Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Ocultación/Teoría de una Ocultación Planetaria o Estelar y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Teoría de una Ocultación Planetaria o Estelar por la Luna y Cálculo de los Elementos Besselianos
[editar]Plano Fundamental o Principal de Referencia según Friedrich Wilhelm Bessel

Ocurrencia de una Ocultación
[editar]En este ejemplo de cálculo he elegido la Ocultación de Júpiter por la Luna ocurrida el 22.01.2013 [1]. Habiendo hallado, por interpolación, el instante de la mínima distancia angular [2] del centro de la Luna con el centro del gigante gaseoso, Júpiter, se procede al cálculo de la distancia siendo perpendicular al Eje del "Cilindro de Luz" del planeta hacia el centro de la Tierra que corre por el Plano Fundamental o de Referencia, esto es, el valor de γ (gamma) en [Radios Terrestres], siendo positivo (+) hacia el Norte del centro de la Tierra y negativo (-) hacia el Sur:
- γ = (((ΔTL * Seno(ΔLJ)) / Seno((90 - (ΔLJ))) / 6.378,14 (1) [3]
Donde ΔLJ es la mínima distancia angular en [°] entre la Luna y Júpiter y ΔTL es la distancia en [kms] entre la Tierra y la Luna en ese mismo instante. Entonces con γ se determina si ocurre o no una Ocultación, según la siguiente condición:
Si -0,9972 < γ < 0,9972 entonces hay una Ocultación, es decir el Eje del "Cilindro de Luz" de Júpiter "dibuja" una ruta sobre la superficie de la Tierra.
Contactos Exteriores e Interiores de la Luna con Júpiter
[editar]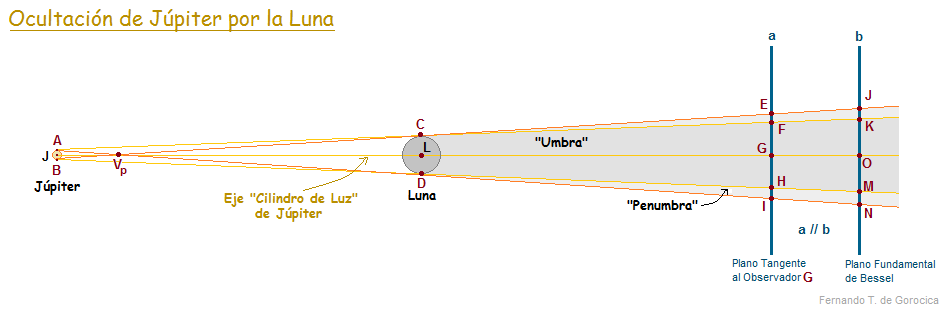
En una Ocultación:
Contactos Interiores de la Luna con Júpiter si el observador está en H (DB) o en F (CA).
Contactos Exteriores de la Luna con Júpiter si el observador está en E (CB) o en I (DA).
La Ocultación Central, es decir el centro de Júpiter se encuentra justo en el centro de la Luna, si el observador está en G.
Vp es el vértice del Cono Penumbral Lunar.
Ecuaciones Fundamentales y Cálculos de los Elementos Besselianos. Ejemplos prácticos según la Ocultación de Júpiter por la Luna del 22.01.2013
[editar]El presente cálculo se basa completamente en el de un Eclipse Solar, lo único que cambiamos es la paralaje media y el semidiámetro medio solar por los de Júpiter. En el caso de una Ocultación de una Estrella la paralaje y su semidiámetro estelar es muy cercana a cero (1E-15).
Plano Fundamental o Principal de Referencia según Bessel
[editar]En la primer figura se describe el Plano Fundamental o Principal de Referencia según Bessel que pasa por el centro de la Tierra y siendo siempre perpendicular al Eje del "Cilindro de Luz" de Júpiter. La línea OZ es paralela a tal Eje y tiene su origen también en el centro de la Tierra, y apunta hacia la esfera celeste, a una Coordenada Ecuatorial Geocéntrica: Ascensión Recta y Declinación del punto Z.
Con el fin de determinar las Coordenadas Rectangulares de la Luna y de Júpiter, el eje de las x va desde el centro de la Tierra hacia el Punto Equinoccial Vernal (Marzo), el eje de las y a 90° del eje de las x y es positivo (+) hacia el punto del Ecuador cuya Ascensión Recta es igual a 90°. El eje de las z es positivo (+) si apunta hacia el hemisferio Norte Celeste.
Efemérides de la Luna y de Júpiter
[editar]Sabiendo que la Conjunción Júpiter-Luna, en Ascensión Recta, ocurre a las 03:07:40 hs. (GMT = Greenwich Meridian Time) [4] tomamos 7 horas para los cálculos respectivos. T₀ = 3 hs. es la hora central y anterior más cercana a tal conjunción, luego se realizan los cálculos para ±3 hs. a partir de esa T₀, es decir para las 0 hs., 1 hs., 2 hs., 3 hs., 4 hs., 5 hs. y 6 hs. (GMT).
Ambos astros están en Coordenadas Ecuatoriales Geocéntricas tomadas de las Efemérides diarias (00:00 GMT), y publicadas, por ejemplo, por The Astonomical Almanac donde las Ascensiones Rectas (α) de la Luna y las de Júpiter están en el formato Hora, Minutos y Segundos, y las Declinaciones (δ) de la Luna y las de Júpiter en el formato °, ' y ". También desde estas efemérides se toman la Paralaje Ecuatorial Horizontal de la Luna π en [°] y la distancia r' Tierra-Júpiter en [U.A.].
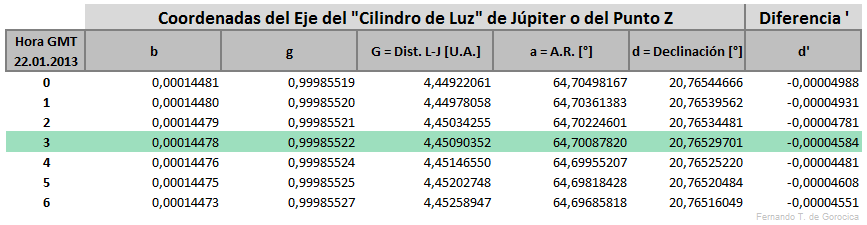
Coordenadas Ecuatoriales Geocéntricas del Eje del "Cilindro de Luz" de Júpiter o del punto Z
[editar]Según la siguiente tabla se tienen las Constantes:

Calcular
- b = Seno(π₀) / (r' * Seno(π)) (2)
luego g y G siendo esta última la distancia Luna-Júpiter (Centro a Centro) en [U.A.]
- g = 1 - b (3)
- G = r' * g (4)
después calcular la Ascensión Recta del punto Z o del Eje del "Cilindro de luz" de Júpiter
- a = α' - (b / ((1 - b) * Seno(δ'))) * Coseno(δ) * (α - α') (5)
y la Declinación del punto Z o del Eje del "Cilindro de Luz" de Júpiter
- d = δ' - (b / (1 - b)) * (δ - δ') (6)
Coordenadas Rectangulares de la Luna x,y,z
[editar]Calcular primero r la distancia Tierra-Luna (Centro a Centro) en [Radios Terrestres]
- r = 1 / Seno(π) (7)
luego las Coordenadas Rectangulares Geocéntricas Lunares x,y,z
- x = r * Coseno(δ) * Seno(α - a) (8)
- y = r * Seno(δ - d) * Coseno((α - a) / 2)^2 + r * Seno(δ + d) * Seno((α - a) / 2)^2 (9)
- z = r * Coseno(δ - d) * Coseno((α - a) / 2)^2 - r * Coseno(δ + d) * Seno((α - a) / 2)^2 (10)
Ángulo y Radio del "Cono Penumbral" Lunar (Contactos Exteriores)
[editar]Calcular el ángulo f₁ con vértice en Vp entre Júpiter y la Luna
- f₁ = Aseno((Seno(H) + k * Seno(π₀)) / (r' * g)) (11)
luego c₁ u OVp que es la distancia desde el vértice del "Cono Penumbral" Lunar Vp hasta el Plano Fundamental o Principal de Referencia (O), por lo tanto siendo siempre positiva (+).
- c₁ = z + k / Seno(f₁) (12)
después el valor de i₁
- i₁ = Tan(f₁) (13)
y por último el Radio del "Cono Penumbral" Lunar l₁ (JO) sobre el Plano Fundamental o Principal de Referencia
- l₁ = i₁ * c₁ (14)
Ángulo y Radio del "Cono de la Sombra (Umbra)" Lunar (Contactos Interiores)
[editar]Calcular el Ángulo f₂ con vértice pasando el Plano Fundamental o de Referencia
- f₂ = Aseno((Seno(H) - k * Seno(π₀)) / (r' * g)) (15)
luego c₂ que es la distancia desde el "vértice" del "Cono de la Sombra (Umbra)" hasta el Plano Fundamental o Principal de Referencia, que en el caso de una Ocultación será siempre negativa (-) dado que el "vértice" del "Cono de la Sombra" Lunar se ubica por debajo (pasa) el Plano Fundamental o de Referencia
- c₂ = z - k / Seno(f₂) (16)
después el valor de i₂
- i₂ = Tan(f₂) (17)
y por último el Radio del "Cono de la Sombra" lunar (Umbra) l₂ (KO) sobre el Plano Fundamental o Principal de Referencia
- l₂ = i₂ * c₂ (18)
Hora Sidérea Aparente y Ángulo Horario de Z en Greenwich (ω = 0)
[editar]Primero tomar de las Efemérides, por ejemplo del The Astonomical Almanac, la Hora Sidérea Aparente μ (00:00 GMT) y en [hms], luego calcularlas en [°] multiplicándolas por 15 (μ⁰). Después hallar el Ángulo Horario μ₁ siendo el ángulo horario del punto Z o Eje del "Cilindro de Luz" de Júpiter también en Greenwich (ω = 0)
- μ₁ = μ⁰ - a (19)
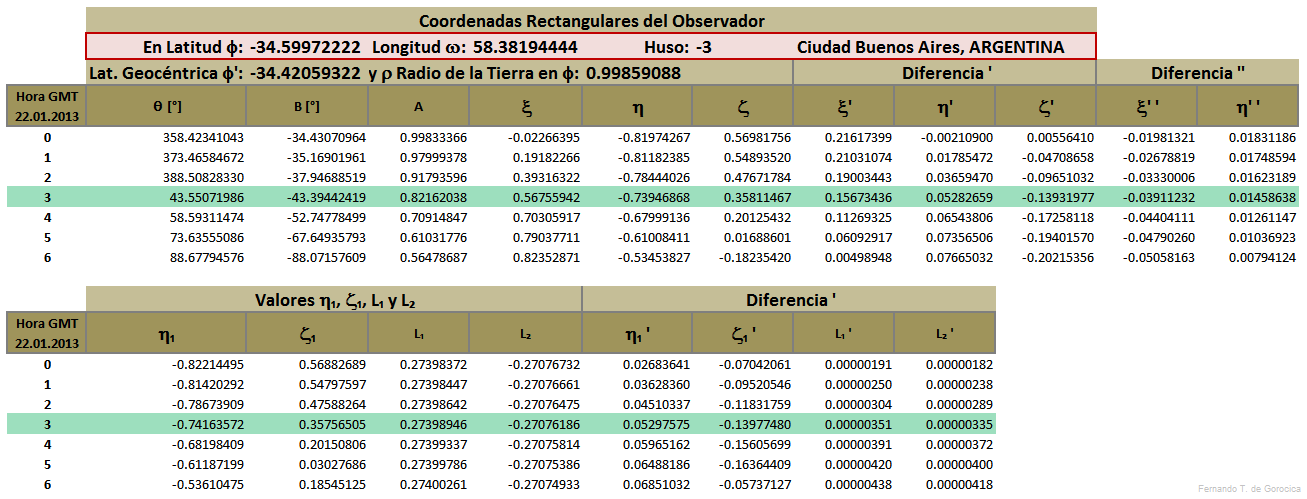
Coordenadas Rectangulares del Observador ξ,η,ζ
[editar]Calcular primero φ' en [°], ρ en [Radios Terrestres], θ en [°], B en [°] y A
φ' es la Latitud Geocéntrica según la siguiente fórmula
- φ' = Atan((Seno(φ) * (1 - e^2)) / Coseno(φ)) (20)
donde φ es la Latitud Geográfica y e es la Excentricidad Terrestre según la tabla de las Constantes mencionada más arriba, o bien
- e = (1 - b^2 / a^2)^0,5 (21)
siendo a el Radio Ecuatorial Terrestre y b el Radio Polar Terrestre, ambos ejes de la Elipsoide Terrestre también dados en la tabla de las Constantes mencionada más arriba.
ρ es la distancia en [Radios Terrestres] desde el Centro de la Tierra hasta la Latitud del Observador, siendo prácticamente constante en toda la ocultación
- ρ = 0,99833132881 + 0,0007271 * Coseno(2 * φ) - 0,0000018 * Coseno(4 * φ) (22)
- θ = μ₁ - ω (23)
donde ω es la Longitud del Observador hacia el Oeste (W) desde Greenwich (0° - 360°) y θ el Ángulo Horario del punto Z o del Eje del "Cilindro de Luz" de Júpiter.
- B = Atan(Seno(φ') / (Coseno(φ') * Coseno(θ))) (24)
- A = ρ * Seno(φ') / Seno(B) (25)
por último, calcular las Coordenadas Rectangulares del Observador ξ,η,ζ
- ξ = ρ * Coseno(φ') * Seno(θ) (26)
- η = A * Seno(B - d) (27)
- ζ = A * Coseno(B - d) (28)
donde ξ,η corresponden al Plano Fundamental o Principal de Referencia (equivalentes a las x,y de la Luna).
Los valores de los cambios horarios para ξ,η,ζ están dados por
- ξ' = μ' * Seno(1) * ρ * Coseno(φ') * Coseno(θ) (29)
- η' = μ' * Seno(1) * ξ * Seno(d) - d' * Seno(1) * ζ (30)
- ζ' = -μ' * Seno(1) * ξ * Coseno(d) + d' * Seno(1) * η (31)
Los valores μ', d y d' los podemos encontrar en las tablas correspondientes (más arriba)
Radio del "Cono de la Penumbra y de la Sombra (Umbra)" Lunar sobre el Plano Tangencial del Observador
[editar]Primero, calcular el Radio del "Cono de la Penumbra" Lunar L₁ sobre el Plano Tangencial del Observador paralelo al Plano Fundamental o Principal de Referencia
- L₁ = (c₁ - ζ) * Tan(f₁) = l₁ - ζ * Tan(f₁) (32)
luego el Radio del "Cono de la Sombra (Umbra)" Lunar L₂ sobre el Plano Tangencial del Observador paralelo al Plano Fundamental o Principal de Referencia
- L₂ = (c₂ - ζ) * Tan(f₂) = l₂ - ζ * Tan(f₂) (33)
- Para el "Cono de la Penumbra" Lunar (c₁ - ζ) es siempre es positivo (+) y por lo tanto también para L₁.
- Para el "Cono de la Sombra (Umbra)" Lunar (c₂ - ζ) es negativo (-) cuando el "vértice" del "cono" se ubica (siempre en una ocultación) por debajo del Plano Tangencial del Observador: por lo tanto L₂ será negativo (-). Usualmente se considera positivo (+) el Radio de la Sombra (Umbra) y en consecuencia se cambia su signo para este caso; aunque para un estudio analítico de nuestras ecuaciones, generalmente será mejor si preservamos el signo negativo (-) de L₂ como una característica de la Ocultación.
Ecuación Fundamental de las Ocultaciones
[editar]Calcular la distancia Δ en [Radios Terrestres] medida desde el Observador hasta el Eje del "Cilindro de Luz" de Júpiter sobre el Plano Fundamental o Principal de Referencia, siendo la Ecuación Fundamental de las Ocultaciones
| Δ = ((x - ξ)^2 + (y - η)^2)^ 0,5 (34) |
Otros Cálculos de Elementos Besselianos
[editar]Cálculo de: d₁, ρ₁, d₂ y ρ₂
[editar]Calcular la declinación d₁ en [°] del Eje del "Cilindro de Luz" de Júpiter o del punto Z según e
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (35)
luego calcular el radio de la Tierra ρ₁ en [Radios Terrestres] en el lugar del instante correspondiente
- ρ₁ = Seno(d) / Seno(d₁) (36)
Después calcular la declinación d₂ en [°] del Eje del "Cilindro de Luz" de Júpiter o del punto Z según e
- d₂ = Atan(Seno(d) * (1 - e^2)^0,5 / Coseno(d)) (37)
luego calcular el radio de la Tierra ρ₂ en [Radios Terrestres] en el lugar del instante correspondiente
- ρ₂ = Coseno(d) / Coseno(d₂) (38)
Los valores ρ₁ y ρ₂ se mantienen prácticamente constantes en toda la Ocultación. e lo podemos hallar en la tabla de las Constantes (más arriba)
Cálculo de: a₁', a₂', b', c₁' y c₂'
[editar]- a₁' = -l₁' - μ' * Seno(1) * i₁ * x * Coseno(d) (39)
- a₂' = -l₂' - μ' * Seno(1) * i₂ * x * Coseno(d) (40)
- b' = -y' + μ' * Seno(1) * x * Seno(d) (41)
- c₁' = x' + μ' * Seno(1) * (y * Seno(d) + i₁ * l₁ * Coseno(d)) (42)
- c₂' = x' + μ' * Seno(1) * (y * Seno(d) + i₂ * l₂ * Coseno(d)) (43)
Los valores μ', d, lᵢ, iᵢ, x, y, x' e y' los podemos encontrar en las tablas correspondientes (más arriba)
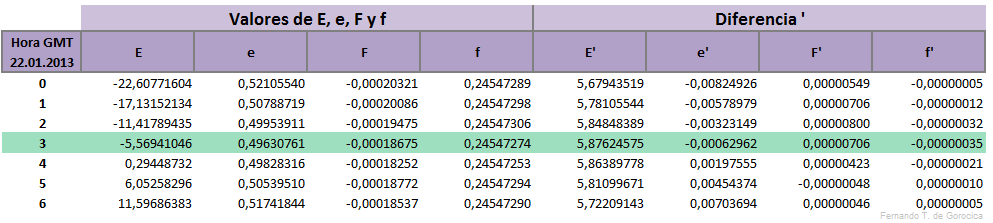
Cálculo de: E, e, F y f
[editar]- E = Atan(b' / c₁') (44)
- e = b' / Seno(E) (45)
- F = Atan(d' / (μ' * Coseno(d)) (46)
- f = (d' * Seno(1)) / Seno(F) (47)
Los valores μ', d y d' los podemos encontrar en las tablas correspondientes (más arriba)
Cálculo de y₁
[editar]- y₁ = y / ρ₁ (48)
Los valores y y ρ₁ los podemos encontrar en las tablas correspondientes (más arriba)
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de una Ocultación |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
Notas de referencia
[editar]- ↑ En el caso de una Ocultación de una Estrella por un Planeta o Asteroide, reemplazar los datos de la Luna por los del Planeta o Asteroide. Y en el caso de una Ocultación de un Planeta por otro Planeta, por ejemplo Venus oculta a Júpiter, los datos de la Luna deben ser reemplazados por los de Venus. También se puede dar el caso de una Ocultación de un Asteroide por un Planeta (Ej. Marte con un Asteroide), los datos de la Luna deben ser reemplazados por los del Planeta.
- ↑ Con las siguientes fórmulas y con las efemérides del The Astonomical Almanac hallar la distancia angular ΔLJ (Luna-Júpiter [°]) para todos los días del año (00:00 GMT):
ΔLJ = Seno(δJ) * Seno(δL) + Coseno(δJ) * Coseno(δL) * Coseno((αJ – αL) * 15)
ΔLJ = (Atan(-ΔLJ / (1 - ΔLJ^2)^0,5) + 2 * Atan(1))
Si ΔLJ < 0,166666666666666 entonces
ΔLJ = (((αL - αJ) * 15 * Coseno((δL + δJ) / 2))^2 + (δJ - δL)^2)^0,5
FinSi
Ambos astros en Coordenadas Ecuatoriales Geocéntricas donde las Ascensiones Rectas de la Luna αL y de Júpiter αJ están en el formato Hora, Minutos y Segundos, y las Declinaciones de la Luna δL y de Júpiter δJ en el formato °, ' y ".
Luego, interpolar con tres pares de valores tabulares (click en la imagen) para hallar un extremo, aquí la mínima distancia angular Luna-Júpiter (ΔLJ) y su instante:

- ↑ De ahora en más, en todas las funciones trigonométricas: Seno, Coseno y Tan los ángulos expresados en radianes deberán pasarse a grados multiplicándolos por π/180. Las funciones Aseno, Acoseno y Atan por 180/π
- ↑ También, por interpolación, hallar la conjunción de la Luna con Júpiter cuando tienen las mismas Ascensiones Rectas. Esto se puede hacer asignando en una variable la diferencia entre Ascensiones Rectas y al cambio de signo interpolar con 0 (cero) y allí nos dará el tiempo de la conjunción. Ver Interpolación con tres pares de valores tabulares (Nota de Referencia N° 1).
- ↑ Interpolación por diferencias (click en la imagen).