Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Ocultación/Curva de la Ocultación Central
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
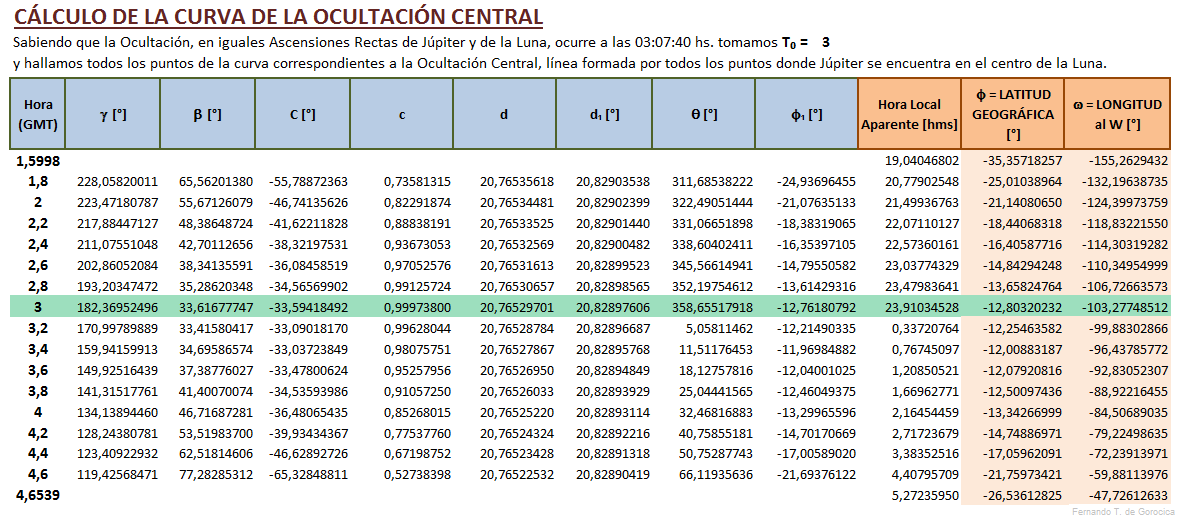
Cálculo de la Curva de la Ocultación Central.
[editar]
Sabiendo que la Conjunción Júpiter-Luna, en Ascensión Recta, ocurre a las 03:07:40 hs. (GMT = Greenwich Meridian Time), tomamos 7 horas para los cálculos respectivos. T₀ = 3 hs. es la hora central y anterior más cercana a tal conjunción, luego se realizan los cálculos para ±3 hs. a partir de esa T₀, es decir para las 0 hs., 1 hs., 2 hs., 3 hs., 4 hs., 5 hs. y 6 hs. (GMT).
Según los tiempos del primer y último contacto del Eje del "Cilindro de Luz" de Júpiter o del punto Z con el horizonte (tangente), que se han hallado en el capítulo anterior, se comienzan los cálculos desde las 1,8 hs. y se repiten (iteración) cada 12 minutos y así sucesivamente hasta las 4,6 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
Comenzamos entonces con γ y en [°]
- γ = Atan(x / y₁) (197)
el ángulo γ debe estar comprendido entre 0° y 360°. Si y₁ es negativo sumar 180° a γ.
Luego β en [°]
- β = Aseno(x / Seno(γ)) (198)
Ahora calcular C en [°] y c
- C = Atan(y₁ / Coseno (β)) (199)
el ángulo C debe estar comprendido entre 0° y 360°. Si Coseno (β) es negativo sumar 180° a C, luego calcular c según C
- c = y₁ / Seno (C) (200)
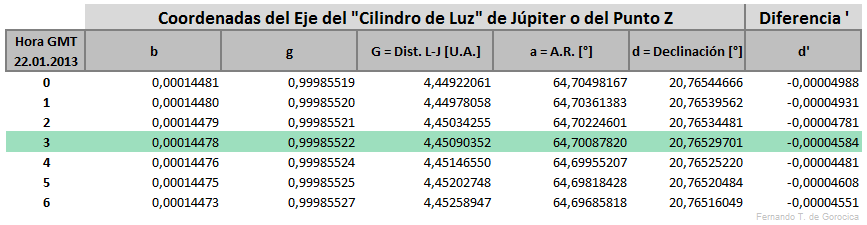
Hallar luego el valor de d en [°], siendo la declinación del Eje del "Cilindro de Luz" de Júpiter o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también d₁ en [°] siendo la declinación del Eje del "Cilindro de Luz" de Júpiter o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (201)
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo)
Seguido calculamos θ que es ángulo horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z en el lugar o bien en la Longitud ω, que es aproximadamente el Ángulo Horario de Júpiter, y correspondiente también a ese instante Tᵢ, entonces
- θ = Atan(x / (c * Coseno(C + d₁))) (202)
el ángulo θ debe estar comprendido entre 0° y 360°, si (c * Coseno(C + d₁)) es negativo (-) sumar 180° a θ. Para el Tiempo Aparente Local que es aproximadamente la Hora Solar Verdadera, dividir θ por 15.
Luego calculamos φ₁ en [°] para hallar después la latitud geográfica φ también en [°]
- φ₁ = Acoseno(c * Seno(C + d₁)) (203)
Por último, hallaremos las coordenadas terrestres para el instante Tᵢ, pero primero μ₁, siendo el ángulo horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z en Greenwich, ángulo comprendido entre 0° y 360°, para el instante Tᵢ interpolando [1] en la tabla correspondiente (más abajo).
Entonces, para el punto de la curva de la Ocultación Central para ese instante Tᵢ tenemos:
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) (204) |
| Longitud ω (al W) = μ₁ - θ (205) |
e lo encontramos en la tabla de las Constantes (más abajo). La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste.
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Ejemplo práctico:
[editar]Tablas para interpolar valores
[editar]Todos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de una Ocultación Planetaria o Estelar y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de una Ocultación |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |