Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Ocultación/Curva del Límite Norte
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
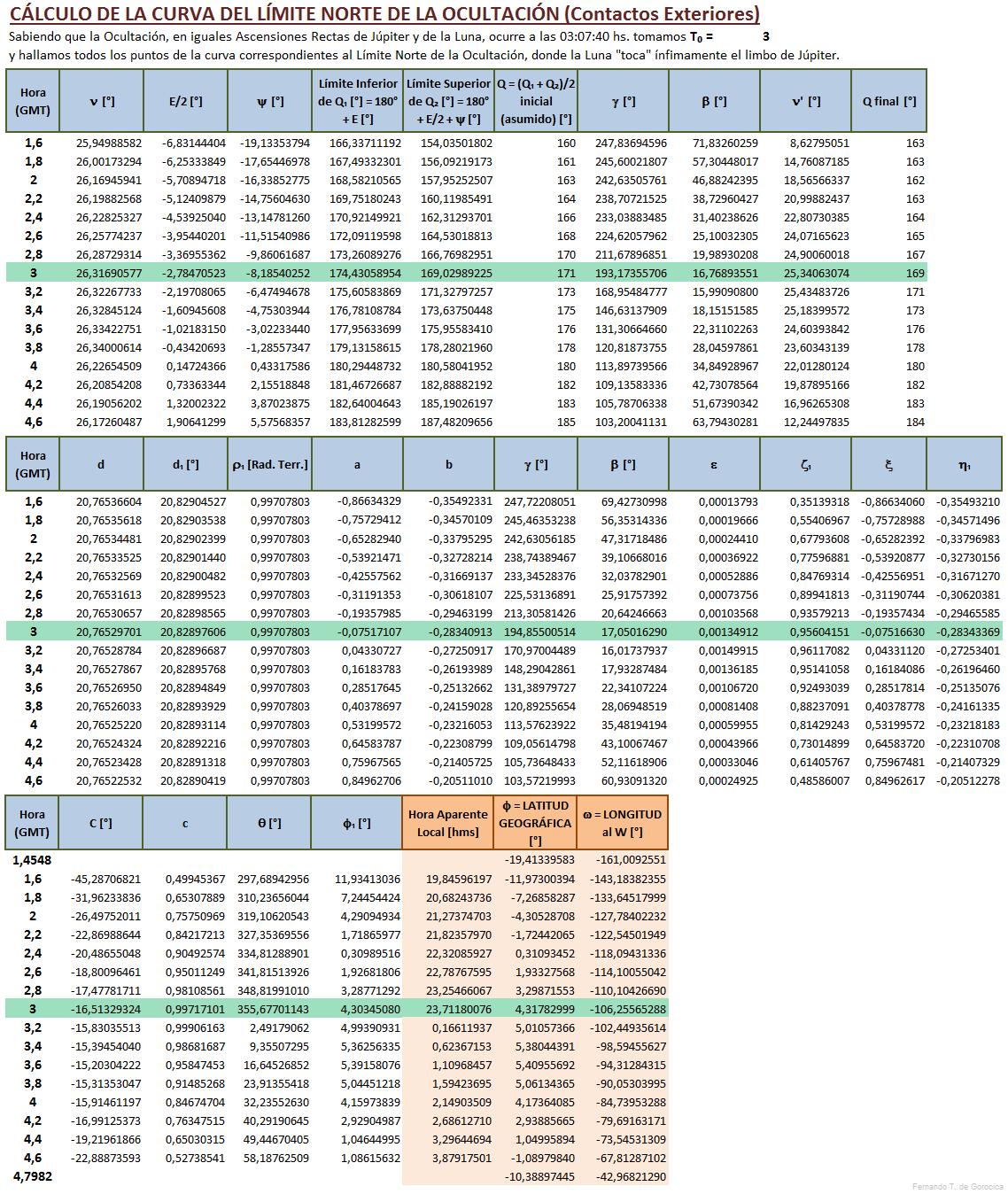
Cálculo de la Curva del Límite Norte - Contactos Exteriores
[editar]
Primero, como lo hemos hecho en el capítulo anterior, se determinará si hay dos límites en la Ocultación, es decir el límite Norte y el Límite Sur. La condición para que ocurran ambos es que el "Cono de la Penumbra" Lunar "pase" enteramente dentro de la Tierra, es decir que llegue totalmente al Plano Fundamental o Principal de Referencia. En este ejemplo práctico de la Ocultación de Júpiter por la Luna del 22.01.2013 se cumple para ambos límites, el Norte y el Sur.
Por lo tanto, en este capítulo vamos a encontrar todos los puntos del límite Norte.
Sabiendo que la Conjunción Júpiter-Luna, en Ascensión Recta, ocurre a las 03:07:40 hs. (GMT = Greenwich Meridian Time), tomamos 7 horas para los cálculos respectivos. T₀ = 3 hs. es la hora central y anterior más cercana a tal conjunción, luego se realizan los cálculos para ±3 hs. a partir de esa T₀, es decir para las 0 hs., 1 hs., 2 hs., 3 hs., 4 hs., 5 hs. y 6 hs. (GMT).
Según los tiempos del primer y último contacto exterior se comienzan los cálculos desde las 1,6 hs. y se repiten (iteración) cada 12 minutos y así sucesivamente hasta las 4,6 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
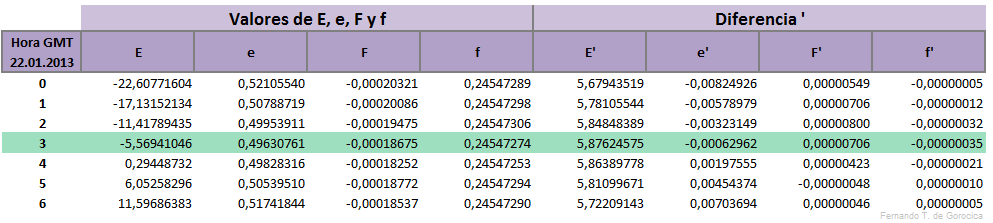
Comenzamos entonces calculando ν en [°] donde f y e para Tᵢ = 1,6 hs., hallando estos valores en las tablas correspondientes (más abajo)
- ν = Atan(f / e) (109)
el ángulo ν debe estar comprendido entre 0° y 180°. Si e es negativo sumar 180° a ν.
Luego calculamos E en [°]
- E = E / 2 (110)
E lo encontramos interpolando en la tabla correspondiente (más abajo).
Seguido hallamos ψ en [°]
- ψ = Atan(Tan(45 + ν) * Tan(E)) (111)
Luego, según las siguientes condiciones, calculamos Qᵢ en [°]
- Para la curva del límite Sur, Q "cae" entre E y E/2 + ψ y
- Para la curva del límite Norte, cálculo en este capítulo, Q "cae" entre 180° + E y 180° + E/2 + ψ, entonces
calculamos los límites inferior Q₁ y superior Q₂ para tal límite Norte, por lo tanto
- Q₁ = 180 + E (112)
- Q₂ = 180 + E/2 + ψ (113)
los ángulos Q₁ y Q₂ deben estar comprendido entre 0° y 360°. Luego hallar el Q inicial (asumido) en [°] hallando el promedio entre Q₁ y Q₂, entonces
- Q = Entero((Q₁ + Q₂) / 2) (114)
el ángulo Q debe estar comprendido entre 0° y 360°. Calculamos luego γ en [°] donde x, y y l₁ para el Tᵢ, hallando estos valores en las tablas correspondientes (más abajo)
- γ = Atan((x - l₁ * Seno(Q)) / (y - l₁ * Coseno(Q))) (115)
el ángulo γ debe estar comprendido entre 0° y 360°. Si (y - l₁ * Coseno(Q)) es negativo (-) sumar 180° a γ.
Luego β en [°]
- β = Aseno((x - l₁ * Seno(Q)) / Seno(γ)) (116)
el ángulo β debe estar comprendido entre 0° y 360°. Seguido, calculamos el valor de ν' en [°]
- ν' = Atan(f * Coseno(β) / e) (117)
los valores de e y f son los hallados anteriormente por interpolación (más arriba). Si e es negativo sumar 180° a ν' .
Con todas estas formulas anteriores encontraremos ahora el valor final de Q para el punto indicado del límite Norte, entonces
- Q = Atan(Tan(45 + ν') * Tan(180 + E / 2)) + 180 + E / 2 (118)
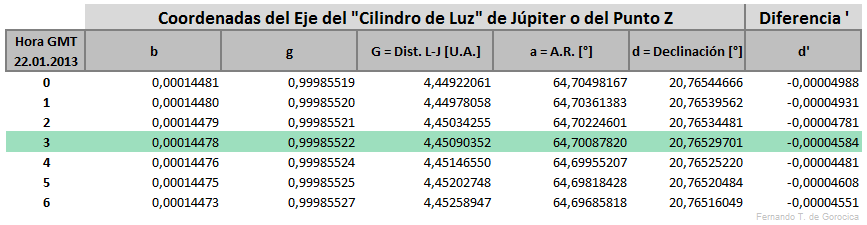
Hallar luego el valor de d en [°], siendo la declinación del Eje del "Cilindro de Luz" de Júpiter o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también d₁ en [°] siendo la declinación del Eje del "Cilindro de Luz" de Júpiter o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (119)
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo)
Luego hallamos el valor de ρ₁ en [Radios Terrestres] también en función de e, la excentricidad terrestre
- ρ₁ = Seno(d) / Seno(Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5))) (120)
después los valores de a y b, primero interpolando los valores x, y y l₁ para el instante en cuestión y según las siguientes fórmulas se tiene
- a = x - l₁ * Seno(Q) (121)
- b = y - l₁ * Coseno(Q) (122)
Luego γ en [°] según
- γ = Atan(a / b) (123)
el ángulo γ debe estar comprendido entre 0° y 360°. Si b es negativo (-) sumar 180° a γ.
Seguido, calculamos β en [°]
- β = Aseno(a / Seno(γ)) (124)
el ángulo β debe estar comprendido entre 0° y 360°. Ahora calculamos ε en [°]
- ε = i₁ * Coseno(Q - γ) / Seno(1) (125)
Luego calcular ζ₁, ξ y η₁ en [Radios Terrestres]
- ζ₁ = Coseno(β) - Seno(β) * Seno(ε) (126)
- ξ = Seno(β) * Seno(γ) + i₁ * ζ₁ * Seno(Q) (127)
- η₁ = Seno(β) * Coseno(γ) + i₁ * ζ₁ * Coseno(Q) (128)
Ahora calcular C en [°] y c
- C = Atan(η₁ / ζ₁) (129)
el ángulo C debe estar comprendido entre 0° y 360°, en el caso ζ₁ sea negativo (-) sumar 180° a C, luego calcular c según C
- c = η₁ / Seno (C) (130)
Por último, hallaremos las coordenadas terrestres para el instante Tᵢ, pero primero μ₁, siendo el ángulo horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z en Greenwich, ángulo comprendido entre 0° y 360°, para el instante Tᵢ interpolando [1] en la tabla correspondiente (más abajo). Seguido calculamos θ que es ángulo horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z en el lugar o bien en la Longitud ω, que es aproximadamente el Ángulo Horario de Júpiter, y correspondiente también a ese instante Tᵢ, entonces
- θ = Atan(ξ / (c * Coseno(C + d₁))) (131)
el ángulo θ debe estar comprendido entre 0° y 360°, si (c * Coseno(C + d₁)) es negativo (-) sumar 180° a θ.
Para el Tiempo Aparente Local que es aproximadamente la Hora Solar Verdadera, dividir θ por 15.
Luego calculamos φ₁ en [°] para hallar después la latitud geográfica φ también en [°]
- φ₁ = Acoseno(ξ / Seno(θ)) (132)
Finalmente, para a ese instante Tᵢ de Eclipse tenemos:
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) (133) |
| Longitud ω (al W) = μ₁ - θ (134) |
e lo encontramos en la tabla de las Constantes (más abajo). La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste.
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Ejemplo práctico:
[editar]Tablas para interpolar valores
[editar]Todos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de una Ocultación Planetaria o Estelar y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de una Ocultación |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |