Ábaco Oriental/Métodos Tradicionales/Uso de la 5ª Cuenta Inferior
Introducción
[editar]

Es un misterio por qué los ábacos tradicionales chinos y japoneses tenían cinco cuentas en su parte inferior, ya que solo se requieren cuatro desde el punto de vista de la representación de números decimales. Como ningún documento antiguo existente parece explicarlo, este misterio probablemente dure para siempre y tendremos que conformarnos con nuestras propias conjeturas para tratar de comprender su origen. En esta línea, podríamos pensar que, cuando aparecieron por primera vez, los ábacos de cuentas fijas fueron concebidos a imagen y semejanza de las varillas de cálculo, de las que heredaron todos los algoritmos. Con las varillas de cálculo, el uso de cinco barras para representar el número cinco era obligatorio para evitar la ambigüedad entre uno y cinco, al menos inicialmente, cuando no se usaba una representación del cero ni un tablero cuadriculado al estilo japonés. Equipar el ábaco con cinco cuentas inferiores permite una manipulación paralela o similar de cuentas y varillas, aportando algún tipo de compatibilidad de "hardware" y "software" a los ábacos de cuentas fijas; de hecho, los primeros libros chinos sobre el ábaco también se ocupaban de las varillas de cálculo, por lo que ambos instrumentos eran aprendidos al mismo tiempo. También podríamos invocar un cierto deseo de compatibilidad entre el ábaco y el sistema de notación derivado de las varillas de cálculo que, de una forma u otra, ha estado en uso hasta los tiempos modernos. Si fuéramos a anotar nuestros resultados usando tal notación, estaríamos interesados en cambiar los cincos de nuestro ábaco para que estén representados por las cinco cuentas inferiores con el fin de evitar errores de transcripción catastróficos.
Las varillas de cálculo, el ábaco más versátil y poderoso de la historia, tenía un defecto: es extremadamente lento de manipular. Como se ha explicado en la sección anterior de este libro, no es una sorpresa que los antiguos matemáticos chinos inventaran la tabla de multiplicar para acelerar la multiplicación y que también descubrieran el uso de dicha tabla de multiplicar para acelerar la división. No ha de ser, por tanto, una sorpresa que también descubrieran que las operaciones de suma y resta se podían simplificar un poco al usar la quinta cuenta inferior del ábaco. Realmente tenían que ser muy sensibles a la lentitud.
A continuación, se presenta un pequeño conjunto de reglas para el uso de la quinta cuenta junto con su razón de ser y alcance de uso. Estas reglas no se establecen explícitamente en ninguna de las obras clásicas, pero se pueden inferir de las demostraciones de suma y resta presentes en ellas[1], especialmente en el: Métodos computacionales con las cuentas en una bandeja (Pánzhū Suànfǎ 盤珠算法) de Xú Xīnlǔ 徐心魯 (1573)[2], por cierto, el libro más antiguo que se conoce enteramente dedicado al ábaco.
Algunos términos y notación
[editar]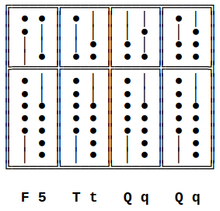
En lo que sigue usaremos los siguiente conceptos y forma de notación en referencia al uso (o no) de la quinta cuenta inferior (véase la figura acompañante a la derecha).
- F: para denotar un cinco inferior (cinco cuentas inferiores activadas) en lugar de:
- 5: cinco superiores (una cuenta superior activada).
- T: diez en una varilla (una cuenta superior y cinco cuentas inferiores activadas). En el ábaco de tipo 5 + 2, también es un diez inferior en lugar de t un diez superior (dos cuentas superiores activadas).
- Q: quince inferior en una varilla (dos cuentas superiores y cinco cuentas inferiores activadas) en lugar de q quince superior (cuenta superior suspendida en el 5+2, tres cuentas superiores activadas en el 5+3).
- acarreo: esto representa el número 1 cuando se debe agregar a una columna como un acarreo desde la derecha (adición).
Reglas para la adición
[editar]- a1: No utilice nunca la quinta cuenta, excepto en los dos casos siguientes:
- a2: 4 + acarreo = F
- a3: 9 + acarreo = T
Es decir, al sumar 1 a una varilla se actúa como de costumbre, por ejemplo:
| A | A | |
|---|---|---|
| A + 1 = | ||
| 4 | 5 |
y
| A | B | A | B | |
|---|---|---|---|---|
| B + 1 = | ||||
| 0 | 9 | 1 | 0 |
pero al sumar 1 como resultado de un acarreo o llevada, se usa la quinta cuenta inferior en la forma:
| A | B | A | B | |
|---|---|---|---|---|
| B + 5 = | ||||
| 4 | 6 | F | 1 |
y
| A | B | A | B | |
|---|---|---|---|---|
| B + 5 = | ||||
| 9 | 6 | T | 1 |
Puede ver las reglas de adición anteriores mencionadas de una manera ligeramente diferente por Chen[3].
La lógica de estas reglas
[editar]El objetivo de la regla a1 es simplemente procurar dejar siempre una cuenta inferior sin usar a nuestra disposición para el caso de que la columna actual tenga que recibir posteriormente un acarreo desde la derecha, mientras que las reglas a2 y a3 dictan el uso de la quinta cuenta ante tal situación. Entonces, podemos esperar obtener:
- una reducción del número de movimientos de dedos porque evitamos tratar con las cuentas superiores e inferiores a la vez
- evitar algunos saltos de varillas y reducir el intervalo de desplazamiento izquierda-derecha de la mano
- cortar cualquier "acarreo múltiple" hacia la izquierda (piense en 99999 + 1 = 999T0 en lugar de 99999 + 1 = 100000)
La ventaja
[editar]Las ventajas anteriores se obtienen automáticamente mediante el uso de las reglas a2 y a3, pero la regla a1 es de naturaleza diferente. La regla a1 es una previsión para el futuro, simplificará las cosas si un acarreo futuro realmente cae en la columna actual (lo que ocurre aproximadamente el 50% de las veces en promedio), pero no simplificará nada en caso contrario. La regla a1 es una especie de apuesta (las reglas para la resta a continuación también son de la misma naturaleza).
El ámbito de uso
[editar]Las reglas a1, a2 y a3 son para columnas que pueden recibir un acarreo, lo que excluye la última columna a la derecha en la operación normal (es decir, operando de izquierda a derecha).
En la operación inversa (operando de derecha a izquierda), ninguna columna recibirá posteriormente un acarreo desde la derecha, por lo que la regla a1 no es aplicable, pero las reglas a2 y a3 siempre deberán usarse. (Esto se menciona porque una técnica antigua, ahora caída en el olvido, utilizaba la operación hacia la izquierda en alternancia con la operación normal en sumas y restas de varios números para evitar largos desplazamientos de la mano. No es de utilidad general, pero sí un ejercicio extremadamente interesante y recomendable para un usuario avanzado para mejorar su "comprensión de las cuentas").
Excepcionalmente, si sabe que alguna columna nunca recibirá un acarreo, también podemos olvidarlos de la regla a1. (Esto puede parece un comentario extraño aquí, pero debemos hacerlo para lo que seguirá).
Reglas para la sustracción
[editar]- s1 Utilice siempre cinco inferiores (F) en lugar de cinco superiores (5). Por ejemplo: 7-2 = F
- s2 Nunca deje una varilla despejada (0) si puede tomar prestado de la varilla inmediatamente a la izquierda (¡pero no de una más lejana!), deje T en su lugar, es decir, por ejemplo: 27-7 = 1T
- en lugar de 27-7 = 20.
- Observación
- Estas dos reglas no se aplican a las varillas de las que está tomando prestado; es decir, 112-7 = 10F
- y 62-7 = 5F (no FF).
La lógica de estas reglas
[editar]Ambas reglas tienden a dejar cuentas inferiores activadas a nuestra disposición para el caso en que necesitemos tomar prestado de ellas en el futuro (es como tener dinero suelto en el bolsillo por si acaso), ahorrándonos algunos movimientos y/o desplazamientos de la mano más anchos o más complejos, como tomar prestado de columnas no adyacentes o saltar varillas.
La ventaja
[editar]No se obtiene automáticamente, sólo cuando necesitamos tomar prestado de la varilla actual. En esto es similar a la regla de adición a1.
El ámbito de uso
[editar]Una vez más, la columna de la derecha está fuera del alcance de estas reglas, ya que nunca tomaremos prestado de ella.
Además, en la operación hacia la izquierda o inversa, nunca tomaremos prestado de la columna actual, por lo que estas reglas no se aplican (lo que puede verse como una razón adicional para preferir la operación hacia la derecha en el uso normal).
Ejemplo de uso de las reglas
[editar]

Era común en los libros antiguos sobre el ábaco demostrar la suma y la resta mediante el conocido ejercicio que consiste en sumar el número 123456789 nueve veces a un ábaco puesto a cero hasta llegar al número 1111111101, y luego borrarlo nuevamente restando el mismo número nueve veces. Este ejercicio parece tener el nombre chino: "Jiǔ pán qīng" 九 盤 清, que significa algo así como "limpiar las nueve bandejas".
Precisamente, las reglas de uso de la quinta cuenta inferior ofrecidas aquí se han inferido de la demostración de suma y resta que aparece en el Panzhu Suanfa[2] de Xu Xinlu, por lo que nada mejor que emplear este ejercicio como prueba de dichas reglas. En particular, las reglas permiten reconstruir la serie de resultados intermedios que aparecen en el mencionado libro[4] tras cada adición o sustracción del número 12345689. Para la suma:
000000000, 123456789, 246913F78, 36T36T367, 4938271F6,
617283945, 74073T734, 864197F23, 9876F4312, ...
en este punto, agregar 123456789 una vez más da como resultado 1111111101, pero este número aparece en el Panzhu Suanfa como:
TTTTTTTT1
es decir, el ábaco presenta este aspecto:
| T | T | T | T | T | T | T | T | 1 |
que no se puede obtener mediante el uso de las reglas anteriores únicamente. Una situación similar ocurre al repetir este ejercicio pero comenzando con 999999999 en lugar de un ábaco despejado (ver Tabla 2), llegando a 1TTTTTTTT0. Es por esto por lo que incluimos el último comentario sobre el alcance de las reglas de adición anteriores. Puede ser que, por inspección o intuición, nos demos cuenta de que usar la quinta cuenta aquí no genera ningún acarreo, por lo que podemos prescindir de la regla a1 y proceder a este resultado, ...un tanto teatral por lo demás.
A partir de aquí, por sustracción deberíamos obtener:
TTTTTTTT1, 9876F4312, 864197523, 740740734, 61728394F,
493827156, 36T370367, 246913578, 123456789, 000000000
Como se puede ver, pocas F y T aparecen en los resultados intermedios de esta parte del ejercicio, pero algunas más aparecen durante el cálculo (Tabla 1), siendo inmediatamente convertidas a 4 y 9 al tomar prestado, que es el propósito para el cual fueron introducidas. Las F y T que quedan en los resultados intermedios son sólo las no utilizadas.
Veamos a continuación el detalle del ejercicio. El lector debería estudiarlo detenidamente.
Suma
[editar]
ABCDEFGHI ABCDEFGHI ABCDEFGHI ABCDEFGHI ABCDEFGHI
--------- --------- --------- --------- ---------
000000000 123456789 246913F78 36T36T367 4938271F6
100000000 A+1 223456789 A+1 346913F78 A+1 46T36T367 A+1 5938271F6 A+1
120000000 B+2 243456789 B+2 366913F78 B+2 48T36T367 B+2 6138271F6 B+2
123000000 C+3 246456789 C+3 369913F78 C+3 49336T367 C+3 6168271F6 C+3
123400000 D+4 246856789 D+4 36T313F78 D+4 49376T367 D+4 6172271F6 D+4
123450000 E+5 246906789 E+5 36T363F78 E+5 49381T367 E+5 6172771F6 E+5
123456000 F+6 246912789 F+6 36T369F78 F+6 493826367 F+6 6172831F6 F+6
123456700 G+7 246913489 G+7 36T36T278 G+7 493827067 G+7 6172838F6 G+7
123456780 H+8 246913F69 H+8 36T36T358 H+8 493827147 H+8 617283936 H+8
123456789 I+9 246913F78 I+9 36T36T367 I+9 4938271F6 I+9 617283945 I+9
ABCDEFGHI ABCDEFGHI ABCDEFGHI ABCDEFGHI
--------- --------- --------- ---------
617283945 74073T734 864197F23 9876F4312
717283945 A+1 84073T734 A+1 964197F23 A+1 T876F4312 A+1
737283945 B+2 86073T734 B+2 984197F23 B+2 TT76F4312 B+2
740283945 C+3 86373T734 C+3 987197F23 C+3 TTT6F4312 C+3
740683945 D+4 86413T734 D+4 987597F23 D+4 TTTTF4312 D+4
740733945 E+5 86418T734 E+5 987647F23 E+5 TTTTT4312 E+5
740739945 F+6 864196734 F+6 9876F3F23 F+6 TTTTTT312 F+6
74073T645 G+7 864197434 G+7 9876F4223 G+7 TTTTTTT12 G+7
74073T725 H+8 864197F14 H+8 9876F4303 H+8 TTTTTTT92 H+8
74073T734 I+9 864197F23 I+9 9876F4312 I+9 TTTTTTTT1 I+9
Resta
[editar]
ABCDEFGHI ABCDEFGHI ABCDEFGHI ABCDEFGHI ABCDEFGHI
--------- --------- --------- --------- ---------
TTTTTTTT1 9876F4312 864197523 740740734 61728394F
9TTTTTTT1 A-1 8876F4312 A-1 764197523 A-1 640740734 A-1 F1728394F A-1
98TTTTTT1 B-2 8676F4312 B-2 744197523 B-2 620740734 B-2 49728394F B-2
987TTTTT1 C-3 8646F4312 C-3 741197523 C-3 617740734 C-3 49428394F C-3
9876TTTT1 D-4 8642F4312 D-4 740797523 D-4 617340734 D-4 49388394F D-4
9876FTTT1 E-5 8641T4312 E-5 740747523 E-5 617290734 E-5 49383394F E-5
9876F4TT1 F-6 864198312 F-6 740741523 F-6 617284734 F-6 49382794F F-6
9876F43T1 G-7 864197612 G-7 740740823 G-7 617283T34 G-7 49382724F G-7
9876F4321 H-8 864197532 H-8 740740743 H-8 6172839F4 H-8 49382716F H-8
9876F4312 I-9 864197523 I-9 740740734 I-9 61728394F I-9 493827156 I-9
ABCDEFGHI ABCDEFGHI ABCDEFGHI ABCDEFGHI
--------- --------- --------- ---------
493827156 36T370367 246913578 123456789
393827156 A-1 26T370367 A-1 146913578 A-1 023456789 A-1
373827156 B-2 24T370367 B-2 126913578 B-2 003456789 B-2
36T827156 C-3 247370367 C-3 123913578 C-3 000456789 C-3
36T427156 D-4 246970367 D-4 123F13578 D-4 000056789 D-4
36T377156 E-5 246920367 E-5 123463578 E-5 000006789 E-5
36T371156 F-6 246914367 F-6 123457578 F-6 000000789 F-6
36T370456 G-7 246913667 G-7 123456878 G-7 000000089 G-7
36T370376 H-8 246913587 H-8 123456798 H-8 000000009 H-8
36T370367 I-9 246913578 I-9 123456789 I-9 000000000 I-9
Extensión del ejemplo
[editar]Una vez que comprenda y domine el presente ejercicio, puede extenderlo para ampliar su práctica de uso de la quinta cuenta sin mas que repetirlo sobre un fondo 111111111, 222222222,..., 999999999 en lugar de 000000000. Se ofrecen a continuación los resultados parciales.
0 1 2 3 4
000000000 0111111111 0222222222 0333333333 0444444444
123456789 02345678T0 0345678T11 045678T122 05678T1233
246913F78 0357T24689 046913F7T0 057T246911 0691357T22
36T36T367 0481481478 0592592F89 06T36T36T0 0814814811
4938271F6 0604938267 0715T49378 082715T489 09392715T0
617283945 0728394TF6 08394T6167 09F0617278 1061738389
74073T734 08F18F1845 09629629F6 1074073T67 118F18F178
864197F23 097F308634 1086419745 1197F2T8F6 1308641967
9876F4312 109876F423 1209876F34 1320987645 14320987F6
TTTTTTTT1 1222222212 1333333323 1444444434 1555FFFF45
9876F4312 1098765423 1209876534 132098764F 1432098756
864197523 097F308634 108641974F 1197F30856 1308641967
740740734 08F18F184F 0962962956 0T74074067 118F18F178
61728394F 072839F056 0839F06167 09F0617278 0T61728389
493827156 05T4938267 0716049378 0827160489 093827159T
36T370367 0481481478 0592592589 06T370369T 0814814811
246913578 0357T24689 046913579T 0F7T246911 0691358022
123456789 023456789T 0345678T11 04F678T122 0F678T1233
000000000 0111111111 0222222222 0333333333 0444444444
5 6 7 8 9
0555555555 0666666666 0777777777 0888888888 0999999999
0678T12344 078T1234F5 08T1234F66 0T1234F677 11234F6788
07T2469133 091357T244 0T246913F5 11357T2466 1246913F77
0925925922 1036T36T33 1148148144 12592592F5 136T36T366
1049382711 115T493822 12715T4933 1382715T44 14938271F5
11728394T0 128394T611 1394T61722 1F06172833 1617283944
1296296289 14073T73T0 1F18F18F11 1629629622 174073T733
14197F2T78 1530864189 164197F2T0 17F3086411 1864197F22
1543209867 1654320978 176F431T89 1876F431T0 19876F4311
16666666F6 1777777767 1888888878 1999999989 1TTTTTTTT0
1F43209867 16F4320978 176F432089 1876F4319T 19876F4311
14197F3078 1F30864189 164197529T 17F3086411 1864197522
1296296289 140740739T 1F18F18F11 1629629622 1740740733
117283949T 12839F0611 139F061722 14T6172833 1617283944
0T49382711 115T493822 1271604933 1382716044 149382715F
0925925922 0T36T37033 1148148144 125925925F 136T370366
07T2469133 0913580244 0T2469135F 11357T2466 1246913577
0678T12344 078T12345F 08T1234566 0T12345677 1123456788
0FFF55555F 0666666666 0777777777 0888888888 0999999999
Reglas adicionales
[editar]Por supuesto, las reglas para la suma también se pueden usar directamente en la multiplicación y las reglas para la resta en la división, raíces, etc. Ya lo sabe, todo lo que se puede hacer en el ábaco consiste en una sucesión de sumas y restas.
Adicionalmente, aunque la división tradicional se estudiará en capítulos posteriores, podemos dejar indicada aquí una regla adicional que le es específica y a la que podrá referirse tras estudiar la tabla de división; con ábacos 5+2 o 5+3:
- k1: Utilice siempre cinco, diez y quince inferiores (F, T, Q) cuando sume al resto durante la aplicación de las reglas de división.
Esto es así porque, aunque estemos sumando a una varilla, lo siguiente que haremos será empezar a restar de la misma (si el divisor tiene más de un dígito). Es una especie de extensión de la primera regla para la resta (s1). Por ejemplo, iniciando la división87÷98:
| Ábaco | Comentario |
|---|---|
| ABCDEFG | |
| 87 98 | Dividendo: AB, divisor: FG |
| 8Q 98 | A: Regla 8/9>8+8 |
| -64 | |
| 886 98 | etc. |
Justo después de la aplicación de la regla de división 8/9>8+8 deberíamos tener:
| A | B | C | D | E | F | G | ||
|---|---|---|---|---|---|---|---|---|
| 8 | Q | 0 | 0 | 0 | 9 | 8 |
Por cierto, a veces puede encontrar algo contradictorio el uso de la segunda regla para la resta (s2) en la división tradicional. Por ejemplo, 1167/32 = 36.46875
| Ábaco | Comentario |
|---|---|
| ABCDEFG | |
| 32 1167 | regla 1/3>3+1 |
| 32 3267 | -3*2=-6 in F, use la regla s2 |
| -6 | |
| 32 31T7 |
Ahora bien, ¿qué regla de división debería usarse aquí? 1/3>3+1 o 2/3>6+2? De hecho, podemos usar cualquiera de ellas y revisarlas según sea necesario, pero es más rápido darse cuenta de que el resto es en realidad 3207, de modo que la segunda regla de división es la adecuada, así que simplemente cambie las columnas EF a 62 y continue...
| Ábaco | Comentario |
|---|---|
| ABCDEFG | |
| 32 3627 | |
| ... |
Finalmente, si está utilizando el método de multiplicación tradicional o similar en un 5+2, puede encontrarse con un desbordamiento en algunas columnas, por lo que la regla adicional:
- m1 [14] + acarreo = Q
debe tambien considerarse.
Acerca de la ventaja
[editar]Está claro que el uso de la quinta cuenta puede reducir el número de movimientos de cuentas o de los dedos requeridos en algunos cálculos (piense en 99999 + 1 = 999T0 frente a 99999 + 1 = 100000). Una estimación basada en el ejercicio 123456789 y algunos de sus derivados conduce a una reducción del 10% en promedio (contando los movimientos simultáneos de las cuentas superior e inferior por separado). Esta es una reducción modesta, pero la ventaja de la quinta cuenta va más allá de simplemente reducir el número de movimientos de los dedos, ya que también reduce el número y/o la extensión de otros gestos de la mano requeridos en los cálculos (desplazamientos, cambios de dirección, saltos de varillas, ...). Como ya se ha indicado en otra parte, cada gesto:
- como proceso físico, tarda un tiempo en completarse,
- como lo controla nuestro cerebro, requiere nuestra atención, consumiendo energía (mental o bioquímica),
- como lo hacemos seres humanos (no máquinas), tiene la posibilidad de hacerse de manera incorrecta, introduciendo errores.
Bajo esta óptica, podemos esperar entonces que el uso de la quinta cuenta resulte en un cálculo algo más rápido, más relajado y fiable al reducir el número total de gestos requeridos. No es fácil medir esta triple ventaja utilizando un solo parámetro.
Saltar columnas parece haber sido visto tradicionalmente como algo que debe evitarse como una posible fuente de errores[1][3]. Sin este concepto, la regla de resta (s2) no se puede entender ya que no siempre conduce a una reducción en el número de movimientos de los dedos, pero siempre reduce el rango de movimiento de la mano y la necesidad de saltar barras.
En cualquier caso, la ventaja de usar la quinta cuenta, aunque no despreciable, es solo modesta, y cada uno debe decidir si vale la pena usarla o no. Después de acostumbrarse y dominar el uso de la quinta cuenta, no hay mejor prueba de su eficiencia que usar nuevamente un ábaco moderno 4+1, y ser sensible al trabajo adicional requerido para completar las mismas tareas con él.
Referencias
[editar]- ↑ 1,0 1,1 Chen Yifu (2013) (en Francés). L’étude des Différents Modes de Déplacement des Boules du Boulier et de l’Invention de la Méthode de Multiplication Kongpan Qianchengfa et son Lien avec le Calcul Mental. Université Paris-Diderot (Paris 7). http://www.theses.fr/2013PA070061.
- ↑ 2,0 2,1 Xú Xīnlǔ (徐心魯) (1993) [1573] (en Chino). Pánzhū Suànfǎ (盤珠算法). Zhōngguó kēxué jìshù diǎnjí tōng huì (中國科學技術典籍通彙).
- ↑ 3,0 3,1 Chen Yifu (2018). «The Education of Abacus Addition in China and Japan Prior to the Early 20th Century». En Volkov, Alexei; Freiman, Viktor. Computations and Computing Devices in Mathematics Education Before the Advent of Electronic Calculators. Springer Publishing. ISBN 978-3-319-73396-8. https://link.springer.com/book/10.1007%2F978-3-319-73396-8.
- ↑ Suzuki, Hisao (鈴木 久男) (1982). «Chuugoku ni okeru shuzan kagen-hou 中国における珠算加減法» (en Japonés). Kokushikan University School of Political Science and Economics 57 (3). ISSN 0586-9749. http://id.nii.ac.jp/1410/00008407/.
Otras lecturas
[editar]- Heffelfinger, Totton (2011). «The 5 Earth Bead Advantage». 算盤 Abacus: Mystery of the Bead. Archivado desde el original, el August 1, 2021.
Recursos externos
[editar]Puede practicar online el uso de la quinta cuenta con Soroban Trainer (ver capítulo: Introducción) usando este fichero 123456789-5bead.sbk que tendrá que descargar a su ordenador y después subirlo a Soroban Trainer (Es un archivo de texto que puede inspeccionar con cualquier editor de texto y que puede descargar de forma segura a su computadora.).
