Cursos/E M T/3º Electromecánica - Matemáticas/Texto completo
Introducción
[editar]La Geometría (del latín geometrĭa, que proviene del idioma griego γεωμετρία, geo tierra y metria medida), es una rama de la matemática que se ocupa del estudio idealizado de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, politopos (paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc).
Es la justificación teórica de la geometría descriptiva o del dibujo técnico. También da fundamento a instrumentos como el compás, el teodolito, el pantógrafo o el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales).
Sus orígenes se remontan a la solución de problemas concretos relativos a medidas. Tiene su aplicación práctica en física aplicada, mecánica, astronomía, arquitectura, cartografía, náutica, topografía, balística, etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanías.
Tipos de geometría
[editar]Entre los tipos de geometría se encuentran: geometría plana y del espacio.
Geometría euclidiana
[editar]La geometría euclidiana (o geometría parabólica) es aquella que estudia las propiedades del plano y el espacio tridimensional. En ocasiones los matemáticos usan el término para englobar geometrías de dimensiones superiores con propiedades similares. Sin embargo, con frecuencia, geometría euclidiana es sinónimo de geometría plana y de geometría clásica. Fragmento de Los elementos de Euclides, escrito en papiro, hallado en el yacimiento de Oxirrinco (Egipto). Desde un punto de vista historiográfico, la geometría euclidiana es aquella geometría que postuló Euclides, en su libro Los elementos, dejando al margen las aportaciones que se hicieron posteriormente —desde Arquímedes hasta Jakob Steiner—. Según la contraposición entre método sintético y método algebraico-analítico, la geometría euclidiana sería, precisamente, el estudio por métodos sintéticos de los invariantes de un espacio vectorial real de dimensión 3 dotado de un producto escalar muy concreto (el frecuentemente denominado «producto escalar habitual»). Según el programa de Erlangen, la geometría euclidiana sería el estudio de los invariantes de las isometrías en un espacio euclidiano (espacio vectorial real de dimensión finita, dotado de un producto escalar).
Geometría plana
[editar]La geometría plana es una parte de la geometría euclidiana que trata de aquellos elementos cuyos puntos están contenidos en un plano. La geometría plana está considerada parte de la geometría euclidiana, pues ésta estudia los elementos geométricos a partir de dos dimensiones.
Geometría espacial
[editar]La geometría espacial o geometría del espacio es la rama de la geometría que se ocupa de las propiedades y medidas de las figuras geométricas en el espacio tridimensional o espacio euclídeo. Entre estas figuras, también llamadas sólidos, se encuentran el cono, el cubo, el cilindro, la pirámide, la esfera, el prisma, los poliedros regulares (los sólidos platónicos, convexos, y los sólidos de Kepler-Poinsot, no convexos) y otros poliedros.
La geometría del espacio amplía y refuerza las proposiciones de la geometría plana, y es la base fundamental de la trigonometría esférica, la geometría analítica del espacio, la geometría descriptiva y otras ramas de las matemáticas. Se usa ampliamente en matemáticas, en ingeniería y en ciencias naturales.
Llamamos cuerpos geométricos a las figuras que se han de representar en el espacio tridimensional. Los cuerpos geométricos ocupan siempre un espacio.
Asimismo, los cuerpos que están huecos pueden albergar en su interior otros cuerpos en una cantidad que recibe el nombre de capacidad. Existe una relación directa entre la capacidad de un cuerpo y el volumen que éste ocupa.
La geometría espacial se basa en un sistema formado por tres ejes (X,Y,Z):
- Ortogonales (perpendiculares 2 a 2)
- Normalizados (las longitudes de los vectores básicos de cada eje son iguales)
- Dextrógiros (el tercer eje es producto vectorial de los otros 2)
Geometría No euclidiana
[editar]Se denomina geometría no euclidiana o no euclídea, a cualquier forma de geometría cuyos postulados y propiedades difieren en algún punto de los establecidos por Euclides en su tratado Elementos. No existe un sólo tipo de geometría no euclídea, sino muchos, aunque si se restringe la discusión a espacios homogéneos, en los que la curvatura del espacio la misma en cada punto, en los que los puntos del espacio son indistinguibles pueden distinguirse tres tipos de geometrías:
- La geometría euclidiana satisface los cinco postulados de Euclides y tiene curvatura cero.
- La geometría hiperbólica satisface sólo los cuatro primeros postulados de Euclides y tiene curvatura negativa.
- La geometría elíptica satisface sólo los cuatro primeros postulados de Euclides y tiene curvatura positiva.
Todos estos son casos particulares de geometrías riemannianas, en los que la curvatura es constante, si se admite la posibilidad de que la curvatura intrínseca de la geometría varíe de un punto a otro se tiene un caso de geometría riemanniana general, como sucede en la teoría de la relatividad general donde la gravedad causa una curvatura no homogénea en el espacio tiempo, siendo mayor la curvatura cerca de las concentraciones de masa, lo cual es percibido como un campo gravitatorio atractivo.
Geometría Riemanniana
[editar]En geometría diferencial, la geometría de Riemann es el estudio de las variedades diferenciales con métricas de Riemann; es decir de una aplicación que a cada punto de la variedad, le asigna una forma cuadrática definida positiva en su espacio tangente, aplicación que varía suavemente de un punto a otro. Esto da ideas locales de (entre otras magnitudes) ángulo, longitud de curvas, y volumen. A partir de éstas, pueden obtenerse otras magnitudes por integración de las magnitudes locales.
Fue propuesta por primera vez de forma general por Bernhard Riemann en el siglo XIX. Como casos especiales particulares aparecen los dos tipos convencionales (geometría elíptica y geometría hiperbólica) de geometría No-Euclidiana, así como la geometría euclidiana misma. Todas estas geometrías se tratan sobre la misma base, al igual que una amplia gama de las geometrías con propiedades métricas que varían de punto a punto.
Geometría Analítica
[editar]La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
Geometría Analítica en el plano
[editar]- Introducción
- Coordenadas cartesianas
- La Recta
- La Circunferencia
- La Parábola
- La Elipse
- La Hipérbola
Figuras geométricas
[editar]
Una figura geométrica es un conjunto cuyos elementos son puntos. La geometría plana es una parte de la geometría que trata de aquellos elementos cuyos puntos están contenidos en un plano. La geometría plana está considerada parte de la geometría euclidiana, pues ésta estudia los elementos geométricos a partir de dos dimensiones.
- Adimensional (sin dimensiones)
- Punto
- Unidimensional (lineales)
- Recta
- Semirrecta
- Segmento
- Curva
- Bidimensional (superficiales)
- Plano
Delimitan superficies (figuras geométricas en sentido estricto):
- Polígono
- Triángulo
- Cuadrilátero
- Sección cónica
- Elipse
- Circunferencia
- Parábola
- Hipérbola
- Elipse
Describen superficies:
- Superficie de revolución
- Superficie reglada
- Tridimensional (volumétricas)
Delimitan volúmenes (cuerpos geométricos):
- Poliedro
Describen volúmenes:
- Sólido de revolución
- Cilindro
- Cono
- Esfera
- N-dimensional (n dimensiones)
- Politopo
| Para más información, véase el artículo «Figura Geométrica» en Wikipedia. |
Teorema de Pitágoras
[editar]Ideas previas
[editar]Cateto
[editar]Cada uno de los dos lados que forman el ángulo recto en un triángulo rectángulo.
Cada uno de los dos lados menores de un triángulo rectángulo.
El nombre de cateto solamente aparece en los triángulos rectángulos.
Hipotenusa
[editar]Lado mayor de un triángulo rectángulo, es opuesto al ángulo recto.
La medida de la hipotenusa puede ser calculada si se conoce la medida de ambos catetos, utilizando el teorema de Pitágoras.
El nombre de Hipotenusa solamente aparece en los triángulos rectángulos.
Ángulo recto
[editar]Dos líneas que se cortan perpendicularmente determinan cuatro ángulos iguales, que llamamos rectos.
El ángulo recto es la cuarta parte del ángulo completo.
El ángulo recto mide la mitad de un ángulo llano.
En el sistema sexagesimal mide 90º.
Sus lados son semirrectas perpendiculares con el origen en el mismo punto, el vértice del ángulo
En otros sistemas mide: π/2 radianes y 100g
Teorema de Pitágoras
[editar]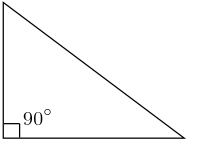
El matemático Pitágoras, basándose en los conocimientos egipcios, descubrió una relación entre los lados de un triángulo rectángulo. Dicha relación es lo que conocemos comúnmente como Teorema de Pitágoras.
Enunciado
[editar]El enunciado del teorema establece que, en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
a2 = b2 + c2
cuadrado de la hipotenusa a = cuadrado del cateto b + cuadrado del cateto cEl teorema de Pitágoras solamente es aplicable a triángulos rectángulos. Un triángulo rectángulo es aquel que posee un ángulo denominado recto o de 90°. Se le nombra catetos a los dos lados que forman el ángulo de 90° y la hipotenusa es el segmento restante opuesto al ángulo recto. Pero con dominio de la geometría se puede extender a otros triángulos e incluso a otras figuras, por ejemplo en un rectángulo, al trazar una de sus diagonales quedan determinados dos triángulos rectángulos.
Otras formas del teorema de Pitágoras
[editar]Se puede obtener una fórmula para obtener el valor de uno de los catetos al despejar la ecuación. Las otras formas del teorema son las siguientes:
- b2 = a2 – c2
- c2 = a2 – b2
Teorema de Tales
[editar]Teorema de Tales
[editar]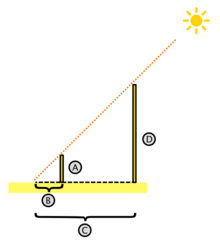
Se nombra así en nombre del geometro griego Tales de Mileto. El teorema de tales sirve para hacer dibujos a escala.
Primer teorema
[editar]Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:
"Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes." A el se debe una de las numerosas aplicaciones que tiene la semejanza, que es la determinación de la distancia entre dos puntos inaccesibles entre sí; para ello se dice que calcula la altura de una de las pirámides de Egipto sin medirla directamente, basándose en la longitud de la sombra de su bastón; así logró realizar una brillante triangulación.
Segundo teorema
[editar]
El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los [ángulos inscritos, consiste en el siguiente enunciado:
"Sea B un punto de la circunferencia de diámetro AC y centro "O", distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo donde <ABC = 90º"
Poliedros
[editar]- Introducción
- Definición de Cuerpo Geométrico
- Clasificación de los Poliedros
- Clasificación de cuerpos Redondos
- Denominación
- Sólidos de Platón
- Sólidos de Arquímedes
- Sólidos de Catalán
- Sólidos de Kepler-Poinsot
- Sólidos de Johnson
- Esferas y domos geodésicos
- Hipercubos
Coordenadas
[editar]- Introducción
- Definiciones
- Métodos fundamentales
- Tipos de Sistemas
- Coordenadas Cartesianas
- Abscisa
- Ordenada
- Sistema de coordenadas ortogonales
- Sistemas de coordenadas polares
- Sistemas de coordenadas cilíndricas
- Sistemas de coordenadas esféricas
- Coordenadas Geográficas
- Otros sistemas de coordenadas
- Funciones y coordenadas
- Resumen de los distintos sistemas
- Biografía de René Descartes
- Paralelas del plano (a revisar)
- Funciones inversas y curvas de función (a revisar)
Trigonometría
[editar]La trigonometría es una rama de las matemáticas que se ocupa del estudio de las relaciones entre los lados y los ángulos de un triángulo. Este estudio da pie a considerar una serie de funciones (seno, coseno, tangente...) que dan lugar a un campo mucho más amplio que el considerado inicialmente y que se aplica sobre todo a fenómenos de tipo periódico, como son las ondas electromagnéticas. En la antigüedad, se uso para los estudios astronómicos y en agrimensura. Hoy en día, además, la trigonometría juega un papel clave en los sistemas de posicionamiento global (GPS). Tomando como punto de partida un triángulo rectángulo, en particular uno de sus ángulos agudos, definimos las siguientes relaciones:
Relación inicial
[editar]
Teorema fundamental de la trigonometría
[editar]
Equivalencia entre las funciones trigonométricas
[editar]| Seno | Coseno | Tangente | Cotangente | Secante | Cosecante | |
|---|---|---|---|---|---|---|
- sin(α+β)=sinα*cosβ+senβ*cosα
- sin(α-β)=sinα*cosβ-sinβ*cosα
- tan(α+Β)=(tanα+tanΒ) / (1-tanα*tanβ)
- cos(α+β)=cosα*cosβ-sinα*sinβ
- cos(α-β)cosα*cosβ+sinα*sinβ
- sin(2α)=2*sinα*cosα
- cos(2α)=cos^2(α)-sin^2(α)
- tan(2α)=2*tan(α)/(1 - tan^2(α))
Funciones trigonométricas
[editar]Dado un ángulo , las funciones trigonométricas y son, respectivamente, las proyecciones sobre los ejes vertical y horizontal de la hipotenusa de un triángulo rectángulo, uno de cuyos ángulos agudos es precisamente . Para ser más preciso, sean , el triángulo (rectángulo) con vértice en el origen de coordenadas, el cateto en el eje de las abscisas, y el cateto paralelo al eje de las ordenadas.
Entonces las igualdades son válidas, en concordancia con la relación de proporcionalidad de lados en un triángulo que asegura el teorema de Thales.
En el caso en el que el ángulo no esté en el intervalo , se conviene en darle a las dos expresiones definidas anteriormente el signo que tiene la coordenada en los numeradores de dichas expresiones (esto es, es positivo en el primer y segundo cuadrantes, y es positivo en el primer y cuarto cuadrantes; negativos ambos en los otros casos). Adicionalmente, si , se define en la forma siguiente: y ahora el signo de esta función se calcula como el cociente de los signos que tienen y . Otras funciones trigonométricas útiles son tomando las precauciones necesarias para que los denominadores sean no nulos.
















































![{\displaystyle x\in [0,\pi /2]\subset R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee23430dd15b91ed782189336aa377d0174168e1)





![{\displaystyle \displaystyle [0,\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506d138bca316db9477abdbac7edf5a6d62a121b)





