Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Solar/Curva del Eclipse Total Central. Eclipse Máximo y Ancho de la Sombra
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Cálculo de la Curva del Eclipse Total Central. Eclipse Máximo y Ancho de la Sombra
[editar]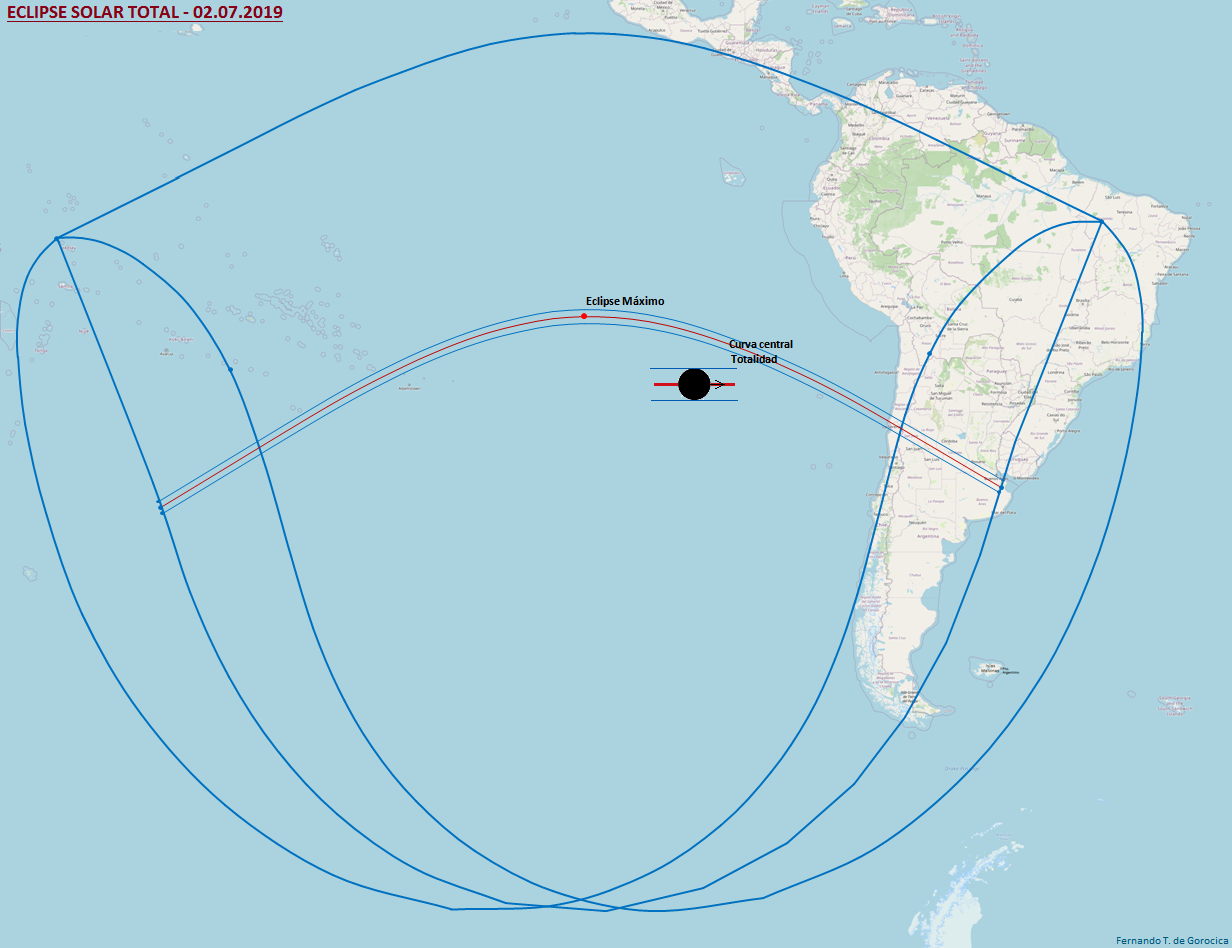
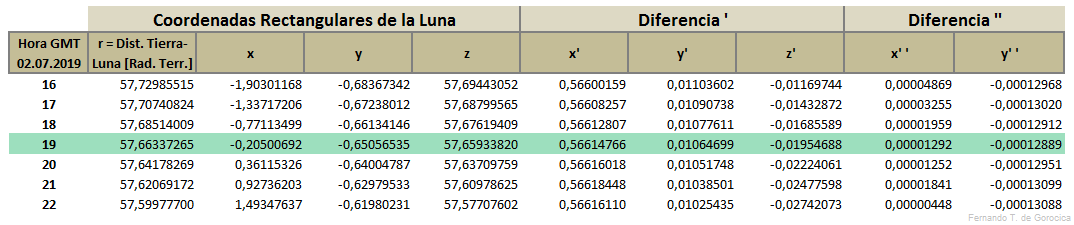
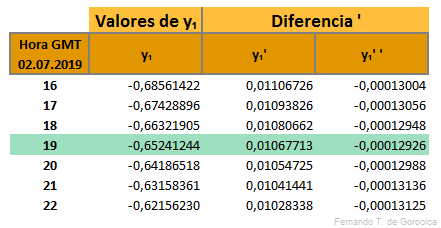
Sabiendo que la Conjunción Sol-Luna, en Ascensión Recta, ocurre a las 19:21:36 hs. (GMT = Greenwich Meridian Time), tomamos 7 horas para los cálculos respectivos. T₀ = 19 hs. es la hora central y anterior más cercana a tal conjunción, luego se realizan los cálculos para las tablas para ±3 hs. a partir de esa T₀, es decir para las 16, 17, 18, 19, 20, 21 y 22 hs. (GMT).
Según los tiempos del primer y último contacto del Eje de Cono de la Sombra Lunar o del punto Z con el horizonte (tangente), que se han hallado en el capítulo anterior, se comienzan los cálculos desde las 18 hs. y se repiten (iteración) cada 12 minutos y así sucesivamente hasta las 20,8 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
Comenzamos entonces con γ y en [°]
- γ = Atan(x / y₁) (173)
el ángulo γ debe estar comprendido entre 0° y 360°. Si y₁ es negativo sumar 180° a γ.
Luego β en [°]
- β = Aseno(x / Seno(γ)) (174)
el ángulo β debe estar comprendido entre 0° y 360°.
Ahora calcular C en [°] y c
- C = Atan(y₁ / Coseno (β)) (175)
el ángulo C debe estar comprendido entre 0° y 360°. Si Coseno (β) es negativo sumar 180° a C, luego calcular c según C
- c = y₁ / Seno (C) (176)
Hallar luego el valor de d en [°], siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también d₁ en [°] siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (177)
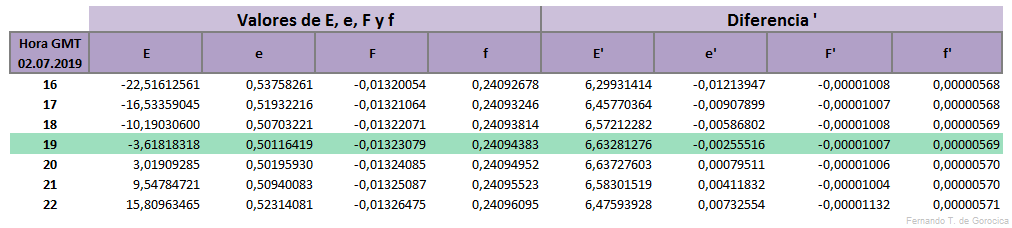
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo)
Seguido calculamos θ que es ángulo horario del Eje del Cono de la Sombra Lunar o del punto Z en el lugar o bien en la Longitud ω, que es aproximadamente el Ángulo Horario del Sol, y correspondiente también a ese instante Tᵢ, entonces
- θ = Atan(x / (c * Coseno(C + d₁))) (178)
el ángulo θ debe estar comprendido entre 0° y 360°, si (c * Coseno(C + d₁)) es negativo (-) sumar 180° a θ. Para el Tiempo Aparente Local que es aproximadamente la Hora Solar Verdadera, dividir θ por 15.
Luego calculamos φ₁ en [°] para hallar después la latitud geográfica φ también en [°]
- φ₁ = Acoseno(c * Seno(C + d₁)) (179)
Después los valores de L y a, primero interpolando, en las tablas correspondientes (más abajo), los valores l₂, i₂, b', c₂' y f para el instante en cuestión y según las siguientes fórmulas se tiene
- L = Abs(l₂ - i₂ * Coseno(β)) (180)
- a = c₂' - f * Coseno(β) (181)
el valor de f, de ésta última fórmula, lo hallamos en la tabla E, e, F y f (más abajo).
Con las formulas anteriores encontraremos ahora el valor Q en [°]
- Q = Atan(a / b') (182)
el ángulo Q debe estar comprendido entre 0° y 360°. Si b' es negativo (-) sumar 180° a Q.
Por último, hallaremos las coordenadas terrestres para el instante Tᵢ, pero primero μ₁, siendo el ángulo horario del Eje del Cono de la Sombra Lunar o del punto Z en Greenwich, ángulo comprendido entre 0° y 360°, para el instante Tᵢ interpolando [1] en la tabla correspondiente (más abajo).
Entonces, para el punto de la curva del Eclipse Total Central para ese instante Tᵢ tenemos:
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) (183) |
| Longitud ω (al W) = μ₁ - θ (184) |
e lo encontramos en la tabla de las Constantes (más abajo). La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste.
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Seguido calcularemos para cada instante Tᵢ y su coordenada terrestre la duración de la totalidad en [minuto], el comienzo y su fin ambos en [hora]. Entonces tenemos
| T (Comienzo) = Tᵢ - t / 120 (185) |
| t (duración) = 120 * L * Seno(Q) / a (186) |
| T (Fin) = Tᵢ + t / 120 (187) |
Para el Ancho del Cono de la Sombra Lunar sobre la superficie terrestre calcularemos primero para cada instante Tᵢ y su respectiva coordenada los siguientes valores B², L₂, A y n² según el método de Mikhailov. Tal Ancho del Cono de la Sombra Lunar sobre la superficie terrestre es siempre perpendicular a la dirección del movimiento del centro de la elipse formada por el cono.
- B² = 1 - x^2 - y₁^2 (188)
- L₂ = l₂ - B²^0,5 * Tan(f₂) (189)
- A = c₂ - B²^0,5 * μ' * Seno(1) * Coseno(d) (190)
- n² = A^2 + b'^2 (191)
Los valores x, y₁, l₂, f₂, c₂, μ' y b' deben ser hallados en las tablas correspondientes (más abajo).
Por último el Ancho del Cono de la Sombra Lunar en [km] será
| Ancho = Abs((2 * 6377,39715 * L₂) / (B² + (x * A - y₁ * b')^2 / n²)^0,5) (192) |
Para la Máxima Duración en todo el Eclipse Total Central interpolar un extremo por el método del polinomio de Lagrange [2] con tres pares de valores (Xᵢ;Yᵢ) según t = Duración de la totalidad [ms].
Para el Eclipse Total Central al Mediodía = 12:00 Hora Aparente Local interpolar por el método del polinomio de Lagrange [2] con tres pares de valores (Xᵢ;Yᵢ) según la Hora Local Aparente (12:00 h).
Ejemplo práctico:
[editar]Tablas para interpolar valores
[editar]Todos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de un Eclipse Solar |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |