Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Solar/Curva del Eclipse Máximo en el Horizonte
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Cálculo de la Curva del Eclipse Máximo en el Horizonte
[editar]
Como ejemplo práctico tomamos el Eclipse Solar Total del 02.07.2019 y sabiendo que la Conjunción Sol-Luna, en Ascensión Recta, ocurre a las 19:21:36 hs. (GMT = Greenwich Meridian Time) tomamos también 7 horas para los cálculos respectivos. T₀ = 19 hs. es la hora central y anterior más cercana a tal conjunción.
Se comienzan los cálculos desde las 16 hs. y se repiten (iteración) cada 12 minutos y así sucesivamente hasta las 22 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
Comenzamos entonces calculando M en [°] y Tᵢ = 16 hs.
- M = Atan(x / y) (93)
Donde x e y son las Coordenadas Rectangulares de la Luna, el ángulo M debe estar comprendido entre 0° y 360°. Si y es negativo sumar 180° a M para que luego m sea positivo (+).
Luego m
- m = x / Seno(M) (94)
Después calculamos E en [°] que nos servirá para determinar si el Eclipse está comenzando o finalizando
- E = Atan(b' / c₁') (95)
donde b' y c₁' los hallamos interpolando en las tablas correspondientes (más abajo). Si c₁' es negativo sumar 180° a E.
Luego si se cumple la siguiente condición, se podrán calcular para cada instante Tᵢ los límites del Eclipse Máximo en la Salida o en la Puesta
- |m * Seno(M - E)| < 1 (96)
por lo tanto, en el presente caso práctico del Eclipse Solar Total del 02.07.2019, se cumple tal condición para los instantes desde las 18 hs. hasta las 20,8 hs. ambos inclusive, los >= se excluyen.
Hallar luego el valor de d en [°], siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también ρ₁ en [Radios Terrestres]
- ρ₁ = Seno(d) / Seno(Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5))) (97)
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo).
Calcular ahora el valor de ψ₁ y ψ₂ ambos en [°]
- ψ₁ = Aseno(m * Seno(M - E) / 10^(Log(ρ₁) / 2)) (98)
- ψ₂ = Aseno(m * Seno(M - E) / 10^(Log(ρ₁) / 2)) + 180 (99)
Los ángulos ψ₁ y ψ₂ deben estar comprendidos entre 0° y 360°.
Seguido hallar, interpolando en la tabla correspondiente (más abajo), el valor de l₁ siendo el Radio Penumbra en el Plano Fundamental o Principal de Referencia
luego calcular Δ
- Δ = Coseno(ψᵢ) * 10^(Log(ρ₁) / 2) - m * Coseno(M - E) (100)
eligiendo, para esta fórmula, alguno de los dos ψᵢ donde
- Los lugares que satisfacen la solución son aquellos que están dentro de la Sombra, es decir aquellos donde se cumple la condición Δ < l₁, o al menos Δ <= l₁. Si Δ > l₁ no se toma en cuenta el correspondiente ψᵢ, es decir que tendremos siempre una solución para alguno de los dos ψᵢ. Entonces
Calcular luego γ en [°]. Si se tomó ψ₁, ψᵢ será positivo (+), pero si se tomó ψ₂, ψᵢ será negativo (-), entonces
- γ = ψᵢ + E (101)
Habiendo hallado el verdadero valor de ψ y γ calculamos γ' en [°]
- γ' = Atan(ρ₁ * tan(γ)) (102)
recordar que γ' en [°] es un valor muy similar a γ, por lo tanto el primero tiene que estar en el mismo cuadrante que el segundo. Ambos ángulos comprendidos entre 0° y 360°.
Luego hallamos, con estos nuevos valores, las coordenadas terrestres para cada instante, pero primero
el d₁ en [°] siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (103)
luego θ que es el Ángulo Horario del Eje del Cono de la Sombra Lunar o del punto Z en el lugar (Ángulo Horario del Sol)
- θ = Atan(Seno(γ') / (-Coseno(γ') * Seno(d₁))) (104)
Si (-Coseno(γ') * Seno(d₁)) es negativo (-) sumar 180° a θ. Tal ángulo debe estar comprendido entre 0° y 360°. Si dividimos a θ por 15 nos dará la Hora Local Aparente del lugar para ese instante, hora similar a la verdadera solar, entonces
| Hora Local Aparente = θ / 15 (105) |
El valor de e en la tabla de las Constantes (más abajo).
Después calcular el valor de φ₁ en [°]
- φ₁ = Aseno(Coseno(γ') * Coseno(d₁)) (106)
La Latitud Geográfica φ y la Longitud ω, ésta última al Oeste (W) de Greenwich, serán
| Latitud Geográfica φ = Atan(Tan(φ₁) / (1 - e^2)^0,5) (107) |
| Longitud ω (al W) = μ₁ - θ (108) |
La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste. El valor de μ₁ lo hallamos interpolando para ese instante y en la tabla correspondiente (más abajo) y e en la tabla de las Constantes (más abajo).
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
El Porcentaje de Oscurecimiento del Eclipse Máximo tanto en la Salida como en la Puesta será
| % de Oscurecimiento = ((Promedio l₁) - Abs(Δ)) / ((Promedio l₁) + (Promedio l₂)) (109) |
Δ según la fórmula (100), los promedios de l₁ y l₂ en las tablas correspondientes (más abajo).
Por último, para cada instante, averiguar si el Eclipse Máximo ocurre en la Salida o en la Puesta según la siguiente condición (MS-Excel "Si") y con θ según la fórmula (104)
| Si(θ >= 180); "Eclipse Máximo en la Salida"; "Eclipse Máximo en la Puesta") (110) |
Es decir, la explicación según esta última condición es:
- En un instante dado el Sol está saliendo o poniéndose en un lugar determinado de acuerdo a θ siendo el Ángulo Horario del Eje del Cono de la Sombra Lunar o del punto Z, que comprendido entre más de los 180° y menos de los 360° es para la salida del Sol y entre 0° y 180° es para la puesta.
Ejemplo práctico:
[editar]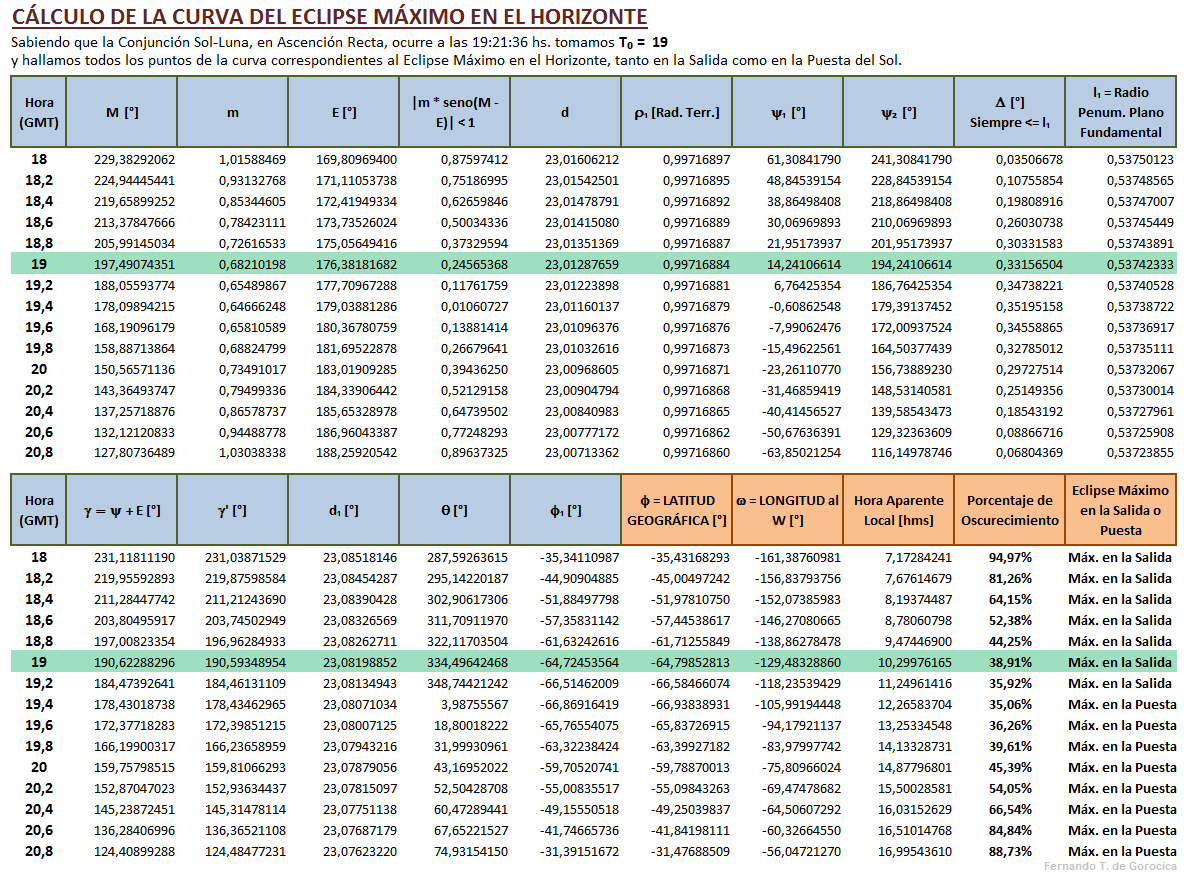
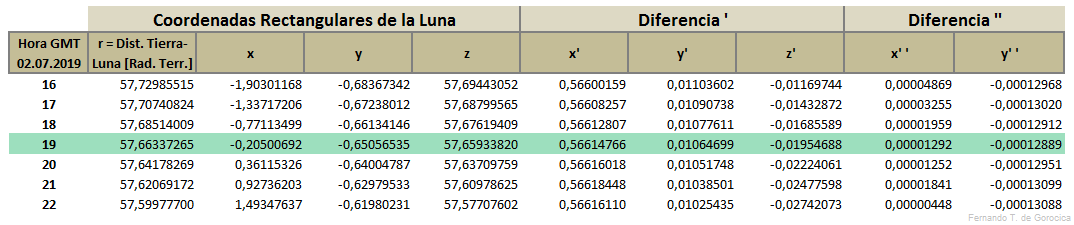
Tablas para interpolar valores
[editar]Todos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de un Eclipse Solar |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |