Curso de alemán para principiantes con audio/Lección 085b
Apariencia
- índice
- Lección 084b ← Lección 085 → Lección 086b
- Lección 085
- Mathematik auf Deutsch - 35
BM1701 - BM1710
[editar]BM1701

Dreieck - Dreiecksungleichung (Wiederholung aus der vorhergehenden Lektion)
- ---
- Die Gesamtlänge zweier Seiten eines Dreiecks ist immer größer als die Länge der dritten Seite. Diese Beziehungen lassen sich in der so genannten Dreiecksungleichung ausdrücken.
- Nach der Dreiecksungleichung ist im Dreieck die Summe der Längen zweier Seiten a und b stets mindestens so groß wie die Länge der dritten Seite c. Das heißt formal:
- Man kann auch sagen, der Abstand von A nach B ist stets höchstens so groß wie der Abstand von A nach C und von C nach B zusammen, oder um es populär auszudrücken: „Der direkte Weg ist immer der kürzeste.“
- ---
- Sind a, b und c die Längen der Seiten eines Dreiecks, so gelten folgende Ungleichungen:
- Also gilt:
- SATZ:
- In jedem Dreieck ist die Summe zweier Seiten größer als die dritte Seite.
- ---
- Der direkte Weg ist immer der kürzeste.
- Die kürzeste Verbindung zwischen zwei Punkte ist die Gerade.
BM1702

- Kongruenz von Dreiecken
- Anwendung des Kongruenzbegriffs auf Dreiecke
- kongruent = deckungsgleich
- ---
- Zwei Dreiecke sind kongruent genau dann, wenn es eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen ist.
- ---
- Das Dreieck ist das Bild eines Dreiecks bei der Spiegelung an der Geraden .
- Die Dreiecke und sind also kongruent.
- Wir schreiben: .
BM1703

Bild 1 
Bild 2 - Eigenschaften kongruenten Dreiecken
- --
- Die Kongruenz von Dreiecken ist eine Beziehung zwischen jeweils zwei Dreiecken.
- Wenn ist, so gibt es eine Bewegung, bei der das Dreieck das Bild des Dreiecks ist.
- ---
- SATZ:
- Wenn zwei Dreiecke kongruent sind, dann stimmen sie in den Seiten und in den Winkeln überein.
- ---
- Ein Beweis dieses Satzes ergibt sich durch die Anwendung der Definition für die Kongruenz.
- (Definition: Geometrische Figuren heißen kongruent [deckungsgleich] genau dann, wenn es eine Bewegung gibt, die eine Figur auf die andere abbildet.)
- Sind nämlich zwei Dreiecke kongruent, so gibt es eine Bewegung, bei der jeder Seite des Originaldreiecks genau ein Seite des Bilddreiecks und jedem Winkel des Originaldreiecks genau ein Winkel des Bilddreiecks zugeordnet ist. Die einander zugeordneten Seiten bzw. Winkel sind dann kongruent. Die beiden Dreiecke stimmen also in den Seiten und in den Winkels überein.
BM1704
- Hier nochmals der SATZ aus der vorherigen Übung:
- Wenn zwei Dreiecke kongruent sind, dann stimmen sie in den Seiten und in den Winkeln überein.
- ---
- Es gilt auch die Umkehrung des Satzes:
- Wenn zwei Dreiecke in den Seiten und in den Winkeln übereinstimmen, dann sind die Dreiecke kongruent.
- ---
- Um diesen Satz zu beweisen, müsste gezeigt werden, dass es auf Grund der in dem Satz genannten Voraussetzugen stets eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen Dreiecks ist.
- Wir verzichten an dieser Stelle auf einen Beweis.
BM1705

Bild 1: Gestieltes Laubblatt des Spitz-Ahorns (Acer platanoides) 
Bild 2: verschiedene Ebene Vielecke - Unter Planimetrie (von lat. planum für Ebene; und von altgriech. metreo für ich messe; Messung in der Ebene) versteht man allgemein metrische Problemstellungen der ebenen Geometrie, insbesondere die Flächeninhaltsberechnung in der Ebene. (Mit der Flächenberechnung im Raum befasst sich die Stereometrie.)
- Der Flächeninhalt einfacher Flächen in der Ebene kann aus bekannten Längenwerten berechnet werden. Die Errechnung komplizierterer Flächen wird meist über Zerlegung in Flächenstücke, die sich leichter errechnen lassen, erreicht. Unregelmäßige Flächen, wie z. B. die Fläche eines Ahornblattes, müssen analytisch mit dem Kurvenintegral – sofern die Kurve analytisch vorliegt – errechnet, mit planimetrischen Methoden abgeschätzt oder planimetriert (ausgemessen) werden.
- Dabei zeigt das Beispiel eines Ahornblattes besonders deutlich, dass es um Abstraktion und Näherungsverfahren geht. Planimetrisch berechnet wird nicht die (Ober-)Fläche des (nicht flachen) Ahornblattes, sondern die abstrahierte Fläche, welche seine (mathematisch gedachte) Grundrisszeichnung auf dem Papier einnimmt. Physikalisch allerdings ist auch das Papier nicht flach und die Fläche müsste als Oberfläche stereometrisch berechnet werden, doch da finden sich schon vor der Genauigkeit im Nanobereich riesige Höhlen und Berge, fraktale Klüftungen, dass man darüber fast auf die „Quanten-Frage“ stößt, ob denn die Oberfläche eines Ahornblattes wirklich endlich ist.
BM1706
- In der Planimetrie hat man häufig die Kongruenz zweier Dreieck nachzuweisen:
- Wir haben dazu zwei Möglichkeiten:
- 1.) Wir weisen nach, dass es eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen ist.
- 2.) Wir weisen nach, dass die Dreiecke in den Seiten und in den Winkeln übereinstimmen.
- Das zweite Verfahren kann vereinfacht werden.
- Die drei Seiten und die drei Innenwinkel eines Dreiecks nennt man seine Bestimmungsstücke, kurz Stücke.
- ---
- Zunächst überzeugen wir uns an Beispielen davon, dass zwei Dreiecke im Allgemeinen NICHT kongruent sind, wenn sie nur in
- a) einem Stück bzw. b) zwei Stücken übereinstimmen
- ---

Bild 1 - In Bild 1 stimmen die beiden Dreiecke und zwar in den Seiten und überein, sind jedoch nicht kongruent.
- ---
- Die beiden Dreiecke und in Bild 1 stimmen zwar einerseits in den Seiten und sowie andererseits in den Seiten und überein, sind jedoch nicht kongruent.
- Der Winkel ist nämlich ein rechter Winkel und der Winkel ein spitzer Winkel.
BM1707
- Stimmen zwei Dreiecke in drei Stücken überein, so können sie kongruent sein. Diese Fälle werden wir in den nächsten Übungen untersuchen
- ---
- Kongruenzsatz SWS
- ---
- Seite = S
- Winkel = W
- SWS: Seite-Winkel-Seite
- ---

Bild 1 - Wir betrachten zunächst den Fall, dass zwei Dreiecke in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen.
- Diesen Fall bezeichnen wir mit (sws)
- Seite-Winkel-Seite
- „Ein Winkel wird von beiden Seiten eingeschlossen“ bedeutet, dass die Seiten auf den Schenkeln des Winkels liegen.
- ---

Bild 2 - Kongruenzsatz (sws):
- Zwei Dreiecke, die in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen, sind kongruent.
- ---
- Damit wir sicher sind, dass der Kongruenzsatz (SWS) für alle möglichen Paare von Dreiecken zutrifft, die den Bedingungen (Voraussetzungen ) des Satzes genügen, müssen wir ihn unabhängig von Beispielen beweisen. Wir zeigen dazu, dass es auf Grund der im Satz genannten Voraussetzungen eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen ist.
- Der Beweis folgt in der nächsten Übung.
BM1708

Bild 1 - Beweis des Kongruenzsatzes (SWS)
- ---
- Für zwei beliebige Dreiecke und seien folgende Bedingungen erfüllt:
- ---
- 1.)
- Wegen gibt es eine Bewegung, bei der
- a) der Punkt Q das Bild des Punktes B,
- b) der Strahl QP das Bild des Strahls BA und
- c) der Strahl QR das Bild des Strahls BC ist.
- 2.)
- Bei dieser Bewegung ist
- a) wegen der Punkt P das Bild des Punktes A und
- b) wegen der Punkt R das Bild des Punktes C.
- ---
- Das Dreieck ist also das Bild des Dreiecks bei dieser Bewegung.
- Demnach gilt: .
- w.z.b.w.
BM1709
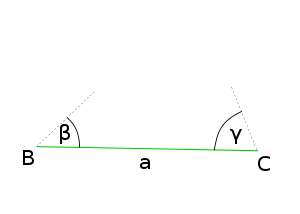
Bild 1 
Bild 2 - Kongruenzsatz WSW
- ---
- Seite = S
- Winkel = W
- WSW: Winkel-Seite-Winkel
- ---
- Für die beiden Dreiecke in Bild 1 nehmen wir an, dass sie in einer Seite und den beiden anliegenden Winkels übereinstimmen.
- Diesen Fall bezeichnen wir als (WSW)
- ---
- Kongruenzsatz (wsw)
- Zwei Dreiecke, die in einer Seite und den beiden anliegenden Winkeln übereinstimmen, sind kongruent. (deckungsgleich)
- ---
- Beweis des Kongruenzsatzes (WSW)
- Für zwei beliebige Dreiecke und seien folgende Bedingungen erfüllt:
- ---
- 1.)
- Wegen gibt es eine Bewegung, bei der
- a) der Punkt P das Bild des Punktes A,
- b) der Strahl PQ das Bild des Strahls AB und
- c) der Strahl PR das Bild des Strahls AC ist.
- 2.)
- Bei dieser Bewegung ist
- wegen der Punkt Q das Bild des Punktes B.
- 3.)
- Das Bild von bei dieser Bewegung liegt auf dem STrahl PR.
- Aus und der Voraussetzung
- ergibt sich . Daraus folgt
- Das Dreieck ist also das Bild des Dreiecks bei dieser Bewegung.
- Demnach gilt
- w.z.b.w.
BM1710

Bild 1: Kongruenzsatz (sss) 
Bild 2: Kongruenzsatz (ssw) 
Bild 3: Kongruenzsatz (ssw) 
Bild 4 
Bild 5 - Insgesamt gibt es 4 Kongruenzsätze für Dreiecke.
- Wir hatten bisher: sws und wsw
- Es fehlen uns noch: sss und ssw
- ---
- Kongruenzsatz (sss)
- Zwei Dreiecke, die in den drei Seiten übereinstimmen, sind kongruent.
- ---
- Kongruenzsatz (ssw)
- Zwei Dreiecke, die in den zwei Seiten und dem Gegenwinkel der größeren Seite übereinstimmen, sind kongruent.
BM1711 - BM1720
[editar]BM1711
- Zeige an je einem Beispiel; dass in den folgende Fällen die beiden Dreiecke nicht kongruent zu sein brauchen:
- 1.) Zwei Dreiecke stimmen in zwei Seiten und Winkel, der der kleineren Seite gegenüberliegt, überein.
- 2.) Zwei Dreiecke stimmen in den drei Winkeln überein.
2. Lösung BM1711
BM1712

Bild 1 
Bild 2 
Bild 3 
Bild 4 - Für kongruente Dreiecke braucht man immer drei Größen.
- Aber drei gegebenen Winkel reichen nicht um ein eindeutiges Dreieck zu konstruieren.
- Es kann durchaus zwei nicht kongruente Dreiecke geben, die in allen drei Winkeln übereinstimmen.
- ---
- Drei Seiten im Dreieck reichen immer aus, um ein Dreieck eindeutig festzulegen. Stimmen zwei Dreiecke also in allen Seiten überein, so sind sie kongruent.
- ---
- Zwei Seiten und der von ihnen eingeschlossene Winkel reichen auch immer aus, um ein Dreieck eindeutig zu bestimmen.
- Achtung: Der Winkel muss eingeschlossen sein, denn sonst sind die Dreiecke meistens mehrdeutig.
- ---
- Dreiecke, die deckungsgleich sind, sind auch immer flächengleich.
- Die Umkehrung gilt aber nicht.
- Dreiecke, die flächengleich sind, sind NICHT immer deckungsgleich.
- ---
- Ordne die vier Kongruenzsätze für Dreiecke den vier Abbildungen zu!
BM1713
BM1714

Bild 1 - Begründe, warum durch die Konstruktion der Mittelsenkrechten - wie in der vorherigen Übung beschrieben - die Strecke halbiert wird!
BM1715

Bild 1 - Konstruiere den Mittelpunkt der Strecke !
- Als zusätzliches Problem ist hier aber die Strecke so lang, dass der zur Verfügung stehende Zirkel zu klein ist, um ausreichend große Kreis zu zeichnen. Die maximal mögliche Größe des Kreise ist der Abbildung zu entnehmen.
Lösung BM1715
BM1716
- Wie halbiert man einen Winkel?
BM1717
Lösung BM1717 - Begründung:
- Die Dreiecke SAC und SBC sind nach dem Kongruenzsatz (SSS) kongruent.
- Daraus folgt:
- Der Strahl SC ist also Winkelhalbierende des gegebenen Winkels.
BM1718
BM1719

- Begründe, warum wir sicher sein können, dass wir mit der Konstruktion aus der vorhergehenden Übung die Senkrechte in Punkt A errichtet haben!
1. Lösung BM1719 - Begründung:
- Die Dreiecke und sind nach Kongruenzsatz (sss) kongruent.
- Kannst du das genauer erläutern?
2. Lösung BM1719
- Die Dreiecke und sind nach Kongruenzsatz (sss) kongruent, denn
- die Strecken und sind gleich lang, ihre Länge ist gleich dem Radius des roten Kreisbogens,
- die Strecken und sind gleich lang, ihre Länge ist gleich dem Radius des blauen bzw. grünen Kreisbogens, die laut Konstruktionsanweisung gleich sind.
- die Streckn wird von beiden Dreiecken verwendet, sie ist deshalb in beiden Dreiecken gleich lang.
- ---
- Weiter mit der Begründung:
- Da dann die Winkel BAD und CAD zueinander kongruente Nebenwinkel sind, ist jeder der beiden ein rechter Winkel.
- (Zwei kongruente Nebenwinkel müssen immer 90° große sein.)
- Die Gerade DA steht also in Punkt A senkrecht auf der gegebenen Geraden.
- (rechter Winkel, senkrecht und 90° bedeuten das gleiche)
- Die Dreiecke und sind nach Kongruenzsatz (sss) kongruent, denn
BM1720
-
Bild 1
-
Bild 2
-
Bild 3
-
Bild 4
-
Bild 5
- Was ist auf den Abbildungen dargestellt?
BM1721 - BM1730
[editar]BM1721

Bild 1:Zirkel und Lineal 
Bild 2:Die Konstruktion eines regelmäßigen Sechsecks nur mit Zirkel und Lineal - Konstruktion mit Zirkel und Lineal
- ---
- In der euklidischen Geometrie versteht man unter einer Konstruktion mit Zirkel und Lineal die Entwicklung der exakten zeichnerischen Darstellung einer Figur auf der Grundlage vorgegebener Größen, wobei in der Regel nur Zirkel und Lineal verwendet werden dürfen. Das Lineal hat keine Markierungen; man kann damit also nur Geraden zeichnen, aber keine Strecken abmessen.
- In der Geometrie werden Zirkel und Lineal auch als euklidische Werkzeuge bezeichnet. Problemlösungen, die auf andere Hilfsmittel zurückgreifen, wurden von den Griechen der klassischen Periode (und auch später von den meisten Geometrietreibenden bis ins 20. Jahrhundert) als nicht zufriedenstellend betrachtet.
- ---
- Euklidische Werkzeuge:
- Die Beschränkung auf die „euklidischen Werkzeuge“ leitete sich aus den Postulaten ab, die Euklid am Anfang seines Lehrbuches Die Elemente zusammengestellt hatte. Daraus ergeben sich als einzige zugelassene Anwendungen dieser Werkzeuge:
- das Ziehen einer Geraden mit unbeschränkter Länge durch zwei beliebig gegebene, voneinander verschiedene Punkte,
- das Ziehen eines Kreises, der einen beliebig gegebenen Punkt als Mittelpunkt hat und durch einen beliebig gegebenen anderen Punkt verläuft, und
- das Übertragen bzw. Abschlagen einer Strecke auf einer Geraden oder einer Kreislinie.
- Ein Beispiel wäre die Konstruktion eines Dreiecks aus drei Vorgaben, etwa zweier Seiten und eines Winkels.
- ---
- Geschichte:
- In der Antike forderte man vorerst kollabierende Zirkel.
- (Erläuterung: In den ursprünglichen Konstruktionsproblemen des Euklid wurde von einem kollabierenden Zirkel ausgegangen, dessen Radius beim Hochheben vom Blatt nicht festgehalten werden kann, um einen weiteren Kreis mit diesem Radius zu zeichnen.)
- Später war auch der nicht-kollabierende Zirkel für Konstruktionen erlaubt – nicht zuletzt, weil mit Lineal und kollabierendem Zirkel dieselben Punkte konstruiert werden können wie mit Lineal und nicht-kollabierendem Zirkel.
- Die Konstruktion nur mittels Zirkel und (unskaliertem) Lineal galt viele Jahrhunderte als die Krone mathematischer Logik. Sie galt aber lange als weitgehend ausgereizt. Die Entdeckung einer Konstruktionsmethode für das regelmäßige Siebzehneck am 29. März 1796 durch Carl Friedrich Gauß war die erste wesentliche Neuerung seit zweitausend Jahren.
- Viele Mathematiker haben sich jahrelang an – wie man heute weiß unlösbaren – Aufgaben wie der Quadratur des Kreises versucht.
- Nach dem Satz von Mohr-Mascheroni können Konstruktionsaufgaben mit Zirkel und Lineal auch mit dem Zirkel allein ausgeführt werden und nach dem Satz von Poncelet-Steiner auch mit dem Lineal und einem vorgegebenen Kreis.
- ---
- Unmögliche Konstruktionen:
- Viele geometrische Figuren können nicht allein mit Zirkel und Lineal exakt konstruiert werden. Darunter sind die klassischen Probleme der antiken Mathematik:
- die Dreiteilung des Winkels,
- die Verdoppelung des Würfels,
- die Quadratur des Kreises.
BM1722

Lot von einem Punkt auf eine Gerade mit Lotfußpunkt - Lot
- ---
- Ein Lot ist in der Geometrie eine Strecke oder Gerade, die auf einer gegebenen Geraden oder Ebene senkrecht steht. Je nachdem, ob es sich um eine Gerade oder um eine Strecke handelt, spricht man auch von Lotgerade oder Lotstrecke. Der Schnittpunkt des Lots mit der gegebenen Geraden oder Ebene wird Lotfußpunkt genannt. Das Lot kann auf verschiedene Weisen mit Zirkel und Lineal geometrisch konstruiert werden.
- ---
- Definition:
- Eine Strecke oder Gerade heißt Lot auf eine Gerade , wenn
- gilt, wenn sie also senkrecht auf der Geraden oder Ebene steht und somit mit ihr einen rechten Winkel bildet. Der Lotfußpunkt ist dann der Schnittpunkt des Lots mit der Geraden.
BM1723
- Geometrische Konstruktionen des Lots
- ---
- In zwei Dimensionen lässt sich das Lot auf eine Gerade auf einfache Weise mit Zirkel und Lineal konstruieren. Je nachdem, ob ein gegebener Punkt auf der Geraden oder außerhalb liegt, spricht man vom Errichten oder vom Fällen des Lots.
- ---

Bild 1: Errichten eines Lots als Mittelsenkrechte zweier Punkte. - Errichten des Lots
- ---
- Ist ein Punkt auf der Geraden gegeben, dann findet man die Lotgerade durch diesen Punkt wie folgt:
- Man sticht den Zirkel in den Punkt ein und bestimmt durch Ziehen eines beliebigen Kreisbogens zwei Punkte auf mit gleichem Abstand von . Dann vergrößert man den Winkel des Zirkels, sticht ihn jeweils in einen der beiden gefundenen Punkte auf ein und findet durch Ziehen zweier Kreisbögen einen Punkt (von zwei möglichen) außerhalb der Geraden mit gleichem Abstand von den beiden Punkten. Die Gerade, die durch diesen Punkt und den gegebenen Punkt verläuft, ist dann die Lotgerade zu durch .
- ---

Bild 2: Errichten eines Lots mit Hilfe des Thaleskreises (siehe spätere Lektionen: „Satz des Thales“). Die Position des Punktes ist frei wählbar. - Eine Alternative, auf einer Geraden durch den Punkt mit eingeschränkten Platzverhältnissen ein Lot zu errichten, zeigt Bild 2. Die einfache Konstruktion lässt sich auf folgende Art und Weise beschreiben: Man schlägt um einen frei wählbaren Punkt (z. B. eine gedachte Linie von zu bildet mit der Geraden einen Winkel ca. 45°) einen Kreisbogen mit dem Radius , bis er die Gerade in schneidet. Es folgt das Zeichnen einer Linie ab durch , bis sie den Kreisbogen in schneidet. Die abschließende Linie, die durch und verläuft, ist dann die Lotgerade zu durch .
BM1724
- Fällen des Lots

Bild 1: Fällen des Lots - Ist ein Punkt außerhalb der Geraden gegeben, dann findet man das Lot durch auf wie folgt: Man sticht den Zirkel in den Punkt ein und bestimmt durch Ziehen eines Kreisbogens mit entsprechend großem Radius zwei Punkte auf mit gleichem Abstand von . Dann sticht man jeweils in einen der beiden gefundenen Punkte auf ein und findet durch Ziehen zweier Kreisbögen (mit hinreichend großem Radius) einen weiteren Punkt mit gleichem Abstand von den beiden Punkten. Die Gerade, die durch diesen Punkt und den gegebenen Punkt verläuft, ist dann die Lotgerade zu durch und der Schnittpunkt dieser Lotgeraden mit ist der Lotfußpunkt .
- ---

Bild 2: Alternative Methode zum Fällen des Lots - Eine alternative Konstruktion (Bild 2), von einem gegebenen Punkt das Lot auf eine Gerade zu fällen, besteht darin, den Zirkel an zwei beliebigen Punkten und auf der Geraden einzustechen und jeweils den Kreis, der durch den gegebenen Punkt verläuft, einzuzeichnen. Diese beiden Kreise schneiden sich dann in einem weiteren Punkt außerhalb der Gerade und die Linie die durch und verläuft, ist dann die Lotgerade durch . Diese Konstruktion kann auch für Spiegelungen benutzt werden.
BM1725
- Gegeben: Eine Gerade g und ein Punkt P außerhalb der Gerade.
- 1.) Zeichne um zwei verschiedene Punkte (A , B) der Geraden jeweils einen Bogen vom Punkt P auf die andere Seite.
- 2.) Der andere Schnittpunkt ist die Spiegelung P' des Punktes P an der Geraden.
- 3.) Verbinde die Punkte mit einer Geraden. Diese ist das Lot von P auf die Gerade g mit dem Fußpunkt F.
- Hinweis:
- Die in vielen Lehrbüchern dargestellte Konstruktion mit zwei gleichen Radien ist mathem. nicht notwendig und nur sinnvoll, wenn der Punkt so nahe an der Gerade liegt, dass die Konstruktion zu ungenau wird.
BM1726
- Errichten einer Senkrechten zu einer Geraden (Errichten des Lotes)
- ---

- Gegeben: Eine Gerade und ein Punkt auf der Geraden.
- 1.) Markiere mit dem Zirkel von dem Punkt aus zwei weitere Punkte mit gleichem Abstand zu auf der Geraden (, )
- 2.) Zeichne um diese Punkte jeweils einen Kreis mit größerem Radius als zuerst mit dem Zirkel abgetragen.
- 3.) Die Gerade durch und den Schnittpunkt der Kreise ist die Senkrechte zu im Punkt und die Mittelsenkrechte der Stecke .
BM1727

Die Parallele zu einer Geraden durch einen Punkt ist die Menge von Punkten, die alle den gleichen Abstand von haben. - Eigenschaften von Parallelen.
- SATZ:
- Sind zwei Geraden zueinander parallel, dann haben alle Punkte der einen Geraden den gleichen rechtwinkigen Abstand von der anderen Geraden.
- ---
- Beweis:
- Wir wählen zwei beliebige zueinander parallele Geraden und und auf zwei beliebige Punkte und .
- Wir fällen von und ein Lot auf und bezeichnen die Fußpunkte mit L1 und L2.
- Dann sind die Dreiecke und nach dem Kongruenzsatz (wsw) kongruent.
- Also gilt: .
- Die Punkte und haben also von denselben Abstand.
- w.z.b.w.
BM1728
- Gegeben: Eine Gerade und ein Abstand .
- 1.) In zwei beliebigen aber verschiedenen Punkten und der Gerade werden die Senkrechten und errichtet.
- 2.) Trage auf den Senkrechten (auf einer Seite der Gerade ) jeweils den Abstand ab.
- 3.) Die Gerade durch die so gefundenen Punkte und ist zu parallel und hat den Abstand
- ---
- Hinweis:
- Je länger die Strecke gewählt wird, desto genauer kann gezeichnet werden.
BM1729
- Gegeben: Eine Gerade und ein Punkt außerhalb von .
- ---
- Möglichkeit 1:
- Zeichne einen Bogen mit einem Radius um , welcher die Gerade in einem Punkt schneidet.
- Trage ab den Radius auf der Geraden ab (Punkt ).
- Zeichne einen Bogen mit dem Radius um , welcher den ersten Bogen in Punkt schneidet.
- Die Gerade durch und ist die Parallele.
- ---
- Möglichkeit 2:

Bild 2 - Zeichne einen unterbrochenen Kreisbogen um den auf der Geraden gewählten Punkt durch den Punkt mit dem Radius . Er schneidet die Gerade in den Punkten und .
- Zeichne einen Kreisbogen mit dem Radius , entspricht dem Abstand , um den Punkt bis er den Kreisbogen um in schneidet.
- Die Gerade durch und ist die Parallele.
- ---
- Möglichkeit 3 mit kollabierendem Zirkel:

Bild 3 - Zeichne einen Kreis um den auf der Geraden gewählten Punkt durch den Punkt . Er schneidet die Gerade im Punkt .
- Zeichne einen Kreis um den Punkt durch den Punkt .
- Zeichne einen Kreis um den Punkt durch den Punkt . Er schneidet den Kreis um in .
- Die Gerade durch und ist die Parallele.
BM1730

- Antragen eines Winkels in einem Punkt an eine Gerade
- ---
- Gegeben: Ein Winkel α und eine Gerade mit einem Punkt P darauf.
- 1.) Mit dem Zirkel in den Scheitelpunkt S des Winkels einstecken und einen Bogen durch beide Schenkel zeichnen (Punkte A und B).
- 2.) Den gleichen Bogen auch um den Punkt P der Geraden zeichnen. Es ergibt sich Punkt C .
- 3.) Den Zirkel auf den Abstand der beiden Punkte A und B einstellen und einen Bogen um C zeichnen.
- 4.) Die Schnittpunkte der beiden Kreise um P und C ergibt den möglichen Punkt D auf dem anderen Schenkel des Winkels.
- 5.) Es gibt durch zweifache Spiegelung vier (!) Möglichkeiten.
BM1731 - BM1740
[editar]BM1731
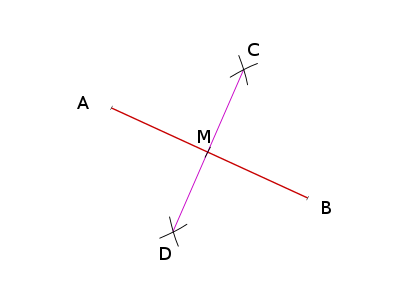
- Eigenschaften von Mittelsenkrechten
- ---
- SATZ:
- Wenn ein Punkt C auf der Mittelsenkrechten einer Strecke liegt, dann sind die Strecken und kongruent.
- ---
- Beweis:
- sei ein beliebiger Punkt der Mittelsenkrechten einer Strecke . Der Mittelpunkt der Strecke sei .
- Die Dreiecke und sind nach dem Kongruenzsatz kongruent.
- Welcher Kongruenzsatz?
- a) sws
- b) wsw
- c) sss
- d) ssw
Lösung BM1731 - a) sws (Seite ; Winkel ; Seite )
- ---
- Weiter mit dem Beweis:
- Also gilt: (denn in kongruente Deiecken sind alle 3 Seiten kongruent)
- w.z.B.w.
BM1732

Bild 1 - Diejenigen Punkte der Ebene, die nicht auf der Mittelsenkrechten einer Strecke liegen liegen, haben von und verschiedene Entfernungen.
- Für sie gilt deshalb NICHT die Kongruenz der Strecken und .
- ---
- Die Mittelsenkrechte einer Strecke ist also die Menge von Punkten, die jeweils von und gleich weit entfernt sind.
- ---

Bild 2 - Definition:
- Eine Gerade, deren Punkte von zwei zueinander parallelen Geraden denselben Abstand haben, nennt man Mittelparallele oder Mittellinie dieser parallelen Geraden.
-
BM1733

- Winkelhalbierende
- ---
- SATZ über die Winkelhalbierende:
- Wenn ein Punkt B auf der Winkelhalbierenden w eines Winkels liegt, dann hat er von den Schenkeln des Winkels gleichen Abstand.
- Formal kann man diesen Satz so formulieren:
- (Lies: B ist Element von w genau dann wenn gilt: die Strecke BC hat die gleiche Länge wie die Strecke BD.)
- ---
- Beweise diesen Satz!
1. Lösung BM1733 - 1.) Die Dreiecke und sind kongruent, denn dieser Fall lässt sich auf den Konkruenzsatz (wsw) zurückführen.
- ---
- Erläutere das bitte genauer!
- ---

- Umkehrung des obigen SATZES:
- Oben hatten wir den Satz formal folgendermaßen formulieren:
- Bisher haben wir aber nur folgenden SATZ bewiesen:
- Wir müssen noch die Umkehrung beweisen:
- .
- Nur dann kann der Pfeil in beide Richtungen zeigen. ()
- Man könnt sagen:
- Voraussetzung und Folgerung des obigen Satzes muss also vertauscht werden.
- Formuliere bitte, wie die Umkehrung des folgenden Satzes lauten muss!
- „Wenn ein Punkt B auf der Winkelhalbierenden w eines Winkels liegt, dann hat er von den Schenkeln des Winkels gleichen Abstand.“
3. Lösung BM1733 - Wenn ein Punkt B von den Schenkeln des Winkels den gleichen Abstand hat, dann liegt er auf der Winkelhalbierenden w dieses Winkels.
- ---
- Formal kann man diesen Satz so formulieren:
- (Lies:Wenn die Strecke BC die gleiche Länge wie die Strecke BD hat, dann ist B Element von w.)
- Den Pfeil nach rechts ließt man also als: „wenn ... dann...“
- Oder: „Wenn die Bedingung A zutrifft, dann folgt daraus, dass auch B zutrifft.“
- Oder auch: „Wenn A wahr ist, dann folgt daraus, dass auch B wahr ist.“
- Oder kürzer: „Wenn A, dann B wahr.“
- ---
- Wenn der Pfeil in beide Richtungen zeigt, dann bedeutet das, dass auch die Umkehrung zutrifft.
- Dann sagt man: „... genau dann wenn ...“
- Oder: „A gilt genau dann, wenn B.“
- Oder: „A gilt genau dann, wenn B gilt.“
- Oder auch: „A gilt dann und nur dann, wenn B.“
- Das unterscheidet sich eigentlich nicht wirklich von: A = B
- ---
- Beweise den SATZ:
- Wenn ein Punkt B von den Schenkeln des Winkels den gleichen Abstand hat, dann liegt er auf der Winkelhalbierenden w dieses Winkels.
BM1734
- Besondere Linien im Dreieck
- ---
- Mittelsenkrechte des Dreiecks

Bild 1 - Das Dreieck mit den drei Mittelsenkrechten auf den Seiten a, b und c.
- Die Mittelsenkrechte steht senkrecht auf der Seite a.
- ---

Bild 2 - Die Mittelsenkrechte steht senkrecht auf der Seite b.
- ---

Bild 3 - Die Mittelsenkrechte steht senkrecht auf der Seite c.
BM1735

Bild 1 - Die Mittelsenkrechten , und der Seiten , und eines Dreiecks nennt man Mittelsenkrechten des Dreiecks.
- ---
- SATZ:
- Die Mittelsenkrechten eines Dreiecks schneiden einander in einem Punkt.
- ---
- Wie würdest du diesen Satz beweisen?
BM1735
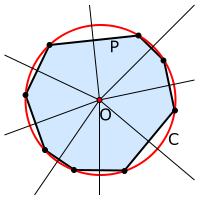
Bild 1 
Bild 2 
Bild 3 - Umkreis
- ---
- In der ebenen Geometrie ist ein Umkreis ein Kreis, der durch alle Eckpunkte eines Polygons (Vielecks) geht.
- Nicht für jedes Polygon existiert ein solcher Umkreis. Allgemein besitzt ein konvexes Polygon genau dann einen Umkreis, wenn die Mittelsenkrechten aller Seiten einander in einem Punkt schneiden. In diesem Fall ist der gemeinsame Punkt der Mittelpunkt des Umkreises.
- ---

Bild 4: Dreieck mit Mittelsenkrechten und Umkreis; U = Umkreismittelpunkt - Umkreis eines Dreiecks
- Definition: Es sei ein Dreieck. Ein Kreis, auf dem alle Eckpunkte von liegen, heißt Umkreis von .
- Eine besonders große Bedeutung hat der Umkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Umkreis, wie im Folgenden begründet wird.
- Alle Punkte der Mittelsenkrechten zu sind von und gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu übereinstimmende Entfernungen von und . Der Schnittpunkt dieser beiden Mittelsenkrechten ist also von allen drei Ecken (, und ) gleich weit entfernt. Er muss also auch auf der dritten Mittelsenkrechten liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.
- ---

Bild 5: Umkreis am rechtwinkligen Dreieck - Sonderfälle:
- Für spitzwinklige Dreiecke liegt der Umkreismittelpunkt im Inneren des Dreiecks. Beim rechtwinkligen Dreieck ist der Mittelpunkt der Hypotenuse (das ist die Seite, die dem rechten Winkel gegenüber liegt) zugleich Umkreismittelpunkt.
- ---

Bild 6: Umkreis am stumpfwinkligen Dreieck 
Bild 7: Umkreis am spitzwinkligen Dreieck - Im Falle eines stumpfwinkligen Dreiecks (mit einem Winkel über 90°) befindet sich der Umkreismittelpunkt außerhalb des Dreiecks.
BM1736

Bild 1 - Gegeben sind drei Punkte (Abb. 1).
- Zeichne einen Kreis, der durch alle drei Punkte geht!
- Wie würdest du vorgehen?
- Geht das überhaupt?
- Liegen diese drei Punkte auf einem Kreis?
2. Lösung BM1736
BM1737

Bild 1: Höhe des Dreiecks (rot) 
Bild 2 
Bild 3 
Bild 4: Die Höhe in einem gleichschenkligen Dreieck fällt mit der Mittelsenkrechten und der Winkelhalbierenden zusammen - Höhen des Dreiecks
- ---
- Die Lote , und von den Eckpunkten des Dreiecks auf die gegenüberliegenden Seiten , und oder deren Verlängerungen nennt man die Höhe des Dreiecks.
- Die Fußpunkte diese Lote heißen Höhenfußpunkte.
- Unter de Länge einer Höhe verstehen wir den Abstand des betreffenden Eckpunktes von der gegenüberliegenden Seite.
BM1738
- SATZ:
- Die Höhen eines Dreiecks schneiden einander in einem Punkt.
- ---
- Den Beweise für diesen Satz wollen wir mit Hilfe des bereits weiter oben bewiesenen Satzes („Die Mittelsenkrechten eines Dreiecks schneiden einander in einem Punkt.“) führen.
- Na, dann leg mal los!
- Hast du schon eine Idee?
- Streng mal deine grauen Zellen etwas an!
1. Lösung BM1738
- Zum Beweis, dass sich alle drei Höhen des Dreiecks in einem Punkt schneiden, zeichnet man die Parallelen zu den Dreiecksseiten durch die gegenüberliegenden Ecken, sodass ein größeres Dreieck entsteht. Je zwei der vier Teildreiecke des neuen Dreiecks bilden ein Parallelogramm.
- ---
- In einem Parallelogramm sind gegenüberliegende Seiten gleich lang. Daher sind die Seiten des neuen Dreiecks doppelt so lang wie die entsprechenden Seiten des ursprünglichen Dreiecks. Die Höhen des ursprünglichen Dreiecks stimmen daher mit den Mittelsenkrechten des neuen Dreiecks überein.
- ---
- Kannst du das bitte näher erklären! Schritt für Schritt, damit es jeder verstehen kann!
BM1739
- SATZ:
- Der Schnittpunkt der Mittelsenkrechten eines Dreiecks fällt mit dem Schnittpunkt seiner Höhen zusammen.
- ---
- Beweise diesen Satz!
BM1740

Bild 1 - Bild 1: In das Dreieck wurden die drei Winkelhalbierenden eingezeichnet. Sie treffen sich im einem Punkt (Z). Den Beweis dazu treten wir in einer späteren Übung an (s. u. BM1750).
- ---

Bild 2 - Bild 2: Wenn man einen Kreis mit dem Schnittpunkt der Winkelhalbierenden eines Dreiecks als Zentrum zeichnet (Z), dann erhält man einen Inkreis - wenn der Kreis den entsprechenden Radius hat.
- ---

Bild 3 - Bild 3: Wenn man einen Kreis mit dem Schnittpunkt der Mittelsenkrechten zeichnet (M; blau), dann erhält man den Umkreis. Der Umkreis geht durch alle drei Ecken des Dreiecks.
- ---
- Wenn man einen Kreis mit dem Schnittpunkt der Höhen im Dreieck zeichnet (P; rot), dann erhält man weder einen Innkreis noch einen Umkreis. Dafür kann man aber mit diesen Höhen die Fläche eines Dreiecks berechnen.
BM1741 - BM1750
[editar]BM1741

Bild 1: Seitenhalbierende (rot) und Mittelsenkrechte (blau) auf 
Bild 2: Seitenhalbierende (rot) und Mittelsenkrechte (blau) auf 
Bild 3: Seitenhalbierende (rot) und Mittelsenkrechte (blau) auf - Seitenhalbierende
- ---
- Eine Seitenhalbierende (auch Schwerlinie) in einem Dreieck ist eine Strecke, die eine Ecke des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
- ---
- Die Mittelsenkrechte dagegen beginnt zwar auch am Mittelpunkt einer Seite. Sie steht aber immer senkrecht auf dieser Seite und geht nicht zwangsläufig zur gegenüberliegenden Ecke.
- ---

Bild 4 - Die drei Seitenhalbierenden eines Dreiecks sind somit Schwerlinien und schneiden sich in einem Punkt (Q), dem so genannten Schwerpunkt des Dreiecks. (Für den Beweis s. u. Übbung BM1750)
- ---

Bild 5 - Dieser Schnittpunkt der Seitenhalbierenden (S = Schwerpunkt) teilt jede der Seitenhalbierenden im Verhältnis 2:1. Dabei ist die Strecke zwischen Schwerpunkt (S) und Ecke länger als die Strecke zwischen Schwerpunkt und Seitenmittelpunkt.
- ---
- Schwerpunkt:
- Würde man eine dreieckige Metallplatte am Schwerpunkt aufhängen, so würde sie waagerecht zum Boden „hängen“.
BM1742
- Erkläre den Unterschied zwischen:
- 1.) Winkelhalbierende
- 2.) Mittelsenkrechte
- 3.) Höhe
- 4.) Seitenhalbierende
Lösung BM1742 - 1.) Winkelhalbierende: Winkelhalbierende eines Winkels ist die Halbgerade, die durch den Scheitelpunkt des Winkels verläuft und das Winkelfeld in zwei deckungsgleiche Teile teilt.
- 2.) Mittelsenkrechte: Die Mittelsenkrechte ist eine Gerade, die senkrecht zu einer Strecke verläuft und diese Strecke in der Hälfte teilt.
- 3.) Höhe: Die Höhe im Dreieck ist die Strecke des Lots von einer Ecke auf die gegenüberliegende Dreiecksseite
- 4.) Seitenhalbierende: Eine Seitenhalbierende in einem Dreieck ist eine Strecke, die eine Ecke des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
- ---
- Ausgezeichnete Punkte im Dreieck = Besondere Punkte im Dreieck
- Ausgezeichnete Linien im Dreieck = Besondere Linien im Dreieck
- ---
- Alle vier ausgezeichneten Linien treffen sich jeweils in einem Punkt.
- 1.) Die Winkelhalbierenden treffen sich im Inkreismittelpunkt I (Schnittpunkt der Winkelhalbierenden).
- 2.) Die Mittelsenkrechten treffen sich im Umkreismittelpunkt U (Schnittpunkt der Mittelsenkrechten).
- 3.) Die Höhen treffen sich im Höhenschnittpunkt H (Schnittpunkt der Höhen).
- 4.) Die Seitenhalbierenden treffen sich im Schwerpunkt S (Schnittpunkt der Seitenhalbierenden).
BM1743
- Winkelhalbierende im Dreieck
- ---
- Ist in der Dreieckslehre von Winkelhalbierenden die Rede, so bezieht sich dieser Begriff meist auf die Innenwinkel, seltener auf die Außenwinkel.
- Für diese Winkelhalbierenden gelten unter anderem folgende Sätze:

Bild 1 
Bild 2 - Die drei Winkelhalbierenden (der Innenwinkel) eines Dreiecks schneiden sich in einem Punkt. Dieser Punkt ist der Mittelpunkt des Inkreises. (Das sind gleich zwei Aussagen, die wir weiter unten beweisen wollen.)
- Die drei Winkelhalbierenden (der Innenwinkel) eines Dreiecks schneiden sich in einem Punkt. Dieser Punkt ist der Mittelpunkt des Inkreises. (Das sind gleich zwei Aussagen, die wir weiter unten beweisen wollen.)
- ---

Bild 3 - Jede Winkelhalbierende im Dreieck teilt die gegenüberliegende Seite im Verhältnis der anliegenden Seiten. (Diese Aussage wird auch als Winkelhalbierendensatz bezeichnet. Die genauere Erklärung und der Beweis folgt weiter unten.)
- Jede Winkelhalbierende im Dreieck teilt die gegenüberliegende Seite im Verhältnis der anliegenden Seiten. (Diese Aussage wird auch als Winkelhalbierendensatz bezeichnet. Die genauere Erklärung und der Beweis folgt weiter unten.)
- ---

Bild 4 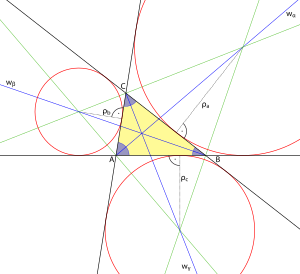
Bild 5 - Der Ankreise eines Dreiecks berührt eine Dreiecksseite und die Verlängerungen der beiden anderen Seiten. Es gibt insgesamt drei Ankreis am Dreieck. Die Mittelpunkte der Ankreise ergeben sich dadurch, dass man jeweils die Winkelhalbierende eines Innenwinkels mit den Winkelhalbierenden der nicht anliegenden Außenwinkel schneidet.
- ---
- Die Schnittpunkte der Außenwinkelhalbierenden mit den verlängerten Gegenseiten der entsprechenden Innenwinkel liegen, sofern sie existieren, auf einer Geraden.
- Die Schnittpunkte der Außenwinkelhalbierenden mit den verlängerten Gegenseiten der entsprechenden Innenwinkel liegen, sofern sie existieren, auf einer Geraden.
BM1744
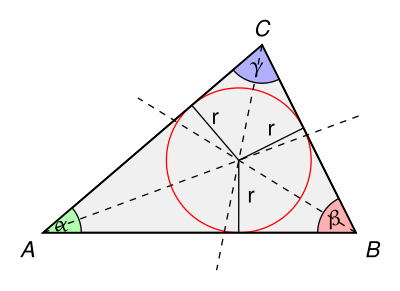
Dreieck mit Inkreis - Inkreis eines Dreiecks
- ---
- Eine besonders große Bedeutung hat der Inkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Inkreis, sein Mittelpunkt liegt im Schnittpunkt der drei Winkelhalbierenden. Zeichnet man um diesen Schnittpunkt einen Kreis, der eine Seite des Dreiecks berührt (die Seite wird somit eine Kreistangente des Inkreises), so berührt dieser Kreis auch die beiden anderen Seiten.
- Alle Punkte der Winkelhalbierenden des Innenwinkels haben den gleichen Abstand von den Seiten und . Entsprechend haben die Punkte der Winkelhalbierenden von den gleichen Abstand von und . Der Schnittpunkt dieser beiden Winkelhalbierenden hat also von allen drei Seiten des Dreiecks (, und ) gleichen Abstand. Er muss also auch auf der dritten Winkelhalbierenden liegen.
- Der Inkreis berührt alle drei Seiten von innen – im Gegensatz zu den drei Ankreisen, die jeweils eine Seite von außen und die Verlängerungen der beiden anderen Seiten berühren.
- Der Inkreismittelpunkt, also der Schnittpunkt der Winkelhalbierenden, zählt zu den ausgezeichneten Punkten des Dreiecks.
BM1745

Dreieck mit Ankreisen (rot) - Ankreis
- ---
- Die drei Ankreise gehören mit dem Umkreis und dem Inkreis zu den besonderen Kreisen eines Dreiecks, die schon in der Antike von griechischen Mathematikern untersucht wurden.
- Die Ankreise sind definiert als Kreise, die jeweils von einer Dreiecksseite von außen und von den Verlängerungen der beiden anderen Seiten tangential berührt werden. Jedes beliebige Dreieck besitzt drei Ankreise. Die Ankreismittelpunkte liegen jeweils auf der Winkelhalbierenden eines Innenwinkels und auf den Winkelhalbierenden der beiden Außenwinkel, die nicht zu dem Innenwinkel gehören.
- Die Ankreismittelpunkte des Dreiecks bilden ein Dreieck, dessen Höhenschnittpunkt der Inkreismittelpunkt des Dreiecks ist.
BM1746

Dreieck mit Mittelsenkrechten und Umkreis - Umkreis eines Dreiecks (Wiederholung)
- ---
- Eine besonders große Bedeutung hat der Umkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Umkreis, wie im Folgenden begründet wird.
- Alle Punkte der Mittelsenkrechten zu sind von und gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu übereinstimmende Entfernungen von und . Der Schnittpunkt dieser beiden Mittelsenkrechten ist also von allen drei Ecken (, und ) gleich weit entfernt. Er muss also auch auf der dritten Mittelsenkrechten liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.
- Der Umkreismittelpunkt, also der Schnittpunkt der Mittelsenkrechten, zählt zu den ausgezeichneten Punkten des Dreiecks.
BM1747

Höhenschnittpunkt - Höhenschnittpunkt
- ---
- Der Höhenschnittpunkt eines Dreiecks ist der Schnittpunkt seiner drei Höhen, d. h. der Lote zu den Dreiecksseiten durch die gegenüberliegenden Ecken. Der Höhenschnittpunkt ist einer der vier klassischen ausgezeichneten Punkte des Dreiecks.
- In der Skizze sind die Höhen mit [AHa], [BHb] und [CHc] bezeichnet. Ist das gegebene Dreieck ABC spitzwinklig, so befindet sich der Höhenschnittpunkt H innerhalb des Dreiecks. Hat das Dreieck dagegen einen stumpfen Winkel (also einen Winkel über 90°), so liegt H außerhalb. Im rechtwinkligen Fall schließlich stimmt H mit dem Scheitel des rechten Winkels überein.
BM1748
- Fagnano-Problem
- ---
- Das Fagnano-Problem ist das folgende nach Giovanni Fagnano benannte Optimierungsproblem.
- Bestimme das in ein spitzwinkliges Dreieck einbeschriebene Dreieck minimalen Umfangs.

- Bild 1: Höhenfußpunktdreieck:
einbeschriebene Dreiecke:
- Hierbei versteht man unter einem einbeschriebenen Dreieck eines Dreiecks ein Dreieck , dessen Ecken auf den Seiten Dreiecks liegen, das heißt , und . Für das Höhenfußpunktdreieck gilt, dass sein Umfang geringer ist als der eines jeden anderen einbeschriebenen Dreiecks und somit ist es die Lösung des Fagnano-Problems.
- Unter allen Dreiecken, die einem spitzwinkligen Dreieck einbeschrieben sind, hat das Höhenfußpunktdreieck den kleinsten Umfang.
- ---

Bild 2: Höhenfußpunktdreieck - Das Höhenfußpunktdreieck ist ein Begriff aus der Dreiecksgeometrie. Es entsteht dadurch, dass die Fußpunkte der drei Höhen (also die Punkte , und , in denen die Lote von den Ecken des Dreiecks auf die gegenüber liegenden Seiten diese Seiten schneiden) miteinander verbunden werden.
BM1749

- Feuerbachkreis
- ---
- Der Feuerbachkreis oder Neun-Punkte-Kreis ist ein besonderer Kreis im Dreieck, der nach Karl Wilhelm Feuerbach benannt ist. Auf ihm liegen neun ausgezeichnete Punkte:
- die Mittelpunkte der Seiten;
- die Fußpunkte der Höhen;
- die Mittelpunkte der oberen Höhenabschnitte (das sind die Mittelpunkte der Strecken zwischen jeweils einer Dreiecksecke und dem Höhenschnittpunkt des Dreiecks).
- Im Bild rechts sind D, E und F die Seitenmittelpunkte, G, H und I die Höhenfußpunkte, J, K und L die Mittelpunkte der oberen Höhenabschnitte und S der Höhenschnittpunkt.
BM1750

Bild 1 - Winkelhalbierende
- ---
- SATZ:
- Die Winkelhalbierenden eines Dreiecks schneiden einander in einem Punkt.
- ---
- Wie kann man das beweisen?
- índice
- Lección 084b ← Lección 085 → Lección 086b
- Lección 085


















































































































































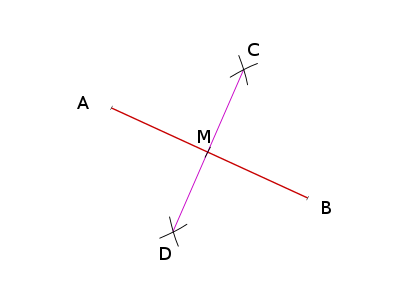































































![{\displaystyle [AB]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0)
![{\displaystyle [BC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)




































































![{\displaystyle [CA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45d1cad430fbae09064e436319693c011c68a748)



























