Curso de alemán para principiantes con audio/Lección 084b
Apariencia
- índice
- Lección 083b ← Lección 084 → Lección 085b
- Lección 084
- Mathematik auf Deutsch - 34
BM1651 - BM1660
[editar]BM1651

Scheitelwinkel - Scheitelwinkel
- ---
- Schneiden sich zwei Geraden, so bezeichnet man das Paar gegenüberliegender Winkel als Scheitelwinkel oder Gegenwinkel.
- Scheitelwinkel sind immer gleich groß.
- Die Bezeichnung Scheitelwinkel kommt daher, dass die beiden Winkel durch Punktspiegelung am Scheitelpunkt aufeinander abgebildet werden.
- ---
- Scheitelwinkel oder Gegenwinkel
- Zwei Winkel mit gemeinsamem Scheitel, deren Schenkel jeweils eine Gerade bilden, heißen Scheitelwinkel. jeder der beiden Winkel heißt der Scheitelwinkel des anderen.
- ---
- Sind zwei Winkel Scheitelwinkel, so ist der eine das Bild des anderen bei einer Drehung um den gemeinsamen Scheitel mit einem gestreckten Winkel (= 180°) als Drehwinkel
- Scheitelwinkel sind kongruent.
- ---

Bild 1 - Bild 1: Zwei Geraden schneiden sich.
- ---

Bild 2 - Bild 2: Die gegenüberliegenden Winkel dieser sich schneidenden Geraden sind Scheitelwinkel (Alpha und Beta)
- ---

Bild 3 - Bild 3: Auch die anderen beiden gegenüberliegenden Winkel sind Scheitelwinkel (hier im Bild: Alpha und Gamma). Alpha ist der Scheitelwinkel von Gamma und umgekehrt. Beta ist der Scheitelwinkel von Delta und umgekehrt.
BM1652

Nebenwinkel (hier: 45° + 135° = 180°) - Nebenwinkel
- ---
- Schneiden sich zwei Geraden, so bezeichnet man ein Paar benachbarter Winkel als Nebenwinkel.
- Nebenwinkel ergänzen sich zu .
- Sie sind also Supplementwinkel (= Ergänzungswinkel).
- ---
- Zeichne zwei Winkel, deren Winkel einen Schenkel haben und deren andere Schenkel eine Gerade bilden!
- ---
- Zwei Winkel, die einen Schenkel gemeinsam haben und deren anderer Schenkel eine Gerade bilden, heißen Nebenwinkel. Jeder der beiden Winkel heißt ein Nebenwinkel des anderen.
- Die Summe zweier Nebenwinkel beträgt 180°.
- ---
- rechter Winkel
- Ein Winkel ist eine rechter Winkel genau dann, wenn er einem seiner Nebenwinkel kongruent ist.
- ---

Bild 1 - Bild 1: Zwei Winkel, die einen Schenkel gemeinsam haben.
- ---

Bild 2 - Bild 2: Zwei Winkel, die einen Schenkel gemeinsam haben UND zusätzlich bilden die anderen Schenkel eine Gerade.
- ---

Bild 3 - Bild 3: Unter welchem Winkel sich die beiden Geraden schneiden ist unerheblich.
- ---

Bild 4 - Bild 4: Ob sich die Geraden schneiden oder nur aneinanderstoßen ist egal.
- ---

Bild 5 - Bild 5: Nebenwinkel gibt es bereits, wenn sich die Geraden nicht völlig schneiden.
- ---

Bild 6 - Bild 6: Alpha und Beta sind Nebenwinkel. Sie ergeben zusammen 180°.
- ---

Bild 7 - Bild 7: Ein Winkel ist eine rechter Winkel genau dann, wenn er einem seiner Nebenwinkel kongruent ist. Wir haben also zwei Nebenwinkel, die beide genauso groß sind. Da die Summe der nebenwinkel 180° ergibt, ist ein rechter Winkel genau halb so groß, also 90°. Der gemeinsame Schenkel der beiden rechten Winkel steht senkrecht (= rechtwinklig) auf der Geraden.
- ---

Bild 8 - Zähle alle möglichen Winkelkombinationen in Bild 8 auf! Wer ist alles Scheitelwinkel von wem? Welche Nebenwinkel haben sie?
Lösung BM1652 - Alpha und Gamma sind Scheitelwinkel. (= Alpha ist der Scheitelwinkel von Gamma. = Gamma ist der Scheitelwinkel von Alpha.)
- Beta und Delta sind Scheitelwinkel. (= Beta ist der Scheitelwinkel von Delta. = Delta ist der Scheitelwinkel von Beta.)
- ---
- Alpha ist der Nebenwinkel von Beta.
- Alpha ist der Nebenwinkel von Delta.
- Beta ist der Nebenwinkel von Alpha.
- Beta ist der Nebenwinkel von Gamma.
- Gamma ist der Nebenwinkel von Beta.
- Gamma ist der Nebenwinkel von Delta.
- Delta ist der Nebenwinkel von Alpha.
- Delta ist der Nebenwinkel von Gamma.
BM1653
-
Bild 1
-
Bild 2
-
Bild 3
- Bild 1: zwei Parallelen
- Bild 2: zwei Parallelen werden geschnitten
- Bild 3: zwei Linien (nicht parallel zueinander) werden geschnitten
- ---
- Wenn zwei Parallelen von einer dritten Linie geschnitten werden, dann gibt es Stufenwinkel und Wechselwinkel. Natürlich gibt es dann auch Scheitelwinkel und Nebenwinkel.
- Wir wollen auch den Fall untersuchen, dass die beiden Parallelen NICHT parallel zueinander verlaufen.
- ---
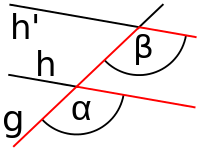
Bild 4: Stufen- oder F-Winkel 
Bild 5: Stufenwinkel - Stufenwinkel an geschnittenen Parallelen
- Schneidet eine Gerade zwei Geraden und , so heißen die Winkel, die auf derselben Seite von und auf einander entsprechenden Seiten von bzw. liegen, Stufen- oder F-Winkel.
- Für den Fall, dass die Geraden und parallel sind, gilt:
- Stufenwinkel an Parallelen sind gleich groß.
- Aus der Winkelgleichheit kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar , von einer weiteren Geraden so geschnitten, dass die Schnittwinkel auf derselben Seite von und auf einander entsprechenden Seiten von und gleich groß sind, so sind die Geraden und parallel.
- ---
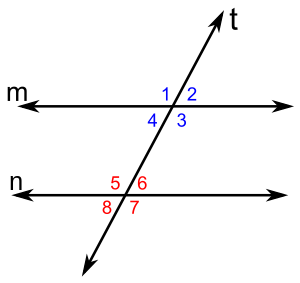
Bild 6 - Die Winkel 7 und 3 sind Stufenwinkel.
- Ebenso: 8 und 4
- 1 und 5
- 2 und 6.
BM1654
- Stufenwinkel
- ---
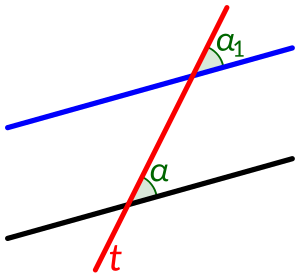
Bild 1 - Schneiden zwei Geraden einander, so entstehen Winkelpaare, die den Scheitel gemeinsam haben (Scheitelwinkel und Nebenwinkel).
- Schneidet eine Gerade zwei andere Geraden, so entstehen außerdem Winkelpaare, deren Winkel voneinander verschiedene Scheitel besitzen. Dabei darf die schneidene Gerade nicht durch den Schnittpunkt der geschnittenen Geraden gehen.
- (Mit anderen Worten: Die drei Geraden dürfen sich nicht in einem einzigen Punkt schneiden. Schließlich werden sich die beiden "fast" parallel zueinander liegenden Geraden irgendwo schneiden.)
- Bild 1: Die Schenkel der Winkel und , die auf der schneidenden Geraden (rot) liegen, sind gleich orientiert. Die Schenkel auf den geschnittenen Geraden (blau und schwarz) liegen auf derselben Seite der Geraden .
- ---
- Zwei Winkel an geschnittenen Geraden heißen Stufenwinkel, wenn sie folgende Eigenschaften besitzen:
- 1.) Sie haben verschiedenen Scheitel.
- 2.) Die Schenkel auf der schneidenden Geraden sind gleich orientiert.
- 3.) Die Schenkel auf der geschnittenen Geraden liegen auf derselben Seite der schneidenden Geraden.
- ---
- SATZ 1:
- Sind zwei Winkel Stufenwinkel und
- sind die geschnittenen Geraden zueinander parallel,
- so sind die beiden Winkel kongruent.
- ---
- In SATZ 1 wird vorausgesetzt, dass zwei Winkel Stufenwinkel und die geschnittenen Geraden zueinander parallel sind. Unter diesen Voraussetzungen wird behauptet, dass die beiden Winkel kongrunent sind.
- Wie eine Behauptung aufgestellt, so muss sie auch bewiesen werden.
- Zum Beweis werden bereits bekannte Eigenschaften oder Sätze bzw. Definitionen verwendet.
- ---
- Beweis von SATZ 1:

Bild 2 - und seien beliebige Stufenwinkel mit den Scheiteln und . Die geschnittenen Geraden (blau und schwarz) seien zueinander parallel.
- Bei der Verschiebung gilt:
- 1.) Die Gerade wird auf sich selber abgebildet.
- 2.) Die Gerade r ist das Bild der Geraden s.
- 3.) Der Scheitel B ist das Bild des Scheitels A.
- 4.) Die Schenkel des Winkels sind die Bilder der Schenkel des Winkels .
- Der Winkel ist also das Bild des Winkels .
- Also gilt: .
- w.z.b.w.
- Man geht also bei diesem Beweis davor aus, dass eine Kongruenzabbildung - z. B. Verschiebung - das Bild winkeltreu, flächenträu und längentreu mit dem Original ist. Dann wurde erläutert, dass die einzelnen Elemente des Winkels Bilder des anderen Winkels sind - also die beiden Schenkel und der Scheitelpunkt. Daraus kann man dann schließen, dass auch die beiden Winkel gleich groß sind.
- Wir erinnern uns, dass in der vorherigen Lektion in Übung BM1620 stand: "Punktspiegelungen sind geraden-, längen- und winkeltreu, also Kongruenzabbildungen." Das gilt auch für Verschiebungen. Und Abbildungen auf sich selber sind auch so etwas wie Verschiebungen.
- Wenn Dir das zu schnell und verwirrend war, dann lies die nächste Übung!
BM1655

- Stufenwinkelsatz
- ---
- Wir wollen nochmals die Gleichheit von Stufenwinkel beweisen.
- Der Stufenwinkelsatz ist ein mathematischer Satz. Er besagt: Wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß.
- Der Stufenwinkelsatz ist umkehrbar, d. h., es gilt: Werden zwei Geraden a und b von einer dritten Geraden c geschnitten und die Stufenwinkel sind gleich groß, so sind a und b parallel.
- ---

Bild 2: Beweis durch Widerspruch: α und β sind die Stufenwinkel - Beweis:
- Bewiesen wird die Umkehrung des Stufenwinkelsatzes, woraus der Beweis für den Stufenwinkelsatz selbst folgt.
- Seien dazu a und b zwei Geraden und schneide die Gerade c die Gerade a im Punkt A und die Gerade b im Punkt C. Weiterhin seien die als Stufenwinkel bezeichneten Winkel α und β gleich groß.
- Annahme des Widerspruchsbeweises: a und b sind nicht parallel. Folge:
- Es existiert also ein Schnittpunkt B der Geraden a und b, sodass ein Dreieck ABC existiert. Nach dem Nebenwinkelsatz ist der Innenwinkel von C = γ = 180° – β. Dann ist
- γ + α = 180° – β + α = 180°, da nach Voraussetzung β = α
- Daraus folgt für den Innenwinkel δ am Punkt B des Dreiecks ABC:
- δ = 180° – (γ + α) = 180° – 180° = 0°.
- Das heißt jedoch, dass gar kein Schnittpunkt von den Geraden a und b existiert; Widerspruch zur Annahme, was zu beweisen war.
- ---
- Wahrscheinlich war dieser Beweis noch verwirrender, als in der vorherigen Übung, da wir noch nicht den Beweis durch Widerspruch (= Widerspruchsbeweis) behandelt haben. Das holen wir in der nächsten Übung nach.
BM1656
- Widerspruchsbeweis
- (Beweis durch Widerspruch)
- ---
- Reductio ad absurdum
- ---
- Die Reductio ad absurdum (von lat. für Zurückführung auf das widrig Klingende, Ungereimte, Unpassende, Sinnlose) ist eine Schlussfigur und Beweistechnik in der Logik. Bei der Reductio ad absurdum wird eine Aussage widerlegt, indem gezeigt wird, dass aus ihr ein logischer Widerspruch oder ein Widerspruch zu einer bereits anerkannten These folgt.
- Als Beweistechnik ist die reductio ad absurdum unter der Bezeichnung „indirekter Beweis“ oder „Widerspruchsbeweis“, „Beweis durch Widerspruch“ bekannt. Dieser indirekte Beweis ist dadurch gekennzeichnet, dass man die zu beweisende Aussage nicht direkt herleitet, sondern dass man ihr kontradiktorisches Gegenteil (d. h. die Annahme, dass die Aussage nicht zutreffe) widerlegt. In der klassischen, zweiwertigen Logik, in der jede Aussage entweder wahr oder falsch ist, ist mit diesem Widerlegen des Gegenteils einer Aussage gezeigt, dass die betroffene Aussage korrekt ist.
- ---
- Erläuterung:
- Ein einfaches Beispiel: Um zu zeigen, dass nicht alle Menschen Griechen sind, wird zunächst das genaue Gegenteil angenommen, nämlich dass alle Menschen Griechen seien. Aus dieser Annahme folgt zum Beispiel, dass Cicero ein Grieche war. Es ist aber bekannt, dass Cicero kein Grieche war (sondern Römer). Dass Cicero aber zugleich sowohl ein Grieche als auch kein Grieche war, ist ein Widerspruch. Damit wurde die Aussage, dass alle Menschen Griechen sind, auf einen Widerspruch zurückgeführt (reductio ad absurdum) und so gezeigt, dass nicht alle Menschen Griechen sind.
- Widerspruch herleiten lässt, gilt: Wenn die Annahme wahr ist, ist auch der Widerspruch wahr. Ein Widerspruch kann aber niemals wahr sein. Die Annahme kann daher nicht wahr sein, muss also falsch sein.
BM1657

- Wechselwinkel an geschnittenen Parallelen
- ---
- Wechselwinkel oder Z-Winkel
- Schneidet eine Gerade zwei Geraden und , so heißen die Winkel, die auf unterschiedlichen Seiten von und entgegengesetzten Seiten von bzw. liegen, Wechsel- oder Z-Winkel. Für den Fall, dass die Geraden und parallel sind, gilt:
- Wechselwinkel an Parallelen sind gleich groß.
- Aus der Winkelgleichheit kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar , von einer weiteren Geraden so geschnitten, dass die Schnittwinkel auf unterschiedlichen Seiten von und unterschiedlichen Seiten von bzw. gleich groß sind, so sind die Geraden und parallel.
- ---
- Die Schenkel der Winkel und , die auf der Geraden liegen, sind entgegengesetzt orientiert. Die Schenkel auf den geschnittenen Geraden und liegen auf verschiednen Seiten der Geraden .
- ---
- Zwei Winkel an geschnittenen Geraden heißen Wechselwinkel, wenn sie folgende Eigenschaften besitzen:
- 1.) Sie haben verschiedenen Scheitel (=Scheitelpunkte)
- 2.) Die Schenkel auf der schneidenden Geraden sind entgegengesetzt orientiert.
- 3.) Die Schenkel auf der geschnittenen Geraden liegen auf verschiedenen Seiten der schneidenden Geraden.
- ---

Bild 2 
Bild 3 
Bild 4 - SATZ:
- Sind zwei Winkel Wechselwinkel
- und sind die geschnittenen Geraden zueinander parallel,
- so sind die beiden Winkel kongruent. (= gleich groß)
- ---
- Beweis:
- und seien zwei beleibige Wechselwinkel mit den Scheiteln A und B. Die geschnittene Geraden und seien zueinander parallel.
- Dann ist das Bild von bei einer Bewegung, sie sich
- 1.) aus der Verschiebung und
- 2.) aus der Drehung um B mit einem gestreckten Winkel als Drehwinkel zusammensetzt.
- Also gilt
- w.z.b.w.
BM1658
- Doppelbruch
- ---
- Ein Doppelbruch ist in der Mathematik ein Term, bei dem ein Bruch (Beispiel: ein Fünftel) durch einen weiteren Bruch geteilt wird. Es ist möglich, statt des üblichen Zeichens für Division einen weiteren Bruchstrich zu schreiben, bei dem Zähler und Nenner wiederum Brüche sind. Doppelbrüche lassen sich durch Erweitern mit einem geeigneten Faktor vereinfachen:
- Hinweis: Dies gilt nur für , denn durch darf nicht dividiert werden.
- Folgende Regel ist bekannter und einfacher zu verstehen: Doppelbrüche werden vereinfacht, indem man den Zählerbruch mit dem Kehrwert des Nennerbruchs multipliziert:
- mit .
- Im ersten Beispiel ist ein Bruch mit dem Nenner 1 :
BM1659
- Division von Brüchen
- ---
- Durch einen Bruch wird dividiert, indem man mit seinem Kehrwert multipliziert.
- Beispiel: .
- Dabei dürfen, wie im Beispiel dargestellt, Zwischenergebnisse gekürzt werden (hier beispielsweise die 3 und die 2 im vorletzten Schritt).
- ---
- 1.)
- 2.)
- 3. )
BM1660

Bild 1 - ---

Bild 2 
Bild 3 
Bild 4 - Erkläre anhand der nebenstehenden Abbildungen die Definition des Wechselwinkels!
BM1661 - BM1670
[editar]BM1661
BM1662

Bild 1: Nach der amerikanischen Schreibweise werden rechte Winkel mit einem kleinen Quadrat gekennzeichnet, üblicherweise aber nicht mit Farbe ausgefüllt, wie hier im Bild. - Zwei Parallelen, die im rechten Winkel geschnitten werden. Hier sind Nebenwinkel, Scheitelwinkel, Stufenwinkel und Wechselwinkel alle 90°. Das ist einfach.
- Aber wofür brauch man den ganzen Quatsch mit Stufenwinkeln, Scheitelwinkeln und Nebenwinkeln?
- Für kompliziertere Sachen, wie sie z. B. in Bild 2 bis 6 zu sehen sind.
-
Bild 2
-
Bild 3
-
Bild 4
-
Bild 5

Bild 6 - Bild 6: Sogar in Indien lernt man das. Es kann also nicht ganz unnütz sein. Das gehört zu den Grundlagen der Geometrie, auf die später viele geometrische Beweise aufbauen.
BM1663
1. Lösung BM1663
2. Lösung BM1663
3. Lösung BM1663
BM1664
1. Lösung BM1664 - Alpha und Delta-Eins sind entgegengesetzt liegende Winkel.
- Das hatten wir noch nicht.
2. Lösung BM1664 - Alpha 1 und Gamma sind Wechselwinkel.
3. Lösung BM1664 - Scheitelwinkel-Paare sind: Alpha und Gamma; Alpha 1 und Gamma 1; Beta und Delta; Beta 1 und Delta 1
- Stufenwinkel-Paare sind: Alpha und Alpha 1; Beta und Beta 1; Gamma und Gamma 1; Delta und Delta 1
- Wechselwinkelpaare sind: Alpha und Gamma 1; Beta und Delta 1; Gamma und Alpha 1; Delta und Beta 1
- Nebenwinkel sind:
- Alpha und Beta; Beta und Gamma; Gamma und Delta; Delta und Alpha
- Alpha 1 und Beta1 ; Beta 1 und Gamma1 ; Gamma 1 und Delta1 ; Delta 1 und Alpha 1
4. Lösung BM1664 - Alpha und Gamma sind Scheitelwinkel.
5. Lösung BM1664 - Alpha und Gamma 1 sind Wechselwinkel.
BM1665

- Wie viel mögliche Winkelpaare können aus 8 Winkeln gebildet werden? (Die Reihenfolge kann dabei unberücksichtigt bleiben.) Erkläre zu jedem Winkelpaar in welcher Beziehung sie stehen!
Lösung BM1665 - Winkel 1 kann ein Paar mit den übrigen 7 Winkeln bilden. So kommt Winkel 1 auf 7 mögliche Winkelpaare. Winkel 1-1 macht keinen Sinn.
- 1-2; 1-3; 1-4; 1-5; 1-6; 1-7 und 1-8.
- Winkel 2 kann auch ein Paar mit den übrigen 7 Winkeln bilden. Allerdings ist der Winkel 2-1 identisch mit dem Winkel 1-2 aus der Zeile davor. Wir lassen dieses Winkelpaar also weg, denn das haben wir schon. Folglich bildet Winkel 2 nur noch 6 Winkelpaare mit den übrigen Winkeln. Auch Winkel 2-2 macht keinen Sinn.
- 2-3; 2-4; 2-5; 2-6; 2-7 und 2-8
- Winkel 3 kann auch ein Paar mit den übrigen 7 Winkeln bilden. Allerdings ist Winkel 3-1 identisch mit 1-3 aus der ersten Zeile. Und Winkel 3-2 ist identisch mit Winkel 3-2 aus der zweiten Zeile. Wir lassen diese Winkelpaare also weg, weil sie schon weiter oben abgedeckt sind. So kommen wir nur noch auf 5 Winkelpaare mit dem Winkel 3. Acuh Winkel 3-3 macht keinen Sinn.
- 3-4; 3-5; 3-6; 3-7; 3-8
- Winkel 4 ergibt nach dem gleichen Schema nur noch 4 mögliche Winkelpaare: 4-5; 4-6; 4-7; 4-8
- Winkel 5 ergibt 3 mögliche Winkelpaare.
- Winkel 6 ergibt 2 mögliche Winkelpaare: 6-7; 6-8
- Winkel 7 ergibt nur noch ein mögliches Winkelpaar: 7-8
- Winkel 8 haben wir schon in allen oberen Zeilen abgearbeitet.
- ---
- Wir haben also insgesamt
- 7+6+5+4+3+2+1=28 unterschiedliche Winkelpaare.
- Nun müssen wir nur noch für jedes Winkelpaar die Beziehung bestimmen:
- Scheitelwinkel, Stufenwinkel; Wechselwinkel, Nebenwinkel und entgegengeetzte Winkel
BM1666
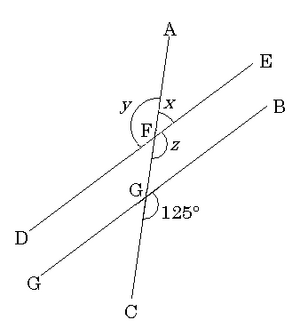
1. BM1666 - Winkel z ist ein Stufenwinkel zu dem Winkel, der mit 125° angegeben wird. Da beide Winkel identisch sind, ist Winkel . Winkel x ist der Nebenwinkel von z.
- also also also .
- y ist ein Stufenwinkel von dem vorgegebenen 125°-Winkel. Also
- Zur Kontrolle: müsste 180° ergeben, denn sie sind Nebenwinkel.
- Auch das stimmt.
2. Lösung BM1666 - Wechselwinkel
BM1667

Bild 1 - Winkel mit paarweise rechtwinkligen Schenkeln
- ---
- Winkel mit paarweise senkrecht aufeinanderstehenden Schenkeln
- Zwei Winkel, deren Schenkel paarweise senkrecht aufeinander stehen, sind gleich groß.
- ---

Bild 2 - Das trifft aber nicht zu, falls der Scheitel des einen Winkels im Inneren des anderen Winkels liegt.
- Diese beiden Winkel ergänzen sich zu . Vergleiche nebenstehende Abbildung.
- Die Winkelsumme im Dreieck beträgt 360°. Wir haben in diesem Viereck zwei rechte Winkel, also 180°. Folglich ergeben die übrigen beiden Winkel (Alpha und Beta) zusammen 180°.
- Also: Die Winkel Alpha und Beta ergänzen sich zu .
BM1668

Bild 1 - Gegeben sind zwei Winkel Alpha und Beta, deren Schenkel paarweise senkrecht aufeinander stehen.
- Beweise, dass diese beiden Winkel deshalb gleich groß sein müssen!
BM1669
- Nachbarwinkel oder E-Winkel
- Entgegengesetzt liegende Winkel an geschnittenen Parallelen
- ---

Nachbar- oder E-Winkel - Schneidet eine Gerade zwei weitere parallele Geraden und , so bezeichnet man die Winkel, die auf derselben Seite von , aber auf unterschiedlichen Seiten von und liegen, als Nachbar- oder E-Winkel.
- Nachbarwinkel ergänzen sich zu .
- Aus der Ergänzung der Winkel zu kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar , von einer weiteren Geraden so geschnitten, dass sich die Schnittwinkel, die auf derselben Seite von , aber jeweils auf unterschiedlichen Seiten von und liegen, zu 180° ergänzen, so sind die Geraden und parallel.
- Die Eigenschaft, dass sich Nachbarwinkel zu ergänzen, folgt direkt aus dem Parallelenaxiom (s. nächste Übung) der euklidischen Geometrie. Die oben genannten Eigenschaften von Stufen- und Wechselwinkeln lassen sich aus der Betrachtung von Neben- und Scheitelwinkeln von Nachbarwinkeln herleiten.
BM1670
- Parallelenaxiom
- ---
- Das Parallelenaxiom ist ein viel diskutiertes Axiom der euklidischen Geometrie. In einer häufig gebrauchten, auf John Playfair zurückgehenden Formulierung besagt es:
- In einer Ebene gibt es zu jeder Geraden und jedem Punkt außerhalb von genau eine Gerade, die zu parallel ist und durch den Punkt geht.
- „Parallel“ bedeutet dabei, dass die Geraden in einer Ebene liegen, aber keinen gemeinsamen Punkt haben.
- Diese eindeutig bestimmte Gerade heißt die Parallele zu durch den Punkt .

Schnittpunkt S von h und k, wenn α+β<180°.
- In den Elementen des Euklid findet sich dieser Satz als das fünfte Postulat (Parallelenpostulat) in folgender Formulierung: „Gefordert soll sein: … dass, wenn eine gerade Linie [] beim Schnitt mit zwei geraden Linien [ und ] bewirkt, dass innen auf derselben Seite entstehende Winkel [ und ] zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien [ und ] bei Verlängerung ins Unendliche sich treffen auf der Seite [von ], auf der die Winkel [ und ] liegen, die zusammen kleiner als zwei Rechte sind.“
- Dies besagt in moderner Formulierung, dass es zu jeder Geraden und jedem Punkt nicht mehr als eine Parallele zu durch geben kann. Dass es mindestens eine solche Parallele gibt, lässt sich aber aus den übrigen Postulaten und Axiomen des Euklid beweisen, sodass die eingangs angegebene Formulierung gerechtfertigt ist.
- Die Benennung des Parallelenpostulats schwankt in der Literatur. Häufig wird es das Fünfte Postulat von Euklid (Elemente, Buch 1) genannt, manchmal wurde es aber auch 11. Axiom oder 13. Axiom genannt.
BM1671 - BM1680
[editar]BM1671

Bild 1 - Nachbarwinkel oder E-Winkel
- Entgegengesetzt liegende Winkel an geschnittenen Parallelen
- ---
- Die Schenkel der Winkel und , die auf der schneidenden Geraden g liegen, sind entgegengesetzt orientiert. Die Schenkel auf den geschnittenen Geraden liegen auf derselben Seite der Geraden g.
- ---
- Zwei Winkel an geschnittenen Geraden heißen entgegengesetzt liegende Winkel (Nebenwinkel), wenn sie folgende Eigenschaften besitzen:
- 1.) Sie haben verschiedene Scheitel.
- 2.) Die Schenkel auf der schneidenden Geraden sind entgegengesetzt orientiert.
- 3.) Die Schenkel auf den geschnittenen Geraden liegen auf derselben Seite der schneidenden Geraden.
- ---
- SATZ:
- Sind zwei Winkel entgegengesetzt liegende Winkel und
- sind die geschnittenen Geraden zueinander parallel,
- so betragen die beiden Winkel zusammen 180°.
- ---

Bild 2 - Beweis:
- und seien zwei beliebige entgegengesetzt liegende Winkel mit den Scheiteln A und B. Die geschnittenen Geraden a und b seien zueinander parallel.
- Bei der Verschiebung ist der Winkel das Bild des Winkels .
- Der Winkel ist Nebenwinkel des Winkels .
- Die Summe der Winkel und beträgt .
- Da und kongruent und damit gleich groß sind, betragen auch die Winkel und zusammen .
- w.z.b.w.
BM1672
- Schneidet eine Gerade zwei andere Geraden, die nicht parallel zueinander liegen, dann haben wir auch solche Winkel, wie bei zwei "Parallelen", die geschnitten werden.
- ---

Bild 1 - Bild 1: Stufenwinkel
- ---

Bild 2 - Bild 2: Wechselwinkel
- ---

Bild 3 - Bild 3: Nebenwinkel (entgegengesetzt liegende Winkel)
- ---

Bild 4 - Bild 4: Nebenwinkel (entgegengesetzt liegende Winkel)
BM1673
- Umkehrung (Teil 1)
- ---

Bild 3 - In dem Satz
- „Wenn ein rechter Winkel ist, dann ist einem seiner Nebenwinkel kongruent.“
- wird vorausgesetzt, dass ein rechter Winkel ist, und behauptet, dass einem seiner Nebenwinkel kongruent ist.
- ---
- Wir vertauschen Voraussetzung und Behauptung und erhalten die
- Umkehrung des Satzes.
- „Wenn einem seiner Nebenwinkel kongruent ist, dann ist ein rechter Winkel.“
- ---
- Wir können uns den Zusammenhang zwischen einem Satz und seiner Umkehrung des Satzes wie folgt veranschaulichen:
| Voraussetzung | Behauptung | |
|---|---|---|
| SATZ | ein rechter Winkel | ist einem seiner Nebenwinkel kongruent |
| Umkehrung | ist einem seiner Nebenwinkel kongruent | ein rechter Winkel |
BM1673

Bild 1 - Umkehrung (Teil 2)
- ---
- Die Summe zweier Nebenwinkel beträgt 180°.
- ---
- Wir können ihn auch so formulieren:
- „Wenn und Nebenwinkel sind, dann beträgt ihre Summe .“
- ---
- Die Umkehrung des Satzes lautet:
- „Wenn die Summe der Winkel und beträgt, dann sind und Nebenwinkel.“
| Voraussetzung | Behauptung | |
|---|---|---|
| SATZ | und sind Nebenwinkel | |
| Umkehrung | und sind Nebenwinkel |
- ---

Bild 2 - Die Umkehrung des Satzes ist nicht wahr. Es gibt nämlich Winkel und , deren Summe zwar 180° beträgt, die aber keine Nebenwinkel sind. (Bild 2)
- Mit anderen Worten: Es gibt Winkel, für die die Umkehrung nicht zutrifft.
- ---
- Die Umkehrung eines Satzes ist also nicht immer auch ein Satz. Deshalb muss stets überprüft werden, ob die Umkehrung eines Satzes gilt.
BM1674

Bild 1: Stufenwinkel 
Bild 2: Wechselwinkel 
Bild 3: Scheitelwinkel - Es gibt Sätze mit mehreren Voraussetzungen. Zu solchen Sätzen gibt es mehrer Umkehrungen.
- ---
- SATZ:
- Sind zwei Winkel Stufenwinkel und sind die geschnittenen Geraden zueinander parallel, so sind die beiden Winkel kongruent.
- ---
- 1. Umkehrung:
- Sind zwei Winkel an geschnittenen Parallelen kongruent, so sind die beiden Winkel Stufenwinkel.
- (Diese Umkehrung trifft NICHT zu, denn es könnten auch Wechselwinkel oder Scheitelwinkel sein.)
- ---
- 2. Umkehrung:
- Sind zwei Stufenwinkel kongruent, so sind die geschnittenen Geraden zueinander parallel.
- (Diese Umkehrung, die für den Nachweis der Parallelität zweier Geraden verwendet werden, lässt sich beweisen. Auf den Beweis verzichten wir an dieser Stelle.)
BM1675
- Ergänze die Sätze!
- ---
- 1.) Schneiden zwei Geraden einander, entstehen ...winkel und ...winkel.
- 2.) Scheitelwinkel sind ...
- 3.) Nebenwinkel betragen zusammen ...
- 4.) Werden zwei Geraden von einer dritten geschnitten, so entstehen ...winkel, ...winkel und entgegengesetzt liegende Winkel.
- 5.) An geschnittenen Parallelen sind Stufenwinkel und Wechselwinkel ...
- 6.) Entgegengesetzt liegende Winkel betragen zusammen ...
Lösung BM1675 - 1.) Schneiden zwei Geraden einander, entstehen Scheitelwinkel und Nebenwinkel.
- 2.) Scheitelwinkel sind kongruent.
- 3.) Nebenwinkel betragen zusammen 180°.
- 4.) Werden zwei Geraden von einer dritten geschnitten, so entstehen Stufenwinkel, Wechselwinkel und entgegengesetzt liegende Winkel.
- 5.) An geschnittenen Parallelen sind Stufenwinkel und Wechselwinkel kongruent.
- 6.) Entgegengesetzt liegende Winkel betragen zusammen 180°.
BM1676
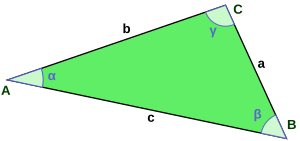
Bild 1 - Dreieck
- ---
- In einem Dreieck seien die Winkel mit , , und die Seiten mit , , , wie in Bild 1, bezeichnet.
- ---
- Dem Winkel liegt die Seite gegenüber.
- Der Winkel und die Seite liegen sich gegenüber.
- Der Seite liegt der Winkel gegenüber.
- ---
- Der Seite liegen die Winkel und an.
- Am Winkel liegen die Seiten und an.
- Der gegenüberliegende Winkel von Seite ist der Winkel .
- ---

Bild 2 - Nebenwinkel
- Wir in einem Dreieck z. B. die Seite über den Eckpunkt hinaus verlängert, so entsteht ein Nebenwinkel der Winkels . (Bild 2)
- Dieser Nebenwinkel heißt Außenwinkel des Dreiecks .
- ---
- Wie viel Außenwinkel kann man an einem Dreick antragen?
- Wie viel Innenwinkel hat ein Dreieck?
Lösung BM1676
BM1677

Bild 1 - Bild 1: Dreiecke, in denen alle drei Seiten gleich lang sind, nennt man gleichseitige Dreiecke.
- ---

Bild 2 - Bild 2: Dreiecke, in denen zwei Seiten gleich lang sind, nennt man gleichschenklige Dreiecke.
- ---
- Jedes Dreieck das gleichseitig ist, ist auch gleichschenklig.
- Ist die Umkehrung dieses Satzes wahr?
1. Lösung BM1677 - Jedes Dreieck das gleichseitig ist, ist auch gleichschenklig.
- Unkehrung:
- Jedes Dreieck das ist gleichschenklig, ist auch gleichseitig .
- Die Umkehrung dieses Satzes ist nicht wahr.
- Ergänze den folgenden Satz und zeichne das Mengendiagramm dazu! Beschreibe mit eigenen Worten, wie das Mengendiagramm dazu aussieht!
- Die Menge aller gleich... Dreiecke ist die Teilmenge aller gleich... Dreiecke, d. h. jedes gleich... Dreieck ist auch gleich...
2. Lösung BM1677

Bild 4 - Die Menge aller spitzwinkligen Dreiecke, die Menge aller rechtwinkigen Dreiecke und die Menge aller stumpfwinkligen Dreiecke besitzen kein gemeinsames Element. Solche Menge nennt man disjunkte Mengen. Sie haben keine Schnittmenge. Oder genauer: Die Schnittmengen dieser Mengen sind leer, d. h. sie enthalten keine Element.
BM1678
- Einteilung der Dreiecke
- ---
- Man kann Dreiecke nach Seiten oder nach Winkeln einteilen.
- einteilen; Einteilung
- klassifizieren; Klassifizierung
- ordnen; Ordnung
- unterscheiden; Unterscheidung
- ---
- Die Einteilung der Dreiecke nach Seiten erfolgt in: unregelmäßige, gleichschenklige und gleichseitig Dreiecke.
- Die Einteilung der Dreiecke nach Winkeln erfolgt in: spitzwinklig, rechtwinklig und stumpfwinklig.
- ---
- Einteilung der Dreiecke nach Seiten
- In einem unregelmäßigen Dreieck sind die Seiten paarweise verschieden lang.
- Ein gleichschenkliges Dreieck hat ein Paar gleich langer Seiten.
- In einem gleichseitigen Dreieck sind alle Seiten gleich lang.
- ---
- In einem spitzwinkligen Dreieck sind alle Winkel spitz. (ODER: Ein spitzwinkliges Dreieck hat nur spitze Winkel.)
- In einem rechtwinkligen Dreieck ist ein Winkel 90°. (ODER: In einem rechtwinkligen Dreieck ist ein Winkel ein rechter Winkel. ODER AUCH: Ein rechtwinkliges Dreieck hat einen rechten Winkel.)
- In einem stumpfwinkligen Dreieck ist ein Winkel stumpf. (Anmerkung: Die anderen beiden Winkel sind spitz, weswegen es aber trotzdem nicht als spitzwinkliges Dreieck bezeichnet wird.)
- ---
-
Bild 1
-
Bild 2
-
Bild 3
-
Bild 4
-
Bild 5
-
Bild 6
-
Bild 7
-
Bild 8
-
Bild 9
- Was für Dreiecke sind das? Hinsichtlich der Einteilung nach Seiten und in Bezug auf die Einteilung nach Winkeln.
- ---
- In einem stumpfwinkligen Dreieck gibt es auch spitze Winkel. Es hat nur einen stumpfen Winkel.
- In einem spitzwinkligen Dreieck gibt es keinen stumpfen Winkel. Die anderen beiden Winkel sind auch spitz. Evtl. ist einer der Winkel ein rechter Winkel.
BM1679
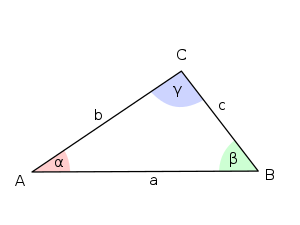
Bild 1 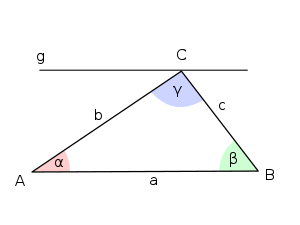
Bild 2 - SATZ:
- In jedem Dreieck beträgt die Summe der Innenwinkel 180°.
- ---
- Die Summe der Innenwinkel in einem ebenen Dreieck beträgt immer 180°.
- Beweis: Wir zeichnen parallel zu einer Seite eine Gerade durch den gegenüberliegenden Punkt. (Bild 2)
- Beweise mit Hilfe von Bild 2, dass die Innenwinkelsumme im Dreieck 180° beträgt!
1. Lösung BM1679
2. Lösung BM1679
4. Lösung BM1679
BM1680

Dreieck - Dreiecksungleichung
- ---
- Die Gesamtlänge zweier Seiten eines Dreiecks ist immer größer als die Länge der dritten Seite. Diese Beziehungen lassen sich in der so genannten Dreiecksungleichung ausdrücken.
- Nach der Dreiecksungleichung ist im Dreieck die Summe der Längen zweier Seiten a und b stets mindestens so groß wie die Länge der dritten Seite c. Das heißt formal:
- Man kann auch sagen, der Abstand von A nach B ist stets höchstens so groß wie der Abstand von A nach C und von C nach B zusammen, oder um es populär auszudrücken: „Der direkte Weg ist immer der kürzeste.“
BM1681 - BM1690
[editar]BM1681

- Hier noch eine leicht abgewandelte Version für den Beweis der Innenwinkelsumme im Dreieck.
- Kannst du den Beweis erläutern?
Lösung BM1681 - Eine Hilfslinie (gestrichelt) ist die Verlänger und der Seite c.
- Die andere gestrichelte Hilfslinie ist eine Parallele zur Seite a und verläuft durch A.
- (drei Nebenwinkel; gestreckter Winkel)
- und sind kongruent, da sie Stufenwinkel an Parallelen sind. ()
- und sind kongruent, da sie Wechselwinkel an Parallelen sind.
- w.z.b.w.
BM1682
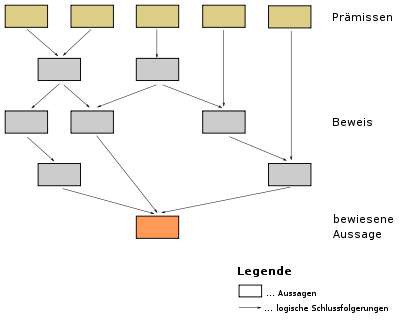
Beispielhafter, schematischer Aufbau eines Beweises - Beweis
- ---
- Mathematische Beweise werden üblicherweise mit „w.z.b.w.“ abgeschlossen - für „was zu beweisen war“.
- Auch die lateinische Form „q.e.d.“ wird verwendet - für: quod erat demonstrandum
- Ebenso verbreitet ist es einen Beweis mit folgendem Symbol ■ (ein kleines schwarzes Quadrat) abzuschließen.
- ---
- Ein Beweis ist in der Mathematik die als fehlerfrei anerkannte Herleitung der Richtigkeit bzw. der Unrichtigkeit einer Aussage aus einer Menge von Axiomen, die als wahr vorausgesetzt werden, und anderen Aussagen, die bereits bewiesen sind.
- ---
- Umfangreichere Beweise von mathematischen Sätzen werden in der Regel in mehrere kleine Teilbeweise aufgeteilt, die oft als Satz und Hilfssatz bezeichnet werden.
BM1683

- Die Summe der Innenwinkel bei Rechtecken ist 360°.
- ()
- ---
- Die Winkelsumme der Innenwinkel in jedem beliebigen Viereck beträgt 360°.
- Kannst du das beweisen?
1. Lösung BM1683
2. Lösung BM1683 - Ein Dreieck hat eine Winkelsumme von 180°. Also haben zwei Dreiecke als Summe der Innenwinkel .
- Folglich hat auch ein Viereck eine Winkelsumme von 360°.
BM1684
- Begründe, dass ein Dreieck höchstens einen rechten Winkel haben kann.
- Begründe, dass ein Dreieck höchstens einen stumpfen Winkel haben kann.
BM1685

Bild 1 - Außenwinkelsatz (Teil 1)
- Jedem Innenwinkel eines Dreiecks sind zwei Außenwinkel zugeordnet.
- Wenn wir von den drei Außenwinkeln eines Dreiecks sprechen, so sind Außenwinkel gemeint, die zu verschiedenen Innenwinkeln gehören.
- ---
Bild 2 - SATZ:
- Jeder Außenwinkel eines Dreiecks ist gleich der Summe der beiden nichtanliegenden Innenwinkel.
- Kannst du diesen Satz beweisen?
Lösung BM1685 - 1.) (Nebenwinkel)
- 2.) (Summe der Innenwinkel)
- 3.) aus 1. und 2. folgt:
- minus auf beiden Seiten ergibt:
- 4.)
- ■
BM1686

- Außenwinkelsatz (Teil 2)
- ---
- Der Außenwinkelsatz ist ein Lehrsatz der Geometrie, der besagt, dass jeder Außenwinkel eines Dreiecks so groß ist wie die beiden nicht anliegenden Innenwinkel zusammen. Er wurde erstmals im 3. Jh. v. Chr. als Satz 32 in Buch 1 der Elemente Euklids bewiesen.
- ---
- Formulierung des Satzes

Innenwinkel α, β, γ und Außenwinkel α′, β′, γ′ eines Dreiecks in der euklidischen Ebene - Der Außenwinkelsatz der euklidischen Geometrie besagt, dass der Außenwinkel an einer Ecke eines Dreiecks stets gleich der Summe der Innenwinkel an den beiden anderen Ecken ist; beispielsweise ist in einem Dreieck die Summe der Innenwinkel an den Ecken und gleich dem Außenwinkel an der Ecke .
- ---
- Beweis des Satzes
- Der Außenwinkelsatz ist eine einfache Folgerung aus dem Satz von der Winkelsumme, denn für die mit , und bezeichneten (Innen-)Winkel des gilt , und somit auch ; wie denn für den Außenwinkel an der Ecke gilt, dass er als Ergänzungswinkel zum Innenwinkel einen Betrag von hat. Womit man prompt den Außenwinkelsatz erhält:
- .
- Analog beweist man und .
- ---
- Schwacher Außenwinkelsatz
- Der schwache Außenwinkelsatz, auch als Satz vom Außenwinkel bezeichnet, sagt:
- Jeder Außenwinkel eines beliebigen Dreiecks ist stets strikt größer als jeder der beiden nichtanliegenden Innenwinkel.
- In Formeln:
- .
- Es folgt, dass jeder Innenwinkel stets strikt kleiner als jeder der beiden nichtanliegenden Außenwinkel ist.
BM1687
1. Lösung BM1687 - 1.) (Nebenwinkel)
- 2.) (Nebenwinkel)
- 3.) (Nebenwinkel)
- 4.) aus 1., 2. und 3. folgt:
- 5.) (Summe der Innenwinkel im Dreieck)
- 6.) wir stellen die Gleichung aus 4. etwas um:
- 7.) für in 6. können wir wegen 5. einfach einsetzen
- 8.) wir rechnen auf beiden Seiten der Gleichung minus und erhalten
- oder
- ■
- ---
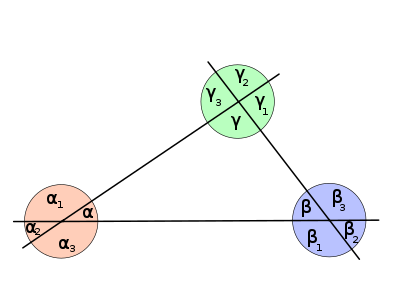
Bild 2 - Man kann diesen Beweis auch etwas abwandeln. Kannst du anhand von Bild 2 den Beweis führen, dass die Summe der Außenwinkel im Dreieck 360° beträgt?
- ---

Bild 3 - Nun wollen wir noch eine 3. Version für den Beweis.
- Beweise den Satz mit Hilfe des Satzes aus der vorherigen Übung BM1685! („Jeder Außenwinkel eines Dreiecks ist gleich der Summe der beiden nichtanliegenden Innenwinkel.“)
- Hast du eine Idee, wie du diesen Beweis führen könntest?
3. Lösung BM1687 - 1.)
- Aus dem bekannten SATZ: „Jeder Außenwinkel eines Dreiecks ist gleich der Summe der beiden nichtanliegenden Innenwinkel.“ folgt:
- 2.)
- (Nebenwinkel)
- (Nebenwinkel)
- (Nebenwinkel)
- 3.)
- (Winkelsumme im Dreieck)
- ---
- Kannst du daraus nun einen Beweis basteln?
4. Lösung BM1687 - (Nebenwinkel)
- Wir stellen die Summaden um. Die Klammern sind nur zur Veranschaulichung:
- Wegen der Winkelsumme können wir schreiben:
- Nun ziehen wir noch auf beiden Seiten 180° ab:
- Jetzt multiplizieren wir noch:
- ■
BM1688

Bild 1 - Winkelhalbierende
- ---
- Ein Strahl m heißt Winkelhalbierende des Winkels , wenn er folgende Eigenschaften besitzt:
- 1.) Sein Anfangspunkt ist der Scheitel des Winkels.
- 2.) Er verläuft innerhalb des Winkels.
- 3.) Winkel (hier grün) und (hier rot) sind kongruent; also
- .
- ---
- In der ebenen Geometrie ist die Winkelhalbierende eines Winkels die Halbgerade (= Strahl), die durch den Scheitelpunkt des Winkels läuft und das Winkelfeld in zwei deckungsgleiche Teile teilt.
- ---

Bild 2 
Bild 3 - Konstruktion der Winkelhalbierenden:
- Ein Winkel ist durch seine beiden Schenkel (Halbgeraden mit gemeinsamen Anfang im Scheitel des Winkels) gegeben. Dann kann die Winkelhalbierende mit einem Zirkel und einem Lineal (Geodreieck) konstruiert werden: Um den Scheitelpunkt wird ein Kreis mit beliebigem Radius gezeichnet (hier blau). An den Schnittpunkten mit den Schenkeln des Winkels wird der Zirkel erneut angesetzt. Dann zeichnet man jeweils einen Kreis mit gleichem Radius (hier rot). Die Schnittpunkte dieser zwei Kreise liegen auf der Winkelhalbierenden.
- Bei dieser Konstruktion wird benutzt, dass die Winkelhalbierende zugleich Mittelsenkrechte (dazu in der nächsten Übung mehr) in dem gleichschenkligen Dreieck ist, das durch den Scheitel und die zwei ersten Hilfspunkte gegeben ist.
BM1689
- ---
- Ein Punkt M einer Strecke heißt Mittelpunkt der Strecke, wenn die Beziehung
- Die Senkrechte im Mittelpunkt einer Strecke auf der Geraden AB heißt MIttelsenkrechte einer Strecke.
- ---
- Die Mittelsenkrechte oder das Mittellot ist eine besondere Gerade, die in der ebenen Geometrie untersucht wird.
- Definition:
- Die Mittelsenkrechte ist die Menge aller Punkte, die von zwei gegebenen Punkten denselben Abstand haben:
- Lies: s ist gleich: die Menge aller X für die gilt: Strecks XA ist gleich Strecke XB
- (Wie erinnern uns bitte: Mengen werden in geschweiften Klammern geschrieben.)
- Die Mittelsenkrechte ist also eine Gerade, die orthogonal (das heißt senkrecht) auf der Verbindungsstrecke der zwei Punkte steht und durch deren Mittelpunkt geht.
BM1690
- Mittelsenkrechte (Teil 2)
- Eine andere Definitionsmöglichkeit für die Mittelsenkrechte lautet:
- Die Mittelsenkrechte ist die Menge der Mittelpunkte aller Kreise, die durch zwei gegebene Punkte gehen.
- ---
- Kannst du das erklären? Stimmt das? Wie muss man sich das vorstellen? Fertige eine Skizze dazu an!
BM1691 - BM1700
[editar]BM1691
Lösung BM1691 - 1.) Einen Kreisbogen mit dem Zirkel zeichnen. Mittelpunkt des Kreisbogens ist der Scheitelpunkt des Winkels. (hier: blau)
- (kurz: Kreisbogen um den Scheitelpunkt zeichnen.)
- 2.) Die dadurch entstandenen zwei Schnittpunkte mit den Schenkels dienen als Mittelpunkt für zwei weitere Kreise. (hier grün). Diese zwei Kreis müssen den gleichen Radius haben. Ihr Radius darf nicht zu klein sein. Er muss mindestens so groß sein, dass sich die Kreis deutlich überlappen.
- 3.) die beiden grünen Kreise bilden an genau zwei Stellen Schnittpunkte miteinander. Diese beiden Punkte definieren unsere Mittelsenkrechte. Wir müssen die Punkte miteinander verbinden und diese Gerade noch etwas in beide Richtungen verlängern. (hier: rot)
BM1692
Lösung BM1692 - Man konstruiert eine Mittelsenkrechte zwischen zwei gegebenen Punkten und , indem man um diese beiden Punkte mit einem Zirkel Kreisbögen zeichnet mit gleichem Radius, der größer als die halbe Strecke zwischen den beiden Punkten sein muss. Die zwei Schnittpunkte dieser beiden Kreislinien bestimmen eine Gerade. Diese Gerade ist die Mittelsenkrechte der Strecke .
BM1693

Ein gleichschenkliges Dreieck.
Es gilt: und- Gleichschenklige Dreiecke
- ---
- Ein gleichschenkliges Dreieck ist ein Dreieck, bei dem mindestens zwei Seiten gleich lang sind. Diese Seiten werden als Schenkel bezeichnet, die dritte Seite heißt Basis des gleichschenkligen Dreiecks. Die beiden Winkel an der Basis (Basiswinkel) sind gleich groß. Der Punkt, an dem beide Schenkel zusammentreffen, wird Spitze genannt, der dortige Winkel ist der Winkel an der Spitze.
- In einem gleichschenkligen Dreieck fallen die Mittelsenkrechte der Basis, die Seitenhalbierende der Basis und die Höhe auf der Basis sowie die Winkelhalbierende des Spitzenwinkels aufeinander.
- ---
- Ein gleichschenkliges Dreieck ist ein Dreieck mit mindestens zwei gleich langen Seiten. Folglich sind auch die beiden Winkel gleich groß, die den gleich langen Seiten gegenüberliegen. Zur vollständigen Bestimmung werden zwei Bestimmungsstücke benötigt, davon zumindest eine Seite.
- Die beiden gleich langen Seiten heißen Schenkel, die dritte Seite heißt Basis. Der der Basis gegenüberliegende Eckpunkt heißt Spitze. Die an die Basis anliegenden Winkel heißen Basiswinkel.
- ---
- Symmetrieeigenschaften gleichschenkiger Dreiecke:
- Jedes gleichschenklige Dreieck ist axialsymmetrisch.
- Jedes gleichschenklige Dreieck ist achsensymmetrisch. Es kann spitzwinklig, rechtwinklig oder stumpfwinklig sein.
BM1694
- Basiswinkelsatz
- Der Basiswinkelsatz besagt, dass in einem gleichschenkligen Dreieck die beiden Basiswinkel, also die Winkel, die den gleich langen Seiten gegenüberliegen, gleich groß sind. Umgekehrt gilt auch: Sind in einem Dreieck zwei Winkel gleich groß, so sind auch die beiden gegenüberliegenden Seiten gleich lang.
- ---
- Gleichschenklige Dreiecke sind achsensymmetrisch. Die Symmetrieachse stimmt mit der Höhe, der Mittelsenkrechten (Streckensymmetrale) und der Seitenhalbierenden (Schwerlinie) der Basis und mit der Winkelhalbierenden (Winkelsymmetrale) des Winkels an der Spitze überein.
- ---
- Da gleichseitige Dreiecke drei gleich lange Seiten haben, sind diese auch gleichzeitig gleichschenklige Dreiecke. Gleichschenklige Dreiecke schließen alos gleichseitige Dreiecke als einen Spezialfall des gleichschenkligen Dreiecks ein. Das war nicht immer so.
- Nach Euklid, also im antiken Griechenland, wurde ein gleichschenkliges Dreieck dadurch definiert, dass es nur zwei gleich lange Seiten besitzt, wohingegen es heute überwiegend als ein Dreieck mit mindestens zwei gleich langen Seiten definiert wird.
BM1695

Bile 1: gleichschenkliges Dreieck 
Bild 2: mit Winkelhalbierender - Basiswinkelsatz
- ---
- In einem gleichschenkligen Dreieck sind die Basiswinkel (hier: Alpha und Beta) gleichgroß.
- Basiswinkelsatz in der Wenn-Dann-Formulierung:
- Wenn ein Dreieck gleichschenklig ist, dann sind die Basiswinkel gleich groß.
- Beweis:
- Voraussetzung:
- Behauptung:
- Beweisidee: Wie zerlegen das Dreieck durch die Winkelhalbierende des Winkels, der nicht Basiswinkel ist, in zwei Teildreiecke und beweisen mit Hilfe der Kongruenzsätze für Dreiecke, dass diese kongruent sind.
- ---
- 1.) (Winkelhalbierende von Gamma)
- 2.) (das folgt aus 1.)
- 3.) (Voraussetzung)
- 4.) ( liegt vollständig in beiden Teildreiecken und )
- 5.) (Dreiecke mit eienr gleichen Seite und gleichen anliegenden Winkeln an dieser Seite sind identisch - dazu später mehr. SWS - Seite-Winkel-Seite sind identisch.)
- 6.) \alpha = \beta</math>
- w.z.b.w.
- Die Basiswinkel eines beliebigen gleichschenkligen Dreiecks sind kongruent.
BM1696

Bild 1 
Bild 2 
Bild 3 
Bild 4 - Der Basiswinkelsatz
- („Die Basiswinkel eines beliebigen gleichschenkligen Dreiecks sind kongruent.“)
- gilt auch für gleichseitige Dreiecke, denn jedes gleichseitige Dreieck ist zugleich auch ein gleichschenkliges Dreieck.
- Also:
- Die Basiswinkel eines gleichseitigen Dreiecks sind kongruent.
- ---
- Da jede Seite eines gleichseitigen Dreiecks Basis eines gleichschenkligen Dreiecks mit den beiden anderen Seiten als Schenkel ist, gibt es in jedem gleichseitigen Dreieck drei Symmetrieachsen (Bild 1-3: rot, grün, blau). Sie schneiden einander in einem Punkt (Bild 4).
BM1697
- Die 3 Winkelhalbierenden des gleichseitigen Dreiecks schneiden sich in einem Punkt.
- Die 3 Winkelhalbierenden des gleichseitigen Dreiecks schneiden sich in einem einzigen Punkt.
- ---
- Beweis:
BM1698

- In jedem gleichseitigen Dreieck betragen alle drei Innenwinkel jeweils 60°.
- Kannst du das begründen?
BM1699

Bild 1 - Seiten-Winkel-Beziehung im Dreieck
- ---
- SATZ:
- In jedem Dreieck liegt der größeren von zwei Seiten auch der größere Winkel gegenüber.
- ---
- Beispiel:
- ⇒
- Wenn die Strecke größer ist als die Strecke , dann folgt daraus, dass der Winkel (der der Strecke gegenüberliegt) größer ist als der Winkel (der der Strecke gegenüberliegt).
- ---
- Auch die Umkehrung diese Satzes gilt:
- In jedem Dreieck liegt dem größeren von zwei Winkeln auch die größere Seite gegenüber.
- („Größere Seite“ bedeutet das gleiche wie „längere Seite“.)
- ---
- Beweise es!
BM1700
- Begründe die folgende Aussage:
- 1.) In jedem rechtwinkligen Dreck ist die Seite, die dem rechten Winkle gegenüberliegt, größer, als die beiden anderen Seiten.
- ---
- 2.) In jedem gleichschenklig-rechtwinkligen Dreieck beträgt jeder der beiden Basiswinkel 45°.
- índice
- Lección 083b ← Lección 084 → Lección 085b
- Lección 084