Teoría musical/Introducción a la notación y el solfeo/Intervalos: Primera Aproximación

← El tono y el semitono		Intervalos: Primera Aproximación	Acordes principales en la tonalidad de Do Mayor →
Teoría musical/Introducción a la notación y el solfeo

La distancia entre dos notas se denomina intervalo. En este capítulo veremos una primera aproximación a los intervalos. El tema se profundizará en el capítulo Intervalos.

Los intervalos se identifican con números ordinales en género femenino (Primera, Segunda, Tercera, etc.).

Para identificar un intervalo debemos contar todas las notas en el recorrido desde la nota inferior hasta la nota superior. Por ejemplo, desde un Fa hasta un La el recorrido es de tres notas (Fa-Sol-La), estamos frente a un intervalo de tercera. Veamos algunos ejemplos:

Ejemplo	Descipción
$\relative c' { \override Staff.TimeSignature #'stencil = ##f <a' a>1 }$	Primera o unísono: Desde una nota hacia la misma nota a la misma altura no hay recorrido, o dicho de otro modo, es un recorrido de una nota, decimos que es un intervalo de primera o unísono.
$\relative c { \clef bass \override Staff.TimeSignature #'stencil = ##f <d e>1 }$	Segunda: De una nota a la nota siguiente hay un recorrido de dos notas. En el ejemplo de Re a Mi.
$\relative c { \clef bass \override Staff.TimeSignature #'stencil = ##f <g' b>1 }$	Tercera: En el ejemplo, de Sol a Si hay un recorrido de tres notas (Sol-La-Si), es una tercera.
$\relative c' { \clef alto \override Staff.TimeSignature #'stencil = ##f <c f>1 }$	Cuarta: En el ejemplo, de Do a Fa hay un recorrido de cuatro notas (Do-Re-Mi-Fa), es una cuarta.
$\relative c' { \clef alto \override Staff.TimeSignature #'stencil = ##f <e, b'>1 }$	Quinta: En el ejemplo, de Mi a Si hay un recorrido de cinco notas (Mi-Fa-Sol-La-Si), es una quinta.
$\relative c' { \override Staff.TimeSignature #'stencil = ##f <f d'>1 }$	Sexta: En el ejemplo, de Fa a Re hay un recorrido de seis notas (Fa-Sol-La-Si-Do-Re), es una sexta.
$\relative c' { \override Staff.TimeSignature #'stencil = ##f <d c'>1 }$	Séptima: En el ejemplo, de Re a Do hay un recorrido de siete notas (Re-Mi-Fa-Sol-La-Si-Do), es una séptima.
$\relative c { \clef bass \override Staff.TimeSignature #'stencil = ##f <b b'>1 }$	Octava: En el ejemplo, de Si a Si hay un recorrido de ocho notas (Si-Do-Re-Mi-Fa-Sol-La-Si), es una octava.

Para dejar esta idea más clara se presentan todos los intervalos desde la nota Do:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c c>1_\markup \center-align{Primera} <c d>_\markup \center-align{Segunda} <c e>_\markup \center-align{Tercera} <c f>_\markup \center-align{Cuarta} <c g'>_\markup \center-align{Quinta} <c a'>_\markup \center-align{Sexta} <c b'>_\markup \center-align{Séptima} <c c'>_\markup \center-align{Octava} \bar "|." }$

Formas de presentar un intervalo

Un intervalo se puede presentar de tres formas: armónico, melódico ascendente o melódico descendente.

Ejemplo	Descipción
$\relative c' { \override Staff.TimeSignature #'stencil = ##f <d f>1 }$	Armónico: ambas notas del intervalo suenan al mismo tiempo
$\relative c' { \override Staff.TimeSignature #'stencil = ##f d2 f }$	Melódico Ascendente: la nota más grave suena primero, en el ejemplo tenemos una tercera melódica ascendente.
$\relative c' { \override Staff.TimeSignature #'stencil = ##f f2 d }$	Melódico Descendente: la nota más aguda suena primero, en el ejemplo tenemos una tercera melódica descendente.

Cabe señalar que los intervalos se calculan siempre desde la nota más grave que se denomina nota raíz.

Clasificación de los intervalos

Los intervalos se clasifican según especie en : Mayores, menores, Justos, Aumentados y disminuidos.

Para identificar cada intervalo utilizaremos la siguiente simbología:

Especie	Símbolo
Mayor	+
menor	-
Justo	J
Aumentado	×
disminuido	°

Por regla general los intervalos Mayores y menores se simbolizan con letras M y m (Mayúscula y minúscula), sin embargo, esta simbología es confusa, sobre todo en los exámenes, dependiendo de la caligrafía del estudiante puede ser difícil distinguir entre una letra y otra.

Intervalo de segunda

El intervalo de segunda se clasifica como Mayor o menor, con el siguiente criterio:

Si es un semitono es una segunda menor.
Si es un Tono es una Segunda Mayor.

A continuación se muestra la clasificación de los intervalos de segunda entre notas naturales:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c d>1_"2+" <d e>_"2+" <e f>_"2-" <f g>_"2+" <g a>_"2+" <a b>_"2+" _"2-" \bar "|." }$

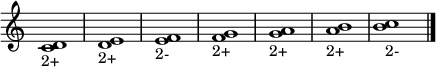
Intervalo de tercera

El intervalo de tercera se clasifica como Mayor o menor, con el siguiente criterio:

Si es un Tono y un semitono es una tercera menor.
Si son dos Tonos es una Tercera Mayor.

A continuación se muestra la clasificación de los intervalos de tercera entre notas naturales:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c e>1_"3+" <d f>_"3-" <e g>_"3-" <f a>_"3+" <g b>_"3+" <a c>_"3-" _"3-" \bar "|." }$

Intervalo de cuarta

El intervalo de cuarta se clasifica como Justa o Aumentada, con el siguiente criterio:

Si son dos Tonos y un semitono es una Cuarta Justa.
Si es tres Tonos es una Cuarta Aumentada.

A continuación se muestra la clasificación de los intervalos de cuarta entre notas naturales:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c f>1_"4J" <d g>_"4J" <e a>_"4J" <f b>_"4×" <g c>_"4J" <a d>_"4J" _"4J" \bar "|." }$

Intervalo de quinta

El intervalo de quinta se clasifica como Justa o disminuida, con el siguiente criterio:

Si son tres Tonos es una quinta disminuida.
Si es tres Tonos y un semitono es una Quinta Justa.

A continuación se muestra la clasificación de los intervalos de quinta entre notas naturales:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c g'>1_"5J" <d a'>_"5J" <e b'>_"5J" <f c'>_"5J" <g d'>_"5J" <a e'>_"5J" _"5°" \bar "|." }$

Intervalo de sexta

El intervalo de sexta se clasifica como Mayor o menor, con el siguiente criterio:

Si son cuatro Tonos es una sexta menor.
Si son cuatro Tonos y un semitono es una sexta Mayor.

A continuación se muestra la clasificación de los intervalos de sexta entre notas naturales:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c a'>1_"6+" <d b'>_"6+" <e c'>_"6-" <f d'>_"6+" <g e'>_"6+" <a f'>_"6-" _"6-" \bar "|." }$

Intervalo de séptima

El intervalo de séptima se clasifica como Mayor o menor, con el siguiente criterio:

Si son cinco Tonos es una séptima menor.
Si son cinco Tonos y un semitono es una séptima Mayor.

A continuación se muestra la clasificación de los intervalos de séptima entre notas naturales:

$\relative c' { \override Staff.TimeSignature #'stencil = ##f \textLengthOn <c b'>1_"7+" <d c'>_"7-" <e d'>_"7-" <f e'>_"7+" <g f'>_"7-" <a g'>_"7-" _"7-" \bar "|." }$

Resumen de la clasificación de los intervalos

A continuación presentamos una tabla que resume los intervalos y su clasificación, con su medida en tonos y semitonos.

Medida	Intervalo
1/2 Tono	Segunda menor
1 Tono	Segunda Mayor
1 1/2 Tonos	Tercera menor
2 Tonos	Tercera Mayor
2 1/2 Tonos	Cuarta Justa
3 Tonos	Cuarta Aumentada o Quinta disminuida
3 1/2 Tonos	Quinta Justa
4 Tonos	Sexta menor
4 1/2 Tonos	Sexta Mayor
5 Tonos	Séptima menor
5 1/2 Tonos	Séptima Mayor
6 Tonos	Octava Justa

Ten en cuenta lo siguiente:

Los intervalos de Primera, Cuarta, Quinta y Octava se clasifican como Justos, Aumentados o disminuidos.
Los intervalos de Segunda, Tercera, Sexta y Séptima se clasifican como Mayores o menores.

Los intervalos de Primera, Cuarta, Quinta y Octava son más consonantes por eso se denominan como Justos o Perfectos.

consejo

No te preocupes si te cuesta calcular un intervalo contando los tonos y semitonos. En el capítulo Intervalos se explicará un método más sencillo.

Consonancia y Disonancia

Uno de los aspectos importantes de los intervalos es reconocer la consonancia y disonancia. La definición de intervalos consonantes o disonantes varía mucho dependiendo del contexto histórico y cultural.

Un aspecto relevante es que la consonancia y la disonancia no significa que suene bien o mal. Actualmente se dice que la disonancia genera tensión y esa tensión necesita una resolución, ya trataremos este tema en Armonía.

Por ahora señalaremos que los intervalos la consonancia y disonancia se define de la siguiente manera:

Consonancia Perfecta: Unísono, Cuarta Justa, Quinta Justa y Octava Justa.
Consonancia Imperfecta: Terceras Mayores y menores; Sextas Mayores y menores.
Disonancia Perfecta: Segundas Mayores y menores; Séptimas Mayores y menores.
Disonancia Condicional: Cuartas Aumentadas y Quintas Disminuidas.

El Tritono

Nos detendremos en el tritono. El tritono es un intervalo de tres tonos, puede ser una cuarta aumentada o una quinta disminuida. Se trata de un intervalo semiconsonante, es decir, aunque no es consonante, su sonido es más agradable que una segunda o una séptima.

Durante el medioevo se evitaba el tritono, muchos músicos evitaban la nota Si, ya que formaba un tritono con el Fa. El tritono fue llamado "Diabolus in Música".

Sin embargo, el tritono adquirió una importancia significativa en la música del período de la práctica común, y está muy presente en muchas composiciones. En el desarrollo de este libro veremos diferentes situaciones en las que aparece el tritono.