Matemáticas Universitarias/Espacios Métricos/Espacios Topológicos
Introducción
[editar]Hemos analizado, en los capítulos anteriores, las posiciones relativas de puntos y conjuntos usando métricas. Hay, sin embargo, situaciones interesantes donde la métrica no es lo más adecuado o, inclusive, puede que no haya una métrica posible; pero que nos interese tener una noción de proximidad. Aquí es donde entra la noción de espacio topológico donde la noción de proximidad será dada por abiertos en lugar de distancias.
Si examinamos lo hecho en los capítulos anteriores, todas las nociones importantes: vecindad, interior, exterior, clausura, puntos aislados, de acumulación, continuidad, etc. fueron definidas usando la noción de abierto.
Por lo que podemos, a partir de una familia de abiertos, tener todas las nociones indicadas arriba. Eso es, precisamente lo que haremos en este capítulo. Nuestro punto de partida será las propiedades de abiertos contenidas en la proposición 5.2.2.
Las Definiciones Básicas
[editar]Definición. (Topología, Espacio Topológico)Una topología en un conjunto X es un conjunto T de subconjuntos de X tal que:
- (I) El conjunto vacío y el conjunto X están en T ;
- (II) La reunión de una familia cualquiera de conjuntos en T está en T ;
- (III) La intersección de dos conjuntos de T está en T .
Un espacio topológico es un par <X, T > donde T es una topología de X. Llamamos puntos del espacio a los elementos de X y (conjuntos) abiertos (de X) a los conjuntos de la topología.
Ejemplos 8.2.1.
- Los espacios métricos son espacios topológicos cuya su topología está determinada por los abiertos definidos a partir de las bolas abiertas. Mirar la proposición 5.2.4. Llamamos a esta topología la topología inducida por la métrica. En particular, llamamos línea real a los Reales R con la métrica usual.
- Llamamos espacio topológico discreto a cualquier espacio donde cualquier subconjunto es abierto.
- Llamamos espacio topológico indiscreto aun espacio donde los únicos abiertos son todo el espacio y el subconjunto vacío.
- Sea X = {a, b, c} y sea T = {X, ∅, {a}, {a, b}, {a, c}}. Es fácil verificar que T es una topología de X. Notemos que no hay abiertos que separen a b y c (la propiedad de Hausdorff). Por lo que el espacio X no puede tener una métrica cuyos abiertos coincidan con los elementos de T . Aunque, por ahora, parezcan una curiosidad, estos espacios topológicos finitos pueden tener algunas aplicaciones interesantes.
Convenios. Como es usual, cuando no haya riesgo de confusión acerca de la topología, hablaremos simplemente del espacio X. De ahora en adelante, además, “espacio” siempre querrá decir “espacio topológico”, a menos que digamos algo distinto.
Cuando digamos que una función f : X → Y es continua, implícitamente suponemos que X y Y son espacios (topológicos).
Los Puntos y los Conjuntos Especiales
[editar]La terminología asociada con espacios topológicos es básicamente la misma que aquella usada para espacios métricos. Enunciaremos las definiciones, principalmente para comparaciones y futuras referencias.
Definición. (Vecindad) Sea X un espacio topológico. Una vecindad de un conjunto A (resp. de un punto p) es cualquier conjunto que contenga un abierto que contenga a A (resp. a p).
Veremos, brevemente las definiciones de cerrado, interior, exterior, clausura y
frontera. Revisar las definiciones para ver que formalmente coinciden con aquellas dadas en el capítulo 5.
Definición. (Cerrado) Un subconjunto de un espacio topológico es cerrado, ssi, su complemento es abierto.
Definición. (Puntos Especiales) Sean X un espacio topológico, A un subconjunto de X y p un punto de X.
- El punto p es interior de A, ssi, hay un abierto U que contiene a p y está contenido en A.
- El punto p es exterior a A, ssi, es interior al complemento de A.
- El punto p es de clausura de A, ssi, cada vecindad abierta de p tiene intersección no vacía con A.
- El punto p es de frontera de A,ssi, es de clausura de A y de su complemento.
- El punto p es de acumulación de A, ssi, cada vecindad de p contiene un punto de A diferente de p.
- El punto p de A es aislado en A, ssi, hay una vecindad de p donde el único punto de A es p.
Definición. (Conjuntos especiales) Sea A un subconjunto de un espacio topológico.
- El interior de A (Int(A) o Ao) es el conjunto de puntos interiores de A.
- El exterior de A (Ext(A) ) es el conjunto de puntos exteriores de A.
- La clausura de A (Cl(A) o A--) es el conjunto de puntos de la clausura de A.
- La frontera de A (Fr(A)) es el conjunto de puntos de la frontera de A.
Claramente las nociones coinciden con las correspondientes de espacios métricos. Queda de ejercicio:
- a) revisar las propiedades enunciadas en el capítulo 5 que no hagan referencias a nociones dependientes de distancias tales como diámetro, distancia entre conjuntos,etc.
- b) verificar su validez en el contexto de espacios topológicos. Ver también los ejercicios
Cada espacio métrico define una topología. Resulta natural preguntarse si podriamos dotar a cada espacio topológico de una métrica de modo que la topología inducida por la métrica coincida con la topología del espacio. La respuesta es negativa, como se puede apreciar en el ejemplo 4 de 8.2.1.
Cuando en un espacio topológico haya una métrica cuya topología inducida coincide con la topología del espacio, diremos que el espacio es metrizable.
Suponiendo que el espacio fuera metrizable, ¿podemos del conocimiento de su topología recuperar la métrica?
La respuesta es negativa, como es fácil de ver. observando que cuando d es una métrica en el conjunto X, entonces d'(x, y) := 2d(x, y) es una métrica que genera los mismos abiertos que d. Más adelante veremos que las normas euclídeas, ciudad y máxima generan la misma topología en los Rn. Es decir que aún métricas muy diferentes pueden generar la misma topología (o sea la misma familia de abiertos).
Observación 8.1 (Topologías definidas por Cerrados). Observamos en el capítulo de abiertos y cerrados, que cerrado era una noción dual a la de abierto. Luego, cuando en un conjunto X tenemos una familia de conjuntos tal que:
- (i) el conjunto vacío y el conjunto X están en ,
- (ii) la intersección de cualquier familia de conjuntos de está en , y
- (iii) la reunión de dos conjuntos en está en ;
tenemos una familia que tiene las propiedades de los cerrados en la proposición 5.3.5. Por lo que podemos definir una topología formada por los complementos de los conjuntos en .
Espacios Hausdorff
[editar]Un espacio Hausdorff es un espacio topológico tal que, para todo p, q en X con p ≠ q hay abiertos disjuntos U y V tales que p está en U y q está en V .
Decimos que tales abiertos separan puntos o distinguen puntos.
Los espacios métricos son espacios Hausdorff, así como los espacios discretos.
Subespacios
[editar]Sean X un espacio (topológico) y Y un subconjunto de X, ¿cuándo Y tendrá una topología relacionada con la topología de X?
La respuesta no consiste simplemente en usar los abiertos de X que son subconjuntos de Y. Miremos, por ejemplo, una situación con espacios métricos. Si X = R y Y = [0, 1], tenemos que [0, 1/2) es un conjunto abierto en Y, aunque no lo sea en X. Los abiertos de Y, recordemos, eran las intersecciones de abiertos de X con Y . Esto motiva la siguiente proposición.
Proposición 8.2.1. Sean <X, T> un espacio topológico, Y un subconjunto de X, y TY := {U ∩ Y : U ∈ T }. Entonces, TY es una topología en el conjunto Y .
-
Demostración. Claramente, el conjunto vacío (∅ = ∅ ∩ Y ) y Y = X ∩ Y están en TY. Sea (Ui), i ∈ I, una familia de conjuntos de TY . Por definición, para cada i en I, hay un abierto Vi de X tal que Ui = Vi ∩ Y. Entonces,
es un abierto de X y como
tenemos que está en TY.
Análogamente, suponiendo que I fuera finito, tenemos que:
lo que prueba que W está en TY. En conclusión, TY es una topología.
Definición. (Subespacio). Sean <X, T > un espacio topológico, Y un subconjunto de X y TY la topología formada por la intersección de los abiertos de X con Y. Decimos que el espacio topológico <Y, TY > es un subespacio (topológico) de <X, T >. Llamamos topología relativa de Y (respecto a X) a la topología TY .
Cuando en el contexto queda claro acerca de que topología estamos hablando,
decimos simplemente que Y es un subespacio de X y supondremos que su
topología es la topología relativa.
Sea A ⊂ X. Aunque cada abierto A de X induce un abierto A ∩ Y de Y , el
recíproco no es válido, en general.
Proposición 8.2.2. Sea Y un subespacio abierto de X (o sea que Y es abierto en X). Entonces, A es abierto en Y , ssi, A es abierto en X.
- Demostración. Ejercicio
Ejercicios 8.2
[editar]- Sea X un espacio topológico y sean A y B subconjuntos cualesquiera de
X. Probar que
- a) El interior de A ∩ B es igual a Int(A) ∩ Int(B)
- b) El interior de A es igual a la reunión de todos los abiertos contenidos en A.
- c) La clausura de A ∪ B es igual a la reunión de las clausuras de A y B.
- d) La clausura de A es igual a la intersección de todos los cerrados que contienen a A.
- e) Si A ⊂ B entonces Int(A) ⊂ Int(B) y Cl(A) ⊂ Cl(B).
- f) El interior del complemento de A es igual al complemento de la clausura de A.
- g) La clausura de A es la reunión de A con su frontera.
- h) El interior de A es A \ Fr(A).
- i) Fr(Cl(A)) ⊂ Fr(A) y Fr(Int A) ⊂ Fr(A).
- j) Fr(A ∪B) ⊂ Fr(A) ∪ Fr(B).
- Sea X = [0,∞[ ⊂ R. Sea T = {∅,X} ∪ {[a,+∞]: a ≥ 0}. Probar que T es una topología de X.
- (Topología del punto especial) Sea X cualquier conjunto no vacío y sea p
un punto de X.
Probar que Tp = {∅} ∪ {A ⊂ X : p ∈ A} es una topología de X. - (Topología del punto excluido) Sea X cualquier conjunto no vacío y sea p un punto de X. Probar que T = {X} ∪ {A ⊂ X : p ∉ A} es una topología de X.
- (Topología de los complementos finitos) Sea X cualquier conjunto infinito. Probar que T = {∅} ∪ {A ⊂ X : X \ A es finito } es una topología de X.
- Sea X un espacio con la topología del punto especial p. ¿Cuál es la clausura de {p}? Probar que cuando F es un subconjunto cerrado propio de X, su interior es vacío.
- (Espacio de Sierpinski) Sea X = {a, b} y sea T = {∅,X, {a}}.
- a) Verificar que T es una topología en X que coincide con la topología del punto especial para a y con la topología del punto excluido para b.
- b) Hallar el interior, el exterior, la clausura y la frontera de los conjuntos {a} y {b}.
- ¿Cuáles de los siguientes espacios topológicos son Hausdorff?
- a) Los Reales.
- b) Un espacio discreto.
- c) Un espacio indiscreto.
- d) Un espacio con la topología de complementos finitos (ver definición en un ejercicio anterior).
- e) Un espacio métrico cualquiera.
- Sean X un espacio y Y, Z subespacios de X con Z ⊂ Y . Probar que la topología relativa de Z como subespacio de Y coincide con la topología relativa de Z como subespacio de X.
- Sean X un espacio, A y B subespacios de X y C un subconjunto de A ∩ B. Si C es abierto respecto a las topologías relativas de A y B, C es abierto en X.
- Probar que un subespacio de un espacio Hausdorff es un espacio Hausdorff.
- Sea X un espacio Hausdorff. Para todo p en X, {p} es cerrado.
- Probar que la topología usual de R coincide con la topología relativa como subespacio de R2 con su topología usual.
- Un subconjunto F de un subespacio Y de X es cerrado, ssi, es la intersección de Y con un cerrado de X.
- Sea +∞ un símbolo que no está en N y sea N♯ = N ∪ {+∞}. Sea T el conjunto formado por los subconjuntos de <N♯ cuyo complemento es finito.Probar que:
- a) T es una topología en N♯, y que
- b) la topología de N como subespacio de N♯ es diferente de la topología de N como subespacio de la línea real.
Funciones Continuas y Homeomorfismos
[editar]Funciones Continuas
[editar]La definición de función continua entre espacios topológicos será formalmente igual a la versión de continuidad global en espacios métricos contenida en la proposición 6.4.1. A nivel de topología, lo interesante es la continuidad global.
Definición. (Función Continua en Espacios Topológicos) Sean X y Y espacios topológicos. Sea f : X → Y una función cualquiera. Decimos que la función f es continua, ssi, para cada abierto V de Y, su preimagen, f-1(V), es un abierto en X.
Notemos que si TX y TY son las topologías de X y Y respectivamente, entonces una función continua de X en Y induce una función , ; por lo que decimos que la función inversa de una función continua preserva (a los conjuntos) abiertos.- Las funciones constantes son continuas.
- Sea Y un subespacio de X. La inyección canónica i (deducida de la inclusión) es continua. (i-1(V ) = V ∩ Y.)
- Cualquier función continua entre espacios métricos es continua para los espacios topológicos inducidos por las métricas (ver la proposición citada arriba). Por lo que no haremos distinción entre ambas nociones.
Proposición 8.3.1 (Composición de Continuas). La composición de funciones continuas es continua.- Demostración. Sean f : X → Y y g : Y → Z funciones continuas. Sea W un abierto de Z, entonces g-1(W) es un abierto en Y. Por lo que (g o f)-1(W) = f-1(g-1(W)) es un abierto de X, lo que prueba la proposición.
(Comparar con la demostración de la proposición 6.3.3 referente a la composición de funciones continuas en espacios métricos.)
Veremos, a continuación, una condición equivalente a la definición de continuidad, pero en términos de vecindades.
Lema 8.3.2. Sea f : X → Y una función entre espacios. Entonces, los enunciados siguientes son equivalentes.- (a) La función f es continua.
- (b) Para cada punto p de X y cada vecindad W de f(p) se cumple que f-1(W) es una vecindad de p.
- Demostración.
[(a) ⇒ (b)] Sea p un punto de X y sea W una vecindad de f(p), entonces hay un abierto V de Y tal que f(p) ∈ V ⊂ W. Luego, f-1(W) contiene a f-1(V) que es un abierto de X que contiene a p. Lo que muestra que f-1(W) es una vecindad de p.
[(b) ⇒ (a)] Sea V un abierto de Y. Si V es vacío, entonces f-1(V) es vacío, por lo que es abierto. Supongamos entonces que hay un y = f(x) en V. Como V es una vecindad de f(x), hay por hipótesis una vecindad U de x tal que U ⊂ f-1(V ). Por definición de vecindad hay un abierto U0 tal que x ∈ U0 ⊂ U ⊂ f-1(V ). Lo que prueba que f es continua.
Lema 8.3.3. Sean f : X → Y una función continua y A un subconjunto de X. Entonces, f(Cl(A)) ⊂ Cl(f(A)).-
Demostración. Sea p un punto de la clausura de A. Sean V un abierto de Y que
contiene a f(p), entonces hay una vecindad U de p tal que f(U) está contenida
en V. Como p es punto de la clausura de A, tenemos que U ∩ A ≠ ∅. Luego, f(U n A) ≠ ∅. Como,
tenemos que f(p) es un punto de la clausura de f(A).
Proposición 8.3.4. Sea f : X → Y una función, X, Y espacios topológicos. Los enunciados siguientes son equivalentes.- (a) f es continua.
- (b) Para todo abierto V de Y , su imagen inversa por f, f-1(V ), es abierto en X.
- (c) Para todo cerrado W de Y , su imagen inversa por f, f-1(W), es cerrado en X.
- (d) Para todo subconjunto A de X, f(Cl(A)) ⊂ Cl(f(A)).
-
Demostración. La definición de continuidad da la equivalencia (a) ⇐⇒ (b). La equivalencia (b) ⇔ (c) sigue de que la preimagen (o imagen inversa) del complemento de un conjunto es igual al complemento de la preimagen del conjunto.
[(d) ⇒ (c)] Sea W cerrado en F y sea W0 = f-1(W). Entonces, f(Cl(W0)) ⊂ Cl(f(W0) )= Cl(f(f-1(W) ) ⊂ Cl(W) = W. Lo que implica que Cl(W0) ⊂ f-1(W) = W0, lo que implica que W0 es cerrado.
[(a) ⇒ (d)] El resultado sigue del lema previo.
Observación 8.2. Notemos que, en general, imágenes de abiertos no son abiertos. Por ejemplo, las funciones numéricas constantes, que son continuas, envían cualquier conjunto en un conjunto con un único punto, que no es abierto (es cerrado).
Para otro ejemplo consideremos la función f : R → R tal que f(t) = sen(t). Entonces, f(] - p, 3p[) = [-1, 1].
Dualmente, las imágenes de cerrados no son necesariamente cerrados. La función t ↦ 1/t de X = R \ 0 en Y = R envía todo el espacio X (que es cerrado, ya que es todo el espacio) en ]-∞ 0[ ∪ ]0,+∞[ que no es cerrado en R.
Los Homeomorfismos
[editar]Las funciones continuas, aunque sean biyectivas, no proporcionan necesariamente “isomorfismos” de espacios topológicos. Necesitaremos algo más.
Ejemplo 8.3.1. Sea Rdiscreto el espacio discreto sobre los Reales. Entonces, se tiene que la función identidad de Rdiscreto en R, t ↦ t, es claramente biyectiva. Además, es continua ya que la preimagen de cada abierto en R es un abierto en Rdiscreto—todos los subconjuntos son abiertos. La función inversa no es continua por la misma razón, no todos los subconjuntos de R son abiertos.
Definición. (Homeomorfismo) Llamamos homeomorfismo de un espacio X en un espacio Y a una función continua biyectiva f : X → Y tal que su inversa también es continua.
Cuando haya un homeomorfismo de un espacio X en un espacio Y , diremos que los espacios X y Y son homeomorfos y escribiremos que X ≅ Y.
Sigue de la definición que la composición de homeomorfismo es un homeomorfismo y que la inversa de un homeomorfismo es un homeomorfismo. Algunas veces,en la literatura (especialmente antigua), aparece la expresión “función bicontinua” para referirse a los homeomorfismos.Ejemplo 8.3.2. Vimos en la proposición 6.5.1, que las funciones t ↦ t + a y t ↦ bt, b ≠ 0 son funciones de R en R continuas, invertibles, y con inversas continuas, por lo que son homeomorfismos
Ejemplo 8.3.3 (♠ Cálculo ). Sea f : R → R tal que f : t ↦ t3, f es biyectiva con inversa . Como ambas funciones son continuas, f y su inversa son homeomorfismos.
Ejemplo 8.3.4. Las isometrías entre espacios métricos son homeomorfismos. Basta con observar que cuando f : E → F es una isometría, las imágenes directas e inversas de bolas abiertas son bolas abiertas de igual radio.
Significado de los Homeomorfismos
[editar]La noción de homeomorfismo es central en el estudio de los espacios topológicos, ya que un homeomorfismo entre dos espacios induce una correspondencia biyectiva entre sus topologías. Como todas las nociones topológicas dependen de la topología, todas las propiedades topológicas de uno, serán propiedades topológicas del otro. También, la correspondencia biyectiva entre los abiertos induce una correspondencia entre sus complementos: los cerrados. Igualmente, para cada noción que dependa de los abiertos: clausura, exterior, punto de acumulación, etc.
Dos espacios homeomórficos son, por lo tanto, indistinguibles para la topología. Desde el punto de vista de la topología, ambos espacios son, esencialmente, el mismo espacio, solamente hay un cambio de nombre de sus elementos.
Propiedad Topológica. Decimos que una propiedad de un espacio es una propiedad topológica, cuando cada espacio homeomórfico al espacio tiene la misma propiedad.
Cada propiedad o noción cuya definición dependa solamente de los abiertos es, por lo tanto, una propiedad topológica. Por ejemplo, abiertos, cerrados, interior, etc. son nociones topológicas. Aunque la métrica de un espacio define una topología, nociones que dependen especialmente de la distancia (y no de los abiertos), [por jemplo conjunto acotado, no serán nociones topológicas, como veremos en ejemplos posteriores.
Propiedad Hereditaria. Decimos que una propiedad P es hereditaria, si cuando un espacio tiene la propiedad, entonces la tienen todos sus subespacios no vacíos.Cuando en el futuro estudiemos propiedades de espacios topológicos, una pregunta natural será acerca de si es heredada por subespacios. Por ejemplo, un subespacio es un espacio Hausdorff es Hausdorff (ver ejercicios de la sección anterior.)
Propiedad Invariante. Sea f : X → Y una función (no necesariamente continua) entre espacios. Diremos que f preserva una propiedad de X o de un subconjunto de X, cuando su imagen por f tiene la propiedad.
Notemos que propiedades invariantes de funciones continuas son propiedades topológicas. La afirmación recíproca no es válida, ya que hay ejemplos de espacios uno de ellos imagen del otro por una función continua, pero tales que uno de ellos es Hausdorff y el otro no.
Proposición 8.3.5. (Propiedades de "es homemorfo con") Sean X, Y y Z espacios topológicos.
Se cumple que:
- (a) X ≅ X.
- (b) X ≅ Y implica que Y ≅ X.
- (c) X ≅ Y y Y ≅ Z entonces X ≅ Z.
-
Demostración. Ejercicio.
Veremos, a continuación, algunos ejemplos no triviales de conjuntos homeomórficos.
Proposición 8.3.6. Dos intervalos abiertos acotados de la línea real son homeomórficos.
-
Demostración. Basta con probar que ]a, b[ ≅ ]0, 1[. Sea f :]0, 1[ → ]a, b[ tal que f(t) = (b - a)t + a. Claramente f es continua y biyectiva. Su inversa es: s : t ↦ (t - a)/(b - a) que también es continua.
Es decir que para un topólogo no hay diferencia entre ambos intervalos. Lo cual es una ventaja, por ejemplo, si queremos estudiar topológicamente a las funciones continuas de ]a, b[ en los Reales, basta considerar el caso a = 0, b = 1.
Sigue, en forma inmediata, de la proposición anterior que diámetro de un conjunto no es una propiedad topológica, ya que, si b-a ≠ 1, se tiene que el diámetro de ]0, 1[ es 1, mientras que aquel de ]a, b[ es b - a. Más espectacular, lo anterior implica que distancia entre puntos no es una propiedad topológica.
El siguiente ejemplo muestra otro aspecto interesante.
Ejemplo 8.3.5 (♠ Cálculo). La función f : R → (-1, 1) tal que f(t) =(2/π) arctan(t) es biyectiva y continua (es derivable) y su inversa g(t) = (π/2) tan(t) también es continua, Luego, la línea real y el intervalo abierto ]-1, 1[ son homeomórficos.
Notemos que mientras que R es un espacio métrico completo, el intervalo abierto no es completo. Completitud es, por lo tanto, una propiedad métrica que no es topológica.
Ejemplo 8.3.6. Sean E = {(x, y, z) : x2+y2+z2 = 1, z ≥ 0} y F = {(x, y, z) ∈ R3 : x2 + y2 = 1, z = 0}.
E es el hemisferio superior de la esfera unitaria de R3 y F es su proyección en el plano z = 0. Claramente, la proyección (x, y, z) ↦ (x, y, 0) es biyectiva con inversa . Se puede verificar que ambas funciones son continuas, por lo que se trata de homeomorfismos.
Notemos que tales homeomorfismos no son isometrías. En general, la distancia euclídea entre dos puntos de la semiesfera es mayor que la distancia de sus proyecciones. Además, la distancia euclídea en E heredada de R3 (distancia por el interior de la Tierra) no es aquella más natural en E. El homeomorfismo nos dice, en cambio, que topológicamente se tratan del mismo espacio, lo que resulta conveniente para muchos estudios.
Proposición 8.3.7. Dos bolas cerradas cualesquiera de Rn son homeomorfas.
-
Demostración. Sea X = B[a; r] una bola cualquiera y sea B la bola con centro el origen y radio 1. Cuando ta es la traslación que envía cada punto p en p + a, tenemos que t-a(B[a; r]) = B[0; r]. Como traslaciones son homeomorfismos, ya que son isometrías, se tiene que una esfera cualquiera es homeomorfa a una esfera del mismo radio, pero con centro en el origen. Sea hr, r > 0, la función que envía cada punto p en rp. Como
||hr(p) - hr(q)|| = r||p - q||, vemos que hr es continua. Además es obviamente biyectiva, con inversa h1/r. Luego se trata de un homeomorfismo. Como hr(B) = B[0; r], se concluye que cualquier bola cerrada es homeomorfa a B.
Análogamente, se verifica que cualquier esfera de Rn es homeomorfa a la esfera unitaria –centro el origen y radio 1. Ver los ejercicios.
Convenio. Denotaremos por Bn a la bola cerrada de centro el origen y radio 1 de Rn. Topológicamente, Bn representa a todas las bolas cerradas de Rn. Por su parte, denotaremos por Sn la esfera unitaria de Rn+1 (que es homeomorfa a todas las esferas en Rn+1).
Funciones Abiertas y Cerradas
[editar]Un homeomorfismo de X en Y envía abiertos en abiertos y cerrados en cerrados. Funciones que tienen esas propiedades reciben nombres especiales.
Definición. (Funciones Abiertas, Cerradas) Una función abierta (resp. cerrada) f de un espacio topológico X en un espacio topológico Y es una función que envía abiertos de X en abiertos de Y (resp. cerrados de X en cerrados de Y ).
Un homeomorfismo es una función biyectiva que es continua, abierta y cerrada.Las nociones son, sin embargo, independientes. Sea A un subconjunto de un espacio topológico X. Entonces, la inclusión i : A ⇒ X es abierta (resp. cerrada), ssi, A es un conjunto abierto (resp. cerrado).
Notamos, anteriormente, que funciones numéricas constantes son continuas, pero no abiertas.
Ejercicios 8.3
[editar]- Explicar cuando una función entre dos espacios topológicos no es continua.
- Explicar por qué una función de un espacio discreto en cualquier espacio es continua.
- Probar que una función cualquiera de un espacio topológico cualquiera en un espacio discreto es una función abierta, que no necesariamente es continua. Probar que dicha función también es cerrada. Si la función fuera biyectiva, ¿debe necesariamente ser un homeomorfismo?
- Probar que la composición de homeomorfismos es un homeomorfismo y que la función inversa de un homeomorfismo es un homeomorfismo.
- (R2) Probar que el cuadrado con vértices (1, 0), (0, 1), (-1, 0) y (0,-1) es homeomórfico a la circunferencia unitaria {(x, y) : x2 + y2 = 1}.
- (R2) Probar que cada celda cerrada [a, b] × [c, d] es homeomórfica al cuadrado unitario I2 = {(x, y) : 0 ≤ x , y \le 1}.
- Sea Sn-1 la esfera unitaria de Rn (todos los puntos que distan 1 del origen). Probar que cualquier esfera de Rn es homeomorfa a Sn-1.
- Sea Sn, n > 0, la esfera unitaria de Rn+1. Se tiene (con respecto a la métrica euclídea) que
Sean
Probar las afirmaciones siguientes.
- Sean X = [0, 1] y Y = {0, 1} con la topología de Sierpinski (topología = {∅, Y, {0}}. Probar que f : X → Y tal que f(x) = 0 si 0 = x < 1/2, y f(x) = 1 en caso contrario, es continua. X es Hausdorff, pero Y no lo es.
- Probar que una función biyectiva es continua, ssi, su inversa es abierta.
- Probar que una función biyectiva continua y abierta es un homeomorfismo.
- Una función f : X → Y es continua, ssi, para todo subconjunto A de X se cumple que f(Int(A)) ⊂ Int(f(A)).
- Probar que si X es un espacio Hausdorff y f : X → Y es un homeomorfismo, entonces Y es un espacio Hausdorff. Es decir que Hausdorff es una propiedad topológica.
- En un espacio normado son homeomorfismos
- a) las traslaciones (x ↦ a + x);
- b) las multiplicaciones por escalar no nulo (x ↦ α x).
- c) las simetrías alrededor de un punto c (x ↦ 2c - x).
- Probar que en un espacio normado todas las bolas abiertas son homeomorfas entre si. Lo mismo pasa con las bolas cerradas y con las esferas.
- (♠) Probar que dos parabolas del plano son siempre homeomórficas. Usar que rotaciones y reflexiones alrededor de líneas son isometrías.
Topologías de un Conjunto
[editar]Sea X un conjunto. Vimos, anteriormente que es posible proveer a X con diferentes métricas. Algo semejante sucede con las topologías. Más adelante, necesitaremos tener topologías especialmente adaptadas a ciertas propiedades. Como las topologías son conjuntos (de conjuntos), podremos comparar a dos topologías mediante la inclusión. En esta sección, introduciremos la nomenclatura usada al respecto y algunas propiedades de la comparación.
Definición. (Comparación de Topologías) Sea T1 y T2 topologías de un mismo conjunto X. Decimos que la topología T1 es menos fina que T2, cuando cada abierto de T1 sea un abierto de T2 (o sea cuando T1 ⊂ T2).
Nomenclatura. Cuando T1 es menos fina que T2, también se dice que:- T2 es más fina que T1;
- T1 es más débil que T2;
- T2 es más fuerte que T1.
En cada conjunto X tenemos una topología discreta—donde cada subconjunto es abierto (y, por lo tanto, cerrado). Esta es la topología más fina posible sobre X. Opuesta a esa topología, está la topología indiscreta que tiene como abiertos solamente al conjunto vacío y a todo el espacio, que es la menos fina de todas las topologías posibles en un conjunto.
Sean T1, T2 dos topologías de un mismo conjunto, probaremos que su intersección, digamos T = T1 n T2 es una topología (menos fina que las topologías originales). Dicha topología consiste de todos los conjuntos que son abiertos en ambas topologías.
Claramente el conjunto vacío y todo el espacio están en T. Sea U = (Ui)i ∈ I, una familia de abiertos de T . Entonces U es una familia de abiertos tanto en T1 como en T2, por lo que su reunión estará tanto en T1 como en T2 y, en consecuencia, en T . Análogamente, si la familia I es finita, la intersección de los conjuntos en la familia será un abierto de T . Lo que prueba lo afirmado.
El razonamiento anterior se puede extender a una familia cualquiera no vacía de topologías de un mismo conjunto. Si tenemos una familia de topologías, (Tk), k ∈ K, de un conjunto X y llamamos T a su intersección, tendremos que: el conjunto vacío y todo el conjunto están en cada una de las topologías, por lo que están en su intersección T .
Si U = (Ui), i ∈ I, es una familia de abiertos de T , la reunión de los conjuntos de la familia estará en cada Tk, por lo que la reunión estará en T .
Si U = (Ui), i ∈ I, es una familia finita de abiertos de T , la intersección de los conjuntos de la familia estará en cada Tk, por lo que dicha intersección estará en T .
Proposición 8.4.1. La intersección de una familia cualquiera de topologías de un conjunto es una topología, que es menos fina (o más débil) que cualesquiera de las topologías de la familia.
Topología Generada por Familias de Subconjuntos. Sea S una familia de subconjuntos de un conjunto X y sea la intersección de todas las topologías posibles de X que contienen a S. La topología discreta es una de esas topologías, por lo que dicha familia no es vacía. Decimos que es la topología de X generada por S. Dicha topología es la topología menos fina (o más débil) que contiene a S.
Proposición 8.4.2. Sea X un conjunto no vacío y sea S un conjunto de subconjuntos de X. Sea T la colección de reuniones arbitrarias de intersecciones de finitos elementos de S. Entonces, T contiene a S y está contenida en cualquier otra topología que contenga a S. Es decir que T =- Demostración. Ejercicio. Considerar la intersección de una familia vacía como el conjunto X y la reunion de una familia vacía como el conjunto vacío.
Subbase. Decimos que una familia de abiertos S de una topología T es una subbase de la topología, cuando T es la topología generada por S.
Base. Decimos que una familia de abiertos B de una topología T es una base de la topología cuando cada abierto de T es una reunión de elementos de B. Un abierto básico es un abierto de una base.
Cuando B sea una base de la topología de un espacio X y la topología quedé clara del contexto, podremos hablar de la base del espacio.
La importancia de bases y subbases reside en que propiedades topológicas de conjuntos abiertos preservadas por intersecciones finitas y reuniones necesitan tan solo verificarse en los elementos de una subbase. Análoga consideración para bases.
Cuando se trabaja alrededor de un punto p de un espacio es interesante considerar al conjunto V{p} formado por todas las vecindades del punto p. Una base para las vecindades de un punto p es una colección de abiertos, vecindades de p, tales que para cada vecindad U de p, hay un A en tal que A ⊂ U.
Ejemplo 8.4.1. En un espacio métrico, cada abierto es una reunión de bolas abiertas, por lo que la familia de todas las bolas abiertas es una base para la topología inducida por la métrica. Las bolas abiertas con centro en un punto p determinan una base para las vecindades del punto.
Ejemplo 8.4.2. (R2) Consideremos al plano con la topología usual. Las preimágenes por las proyecciones son franjas verticales (preimágenes de abiertos de intervalos en el eje X) y franjas horizontales (preimágenes de intervalos en el eje Y).
Sabemos que las celdas—subconjuntos que son productos de intervalos reales acotados (ver ejemplo 5.2.7.) de la sección 5.2.2, son intersecciones de franjas y son, por lo tanto, conjuntos abiertos.
Se puede verificar que para cada conjunto abierto U de R2 y para cada punto p del abierto, hay una celda de las anteriores que contiene al punto y está contenida en el abierto. Es decir que el conjunto de franjas es una subbase de la topología usual del plano.
Ejemplos 8.4.3 (Ejemplos generales).
- Cada topología es una base de ella misma.
- Cada base es una subbase.
- La familia de las intersecciones finitas de conjuntos de una subbase es una base.
Proposición 8.4.3. Sea X un espacio topológico. En orden a que una colección de abiertos B sea una base de la topología de X es necesario, y suficiente, que, para cada abierto no vacío U y cada x en U hay un elemento V de B tal que x ∈V ⊂ U.- Demostración. Supongamos que B fuera una base de X. Sea U un abierto cualquiera de X. Por la definición de base, U es una reunión de una familia (Vi) de abiertos de la base. Si x está en U, x está entonces en algún V = Vi; lo que prueba la necesidad de la condición. Supongamos que se cumple la condición. Sea U un abierto cualquiera no vacío, entonces para cada x de U sea Vx el abierto en B de la condición. Claramente, U es la reunión de todos tales Vx, x ∈ U.
Proposición 8.4.4. Sea f : X → Y una función cualquiera entre espacios. Entonces- (a) f es continua ⇔ la imagen inversa de cada abierto básico es abierto :⇔ la imagen inversa de cada abierto de una subbase es abierto.
- (b) f es abierta ⇔ la imagen de cada abierto básico es abierto.
- Demostración. Los resultados siguen directamente de las siguientes identidades de conjuntos:
Ejercicios 8.4
[editar]- Probar la proposición 8.4.2.
- (Bases) Sea X un espacio topológico.
- a) ¿Siempre hay una base para la topología de X?
- b) ¿Puede una topología tener dos bases distintas?
- c) ¿Pueden dos espacios topológicos diferentes tener bases iguales?
- Probar que cualquier abierto de la línea real es una reunión de intervalos abiertos disjuntos. (Sug: Cuando dos intervalos tiene intersección no vacía, su reunión es un intervalo.) Luego, una base de la topología usual de R consiste de ...
- Sea f : X → Y una biyección. Si X (resp. Y ) es un espacio topológico, se puede proveer a Y (resp. X) de una topología única tal que X y Y sean homeomórficos. Se dice que esa estructura topológica se obtiene por transporte de estructura.
- Sea f : X → Y una función del conjunto X en el espacio topológico Y. Definir T*(f) como el conjunto formado por todos los subconjuntos U de X que son preimágenes de abiertos de Y . Probar que T*(f) es una topología en X (la topología inducida por f) tal que f es continua y que es la menos fina de las topologías con esa propiedad.
- Sea X un espacio y sea A un subconjunto de X. Probar que la topología inducida por la inclusión i : A → X coincide con la topología relativa de subespacio definida en la sección 8.2.
- Sea f : X → Y una función del espacio X en el conjunto Y . Definir T*(f) como el conjunto formado por todos los subconjuntos V de Y cuyas preimágenes son abiertos de X. Probar que T*(f) es una topología en Y (la topología coinducida por f) tal que f es continua y que es la más fina de las topologías con esa propiedad.
- Hallar tres bases diferentes para la topología usual de R2.
- Se llama subbase (resp. base) de cerrados a una colección de conjuntos cerrados cuyos complementos forman una subbase (resp. base). Enunciar y probar teoremas acerca de subbases y bases de cerrados.
Métricas Equivalentes
[editar]El espacio vectorial Rn puede tener varias métricas diferentes; cada una de esas métricas induce una topología en Rn. ¿Cómo comparan esas topologías?
Métricas y Normas Equivalentes. Decimos que dos métricas de un mismo conjunto X son (topológicamente) equivalentes, cuando los abiertos definidos por una de ellas coinciden con los abiertos definidos por la otra. Es decir, cuando definen la misma topología. Análogamente, decimos que dos normas en un espacio vectorial E son equivalentes, cuando definen métricas equivalentes y, por lo tanto, la misma topología.
Por extensión de la terminología, diremos que una norma N1 de un espacio vectorial E es mas fina que una norma N2, cuando la topología inducida por N1 sea más fina que aquella inducida por N2, es decir que los abiertos respecto a la segunda norma son abiertos respecto a la primera. Para que se cumpla lo anterior, bastará con que cada bola abierta respecto a la segunda norma contenga una bola abierta respecto a la primera. Lo anterior pasa cuando la identidad id : E1 → E2 donde Ei es el espacio con norma Ni, i = 1, 2, sea continua.
Lema 8.5.1. Sea E un espacio vectorial y sea Ei el espacio E con norma ||•||i, i = 1, 2. Si hay un número positivo a tal que para todo x se cumple que ||x||2 ≤ a||x||1 entonces ||•||1 es más fina que ||•||2.
- Demostración. Basta probar que cada bola abierta de E2 es abierto en E1.Supongamos que ||x - p||2 < r. Entonces, cuando ||x - p||1 < r/a se tiene que
||x - p||2 ≤ a||x - p||1 < a(r/a) = r. Es decir que una bola de radio r respecto a ||•||2 siempre contiene a la bola de radio r/a respecto a ||•||1. Esto implica lo pedido.
Revisaremos las topologías inducidas por las normas estudiadas de Rn(norma–ciudad, norma euclídea y norma máxima).
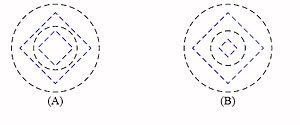
Figura 8.1 La figura 8.1 ilustra gráficamente las equivalencias entre las normas ciudad, euclídea y máxima. Ver la sección 3.3.1.
Formalmente, tenemos lo siguiente.
Lema 8.5.2. Para todo x en Rn se cumple que
- (a) ||x||max ≤ ||x||e ≤ √(n)||x||max,
- (b) ||x||max ≤ ||x||c ≤ n||x||max.
-
Demostración. Probaremos (a) y dejaremos (b) como ejercicio. Sean x = (xi) y M = ||x||max = máx{|xi| : 1 ≤ i ≤ n}. Luego, hay un j, 1 ≤ j ≤ n tal que M = |xj|. Entonces, para todo i = 1, . . . , n, |x_i| ≤ |xi| = M. Tenemos, entonces, que
Proposición 8.5.3. Las normas ciudad, euclídea y maxima de Rnson equivalentes.- Demostración. Directo de los lemas anteriores.
Más adelante, veremos que dos normas cualesquiera de Rn son equivalentes.
Proposición 8.5.4. Dos normas ||·||1 y ||·||2 son equivalentes, cuando hay reales a y b positivos tales que
a ||·||1 ≤ ||·||2 ≤ b || · ||1.
- Demostración. Ejercicio.
Ejercicios 8.5
[editar]- Completar la demostración del lema 8.5.2.
- Probar la proposición 8.5.4.
- Sea <E, d> un espacio métrico y sea d' : E × E → R tal que d'(x, y) = mín {d(x, y), 1}. Probar que d' es una métrica en E que es topológicamente equivalente con d.
Las Sucesiones
[editar]Las sucesiones no tienen un rol tan destacado en los espacios topológicos generales, comparado con lo que pasa en espacios métricos.
La definición de convergencia es aquella de espacios métricos, pero usando solamente abiertos.
Definición. Sea X un espacio topológico, s=(s_n) una sucesión de puntos de X y p un punto de X. Decimos que la sucesión (sn) converge o tiende a p, ssi, para cada vecindad de p, casi todos los términos de lasucción pertenecen a la vecindad. En tal situación, decimos que p es un límite de los sn's.
A pesar de su similitud con la definición para espacios métricos, hay algunas diferencias significativas. Observemos, por ejemplo, que si tiene la topología indiscreta, una sucesión de puntos de tiene como punto límite a cualquier elemento de . Es decir que una sucesión puede converger a varios límites. La unicidad de límite requiere que el espacio sea Hausdorff; en tal situación hay un único límite. La demostración es análoga al caso de espacios métricos. (ver la proposición 7.2.1)
Proposición 8.6.1 En un espacio Hausdorff una sucesión tiene a lo más un límite.
Proposición 8.6.2. (Lema de la Sucesión). Sea un espacio topológico y un subconjunto de . Si es un punto límite de una sucesión de puntos diferentes de , entonces está en .
- Demostración. Por definición de límite, cada vecindad de contiene a casi todos los términos de la sucesión, por lo tanto, al menos un punto de diferente de .
Proposición 8.6.3. Sea una función continua. Entonces, para cada sucesión de , si converge a (no necesariamente único), entonces converge a .
- Demostración. Sea una vecindad de . Como es continua en , hay una vecindad de tal que está contenido en . Como casi todos los están en , casi todos los están en .
Observación 8.3. Se puede verificar que los recíprocos de las proposiciones anteriores son válidos solamente cuando es metrizable o satisface el primer axioma de enumerabilidad (hay una base enumerable de abiertos en la vecindad de cada punto).
Ejercicios 8.6
[editar]- Explicar el significado del enunciado " no es un punto límite de la sucesión ".
- Sean una sucesión de un espacio . Sea una biyección de en si mismo y sea . Probar que si converge a , también lo hace . Es decir que el orden de los términos no afecta la convergencia ni el límite de una sucesión.
- Probar la proposición 8.6.4.
Ejercicios del capítulo 8
[editar]- Probar que A = {(x, y) : 2 < x < 5} es un abierto de R2.
- Probar que C = {(x, y) : 2 < x < 5,-1 < y < -1} es un abierto de R2.
- (T1–topología de R) Sea A consistente del conjunto vacío y los complementos de subconjuntos finitos. Probar que A es una topología de R con respecto a la cual R no es Hausdorff. Denotaremos por RT1 a los Reales con esta topología. ¿Es id : R → RT1 continua? ¿abierta? ¿homeomorfismo?
- (Funciones Abiertas)
- a) Dar ejemplo de una función continua que no sea abierta.
- b) Dar un ejemplo de una función abierta que no es continua.
- c) Probar que la composición de dos funciones abiertas es abierta..
- (Funciones Cerradas)
- a) Dar ejemplo de una función continua que no sea cerrada.
- b) Dar un ejemplo de una función cerrada que no sea continua.
- Sea X un espacio topológico con topología T y sea X* = X ∪ {p}, donde
p no está en X.
Sea T* = {∅} ∪ {A ∪{p} : A ∈ T }. Probar que T* es una topología de X* tal que un subconjunto F de X es cerrado respecto a T, ssi, es cerrado respecto a T*. - Sea F un subespacio cerrado de X. Si f: X → Y es una función cerrada, entonces la restricción de f a F también es cerrada.
- Sea X un conjunto y sea (V{x}), x ∈ X, una familia no vacía de subconjuntos
de X tales que para cada x de X se cumple que:
- (1) x está en cada conjunto de V{x};
- (2) si A está en V{x} y B ⊂ A, entonces B está en V{x};
- (3) la reunión de una familia cualquiera de conjuntos de V{x} es un elemento de V{x}.
- (4) la intersección de una familia finita de conjuntos de V{x} es un conjunto de V{x}.
- (5) para cada A en V{x} hay un B en V{x} tal que A está en V{y} para cada y en B.
- Sea X un espacio topológico y Y un subespacio de X. Sea A un subconjunto de Y . Si A es abierto (resp. cerrado) en X, ¿lo es respecto a Y ?










![{\displaystyle t\mapsto {\sqrt[{3}]{t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/250f57cb6c0dbd48cadf77d2137db8c4492e78c1)




























