Matemáticas Universitarias/Espacios Métricos/Productos y Cocientes
Recordemos que espacio quiere decir espacio topológico, a menos que se indique algo distinto.
Introducción
[editar]Este capítulo está dedicado a la construcción de nuevos espacios a partir de espacios dados. Una construcción básica es la de subespacio, que vimos en el capítulo anterior. En este capítulo, veremos en la sección 9.3 como proveer de topología a un producto cartesiano de espacios. Luego, veremos en la sección 9.4 como proveer de topología a un conjunto cociente de un espacio. Finalmente, en la sección 9.5, veremos algunas construcciones interesantes.
Los Espacios Productos
[editar]El producto cartesiano de conjuntos nos permite formar un conjunto a partir de dos o más conjuntos. Hemos vistos celdas en R2 que son producto de dos intervalos reales. La representación gráfica de tal producto es un rectángulo con lados los intervalos factores. Tal representación nos es familiar y resulta adecuada y confiable para muchos aspectos. Consideremos sin embargo, la siguiente situación A ={a,b,c}, a, b, c arbitrarios, y B un segmento rectilíneo tal como [0,1] ¿cuál de las siguientes representaciones gráficas es la más adecuada?

La respuesta lógica es cualquiera de ellas, no hay nada que nos indique lo contrario. Simplemente, usos tradicionales pueden favorecer una de ellas.
Ejemplo 9.2.1 (Cilindro) Si tomamos el producto cartesiano de la circunferencia unitaria S1 del plano con un intervalo, digamos [0,1], queremos pensar tal producto como un cilindro (sin tapas). Ver la siguiente figura

Sin embargo, las consideraciones anteriores nos dicen que va a depender de como se ubiquen los segmentos respecto a la circunferencia, queremos para un mismo y del segmento, los puntos (x1,y) y (x2,y) estén próximos cuando x1 y x2 lo estén en la circunferencia. En otras palabras, necesitamos una topología que pegue continuamente a los segmentos sobre la circunferencia.
El Producto Cartesiano de Conjuntos
[editar]Antes de introducir topología en un producto de espacios, revisaremos alguno hechos acerca del producto de conjuntos. Nos interesa considerar la generalización del producto de dos elementos a un producto de una familia cualquiera de conjuntos.
Supongamos que tenemos una familia [1] de conjuntos (Xi), i ∈ I. Cuando uno de los Xi sea vacío el producto será el conjunto vacío. En caso contrario, llamamos producto (cartesiano) de los Xi's al conjunto denotado por
y definido como el conjunto formado por todas las familias (xi), i ∈ I, tales que xi, es un elemento de Xi <ref>Suponemos la existencia de tales familias. Formalmente, para un conjunto de índices arbitrario, tal suposición requiere de un axioma especial llamado Axioma de Selección.} Cada uno de los Xi's es un factor del producto. Si k está en I, y x=(xi) es un elemento del producto, decimos que x_k es la coordenada o componente k (o k--ésima) de x. El producto anterior se presenta acompañado de una familia de funciones: las proyecciones, pri :X → Xi, que asocian a cada punto del producto, su i--ésima coordenada.
Claramente, esta noción de producto es una generalización del producto cartesiano usual, ya que podemos considerar a un par (x1, x2) como una familia con conjunto de índices I = {1,2} tal que xi está en Xi.
El producto cartesiano tiene la siguiente propiedad universal.
Proposición (Propiedad Universal del Producto Cartesiano) Sea (Xi), i ∈ I una familia de conjuntos no vacíos y sea X su producto, con las proyecciones pri. Sean Z un conjunto y fi :Z → Xi, i ∈ I, una familia de funciones. Entonces, hay una única función f: Z → X tal que pri ◦ f = fi (*).

- Demostración. Sigue de la relación (*) que tal f debe cumplir con f(z) = (fi(z)) lo que muestra su unicidad y existencia.
Los Espacios Productos
[editar]Volvamos a la consideración del rectángulo R = [a,b] x [c,d] (o región rectangular, si se prefiere) que representamos gráficamente en la figura 9.2.

Esa representación, que es estándar, tiene varios supuestos implícitos. En primer lugar, suponemos que el rectángulo R esta contenido en un plano. En segundo lugar hay una suposición de preservación de cercanías.
Dos puntos, digamos (x1,y1) y (x2,y2) están próximos en la representación, cuando sus primeras coordenadas (x1 y x2) y sus segundas coordenadas (y1 y y2) lo están. Esto quiere decir que tenemos asociada a la imagen una topología. Puntos próximos en los factores, generan puntos próximos en el producto. Con esta idea en mente, veremos como, de forma general, podremos asociar una topología en el producto cartesiano de dos espacios topológicos que esté relacionada con la topología de los factores. La construcción que haremos tiene muchos usos en geometría y topología.
Sean X1, X2 espacios y sea X = X1 x X2.
Sean pri : X1 x X2 → Xi, (x1,x2) ↦ xi, i=1,2. las
proyecciones naturales del producto en sus factores. Las consideraciones
intuitivas de la discusión anterior sugieren que debemos poner una topología en el producto de
manera tal que esas funciones sean continuas. Naturalmente la topología discreta en el producto haría esas funciones continuas, pero no sería muy útil, ya que las proyecciones y cualquier otra función serían continuas; por lo que no habría una relación natural entre la topología de los factores y aquella del producto.
Por lo que definiremos como topología producto a la topología menos fina entre las topologías que hacen que las proyecciones sean continuas. Es decir que las preimágenes de abiertos de los factores serán abiertos en el
producto. Con esa definición, resulta que las celdas serían intersecciones de abiertos como los anteriores. En efecto, cuando U1 y U2 sean abiertos de X1 y X2 respectivamente, U1 x U2 es un abierto en X1 x X2, ya que
La topología producto deberá tener, por lo tanto, a las preimágenes de los abiertos de los factores como una subbase.
La definición anterior de producto puede generalizarse fácilmente a una familia
finita de espacios topológicos. ¿Qué pasa cuando tenemos una familia arbitraria
(<Xi, Ti>), i ∈ I, de espacios topológicos?
Siguiendo lo hecho con el producto cartesiano de dos conjuntos, definimos la
siguiente topología producto general.
Definición. (Topología Producto) Sea (Xi), i ∈ I, una familia no vacía de espacios no vacíos y sea X su producto de conjuntos. Llamamos topología producto de X a la topología menos fina tal que las proyecciones sean continuas. Llamamos espacio topológico producto de los Xi's a X provisto con esta topología.
Sea X = ∏i X_I el espacio topológico producto de los Xi's.
La definición implica lo siguiente.
- Para cada abierto U de X_k, prk-1(U) es abierto en X. Tales preimágenes, con k en I cualquiera, forman una subbase de la topología del producto.
- Cada intersección finita de cada uno de esos abiertos se llama un abierto básico, porque forman una base de la topología producto.
- Un abierto del producto es un producto Π i ∈ Ui, donde cada Ui es un abierto en Xi, igual a Xi, excepto por una cantidad finita de los Ui's. (Recordemos que solamente las intersecciones de finitos abiertos tienen garantía de ser abiertos.)
- Cuando U es un abierto de X, se cumple que pri(U) (por la observación anterior) es un abierto de Xi; o sea que las proyecciones son funciones abiertas
- Tomando complementos, resulta que un conjunto cerrado es un producto prodi Fi donde los Fi son cerrados en Xi, iguales a Xi, excepto para una cantidad finita de los i.
- Cuando tenemos un producto de una familia finita de conjuntos, un abierto del producto es un producto de abiertos de los factores. Análogamente para los conjuntos cerrados.
Proposición (Propiedad Universal del Producto Topológico)
Sea (Xi), i ∈ I, una familia de espacios topológicos y sea fi :Z → Xi, i ∈ I, una familia de funciones continuas. Entonces, hay una única función continua f: Z → ∏i Xi tal que pri o f = fi, para todo i.

- Demostración. La existencia y unicidad de f proviene de la propiedad universal del producto cartesiano de conjuntos. Solamente necesitamos probar que f es continua. Sea U un abierto tal que U = pri-1(V), V un abierto de Xi---es decir que U es un abierto de la subbase que define al producto. Entonces,
Lo que prueba que f-1(U) es un abierto. La continuidad de $f$ sigue, entonces, de la proposición 8.4.4 parte (a), que garantiza la continuidad cuando se la comprueba la continuidad para los abiertos de una subbase.
Corolario 9.3.2 El producto topológico es único, excepto por homeomorfismo.
- Demostración. Sean P y P' productos topológicos de una familia Xi de espacios topológicos. Sigue de la proposición anterior aplicada a P como producto que hay una función continua f:P' → P tal que prif= { pri}'.
Simétricamente, tenemos una función continua g: P → P' tal que { pri}'g = pri. De donde se deduce que
pri fg = pri'g = pri Por la unicidad de la función anunciada por la proposición tenemos que fg=idP. Análogamente, gf=idP'. Luego, f y g son biyectivas, continuas, una inversa de la otra, por lo que son homeomorfismos.
Corolario 9.3.3 Sea f: Z → X una función de un espacio en el producto X = prodi Xi. Entonces, f es continua, ssi, la composición de f con cada proyección es continua.
-
Demostración. Ejercicio. (Mirar la demostración de la
proposición 6.5.5)
Producto de Funciones
[editar]Sean fi : Xi → Yi, i=1,2, un par de funciones. Llamamos producto cartesiano de esas funciones a la función de X1 x X2 → Y1 x Y2 denotada por f1 x f2 y tal que (f1 x f2) (x1, x2) := (f1(x1), f2(x2)).
Proposición 9.3.4 El producto cartesiano de dos funciones continuas (resp. abiertas) es un función continua (resp. abierta).
- Demostración. Ejercicio.
|
Cuando X y Y tienen una cierta propiedad topológica ¿qué podremos decir de su producto? |
El Conjunto de Cantor
[editar]Presentamos en esta sección a un subconjunto muy interesante de los Reales, que usaremos para ejemplos y ejercicios más adelante. Resultará que el llamado "conjunto de Cantor será una extraordinaria figura plana, que por su estructura parecerá desafiar algunas de nuestras intuiciones geométricas preconcebidas---que están usualmente basadas en nuestras intuiciones preconcebidas a partir de los espacios Euclídeos de dimensiones 2 y 3.
Presentaremos inicialmente tres objetos geométricos, que posteriormente veremos son homeomorfos entre sí. La primera versión es un producto infinito de espacios topológicos.
Producto de Espacios Discretos. Sea An = {0,2}, n ≥ 1, una familia de espacios, todos iguales entre si, con dos elementos y la topología discreta. Sea
Expansiones Ternarias Especiales. Sea
Podemos pensar a C3 como las
expansiones ternarias (es decir, usando 3 en lugar de 10) para las expansiones de
los números reales en [0,1] donde la cifra 1 no aparece.
Recordemos que en las expansiones decimales (base =10) se cumple que 0.9999 ... = 1, lo que permite exigir unicidad en la representación, cuando las expansiones decimales finitas se reemplazan usando la igualdad anterior, para tener siempre expansiones decimales infinitas no nulas para los racionales diferentes de 0.
Análogamente se tiene en expansión ternaria que 0.222223 =1 . En efecto, 0.2222 ... 3 es una serie geométrica de razón 1/3 con termino inicial 2/3, por lo que su suma es igual a
Adoptando el convenio anterior, reemplazaremos expansiones ternarias finitas o adonde aparezca unj 1, por expansiones infinitas con ... 2222 ...3, excepto para el 0. Se tiene que C3 representa a todos los números reales en [0,1] cuya expansión ternaria no contiene 1's.
Notemos que la correspondencia es una biyección de CP en C3.
Presentación Gráfica. Esta presentación es más fácil de visualizar. Se basa en el siguiente procedimiento de división de un intervalo cerrado: dividir al a intervalo cerrado en tres partes iguales, y eliminar el interior de los subintervalos del centro para quedarse con los intervalos cerrados de los extremos. Para la construcción empezamos con el intervalo [0,1] y aplicamos el prpcedimentyo a es intervalo. Continuamos aplicando reiteradamente a cada intervalo cerrado que vaya apareciendo.
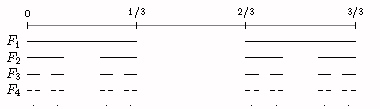
El proceso comienza con el intervalo I = [0,1]. Aplicando el procedimiento descrito, obtenemos
Dividamos cada uno de los intervalos de F1 y formemos F2 como arriba, o sea excluyendo el interior del subintervalo del centro. Es decir que,
Continuando de esta manera, generamos una sucesión (Fn) de conjuntos cerrados en R. Llamamos Conjunto de Cantor a la intersección de todos los Fn y que simbolizaremos aquí por .
¿Qué podemos decir de ? Después de todas las exclusiones,¿quedará algo? Observemos que los puntos de los extremos de los subintervalos son preservados en las sucesivas divisiones, así que 1/3, 1/9, ..., 1/3^n, ... son todos puntos de . No son los únicos puntos como se puede verificar. En F1 están todos los números tales que la primera cifra de su expansión ternaria no es 1. Recordemos que 1/3 = 0.02222...3. En F2 se eliminan todos los números cuya segunda cifra en la expansión ternaria es 1. y así sucesivamente. Lo que muestra que este conjunto coincide con C3
Como cada Fn es una reunión finita de intervalos cerrados, Fn es cerrado. Por lo que su intersección, es un subconjunto cerrado de [0,1] ⊂ R.
Sea α un punto de , entonces cualquier intervalo abierto centrado en α contiene números cuya expansión ternaria tiene al menos un 1, por lo que ese intervalo no puede estar contenido en . Es decir que el conjunto de Cantor no tiene puntos interiores (o sea que es nunca denso).
Computemos el largo de la reunion de intervalos removidos, sumando los largos de los segmentos removidos.
La serie es geométrica con razón 2/3 y término inicial 1/3, luego
Ese resultado implica que el largo de lo que queda, que debe ser igual al largo del segmento [0,1], o sea 1, menos el largo de lo removido, lo que nos dice que el largo del conjunto de Cantor debe ser 1-1=0. !!!!!
Cardinalidad. La cantidad de elementos del conjunto de Cantor es infinita, como fue observado anteriormente. Sin embargo, se trata de un infinito comparable al de los Reales, que es mayor que el infinito de los Naturales. Para ver lo anterior, basta considerar cada expansión ternaria de un elemento de
y cambiar cada 2 que allí aparece por 1. El resultado son todas las expansiones binarias (base 2) de los números en [0,1], que muestra lo indicado.
Largo del Conjunto de Cantor}. El Conjunto de Cantor es un subconjunto de los reales que contiene infinitos números entre 0 y 1, ambos extremos incluidos. Resulta natural preguntarse por su largo. Computaremos dicho largo, mirando al largo de su complemento, que restaremos de 1 (el largo del intervalo [0,1]).
Computemos el largo de la reunion de intervalos removidos, sumando los largos de los segmentos removidos.
La serie es geométrica con razón 2/3 y término inicial 1/3, luego
El largo del Conjunto de Cantor debe ser igual al largo del segmento [0,1]---o sea 1---menos el largo de lo removido, o sea 1-1=0. !!!!!
Ejercicios 9.3
[editar]Cuando Z = X x Y, prX, prY denotan las proyecciones sobre X (Z → X) y sobre Y (Z → Y), respectivamente.
- (Propiedades del Producto de Conjuntos) Sean A, A1, A2 ⊂ X y B, B1, B2 ⊂ Y. Se cumple que
- (A1 ∪ A2) x B = (A1 x B) ∪ (A2 x B).
- (A1 ∪ A2) x (B1 ∪ B2) = (A1 x B1) ∪ (A1 x B2) ∪ (A2 x B1) ∪ (A2 x B2).
- (A1 ∩ A2) x B = (A1 x B) ∩ (A2 x B).
- (A1 x B1) ∩ (A2 x B2) = (A1 ∩ A2) x (B1 ∩ B2).
- (A1 x B1) \ (A2 x B2) = (A1 \ A2) x B1 ∩ A1 x (B1 \ B2).
- (A x B)c = Ac x Y ∪ X x Bc.
- Sea A ⊂ X, entonces prX-1(A) = A x Y ⊂ X x Y.
- (Funciones y Producto Cartesiano) Sea f:X → Y. Llamamos
gráfico de f al subconjunto Γ f de X x Y tal que
- Un subconjunto Z de X x Y es el gráfico de una función X → Y, ssi, para todo a en X se cumple que Z ∩ {a} x Y contiene exactamente un punto.
- Sea f:X → Y, A ⊂ X, B ⊂ Y.
- f(A) = prY ( Γ f ∩ (A x Y )) = prY ( Γ f ∩ prX-1 (A)).
- f-1(B) = prX( Γ f ∩ (X x B)).
- La restricción de prX a Γ f es una biyección.
- La restricción de prY a Γ f es inyectiva, ssi, f es inyectiva.
- Sea H la hipérbola {(x,y): xy=1}. Probar que H es cerrado en R2, pero que su proyección en el eje X no lo es. Es decir que las proyecciones canónicas no son funciones cerradas.
- Sean X, Y y Z espacios topológicos. Probar los enunciados
siguientes.
- X x Y ≅ Y x X.
- X x (Y x Z) ≅ (X x Y) x Z ≅ X x Y x Z.
- X x {p} ≅ X.
- X ≅ Y ⇒ X x Z ≅ Y x Z.
- Probar que Rn con la topología usual es homeomórfico con el producto de n copias de R. Análogamente, el cubo unitario In (como subespacio de Rn) es homeomorfo al producto de n copias del intervalo I=[0,1].
- Probar que f:X → Y es continua, ssi, la proyección de X x Y sobre X restringida a Γf es continua.
- Sea W ⊂ X x Y. Si W es abierto entonces prX(W) es abierto. Concluir que las proyecciones son funciones abiertas. ¿Son funciones cerradas?
- Sea Z = X x Y. Sean A ⊂ X y B ⊂ Y.
- A x B es abierto en Z, ssi, A es abierto en X y B es abierto en Y.
- A x B es cerrado en Z, ssi, A es cerrado en X y B es cerrado en Y.
- Cl(A x B) = Cl(A) x Cl(B).
- ¿Será cierto que Int(A x B) = Int(A) x Int(B)?
- ¿Será cierto que Fr(A x B) = Fr(A) x Fr(B)? En caso negativo, hallar una fórmula para Fr(A x B)?
- Los resultados del ejercicio anterior se pueden generalizar al producto cartesiano de una cantidad finita de espacios topológicos. ¿Cuáles, si alguna, se pueden generalizar a un producto arbitrario de espacios topológicos?
- Probar que el producto de dos espacios Hausdorff es un espacio Hausdorff.
- Sea C el conjunto de Cantor. Probar que
- C no interseca a ]1/2,2/3[.
- C no interseca el intervalo para cualquier par de enteros s y k.
- Probar que el espacio de Cantor no es un espacio discreto, pero que su topología coincide con la topología producto (proyecciones son continuas).
- El ejercicio anterior muestra que el producto de infinitos espacios discretos no es necesariamente discreto. ¿Qué pasa con un producto finito de espacios discretos?
Los Espacios Cocientes
[editar]Conjuntos Cocientes
[editar]Sea X un conjunto no vacío y R una relación de equivalencia en X (o sea que es reflexiva, simétrica y transitiva). Llamamos R--clase de equivalencia o simplemente clase de equivalencia de un elemento x de X, al subconjunto de X denotado por [x] y que está formado por todos los y en X que son equivalentes (respecto a R) con X. Cada elemento de una clase de equivalencia se denomina un representante de la clase.
Las clases de equivalencia forman una partición de X, o sea una colección de subconjuntos no vacíos disjuntos entre si y cuya reunión es todo el conjunto.
En efecto, como cada x está en [x] (reflexividad) se tiene que las clases de equivalencia no son vacías y que su reunión es igual a X.
Supongamos que z fuera un elemento tanto de [x] como de [y]. Entonces, para todo w en [x] se cumple que w ∼ x, x ∼ z y z ∼ y, luego z ∼ y, o sea que w está en [y]. Conclusión, [x] ⊂ [y]. Por la simetría de la situación, tenemos que [y] ⊂ [x], por lo que concluimos que [x] = [y].
Llamamos partición} de un conjunto X a una familia de subconjuntos no vacíos de X disjuntos dos a dos y cuya reunión es todo el conjunto.
Los resultados anteriores muestran que cada relación de equivalencia en un conjunto induce una partición del conjunto cuyos elementos son las clases de equivalencia de la relación.
Supongamos ahora que tenemos una partición de X. Esa partición define una relación de equivalencia en el conjunto de la manera siguiente. Dos elementos están relacionados cuando, y solo cuando, pertenecen al mismo subconjunto de la partición. Cada conjunto de la partición es entonces una clase de equivalencia respecto a esa relación.
Sea X un conjunto cualquiera no vacío y R una relación de equivalencia. Llamamos conjunto cociente de X por la relación R al conjunto formado por todas las clases de equivalencias de R, al que denotamos por X/R. La función ν de X en X/R que asigna a cada x de X su clase de equivalencia se llama suprayección canónica o natural. o también la función cociente.
Ejemplo 9.4.1 Sea f:X → Y un función cualquiera. Definimos una relación x ∼f y en X cuando f(x)= f(y). Es fácil ver que se trata de un relación de equivalencia que denotamos por ∼f o Rf. Las clases de equivalencia son las preimágenes f-1(y), donde y está en f(X). Denotaremos al conjunto cociente por X/f.
El conjunto cociente tiene la siguiente propiedad universal.
Proposición (Propiedad Universal del Conjunto Cociente)
Sea ∼ una relación de equivalencia en un conjunto X y sea ν : X → X/ ∼ la suprayección canónica. Sea f:X → Y una función compatible con la relación de equivalencia---es decir que x ∼ y ⇒ f(x) = f(y), o equivalentemente f es constante en las clases de equivalencia. Entonces, hay una única función inyectiva f*: X/ ∼ → Y tal que f* ° ν = f cuya imagen es f(X). Cuando la función f es suprayectiva, f* es biyectiva.
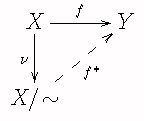
-
Demostración. En order de que f* o ν = f, se debe cumplir que f*([x]) = f(x). Solamente es necesario verificar que tal definición no depende del representante escogido en la clase [x]. Observemos que cuando y está en [x] se cumple, por las hipótesis, que f(y) = f(x), lo que prueba que f* está bien definida.
Notemos que f*([x]) = f*([y]) implica que f(x) = f(y). Lo que, a su vez, implica que [x]=[y]. Esto prueba la inyectividad de f*. Claramente si f es suprayectiva, se tiene que para todo y en Y, hay un x en X con f(x)= y, lo que implica que f*([x]]) = y, probando la suprayectividad de f*.
Nomenclatura. La función f* se dice que es la función deducida de f por paso al cociente.
Ejemplo 9.4.2 Sea g:X → Y un función suprayectiva cualquiera. El conjunto Y puede identificarse (como conjunto) con el conjunto cociente X/g. En efecto, por paso al cociente de g, se tiene que la función g^* :X/g → Y es una biyección.
Ejemplo 9.4.3 Definamos una relación ∼Z en R tal que x ∼Z y , ssi, x-y es un número entero. Claramente, esa relación es de equivalencia. Denotaremos por R/Z al correspondiente conjunto cociente.
Consideremos ahora a una función f : R → R periódica con (menor) periodo igual a 1, o sea tal que para todo t se cumple que f(t+1) = f(t). Probaremos que x ∼f y ⇔ x ∼Z y.
Debemos probar que para cualquier t, cuando m sea entero se cumplirá que f(t+m) = f(t) (*). Tal resultado es evidente si m=0 o m=1. Supongamos que m >0 y que se sabe que f(t+m) = f(t). Entonces, f(t+(m+1)) = f((t+m) + 1 ) = f(t+m) = f(t). Por inducción, tenemos entonces que la relación (*) es válida cuando m es positivo. Sea m <0, entonces f(t+m) = f(t+m + (-m)) = f(t); lo que concluye la prueba.
Por lo tanto, las clases de equivalencia de ambas relaciones coinciden, por lo que sus conjunto cocientes coinciden? ¿Qué más podemos decir del conjunto cociente R/Z (= R/f)? Esperemos a estudiar la topología de la situación.
Cocientes Topológicos
[editar]Sea X un espacio. Una relación de equivalencia R en X o lo que es lo mismo una partición (a veces llamada descomposición en algunos textos de Topología) definen un conjunto cociente, X/ R y una suprayección
ν: X → X/R. Nuestro propósito es dotar a X/R con una topología que haga que
la suprayección canónica sea continua. Claramente la topología indiscreta cumple con esa condición, pero no es la más interesante, ya que no refleja nada especial de la partición La respuesta adecuada será la topología cociente que definiremos a continuación.
Definición. (Topología Cociente) Sean ν: X → X/R como arriba. Llamamos topología cociente a la topología más fina que hace que ν sea continua. Esto es, la topología que contiene a todas las otras topologías en que ν es continua. Esto implica, que un subconjunto U de X/R es abierto, ssi, su preimagen por ν es abierto en X. En tal situación decimos que X/R es el espacio cociente relativo a la relación R o también respecto a la función cociente ν.
Es usual en Topología, llamar identificación a cualquier función f:X → Y entre espacios tal que la topalgia de Y sea tal que un subconjunto de A es abierto, ssi, f-1(A) es abierto. Esto implica que f es continua y que la topología de Y coincide con la topología de X/f, o sea que Y ≅ X/f.
La propiedad universal de los conjuntos cocientes produce una propiedad universal semejante para los espacios cocientes.
Proposición 9.4.2 (Propiedad Universal de los Espacios Cocientes)
Sea R una relación de equivalencia en el espacio topológico X. Sea ν la suprayección canónica sobre el espacio cociente X/R. Sea f:X → Y una función continua compatible con la relación R, o sea tal que x R y implica que f(x) = f(y). Entonces, hay una única función inyectiva continua f* : X /R → Y tal que f = f* o ν. Tal función es biyectiva cuando f es suprayectiva.
-
Demostración. La existencia de la función f* sigue de la propiedad universal de los conjuntos cocientes. Necesitamos tan sólo mostrar que se trata de una función continua. Sea V un abierto de Y y consideremos f-1(V), como
f es continua se trata de un abierto de X. Por la descomposición, f =
f* o ν, tenemos que
Lo que muestra que {f*}-1(V) es abierto, probando la continuidad de f*.
Veremos, en ejemplos, que aunque f sea suprayectiva, la función f* no es necesariamente un homomorfismo, a pesar de ser biyectiva.
Advertencia. Las topologías cocientes pueden, a pesar de la simpleza de su definición, ser bastante patológicas.
Ejemplo 9.4.4 Sean X = [0,2] ⊂ R, Y={0,1} y sea f:X → R tal que f(x) = 0 si x está en [0,1[ y f(x) = 1 si x está en [1,2]. El espacio cociente X/f tiene dos elementos, la clase del 0 y la clase del 1. ¿Cómo es la topología de X/f. Como ν-1([0]) = [0,1] se tiene que el conjunto que contiene solamente a la clase del 0 es un abierto en X/f. Vemos entonces que la clase del 1 es cerrado. Así que X/f tiene la topología de Sierpinski.
Notemos que f* es biyectiva, pero no es un homeomorfismo que Y (como subespacio de R tiene la topología discreta que es diferente de aquella de Sierpinski. Notemos que si f* es la función obtenida de f por paso al cociente, se tiene que f*([0]) = 0 y f*([1]) = 1; lo que muestra que f* es biyectiva, pero no es un homeomorfismo por la diferencia de las topologías.
El siguiente lema muestra que la condición sobre los abiertos de la topología cociente tiene una contrapartida equivalente con cerrados.
Lema 9.4.3 Sea f:X → Y una función entre espacios cualesquiera. Las siguientes propiedades son equivalentes.
- Un subconjunto A de Y es abierto en Y, ssi, f-1(A) es abierto en X.
- Un subconjunto A de Y es cerrado en Y, ssi, f-1(F) es cerrado en X.
- Demostración. Para cualquier función f:X → Y y subconjunto Z de Y se cumple que
De donde se obtiene en forma inmediata la equivalencia (a) ⇔ (b).
La próxima proposición da condiciones para que una función biyectiva, obtenida por paso al cociente, sea un homeomorfismo.
Proposición 9.4.4 Sea f:X → Y una función suprayectiva que es abierta o cerrada .La función f*: X/f → Y obtenida por paso al cociente de f es un homeomorfismo. Es decir que f es una identificación (función cociente)
- Demostración. Sea h= (f*)-1 y ν:X → X/f canónica. Observemos que para todo x en X, f*(ν(x)) = f(x) implica que ν(x) = h(f(x)), o sea que ν= h o f.
Sea U un abierto de X/f. Entonces, ν-1(U) es abierto, pero entonces, f-1(h-1(U)) = ν-1(U) es abierto, Como f es abierta, se tiene que f(f-1(h-1(U))) es abierto en Y, pero como f es suprayectiva,
h-1(U) = f(f-1(h-1(U))), lo que prueba que h es continua. Luego, f* es un homeomorfismo.
Razonamiento análogo para cuando f es cerrada.
|
Cuando X tiene una cierta propiedad, ¿qué podemos decir de un espacio cociente de X? |
Ejercicios 9.4
[editar]- Probar que dada una relación de equivalencia R en un espacio X, el espacio cociente X/R es único, excepto por homeomorfos. Es decir que dos espacios cocientes para la misma relación son siempre homeomorfos.
- Sea X un conjunto cualquiera no vacío. La relación de igualdad = es una relación de equivalencia en X. ¿Qué relación hay entre X y X /=?
- Sea h : [0,1) → S1 tal que f(t) = (cos(2π t), sen(2π t). Probar que h es biyectiva, continua, pero noes un homeomorfismo.
- Sea f:X → Y continua. Definir en X una relación ∼f por x ∼f y ↔ f(x) = f(y). Probar que ∼f es una relación de equivalencia y describir el espacio cociente.
- Sea X = R2 \ {(0,0)}. Definir relaciones R tal que (x,y) R (x',y'), ssi, hay un α >0 tal que x = α x', y = α y'. Probar que el espacio cociente es homeomorfo a una circunferencia.
- Probar que R2 ≅ S1 x ]0, +∞[.
- Sea f: R → R tal que f(x) = x2. Describir el espacio R/f (ver ejercicio anterior).
- Sea f: R → R tal que f(x) = sen(x). Describir el espacio R/f.
}}
Mirando al ejemplo 9.4.4, vemos que un espacio puede ser Hausdorff, pero su cociente no.
Construcción de Conjuntos
[editar]
Gran parte de los ejemplos consiste en hacer todos los puntos de un subconjunto del espacio equivalentes entre si. Sea X un espacio y A un subconjunto de X. Consideremos la partición de X formada por A y por un conjunto de un elemento, para los elementos en el complemento de A. Llamamos contracción de X por A al espacio cociente correspondiente, al que denotaremos por X/A.
Ejemplo 9.5.1 Consideración intuitiva: Sea X un intervalo cerrado de R, digamos [0,1]. Si pegamos 0 con 1, el resultado que se obtiene es una figura homeomórfica a una circunferencia.
Más formal, "pegar" quiere decir que queremos ``identificar 0 con 1. ¿Cómo podemos hacerlo? Simplemente usando una relación de equivalencia donde haya una clase de equivalencia que contenga al 0 y al 1; es decir, haciendo una contracción con A={0,1}. La correspondiente partición sería tal que cada x ≠ 0,1 aporta {x} a la partición, y el único elemento con dos elementos es {0,1}, Sea R la relación definida por esa partición, entonces X/R contiene un punto por cada x ≠ 0,1 y un punto donde se identifican 0 y 1. Notemos que usando la terminología de contracciones, el espacio cociente es [0,1]/{0,1}.
Busquemos una función continua suprayectiva f:[0,1] → S1 (S1 es la circunferencia unitaria) tal que f(0) = f(1) y f(x) = f(y) implica que x=y, cuando 0 < x, y <1. Si esa función es además abierta o cerrada, se tendría una identificación (proposición 9.4.4).
Una posible función es f:[0,1] → S1 tal que f(t) = (cos(2π t), sen(2π t)). Claramente, f es una función continua suprayectiva tal que f(0) = f(1). Sea g:X/f → S1, la función biyectiva que se obtiene al pasar f al cociente. Notemos que f es una función cerrada. Conjuntos cerrados básicos de X son [0,a] con 0 ≤ a < 1 y [b,1] con 0 < b ≤ 1. Entonces, claramente, f([0,a]), el arco desde P= (0,1) a Q=(cos(2π a), sen(2π a)) es un subconjunto cerrado de S1 (intersección de la bola cerrada con centro en el punto medio entre P y Q, de radio la mitad de la distancia de P a Q, con S1. Análogamente, para el otro conjunto cerrado básico. Luego, por la proposición citada, g : X/f → S1 es un homeomorfismo.
Ejemplo 9.5.2. Anteriormente, en el ejemplo 9.4.3, vimos que la relación x ∼Z y, ssi, x-y es un número entero, producía un espacio cociente que al denotamos por R/Z. Considerando al espacio cociente R/ f con f(t) = (cos(2π t), sen(2π t)) y procediendo como en el ejemplo anterior, concluimos que R/Z ≅ S1.
Ejemplo 9.5.3 Sean X, Y espacios topológicos y sea Z = X x Y. Sea x0 un punto de X, definamos una relación de equivalencia, por (x1,y1) R (x2, y2) ↔ y1 = y2.
Se puede observar que la clase de equivalencia de (x,y) consiste de todos los pares cuya segunda coordenada es igual a y. En la representación como ``rectángulo del producto cartesiano, se trata de segmentos paralelos (uno por cada y en Y) al eje de X. Se verifica que prY : X x Y → Y es una identificación, o sea que Y es homeomorfo al correspondiente conjunto cociente.
Ejemplo 9.5.4 (Cilindro) (Intuición) Consideremos un rectángulo y seleccionemos dos de sus lados opuestos. Cada línea paralela a uno de los lados no seleccionados corta a esos dos lados. Identifiquemos esos puntos de corte, o sea imaginemos que pegamos los lados opuestos haciendo corresponder tales puntos de corte. ¿Qué obtenemos? ... un tubo; formalmente llamado cilindro (sin tapas).
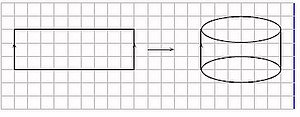
Suponiendo un rectángulo R con vértices (1,0), (1,1), (-1,1) y (-1,0). Definamos una relación en R por (x,y) ∼ (x',y'), ssi, x = 1, x'=-1, y=y' o x =-1, x'=1, y=y', si x &neq; 1 o -1, (x,y) \sim (x',y') solamente cuando x = x', y = y'. R es una relación de equivalencia. Las clases de equivalencia son {(x,y)} cuando x ≠ ± 1, y arbitrario, y {(-1,y)(1,y)}, y cualquiera. Una (función) identificación posible es: h: R → C: (x,y) = (cos(π x), sen(π x),y) donde C = S1 x [0,1] (cilindro).
Ejemplo 9.5.5 (Cinta (o banda) de Moebius) Consideremos nuevamente un rectángulo y seleccionemos dos lados opuestos. Peguemos nuevamente los lados opuestos, pero después de girar por media vuelta uno de ellos. Mirar la figura.

¿Qué obtenemos? ... una superficie conocida como ``cinta de Moebius. Si la lectora o lector no tiene experiencia con este objeto, una experiencia interesante será construir en papel una cinta de Medius (empezar con un rectángulo mucho más largo que ancho: una cinta y pegar los lados menores después de una media vuelta). El resultado será un modelo concreto de la cinta de Moebius. Después de hecho lo anterior, como curiosidad, cortar por el centro de la cinta obtenida ¿qué pasa? Un aspecto importante de la cinta es que tiene una solamente una cara.
Ejemplo9.5.6 (Toro) Una superficie muy interesante es aquella llamando toro, que resulta de hacer girar una circunferencia alrededor de un eje que no la corta. La palabra «toro» proviene del latín ``torus, que significa algo así como ``protuberancia.

Objetos de la vida real que tienen forma de toro son las superficies de los flotadores o de una rosquilla. Topológicamente,un toro se define como el espacio producto S1 x S1. Se puede, también, generarlo como espacio cociente de la manera indicada en la figura, empezando con un rectángulo, pegamos por lados opuestos, obteniendo un cilindro. Luego, pegamos las dos bocas del cilindro.
Ejemplo 9.5.7 (Plano Proyectivo). Sea X = R3 \ {(0,0,0)}. Definir una relación ∼ tal que (x1,x2,x3) ∼ (y1,y2,y3), ssi, hay un número real α ≠ 0 tal que xi = α yi, i=1,2,3. Claramente, la relación ∼ es de equivalencia. El espacio cociente, se llama el plano proyectivo y se denota por . Los puntos del plano proyectivo corresponden a líneas pasando por el origen y se simboliza por [x1:x2:x3] al punto que es la clase de equivalencia de (x1,x2,x3).
Un plano en R3 que pasa por el origen genera una línea del plano proyectivo.
Sea la función cociente natural. Para cada i = 1, 2, 3, sea
Se verifica que cada Ui es un abierto homeomórfico a R3.
Ejercicios 9.5
[editar]- Sea C el cilindro S1 x I donde I=[0,1]. Definir una relación de equivalencia (x,y) R (x',y), ssi, y' = y = 1.
Explicar por qué C/R puede ser llamado ``sombrero cónico.
- Probar que C/R es homeomorfo a un disco cerrado del plano.
- Sea A = {(x,y): y=1}, mostrar que C/A = C/R.
- Sea X el producto de una bola cerrada del plano con un intervalo cerrado, digamos . Si se define una relación R tal que (x,y,t) R (x',y',t'), ssi, t=t'=1, explicar por que podemos decir que el cociente X/R es un cono sólido. es la bola unitaria de \R2.
- Sea Bn cualquier espacio homeomorfo a la bola de radio 1 y centro el origen de Rn. Sea Sn-1 la esfera unitaria de Rn.
- Mostrar que podemos identificar Sn con un subespacio de Bn+1.
- Probar que Bn+1/Sn ≅ Sn+1.
- Probar que un toro y X = S1 x S1 son homeomorfos.
Ejercicios del capítulo 9
[editar]- Sean X={0,1} con la topología discreta y sea Y = X x X con la topología producto. Listar todos los abiertos de Y. ¿Es Y un espacio discreto?
- Sean X={0,1} el espacio de Sierpinski (topología = {∅,{0}, X}) y sea Y = X x X con la topología producto. Listar todos los abiertos de Y.
- En el texto se indicó que el producto cartesiano de dos funciones continuas era continuo. Cuando se tiene una familia f_α : X_α → Y_α , α en I, donde I es un conjunto arbitrario, podemos definir de manera análoga un producto f = ∏α fα tal que f ((xα ))= (fα (xα )). Cuando las fα son continuas, es f necesariamente continua?
- Sea Xi, i ∈ I una familia de espacios topológicos discreto y sea X su producto topológico. ¿Es X necesariamente discreto?
- Cuando g1, g2 son funciones abiertas, también lo es su producto g1 x g2.
- Sea X un espacio cualquiera e I = [0,1] ⊂ R. Sea A = {(x,1): x ∈ X } ⊂ X x I. Sea CX = X/A, el cono basado en X}.
- Si X= Sn entonces CX es homeomorfo a la bola cerrada de radio 1 y centro el origen, Bn+1, n ≥ 1.
- Sea I2 el cuadrado unitario de R2. ¿Cómo podría describirse CX?
- Escribir una relación de equivalencia R en X x I tal que CX = X x I / R.
- Sea X un espacio cualquiera. Se define una partición en X x I, donde I=[-1,1] ⊂ R, integrada por N = {(x,1): x ∈ X},
S = {(x,-1): x ∈ X} y cada punto en el complemento de S ∪ N generando una clase con un único elemento. El conjunto cociente se denota por SX y se llama la suspensión de X.
- Si X= S1 entonces SX= S2 la esfera unitaria de R3
- Si Y fuera un triángulo ordinario (unión de tres segmentos), ¿cómo podríamos describir a SY? ¿Que relación hay entre SY y SX.
- (Homeomorfismos)
- Probar que [0,1]/[1/4,3/4] ≅ [0,1].
- Describir el espacio cociente [0,1]/{1/3,1}. Comparar con una letra del alfabeto.
- Si el punto medio del lado curvo se identifica con el punto medio del segmento rectilíneo de la letra D, ¿qué letra obtenemos?
- Construir otros ejemplos análogos a las situaciones anteriores.
- (Proyección Estereográfica) Sea S la esfera unitaria tridimensional (x2 +y2 +z2 =1) pero sin su polo norte N = (0,0,1). Sea Y el plano z=0 Sea P un punto cualquiera de la esfera. La línea qua pasa por N y P corta el plano en un punto π(P). Probar que π es un homeomorfismo.
- ↑ Suponemos a menos que se diga lo contrario que las familias no son vacías.









![{\displaystyle F_{1}=[0,1/3]\cup [2/3,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec5136ef8c15235f000ece5aac11db7afc18e34)
![{\displaystyle F_{2}=[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1099cb543bd7eaa5b60a673999d892b2095fb98b)





![{\displaystyle ]{\frac {3s+1}{3^{k}}},{\frac {3s+2}{3^{k}}}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfa0756baf52cadd03513a9c09d579707de8e4cf)





![{\displaystyle U_{i}=\{[x_{1}:x_{2}:x_{3}]:x_{i}\neq 0\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/080f41097c69d5d3bd232a46f6d37391dc9420ff)
![{\displaystyle X=\mathbb {B} ^{2}\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa33539647944650545b7c851319dc23a362dc86)
