Matemáticas/Bachillerato LOGSE/Texto completo
- Introducción
- Aritmética
- Álgebra
- Resolución de triángulos
- Números complejos
- Geometría analítica
- Derivadas
- Integrales
- Vectores
- Combinatoria
- Introducción a la trigonometría
- Funciones
- Funciones elementales
- Funciones no elementales
- Sucesos aleatorios
- Distribuciones de probabilidad
- Distribuciones bidimensionales
Introducción
[editar]LOGSE: Ley Orgánica de Ordenación General del Sistema Educativo de España.
Aprobación: 3 de octubre de 1990.
Fue DEROGADA por la ley Orgánica de Educación (LOE), en el año 2006.
Aritmética
[editar]Números
[editar]
Números Racionales
[editar]Se dan por conocidos los números naturales . El conjunto de todos ellos se representa con la letra .
Los enteros () son los naturales y sus opuestos ..., -3, -2, -1, 0, 1, 2, 3, ...
La definición de números racionales es: tales que
Es decir, se dice que un número es racional si se puede escribir como la fracción de dos números enteros.
Los números racionales también se pueden detectar por su forma decimal ya que todos tienen una expresión finita o periódica.
son todos números racionales.
Representación de números racionales sobre la recta
[editar]Aproximación decimal de un número real
[editar]Podemos encontrarnos con números reales que tienen infinitas cifras decimales. ¿Cómo trabajamos con este tipo de números? Para esto hacemos una aproximación al orden de unidad que más nos interese. Existen distintos métodos tales como redondeo o truncamiento.
Intervalos y semirectas
[editar]Se intentará explicar aquí la nomenclatura que existe para designar algunos tramos de la recta real:
Expresión decimal aproximada. Errores
[editar]La motivación de este apartado no es otro que mostrar lo absurdo que puede ser tener muchas cifras significativas si podemos cometer errores de medida.
Por ejemplo la altura de una montaña no tiene sentido decir que es 1245,782m (7 cifras significativas) si hay un escarabajo paseandose por ahí o bien se produce erosión en la cima esa medida no sirve para nada, mejor sería decir que la montaña mide 1250m (3 cifras significativas) o 1245m (4 cifras significativas) si hay que ser preciso. Los dos últimos serían medidas aproximadas.
Cuando damos una medida aproximada el valor que damos no coincidirá en general con el valor exacto (que desconocemos y que normalmente ni siquiera es constante) esta diferencia entre lo real y el valor que damos es el error absoluto.
El error absoluto es desconocido porque el valor real también lo es, pero podemos acotarlo, esto es asegurar que por debajo de cierto valor seguro que no estará y que por encima de otro tampoco. Por ejemplo yo puedo decir que la montaña mide entre 1250 y 1240 metros esto quiere decir que el error que yo cometería sería inferior a 5 metros.
El problema del error absoluto es que engaña, no es lo mismo si digo que el error de medición de un bonsai que mide 0,4m es de 0,2 metros que si digo que el error de medición de una secuoya (de 20m) es de 0,2m. En el segundo caso casi ni se nota en el primero si. Para eso se tiene el error relativo que es la relación entre error absoluto y el valor real.
Notación científica
[editar]La notación científica es muy útil para expresar números muy grandes o muy pequeños.
Tiene tres partes:
- Una parte entera de una sola cifra
- Las otras cifras significativas como la parte decimal
- Una potencia de base diez que da el orden de magnitud de la cifra
Ejemplo:
Operaciones con números en notación científica
[editar]Productos
[editar]
Vemos que tanto el primer caso como el segundo son inmediatos esto pasa siempre con los productos, sin embargo habría que prestar atención al segundo ejemplo en el que hay que correr la coma hacia la izquierda y aumentar el exponencial para que la notación siga siendo científica.
Cocientes
[editar]
Sumas y restas
[editar]
Fijémonos en el método seguido: primero hemos puesto todas los números con un exponente común, y luego cuando ya lo hemos calculado todo lo hemos dejado en notación científica otra vez.
Álgebra
[editar]Ecuaciones de segundo grado
[editar]Seguramente ya se ha visto como resolver ecuaciones de segundo grado en cursos anteriores la motivación ahora es recordarlo y ampliarlo si es posible.
La forma general de las ecuaciones de segundo grado es:
con
Siendo a, b y c números reales
Y obtenemos la solución mediante:
Al radicando se le llama discriminante y se le nota . En función del signo del discriminante se tiene el número de soluciones reales de la ecuación, a saber:
- Si hay dos soluciones reales.
- Si hay una solución reala.
- Si no hay solución real, pero si dos soluciones complejas.
Si la ecuación es incompleta, esto es si b=0 o c=0 no es necesario aplicar la fórmula anterior:
se despeja
Ecuaciones bicuadradas
[editar]Son ecuaciones de cuarto grado pero tienen una característica que las hace especiales: no tienen terminos de grado impar, es decir son de la forma
El truco para resolverlas es hacer el cambio de variable entonces la ecuación quedará como una de segundo grado
La resolvemos, y entonces desechamos las ya que no dan solución en las pero las positivas nos daran dos valores de
Ejemplos
[editar]
Soluciones:
Soluciones:
Soluciones:
Ecuaciones con radicales
[editar]Hay veces que nos encontraremos con ecuaciones que tienen la x dentro de raices cuadradas para solucionarlas hay que aislar las raices una a una e ir elevando al cuadrado para eliminarlas.
Al elevar al cuadrado y buscar la solución aparecen soluciones debidas al proceso (de elevar al cuadrado para eliminar las raíces) estas soluciones son erroneas y hay que rechazarlas. Hay que hacer la comprobación en la ecuación inicial siempre para detectar las soluciones erroneas.
Ejemplos
[editar]
Se elevan al cuadrado los dos lados del igual
Comprobación:
Despejamos la primera raíz (Podíamos haber empezado por la segunda)
Se elevan al cuadrado los dos lados del igual
Aislamos la raíz
Se elevan al cuadrado los dos lados del igual
Comprobación
Nociones básicas para la factorización de polinomios
[editar]La motivación de este apartado es la misma que la que se podría encontrar para la factorización de números; factorizar un número cualquiera es muy útil para calcular el mcm y el MCD además de para simplificar fracciónes o sacar factores de un radical. Factorizar polinomios nos servirá para simplificar fracciones algebraicas, hacer el mcm y el MCD de los polinomios, que también los tiene, y si alguno va a la universidad le serán muy útiles (por ejemplo para hacer transformadas). El concepto fundamental para factorizar polinomios es el de polinomio irreducible, esto es en el cuerpo de los números reales, un polinomio sin raíces reales. Se puede comprobar (con ayuda del cálculo diferencial, por ejemplo) que cualquier polinomio de grado impar tiene al menos una raíz real, por tanto los polinomios irreducibles han de ser de grado par. Aplicando razonamientos sencillos con números complejos se puede deducir, además, que cualquier polinomio de grado par se puede expresar como producto de polinomios de grado dos. Por tanto, los polinomios irreducibles son los de primer grado y los de segundo grado cuyo discriminante es negativo. Tenemos así determinados los equivalentes a los números primos en el caso de los enteros, en el conjunto de los polinomios con coeficientes reales de variable real.
Podemos ver que:
es el polinomio factorizado. Un polinomio está factorizado cuando está expresado como productos de polinomios de menor grado posible es decir de la forma es decir como producto de polinomios de primer grado, y de como máximo de segundo grado cuando no existen soluciones en los reales.
En el ejemplo y serían raíces del polinomio.
Factorización de polinomios de segundo grado
[editar]Los polinomios de segundo grado se pueden factorizar de esta manera (teniendo en cuenta que tendrá como máximo 2 raíces reales):
- Si el polinomio tiene dos raices entonces
Ejemplo
- Si sólo tiene una raíz entonces
Ejemplo
- Si no tiene ninguna raíz real, su descomposición constará de dos factores de grado 1 con coeficientes imaginarios.
Ejemplo
Factorización de polinomios de grado mayor que dos
[editar]Imaginemos que queremos factorizar un polinomio de la forma Para hacerlo no tenemos la ayuda de una fórmula general como en el caso de los polinomios de 2º grado, para hacerlo no queda más remedio que ir encontrando las raíces una a una:
- Si un polinomio tiene raíces enteras estas tienen que ser divisores del término independiente.
- Si es una raiz del polinomio entonces se divide por obtenemos que es un grado menor y repetimos hasta llegar al grado menor posible (que siempre es 1 o máximo 2).
Para hacerlo más cómodo se emplea la regla de Ruffini.yii
Regla de Ruffini
[editar]Seguramente esto ya se ha visto anteriormente, por lo que aquí solamente lo refrescaremos.
Tenemos un polinomio como este y queremos dividirlo por
|
|
|
El resultado significa que el cociente de la división y el resto es
Teorema del resto
[editar]Imaginemos que hacemos la división de un polinomio por y nos da un resto que llamaremos , bien pues si hiciesemos en el polinomio es decir el resultado sería es decir Eoo
Este resultado se puede extender a polinomios de grado cualquiera.
Demostración
|
|
Localización de las raíces enteras de un polinomio
[editar]Tenemos un polinomio con raíces entera y queremos encontrarlas, para hacerlo tenemos que ir probando de dividirlo por , pero ¿qué valor puede tomar ? pues tiene que ser un divisor del termino independiente.
Intuitivamente podemos ver que tenemos que conseguir el opuesto del termino idependiente para hacerlo no queda mas remedio que multiplicar algo por a, por eso es necesario que a sea un divisor del termino independiente, ya que el termino independiente tiene que ser multiplo de .
Procedimiento para la factorización de un polinomio
[editar]Para factorizar un polinomio aplicaremos Ruffini sucesivamente hasta que nos quede un polinomio de segundo grado, cuando estemos en este punto aplicaremos la fórmula y obtendremos las dos últimas raíces o si es negativo sabremos que no lo podemos descomponer más
Ejemplo Tenemos el polinomio siguiente y queremos descomponerlo
- Primero sacamos y factores comunes:
- Ahora aplicamos Ruffini, los divisores de son Empezaremos probando con el
El resto es cero, fantástico, eso quiere decir que hemos encontrado una de las raíces.
- Seguimos aplicando Ruffini, probamos con 1
El resto es diferente de cero con lo que tenemos que seguir probando, con el -1:
El resto vuelve a ser diferente de cero, probamos con 2:
Fantastico, ya hemos encontrado otra raíz con lo cual el polinomio quedará de la siguiente forma:
- Finalmente para encontrar las dos últimas raíces utilizamos la fórmula para resolver polinomios de 2º grado:
Vemos que con lo cual podemos descomponer el polinomio y que sus raíces son 5 y -7. Entonces:
- Ya hemos descompuesto el polinomio. Ya que todos los factores son de primer grado
Resolución de ecuaciones por factorización de polinomios
[editar]Cuando un polinomio esta factorizado podemos encontrar las raíces facilmente, es decir podemos resolver ecuaciones de grado n.
Ejemplos
Queremos resolver la ecuación afortunadamente este es el mismo polinomio que en el apartado anterior con lo cual ya sabemos las soluciones, que son
Ahora queremos resolver
Sacamos factor común , aplicamos después Ruffini y encontramos las raíces 2 y -3 finalmente nos queda la ecuación no tiene solución, por eso no podemos descomponer más. Las soluciones del polinomio son: Como podemos ver aunque el polinomio es de grado 7 y debería tener 7 soluciones, dos de ellas no están porque hay una ecuación de segundo grado que no podemos descomponer.
Nota final
[editar]Aunque durante los dos últimos apartados se ha presentado los polinomios como fácilmente factorizables, no es así. Como norma general la raíz de un polinomio es un número no entero, 0,3242 por ejemplo, para encontrar estas raíces tiene que hacerse lo siguiente: Las soluciones racionales de una ecuación polinómica con coeficientes enteros se encuentran entre los números donde p es uno de los divisores del término independiente y q uno de los divisores del coeficiente director.
Ejemplos
Hallar las raíces de . Los divisores del termino independiente serán, en este caso, 1, -1, 2, -2, 4, -4 y del coeficiente director 1, -1. Por tanto las posibles raíces son 1, -1, 2, -2, 4, -4 que introduciendolos en el polinomio nos dara que la solución es 2. Hallar las raíces de . Ahora tenemos como divisores del término independiente 1, -1 y del coeficiente director 1, -1, 2, -2. De lo que tenemos como posibles soluciones 1/2, -1/2, 1, -1 e introduciendolas en el polinomio comprobamos que las soluciones son -1/2 y -1. El número de soluciones que faltan para correponderse con el grado de estas ecuaciones corresponde a soluciones de números complejos.
Aun con esto muchas veces tampoco podremos encontrar las soluciones de un polinomio como ya que se trata de soluciones irracionales a las que solo nos podemos aproximar, o soluciones de números complejos
Fracciones algebráicas
[editar]Una fracción algebraica es un cociente entre dos polinomios de la forma y funcionan casi igual que las numéricas.
Simplificación
[editar]Al igual que con las numéricas podemos dividir el denominador y el numerador por el mismo polinomio y de esta manera simplificarla.
Ejemplo
Fracciones equivalentes
[editar]Son aquellas que al simplificarse dan la misma fracción o aquellas que al dividirlas entre si dan como resultado 1
Ejemplo
y són equivalentes ya que las dos dan 1 al dividirse entre si o también se puede ver porque al simplificarse las dos dan
Reducción a común denominador
[editar]Supongamos que queremos sumar
Para hacerlo primero debemos reducir a común denominador, para hacerlo multiplicamos el denominador y el numerador de una por el denominador de la otra, esto es:
Suma resta multiplicación y división de fracciones algebraicas
[editar]- Suma (y resta): Ya hemos visto en realidad un ejemplo de suma de polinomios el metodo es
Ejemplo:
- División: Se multiplica la fraccion dividendo por la inversa de la fracción divisor
Ejemplo:
Ecuaciones exponenciales y logarítmicas
[editar]Ecuaciones exponenciales
[editar]Las ecuaciones exponenciales son las que tienen la incógnita en el exponente. Para sacarlo de allí hay que expresar lado y lado del igual con una potencia de la misma base y si esto no se puede hacer entonces se recurre a los logaritmos, aun así hay algunas en las que deberemos usar el ingenio y otras (aunque aquí no veremos ninguna) no se pueden resolver analíticamente.
Ejemplos
Si factorizamos nos damos cuenta de que es y que por lo tanto La cosa queda como sigue:
Ponemos el segundo miembro como potencia de es decir:
Al no poder escribir 3 como potencia de 5 debemos coger logaritmos
Hacemos un cambio de variable
Ecuaciones logarítmicas
[editar]Son las que tienen la x dentro de un logaritmo. Para resolverlas uno debe coger las propiedades de los logaritmos y utilizarlas para resolver la ecuación, muchas veces (aunque no veremos ninguna) no se pueden resolver analiticamente. Hay que comprobar la ecuación inicial
Ejemplos
Nota curiosa: Fijemonos que si la ecuación inicial hubiese sido las dos soluciones serían correctas.
Sistemas de ecuaciones
[editar]Se supone que el alumno ya está familiarizado con los sistemas de ecuaciones, por eso simplemente repasaremos los procedimientos y unos cuantos conceptos.
- Para que un conjunto de valores sea solución de una ecuación ese conjunto de valores debe cumplirla, por ejemplo para: una solución podria ser pero también
- Un sistema de ecuaciones es un conjunto de ecuaciones en las que siguiendo unos pasos podemos encontrar una solución común
- Un sistema de ecuaciones con más incognitas que ecuaciones suele tener infinitas soluciones
Ejemplos
[editar]Lo resolveremos mediante substitución, tomamos la primera ecuación despejamos la y:
Ahora substituimos y en la segunda ecuación:
Resolvemos la ecuación con una incognita, primero elevando al cuadrado los dos miembros
Aplicamos el metodo de reducción sumamos las dos ecuaciones:
Por tanto si
Resolvemos por igualación
Sistemas de tres ecuaciones (método de Gauss)
[editar]El método de Gauss consiste en convertir un sistema de tres ecuaciones con tres incógnitas en un sistema con una 1ª ecuación de tres incógnitas, una 2ª ecuación de dos incógnitas y, por último una 3ª ecuación de solo una incógnita. Por lo que se reduce sustancialmte la dificultad del problema.
Ejemplo
En un primer paso, la primera ecuación se deja siempre igual, mientras que en las otras ecuaciones eliminamos el término de la x usando el método de la reducción con la primera ecuación.
Ahora no cambiaremos ni la 1ª ecuación ni la 2ª ecuación y anularemos el término y de la 3ª ecuación usando la reducción con la 2ª ecuación.
Ahora la resolución del sistema se convierte en una trivialidad. De la 3ª ecuación obtenemos z=2, que introducimos en la 2ª ecuación para hallar y=5, y por último introducimos z e y en la 1ª ecuación para hallar x=-1.
Resolución de triángulos
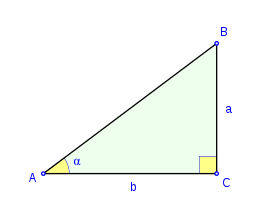
[editar]Razones trigonométricas de un ángulo agudo
[editar]
Si miramos el triángulo de la izquierda podemos describir tres razones que son intrínsecas de los ángulos agudos, ya que las razones sólamente dependen del ángulo debido al teorema de Thales.
- Gracias a estas definiciones podemos calcular razones trigonométricas aproximadamente dibujando y midiendo simplemente.
- Estas razones trigonométricas evidentemente no dependen del triángulo que tracemos sólo dependen del ángulo.
Ejemplo
[editar]
Tenemos un triángulo como el de la figura y queremos saber sus razones trigonométricas así que medimos sus tres lados a= 60mm b= 80mm c= 100mm
Relaciones entre las razones trigonométricas del mismo ángulo
[editar]Las razones trigonometricas, es decir el sin, cos, tan son dependientes, esto quiere decir que si sabemos una, sabemos las tres. Estas relaciones son las siguientes:
Relaciones trigonométricas fundamentales
[editar]
Nota importante: El cuadrado de estas razones no se expresa sino así Es conveniente que se aprendan, hay que tener en cuenta que la mayor parte (seguramente toda) de la literatura matemática usa esa notación.
Demostración
[editar]Ejemplos
[editar]Se conoce el y se quiere calcular cuánto valen
Se conoce la tangente de un ángulo y se quiere calcular cuánto valen
Utilización de la calculadora en trigonometría
[editar]Todas las calculadoras científicas del mercado disponen de teclas para las funciones trigonométricas seno, coseno y tangente. Sin embargo, es importante tener en cuenta dos factores de interés:
- En algunos modelos se introduce el valor del ángulo y luego se pulsa la tecla de la razón trigonométrica para obtener su valor, mientras que en otros se hace justamente al revés, primero se pulsa la tecla de la razón deseada, luego se introduce el valor del ángulo y por último la tecla de resultado (generalmente =) nos muestra el resultado en la pantalla.
- Las calculadoras científicas utilizan tres sistemas de medida angular, los radianes (RAD), los grados sexagesimales (DEG) y los gradianes (GRAD). Es muy importante tener en cuenta este factor, ya que no es lo mismo que o . La conversión entre los sistemas es la siguiente:
Resolución de triangulos rectángulos
[editar]Cuando decimos resolver un triángulo nos referimos a que encontramos todas sus magnitudes desconocidas, es decir la longitud de sus tres lados y la medida de sus tres ángulos, a partir de las conocidas.
Triángulos rectángulos
[editar]
Si un triángulo es rectángulo en realidad ya sabemos una cosa, que tiene un ángulo de 90º, así que nos hará falta menos información para resolverlo. Podemos resolver un triángulo rectángulo si conocemos:
- Dos lados
- Podemos calcular el tercer lado con el Teorema de Pitágoras
- Cuando sabemos lo que miden los tres lados es fácil encontrar los ángulos a partir de las razones trigonométricas y de la relación entre los ángulos de un triángulo.
Ejemplo

Tenemos este triángulo y sabemos que
- Un ángulo y un lado
- Los lados se calculan mediante la razón trigonométrica del ángulo que tenemos y con la longitud del lado que tenemos
- El ángulo que nos falta se calcula recordando que los ángulos de un triángulo suman entre los tres 180º siempre.
Ejemplo

Tenemos este triángulo y conocemos
Resolución de triángulos no rectángulos. Estrategia de la altura
[editar]
Queremos resolver un triángulo como el de la figura. Sabemos que miden dos de sus lados y el ángulo
Para resolverlo lo que hacemos es trazar la siguiente altura h, obtenemos así dos triángulos rectángulos:
Del primer triángulo (el 1) conocemos obtendremos x e y.
Para encontrar y aplicamos Pitágoras:
Y por fin:

Tenemos un triángulo como el siguiente y queremos encontrar que vale h, sabemos que:
con lo que tenemos
Que resulta:
Algunos resultados muy útiles
[editar]Esto que viene a continuación uno podria deducirlo. Pero igual que las tablas de multiplicar que se pueden deducir sumando repetidas veces un número es mejor memorizarlo ya que aparecen con frecuencia.
Proyección de un segmento

Cuando proyectamos un segmento sobre una recta la longitud de dicha proyección es la misma que la del segmento multiplicada por el coseno del angulo que formar segmento y recta.
Altura de un triangulo

Si cojemos cualquier lado del triángulo (que no sea la base) y lo multiplicamos por el seno del ángulo que forma este con la base obtendremos la altura del triángulo.
Area de un triangulo
El area del triangulo es la misma que la mitad del producto de dos de sus lados multiplicado por el seno que forman
Razones trigonométricas de ángulos obtusos
[editar]
Si queremos conocer las razones trigonométricas de un angulo obtuso , basta fijarse en la figura para ver que son fáciles de obtener, a través de su angulo suplementario
La tngente es un poco menos intuitiva, pero también es facil de entender: La tangente de un angulo obtuso es siempre negativa.
Resolución de triangulos cualesquiera
[editar]Podría parecer que este apartado es inútil debido a que ya se ha aprendido a resolver triangulos cualesquiera con la estrategia de la altura. Sin embargo existen dos teoremas que no agilizarán mucho las cosas sin que tengamos que hacer tantos pasos como con la estratégia de la altura.
Teorema del seno
[editar]
Intuitivamente uno puede ver que el angulo mayor de un triangulo tiene enfrente el lado mayor, y el angulo menor de un triangulo tiene enfrente el lado menor.
El teorema del seno dice esto precisamente, un poco más formalmente:
Si tenemos un triangulo de lados y ángulos
Se cumple que:
Demostración
[editar]
Lo demostraremos a partir de la estrategia de la altura.
Dibujamos la altura h desde el vértice C. Los triángulos APC y BCP son rectángulos los dos.
Tenemos que:
Para encontrar la igualdad trazamos h desde el vértice B y procedemos igual que antes.
Aplicaciones
[editar]Antes de continuar hay que advertir que cuando nuestra incognita sea uno de los angulos y apliquemos el teorema del seno hay dos soluciones debido a que los angulos suplementarios tienen el mismo seno. Tendremos que comprobar si las soluciones son validas.
- Triangulos cualesquiera con dos ángulos y un lado conocidos
Ejemplo

Tenemos un triangulo como el de la figura, y queremos resolverlo.
Conocemos un lado y dos ángulos ¿ cuanto miden los lados a y c.?
Sabiendo que:
Aplicando el teorema del seno:
con los valores numéricos:
tenemos:
y tenemos:
- Dos lados y el angulo opuesto de uno de ellos conocido
Ejemplo

Ahora nos encontramos con el siguiente problema:
Conocemos tenemos que encontrar
Con el teorema del seno:
y los valores:
sabiendo:
tenemos
y por fin:
Teorema del coseno
[editar]imagen por hacer Si cogemos un triangulo rectángulo y conservando la longitud de los catetos, el angulo de 90° lo disminuimos es intuitivo de que la "hipotenusa" se hará más corta, y si lo hago más grande esta se hará más grande. Pues esto es lo que nos dice el teorema del coseno, en realidad podríamos decir que el teorema del coseno es el teorema de Pitágoras versión 2.0

Tenemos un triangulo cualquiera, se cumple que:
Demostración
[editar]Dibujamos la altura h, perpendicular a b
Aplicamos Pitagoras a AHB y BHC
Se puede comprobar que tanto para todos los tipos de triángulos sale la misma fórmula.
Aplicaciones
[editar]Hay cuatro casos de problemas que se aconsejan resolver por el teorema del coseno
- Conocemos tres lados y queremos conocer cualquier angulo
- Conocemos dos lados y el angulo opuesto a uno de ellos y queremos conocer el otro lado
- Conocemos dos lados y el angulo que forman y queremos saber el otro lado
- Conocemos dos lados y el angulo que forman y queremos conocer otro angulo. Para este último caso deberemos aplicar el teorema del coseno primero para saber el lado que nos falta y después el teorema del seno para saber el angulo
Números complejos
[editar]Qué son los números complejos
Si intentamos resolver esta ecuación veremos que no tiene solución en números reales.
Para ello recurrimos a los números imaginarios o números complejos.
Sin embargo para entender mejor el problema y luego la solución, primero debemos recurrir a la ley de los signos en la multiplicación, al multiplicar dos signos negativos o dos positivos, el resultado es un numero positivo siempre, es decir si elevo al cuadrado cualquier numero sea positivo o negativo, el resultado es siempre positivo, por tanto no hay manera de encontrar la raíz de un numero negativo. es allí donde se da la solución introduciendo el valor imaginario,es decir aislando el termino insoluble y dejándolo tal como esta , pues si bien es cierto este no tiene solución y tampoco necesitamos que tenga solución, pues manteniéndolo tal como esta como una expresión matemática , nos sirve para dar la solución y se hace así: si mantengo este [sin necesidad de llamarlo i ] puedo operar: por ejemplo sería igual a .(-1) y como se puede aplicar propiedad distributiva a la raíz, se tiene: = . operando se tiene = 3.
esta es la solución, pero alguien me dirá, pero sigue ahí el problema, que no se sabe cuanto es exactamente , yo le respondo que si llamamos "i" a , entonces la solucion es 3i, y ésta solución pasa la prueba, porque en este caso si elevo al cuadrado esta solución, "ahora si me da un numero NEGATIVO" pues: es por = 9 por (-1) = -9
como ven, nunca se solucionó en realidad la raíz de un numero negativo, sino que se lo dejo en "durmiendo" para que cuando se aplique lo contrario ( el cuadrado o potencia par ) se elimine la raiz par y quede el MENOS 1 que hace negativo al numero solucion de un cuadrado o potencia par.
Operaciones con números complejos
[editar]- Suma
- Resta
- Multiplicación
- División
- Igualdad
Números complejos en forma polar
[editar]Paso de forma binómica a polar
[editar]Dado un complejo en forma binómica , definimos su modulo r como:
y su argumento como
La expresión la llamaremos forma polar del número complejo u.
Paso de forma polar a binómica
[editar]La parte real de un complejo es
y la parte imaginaria es
con lo cual su forma binómica será
Operaciones con números complejos en forma polar
[editar]La raiz de indice n de un numero complejo tiene n soluciones, todas ellas con el mismo modulo, que es la raiz n-esima del modulo de radicando y se obtienen al sumarle a este valor, 360/n sucesivas veces hasta completar una vuelta.
Referencias
[editar]Lección sobre Números Complejos (Con ejemplos graficos)
Geometría analítica
[editar]Definición
[editar]La recta L, determinada por los puntos A y B, es el conjunto de puntos P del plano XOY, tal que AP = kAB (1), o L= {P(x,y}/AP =kAB}.
- En efecto, AP= (x-x1, y-y1), AB= (x2-x1,y2-y1), kAB=(k(x2-x1),k(y2-y1)).
- Usando la ecuación (1) y comparando los pares ordenados respectivos resulta x-x1=k(x2-x1), y-y1 = k(y2-y1): Eliminando k se obtienen las formas
- Dos puntos
- Punto pendiente, definiendo este concepto como la razón la ordenada de AB sobre sobre su abscisa.
Ecuaciones de la recta
[editar]Cuando representamos una ecuación de primer grado en un gráfico de 2 dimensiones (dos ejes: ordenadas y abscisas) se hace una recta.
es la pendiente de la recta, coincide con la tangente del ángulo que forma la recta respecto al eje de abscisas.
es la ordenada de origen, el punto en el eje de ordenadas en el cual la recta corta. La parábola es el lugar geométrico de todos los puntos cuyas distancias a una recta fija, llamada directriz, y a un punto fijo, llamado foco son iguales
Aplicación de los vectores a problemas métricos
[editar]Problemas con rectas en paramétricas
[editar]Ecuación explicita de la recta. Pendiente
[editar]La ecuación explicita de la recta se obtiene despejando la "y" en la ecuación general de la recta (ax + by + c = 0):
Sustituyendo y obtenemos:
Donde es el coeficiente angular de la recta y es la intersección de la recta con el eje Oy.
Relacion entre las pendientes m1 y m2 de dos rectas r1 r2
[editar]Inclinación y pendiente. Dado un segmento cualquiera, la inclinación de ésta es el menor de los ángulos ()que forma con el semieje positivo X y se mide desde el eje hacia el segmento o la recta L. la inclinación es positiva si el ángulo se mide en el sentido contrario a las agujas del reloj, en caso contrario es negativo.
Posición relativa de dos rectas dadas en forma general
[editar]ACLARACION EXAGERADA Si la ecuación general de una recta es Ax + By + C = 0, se observa, que es una expresión de primer grado (o lineal) "toda ecuación de primer grado (en dos variables cuyo exponente es la unidad) tiene como gráfica una recta" determinados los coeficientes A, B y C, tenemos la ecuación de la recta. Lo mismos ocurrirá cuando determinemos las ecuaciones de las cónicas, "una vez encontrada la ecuación general, bastará determinar los coeficientes, para tener la ecuación particular a ese problema". Estos coeficientes se hallan en relación a propiedades y características de la curva, condiciones iniciales y de contorno, más los datos del problema.
Derivadas
[editar]Medida del crecimiento de una función
[editar]El resultado de derivar una función es una segunda función que nos indica el crecimiento de la función original. Esto es, en un punto determinado, la pendiente de la función original. Desde un punto de vista gráfico para facilitar su comprensión, una línea recta dibujada horizontalmente tiene una función, una ecuación, asociada como la siguiente: , donde n es un número. La derivada de esta función es 0, puesto que n es una constante. En este caso la derivada nos explica que la función ni crece ni decrece.
Ahora imaginemos una recta creciente de función , donde n (la pendiente) es un número positivo. Si derivamos la función obtendremos de resultado una constante de valor n (la pendiente de la función anterior). Siendo este número positivo sabemos que la función crece.
Conclusión: La derivada de una función nos dice la pendiente de la función.
¿Es esto siempre válido? Con matices. En el caso de las funciones de recta (polinomios de 1r grado) lo es porque independientemente del punto en el que derives el resultado es constante.
¿Y en el caso de curvas (polinomios de grado superior a 1 u otras funciones)? Es válido. PERO: La derivada genérica de la función nos devolverá una función derivada que nos dará toda la información del crecimiento de la función original, para cada punto de esta, por lo que para obtener la información de crecimiento en un punto concreto debemos evaluar la función derivada en ese punto. Es decir, nos dará la tasa de crecimiento de la función para puntos infinitesimalmente cercanos a 1.
Definición
[editar]Sea una función continua, y su curva. Sea la abscisa de un punto regular, es decir donde no hace un ángulo. En el punto de se puede trazar la tangente a la curva. Su coeficiente director, o sea su pendiente, es , el número derivado de en .
La función es la derivada de .

En el punto de contacto, conociendo la pendiente de la tangente, es decir , se puede saber a qué ritmo crece o decrece la función. El signo de determina si la función crece o decrece.

En este gráfico se ve que donde es creciente, las tangentes apuntan hacia arriba (mirando de izquierda a derecha), y por lo tanto es positiva, como en el punto (), mientras que donde es decreciente, las tangentes apuntan hacia abajo y es negativa, como en el punto (). En los puntos y , que son máximo y mínimo local, la tangente es horizontal, luego .
La función derivada se puede calcular sin dibujar la curva de . En efecto, gracias a una propiedad geométrica de la tangente, se tiene la fórmula:
Interpretación geométrica
[editar]
Sea una función cualquiera.
Si trazamos una recta entre dos de sus puntos, podemos hallar la Tasa de Valor Medio como los incrementos en la ordenada respecto de la variable independiente. Es decir, la pendiente de la recta secante a la función por los puntos es: , o de forma abreviada, .
Ahora acerquemos y uno al otro. Cuando se confundan en un punto, también lo harán la recta tangente con la secante. De este modo, por la definición de límite, tema de este curso, podemos hallar la función como sigue:
Esta es la definición formal de función derivada. Sale directamente de la fórmula de la pendiente, acercando los puntos y .
En resumen, la interpretación geométrica de la función derivada es: la función que nos devuelve la pendiente de la función original en cada punto.
Crecimiento de una función en un punto
[editar]Función derivada de otra
[editar]Reglas para obtener las derivadas de algunas funciones
[editar]Las reglas básicas que hay que conocer para derivar funciones tan complejas como uno quiera son:
- , siendo c=cte.
- , siendo c=cte. y f(x) cualquier función.
- , siendo n=cte no nula.
Y la regla de la cadena:
Aplicaciones de las derivadas
[editar]Dada una función que es derivada de otra función
se anula en los puntos donde hay un máximo o un mínimo en la función primitiva, o sea en esos puntos cambia el crecimiento de la función
La derivada segunda (derivada de la derivada) se anula en los puntos en los cuales se encuentran puntos de inflexión en la función original,que es donde cambia la curvatura de la función
Ejemplos
[editar]Ejemplo #1
[editar]Consideremos la siguiente función:
Entonces:
Esta función es constante, para cualquier punto de su dominio vale 5 (por eso f(x+h)=5). Nótese el último paso, donde h tiende a cero pero nunca lo alcanza. Si pensamos un poco, observaremos que la derivada además de ser la pendiente de la recta tangente a la curva, es a la vez, la recta secante a la misma curva.
Ejemplo #2
[editar]Utilizando la definición de derivada de una función, determinar la derivada de la función.
Sustituir datos:
Desarrollar:
Entonces, la derivada de la función es:
Ejemplo #3
[editar]Encuentra la derivada de:
Racionalizando:
Calculamos el límite:
Algunos ejemplos de cómo utilizar este cociente:
Ejemplo #4
[editar]Mediante esta diferenciación, se puede calcular la pendiente de una curva. Consideremos que:
Entonces:
Para cualquier punto x, la pendiente de la función es .
Ejemplo #5
[editar]Sea la función , definida sobre el conjunto de los números reales (denotado por ). Para conocer sus variaciones se observa su derivada:
Para encontrar el signo de , se tiene que factorizar:
lo anterior que se hace resolviendo una ecuación de segundo grado.
También se observa su segunda derivada:
Dado que y entonces tiene un mínimo local en 1 y su valor es .
Dado que y entonces tiene un máximo local en -4 y su valor es .
Nótese que la derivada es diferenciable en todo su dominio y hay exactamente 2 valores de tales que , los cuales son y , tomando en cuenta el teorema del valor medio y que entonces la derivada es negativa en el intervalo por lo tanto la función es decreciente en el intervalo .
Al ser una función basada en un polinomio cúbico no está acotada ni por arriba ni por abajo y como su derivada es una función cuadrática entonces no tiene más de 2 puntos con derivada igual a cero, por tanto la función es creciente en el intervalo y en el intervalo .
Véase también
[editar]http://ballz.ababa.net/silvana/derivada.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t3-DerivadaParcial/node1.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/derivada-direccional/node1.html
Integrales
[editar]Área bajo una curva
[editar]El concepto de integral proviene del deseo de conocer el área comprendida entre el eje de coordenadas y una curva, también llamada área bajo la curva. Originalmente para calcular dicha área se propuso dibujar rectángulos de altura y base conocidas para poder así sumar sus áreas. Obviamente el método no es exacto. Para obtener más precisión se han de hacer los rectángulos con una base más pequeña para que la diferencia sea cada vez menor. El único método exacto es crear rectángulos de base infinatamente pequeñas, usando diferenciales, con lo que se obtiene una serie de áreas infinitamente pequeñas. La integral es la suma de dichas áreas aprovechando las bases diferenciales, con lo que se eliminan las inexactitudes.
Relación analítica entre el area y la función
[editar]Iniciación al cálculo de primitivas
[editar]Regla práctica para el cálculo de integrales
[editar]Aplicaciones de las integrales
[editar]Vectores
[editar]Conceptos básicos
[editar]Es necesario conocer algunos conceptos: definición de vector fijo. Un vector fijo es un segmento orientado. Es decir, un par ordenado de puntos. El primero se denomina origen y el segundo extremo del vector. Cuando ambos puntos coinciden se denomina vector nulo.
 |
 |
Para describir un vector fijo se nombran su origen y su extremo con una flecha por encima:
Propiedades de un vector fijo:
MÓDULO: es la distancia entre su origen y su extremo. Se representa
DIRECCIÓN: es la clase formada por todas las rectas paralelas al vector. Dos vectores tienen la misma dirección cuando son paralelos y diferente cuando no lo son. Un vector nulo no tiene dirección.
SENTIDO: Entre dos vectores fijos con la misma dirección, la recta que une sus dos orígenes divide al plano en dos semiplanos. Si los extremos de ambos vectores están en el mismo semiplano, entonces se dice que los vectores tienen el mismo sentido, mientras que si están en diferente el semiplano tienen sentidos opuestos.
equipolencia Dos vectores fijos se dice que son equipolentes cuando tienen la misma dirección, el mismo módulo y el mismo sentido. Dicho de otra forma, dos vectores equipolentes se diferencian sólo en sus puntos de origen y extremo. La equipolencia establece una relación de equivalencia en el conjunto de todos los vectores fijo.
definición de vector libre Un vector libre es cada una de las clases de equivalencia establecidas en el conjunto de los vectores fijo por la anterior relación de equivalencia. Los vectores que forman parte de una misma clase de equivalencia tienen el mismo módulo, dirección y sentido, por lo que un vector libre se puede considerar como un vector sin origen ni extremo. Así pues, mientras que un vector fijo representa un desplazamiento concreto desde un punto del plano a otro, un vector libre representa un desplazamiento genérico en el plano, sin considerar el punto de partida. Por ejemplo: Mientras que un vector fijo sería el desplazamiento de Pamplona a Logroño, el correspondiente vector libre sería un desplazamiento de 85 km en dirección suroeste. Dos segmentos de recta dirigidos (flechas) con longitudes no nulas representan el mismo vector si y sólo si tienen la misma longitud y la misma dirección. Para denotar los vectores libres usaremos letras latinas con una barra encima. Si el punto inicial y terminal del vector son los puntos A y B respectivamente, también podemos escribir
Nombrar vectores y coordenadas de un vector
[editar]Un vector puebe nombrarse con una sola letra, que lo designa que se coloca junto a la flecha que indica el sentido.
 |
 |
Las proyecciones del vector sobre los ejes son las coordenadas del vector, respecto a ese sistema de coordenadas.
 |
 |
En el caso de dos dimensiones, en el plano x-y, las coordenadas del vector son: que se representa:
En un sistema de tres dimensiones de ejes x-y-z las cooredenadas del vector seran
 |
 |
¿Cómo hallar el módulo de un vector?
[editar]Bien. Ahora, regresemos al pasado y recordemos la fórmula del teorema de Pitágoras.
, para averiguar el modulo del vector vamos a aplicar la misma fórmula. Nos imaginamos que el modulo del vector es la hipotenusa de un triángulo rectangulo:
para este vector
Operaciones con vectores
[editar]1. PRODUCTO DE UN VECTOR POR UN NÚMERO.
Hacer esta operación no entraña ninguna dificultad, pero tienes que saber algunas cosas del vector resultante. Si K es un número real y un vector no nulo, el producto será otro vector con las siguientes características:
- Su módulo es igual al módulo de multiplicado por el valor absoluto de K.
- Su dirección es la misma que la de .
- Su sentido es el mismo de si K es positivo o el contrario si K es negativo.
- Cuando es el vector nulo, o K=0, el resultado es el vector nulo:
2. SUMAS Y RESTAS DE VECTORES.
Gráficamente pueden sumarse mediante el teorema del paralelogramo. Matemáticamente, se emplea la forma:
3. COMBINACION LINEAL DE VECTORES.
Definicion: dados dos vectores, X¯ e Y¯ y dos números A y B, el vector AX¯+BY¯ se dice que es una COMBINACION LINEAL de X¯ e Y¯.
Entonces tu lo haces gráficamente.... dibujas los vectores X¯ e Y¯ y el vector V¯ lo dibujas como si fuera el módulo de los anteriores... pero claro este será más grande que el módulo real de X¯ e Y¯ entonces tendrás que multiplicar los vectores X¯ e Y¯ por dos números hasta que el vector V coincida con el módulo de los nuevos vectores dibujados.
· DE ESTO SE SACA QUE: cualquier vector se puede escribir como combinación lineal de otros dos.
· Y que esta combinación de números (A y B) es única, es decir: no hay otra.
Coordenadas de un vector
[editar]1. BASE
Este es un concepto muy importante que te servira bastante de aqui en adelante.
· DEFINICIÓN: forman base dos vectores con distinta dirección, porque cualquier vector del
·plano se puede poner como combinacion lineal entre ellos.
TIPOS DE BASES:
B. ORTOGONAL. si los vectores que la forman son perpendiculares entre sí.
B. ORTONORMAL: es una base ortogonal cuyos vectores son además unitarios.
Aclaracion: un vector es unitario si su módulo es = 1
B. CANÓNICA: La base canónica es la más común de todas las bases y la que se usará a este nivel. Se caracteriza por estar formada por vectores unitarios que tienen todas las componentes nulas (iguales a 0) excepto una. Por ejemplo, la base canónica en el espacio es {(1,0,0);(0,1,0);(0,0,1)} y en el plano {(1,0);(0,1)}.
B. GENÉRICA: Los vectores que la forman no tienen por que ser ortogonales ni unitarios. Cambian algunas expresiones como la del producto escalar. No se usarán en este curso pero existen.
Producto escalar de vectores
[editar]siendo:
Existen dos fórmulas fundamentales:
- (Expresión geométrica)
- (Expresión algebraica)
Simplemente, aplica estas dos fórmulas según lo que te pidan. Y estúdiate las propiedades del producto escalar que seguro que vienen en tu libro.
Combinatoria
[editar]La combinatoria estudia las diferentes formas en que se pueden agrupar u ordenar los elementos de un conjunto. El punto de partida será el principio de la multiplicación o estrategia del producto.
Principio de la multiplicación o estrategia del producto
[editar]- Ejemplo 1: Un equipo de baloncesto tiene que elegir un nuevo uniforme. Para ello debe escoger entre 4 camisetas y 5 pantalones con diferentes colores. ¿Cuántos uniformes distintos se pueden componer con las camisetas y pantalones disponibles?
- Para resolver este problema hemos de tener en cuenta que cada una de las camisetas se podrá combinar con cada uno de los pantalones disponibles. Si tuviéramos una única camiseta, podríamos componer 5 uniformes diferentes, resultado de combinar dicha camiseta con cada uno de los 5 pantalones. Si tuviéramos 2 camisetas, podríamos componer 5 uniformes distintos para cada camiseta, resultado de combinar cada camiseta con cada uno de los 5 pantalones. Tendríamos por tanto 2 · 5 = 10 combinaciones posibles. Siguiendo el mismo razonamiento, llegaríamos a la conclusión de que con 4 camisetas y 5 pantalones, podríamos componer 4 · 5 = 20 uniformes diferentes.
Lo que hemos utilizado es lo que se conoce con el nombre de principio de la multiplicación, que puede enunciarse de la siguiente forma:
| Principio de la multiplicación. Si tenemos a opciones para escoger un objeto, b opciones para elegir un segundo objeto, c opciones para escoger un tercero, etc., el número total de formas de combinar los distintos objetos es el producto a · b · c · ..... |
- Ejemplo 2: ¿Cuántos números de tres cifras se pueden formar con los dígitos 0, 1, 2, 3 y 4, sin que se repita ninguna cifra?
- Las opciones para escoger la primera cifra son cuatro, pues ésta no puede tomar el valor 0, ya que ningún número de tres cifras comienza por 0. Para la segunda cifra tendremos también cuatro opciones, pues aunque en este caso si puede tomar el valor 0, tendremos que descartar el valor que haya tomado la primera cifra, por no poderse repetir ninguna. Por último, para la tercera cifra tendremos tres opciones, resultado de descartar los valores empleados en las dos primeras cifras, para evitar repeticiones.
- Por tanto, aplicando el principio de la multiplicación, se obtiene que hay 4 · 4 · 3 = 48 números de tres cifras distintos con los dígitos indicados en el enunciado.
Diagrama de árbol
[editar]Un diagrama de árbol es una representación gráfica que ilustra las formas en las que se llevan a cabo las agrupaciones de elementos. Volviendo al ejemplo 1, si llamamos a las diferentes camisetas y a los distintos pantalones, obtendríamos el diagrama de árbol que se muestra en la figura 1. Si contamos los resultados, comprobamos que obtenemos los 20 que indicaba el principio de la multiplicación.
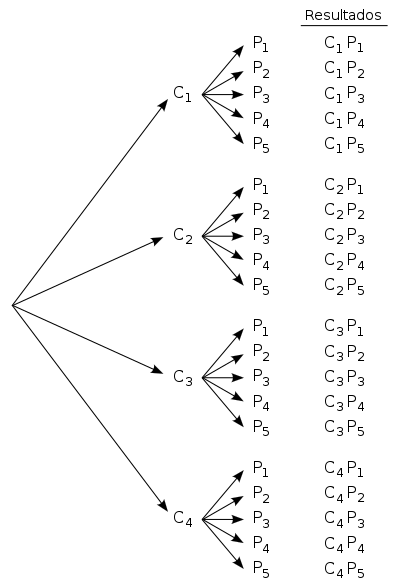
En los diagramas de árbol se emplea una nomenclatura propia, que describimos a continuación:
- Árbol: es el diagrama completo.
- Raíz: es el punto en el cual se origina el árbol. En la figura 1, la raíz sería el punto desde donde parten las cuatro flechas que llegan hasta las cuatro opciones de camiseta.
- Ramas: son las distintas bifurcaciones. En la figura 1 se corresponden con las flechas del gráfico.
- Nodos o nudos: son los puntos desde los que surgen nuevas bifurcaciones. En la figura 1, los nodos serían los puntos en los que tenemos las 4 opciones de camiseta: .
- Hojas: son los puntos finales, desde los cuales no surgen nuevas bifurcaciones. En la figura 1, las hojas son los puntos correspondientes a las 5 opciones de pantalón (todos los nombrados como , 20 puntos en total).
- Nivel: es el número de ramas que separa a un nodo u hoja de la raíz. La raíz corresponde al nivel 0 y, en la figura 1, las opciones de camiseta estarán en el nivel 1 y las de pantalón en el nivel 2.
- Camino: es cualquier recorrido por las ramas del árbol, desde la raíz hasta alguna de sus hojas. En la figura 1 tenemos 20 caminos diferentes.
Variaciones sin repetición
[editar]- Ejemplo 3: En una carrera de natación participan 8 nadadores. ¿De cuántas formas posibles pueden ocuparse los tres primeros puestos?
- Veamos las posibles opciones: Cualquiera de los nadadores participantes podría ser el primero, por lo que el número de opciones para escoger al primero es 8. El segundo puesto lo podría ocupar cualquiera de los nadadores restantes; por tanto, el número de opciones en este caso será 7. Por último, el tercer puesto lo podría ocupar cualquiera de los nadadores que no haya sido primero ni segundo; en este caso las opciones serán 6. Aplicando el principio de la multiplicación, habría 8 · 7 · 6 = 336 posibilidades distintas.
- A cada grupo de 3 nadadores, de los 336 posibles, le llamaremos variación de 8 elementos tomados de 3 en 3.
| Variaciones sin repetición o variaciones ordinarias de m elementos tomados de n en n (n m), son los distintos grupos de n elementos no repetidos que se pueden formar, escogidos de entre los m elementos posibles, de forma que en cada grupo haya algún elemento distinto, o tenga los mismos elementos que otro grupo, pero colocados en distinto orden. Cada uno de los posibles grupos es una variación. Se representa por o . |
Como el primero de los elementos puede ser cualquiera de los m disponibles, el segundo cualquiera de los (m – 1) restantes, el tercero cualquiera de los (m – 2) que quedan y así sucesivamente, aplicando el principio de la multiplicación se obtiene:
|
|
Permutaciones sin repetición. Factorial
[editar]Factorial
[editar]|
Sea el número natural n mayor que 1. Se conoce como factorial de n, y se representa por n!, al producto de los n primeros números naturales: |
Por convenio se definen 1! = 1 y 0! = 1 (son excepciones a la definición, ya que en ambos n no es mayor que 1).
- Ejemplo 4:
- 3! = 3·2·1 = 6
- 5! = 5·4·3·2·1 = 120
- 1! = 1
Teniendo en cuenta la definición de factorial de un número, se puede escribir la expresión para la obtención de las variaciones de m elementos tomados de n en n, de la siguiente forma:
|
|
Permutaciones sin repetición
[editar]- Ejemplo 5: En el bombo de un juego de lotería, quedan 5 bolas. ¿De cuántas formas podrán salir las cinco bolas?
- La primera bola en salir podrá ser cualquiera de las 5. La segunda bola tendrá que ser una cualquiera de las 4 restantes, etc. Si aplicamos a este problema la definición de variación sin repetición que ya hemos visto, se obtiene que las formas posibles de salir las bolas son:
En este caso, vemos que en todas las variaciones intervienen todos los elementos, y que la única diferencia entre una variación y otra está en el orden de dichos elementos. A las variaciones de n elementos tomados de n en n, se las llama permutaciones de n elementos.
|
Permutaciones ordinarias de n elementos son las distintas formas de ordenar dichos elementos. Cada forma de ordenarlos es una permutación. El número de permutaciones de n elementos se representa por , y su valor es: |
Permutaciones circulares
[editar]- Ejemplo 6: ¿De cuántas formas pueden colocarse 7 niños formando un círculo?
- Hay que tener cuidado, ya que no se trata de ordenar simplemente a los 7 niños, pues hay que tener en cuenta que si desplazamos a todos los niños un lugar hacia la derecha, se obtiene una ordenación idéntica a la anterior. En este caso no nos interesa la posición exacta de los niños dentro del círculo, sino la posición relativa entre ellos (no existe un primer niño, ni un último). Cuando el único orden que interesa es el orden relativo entre los n elementos, se dejará fijo a uno de los elementos y se permutará el resto de elementos de todas las formas posibles.
- Operando de esta forma se obtiene que el número de formas de posicionarse es:
|
A estas permutaciones se las llama permutaciones circulares de n elementos: |
Cuando no importa el orden. Combinaciones
[editar]Combinaciones sin repetición
[editar]- Ejemplo 7: A un concursante en un programa de televisión, le dejan elegir 3 regalos entre los siguientes: lavadora, frigorífico, lavavajillas, motocicleta, televisor y viaje. ¿Cuántas posibilidades de elección tiene el concursante?
- Se podría pensar en un principio, que se trata de las variaciones de 6 elementos tomados de 3 en 3, pero hay que tener en cuenta que hay distintas variaciones que dan lugar a la misma elección del concursante.
- Considérese el caso en que el concursante elige la motocicleta, el televisor y el viaje. Dentro del conjunto de todas las variaciones, dicha elección estaría repetida 3! = 6 veces, que son las distintas formas de ordenar dichos regalos. Por tanto, tendríamos que dividir el número de variaciones, entre el número de ordenaciones posibles de los regalos elegidos. En este caso:
|
Combinaciones ordinarias o combinaciones sin repetición de m elementos tomados de n en n (n m) son los distintos grupos que se pueden formar con los m elementos disponibles, de modo que en cada grupo haya n elementos distintos. En este caso para que dos grupos sean distintos, han de tener algún elemento diferente; no basta con que tengan distinto orden de colocación. Se representa por o y su valor viene dado por:
|
Números combinatorios
[editar]El número se conoce también como número combinatorio .
Propiedades de los números combinatorios
[editar]1.
- Demostración:
2.
- Demostración:
3.
- Demostración:
Triangulo de Tartaglia
[editar]A partir de las propiedades de los números combinatorios, se puede construir el llamado triángulo de Tartaglia o de Pascal, que permite obtener los valores de los números combinatorios sin necesidad de realizar las operaciones de la fórmula. Para obtener el triángulo se interpretan las propiedades de los números combinatorios de la siguiente forma:
- 1.Los extremos de las filas del triángulo toman el valor 1 (propiedad 1).
- 2.Todas las filas del triángulo son simétricas (propiedad 2).
- 3.Cada número se obtiene mediante la suma de los dos que tiene encima en el triángulo, excepto los extremos, cuyo valor es 1, según se indicó en el punto 1 (propiedad 3).
Con esto es muy sencillo construir el triángulo para las primeras filas. En la figura 2 se muestra el triángulo para las 10 primeras filas.
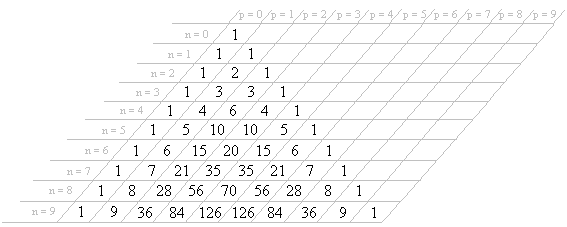
El valor correspondiente al número combinatorio , será el que se encuentra en la fila n y columna p del triángulo.
Así estaría en la fila n = 7 y p = 4, luego sería igual a 35.
Variaciones con repetición
[editar]- Ejemplo 8: ¿Cuántos números de tres cifras se pueden formar con los dígitos 1, 2, 3, 4 y 5?
- La primera cifra podrá ser una cualquiera de las 5. La segunda cifra también podrá ser una cualquiera de las cinco ya que puede repetirse, y lo mismo ocurre para la tercera cifra. Aplicando el principio de multiplicación, hay 5 · 5 · 5 = 125 números de tres cifras.
- Vemos que en este caso importa el orden, pues aún teniendo las mismas cifras, 123 y 231 son números diferentes. Además se han tomado 3 elementos de entre los 5 posibles, luego son variaciones, pero en este caso se puede elegir un elemento de los 5 más de una vez. A este tipo de variaciones se las llama variaciones con repetición.
|
Variaciones con repetición de m elementos tomados de n en n, son los distintos grupos de n elementos repetidos o no que se pueden formar, escogidos de entre los m elementos posibles. En este caso, dos grupos son distintos si tienen algún elemento diferente o si, siendo todos los elementos iguales, están colocados con distinto orden. Se representa por ó . |
Permutaciones con repetición
[editar]- Ejemplo 9: ¿Cuántas palabras de 5 letras, con sentido o sin él, se pueden formar con tres A y dos B?
- Se trata en este caso de obtener las distintas ordenaciones posibles de AAABB. Si las A fuesen distinguibles entre sí, y lo mismo ocurriera con las B, se trataría de ordenar 5 elementos distintos y estaríamos ante el caso de las permutaciones sin repetición visto anteriormente.
- Al ser indistinguibles, muchas de las permutaciones consideradas serán idénticas. Veamos, por ejemplo, el caso en que las 3 A aparezcan al principio de la palabra; la diferencia entre los casos en que las letras sean distinguibles e indistinguibles se recogen en la tabla siguiente (las hemos hecho distinguibles dotándolas de un subíndice).
| Indistinguibles | Distinguibles |
|---|---|
- Vemos que para el caso de las letras distinguibles, el número de palabras resulta de multiplicar las permutaciones de por las de , obteniéndose que el número de permutaciones es 3! · 2! = 12 , de las cuales sólo tenemos que considerar 1. Hemos considerado el caso en que las 3 A aparezcan al principio de la palabra; considerando todos los demás casos obtendremos que el número de palabras es
A partir del ejemplo anterior llegamos a la siguiente definición:
|
Dados n elementos, de los cuales el primer elemento se repite a veces, el segundo b veces, ..., el último r veces (a + b + ..... + r = n), llamaremos permutaciones con repetición de esos n elementos a los distintos grupos que se pueden formar, de forma que en cada grupo de n elementos, el primer elemento esté repetido a veces, el segundo b veces, ..., el último r veces. La única diferencia entre los grupos está en el orden de colocación de sus elementos distinguibles. El número de permutaciones con repetición de n elementos se representa por
|
Procedimiento para resolver problemas de combinatoria
[editar]
El algoritmo representado en la figura 3 puede resultar de ayuda en la resolución de problemas de combinatoria. Partiremos del símbolo con la leyenda Inicio y seguiremos un camino que será función de las respuestas que demos a las preguntas de los rombos por los que pasemos. El camino concluye al llegar a uno de los rectángulos que nos indican el tipo de agrupamiento.
- Ejemplo 10: Utilizaremos el procedimiento de la figura 3 para resolver el problema del ejemplo 9.
- Partimos del inicio y descendemos a la primera pregunta: ¿Importa el orden? La respuesta en este caso es Sí, puesto que no es lo mismo AAABB que ABAAB.
- Seguimos la flecha correspondiente a la respuesta Sí y llegamos a la segunda pregunta: ¿Hay que utilizar todos los elementos? La respuesta vuelve a ser Sí, pues así nos lo indicaban en el enunciado del ejemplo 9.
- Seguimos de nuevo la flecha correspondiente a la respuesta Sí y llegamos a la tercera pregunta: ¿Hay elementos indistinguibles? La respuesta es de nuevo Sí, como ya se vió en el ejemplo 9.
- Siguiendo por último la flecha correspondiente a la respuesta Sí, llegamos al rectángulo que nos indica que se trata de Permutaciones con repetición.
- Ejemplo 11: Utilizaremos el procedimiento de la figura 3 con el problema del ejemplo 7.
- Partimos del inicio y descendemos a la primera pregunta: ¿Importa el orden? La respuesta en este caso es No, puesto que cuando el concursante elige tres regalos, pongamos por caso que sean lavadora, frigorífico y lavavajillas, el conjunto de premios que se llevará el concursante será el mismo, idependientemente de la forma en que se ordenen dichos premios.
- Siguiendo la flecha correspondiente a la respuesta No, llegamos al rectángulo que nos indica que se trata de Combinaciones.
Potencias de un binomio. Teorema del binomio
[editar]El Teorema del binomio de permite desarrollar la potencia de una suma o diferencia de dos monomios.[1]
Siendo .
Demostración
[editar]Demostraremos la fórmula anterior por inducción sobre N.
Base de inducción
[editar]Comprobamos que la fórumula se verifica para n = 1:
Paso de inducción
[editar]Se trata de comprobar que, si la fórmula se verifica para el valor n, entonces se verifica para n + 1.
Puesto que , se tiene
[...]
Importante
[editar]El teorema del binomio dio un vuelco cualitativo cuando el exponente de la potencia de un binomio , se considera un número racional; obviamente con una cantidad infinita de términos, si se trata de exponentes enteros negativos o números fraccionarios, y, correlativamente, los los números combinatorios que se se usan en dichos casos, difieren del típico número combinatorio de enteros no negativos.<ref> Banach, Stefan: "Cálculo diferencial e integral", ISBN 968-18-3949-8, (1991)
Notas y referencias
[editar]- ↑ A Isaac Newton le cupo ampliar para potencia racional que es un desarrollo infinito
Introducción a la trigonometría
[editar]
La trigonometría (del griego τριγωνο <trigōno> "triángulo" + μετρον <metron> medida, "medición de triángulos"), es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para ello se vale de las funciones o razones trigonométricas seno, coseno y tangente.
Circunferencia goniométrica
[editar]
La circunferencia goniométrica (trigonométrica o unitaria) es una herramienta muy útil a la hora de visualizar y definir razones trigonométricas de ángulos cualesquiera.
Se trata de una circunferencia de radio 1, situada en el origen de coordenadas. En ella se dibujan los ángulos de la siguiente forma:
- El vértice en el origen de coordenadas.
- Uno de sus lados en el eje de las x.
- El otro lado se sitúa con la amplitud deseada: se mide el ángulo en sentido contrario a las agujas del reloj.
La circunferencia goniométrica se divide en cuatro partes, denominadas cada una de ellas cuadrantes. Los cuadrantes se numeran a partir del semieje positivo de las x, en sentido antihorario: primero, segundo, tercero y cuarto:
- La parte del plano comprendida entre el semieje positivo de las x y el semieje positivo de las y es el primer cuadrante.
- La parte del plano comprendida entre el smieje positivo de las y, y el semieje negativo de las x es el segundo cuadrante
Y así sucesivamente. Tomando en cuenta los ángulos de la figura adjunta tenemos:
- Primer cuadrante: de 0 a 90º, x>0, y >0
- Segundo cuadrante: de 90 a 180º, x<0, y>0
- Tercer cuadrante: de 180º a 270º, x<0, y<0
- Cuarto cuadrante: de 270º a 360º, x>0, y<0
Como se verá más adelante, dependiendo del cuadrante considerado, las funciones trigonométricas seno, coseno y tangente tienen un valor positivo o negativo.
Seno y coseno de un angulo entre 0 y 360 grados
[editar]
Fijémonos en la figura. Si situamos un ángulo cualquiera son las coordenadas del punto en que el lado corta la circunferencia goniométrica.
Nota: Recordemos que
Si miramos la figura veremos que se cumple que:

|
 |
Tangente de un ángulo entre 0 y 360 grados
[editar]
Si trazamos una recta t tangente al punto U de la circunferencia, ya podemos representar gráficamente la tangente. Cojamos ahora un ángulo cualquiera prolonguemos el segundo lado hasta que corte a t por un punto T. La tangente del ángulo es la longitud del segmento UT, con el signo que le toque.
Los ángulos 90º y 270º no tienen tangente.
Ángulos de medidas cualquiera
[editar]La motivación de este apartado no es otra que dar respuesta a la pregunta ¿cual es el seno de ?
Si hacemos esto quiere decir que 420 es una vuelta entera y 60 grados. Con esta sencilla operación se definen todos los ángulos posibles
Ángulos negativos
[editar]Si a 310º le restamos 360º obtenemos -50º. Es decir 310º puede expresarse como -50º. Es más, normalmente los ángulos que están por debajo del eje de las x se escriben con una medida negativa, es decir que todos los ángulos posibles se suelen escribir con valores comprendidos entre -180º y 180 grados
Ejemplo
[editar]Escribir con valores comprendidos entre -180º y 180º estos ángulos:
|
| ||
|
| ||
Relaciones entre las razones trigonométricas de algunos ángulos
[editar]
Esto que viene ahora es tremendamente útil, y no sólo para ahora. No es necesario aprenderlas de memoria porque si las razonas un par de veces las visualizarás sin pensar
Ángulos que difieren en 90 grados: x y 90º-x
[editar]
Ángulos que difieren en 90 grados: x y 90º+x
[editar]
Ángulos que difieren en 180 grados: x y 180º-x
[editar]
Ángulos que difieren en 180 grados: x y 180º+x
[editar]
Ángulos que difieren en 270 grados: x y 270º-x
[editar]
Ángulos que difieren en 270 grados: x y 270º+x
[editar]
Ángulos opuestos: x y -x
[editar]
para reducir razones trigonométricas de un angulo negativo, -x, basta con darse cuenta de que si sumamos una vuelta a este angulo. obtenemos un angulo equivalente que sunma 360ºcon el opuesto a -x.
Una nueva unidad para medir ángulos: el radian
[editar]Los costumbre de medir los ángulos en grados, proviene de los babilonios que dividieron el ciclo anual en 360 partes, así, el arco recorrido en un día era casi un grado. Y esta forma de medición ha perdurado hasta nuestros días.
Sin embargo el radian aporta algunas ventajas y por eso es interesante conocerlo
Visualización de un radian
[editar]
- Coge un vaso o cualquier objeto cilíndrico. Apóyalo sobre un papel y dibuja su contorno (es decir una circunferencia).
- Localiza el centro de la circunferencia (dibuja dos segmentos haz las mediatrices y donde se corten ese es el centro.
- Coge una cuerda y pon el extremo en el centro y marca con un rotulador el punto donde coincida con la circunferencia.
- Vuelve a poner el vaso en la circunferencia y enrolla la cuerda en el, marca en la circunferencia los dos puntos señalados en la cuerda.
- Dibuja los radios correspondientes a los dos puntos y ya tienes un radian. Mídelo si quieres y verás que son aproximadamente 57º
Definición formal
[editar]Llamamos radián a aquel ángulo tal que el arco que abarca tiene la misma longitud que el radio del arco.del mismo angulo
Conversión radian-grado grado-radian
[editar]Una circunferencia tiene una longidud de y un radian mide r es decir en una circunferencia caben radianes. A su vez en una circunferencia caben 360º. Es decir que:
Paso de grados a radianes:
Paso de radianes a grados:
El valor de un radian es:
Utilidad de los radianes
[editar]Al nivel en que nos encontramos "solamente" sirven para las funciones trigonométricas, no obstante la utilidad del radian es indiscutible para muchas otras cosas que no podremos explicar aquí.
Sin embargo su utilidad es fundamental para problemas tanto matemáticos como para problemas de física, en el tema de la dinámica.
Su utilidad ha servido mucho a la ciencia, su uso es solamente para circunferencias, círculos, y la mayoría de líneas curvas, pues siempre los radianes y los grados han estado correlacionados.
Calculadora
[editar]Funciones circulares
[editar]Vamos a dibujar unas funciones que para cada ángulo expresado en radianes nos den un valor para y:

Fuciones circulares definidas en todo
[editar]Como ya hemos visto un ángulo de 400º es igual a uno de 40º uno de 410º equivale a uno de 50. por lo tanto las funciones circulares son periódicas.
Fórmulas trigonométricas
[editar]LAS ECUACIONES TRIGONOMETRICAS CONTIENEN RESULTADOS CUADRADOS EQUIDISTANTES
Funciones
[editar]Concepto de función
[editar]Tipo de relación donde dada una variable o cantidad y procesada de acuerdo a unas condiciones preestablecidas da como resultado un único resultado.

Ej. Dado cualquier número se elevara al cuadrado y al resultado se le restara uno. Con este ejemplo de función se puede realizar la siguiente tabla donde los datos de la primera columna son datos arbitrarios y la segunda columna son datos obtenidos al procesar el dato de la izquierda.
| X | Y |
|---|---|
| 2 | 3 |
| 3 | 8 |
Observamos que a los datos de entrada se les llamó X y a los de salida se les llamó Y, entonces podemos escribir una formula que muestre lo anteriormente expresado: donde X es cualquier número, é Y es el valor que se obtiene al remplazar la X por el valor arbitrario.
Para dar una mayor idea al respecto y esperando que se profundice en el tema, diremos que una función es como una maquina que siempre le hace a lo que le introduzcan lo mismo, claro que de acuerdo a lo que le introduzcan dará un resultado diferente.
Producto inicial
(x) » » »
(función) Producto final
(y).
El anterior esquema representa un proceso industrial, matemáticamente podríamos decir que el producto inicial es como el valor izquierdo de la tabla, los valores de X; el producto final será el valor de Y que es lo que sale de la maquina, y finalmente la maquina será la función, la que convierte mediante un proceso propio de cada maquina un producto inicial en otro final.
Dominio de definición de una función
[editar]El dominio de una función es el conjunto de valores que pueden entrar para operar. Es decir, los valores que puede tener la variable independiente.
tiene como dominio todo número real ademas cuando tiene en coma.
tiene como dominio todo número real positivo incluído el cero
Discontinuidades. Continuidad
[editar]Una función es continua en un punto si, y solo si el límite de la función cuando tiende a tal punto tanto por la derecha y por la izquierda es el mismo, y es igual al valor que toma la función a tal punto.
La función es continua en el punto si se cumple la siguiente condición:

En caso de no cumplirse esta condición, la función es discontinua. Dicha discontinuidad puede ser evitable, si existen los límites por la derecha y por la izquierda (y son iguales, por lo tanto, existe el límite), pero no coinciden con el valor de la función (en tal caso, bastaría definir una nueva función "a trozos", de manera que se asignase el valor de los límites a la función en el punto para que esta fuese contínua), o inevitable, caso de que no existan o sean distintos.
La discontinuidad evitable también aparece cuando existe el límite y existe la imagen pero son diferentes.
Límites en un punto
[editar]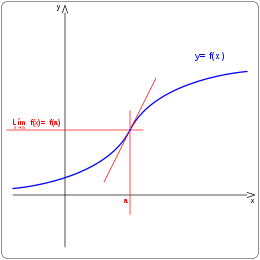
Una función f(x) es continua en un punto x=a si se cumplen la siguientes condiciones:
- Que el punto x=a tenga imagen.
- Que exista el límite de la función en el punto x=a.
- Que la imagen del punto coincida con el límite de la función en el punto.
Cálculo de límites cuando x -> a
[editar]Cálculo del límite de un cociente de polinomios cuando x -> a
[editar]Comportamiento de una función cuando x -> infinito
[editar]El comportamiento de una función cuando x tiende a son los distintos valores del , estos pueden ser ó . Si la función es un polinomio , siendo k el grado del polinomio,serà cuando , independiente si k es par o impar, y será cuando y k impar y será cuando y k par.
Ramas infinitas y asíntotas
[editar]En el estudio de la función, es importante analizar los puntos en los que esta tiende hacia el infinito (ramas infinitas), o las direcciones constantes que toma al alejarse hacia o (caso de que las haya). Una buena forma de enfocar este estudio podría ser el siguiente: localizar los puntos singulares de la función (denominador que se anula, logaritmo negativo ...), estudiar el límite en y por último buscar asíntotas verticales.
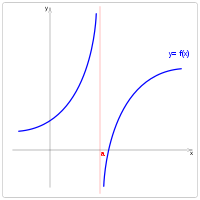
Asíntotas Verticales: Indican un valor a de la variable independiente x, tal que . Si ya hemos hecho un análisis del dominio de la función, encontrarlas es mucho más facil; son los ceros del denominador, los puntos en los que el argumento de un logaritmo se anula ... Para la posterior representación gráfica, es recomendable dibujar con trazo discontínuo las A. V. como rectas
Asíntotas Horizontales: Son tales que . Intuitivamente, es el valor al que se va acercando la función al crecer el valor de la variable independiente. Análogamente al caso anterior, es recomendable dibujar con trazo discontínuo la A.H. como una recta .
Asíntotas Oblícuas: a una dirección constante en el plano cartesiano. Para ello, es necesario calcular dos límites, que nos proporcionan diversa información:
- . Si , se trata de una rama parabólica de dirección OY; si es una rama infinita de dirección OX. Si , es una rama asintótica de pendiente k.
- Para determinar completamente dicha asíntota, tenemos que obtener el límite .
La asíntota será la recta de ecuación .
Comportamiento de una función cuando
[editar]Se calcula exactamente igual que cuando X-> infinito, pero teniendo en cuenta las reglas de los signos (ya sea suma, resta, multiplicación, división, potencia o raíz).
Funciones elementales
[editar]Dada una función real de variable real. función elemental:
Las funciones elementales son funciones recursivamente construibles a partir de alguna de los siguientes conjuntos:
- Conjunto de funciones polinómicas
- Función exponencial
- Funciones trigonométricas
Mediante alguna de las siguientes operaciones
- Operaciones de álgebra elemental (suma, resta, multiplicación, división) entre funciones de los anteriores conjuntos
- Composición de funciones elementales de los anteriores conjuntos
- Recíproco de funciones elementales (dada una función elemental su recíproca también es elemental por definición).
Representación de una función
[editar]Representación gráfica de funciones Se llama estudiar una función al conjunto de las tareas encaminadas a determinar los elementos que definen su comportamiento para los diferentes intervalos de valores de su dominio. Crecimiento, concavidad, tendencias asintóticas y otras informaciones relacionadas sirven de ayuda para conocer la conducta de las funciones matemáticas y extraer datos de optimización relevantes para los problemas prácticos.
La abscisa de un punto en el que la grafica de una función intercepta al eje al eje x se denomina intersección con el eje x o raíz de la función. La intersección con el eje x es también una solución real o raíz de la ecuación f(x)=0. La ordenada de un punto en el que la grafica de una función cruza el eje y se denomina intersección con el eje y de la función.
Para estudiar el comportamiento de una función, se aplica un procedimiento sistemático que comprende los puntos siguientes:
- Determinación de su dominio de definición.
- Búsqueda de simetrías y periodicidades.
- Fijación de los puntos de corte con los ejes.
- Cálculo de las asíntotas.
- Tendencias de crecimiento y decrecimiento, con determinación de los máximos y los mínimos relativos.
- Concavidad, convexidad y puntos de inflexión.
- Análisis del comportamiento de la función en las distintas regiones del plano.
En las aplicaciones, es frecuente que una gráfica muestre la relación entre dos variables con mayor claridad que una ecuación o una tabla.
Cuando la regla que define una función f está dada mediante una ecuación en x y y, la gráfica de f es la gráfica de la ecuación, es decir, el conjunto de puntos (x, y) en el plano xy que satisfacen dicha ecuación.
No toda colección de puntos en el plano xy representa la grafica de una función. Para una función cada numero x en el dominio de f tiene una, y solo una, imagen f(x). Así, la grafica de una función no puede contener dos puntos con la misma abscisa y diferentes ordenadas. Por lo tanto, la grafica de una función debe satisfacer el siguiente criterio de la recta vertical: Un conjunto de puntos en el plano xy es la grafica de una función si, y solo si, una recta vertical interseca la grafica a lo mas en un punto. De esto concluimos que si una recta vertical interseca una grafica en más de un punto, esa grafica no es la de una función.
Representar una función
[editar]es un tipo de representación gráfica de modo f(x)=y+x Pubertad Universidad Tecnológica Amistad
Función constante
[editar]
Una función contante es la que tiene la forma:
Siendo a un valor real costante y conocido. Por ejemplo:
Funciones líneales
[editar]
Una función es lineal si tiene la forma:
Donde a y b son valores reales constantes y conocidos. Por ejemplo:
- Dominio de definición.
La función esta definida para todo x real.
- Corte con el eje y.
- Corte con el eje x.
Función cuadrática
[editar]
Una función cuadrática es de la forma:
Donde a, b y c son valores reales constantes y conocidos.
Función cubica
[editar]
Una función cubica es de la forma:
Donde a, b, c y d son valores reales constantes y conocidos.
Función polinómica, caso general
[editar]
Una función polinómica es de la forma, en un caso general:
Representación de funciones racionales
[editar]Funciones trigonométricas
[editar]-
Seno: y= sen x
-
Coseno: y= cos x
-
Tangente: y= tan x
-
Cosecante: y= csc x
-
Secante: y= sec x
-
Cotangente: y= ctg x
Todas:

Funciones exponenciales
[editar]Funciones logarítmicas
[editar]
Funciones no elementales
[editar]Dada una función real de variable real. función no elemental:
se dice que la función f es no elemental si no cumple las condiciones de función elemental. Existen un número inlimitado de funciones no elementales, presentaremos unos ejemplos de funciones de este tipo.
Funciones de partes de x
[editar]
Dada la función id(x) que asocia a y el mismo valor de x, definida así:
con la representadión grafica de la derecha.
La función id(x) esta definida para todo x real, es continua u derivable, y creciento en todo su entorno de definición.
Es función impar:
Es función idempotente:
Función signo
[editar]
La función signo es una función no elemental definida para todo x real:
Asigna a y el volor 1 si x es positivo, 0 si x es 0 y -1 si x es negativo:
La función sgn(x) esta derinida para todo x real, es discontinua para x= 0, para los valores distintos de cero es continua y derivable, y estacionaria (no es creciente ni decreciente).
Es función impar:
Ademas:
Es función idempotente:
Función valor absoluto
[editar]
La función valor absoluto asocia a y el valor de x sin signo:
La función esta definida paro todo x real, es continua y no deribable para x= 0.
La función abs nunca toma valores negativos, es decreciente para x negativo y es creciente para x positivo, para x= 0 la función tambien vale cero (y= 0).
Es función par:
Es función idempotente:
podemos ver que:
Escalón de Heaviside
[editar]
La función escalón de Heaviside, también llamada función escalón unitario, debe su nombre al matemático inglés Oliver Heaviside. Es una función discontinua cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo, incluido el cero:
Esta función queda definida de esta forma:
Función rampa
[editar]
La función rampa definida para valores reales:
Que se puede especificar de esta forma:
Esta función es continua, y no es derivable para x = 0.
Es función idempotente:
Puede verse que:
Función entero de x
[editar]
Esta función asocia a y el mismo valor de x cuando x en un número entero, si x es positivo y se obtiene eliminando la parte decimas, si x tiene valor negativo y es el valor de x sin parte decimal menos una unidad.
La función entero asocia a y el maximo número entero menor o igual a x, esto es, de todos los números enteros menores o iguales que x, el mayor de ellos:
Representada en la figura de la derecha.
La función E(x) esta definida paro todo x real, es discontinua para x número entero, y para los valores en los que es continua es estacionaria.
Función mantisa de x
[editar]
La función mantisa o parte decimal de x, es una función que asocia a y el valor que falta desde el número entero inferior a x
Ver la figura de la derecha, si x es un número entero M(x) es cero, si x en un número positivo M(x) es la parte decimal de x, cuando x tiene valor negativo entonces M(x) es lo que le falta hasta en número entero inferior a x. M(x) nunca toma valores negativos.
La función M(x) esta definida para todo x real, es discontinua para x número entero y para los valores en los que es continua es creciente.
Puede verse que:
Ver la figura de la derecha.
Función parte entera de x
[editar]
La función parte entera de x es el resultado de eliminar la parte decimal del número, de forma que se conserva el signo y la parte entera. Es una funcion definida para todo número real:
La función parte entera se define como:
para x menor que cero: es el minimo entero mayor o igual que x y para x mayor o igual que cero: es el maximo entero menor o igual que x.
Esta función es impar:
Función parte decimal de x
[editar]
La función parte decimal de x es el resultado de eliminar la parte entera del número, de forma que se conserva el signo y la parte decimal. Es una funcion definida para todo número real:
Para x negativo frac int(x) es no positivo, para x positivo frac int(x) es no negativo.
Esta función es impar:
Puede verse que:
Función redondeo de x
[editar]
La funcion redondeo de x esta definida para todo número real:
Esta función asocia a todo x número real el número entero más proximo, en caso de enteros igualmente proximos se tomara el de menor valor absoluto. La función parte entera se define como:
Esta función es impar:
Función fracción de redondeo de x
[editar]
La funcion fracción de redondeo de x esta definida para todo número real:
Esta función asocia a todo x número real el número fraccionario más proximo a un número entero.
Esta función es impar:
se puede ver que:
Función suelo
[editar]
Esta función es equivalente a la funcios parte entera: :
La función suelo asocia a y el maximo número entero menor o igual a x:
Función fracción de suelo
[editar]
La función fracción de suelo es equivalente a mantisa o parte decimal, asocia a y el valor que falta desde el número entero inferior a x
Puede verse que:
Ver la figura de la derecha.
Función techo
[editar]
La función techo asocia a y el valor entero de x por esceso, compararla con la función suelo:
El valor de la función techo es el minimo valor entero mayor o igual que x:
Función fracción de techo
[editar]
La función fracción de techo asocia a y el valor que falta desde el número entero superios a x
Puede verse que:
Ver la figura de la derecha.
Funciones escalonadas
[editar]Función rectangular
[editar]
La función rectangular (también llamada función ventana unitaria o pulso unitario) se define como:
Función escalonada
[editar]
Una función es escalonada si toma valores constantes en distintos intervalos, por ejemplo podemos ver la función y= s(x) de la figura:
Sucesos aleatorios
[editar]Experiencias aleatorias. Sucesos
[editar]Una experiencia aleatoria o experimento aleatorio es todo fenóneno cuyo resultado no es predecible.Por ejemplo, no es posible saber el resultado del lanzamiento de una moneda antes de lanzarla, por tanto lanzar una moneda es un experimento aleatorio.
Se llama Suceso a todo resultado posible de una experiencia aleatoria o experimento aleatorio. Por ejemplo, que una moneda caiga mostrando una cara es un resultado posible del experimento lanzar una moneda, por tanto "salir cara" es un suceso de la experiencia aleatoria "Lanzar una moneda"
El conjunto de todos los posibles resultados de un experimento aleatorio se denomina Espacio muestral. Por ejemplo el espacio muestral de la experiencia aleatoria "Lanzar una moneda" estará compuesto por los sucesos "salir cara" y "salir cruz"
Entre los sucesos posibles de una experiencia aleatoria se pueden distinguir varios tipos:
- Sucesos elementales: Son aquellos sucesos que solo pueden ocurrir con un resultado del espacio muestral. Por ejemplo en la experiencia aleatoria lanzar un dado, el suceso "sacar 1" solo se puede obtener si se obtiene el resultado 1, es por tanto un suceso elemental. En cambio el suceso "sacar un número par" no es un suceso elemental por que se puede obtener si sale 2, 4 o 6.
- Sucesos compatibles: Son aquellos sucesos que se pueden dar a la vez. Por ejemplo en la experiencia aleatoria lanzar un dado, los sucesos "salir par" y "salir primo" se satisfacen a la vez si se obtiene el resultado 2.
- Sucesos incompatibles: Son aquellos sucesos que no pueden ocurrir a la vez. Ejemplo, en la experiencia aleatoria lanzar un dado, no pueden ocurrir a la vez los sucesos "salir par" y "salir impar". Todos los sucesos elementales son incompatibles entre si.
- Suceso contrario: El suceso contrario a un suceso A es aquel que sucede si no ocurre A. Por ejemplo el suceso contrario a que salga cara en el lanzamiento de una moneda es que salga cruz, El suceso contrario a que salga par en el lanzamiento de un dado es que salga impar, El suceso contrario a que salga Oro en la extracción de una carta en una baraja es que No salga Oros.
- Suceso seguro: Es aquel suceso que ocurre sea cual sea el resultado de la experiencia. Por ejemplo en al lanzar un dado será suceso seguro "obtener un número menor o igual a 6"
Para sistematizar todas estas ideas se puede utilizar el álgebra de conjuntos.
El espacio muestral es el conjunto de todos los sucesos posibles de una experiencia aleatoria. Llamemoslo
Un suceso seria cualquier subconjunto que se pudiera formar con los elementos del espacio muestral. A
Un suceso elemental sería aquel subconjunto del espacio muestal que solo contuviera un único elemento del espacio muestral.
Dos sucesos serian compatibles si su intersección tuviera al menos un elemento
A es compatible con B si
Dos sucesos serian incompatibles si su intersección fuera el conjunto vacío, es decir no contuviera ningun elemento.
El suceso contrario a un suceso A es aquel suceso B, subconjunto del espacio muestral cuyos elementos son todos aquellos que no pertenecen al subconjunto A.
El suceso seguro seria el propio espacio muestral, que es un subconjunto de si mismo.
Analicemos con estas ideas un ejemplo sencillo, la experiencia aleatoria lanzar un dado.
Espacio muestral:
Sucesos elementales: Los elementos individuales del espacio muestral: Obtener 1, Obtener 2,...,Obtener 6
Suceso: Cualquier subconjunto que podamos formar con los elementos del espacio muestral, tengan sentido como grupo o no.
A y B son ejemplos de sucesos incompatibles, no contienen ningún elemento en común,la teoría de conjuntos diria que tienen la intersección vacía.
--Kuhn2012 (discusión) 12:21 11 ene 2013 (UTC)
Frecuencia y probabilidad
[editar]El estudio de las experiencias aleatorias comienza con un estudio estadístico. Se repite la experiencia aleatoria un gran número de veces y se analizan los resultados. Tomemos como ejemplo el estudio de la experiencia aleatoria lanzar un dado. Si lo lanzamos un número grande de veces, N, cada resultado posible se obtendrá un número de veces, fi con i variando de 1 a 6.
Al número de veces que se obtiene un resultado después de N repeticiones de una experiencia aleatoria se denomina Frecuencia
Es evidente que la suma de todas las frecuencias debe ser igual al número de veces que se ha realizado la experiencia aleatoria N
Si las distintas frecuencias se dividen por el número total de veces que se ha realizado la experiencia aleatoria fri=fi/N se obtiene lo que se denomina frecuencia relativa.
También resulta evidente que la suma de todas las frecuencia relativa debe ser 1.
Si repetimos un número virtualmente infinito de veces la experiencia aleatoria, las frecuencia relativas tienden a estabilizarse en un valor determinado.
Se denomina Probabilidad de un suceso al valor al que tiende su frecuencia relativa cuando el número de veces(N) que se realiza la experiencia aleatoria tienda a infinito.
Ley de Laplace
[editar]La probabilidad de que ocurra un suceso en una experiencia aleatoria es la relación entre el número de casos favorables a tal suceso que contiene el espacio muestral y el número de casos totales que contiene el espacio muestral.
P=número de casos favorables/Número de casos posibles
Un ejemplo simple: La probabilidad de obtener cara en el lanzamiento de una moneda sería 1/2 (un caso favorable/2 casos posibles)
En esta ley se hace la suposición implícita de que todos los sucesos elementales del espacio muestral de la experiencia aleatoria son igualmente probables, lo cual no siempre es cierto, pero como aproximación a la realidad es bastante aceptable.
Para realizar un estudio más exacto de una experiencia aleatoria sin la suposición de que todos sus resultados son igualmente probables seria necesario realizar un estudio estadístico y hacer una estimación de las probabilidades de los sucesos elementales del espacio muestral de dicha experiencia aleatoria. En la mayoría de los casos los resultados obtenidos discrepan de la ley de Laplace en una cantidad insignificante.
Probabilidad condicionada. Sucesos independientes
[editar]Dos sucesos se denominan independientes, cuando la probabilidad de que ocurra uno de ellas no afecta a la probabilidad de que ocurra el otro. Ejemplo, el lanzamiento de dos dados, el resultado que se haya obtenido en un dado no afecta al resultado que se obtiene en el otro dado.
Dos sucesos son dependientes cuando la probabilidad de que ocurra uno de ellos depende de que el otro haya ocurrido anteriormente o no.
Analicemos un ejemplo clásico, la experiencia aleatoria extraer dos cartas de una baraja. Para fijar ideas, la baraja es de española de 40 cartas.
Si la primera carta que se extrae se vuelve a poner en la baraja para que este disponible en la segunda extracción, se dice que la experiencia es una extracción con reposición
Si la primera carta que se extrae no se vuelve a poner en la baraja, no estará disponible en la segunda extracción, se dice entonces que la experiencia es una extracción sin reposición
En el caso de que la extracción sea con reposición, la probabilidad de que salga una carta concreta en la segunda extracción es: 1/40, independientemente de la carta que haya salido en la primera extracción.
En el caso de que la extracción sea sin reposición, la probabilidad de que salga una carta concreta en la segunda extracción es: 1/39, a menos que ya haya salido la carta en la primera extracción, en cuyo caso la probabilidad es cero (la carta ya no está en la baraja)
Se denomina Probabilidad de un suceso A condicionada a otro suceso B P(A/B) a la probabilidad que tiene un suceso A de ocurrir cuando anteriormente ha ocurrido el suceso B.
En el experimento de la extracción de dos cartas de una baraja española de 40 cartas. Supongamos que sacamos una carta y resulta ser el As de Oros y nos planteamos la pregunta de cual será la probabilidad de obtener otra vez oros.
A= Obtener oros.
B= Obtener el As de oros.
Si la experiencia se realiza sin reposición:
La probabilidad de obtener Oros habiendo obtenido el As de oros es: P(A/B)=9/39, la razón es que el As de oros es un resultado posible del suceso obtener oros y ya no está disponible y además hay una carta menos en la baraja.
En este caso se dice que los sucesos A y B son dependientes.
Si la experiencia se realiza con reposición:
La probabilidad de obtener Oros habiendo obtenido el As de oros es: P(A/B)=10/40, la razón es que el As de oros está disponible en la segunda extracción y vuelven a ser cuarenta cartas en la baraja. Se observa que el resultado es independiente de que se haya obtenido anteriormente el As de oros.(La probabilidad de obtener oros en una extracción es según la ley de Laplace 10/40)
En este caso se dice que se los sucesos A y B son independientes.
Vemos que un par de sucesos son independientes cuando: P(A/B)=P(A)
Si dos sucesos son dependientes, ¿Cuál sería la fórmula para calcular la probabilidad de modo general?:
P(A/B)
Sabemos, que ha sucedido B, por tanto los casos favorables estarán dentro del conjunto intersección de , serán aquellas posibilidades comunes a A y B. Los casos totales estarán dentro del suceso B, el que sabemos que ha ocurrido previamente, es decir que
Tablas de contingencia
[editar]Las tablas de contingencia son un método útil de determinar probabilidades. Consisten en tablas de doble entrada en cuyas celdas se localizan posibilidades de determinados sucesos. La utilidad radica en que se pueden determinar muchas probabilidades de sucesos relacionados. Pongamos un ejemplo. En una empresa se hace recuento de los empleados bajo dos criterios, su sexo y su actitud hacia el tabaco. Los resultados se resumen en una tabla de doble entrada:
| Fumadores | No fumadores | Totales | |
|---|---|---|---|
| Mujeres | 123 | 161 | 284 |
| Hombres | 177 | 152 | 329 |
| Totales | 300 | 313 | 613 |
Si realizamos la siguiente experiencia aleatoria: Extraemos la ficha al azar de un empleado de esta empresa, ¿Cuál será la probabilidad de que sea Mujer?
Respuesta: Son 284 mujeres entre 613 empleados, por tanto, aplicando la Ley de Laplace: P(mujer)=284/613
¿Cuál es la probabilidad de que extraída la ficha de un empleado al azar, sea hombre y fumador?
Son 177 hombres fumadores de 613 empleados, aplicando la ley de Laplace: P(Hombre y fumador)=177/613
Las tablas de contingencia también permiten calcular probabilidades condicionadas:
Se extrae una ficha de empleado al azar, se lee el nombre y resulta ser hombre,¿Cuál es la probabilidad de que se trate de una fumadora?
Son 123 de 284 mujeres, por tanto: P(Fumador/Mujer)=123/284
Pruebas compuestas
[editar]Las pruebas compuestas o experimentos compuestos son aquellas experiencias aleatorias que se desarrollan en dos o más etapas. Por ejemplo la experiencia aleatoria ya comentada en el apartado de los sucesos dependientes e independientes, extraer dos cartas de una baraja.
La probabilidad de que ocurra un suceso A y luego otro B sería
Recordando la definición de probabilidad condicionada:
Como la , ocurre que tenemos dos igualdades:
y
Si los sucesos son independientes ocurre que la fórmula anterior se convierte simplemente en:
Pongamos un ejemplo con sucesos independientes:
Extraer dos cartas de una baraja con reemplazamiento es un ejemplo de experiencia aleatoria compuesta con sucesos independientes, supongamos que la baraja es de 40 cartas. La probabilidad de obtener Oros y luego Copas es: , es decir
Pongamos un ejemplo con sucesos dependientes:
Extaer dos cartas de una baraja sin reemplazamiento es un ejemplo de experiencia aleatoria compuesta con sucesos dependientes. La probabilidad de obtener Oros y luego Copas es:
La diferencia es que en la segunda extracción hay una carta menos en la baraja.
La diferencia se nota aun mas si nos planteamos la probabilidad de sacar dos oros consecutivos, en ese caso la probabilidad pasa a ser , en este caso hay una posibilidad menos de obtener oros por que ya ha salido oros en la anterior extracción y no se ha devuelto a la baraja y además hay una carta menos en la baraja.
Probabilidad total
[editar]Imaginemos un suceso que puede ocurrir en diversas situaciones, situaciones que no pueden darse simultáneamente. Por ejemplo la probabilidad de alguien sufra un accidente montando en bici es diferente si hace buen tiempo que si está lloviendo. Nos interesa saber cual es la probabilidad global de que alguien sufra un accidente montando en bici, independientemente de las circunstancias. A esta probabilidad se le llama probabilidad total.
El teorema de la probabilidad total es un resultado que nos permite calcular la probabilidad total de un suceso cuando conocemos las probabilidades concicionadas de ese suceso en las diversas circunstancias en las que se puede presentar.
Se llama sistema completo de sucesos a un conjunto de sucesos A1,A2,A3,...,An de un espacio muestral Ω que cumplan los siguientes requisitos:
- Son incompatibles entre si dos a dos: con
para todo i,j con valores entre 1 y n
- La unión de todos ellos es el suceso seguro (el espacio muestral completo):
El teorenma de la probabilidad total dice que:
Si tenemos un sistema completo de sucesos A1,...,An tal que la probabilidad de ningnuno de ellos es nula, y tenemos un suceso B del que se conocen todas la probabilidades condicionadas P(B/Ai), entonces la probabilidad total de que el suceso B ocurra es;
Analicemos el ejemplo del inicio de la sección: Supongamos que la probabilidad de que alguien sufra un accidente montando en bici cuando hace buen tiempo es del 0,1 y cuando llueve 0,2, si hace buen tiempo con probabilidad del 0,6 y llueve 0,4, podemos calcular la probabilidad de que alguien sufra un accidente montando en bici:
Probabilidades "a posteriori". Formula de Bayes
[editar]El teorema de Bayes relaciona la probabilidades condicionadas de dos sucesos: P(A/B) con P(B/A). Un ejemplo, una enfermedad tiene una serie de síntomas con ciertas probabilidades, estas son probabilidades condicionadas de tener un determinado síntoma cuando se sufre la enfermedad, nos puede interesar saber la probabilidad de que alguien sufra la enfermedad cuando muestra un determinado síntoma. Mas concreto, A= Gripe, B=Dolor de cabeza, la probabilidad de tener dolor de cabeza cuando se tiene gripe P(B/A), probabilidad de tener gripe cuando se tiene dolor de cabeza P(A/B). El teorema nos permitirá relacionar ambas probabilidades. También se le llama de las probabilidades "A posteriori" por que relaciona un hecho anterior con los hechos que le acompañan después, tener gripe lleva a tener fiebre, dolor de cabeza, etc.
Matemáticamente el teorema de Bayes se establece en las mismas condiciones que el teorema de la probabilidad total:
Un sistema completo de sucesos A1,A2,A3,...,An de un espacio muestral Ω que cumplan los siguientes requisitos:
- Son incompatibles entre si dos a dos: con para todo i,j con valores entre 1 y n
- La unión de todos ellos es el suceso seguro (el espacio muestral completo):
Si tenemos un sistema completo de sucesos A1,...,An tal que la probabilidad de ninguno es nula. B un suceso cualquiera del que se conocen las probabilidades P(B/Ai) entonces la probabilidad P(Ai/B) viene dada por:
Distribuciones de probabilidades
[editar]Matemáticas/Bachillerato LOGSE/Distribuciones de probabilidades
Distribuciones bidimensionales
[editar]Nubes de puntos. Correlación
[editar]Medida de la correlación
[editar]Rectas de regresión
[editar]Recta de regresión de x sobre y:
- x=media de x+(sigma xy/sigma y^2)·(y-media de y)
- y=media de y+(sigma xy/sigma x^2)·(x-media de x)









![{\displaystyle [a,b]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08268f073d76e500a09a309a45bcc9f19e599db4)

![{\displaystyle (a,b]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/971a5742ccdd3be8c11ceb4ad00e495da0fb261b)





![{\displaystyle (-\infty ,a]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b996c00936430b9a3171b447986950df638d231)

































































































































































































































































































![{\displaystyle D[f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83a62e6fa818dc5f18ae0a8d668e9fec645aaa09)
![{\displaystyle D[f(1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de92295bcd4c5a0e7f5668ebee6c3a2a83e3409)


























![{\displaystyle D[c]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/574214906d11ac571491ec635218958eaa7c703f)
![{\displaystyle D[c\cdot f(x)]=c\cdot D[f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3898c88d789d9179b58141ff643121fcc88db5d)
![{\displaystyle D[x^{n}]=n\cdot x^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e859b593713b3206fcf95bda059cf2652845ad1)
![{\displaystyle D[\sin(x)]=\cos(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93ff6e0e29fe433176cb295b2c16c005ea73f9f6)
![{\displaystyle D[\cos(x)]=-\sin(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41fd759f457270434f23655e9e698537844f9043)
![{\displaystyle D[\tan(x)]=1/\cos ^{2}(x)=1+\tan ^{2}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c575f7c5c67dd51b328dbabd5c524cf3850f29)
![{\displaystyle D[\ln(x)]=1/x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/650436fcac5841d0a53daea749e54433a3d2896c)
![{\displaystyle D[e^{x}]=e^{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aae8145c82845e8fdf34cb8d5e7cddfead7a6eab)
![{\displaystyle D[f(g(x))]=g'(x)\cdot f'(g(x))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd40d03a387df9a54c164d4121c08e195e876806)















































![{\displaystyle [-4,1]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/699798f05200fee2074341f31b8336136ffa2a85)

![{\displaystyle (-\infty ,-4]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ee7bbe19585688353a944ccb0fcc2197c684359)