Curso de alemán para principiantes con audio/Lección 095b
Apariencia
- índice
- Lección 094b ← Lección 095b → Lección 096b
- Lección 095
- Mathematik auf Deutsch - 45
BM2201 - BM2210
[editar]BM2201

Kreis mit Mittelpunkt M und Radius r - Kreis
- ---
- Ein Kreis ist eine ebene geometrische Figur. Er wird definiert als die Menge aller Punkte einer Ebene, die einen konstanten Abstand zu einem vorgegebenen Punkt dieser Ebene (dem Mittelpunkt) haben. Der Abstand der Kreispunkte zum Mittelpunkt ist der Radius oder Halbmesser des Kreises, er ist eine positive reelle Zahl. Der Kreis gehört zu den klassischen und grundlegenden Objekten der euklidischen Geometrie.
- Schon die alten Ägypter und Babylonier versuchten, den Flächeninhalt des Kreises näherungsweise zu bestimmen. Besonders in der griechischen Antike war der Kreis wegen seiner Vollkommenheit von großem Interesse. Beispielsweise versuchte Archimedes erfolglos, mit den Werkzeugen Zirkel und Lineal den Kreis in ein Quadrat mit gleichem Flächeninhalt zu überführen, um so den Flächeninhalt des Kreises bestimmen zu können. Ein solches Verfahren zur Berechnung des Flächeninhalts nennt man die Quadratur des Kreises. Erst 1882 konnte Ferdinand von Lindemann durch Nachweis einer besonderen Eigenschaft der Kreiszahl zeigen, dass diese Aufgabe unlösbar ist.
- ---
- Kreisflächen:
- Nach der eingangs genannten Definition ist ein Kreis eine Kurve, also ein eindimensionales Gebilde, und keine zweidimensionale Fläche. Da das Wort „Kreis“ aber oft ungenau auch für die eingeschlossene Fläche benutzt wird, verwendet man zur Verdeutlichung häufig die Begriffe Kreislinie, Kreisrand oder Kreisperipherie anstatt Kreis – im Gegensatz zur Kreisfläche oder Kreisscheibe. Mathematiker unterscheiden dann noch zwischen der abgeschlossenen Kreisfläche oder -scheibe und der offenen (oder dem Kreisinneren), je nachdem ob die Kreislinie dazugehört oder nicht.
- ---
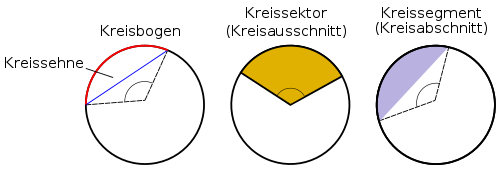
Kreisbogen, Kreissektor und Kreissegment 
Kreisring - Bogen, Sehne, Sektor, Segment und Ring:
- Eine zusammenhängende Teilmenge des Kreises (also der Kreislinie) ist ein Kreisbogen. Eine Verbindungsstrecke von zwei Punkten auf der Kreislinie bezeichnet man als Kreissehne. Zu jeder Sehne gehören zwei Kreisbögen. Die längsten Kreissehnen sind diejenigen, die durch den Mittelpunkt verlaufen, also die Durchmesser. Die zugehörigen Kreisbögen heißen Halbkreise. Ist die Kreissehne kein Durchmesser, so sind die Kreisbögen unterschiedlich lang.
- Ein Kreissektor (Kreisausschnitt) ist eine Fläche, die von zwei Radien und einem dazwischen liegenden Kreisbogen begrenzt wird. Bilden die zwei Radien einen Durchmesser, wird der Sektor auch als Halbkreis bezeichnet.
- Kreissegmente (Kreisabschnitte) werden von einem Kreisbogen und einer Kreissehne eingeschlossen.
- Ein Kreisring entsteht, wenn man aus einem Kreis einen kleineren Kreis mit demselben Mittelpunkt herausschneidet.
- ---

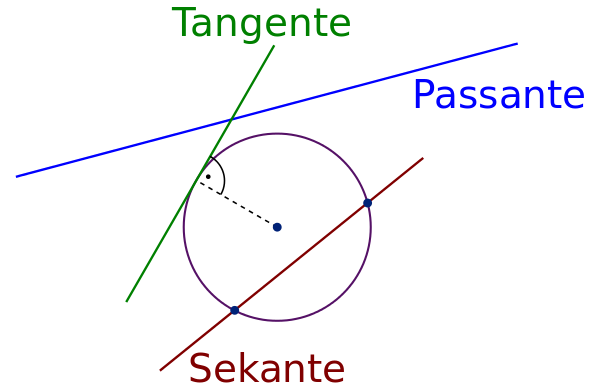
Beziehung von Kreis zu Tangente, Passante und Sekante - Tangente, Passante und Sekante:
- Für die Lage einer Geraden in Bezug auf einen gegebenen Kreis gibt es drei Möglichkeiten:
- Ist der Abstand zwischen Mittelpunkt und Gerade kleiner als der Kreisradius, so haben Kreis und Gerade zwei (verschiedene) Schnittpunkte und man nennt die Gerade Sekante (lateinisch secare = schneiden). Manchmal bezeichnet man den Spezialfall einer Sekante, die durch den Mittelpunkt eines Kreises verläuft, als Zentrale.
- Stimmt der Abstand des Mittelpunkts zu der Geraden mit dem Radius überein, so gibt es genau einen gemeinsamen Punkt. Man sagt, dass die Gerade den Kreis berührt, und nennt die Gerade eine Tangente (lateinisch tangere = berühren). Eine Tangente steht im Berührpunkt senkrecht (orthogonal, normal) zum entsprechenden Radius.
- Wenn der Abstand des Kreismittelpunkts von der Geraden größer ist als der Kreisradius, dann haben Kreis und Gerade keinen Punkt gemeinsam. In diesem Fall bezeichnet man die Gerade als Passante. Diese Bezeichnung hat keinen unmittelbaren lateinischen Ursprung, sondern wurde wohl nach franz. oder ital. passante = Vorbeigehende gebildet. Die lat. Wurzel ist passus = Schritt.
BM2202

Ein Kreis mit Mittelpunkt , Radius und Durchmesser . - Formale Definition des Kreises
- ---
- In einer Ebene ist ein Kreis mit Mittelpunkt und Radius die Punktmenge
- Dabei ist der Radius eine positive reelle Zahl, und bezeichnet die Länge der Strecke .
- Der doppelte Radius heißt Durchmesser und wird oft mit bezeichnet. Radius und Durchmesser sind durch die Beziehungen oder miteinander verknüpft.
- Manchmal wird auch jede Strecke, die den Mittelpunkt mit einem Punkt auf der Kreislinie verbindet, als Radius bezeichnet, und jede Strecke, die durch den Mittelpunkt geht, und deren beide Endpunkte auf der Kreislinie liegen, als Durchmesser. Bei dieser Sprechweise ist die Zahl die Länge jedes Radius und die Zahl die Länge jedes Durchmessers.
- Die offene Kreisfläche ist formal definiert als die Punktmenge
- die abgeschlossene Kreisscheibe als
BM2203

Fragment des Papyrus Rhind 
Annäherung der Kreisfläche im Papyrus Rhind, die Figur oben wird als unregelmäßiges Achteck gedeutet, darunter die Rechenschritte am Beispiel d=9 (Chet). - Kreis, Geschichte (Teil 1)
- Zeit der Ägypter und Babylonier
- ---
- Der Kreis gehört neben dem [Punkt und der geraden Linie zu den ältesten Elementen der vorgriechischen Geometrie. Schon vor viertausend Jahren beschäftigten sich die Ägypter mit ihm in ihren Studien zur Geometrie. Sie konnten den Flächeninhalt eines Kreises näherungsweise bestimmen, indem sie vom Durchmesser d ein Neuntel seiner Länge abzogen und das Ergebnis mit sich selbst multiplizierten. Sie rechneten also
- und bestimmten so näherungsweise (mit einer Abweichung von nur etwa +0,6 %) den Flächeninhalt einer Kreisfläche. Diese Näherung wurde in der altägyptischen Abhandlung Papyrus Rhind gefunden, sie lässt sich erhalten, wenn man den Kreis durch ein unregelmäßiges Achteck annähert.
- Die Babylonier (1900 bis 1600 vor Christus) benutzten eine ganz andere Methode, um den Flächeninhalt der Kreisscheibe zu berechnen. Im Gegensatz zu den Ägyptern gingen sie vom Kreisumfang aus, den sie als dreimal den Kreisdurchmesser schätzten. Der Flächeninhalt wurde dann auf ein Zwölftel des Quadrates des Umfanges geschätzt, also
- mit einer Abweichung von −4,5 % ein deutlich schlechteres Ergebnis.
- Die Babylonier beschäftigten sich aber auch schon mit Kreissegmenten. Sie konnten die Länge der Sehne oder die Höhe des Kreissegments (die senkrecht auf der Sehnenmitte stehende Strecke zwischen Sehne und Umfang) berechnen. Damit begründeten sie die Sehnengeometrie, die später von Hipparch weiterentwickelt wurde und die Claudius Ptolemaios an den Anfang seines astronomischen Lehrbuches Almagest stellte.
BM2204

Titelblatt von Henry Billingsleys englischer Übersetzung der Elemente (1570) - Kreis, Geschichte (Teil 3)
- Antike
- ---
- Die Griechen werden meist als die Begründer der Wissenschaft von der Natur angesehen. Als der erste bedeutende Philosoph dieser Zeit, der sich mit Mathematik beschäftigte, gilt Thales von Milet (624–546 v. Chr.). Er brachte Wissen über die Geometrie aus Ägypten mit nach Griechenland, wie zum Beispiel die Aussage, dass der Durchmesser den Kreis halbiert. Andere Aussagen zur Geometrie wurden von Thales selbst aufgestellt. Der heute nach Thales benannte Satz (Satz von Thales) besagt, dass Peripheriewinkel im Halbkreis rechte Winkel sind. Insbesondere war Thales der erste, bei dem der Begriff des Winkels auftrat.
- Die erste bekannte Definition des Kreises geht auf den griechischen Philosophen Platon (428/427–348/347 v. Chr.) zurück, die er in seinem Dialog Parmenides formulierte:
- "Rund ist doch wohl das, dessen äußerste Teile überall vom Mittelpunkt aus gleich weit entfernt sind." (Platon: Parmenides)
- Zirka 300 Jahre vor Christus lebte der griechische Mathematiker Euklid von Alexandria. Über ihn selbst ist wenig bekannt, aber sein Werk im Bereich der Geometrie war beachtlich. Sein Name ist heute noch in Zusammenhängen wie euklidischer Raum, euklidische Geometrie oder euklidische Metrik in Gebrauch. Sein wichtigstes Werk waren Die Elemente, eine dreizehnbändige Abhandlung, in der er die Arithmetik und Geometrie seiner Zeit zusammenfasste und systematisierte. Er folgerte die mathematischen Aussagen aus Postulaten und begründete damit die euklidische Geometrie. Der dritte Band der Elemente beschäftigte sich mit der Lehre über den Kreis.
- Von Archimedes, der vermutlich zwischen 287 v. Chr. und 212 v. Chr. auf Sizilien lebte, ist eine ausführliche Abhandlung mit dem Titel Kreismessung überliefert. Er bewies in dieser Arbeit, dass der Flächeninhalt eines Kreises gleich dem Flächeninhalt eines rechtwinkligen Dreiecks mit dem Kreisradius als der einen und dem Kreisumfang als der anderen Kathete ist. Der Flächeninhalt des Kreises lässt sich also als "½ · Radius · Umfang" angeben. Mit dieser Erkenntnis führte er das Problem der Quadratur des Kreises auf die Frage der Konstruierbarkeit des Umfangs aus dem vorgegebenen Radius zurück.
- In seiner Abhandlung Kreismessung konnte Archimedes ebenfalls zeigen, dass der Umfang eines Kreises größer als 310/71 und kleiner als 31/7 des Durchmessers ist. Für praktische Zwecke wird diese Näherung 22/7 (~ 3,143) heute noch verwendet.
- Aus diesen beiden Aussagen folgert man, dass sich der Flächeninhalt eines Kreises zum Quadrat seines Durchmessers nahezu wie 11/14 verhält. Euklid war bereits bekannt, dass sich der Flächeninhalt eines Kreises proportional zum Quadrat seines Durchmessers verhält. Archimedes gibt hier eine gute Näherung der Proportionalitätskonstante an.
BM2205

Umfang des Kreises mit d = 1 - Kreisberechnung
- ---
- Kreiszahl:
- Da alle Kreise ähnlich sind, ist das Verhältnis von Kreisumfang und Kreisdurchmesser für alle Kreise konstant. Der Zahlenwert dieses Verhältnisses wird in der Elementargeometrie als Definition für die Kreiszahl verwendet. Es handelt sich hierbei um eine transzendente Zahl, bei der sich außerdem gezeigt hat, dass sie in vielen Bereichen der höheren Mathematik eine herausragende Bedeutung besitzt.
- ---
- Umfang
- Im Rahmen der Elementargeometrie ist das Verhältnis von Kreisumfang zu dessen Durchmesser , und zwar für beliebige Kreise. Somit gilt
- Mit ist der Radius des Kreises gemeint.
- ---

Die Zeichnung verdeutlicht, dass der Flächeninhalt einer Kreisscheibe kleiner als sein muss. 
Darstellung einer Näherung für die Kreisfläche - Kreisfläche:
- Der Flächeninhalt der Kreisfläche (lat. area: Fläche) ist proportional zum Quadrat des Radius bzw. des Durchmessers des Kreises. Man bezeichnet ihn auch als Kreisinhalt.
- Um die Formel für den Kreisinhalt zu erhalten, sind Grenzwert-Betrachtungen unerlässlich. Recht anschaulich ergibt sich eine solche aus der nebenstehenden Zeichnung:
- Die Kreisfläche ist zerlegungsgleich mit der Fläche der rechten Figur. Diese nähert sich bei feiner werdender Sektoreinteilung einem Rechteck an mit der Länge und der Breite . Die Flächenformel ist somit
- ---
- Durchmesser:
- Der Durchmesser eines Kreises mit Flächeninhalt und mit Radius lässt sich durch
- berechnen.
- Das hatten wir auch schon 12 Zeilen weiter oben:
BM2206
- Kreis
- Näherungen für den Flächeninhalt
- ---
- Da die Kreiszahl eine transzendente Zahl ist, gibt es kein Konstruktionsverfahren mit Zirkel und Lineal, mit dem man den Flächeninhalt exakt bestimmen kann. Außerdem sind transzendente Zahlen auch irrational, und daher hat auch keine endliche Dezimalbruchentwicklung, weshalb der Kreisflächeninhalt bei rationalem Radius auch keine endliche Dezimalbruchentwicklung besitzt. Aus diesen Gründen wurden bis heute unterschiedliche Näherungsverfahren für den Flächeninhalt und somit auch den Umfang eines Kreises entwickelt. Manche der Näherungsverfahren, wie beispielsweise das im Abschnitt Annäherung durch Vielecke erläuterte Verfahren, können durch mehrfache Wiederholung ein beliebig genaues Ergebnis liefern.
- ---
- Auszählen in einem Raster:
- Die Kreisfläche lässt sich annähernd bestimmen, indem man ihr viele kleine Quadrate unterlegt (z. B. mit Millimeterpapier). Zählt man alle Quadrate, die vollständig innerhalb des Kreises liegen, so erhält man einen etwas zu niedrigen Wert für die Fläche, zählt man auch alle Quadrate mit, die den Kreis lediglich schneiden, so ist der Wert zu groß. Der Mittelwert beider Ergebnisse ergibt eine Näherung für den Flächeninhalt des Kreises, deren Güte mit der Feinheit des Quadratrasters steigt.
BM2207

Kreiswinkel: Der Umfangswinkel hängt nicht von der Lage des Punktes C auf dem Kreisbogen ab. Er ist halb so groß wie der Zentriwinkel und genauso groß wie der Sehnentangentenwinkel . 
Halbkreis mit rechtwinkligen Dreiecken - Kreiswinkel und Winkelsätze
- ---
- Eine Kreissehne mit Endpunkten A und B teilt einen gegebenen Kreis in zwei Kreisbögen. Ein Winkel mit Scheitel C auf einem der Kreisbögen wird Umfangswinkel oder Peripheriewinkel genannt. Der Winkel mit Scheitel im Mittelpunkt M heißt Mittelpunktswinkel oder Zentriwinkel.
- Im Spezialfall, dass die Sehne den Mittelpunkt enthält, also ein Durchmesser des Kreises ist, ist der Mittelpunktswinkel ein gestreckter Winkel mit 180°.
- In dieser Situation gilt eine grundlegende Aussage der Kreisgeometrie, der Satz von Thales: Er besagt, dass Umfangswinkel über einem Durchmesser stets rechte Winkel sind, also 90° betragen. Der Kreis um das rechtwinklige Dreieck wird in dieser Situation auch Thaleskreis genannt.
- Auch im Fall einer beliebigen Kreissehne sind alle Umfangswinkel, die auf dem gleichen Kreisbogen liegen, gleich groß. Diese Aussage wird auch Umfangswinkelsatz genannt. Der Kreisbogen, auf dem die Scheitel der Umfangswinkel liegen, heißt Fasskreisbogen. Liegen Umfangswinkel und Zentriwinkel auf der gleichen Seite der Sehne, dann ist der Zentriwinkel doppelt so groß wie der Umfangswinkel (Kreiswinkelsatz). Zwei Umfangswinkel, die auf gegenüberliegenden Seiten der Sehne liegen, ergänzen einander zu 180°.
- Der Umfangswinkel ist genauso groß wie der spitze Sehnentangentenwinkel zwischen der Sehne und der durch einen ihrer Endpunkte verlaufenden Tangente (Sehnentangentenwinkelsatz).
BM2208
- Kreiswinkel
- ---
- Für viele Fragestellungen der Elementargeometrie, bei denen es um Winkel an Kreisen geht, lassen sich die im Folgenden erklärten Begriffe und Aussagen verwenden.
- ---
- Begriffe
- ---
- Verbindet man die voneinander verschiedenen Endpunkte A und B eines Kreisbogens mit seinem Mittelpunkt M und einem Punkt P auf dem Kreisbogen, so liegen folgende Winkel vor:
- Umfangswinkel oder Peripheriewinkel (Φ) nennt man einen Winkel , dessen Scheitel P auf demjenigen Kreisbogen liegt, der den gegebenen Kreisbogen über [AB] zum vollständigen Kreis (dem Umkreis des Dreiecks ABP) ergänzt.
- Mittelpunktswinkel (μ): Ist M der Mittelpunkt des gegebenen Kreisbogens, so bezeichnet man den Winkel als den zugehörigen Mittelpunktswinkel (Zentriwinkel).
- Ein Sehnentangentenwinkel (τ) zum gegebenen Kreisbogen wird begrenzt von der Sehne [AB] und der Kreistangente im Punkt A bzw. B.
- Viele Autoren von Geometrie-Lehrbüchern nehmen bei Umfangswinkeln, Mittelpunktswinkeln und Sehnentangentenwinkeln nicht Bezug auf einen gegebenen Kreisbogen, sondern auf eine gegebene Kreissehne [AB]. Legt man eine solche Definition zugrunde, so muss man zwei Arten von Umfangswinkeln unterscheiden, nämlich spitze und stumpfe Umfangswinkel. Als Mittelpunktswinkel definiert man in diesem Fall den kleineren der beiden Winkel, die von den Kreisradien [MA] und [MB] eingeschlossen werden. Die Formulierung der Sätze im nächsten Abschnitt muss bei Verwendung dieser Definition ein wenig variiert werden.
- ---

Umfangs-, Mittelpunkts- und Sehnentangentenwinkel - Kreiswinkelsatz (Zentriwinkelsatz)
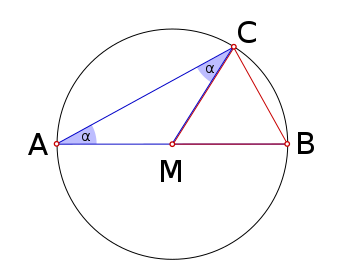
- ---
- Der Mittelpunktswinkel (Zentriwinkel) eines Kreisbogens ist doppelt so groß wie einer der zugehörigen Umfangswinkel (Peripheriewinkel).

Skizze zum Kreiswinkelsatz 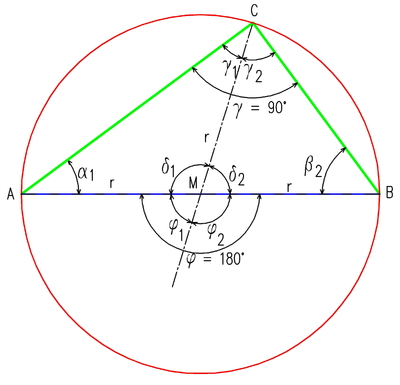
Satz des Thales - Der Beweis dieser Aussage ist in dem links skizzierten Spezialfall besonders einfach. Die beiden Winkel bei B und P sind als Basiswinkel in dem gleichschenkligen Dreieck MBP gleich groß. Der dritte Winkel des Dreiecks MBP (mit dem Scheitel M) hat die Größe . Der Satz über die Winkelsumme ergibt folglich
- und weiter, wie behauptet, .
- Im allgemeinen Fall liegt M nicht auf einem Schenkel des Umfangswinkels. Die Gerade PM teilt dann Umfangswinkel und Mittelpunktswinkel in zwei Winkel ( und bzw. und ), für die jeweils einzeln die Aussage gilt, da die Voraussetzungen des bewiesenen Spezialfalls erfüllt sind. Deshalb gilt die Aussage auch für den gesamten Umfangswinkel und den gesamten Mittelpunktswinkel . Außerdem ermöglicht die Gültigkeit des Peripheriewinkelsatzes (siehe unten) eine Überführung des allgemeinen Falles in den Spezialfall, ohne die Allgemeinheit des bereits für den Spezialfall erbrachten Beweises einzuschränken.
- Ein besonders wichtiger Sonderfall liegt vor, wenn der gegebene Kreisbogen ein Halbkreis ist: In diesem Fall ist der Mittelpunktswinkel gleich 180° (ein gestreckter Winkel), während die Umfangswinkel gleich 90°, also rechte Winkel sind. Damit erweist sich der Satz des Thales als Spezialfall des Kreiswinkelsatzes.
BM2209
- Satz des Thales
- ---
- Der Satz des Thales ist ein Satz der Geometrie und ein Spezialfall des Kreiswinkelsatzes. Vereinfacht lautet er: Alle Winkel am Halbkreisbogen sind rechte Winkel.
- Der erste Beweis wird dem antiken griechischen Mathematiker und Philosophen Thales von Milet zugeschrieben. Die Aussage des Satzes war bereits vorher in Ägypten und Babylonien bekannt.
- ---
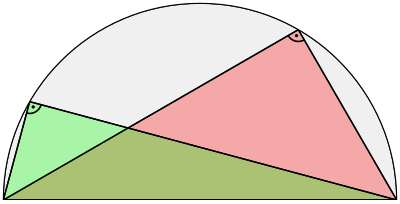
Halbkreis mit rechtwinkligen Dreiecken - Formulierung des Satzes und seiner Umkehrung
- ---
- Exakte Formulierung: Konstruiert man ein Dreieck aus den beiden Endpunkten des Durchmessers eines Halbkreises (Thaleskreis) und einem weiteren Punkt dieses Halbkreises, so erhält man immer ein rechtwinkliges Dreieck.
- Oder: Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C immer einen rechten Winkel.
- Auch die Umkehrung des Satzes ist korrekt: Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse, also der längsten Seite des Dreiecks, die dem rechten Winkel gegenüberliegt.
- Oder: Hat das Dreieck ABC bei C einen rechten Winkel, so liegt C auf einem Kreis mit der Hypotenuse AB als Durchmesser.
- ---
- Beweise
- ---
- Euklid leitet den Satz des Thales im dritten Band seiner Elemente mit Hilfe folgender Sätze, die ebenfalls Thales zugeschrieben werden und im ersten Band enthalten sind, her:
- In jedem gleichschenkligen Dreieck sind die Winkel an der Basis gleich.
- Die Winkelsumme im Dreieck ist 180°.
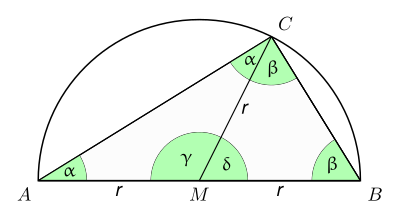
Halbkreis mit Dreieck und Mittelpunkt M - ABC sei ein Dreieck innerhalb eines Kreises mit [AB] als Kreisdurchmesser und dem Radius r. Dann ist der Mittelpunkt M der Strecke [AB] auch der Kreismittelpunkt. Die Streckenlängen [AM], [BM] und [CM] sind also gleich dem Radius r.
- Die Strecke [CM] teilt das Dreieck ABC in zwei Dreiecke AMC und BCM auf, die gleichschenklig sind. Die Basiswinkel dieser Dreiecke, also die Winkel an der Grundseite [AC] bzw. [BC], sind daher jeweils gleich ( beziehungsweise in der Abbildung).
- Die Winkelsumme im Dreieck ABC beträgt 180°:
- Dividiert man diese Gleichung auf beiden Seiten durch 2, so ergibt sich
- .
- Damit ist gezeigt, dass der Winkel mit Scheitel C ein rechter Winkel ist.
- Die Umkehrung des Satzes von Thales lässt sich auf die Aussage zurückführen, dass die Diagonalen eines Rechtecks gleich lang sind und sich gegenseitig halbieren.
BM2210

- Satz des Thales
- ---
- Der Satz des Thales besagt, dass jedes Dreieck rechtwinklig ist, wenn auf einem Halbkreis über liegt.
- ---
- Beweis 1
- ---
- Da sind und gleichschenklige Dreiecke. Weil die beiden Basiswinkel in einem gleichschenkligen Dreieck gleich groß sind, gilt:
- (1)
- und
- (2)
- Da alle Winkel in einem Dreieck addiert ergeben, gilt für das Dreieck :
- (3)
- Setzt man nun (1) und (2) ein, erhält man:
- (3.1)
- (3.2)
- (3.3)
- (3.4)
- (3.5)
- Damit ist der Satz des Thales bewiesen, denn das Dreieck enthält immer den rechten Winkel bei und ist somit immer rechtwinklig.
BM2211 - BM2220
[editar]BM2211
- Sind A, B, C drei Punkte, die nicht auf einer Geraden liegen, also ein nicht ausgeartetes Dreieck bilden, dann existiert ein eindeutig bestimmter Kreis durch diese Punkte, nämlich der Umkreis des Dreiecks ABC. Der Mittelpunkt des Umkreises ist der Schnittpunkt der drei Mittelsenkrechten des Dreiecks. Ebenso kann jedem Dreieck ein eindeutig bestimmter Kreis einbeschrieben werden, der die drei Seiten berührt, d. h., die Dreiecksseiten bilden Tangenten des Kreises. Dieser Kreis wird Inkreis des Dreiecks genannt. Sein Mittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden.
- In der Elementargeometrie werden noch weitere Kreise am Dreieck betrachtet: Die Ankreise liegen außerhalb des Dreiecks und berühren eine Seite und die Verlängerungen der beiden anderen Seiten. Ein weiterer interessanter Kreis am Dreieck ist der Feuerbachkreis, benannt nach Karl Wilhelm Feuerbach. Auf ihm liegen die drei Seitenmittelpunkte und die drei Fußpunkte der Höhen. Da auf ihm außerdem die drei Mittelpunkte der Strecken zwischen dem Höhenschnittpunkt und den Ecken des Dreiecks liegen, wird der Feuerbachkreis auch Neunpunktekreis genannt. Sein Mittelpunkt liegt wie der Schwerpunkt, der Umkreismittelpunkt und der Höhenschnittpunkt auf der eulerschen Geraden.
- Im Gegensatz zu Dreiecken besitzen Polygone mit mehr als drei Ecken im Allgemeinen keinen Umkreis oder Inkreis. Für regelmäßige Vielecke existieren beide allerdings stets. Ein Viereck, das einen Umkreis besitzt, wird Sehnenviereck genannt. Ein konvexes Viereck ist genau dann ein Sehnenviereck, wenn sich gegenüberliegende Winkel zu 180° ergänzen. Ein Viereck, das einen Inkreis besitzt, wird Tangentenviereck genannt. Ein konvexes Viereck ist genau dann ein Tangentenviereck, wenn die Summe der Seitenlängen zweier gegenüberliegender Seiten gleich der Summe der beiden anderen Seitenlängen ist.
BM2212

Tangenten mit Hilfe des Thaleskreises durch Punkt an den Kreis
- Thaleskreis
- ---
- Für die Konstruktion des Thaleskreises über einer gegebenen Strecke wird zunächst der Mittelpunkt dieser Strecke konstruiert, der auch der Mittelpunkt des Thaleskreises ist. Dazu werden um und jeweils zwei kurze Kreisbögen mit dem gleichen Radius geschlagen, wobei so groß gewählt werden muss, dass die vier Kreisbögen sich in zwei Punkten und schneiden. Das ist z. B. für der Fall. Die Strecke schneidet dann im Mittelpunkt
- .
- Der gesuchte Thaleskreis ist nun der Kreis mit Mittelpunkt und Radius
- .
- ---
- Konstruktion von Tangenten:
- Gegeben sei ein Punkt außerhalb eines Kreises mit Mittelpunkt und es sollen die beiden Tangenten an den Kreis konstruiert werden, die durch den Punkt laufen. Diese elementare Konstruktionsaufgabe lässt sich einfach mit Hilfe des Satzes von Thales lösen: Man konstruiert den Thaleskreis mit der Strecke als Durchmesser. Die Schnittpunkte dieses Kreises mit sind dann die Berührpunkte der gesuchten Tangenten.
BM2213

Ein Kleinkreis (blau) und ein Großkreis (rot) - Kleinkreis
- ---
- Unter Kleinkreis versteht man jene Kreise auf einer Kugeloberfläche, deren Ebenen nicht den Kugelmittelpunkt enthalten.
- Der Name „Kleinkreise“ wurde als Gegensatz zu den „Großkreisen“ geprägt, deren Ebenen das Kugelzentrum enthalten und die alle größtmöglichen Kreise auf einer Kugeloberfläche umfassen.
- Die wichtigsten Kleinkreise sind
- die Breitenkreise (konstante geografische Breite) und
- die Entfernungskreise (Kreise gleicher Entfernung zu einem gegebenen Punkt).
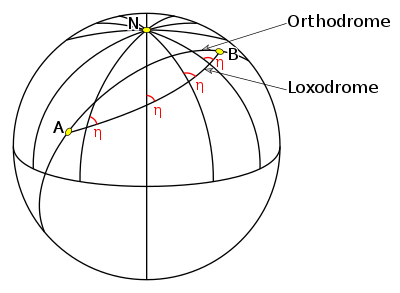
- Sie eignen sich aber nicht für trigonometrische Berechnungen. Für deren Formeln sind ausschließlich Großkreise zu verwenden – zum Beispiel Meridiane oder „Orthodromen (kürzeste Verbindungslinien zwischen Kugelpunkten)“. Ein Dreieck aus solchen Großkreisen heißt nach seinen wichtigsten Anwendungen astronomisches oder nautisches Dreieck, wird aber auch nach seinen Eckpunkten Pol-Zenit-Stern-Dreieck genannt.
- ---

Großkreis (rot) und Kleinkreis (blau) 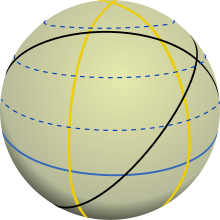
Verschiedene Großkreise (durchgezogene Linien). Die gelben Großkreise sind hier Längenkreise. Neigung der 2 schwarzen Großkreise gegen den Äquator (blau) ca. 55° und 60° 
Großkreiskarte für die Schweiz - Großkreis
- ---
- Ein Großkreis ist ein größtmöglicher Kreis auf einer Kugeloberfläche. Sein Mittelpunkt fällt immer mit dem Mittelpunkt der Kugel zusammen und ein Schnitt auf dem Großkreis teilt die Kugel in jedem Fall in zwei („gleich große“) Hälften. Da es unendlich viele Möglichkeiten gibt, eine Kugel so zu zerschneiden, dass die Schnittebene den Kugelmittelpunkt trifft, gibt es auch unendlich viele Großkreise.
- Großkreise spielen z. B. in der Geographie sowie der Schiff- und Luftfahrt eine bedeutende Rolle. Anhand von ihnen werden auch die Zeitzonen festgelegt. Die Sphärische Geometrie beinhaltet Großkreise als elementaren Bestandteil. Das Verständnis der Orthodrome als kürzeste Verbindung zweier Punkte auf einer Kugeloberfläche ist unerlässlich für das Verständnis der „geradlinigen“, unbeschleunigten (Abkehr vom Konzept der Gravitation) Bewegung im gekrümmten Raum (allgemeine Relativitätstheorie, Raumkrümmung).
- Im geografischen Koordinatensystem der Erde gibt es Sonderfälle von Großkreisen. Sie sind besonders gelagerte Großkreise. Diese Sonderfälle sind der Äquator (hier durchgezogene blaue Linie) sowie die Längenkreise (hier gelbe Linie). Der Äquator ist der Großkreis, der die Erdkugel in der Mitte zwischen Süd- und Nordpol trennt. Die Längenkreise gehen durch den Süd- und durch den Nordpol. Auf ihnen liegen die Meridiane, die sich jeweils vom Nord- zum Südpol erstrecken. Wie z. B. der Nullmeridian (0°) und der 180°-Meridian. Die Meridiane werden auch Längengrade genannt. Hingegen sind die Breitenkreise (hier gestrichelte Linien), mit Ausnahme des Äquators, keine Großkreise, sondern kleiner als der maximale Kugelumfang. Man nennt sie deshalb Neben- oder Kleinkreise.
- Auf Großkreisen der Erde entspricht eine Bogenminute einer Seemeile, abgekürzt sm (engl. nautical mile, nm oder NM). Sie wird (also als „Längenminute“ bzw. als „Breitenminute am Äquator“) mit 1852 Metern errechenbar bei einem angenommenen Erdumfang von 40.000 km. Der mittlere Erdradius beträgt 6371 km.
- Die kürzeste Verbindung zwischen zwei Punkten auf einer Kugeloberfläche – die sogenannte Orthodrome – ist immer Teil eines Großkreises (der sogenannte Hauptbogen). Deshalb führen Schifffahrts- und vor allem Flugrouten meist entlang von Großkreisen. Das Befahren der Erdkugel auf Orthodromen wird Großkreissegeln genannt; bei Start- und Zielpunkt auf ähnlicher geographischer Breite verlaufen die „Großkreiskurse“ dabei über etwas größere Breiten (z. B. München–Peking über Sibirien).
- ---
- Orthodrome
- ---

Orthodrome auf der Erdkugel zwischen Los Angeles und London - Die Orthodrome (griech. orthos für „gerade“, dromos für „Lauf“) ist die kürzeste Verbindung zweier Punkte auf einer Kugeloberfläche.
- Die Orthodrome ist eine Geodäte für den speziellen Fall einer Kugeloberfläche. Die Orthodrome ist immer ein Teilstück eines Großkreises. In der Luftfahrt fliegt man meist entlang dieser Orthodrome, um die geringste Flugstrecke zurücklegen zu können. Die umgangssprachlich häufiger gebrauchte synonyme Bezeichnung ist Luftlinie.
- ---
- Loxodrome
- ---
- Eine Loxodrome (gr. loxos „schief“, dromos „Lauf“) ist eine Kurve auf einer Kugeloberfläche – z. B. der Erdoberfläche –, die die Meridiane im geographischen Koordinatensystem immer unter dem gleichen Winkel schneidet und daher auch Kursgleiche, Winkelgleiche oder Kurve konstanten Kurses genannt wird.

Der kürzeste Weg auf der Kugeloberfläche zwischen Punkt A und B ist eine Orthodrome. 
Die Loxodrome von A nach B schneidet alle Meridiane im konstanten Winkel
BM2214

Kreis mit Tangente, Sekante und Passante - Tangente
- ---
- Eine Tangente (von lateinisch: tangere ‚berühren‘) ist in der Geometrie eine Gerade, die eine gegebene Kurve in einem bestimmten Punkt berührt. Beispielsweise ist die Schiene für das Rad eine Tangente, da der Auflagepunkt des Rades ein Berührungspunkt der beiden geometrischen Objekte, Gerade und Kreis, ist. Tangente und Kurve haben im Berührungspunkt die gleiche Richtung. Die Tangente ist in diesem Punkt die beste lineare Näherungsfunktion für die Kurve.
- Besonders einfach sind die Verhältnisse beim Kreis: Alle Geraden können bezüglich eines Kreises unterschieden werden in Sekanten, Tangenten und Passanten – je nachdem, ob sie mit dem Kreis zwei Punkte, einen oder gar keinen Punkt gemeinsam haben. Die Kreistangente trifft den Kreis also in genau einem Punkt. Sie steht dort senkrecht auf dem zu diesem Punkt gehörenden Berührungsradius.
BM2215
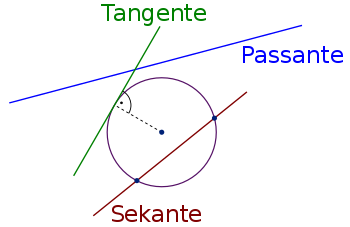
Bild 1 - Kreistangente
- ---
- Tangente eines Kreises ist jede in der gleichen Ebene verlaufende Gerade, die mit dem Kreis genau einen Punkt gemeinsam hat.
- Die in der Kreisebene verlaufenden Geraden lassen sich einteilen in Sekanten, Tangenten und Passanten. Die Tangenten stellen dabei in gewisser Weise den Grenzfall dar zwischen Sekanten und Passanten.
- Eine Grundeigenschaft der Tangente ist es, dass sie orthogonal (im rechten Winkel) zu ihrem Berührungsradius verläuft, also zur Verbindungslinie zwischen dem Berührpunkt und dem Kreismittelpunkt. Umgekehrt ist jede Gerade, die im Endpunkt eines Radius senkrecht auf diesem steht, auch eine Tangente des Kreises. Dies hängt damit zusammen, dass die Gerade, zu der der Radius gehört (wie jede Gerade durch den Mittelpunkt) Symmetrieachse des Kreises ist.
- ---
- Konstruktion der Tangente
- ---
- Für eine Konstruktion mit Zirkel und Lineal reicht es keinesfalls aus, nach Augenmaß eine Gerade zu finden, die den Kreis k „gerade noch“ berührt.
- Wenn der Berührpunkt gegeben ist (oder beliebig gewählt werden darf), so ist zuerst der Berührungsradius einzuzeichnen und dann das Lot dazu im Berührpunkt.
- Wenn ein Punkt P außerhalb des Kreises gegeben ist, durch den die Tangente gehen soll, so muss zunächst der Berührpunkt gefunden werden. Da hierbei ein rechter Winkel entstehen muss, hilft der Satz des Thales:
Man verbindet den Punkt P mit dem Kreismittelpunkt M und zeichnet über der Strecke [PM] den Thaleskreis. Dieser schneidet den Kreis k in zwei Punkten, die als Berührpunkte geeignet sind. Man erhält also durch den Punkt P zwei mögliche Kreistangenten. Die durch die beiden Berührpunkte bestimmte Gerade heißt Polare des Punktes P bezüglich des Kreises k.
- Wenn ein Punkt P außerhalb des Kreises gegeben ist, durch den die Tangente gehen soll, so muss zunächst der Berührpunkt gefunden werden. Da hierbei ein rechter Winkel entstehen muss, hilft der Satz des Thales:

- Eine Alternative zur Konstruktion mit Hilfe des Thaleskreises ist die Konstruktion direkt über die zum Punkt P gehörende Polare. Hierzu zeichnet man zwei vom P ausgehende beliebige Sekanten und teilt dann die von ihnen erzeugten Sehnen harmonisch, wobei der Punkt P jeweils der äußere Teilungspunkt der harmonischen Teilung der Sehne ist. Die beiden inneren Teilungspunkte der Sehnen liegen dann auf der Polaren zu P und die Polare schneidet den Kreis in den beiden Berührungspunkten der zu konstruierenden Tangenten. Den inneren Teilungspunkt der harmonische Teilung einer Sehne kann man dabei wie folgt konstruieren. Man zeichnet eine beliebige durch P verlaufende Hilfsgerade und wählt auf dieser einen (beliebigen) von P verschiedenen Punkt X. Dann zeichnet man die Verbindungsgerade zwischen X und dem hinteren Endpunkt B der Sehne und anschließend eine Parallele zu dieser Geraden durch den vorderen Endpunkt A der Sehne. Diese Parallele schneidet die ursprüngliche Hilfsgerade in einen Punkt Y und man trägt nun auf der anderen Seite von A eine Strecke der Länge |AY| ab und verbindet deren Endpunkt Z mit X. Die Strecke ZX schneidet dann die Sehne AB im Punkt Q, welcher der innere Teilungspunkts der harmonischen Teilung von AB ist. Das heißt P und Q teilen die Sehne AB harmonisch und Q liegt auf der zu P gehörenden Polaren. Diese Konstruktion mit Hilfe der Polaren lässt sich auch auf anderen Kegelschnitte anwenden, das heißt man kann auf die Weise auch Tangenten an Ellipse, Parabeln und Hyperbeln konstruieren.

BM2216
Ein Sehnenviereck ABCD mit Umkreis k - Sehnenviereck
- ---
- Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Kreis liegen, dem Umkreis des Vierecks. Folglich sind alle Seiten des Sehnenvierecks Sehnen des Umkreises. Üblicherweise meint man mit Sehnenviereck ein nicht überschlagenes Sehnenviereck, dieses ist notwendigerweise konvex.
- ---

Ein Tangentenviereck ABCD mit Inkreis k - Tangentenviereck
- ---
- Ein Tangentenviereck ist ein Viereck, dessen Seiten Tangenten eines Kreises sind. Diesen Kreis nennt man den Inkreis des Tangentenvierecks.
- Die (hier grün dargestellten) Senkrechten vom Inkreismittelpunkt (M) auf die vier Seiten zerlegen das Tangentenviereck in vier Drachenvierecke (mit grau gezeichneten Symmetrieachsen).
BM2217

Bild 1: rot = Kreisbogen der Länge b; blau = Kreissehne der Länge l - Kreisbogen
- ---
- Legt man auf einem Kreis zwei beliebige Punkte fest und verbindet diese durch Strecken mit dem Mittelpunkt des Kreises, so stellen die beiden Teile der Kreisfläche, die durch diese Strecken voneinander getrennt werden, Kreisausschnitte (auch Kreissektor genannt) dar. Ein Kreisausschnitt wird also gleichsam von zwei Radien aus einem Kreis „herausgeschnitten“. Der zu einem Kreissektor gehörende Teil der Kreislinie wird als Kreisbogen bezeichnet, der Winkel zwischen den beiden Radien als Mittelpunktswinkel.
- ---
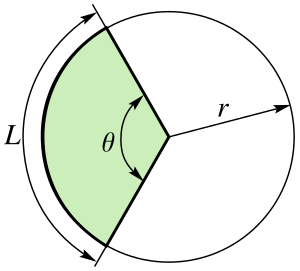
Bild 2: Kreissektor - Kreissektor
- ---
- Ein Kreissektor (auch Kreisausschnitt) ist in der Geometrie die Teilfläche einer Kreisfläche, die von einem Kreisbogen und zwei Kreisradien begrenzt wird (im Gegensatz zum von einem Kreisbogen und einer Kreissehne begrenzten „Kreissegment/Kreisabschnitt“). Von oben betrachtet sieht diese Teilfläche aus wie ein Tortenstück.
- ---

Bild 3: Kreissegment - Kreissegment
- ---
- Ein Kreissegment (auch Kreisabschnitt) ist in der Geometrie die Teilfläche einer Kreisfläche, die von einem Kreisbogen und einer Kreissehne begrenzt wird (im Gegensatz zum von einem Kreisbogen und zwei Kreisradien begrenzten „Kreissektor/Kreisausschnitt“).
- Größen des Kreissegments:
- α = Mittelpunktswinkel
- b = Kreisbogen
- h = Segmenthöhe
- r = Radius
- s = Kreissehne
- A = Segmentfläche
- M = Kreismittelpunkt
- Der Flächeninhalt eines Kreissegments lässt sich aus dem Kreisradius und dem zugehörigen Mittelpunktswinkel berechnen. Man ermittelt dazu die Flächeninhalte des entsprechenden Kreissektors und des in der Skizze dargestellten gleichschenkligen Dreiecks AMB. Ist der Mittelpunktswinkel kleiner als 180°, so muss man diese Flächeninhalte subtrahieren (Sektorfläche minus Dreiecksfläche). Bei einem Mittelpunktswinkel über 180° sind die Flächeninhalte zu addieren. Wenn der Mittelpunktswinkel genau 180° beträgt, ist das Kreissegment eine Halbkreisfläche, und die Fläche des Dreiecks ist 0.
BM2218
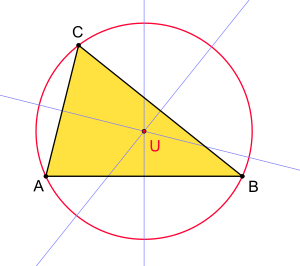
Dreieck mit Mittelsenkrechten und Umkreis - Umkreis von Dreiecken
- ---
- Der Umkreismittelpunkt ist der Schnittpunkt der Mittelsenkrechten.
- Eine besonders große Bedeutung hat der Umkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Umkreis, wie im Folgenden begründet wird.
- Alle Punkte der Mittelsenkrechten zu sind von und gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu übereinstimmende Entfernungen von und . Der Schnittpunkt dieser beiden Mittelsenkrechten ist also von allen drei Ecken (, und ) gleich weit entfernt. Er muss also auch auf der dritten Mittelsenkrechten liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.
- ---
- Sonderfälle:
- Für spitzwinklige Dreiecke liegt der Umkreismittelpunkt im Inneren des Dreiecks. Beim rechtwinkligen Dreieck ist der Mittelpunkt der Hypotenuse zugleich Umkreismittelpunkt (siehe Satz des Thales). Im Falle eines stumpfwinkligen Dreiecks (mit einem Winkel über 90°) befindet sich der Umkreismittelpunkt außerhalb des Dreiecks.
- ---

Dreieck mit Inkreis - Inkreis
- ---
- Eine besonders große Bedeutung hat der Inkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Inkreis, sein Mittelpunkt liegt im Schnittpunkt der drei Winkelhalbierenden. Zeichnet man um diesen Schnittpunkt einen Kreis, der eine Seite des Dreiecks berührt (die Seite wird somit eine Kreistangente des Inkreises), so berührt dieser Kreis auch die beiden anderen Seiten.
- Alle Punkte der Winkelhalbierenden des Innenwinkels haben den gleichen Abstand von den Seiten und . Entsprechend haben die Punkte der Winkelhalbierenden von den gleichen Abstand von und . Der Schnittpunkt dieser beiden Winkelhalbierenden hat also von allen drei Seiten des Dreiecks (, und ) gleichen Abstand. Er muss also auch auf der dritten Winkelhalbierenden liegen.
- Der Inkreis berührt alle drei Seiten von innen – im Gegensatz zu den drei Ankreisen, die jeweils eine Seite von außen und die Verlängerungen der beiden anderen Seiten berühren.
BM2219
- 1.) Wie ist ein Kreis definiert?
- 2.) Was ist ein Radius?
- 3.) Was ist ein Durchmesser?
- 4.) Was ist eine Tangent?
- 5.) Was ist eine Sekante?
- 6.) Was ist eine Sehne?
- 7.) Was ist der Unterschied zwischen einer Sehne und einer Sekante?
- 8.) Was ist eine Passante?
BM2220
-
Bild 1
-
Bild 2
-
Bild 3
-
Bild 4
- Tangente
- ---
- Durch einen Punkt eines Kreises lassen sich viele Geraden legen (Bild 1 - 4). Es gibt jedoch nur eine einzige Gerade durch , die Tangente dieses Kreises ist (Bild 3).
- Mit Hilfe eines Lineals lässt sich die Tangente in einem Punkt des Kreises nur näherungsweise zeichnen.
- ---
- Der Radius, der den Berührungspunkt mit dem Mittelpunkt des Kreises verbindet, heißt der Berührungspunkt dieser Tangente.
- SATZ: Wenn der Berührungspunkt einer Tangente an einem Kreis um ist, so steht der Radius senkrecht auf .
- ---
- Beweis: Um das Lot von auf zu fällen gibt es zwei Möglichkeiten:
- a) Der Fußpunkt des Lotes ist der Punkt . In diesem Fall ist der Satz bewiesen. (Bild 5)
- b) Der Fußpunkt des Lotes ist von verschieden (Bild 6 und 7). In diesem Fall bestimmen wir das Bild der Geraden und des Kreises bei der Spiegelung der Geraden . Das Bild des Punktes liegt dann sowohl auf der Geraden als auch auf dem Kreis, da wegen des rechten Winkels auf sich selbst abgebildet wird. Die Gerade hat also mit dem Kreis zwei gemeinsame Punkte und ist demnach nicht Tangente an dem Kreis. Da wir vorausgesetzt hatten, dass Tangente sein soll, ist der Fall b) nicht möglich. Es kann immer nur der Fall a) eintreten.
BM2221 - BM2230
[editar]BM2221
-
Bild 1
-
Bild 2
-
Bild 3
- Erkläre mit deinen Worten, warum der Radius senkrecht auf der Tangente steht!
- ---
- Wer hat den Beweis aus der vorigen Übung wirklich verstanden?
- Wäre es nicht denkbar, dass es durch einen Punkt des Kreises eine Gerade gibt, die nicht unbedingt rechtwinklig zum Radius dieses Punktes steht?
- Wäre es nicht denkbar, dass durch diesen Punkt verschiedene Geraden gehen? Mit leicht unterschiedlichen Neigungen? (Bild 1-3)

Bild 4 - Die Geraden müssen ja nicht so stark geneigt sein, dass sie den Kreis in zwei Punkten schneiden (Bild 4). (Wenn die Gerade den Kreis in zwei Punkten schneiden würde, dann wäre es keine Tangente mehr, sondern eine Sekante. Das wäre dann eine ganz andere Geschichte.)
- Erkläre mit deinen Worten, warum der Radius senkrecht auf der Tangente steht!
BM2222
- SATZ: Wenn der Berührungspunkt einer Tangente an einem Kreis um ist, so steht der Radius senkrecht auf .
- ---
- Wie lautet die Umkehrung dieses Satzes?
1. Lösung BM2222 - SATZ: Steht der Radius eines Kreises senkrecht auf einer Geraden durch den Punkt , so ist die Gerade Tangente an dem Kreis im Punkt .
- ---
- Welcher Satz ergibt sich aus den beiden Sätzen?
- 1.) Wenn der Berührungspunkt einer Tangente an einem Kreis um ist, so steht der Radius senkrecht auf .
- und
- 2.) Steht der Radius eines Kreises senkrecht auf einer Geraden durch den Punkt , so ist die Gerade Tangente an dem Kreis im Punkt .
2. Lösung BM2222 - SATZ: Eine Gerade durch einen Punkt eines Kreises um ist Tangente das Kreises genau dann, wenn der Radius senkrecht auf steht.
BM2223
- Ein Satz und seine Umkehrung
- ---
- Die Umkehrung einer wahren Aussage muss nicht unbedingt wieder eine wahre Aussage sein.
- Beispiel:
- Wenn es eine Wiese ist, dann ist es grün. (wahr!) (Voraussetzung: es ist ene Wiese; Behauptung: es ist grün)
- Wenn es grün ist, dann ist es eine Wiese (falsch!)
- ---
- Wenn ein Satz und seine Umkehrung gilt („wenn A dann B“; Umkehrung: „wenn B dann A“), dann sind Voraussetzung und Behauptung äquivalent.
- ---
- (A ist notwendig für B); (aus A folgt B); (A ist eine notwendige Bedingung für B); („eindeutig“) und
- (B ist notwendig für A); (aus B folgt a); (B ist eine notwendige Bedingung für A);
(„eindeutig“)
- („eineindeutig“)
- ---
- („wenn A dann B“)
- („genau dann, wenn“); („A genau dann, wenn B“); („dann und nur dann“); („A dann und nur dann wenn B“)
BM2224
- Notwendige und hinreichende Bedingung
- ---
- Notwendige Bedingung und hinreichende Bedingung sind Begriffe aus der Theorie wissenschaftlicher Erklärungen, die Bedingungen in zwei verschiedene Typen unterteilen. Die unterschiedlichen Beziehungen zwischen Bedingendem und Bedingtem werden auch in der Logik, vor allem in der Aussagenlogik, behandelt.
- Kausal verstanden betreffen beide Begriffe die Frage, ob bestimmte Ereignisse als Ursachen anderer Ereignisse unersetzlich sind, und ob die anderen Ereignisse zwangsläufig einträten, wenn die bestimmten Ereignisse vorliegen würden.
- ---

Gemahlene Bohnen sind eine notwendige Bedingung, um Kaffee zu kochen – ohne sie geht es nicht. Aber sie sind nicht hinreichend. - Notwendige Bedingung
- Aussagenlogisch betrachtet ist eine notwendige Bedingung für eine Aussage eine Aussage, die zwingend wahr (erfüllt) sein muss, wenn wahr ist. Es kommt also nicht vor, dass erfüllt ist, ohne dass erfüllt ist.
- Der Zusammenhang wird durch die symbolische Schreibweise ausgedrückt, sprich „K impliziert B“ oder „aus K folgt B“. Der Pfeil, der den Zusammenhang symbolisiert, steht für die mögliche Schlussfolgerung. Wenn sicher ist, dass erfüllt ist, kann man sicher sein, dass auch erfüllt ist; es kann also von auf geschlossen werden. Dabei ist es unerheblich, ob zeitlich vor oder nach stattfindet. Oft geht es gerade darum, aus dem Vorliegen von einen Schluss auf die vorangegangenen Bedingungen anzustellen. Gibt es mehrere notwendige Bedingungen , d. h. gilt , so müssen alle gleichzeitig erfüllt sein, wenn erfüllt ist (logische Konjunktion):
- Gibt es verschiedene, voneinander logisch unabhängige, notwendige Bedingungen, sodass für alle Paare von Bedingungen mit gilt, so kann keine für sich allein hinreichend sein, da dies dem widerspräche, dass die anderen notwendig sind.
- Eine notwendige Bedingung ist also unersetzlich für das Eintreten eines Ereignisses. Wenn sie aber nicht zugleich hinreichend ist, genügt sie allein nicht, damit das Ereignis eintritt. Mit anderen Worten: Ohne sie geht es nicht (daher auch der Ausdruck Conditio-sine-qua-non), für das Eintreten von ist aber eventuell noch etwas anderes nötig.
- ---
Heu zu fressen, stillt den Hunger des Hamsters hinreichend, doch Heu ist für seine Sättigung nicht notwendig. Sie kann auch anders erreicht werden (z. B. mit Karotten). - Hinreichende Bedingung:
- Eine hinreichende Bedingung sorgt zwangsläufig für das Eintreten des bedingten Ereignisses. Wenn die Bedingung nicht zugleich notwendig ist, dann gibt es andere hinreichende Bedingungen, die ebenfalls zum Eintreten des Ereignisses führen. Die hinreichende, nicht notwendige Bedingung ist also ersetzbar bzw. umgehbar (multiple Erfüllbarkeit). Mit anderen Worten: Wenn eine hinreichende Bedingung vorliegt, dann tritt das bedingte Ereignis zwangsläufig ein. Ist das Ereignis bereits eingetreten, kann aber nur auf seine notwendigen Bedingungen zurückgeschlossen werden, denn wenn eine in Betracht gezogene hinreichende Bedingung nicht notwendig ist, so muss es immer andere mögliche Bedingungen geben, die ebenso hinreichend sind. Welche der hinreichenden Bedingungen vorliegt, kann ausgehend vom bedingten Ereignis nicht entschieden werden.
- Aussagenlogisch betrachtet: Hat eine Aussage mehrere hinreichende Bedingungen , d. h. gelten die Subjunktionen , so genügt es, dass mindestens eine erfüllt ist (logische Disjunktion), damit gilt: .
- ---
- Äquivalente Bedingung
- Eine Bedingung, die sowohl notwendig als auch hinreichend ist, wird äquivalente Bedingung genannt. Aussagenlogisch ist dafür das Kürzel iff – engl. if and only if üblich; deutschsprachige Entsprechungen sind g. d. w., abgekürzt für genau dann, wenn und dann und nur dann, Formelzeichen .
- Zu jedem Bedingten kann es nur eine einzige zugleich notwendige-und-hinreichende Bedingung geben. Gäbe es alternative hinreichende Bedingungen, so wäre sie nicht notwendig; gäbe es zusätzliche notwendige Bedingungen, so wäre sie nicht hinreichend. Bedingung und Bedingtes stehen somit in der logischen Relation des Bikonditionals: , sie sind äquivalent.
- ---
- Aussagenlogischer Zusammenhang:
- Notwendige und hinreichende Bedingung stehen in engem Zusammenhang. Im Rahmen der Aussagenlogik bedeutet (gesprochen „K impliziert B“): Wenn eine hinreichende Bedingung für einen Sachverhalt ist, dann ist zugleich eine notwendige Bedingung für .
- Auch der Umkehrschluss hinsichtlich des Typs der Bedingung ist gültig: Falls eine notwendige Bedingung für ist, dann ist eine hinreichende Bedingung für . In der Aussagenlogik lassen notwendige und hinreichende Bedingungen allein keine weiteren Schlüsse auf die Art des Zusammenhangs zwischen Bedingung und Bedingtem zu.
BM2225

Bild 1 
Bild 2 - Symmetrie am Kreis
- ---
- SATZ: Jeder Kreis ist sowohl axialsymmetrisch als auch zentralsymmetrisch. Jede Gerade durch den Mittelpunkt ist Symmetrieachse. Der Mittelpunkt selbst ist Symmetriezentrum des betreffenden Kreises.
- ---
- Jeder Kreis wird bei jeder Drehung um seinen Mittelpunkt aus sich selbst abgebildet. Geometrische Figuren, die bei einer Drehung um einen Punkt aus sich selbst abgebildet weden, heißen zentralsymmetrisch mit dem Symmetriezentrum .
- ---
- Gibt es eine Spiegelung an einer Geraden, durch die eine geometrische Figur auf sich abgebildet wird, so heißt diese Figur axialsymmetrisch. Die betreffende Gerade heißt Symmetrieachse dieser geometrischen Figur.
BM2226
- Was ist ein
- a) Zentriwinkel?
- b) Peripheriewinkel?
- c) Sehnentangentenwinkel?
- d) Umfangswinkel?
Lösung BM2226
BM2227
Sehnenviereck - SATZ über die Gegenwinkel eines Sehnenvierecks:
- In jedem (konvexen) Sehnenviereck betragen die Gegenwinkel zusammen 180°.
- ---
- Der folgende Satz gilt nur für nicht überschlagene Sehnenvierecke ABCD:
- SATZ: Gegenüberliegende Winkel ergänzen sich zu 180°, also
- ---
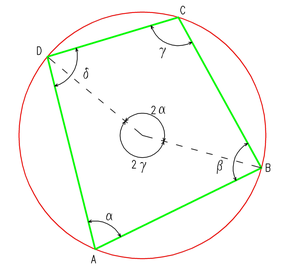
- Gegenüberliegende Winkel im Sehnenviereck:
- Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel 180°.
- Der Beweis ergibt sich unmittelbar aus dem Kreiswinkelsatz, da zwei gegenüberliegende Winkel des Sehnenvierecks Umfangswinkel über zwei komplementären Kreisbögen sind, deren Mittelpunktswinkel sich zu 360° ergänzen. Da Umfangswinkel halb so groß sind wie Mittelpunktswinkel über dem gleichen Bogen, müssen sich die Umfangswinkel zu 360°/2 = 180° ergänzen.
- Die Umkehrung dieser Aussage stimmt auch, d. h. ist in einem Viereck die Summe gegenüberliegender Winkel 180°, so ist es ein Sehnenviereck.
- ---
- Kreiswinkelsatz (Zentriwinkelsatz):
- Der Mittelpunktswinkel (Zentriwinkel) eines Kreisbogens ist doppelt so groß wie einer der zugehörigen Umfangswinkel (Peripheriewinkel).
BM2228
- Gegenüberliegende Winkel im Sehnenviereck
- Beweis 1
- ---
- Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel .
- Dieses lässt sich wie folgt beweisen:
- Winkelsumme im
- Umfangswinkel über Sehne (sind gleich)
- Umfangswinkel über Sehne (sind gleich)
- (Alle Umfangswinkel [Peripheriewinkel] über einem Kreisbogen sind gleich groß. Dieser Kreisbogen heißt dann Fasskreisbogen.)
- eingesetzt ergibt sich
- mit
- Analog gilt für
BM2229

- Gegenüberliegende Winkel im Sehnenviereck
- Beweis 2
- ---
- Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel .
- Der Beweis ergibt sich unmittelbar aus dem Kreiswinkelsatz bzw. Mittelpunktswinkel-Umfangswinkel, da zwei gegenüberliegende Winkel des Sehnenvierecks Umfangswinkel über zwei komplementären Kreisbögen sind, deren Mittelpunktswinkel sich zu ergänzen. Da Umfangswinkel halb so groß sind wie Mittelpunktswinkel über dem gleichen Bogen, müssen sich die Umfangswinkel zu
- ergänzen.
BM2230
- Peripheriewinkelsatz
- ---
- SATZ: Peripheriewinkel über derselben Sehne eines Kreises sind gleich groß.
- ---
- Beweis:
- und seien beliebige Peripheriewinkel über derselben Sehen . Ihre Scheitel seien und .
- Wir wählen einen Punkt des Kreises, der mit und damit auch mit auf verschiedenen Seiten der Geraden liegt.
- Den Winkel bezeichnen wir mit . Dann gilt nach dem Satz über die Gegenwinkel eines Sehnenvierecks (für den Beweis s. nächste Übung)
- und .
- Daraus folgt
- w.z.b.w.
BM2231 - BM2240
[editar]BM2231
- SATZ über die Gegenwinkel eines Sehnenvierecks:
- In jedem (konvexen) Sehnenviereck betragen die Gegenwinkel zusammen 180°.
- ---
- Beweis:
- Wir bezeichnen die Winkel eines Sehnenvierecks mit , , und und den Kreismittelpunkt mit .
- Der Punkt kann entweder innerhalb oder außerhalb des Vierecks oder auf einer Seite des Vierecks liegen.
- Wir beweisen hier den Satz nur für den Fall, dass innerhalb des Sehnenvierecks liegt.
- Wir verbinden mit den Eckpunkten des Vierecks und erhalten vier gleichschenklige Dreiecke, in denen die Basiswinkel jeweils gleich groß sind.
- Die Basiswinkel bezeichnen wir wie in Bild 6.
- Aus (Winkelsumme im Viereck)
- folgt wegen
- , , und (gleichschenklige Dreiecke)
1. Details BM2231 - (umgestellt)
- (umstellen: , , und )
- (einsetzen: , , , und )
- bzw.
2. Details BM2231 - (Die 2 ausklammern)
- (Durch 2 dividieren)
- Da und ist, finden wir
- .
- Ebenso ergibt sich
- .
- w.z.b.w.
- SATZ: In jedem Sehnenviereck betragen die Gegenwinkel zusammen 180°.
- ---
- Die beiden anderen Fälle (Mittelpunkt außerhalb oder auf einer Kante) lassen sich entsprechend beweisen.
BM2232

Bild 1 
Bild 2 
Bild 3 - Satz des Thales:
- Jeder Peripheriewinkel über einem Durchmesser eines Kreises ist ein rechter Winkel.
- ---
- Beweis:
- Der Winkel sei ein beliebiger Peripheriewinkel über einem Durchmesser eines Kreises um . Die Mittelsenkrechte der Strecke schneide den Kreis in .
- Wegen des Satzes „Peripheriewinkel über derselben Sehne eines Kreises sind gleich groß.“ (für den Beweis siehe Übung BM2230) gilt:
- Wir zeigen in der Folge, dass der Winkel ein rechter Winkel ist.
- Die Dreiecke und sind gleichschenklig-rechtwinklige Dreiecke, die bezüglich der Geraden spiegelbildlich liegen.
- Da die Basiswinkel gleichschenklig-rechtwinkliger Dreiecke stets 45° betragen, ist der Winkel ein rechter Winkel. Damit ist auch der Winkel ein rechter Winkel.
- w.z.b.w.
BM2233

Bild 1 - Satz des Thales:
- Jeder Peripheriewinkel über einem Durchmesser eines Kreises ist ein rechter Winkel.
- ---
- 2. Beweis für den Satz des Thales:
- ---
- Wir haben das Dreieck im Thaleskreis - Dreieck mit den Winkeln , und . (Bild 1)
- ---

Bild 2 - Das Dreieck wird durch die Strecke in zwei Teildreiecke zerlegt:
- Dreick (blau) und
- Dreieck (rot). (Bild 2)
- ---

Bild 3 - Diese beiden Teildreiecke (rot und blau) sind gleichschenklig, denn die von ausgehenden Strecken haben alle die gleich Länge, die dem Radius des Thaleskreises entspricht (Schenkellänge ). Deshalb können wir die beiden gleichgroßen Basiswinkel jeweils mit dem gleichen Buchstaben bezeichnen (Bild 3)
- ---

Bild 4 - Die Bezeichnung der Winkel bei (Delta und Epsilon) können wir weglassen, da diese Winkel für unsere weitere Betrachtung und Beweisführung keine Bedeutung haben. (Bild 4)
- ---

Bild 5 - Bei wird der Winkel folglich in und aufgeteilt. (Bild 5)
-
- ---

Bild 6 - (Winkelsumme im Dreieck) (Bild 6)
- (Wegen können wir für auch einsetzen.)
- (umstellen und zusammenfassen)
- (Wie dividieren jetzt die Gleichung auf beiden Seiten durch 2.)
- Da (s. Bild 5) ist damit bewiesen, dass ist.
- q.e.d.
BM2234

Bild 1 
Bild 2 - Satz des Thales:
- Jeder Peripheriewinkel über einem Durchmesser eines Kreises ist ein rechter Winkel.
- ---
- Umkehrung:
- SATZ: Der Scheitel des rechten Winkels in einem rechtwinkligen Dreieck liegt stets auf dem Kreis um den Mittelpunkt von mit dem Radius .
- ---
- Anwendung:
- Die Umkehrung des Thalessatzes wird bei vielen Konstruktionsaufgaben angewendet.
- Es soll ein rechtwinkliges Dreieck mit dem Scheitel des rechten Winkels bei konstruiert werden, wenn und .

Bild 3: Wir zeichnen einen Kreis mit dem Radius 2,5 cm und erhalten so die 5 cm lange Strecke 
Bild 4: Bei tragen wir den Winkel an. 
Bild 5: Wir erhalten den Schnittpunkt mit dem Kreis. 
Bild 6: Der Schnittpunkt mit dem Kreis gibt uns Punkt . 
Bild 7: Der Winkel bei ist ein rechter Winkel. Wir haben also ein rechtswinkliges Dreieck mit und konstruiert.
BM2235

- Satz des Thales:
- Jeder Peripheriewinkel über einem Durchmesser eines Kreises ist ein rechter Winkel.
- ---
- Alternative Formulierung (die ursprüngliche Formulierung von Thales)
- Konstruiert man ein Dreieck aus den beiden Eckpunkten des Durchmessers eines Halbkreises und einem weiteren Punkt dieses Halbkreises, so erhält man immer ein rechtwinkliges Dreieck.
BM2236
- Konstruiere ein rechtwinkliges Dreieck mit der Hypotenuse cm und einer Kathete cm!
BM2237
- Konstruiere die Tangente an einem gegebenen Kreis, die durch einen gegebenen Punkt geht, der außerhalb des Kreises liegt!

Geometrie auf der gekrümmten Erdoberfläche (Kugeloberfläche) = sphärische Geometrie - Wofür braucht man solche Konstruktionen?
- In späteren Lektionen lernen wir solche Konstruktionen zusätzlich zu berechnen. Das ist das Gebiet der analytischen Geometrie.
- Dafür ist es hilfreich, wenn man die Methoden der Konstruktion mit Zirkel und Lineal beherrscht.
- Beispielsweise kann die Lage und der Verlauf von Eisenbahnlinien auf einer Planungskarte gezeichnet und berechnet werden.
- Oder der Flug eines Flugzeuges soll geplant werden. Beispielsweise soll bei einem Flug ein Sicherheitsradius von einem Kernkraftwerk eingehalten werden. Dann fließt dieses Wissen über geometrische Konstruktionen in die Berechnung mit Hilfe der analytischen Geometrie ein und wird in einem Computerprogramm programmiert.
- Auch wenn man später keine praktische Anwendung für dieses geometrische Wissen in seinem Beruf hat, so gehört es doch zur mathematischen Grundbildung und hilft dabei sich abstrakte Sachverhalte vorstellen zu können.
- Bei der Geometrie im dreidimensionalen Raum (Stereometrie; Astronomie) wird es dann später viel komplizierter und man kann sich die räumlichen Konstruktionen nicht ganz so einfach vorstellen, da die erklärenden Zeichnungen nur zweidimensional sind.
- Schon die sphärische Geometrie (Geometrie auf einer Kugelfläche, z. B. Navigation auf der Erdoberfläche für Schiffe oder Flugzeuge) ist etwas komplizierter, als die bis jetzt abgehandelte zweidimensionale Geometrie (Planimetrie).
BM2238
- Konstruiere die Tangente an zwei gegebenen Kreisen!
- Gegeben sind zwei Kreise .
- Der Abstand zwischen den beiden Kreisen beträgt 12 cm .
- Gesucht sind die äußeren Tangenten.
BM2239
- Konstruiere die innere Tangente an zwei gegebenen Kreisen!
- Gegeben sind zwei Kreise und der Abstand zwischen den beiden Kreisen.
1. Lösung BM2239 - Die Grundidee der Konstruktion ähnelt der Lösung der vorherigen Übung zur Konstruktion einer äußeren Tangente an zwei Kreisen.
- Allerdings wird der Hilfskreis diesmal nicht IM großen Kreis gezeichnet, sondern der Hilfskreis ist noch größer als der große Kreis.
- ---
- Kommst du jetzt alleine auf die Lösung?
2. Lösung BM2239 - Der Radius des Hilfskreises ist
- NICHT
- SONDERN
- ---
- Kommst du jetzt alleine auf die Lösung?
3. Lösung BM2239
BM2240
- Welche gegenseitige Lage können zwei Kreise zueinander haben?
- Wie viel Möglichkeiten gibt es?
1. Lösung BM2240 - Wir wollen zwei Fälle unterscheiden:
- a) die Kreise sind gleich groß
- b) die Kreise sind unterschiedlich groß
2. Lösung BM2240 -
Bild 1
-
Bild 2
-
Bild 3
-
Bild 4
- a) die Kreise sind gleich groß
- Bild 1: Die beiden Kreise haben keinen Punkt gemeinsam. Die Entfernung der Mittelpunkte beider Kreise ist größer als die Summe der Radien beider Kreise.
- Bild 2: Die beiden Kreise haben genau einen Punkt gemeinsam. Sie berühren einander von außen. Die Entfernung der Mittelpunkte beider Kreise ist gleich der Summe der Radien beider Kreise.
- Bild 3: Die beiden Kreise haben genau zwei Punkte gemeinsam. Die beiden Kreise schneiden einander. Die Entfernung der Mittelpunkte beider Kreise ist größer als die Differenz und kleiner als die Summe der Radien beider Kreise.
- Bild 4: Die beiden Kreise haben drei Punkte gemeinsam. Die beiden Kreise haben alle Punkte gemeinsam. Die beiden Kreise sind identisch.
- ---
-
Bild 5
-
Bild 6
-
Bild 7
-
Bild 8
-
Bild 9
-
Bild 10
- b) die Kreise sind unterschiedlich groß
- Bild 5: Die beiden Kreise haben keinen Punkt gemeinsam. Die Entfernung der Mittelpunkte beider Kreise ist größer als die Summe der Radien beider Kreise.
- Bild 6: Die beiden Kreise haben genau einen Punkt gemeinsam. Sie berühren einander von außen. Die Entfernung der Mittelpunkte beider Kreise ist gleich der Summe der Radien beider Kreise.
- Bild 7: Die beiden Kreise haben genau zwei Punkte gemeinsam. Die beiden Kreise schneiden einander. Die Entfernung der Mittelpunkte beider Kreise ist größer als die Differenz und kleiner als die Summe der Radien beider Kreise.
- Bild 8: Die beiden Kreise haben genau einen Punkt gemeinsam. Sie berühren einander von innen. Die Entfernung der Mittelpunkte beider Kreise ist gleich der Differenz der Radien beider Kreise.
- Bild 9: Einer der beiden Kreise liegt innerhalb des anderen. Die Mittelpunkte beider Kreis sind verschieden. Die Entfernung der Mittelpunkte beider Kreise ist kleiner als die Differenz der Radien beider Kreise.
- Bild 10: Einer der beiden Kreise liegt innerhalb des anderen. Beide Kreise haben einen gemeinsamen Mittelpunkt.
- ---
- Zusammenfassung
- a) die Kreise sind gleich groß: Es gibt 4 verschiedene mögliche Lagepositionen.
- b) die Kreise sind unterschiedlich groß: Es gibt 6 mögliche verschiedene Lagepositionen.
-
BM2241 - BM2250
[editar]BM2241
- Zentriwinkel-Peripheriewinkel-Satz:

Bild 4: Der Zentriwinkel (Beta) ist doppel so groß wie der Paripheriewinkel (Alpha) - IMMER - Zentriwinkel-Peripheriewinkel-Satz:
- Jeder Zentriwinkel ist doppelt so groß wie jeder Peripheriewinkel über derselben Sehne.
- ---
- Beweis:
- Der Winkel sei ein beliebiger Zentriwinkel und sei ein beliebiger Peripheriewinkel.
- Der Punkt liegt nicht auf , jedoch mit auf derselben Seite von .
- Der Mittelpunkt liegt dann entweder auf einem Schenkel (1. Fall) oder innerhalb des Winkels (2. Fall) oder außerhalb des Winkels (3. Fall).

Bild 5: 1. Fall - Bild 5:
- 1. Fall: liegt auf
- Das Dreieck ist gleichschenklig: Es gilt .
- Der Winkel ist Außenwinkel des Dreiecks . Es gilt: .
- Daraus folgt:
-
- (Zur Erinnerung: SATZ: Jeder Außenwinkel eines Dreiecks ist gleich der Summe der beiden nichtanliegenden Innenwinkel. Den Beweis hatten wir in Lección 084b, Übung BM1685)
- ---

Bild 6: 2. Fall - Bild 6:
- 2. Fall: liegt innerhalb des Winkels
- Der Strahl schneidet den Kreis in .
- Nach Fall 1 gilt: und .
- Daraus folgt .
- Wegen und ergibt sich:
-
- ---

Bild 7: 3. Fall - Bild 7:
- 3. Fall: liegt außerhalb des Winkels
- Der Strahl schneidet den Kreis in .
- Nach Fall 2 gilt: und .
- Daraus folgt .
- Wegen und ergibt sich:
-

Bild 8: 3. Fall
BM2242
- 1.) Wie heißt der größte Breitenkreis auf der Erde?
- 2.) Wo liegt der Nullte Längenkreis?
- 3.) Sind Breitenkreise oder Längenkreise keine Großkreise?
- 4.) Ist das Navigieren nach einer Loxodrome oder nach einer Orthodrome einfacher?
- 5.) Bevorzugt man für die Langstreckennavigation den Kurs nach einer Loxodrome oder nach einer Orthodrome?
- 6) Wie heißt die größte Sehne eines Kreises?
Lösung BM2242 - 1.) Wie heißt der größte Breitenkreis auf der Erde? - Äquator
- 2.) Wo liegt der Nullte Längenkreis? - London, Greenwich
- 3.) Sind Breitenkreise oder Längenkreise keine Großkreise? - Breitenkreise sind keine Großkreise, mit Ausnahme des Äquators. Das Zentrum eines Großkreises muss im Zentrum der Kugel liegen, für den Fall der Erdkugel also im Zentrum des Erdmittelpunktes.
- 4.) Ist das Navigieren nach einer Loxodrome oder nach einer Orthodrome einfacher? - Das Navigieren nach einer Loxodrome ist einfacher, da immer nur der gleiche Kurs gesteuert werden muss. - Eine Loxodrome ist eine Kurve auf einer Kugeloberfläche – z. B. der Erdoberfläche –, die die Meridiane im geographischen Koordinatensystem immer unter dem gleichen Winkel schneidet und daher auch Kursgleiche, Winkelgleiche oder Kurve konstanten Kurses genannt wird. - Eine Orthodrome ist die kürzeste Verbindung zweier Punkte auf einer Kugeloberfläche, also ein Teilstück eines Großkreises. - Das Steuern nach einer Orthodrome verlangt eine regelmäßige Kurskorrektur, theoretisch muss der Steuerkurs ständig leicht geändert werden.
- 5.) Bevorzugt man für die Langstreckennavigation den Kurs nach einer Loxodrome oder nach einer Orthodrome? - Für die Langstreckennavigation (Schiff, Flugzeug) bevorzugt man einen Kurs, der einer Orthodrome entspricht oder zumindest nahe an einer Orthodrome liegt. So ist die Wegstrecke insgesamt wesentlich kürzer.
- 6) Wie heißt die größte Sehne eines Kreises? - Durchmesser
BM2243

Bild 1: Zentriwinkel-Peripheriewinkel-Satz 
Bild 2: Satz des Thales 
Bild 3: Der Satz des Thales ist ein Speziallfall des Zentriwinkel-Peripheriewinkel-Satzes. - 1.)
- Zentriwinkel-Peripheriewinkel-Satz:
- Jeder Zentriwinkel ist doppelt so groß wie jeder Peripheriewinkel über derselben Sehne.
- ---
- 2.)
- Satz des Thales:
- Jeder Peripheriewinkel über einem Durchmesser eines Kreises ist ein rechter Winkel.
- ---
- 3.)
- Der Durchmesser eines Kreises ist seine größte Sehne.
- ---
- Definition: Die Sehne eines Kreises teilt den Kreis in zwei Kreisbögen. (Diese Kreisbögen sind in der Regel ungleich groß.)
- Definition: Die Sehne eines Kreises ist eine Verbindungsstrecke zweier Punkte auf dem Kreis.
- ---
- Aus 1.), 2.) und 3.) folgt, dass der Satz des Thales ein Speziallfall des Zentriwinkel-Peripheriewinkel-Satzes ist.
- ---
- Der Durchmesser (die größe Sehne eines Kreises) kann als gestreckter Winkel betrachtet werden .
- Wenn der Zentriwinkel ist, dann ist gemäß Zentriwinkel-Peripheriewinkel-Satz der Peripheriewinkel .
- ---
- Genau das gleiche besagt auch der Satz des Thales: „Jeder Peripheriewinkel über einem Durchmesser eines Kreises ist ein rechter Winkel, also .“
- ---
- Der Satz des Thales ist ein Speziallfall des Zentriwinkel-Peripheriewinkel-Satzes.
- ---
- Für den Beweis des Thalessatzes ist also der Beweis des Zentriwinkel-Peripheriewinkel-Satzes ausreichend.
BM2244

Bild 1: Sehnentangentenwinkel 
Bild 2: Sehnentangentenwinkel; Tangente (blau) rechtwinklig zum Radius (grün)
- Sätze über den Sehnentangentenwinkel
- ---
- SATZ:
- Jeder Zentriwinkel eines Kreises ist doppelt so groß wie ein zugehöriger Sehnentangentenwinkel.
- ---
- Beweis:
- Bild 3: sei Zentriwinkel und sei ein zugehöriger Sehnentangentenwinkel.

Bild 3 - Den Mittelpunkt von bezeichnen wir mit .
- Die Mittelsenkrechte von geht durch .
- Da das Dreieck gleichschenklig ist, ist die Mittelsenkrechte zugleich Winkelhalbierende des Zentriwinkels .
- Den Winkel bezeichnen wir mit .
- Da der Radius senkrecht auf auf der Geraden steht, gilt .
- Für das Dreieck ist die Winkelsumme .
- Da das Dreieck rechtwinklig ist, gilt .
- Daraus folgt bzw.
- .
- w.z.b.w.
- ---
- Wie kommt man von
- zu ?
Lösung BM2244 - Aus und folgt:
- ---
- SATZ:
- Jeder Peripheriewinkel eines Kreises ist genauso groß wie ein zugehöriger Sehnentangentenwinkel.
- ---

Bild 4 - Beweis:
- Bild 4: sei Zentriwinkel, ein zugehöriger Peripheriewinkel und ein zugehöriger Sehnentangentenwinkel.
- Aus (bewiesen in der vorherigen Übung BM2243)
- und (was wir soeben im vorhergehenden Beweis bewiesen haben) folgt
- w.z.b.w.
- ---
- Die Sätze über den Sehnentangentenwinkel werden zu Dreieckskonstruktionen herangezogen.
- ---
- Konstruiere ein Dreieck aus folgenden gegebenen Teilen (Bild 1 und 2):
- und
- .

Bild 7 - 1.)
- Wir zeichnen die Strecke und die Mittelsenkrechte dieser Strecke.
- In tragen wir an den Winkel als Sehnentangentenwinkel an.
- Wir errichten in die Senkrechte auf dem freien Schenkel von .
- Der Schnittpunkt der Mittelsenkrechten und des Lotes liefert den Mittelpunkt für den Kreis, in dem Sehnentangentenwinkel ist.
- Der Kreis um mit dem Radius ergibt eine Bestimmungslinie für den Punkt .
- 2.)
- Im Abstand ziehen wir eine Parallele zu .
- Diese Parallele schneidet den Kreis um in zwei Punkten, die wir mit und bezeichnen.
- Wir erhalten die Dreiecke bzw. , die beide die Bedingungen der Aufgabe erfüllen.
BM2245
- Kreisumfang
- ---
- 1.) Wie berechnet man den Kreisumfang im Verhältnis zum Durchmesser ?
- 2.) Wie berechnet man den Kreisumfang im Verhältnis zum Radius ?
- 3.) Wie berechnet man den Kreisumfang im Verhältnis zum Flächeninhalt ?
2. Lösung BM2245: Kreisumfang im Verhältnis zum Radius
BM2246

Bild 1: rot = Kreisbogen der Länge b; blau = Kreissehne der Länge l - Kreisbogen
- ---
- Legt man auf einem Kreis zwei beliebige Punkte fest und verbindet diese durch Strecken mit dem Mittelpunkt des Kreises, so stellen die beiden Teile der Kreisfläche, die durch diese Strecken voneinander getrennt werden, Kreisausschnitte (auch Kreissektor genannt) dar. Ein Kreisausschnitt wird also gleichsam von zwei Radien aus einem Kreis „herausgeschnitten“. Der zu einem Kreissektor gehörende Teil der Kreislinie wird als Kreisbogen bezeichnet, der Winkel zwischen den beiden Radien als Mittelpunktswinkel.
- ---
- Zu jedem Zentriwinkel eines Kreises gehört ein Kreisbogen, der innerhalb des betreffenden Winkels liegt. Wir sagen, dass der Kreisbogen dem Zentriwinkel zugeordnet oder zugehörig ist.
- ---

Bild 2 - Die Länge eines Kreisbogens mit dem Radius , der einem Zentriwinkel von zugehörig ist, beträgt:
- .
- Dabei ist der Umfang des Kreises.
- Die Länge eines Kreisbogens mit dem Radius , der einem Zentriwinkel von zugehörig ist, beträgt das -fache von :
- .
- Aus dieser Beziehung finden wir die Verhältnisgleichung
- ---
- Mit Hilfe dieser Verhältnisgleichung können wir die Länge des Kreisbogens berechnen, falls außer der Länge des Umfangs die Größe des zugehörigen Zentriwinkels gegeben ist.
- Umgekehrt können wir die Größe des Zentriwinkels berechnen, wenn außer der Länge des Umfangs die Länge des Kreisbogens gegeben ist.
- ---
- Gesucht ist die Länge eines Kreisbogens, der einen Zentriwinkel von zugehörig ist. Der Radius des Kreises beträgt .
1. Lösung BM2246 - Aus ergibt sich
- .
- Wir setzen die Formel für den Umfang ein und die für .
- .
- Mit dem Taschenrechner erhalten wir
- .
- ---
- Gesucht ist die Größe eines Zentriwinkels, der einem Kreisbogen von der Länge zugehörig ist. Der Radius des Kreises beträgt .
2. Lösung BM2246 - Aus ergibt sich
- Wir setzen die Werte und die Umfangsformel ein:
- Mit dem Taschenrechner erhalten wir:
- ---
- Gesucht ist der Radius eines Kreises, in dem ein Kreisbogen von Länge einem Zentriwinkel von zugehörig ist.
3. Lösung BM2246 - Aus ergibt sich
- Wir setzen diedie Umfangsformel ein:
- Und stellen nach <mathr</math> um:
- Nun setzen wir die gegebenen Werte ein:
- Mit dem Taschenrechner erhalten wir:
- ---
- Kreisausschnitt = Kreissektor
- ---
- Eine Fläche, die von einem Kreisbogen und den Schenkels des zugehörigen Zentriwinkels begrenzt wird, heißt Kreisausschnitt oder Kreissektor.
- Der Zentriwinkel wird auch Öffnungswinkel des Kreisausschnittes genannt.
- ---
- Der Flächeninhalt eines Kreisausschnittes mit dem Öffnungswinkel von beträgt:
- ---
- Der Flächeninhalt eines Kreisausschnittes mit dem Öffnungswinkel beträgt das -fache von :
- .
- ---
- Aus dieser Beziehung finden wir die Verhältnisfleichung
- .
BM2247
- Stereometrie
- ---
- Stereometrie ist ein Teilgebiet der Geometrie und damit der Mathematik. Sie befasst sich – im Gegensatz zur ebenen Geometrie (Planimetrie) – mit geometrischen Gebilden im (dreidimensionalen) Raum. Statt Stereometrie sagt man auch Raumgeometrie oder räumliche Geometrie.
- Zur Stereometrie gehört unter anderem die Berechnung der Oberfläche (Flächenberechnung) bzw. der Mantelfläche und des Volumens (Volumsberechnung) einfacher und zusammengesetzter geometrischer Körper sowie die Stereotomie.
- Die Stereometrie stellte im antiken Griechenland einen der Wissenschaftsbereiche dar, die von herausragender Bedeutung waren. So versuchten sich verschiedene namhafte Denker dieser Zeit an der Lösung des stereometrischen Problems der Würfelverdoppelung. Platon fordert gar in seinem Werk Der Staat (Politeia), dass die Stereometrie neben der Planimetrie in das wissenschaftliche Propädeutikum (Vorbereitungsveranstaltung) mit aufgenommen werden solle.
- ---

Bild 1: Gerader Kreiszylinder mit abgerollter Mantelfläche 
Bild 2: Kegelstumpf und seine abgewickelte Mantelfläche - Mantelfläche
- ---
- Als Mantelfläche (auch Hüllfläche) bezeichnet man die Oberfläche eines Volumens, das durch Rotation eines Graphen einer Funktion um eine Koordinatenachse entsteht. „Boden“ (Grundfläche) und „Deckel“ (Deckfläche) werden, falls vorhanden, in der Regel nicht zur Mantelfläche gezählt.
- Auch bei Nicht-Rotationskörpern - wie Pyramide, Prisma etc. - spricht man von einer Mantelfläche.
- ---
- Mantelfläche des Kreiszylinders:
- Die blaue Fläche im nebenstehenden Bild 1 entspricht der Mantelfläche des gezeigten Kreiszylinders. Dieser könnte etwa durch Rotation einer konstanten Funktion um eine Koordinatenachse entstehen.
- ---
- Erdmantel - Erdkern
- „Vier Millionen Tonnen entsprechen dem dem Gewicht von neunundachtzig Millionen Mantelpavianen, mit Mantel.“ (Loriot)
BM2248

Bild 1: Ein Prisma mit einem Sechseck als Grundfläche - Prisma
- ---
- Ein Prisma (Mehrzahl: Prismen) ist ein geometrischer Körper, der durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht (man spricht auch von einer Extrusion des Vielecks). Ein Prisma ist damit ein spezielles Polyeder.
- Das gegebene Vieleck wird als Grundfläche bezeichnet, die gegenüberliegende Seite (oder Begrenzungsfläche) als Deckfläche. Die Gesamtheit aller übrigen Begrenzungsflächen heißt Mantelfläche. Die Seitenkanten des Prismas, die Grund- und Deckfläche verbinden, sind zueinander parallel und alle gleich lang. Grund- und Deckfläche sind zueinander kongruent (deckungsgleich) und parallel.
- ---
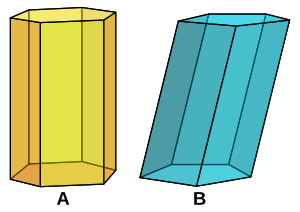
Bild 2: A: gerades Prisma; B: schiefes Prisma 
Bild 3: Spezialfall eines schiefen Prismas: Parallelepiped, hier sogar ein Rhomboeder - Gerades und schiefes Prisma:
- Erfolgt die Parallelverschiebung des Vielecks senkrecht zur Grundfläche, spricht man von einem geraden Prisma, ansonsten von einem schiefen Prisma. Die Mantelfläche eines geraden Prismas besteht aus Rechtecken, im allgemeinen Fall besteht sie aus Parallelogrammen.
- ---
- Sonderfälle:
- Eine besondere Form des Prismas ist der Quader. Beim Quader kann jede Seite als Grundfläche des Prismas aufgefasst werden.
- Das Prisma ist in der Mathematik ein Spezialfall des allgemeinen Zylinders.
- ---
- Prisma (Optik):
- Unter einem Prisma wird in der Optik ein Bauelement in Form des geometrischen Körpers Prisma verstanden, das für unterschiedliche optische Effekte eingesetzt wird, z. B. als dispersives (Licht nach Wellenlängen auffächerndes) Element oder zur Umlenkung eines Lichtstrahls. Bei der Form handelt es sich häufig um ein gerades Prisma mit einem Dreieck als Grundfläche.

Bild 4: Prisma mit gleichseitigem Dreieck als Grundfläche 
Bild 5: Lichtbrechung im Prisma; Teilreflexion an beiden brechenden Flächen als Nebeneffekt 
Bild 6: Lichtbrechung im Prisma, schematisch
- ---

Bild 7: senkrechter Kreiszylinder: Höhe , Radius - Zylinder
- ---
- Ein Zylinder (lat. cylindrus, altgr. κύλινδρος kýlindros, von κυλίνδειν kylíndein ‚rollen‘, ‚wälzen‘) ist im einfachsten Fall eine
- Fläche, deren Punkte von einer festen Gerade, der Achse, denselben Abstand haben.
- Da solch eine Fläche unendlich ausgedehnt ist, beschneidet man sie normalerweise mit zwei parallelen Ebenen der Distanz (s. Bild).
- Sind die Schnittebenen senkrecht zur Achse, entsteht ein senkrechter (oder gerader) Kreiszylinder mit Radius und Höhe . Die so beschnittene Fläche heißt Mantelfläche des Zylinders.
- Da man sich einen geraden Kreiszylinder auch durch Rotation einer Strecke um die (parallele) Zylinderachse erzeugt denken kann, wird er auch Drehzylinder genannt. Die erzeugenden Strecken nennt man Mantellinien des Zylinders oder auch Erzeugende.
- In der Technik versteht man unter einem Zylinder oft den Körper, der von der Mantelfläche und den beiden Schnittkreisflächen eingeschlossen wird.
BM2249
- Prisma
- Formeln für Volumen, Mantel- und Oberfläche
- ---
- Das Volumen eines Prismas ist gegeben durch
- ,
- wobei den Flächeninhalt der Grundfläche und die Höhe des Prismas bezeichnet.
- Zwei Prismen (etwa ein gerades und ein schiefes Prisma) besitzen bei gleicher Grundfläche und Höhe das gleiche Volumen.
- Die Mantelfläche eines geraden Prismas ist gegeben durch
- ,
- wobei für den Umfang der Grundfläche und für die Höhe des Prismas steht.
- Die gesamte Oberfläche eines Prismas ergibt sich aus
- ,
- wobei und dem Inhalt von Grund- und Mantelfläche entsprechen.
- ---

Bild 1: Gerader Kreiszylinder mit abgewickeltem Mantel - Kreiszylinder
- senkrechter Kreiszylinder
- ---
- Es ergibt sich für
- das Volumen (Grundfläche x Höhe)
- die Mantelfläche (die Abwicklung ist ein Rechteck der Länge und Höhe )
- die Oberfläche
- Ein gerader Kreiszylinder mit h = 2r heißt gleichseitiger Zylinder. Diese Bezeichnung erklärt sich wie folgt: Schneidet man einen solchen Zylinder mit einer Ebene, die die Achse enthält, so erhält man ein Quadrat.
- ---

Bild 2: Hohlzylinder - Hohlzylinder
- ---
- Besitzt ein gerader Kreiszylinder eine Bohrung entlang seiner Achse, so spricht man von einem Hohlzylinder.
- Für einen Hohlzylinder – etwa ein gerades Rohrstück – sind die bestimmenden Größen neben der Höhe der Außenradius und der Innenradius . Die Wanddicke b ist somit .
- Das Volumen ist
- die Mantelfläche (innen und außen)
- die Oberfläche
BM2250
- Was berechnet man mit den folgenden Formeln?
- Wofür stehen jeweils die Buchstaben a, b bzw. c in der Formel?
- 1.)
- ---
- 2.)
- ---
- 3.)
- ---
- 4.)
- ---
- 5.)
- ---
- 6.)
- ---
- 7.)
- ---
- 8.)
- ---
- 9.)
- ---
- 10.)
- ---
- 11.)
- ---
- 12.)
- ---
- 13.)
- ---
- 14.)
Lösung BM2250 - 1.)
- Volumen eines geraden Hohlzylinders
- ---
- 2.)
- Flächeninhalt eines Rechtecks
- ---
- 3.)
- Volumen eines Würfels
- ---
- 4.)
- Oberflächeninhalt eines Kreiszylinders
- ---
- 5.)
- Volumen eines geraden Hohlzylinders
- ---
- 6.)
- Mantelfläche eines Kreiszylinders
- ---
- 7.)
- Volumen eines Kreiszylinders
- ---
- 8.)
- Flächeninhalt eines Quadrats
- ---
- 9.)
- Flächeninhalt eines Dreiecks
- ---
- 10.)
- Oberflächeninhalt eines Kreiszylinders
- ---
- 11.)
- Oberflächeninhalt eines Hohlzylinders
- ---
- 12.)
- Mantelfläche eines Kreiszylinders
- ---
- 13.)
- Volumen eines Kreiszylinders
- ---
- 14.)
- Volumen eines Quaders
- índice
- Lección 094b ← Lección 095b → Lección 096b
- Lección 095















![{\displaystyle [\mathrm {MX} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df392cf388e4c6cf3cd7223cc72665a3b88d1baa)







































































































![{\displaystyle [AB]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0)

![{\displaystyle [BC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)


![{\displaystyle [CA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45d1cad430fbae09064e436319693c011c68a748)