Curso de alemán para principiantes con audio/Lección 094b
Apariencia
- índice
- Lección 093b ← Lección 094b → Lección 095b
- Lección 094
- Mathematik auf Deutsch - 44
BM2151 - BM2160
[editar]BM2151

A. Dürer: Zentralprojektion einer Laute 
Auf- und Seitenriss eines Hauses 
a) senkr. Parallelprojektion
b) Zentralprojektion eines Hauses- Darstellende Geometrie
- ---
- Darstellende Geometrie ist der Teilbereich der Geometrie, der sich mit den geometrisch-konstruktiven Verfahren von Projektionen dreidimensionaler Objekte auf eine zweidimensionale Darstellungsebene befasst. Die Anwendungsbereiche ihrer Methoden sind breit gefächert und erstrecken sich neben den heute bekanntesten Anwendungen in der Technik- und Architekturdarstellung auch auf Kunst, Malerei, Kartenwesen und Computergraphik. Die Darstellende Geometrie beschränkt sich nicht nur auf das Darstellen von räumlichen Objekten, sondern bietet auch Möglichkeiten raumgeometrische Probleme zeichnerisch zu lösen: z. B. die Bestimmung des Schnittpunktes einer Gerade mit einer Ebene oder die Schnittkurve zweier Flächen oder den Schatten eines Objektes.
- Im Gegensatz zu früher ist die Darstellende Geometrie nicht mehr das einzige Mittel, um räumliche Objekte anschaulich darzustellen oder raumgeometrische Probleme zu lösen. Hierfür verwendet man heute Computer und Geometrische Modellierung). Die Bedeutung der Darstellenden Geometrie liegt heute vielmehr im Training der Benutzer geometrischer Software, damit sie verstehen, was eine Software kann und an Eingaben verlangt. Für erste Skizzen einer (räumlichen) Idee oder Interpretationen und Ergänzungen von Computerzeichnungen ist das Zeichnen mit Zirkel und Lineal eine hervorragende Übung.
- Bei der Darstellung räumlicher Objekte in einer Zeichenebene spielen zwei konkurrierende Gesichtspunkte eine wesentliche Rolle. Will man Maßgenauigkeit erreichen, so ist dies meistens nur unter Verlust von Anschaulichkeit möglich. Z. B. lassen die beiden folgenden Bilder eines Hauses leicht auf Länge, Breite und Höhe schließen; sie sind aber nicht sehr anschaulich.
- Dagegen bringen die nächsten beiden Bilder den räumlichen Eindruck mehr zur Geltung. Genaue Abmessungen lassen sich aber (insbesondere aus dem rechten Bild) nur schwer ablesen.
BM2152
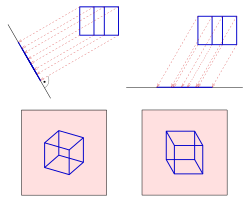
Parallelprojektion eines Würfels:
a) orthogonal
b) schief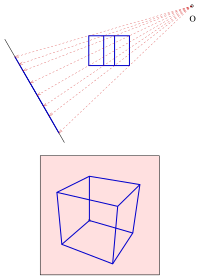
Zentralprojektion eines Würfels 
Parallelprojektion bzw. Zentralprojektion einer Häuserreihe - Abbildungsverfahren in der darstellenden Geometrie
- In der Darstellenden Geometrie bedient man sich im Wesentlichen zweier Abbildungsverfahren. Dabei werden Punkte und Kurven eines Objektes mit Hilfe von Strahlen (Geraden) auf eine Bildtafel (Ebene) projiziert:
- ---
- 1.) Parallelprojektion:
- Die Abbildungsstrahlen sind parallel, wie z. B. beim Sonnenlicht. Dabei unterscheidet man noch die beiden Fälle:
- Die Strahlen stehen senkrecht auf der Bildtafel (senkrechte Parallelprojektion oder Orthogonalprojektion oder Normalprojektion).
- Die Strahlen stehen nicht senkrecht zur Bildtafel (schiefe oder schräge Parallelprojektion).
- Parallelprojektionen werden gerne von Ingenieuren verwendet wegen ihrer Teilverhältnistreue (Teilverhältnisse auf Geraden bleiben invariant). Der Spezialfall Vogelperspektive ist eine schiefe Parallelprojektion, die insbesondere zur Veranschaulichung von Stadtplänen verwendet wird. Sie lässt sich relativ einfach von Hand herstellen. Parallelprojektionen lassen sich schnell als axonometrische Bilder oder bei umfangreicheren Objekten mit Hilfe des Einschneideverfahrens herstellen.
- Für fast alle Konstruktionen in der Darstellenden Geometrie verwendet man Grund- und Aufriss eines Objektes. Das sind senkrechte Parallelprojektionen auf eine horizontale (Grundriss) bzw. senkrechte Ebene (Aufriss). Durch sie ist (mit den entsprechenden Bezeichnungen) ein Objekt räumlich eindeutig beschrieben.
- ---
- 2.) Zentralprojektion:
- Alle Abbildungsstrahlen gehen durch einen Punkt, dem Projektionszentrum oder Augpunkt. Bei Parallelprojektion sind die Bilder paralleler Geraden i. A. wieder parallel. Bei Zentralprojektionen schneiden sich die Bilder paralleler Geraden i. A. in einem Punkt, dem Fluchtpunkt des Parallelbüschels.
- Dass eine Zentralprojektion den besten optischen Eindruck verschafft, zeigen die Bilder mit einer Häuserreihe. Bei dem Bild in Parallelprojektion erscheint das hintere Haus größer als das erste. Dies liegt an einer optischen Täuschung. Das Auge erkennt das Haus als räumliches Objekt und erwartet, dass ein gleich großes, entferntes Haus kleiner ist, was bei Parallelprojektion aber nicht der Fall ist.
- ---
- Darstellung realer Objekte:
- Um Objekte wie Häuser, Brücken, ... in einer handlichen Zeichenebene oder auf einem Bildschirm darstellen zu können, werden die Abmessungen der Objekte üblicherweise vor einer Projektion geeignet skaliert (verkleinert), z.B. mit Faktoren 1/10, 1/50 oder 1/100.
BM2153
- Hilfsmittel in der darstellenden Geometrie
- ---
- Technische Hilfsmittel:
- Klassische Hilfsmittel bei der Erstellung von Zeichnungen sind: Papier als ebene Zeichenfläche, Bleistift, Zirkel, Lineal, Geodreieck und Kurvenlineal als Zeichengeräte. Computer mit geeigneter Software (z. B. Cinderella (Software)|Cinderella, GeoGebra, Inkscape, Xfig, ...) können heute all diese Hilfsmittel ersetzen. Manuell steuert man solch einen graphikfähigen Computer mit einer Computer-Maus. Will man das Ergebnis schwarz auf weiß auf Papier vor sich haben, verwendet man einen computergesteuerten Drucker. Allerdings werden die klassischen Hilfsmittel (ohne Computer) auch heute noch als Grundlage bei der Ausbildung von Architekten und Ingenieuren verwendet.
- ---
- Theoretische Hilfsmittel:
- Als theoretische Hilfsmittel verwendet man grundlegende Aussagen aus der klassischen Geometrie: Strahlensätze, die Sätze von Pythagoras und Thales, Sätze über Dreiecke, Sätze über Kegelschnitte (Ellipsen, ...), Eigenschaften von Quadriken (Kugel, Kegel, Zylinder, ...).
BM2154

Zentralprojektion einer Brücke in Frontalperspektive 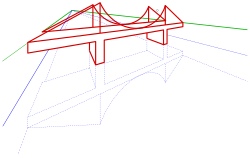
Zentralprojektion einer Brücke mit Spiegelung 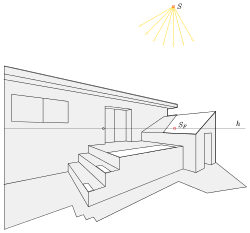
Zentralprojektion mit Schatten bei parallelem (Sonnen-) Licht 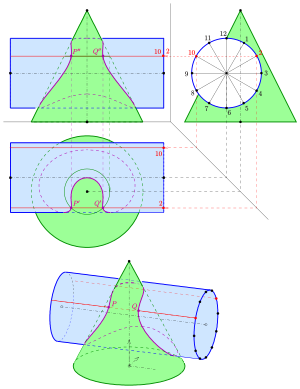
Schnitt Kegel-Zylinder: Mantellinienverfahren 
Frontalperspektive - Methoden der Darstellenden Geometrie
- ---
- Projektionen: Zweitafelprojektion, Axonometrie, Architektenanordnung, Frontalperspektive:
- Die wichtigsten Arbeitsmittel in der Darstellenden Geometrie sind Grund- und Aufriss und deren Zuordnungen. Sie liefern die räumlichen Informationen für spezielle Darstellungen und Konstruktionen. Das Wissen darüber lernt man in
- Zweitafelprojektion: Gelegentlich ist es nötig, weitere Risse einzuführen. Man spricht dann auch von Umprojektionen und Mehrtafelprojektionen.
- Mit Grund- und Aufriss lassen sich dann mit Hilfe von
- Axonometrie,
- Einschneideverfahren,
- Orthogonaler Axonometrie und
- Umrisskonstruktion (für gekrümmte Flächen; siehe hierzu auch Kanalflächen)
- anschauliche Bilder von räumlichen Objekten in Parallelprojektion herstellen.
- Bilder in Zentralprojektion konstruiert man am besten mit der
- Architektenanordnung (ähnlich dem Einschneideverfahren für Parallelprojektionen) und der
- Frontalperspektive (Perspektive mit einem wesentlichen Fluchtpunkt, dem Hauptpunkt).
- Um verzerrt wirkende Bildteile zu vermeiden, sollte man nach der Wahl der Lage von Bildtafel, Hauptpunkt und Augpunkt zunächst den
- Sehkreis
- einzeichnen. Denn nur Bildteile innerhalb des Sehkreises erscheinen im perspektiven Bild unverzerrt.
BM2155
- Durchdringungen: Schnittpunkte und Schnittkurven:
- Eine wichtige Grundaufgabe der Darstellenden Geometrie ist die (zeichnerische) Bestimmung des Schnittpunktes einer Gerade und einer Ebene. Das Verfahren hierzu heißt
- Durchstoßpunkt-Verfahren (Schnittpunkt einer Gerade mit einer Ebene).
- Durchstoßpunkte werden z. B. benötigt bei der
- Schattenkonstruktion.
- Zu den Grundaufgaben gehören auch die Bestimmung der
- Schnittpunkte einer Gerade mit Kugel, Kegel oder Zylinder.
- Für die Konstruktion von Punkten der Schnittkurve zweier Flächen (Zylinder, Kegel, Kugel, Torus, Rotationsfläche) gibt es vier Standardverfahren:
- das Hilfsebenenverfahren,
- das Mantellinienverfahren,
- das Pendelebenenverfahren und
- das Hilfskugelverfahren.
- (Rechnerische Verfahren zur Bestimmung einer Schnittkurve werden hier nicht weiter erörtert.)
- Bei der Herstellung von Modellen sich durchdringender Zylinder und/oder Kegel werden oft aufgewickelte Abwicklungen dieser Flächen verwendet. Wie man Zylinder und Kegel abwickelt, wird in
- Abwicklung
- beschrieben.
BM2156

Kotierte Projektion einer Straße mit einem Teil einer Böschungsfläche 
Zentralprojektion eines Turmes mit einem Tor (Kreise) 
Zentralprojektion zweier Kugeln 
Zimmer in Zentralprojektion mit Wandspiegel - Eintafelprojektionen: kotierte Projektion, Dachausmittlung:
- ---
- Neben den Zwei- und Mehrtafelprojektionen gibt es noch spezielle Eintafelprojektionen. Dabei handelt es sich um Grundrisse mit Zusatzinformationen, die die Objekte räumlich beschreiben. Im Straßenbau verwendet man die
- Kotierte Projektion, um
- Böschungsflächen zu konstruieren und darzustellen.
- Mit der Konstruktion von Grat-, Kehl- und Firstlinien (Schnittgeraden) von ebenen Dachflächen befasst sich die
- Dachausmittlung.
- ---
- Wahre Länge, wahre Gestalt und Rekonstruktion:
- Geneigte Strecken oder ebene Figuren in Parallelprojektionen entzerrt man mit
- wahrer Länge und wahrer Gestalt.
- Analoge Methoden für Zentralprojektionen (Fotos) bietet die
- Rekonstruktion.
- ---
- Kreis und Kugel:
- Kreise und Ellipsen spielen insbesondere als Berandungskurven von Objekten wie Zylindern, Kegeln und Rotationsflächen eine wichtige Rolle (s. Bilder: Turm mit Tor, Brücke in Frontalperspektive).
- Die Darstellung einer Kugel ist bei senkrechter Parallelprojektion sehr einfach. Ihr Umriss ist ein Kreis mit dem Radius der Kugel. Bei allen anderen wesentlichen Projektionsarten, wie Vogelperspektive, Kavalierperspektive und Zentralprojektion, erscheint der Umriss einer Kugel, von Sonderfällen abgesehen, als Ellipse.
BM2157
- Spezielle Perspektiven (Ansichten):

Parallelprojektion:
a) Grund- und Aufriss
b) Kavalierperspektive
c) Vogelperspektive
Zentralprojektion:
a) Froschperspektive
b) Vogelperspektive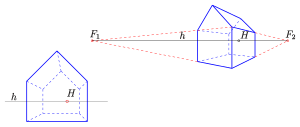
Haus mit zwei Fluchtpunkten (oben) bzw. einem Fluchtpunkt (Frontalperspektive, unten) - Die Grundlage für fast alle Darstellungen und Konstruktionen in der Darstellenden Geometrie sind
- Grund- und Aufriss: Senkrechte Parallelprojektionen auf eine horizontale bzw. senkrechte Bildtafel.
- Das Wort Perspektive wird in der Darstellenden Geometrie vielfach benutzt, um besondere anschauliche Ansichten eines räumlichen Objektes zu benennen:
- Die Kavalierperspektive oder Kabinettperspektive ist eine schiefe Parallelprojektion (s. Axonometrie) auf eine senkrechte Bildtafel. Alle ebenen Figuren, die parallel zur Bildtafel sind, werden unverzerrt abgebildet (s. Bild).
- Die Vogelperspektive oder Militärperspektive ist
- im einen Fall eine schiefe Parallelprojektion (s. Axonometrie), deren Bildtafel horizontal ist, d. h., alle ebenen horizontalen Figuren werden unverzerrt abgebildet (s. Bild) und
- im anderen Fall ist die Vogelperspektive eine Zentralprojektion, deren Augpunkt deutlich höher liegt als die größte Höhe des Objektes, und deren Bildtafel geneigt ist.
- Eine Ingenieurprojektion ist ein axonometrisches Bild mit einfachen Verkürzungen (0.5, 1, 1). Die Bilder der x- bzw. y-Achse schließen mit dem Bild der z-Achse Winkel von 132° bzw. 97° ein. Ihre Vorteile sind: a) einfache Verkürzungen, b) gute Bildwirkung, c) (skalierte) Orthogonalprojektion, d) Umrisse von Kugeln sind Kreise.
- Eine Isometrie ist ein axonometrisches Bild, bei dem die Verzerrungen in x-, y- und z-Richtung alle gleich sind. Bei der Standardisometrie gilt außerdem: Die Bilder der Koordinatenachsen schneiden einander im Winkel von 120°. Eine typische Eigenschaft ist: In der Projektion eines achsenparallelen Würfels fallen zwei Punkte zusammen.
- Die Froschperspektive ist eine Zentralprojektion, deren Augpunkt nahe der Standebene liegt (s. Bild).
- Zentralperspektive ist eine Zentralprojektion.
- Perspektive wird oft als Kurzform für Zentralperspektive verwendet.
- Frontalperspektive ist eine Zentralprojektion eines Objektes mit drei wesentlichen zueinander orthogonalen Richtungen (z. B. Quader, Haus), wobei zwei dieser Richtungen parallel zur Bildtafel verlaufen und damit deren Fluchtpunkte im „Unendlichen“ liegen. Man nennt so eine Ansicht auch Perspektive mit einem Fluchtpunkt (s. Bild). Der eine besondere Fluchtpunkt ist in der Regel der Hauptpunkt. Der Vorteil einer Frontalperspektive: Alle ebenen Figuren in Ebenen parallel zur Bildtafel werden nur skaliert, aber unverzerrt, abgebildet (s. Beispiele: Brücke und Haus in Frontalperspektive).
- Perspektive mit zwei Fluchtpunkten ist eine Zentralprojektion, bei der die Fluchtpunkte zu zwei zueinander senkrechten orthogonalen Richtungen (meist horizontal) eine wesentliche Rolle spielen (s. Bild).
- Perspektive mit drei Fluchtpunkten ist eine Zentralprojektion bei der drei Fluchtpunkte eine wesentliche Rolle spielen. Hier ist die Bildtafel geneigt (s. Haus in Vogelperspektive der Zentralprojektion).
- Parallelperspektive ist eine Parallelprojektion.
- Polarperspektive ist eine frühere Bezeichnung für Zentralprojektion.
BM2158
- Darstellende Geometrie ist heute ein Unterrichtsfach in technisch-berufsbildenden Schulen und ein grundlegendes Fach in der Ausbildung von Ingenieuren an einer Technischen Universität oder Fachhochschule.
- Thema ist die Erfassung und Darstellung von räumlichen, insbesondere technischen Strukturen (geometrische Körper, Bauwerke, Darstellung des Geländes usw).
- Wichtigste Hilfsmittel sind Konstruktionszeichnungen, Perspektive (Zentralprojektion), Axonometrie, Kotierte Projektion und Ähnliches. Neben dem Erlernen von Zeichentechniken sollen die räumliche Vorstellungskraft und Ausdrucksweise gefördert sowie Querverbindungen zu Mathematik, zur Technik und zur Bildenden Kunst hergestellt werden.
- Noch bis in die 2000er Jahre ein rein graphisches Fach (angewandtes geometrisches Zeichnen), ist es heute in weiten Bereichen eines der Computergrafik.
- In den letzten Jahren hatte die Bedeutung des Faches zwar nicht generell, aber in der Ausbildung abgenommen, weil die computergestützte Konstruktion (CAD) andere Fertigkeiten verlangt als die zeichnerische Darstellung von Hand. Seit auch Schulen gut mit Computern im Unterricht ausgestattet sind, gehört das Fach wieder zu den bedeutendsten technischen Grundlagenausbildungen überhaupt und umfasst auch das Erlernen zugehöriger Programme – im Allgemeinen marktführender Spezial-CAD-Anwendungen der Branche.
- Die eigentliche Denkarbeit, das Umsetzen der 2D-Darstellung (ob Papier oder Bildschirm) in ein 3D-(Denk-)Modell bleibt auch bei Benutzung von CAD dem Konstrukteur oder Entwerfer erhalten. Dagegen wird es schwieriger, räumliche Konstruktionsprobleme (z. B. Anschlussprofile bei schrägen Anschnitten) zu erkennen, wenn (und weil) man sich auf die Software verlässt.
- "Darstellende Geometrie ist nicht in einem oberflächlichen Sinn Voraussetzung, ein CAD-Programm zu beherrschen. Sie zu üben, ist vielmehr eine Primärerfahrung, indem die räumliche Vorstellungskraft, das Abschätzen und Auswählen von Lösungsstrategien und die Präzision des Denkens trainiert werden."
BM2159
- Zur Geschichte der Darstellenden Geometrie
- ---

Vitruvius: Grundriss eines griechischen Hauses 
A. Dürer: Grund-, Auf- und Kreuzriss eines Fußes 
A. Dürer: Hieronymus-im-Gehäus (Frontalperspektive) - Bei der systematischen Errichtung von Bauwerken spielen Pläne mit konkreten Vorgaben eine wichtige Rolle. Schon im Altertum wurden Grund- und Aufrisse verwendet. Der älteste schriftliche Beleg dafür ist das Werk Zehn Bücher über Architektur des römischen Baumeisters Vitruvius. Aber erst Albrecht Dürer (1471–1528) schrieb in der Frühen Neuzeit das erste wirkliche Lehrbuch der Darstellenden Geometrie: Underweysung mit dem Zirkel und Richtscheydt (Nürnberg 1525). Auf den Seiten 34–37 des ersten Buches treten auch schon die Kegelschnitte Ellipse, Parabel und Hyperbel auf. Gaspard Monge (1746–1818) führte in seinem Buch Geometrie descriptive zum ersten Mal die strenge Zuordnung von Grund- und Aufriss ein, um räumliche Probleme zeichnerisch zu lösen. Die Grundaufgaben der Darstellenden Geometrie sind dort schon in der noch heute gebräuchlichen Fassung zu finden.
- Die Grundlagen der Zentralprojektion waren schon den Griechen und Römern bekannt. Aber erst in der Renaissance wurde diese Art der Darstellung räumlicher Gegebenheiten durch die Malerei wiederentdeckt und zur Blüte weiterentwickelt. Siehe hierzu Leon Battista Alberti#De Pictura (Über die Malkunst) 1435/1436|De pictura von Leon Battista Alberti (1404). Die Meister dieser Zeit waren Albrecht Dürer (1471–1528), Leonardo da Vinci (1452–1519) und Michelangelo (1475–1564).
BM2160
Bild 1 Bild 2 
Bild 3 
Bild 4: Strahlengang; Z = Zentrum; O = Original; B = Bild;
a) Bild 1; b) Bild 2; c) Bild 3
Bild 5: = Zentrum; = Originalpunkt; = Bildpunkt - Projektion
- ---
- Als Projektion bezeichnet man die vergrößerte, verkleinerte oder anders modifizierte Übertragung eines Bildes auf eine Projektionsfläche. Typisches Beispiel ist die Projektion auf eine Bildwand mit Hilfe eines Projektors.
- ---
- Oft genügt ein Bild (Foto, Zeichnung, Skizze), um eine klare Vorstellung von einem Gegenstand zu bekommen. Es gibt verschiede Verfahren, nach denen man geometrische Gebilde auf ein Zeichenblatt abbildet. Diese Verfahren machen es möglich, dass man sich auf Grund der Zeichnung auch geometrische Gebilde des Raumes genau vorstellen kann.
- Es gibt verschiedene Möglichkeiten, wie wir von Gegenständen Bilder erhalten:
- Lichtprojektion des Objektes auf eine Leinwand. (Bild 1 und 2)
- Durchzeichnen durch eine Glasscheibe (Vor dem zu zeichnenden Objekt (Motiv) steht eine Glasscheibe. Das Motiv wird durch die Glasscheibe betrachtet und direkt auf der Glasscheibe nachgezeichnet.) (Pausen ist Durchzeichnen durch ein Transparentpapier.)
- Abbildung auf der Rückwand einer Kamera. (Das Bild steht dabei auf dem Kopf.) (Bild 3: Funktionsweise einer Camera obscura)
- in allen drei Fällen erhalten wir vom Gegenstand, den wir allgemein Original nennen, ein Bild auf der Bildebene.
- Originalpunkte sind mit ihren Bildpunkten durch Geraden verbunden, die alle durch einen Punkt (Lichtquelle, Auge, Lochblende) gehen. Diesen Punkt bezeichnen wir mit (Zentrum), die Geraden nennen wir Projektionsgeraden, den ganzen Vorgang Projektion. (Bild 4)
- Um in Abb. 5 das Bild vom Original unterscheiden zu können, versehen wir die Buchstaben der Bildpunkte mit einem Strich, z. B. Originalpunkt ; Bildpunkt .
- ---
- In der darstellenden Geometrie werden geometrische Gebilde des Raumes auf einer Zeichenebene so abgebildet, dass man aus der ebenen Zeichnung auf das geometrische Gebilde des Raumes schließen kann.
- Die Verbindunsgeraden von Originalpunkten mit den Bildpunkten nennt man Projektionsgeraden.
BM2161 - BM2170
[editar]BM2161

Bild 1: Würfel 
Bild 2: Quader - Parallelprojektion
- ---
- An einem Quader wollen wir die Breite, die Höhe und die Tiefe unterscheiden. Blicken wir in Bild 1 in der angegebenen Blickrichtung auf den Würfel, so können wir feststellen:
- 1.) vier Kanten liegen in Tiefenrichtung,
- 2.) vier Kanten liegen in Breitenrichtung,
- 3.) vier Kanten liegen in Höhenrichtung.
- ---
- Wie heißen diese vier Kanten jeweils?
Lösung BM2161 - 1.) vier Kanten liegen in Tiefenrichtung: ; ; ; .
- 2.) vier Kanten liegen in Breitenrichtung: ; ; ; .
- 3.) vier Kanten liegen in Höhenrichtung: ; ; ; .
BM2162

Parallelprojektion eines Würfels: a) orthogonal, b) schief - Parallelprojektion
- ---
- Eine Parallelprojektion ist eine Abbildung von Punkten des dreidimensionalen Raums auf Punkte einer gegebenen Ebene, wobei die Projektionsstrahlen zueinander parallel sind. Treffen die Projektionsstrahlen im rechten Winkel auf die Projektionsebene, handelt es sich um eine Orthogonalprojektion. Eine Parallelprojektion kann als Grenzfall einer Zentralprojektion angesehen werden, bei der sich das Projektionszentrum im Unendlichen befindet. Parallelprojektionen dienen häufig dazu, Schrägbilder von geometrischen Körpern herzustellen.
- ---
- Beschreibung
- Den Bildpunkt eines beliebigen Punktes im Raum erhält man bei einer Parallelprojektion dadurch, dass man die Parallele zur Projektionsrichtung durch diesen Punkt mit der Projektionsebene zum Schnitt bringt. Geraden werden durch eine Parallelprojektion im Allgemeinen wieder auf Geraden abgebildet. Das gilt jedoch nicht für Parallelen zur Projektionsrichtung, da diese in Punkte übergehen. Die Bildgeraden von parallelen Geraden sind – soweit definiert – ebenfalls parallel zueinander. Die Länge einer Strecke bleibt erhalten, wenn diese parallel zur Projektionsebene verläuft. Die Größe eines projizierten Winkels stimmt normalerweise nicht mit der Größe des ursprünglichen Winkels überein. Aus diesem Grund wird ein Rechteck im Allgemeinen auf ein Parallelogramm abgebildet, aber nur in Ausnahmefällen auf ein Rechteck. Ähnliches gilt für Kreise, die im Allgemeinen in Ellipsen übergehen.
- Im Allgemeinen treffen die Projektionsstrahlen schräg auf die Projektionsfläche. Man spricht dann von einer schrägen oder schiefen Parallelprojektion. Beispiele hierfür sind die Kavalierprojektion und Vogelperspektive.
- Am häufigsten wird eine Orthogonalprojektion (auch orthogonale oder orthographische Parallelprojektion genannt) angewendet. Hier treffen die Projektionsstrahlen im rechten Winkel auf die Projektionsebene. Auf dieser Projektion beruhen die technischen Zeichnungen der Ingenieure und Architekten, wobei der Sonderfall dominiert, dass eine der drei Hauptebenen der oft würfelförmigen technischen Gegenstände parallel zur Projektionsfläche ist (Dreitafelprojektion). Um Zeichnungen mit räumlichem Eindruck zu erstellen, wird diese Parallelität aufgehoben. Die Gegenstände werden geneigt. Je nach Neigungswinkel(n) entstehen zum Beispiel Isometrien oder Dimetrien. Die so erhaltenen Bilder werden oft fälschlicherweise als Bilder in Kavalierperspektive angesehen. Die Orthogonalprojektion entspricht einer Fotografie mit einem telezentrischen Objektiv oder näherungsweise einer Fotografie aus großer Entfernung, vorteilhaft mit einem Teleobjektiv aufgenommen.
BM2163

Orthogonalprojektion eines Punkts auf eine Ebene : Der Verbindungsvektor zwischen dem Punkt und seinem Abbild bildet mit der Ebene einen rechten Winkel. - Orthogonalprojektion
- rechtwinklige Parallelprojektion
- ---
- Eine Orthogonalprojektion (von gr. ὀρθός orthós gerade, γωνία gōnía Winkel), orthogonale Projektion oder senkrechte Projektion ist eine Abbildung, die in vielen Bereichen der Mathematik eingesetzt wird. In der Geometrie ist eine Orthogonalprojektion die Abbildung eines Punkts auf eine Gerade oder eine Ebene, sodass die Verbindungslinie zwischen dem Punkt und seinem Abbild mit dieser Gerade oder Ebene einen rechten Winkel bildet. Das Abbild hat dann von allen Punkten der Gerade oder Ebene den kürzesten Abstand zum Ausgangspunkt. Eine Orthogonalprojektion ist damit ein Spezialfall einer Parallelprojektion, bei der die Projektionsrichtung gleich der Normalenrichtung der Gerade oder Ebene ist.
- ---

- Orthogonalprojektion in der Darstellenden Geometrie
- ---
- In der arstellenden Geometrie und im technischen Zeichnen dienen Projektionen dazu, zweidimensionale Abbildungen von dreidimensionalen geometrischen Körpern herzustellen. Neben der Zentralprojektion kommen hierbei häufig Parallelprojektionen zum Einsatz. Eine Parallelprojektion ist eine Abbildung, die Punkte des dreidimensionalen Raums auf Punkte einer gegebenen Bildebene abbildet, wobei die Projektionsstrahlen zueinander parallel sind. Treffen die Projektionsstrahlen im rechten Winkel auf die Projektionsebene, so spricht man von einer Orthogonalprojektion.
- Werden statt einer Bildebene drei Projektionsebenen verwendet, die aufeinander senkrecht stehen, dann handelt es sich um eine Dreitafelprojektion oder Normalprojektion. Meist liegen dabei die Projektionsebenen parallel zu den Achsen des verwendeten (kartesischen) Koordinatensystems. Besitzt ein Punkt im Raum dann die Koordinaten , so erhält man die Orthogonalprojektionen des Punkts auf die drei Koordinatenebenen durch
BM2164

Orthogonalprojektion eines Punkts auf eine Gerade . Das Lot steht auf der Gerade senkrecht. - Orthogonalprojektion
- Projektion auf eine Gerade
- Definition
- ---
- In der euklidischen Ebene ist eine Orthogonalprojektion die [Abbildung eines Punkts auf eine Gerade , derart dass die Verbindungslinie zwischen dem Punkt und seinem Abbild einen rechten Winkel mit der Gerade bildet. Eine Orthogonalprojektion muss demnach die beiden Bedingungen
- (Projektion)
- (Orthogonalität)
- erfüllen. Die Linie heißt Lot des Punkts auf die Gerade und der projizierte Punkt wird Lotfußpunkt genannt. Die zeichnerische Konstruktion des Lots mit Zirkel und Lineal ist eine Standardaufgabe der euklidischen Geometrie und man spricht dabei vom Fällen des Lots.
BM2165

Zentralprojektion eines Würfels 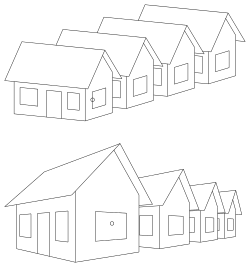
Parallelprojektion bzw. Zentralprojektion einer Häuserreihe - Zentralprojektion
- ---
- Mit Hilfe der Zentralprojektion stellt man in der darstellenden Geometrie anschauliche Bilder von räumlichen Objekten her. Im Gegensatz zur Parallelprojektion, in der man parallele Strahlen zur Projektion auf eine Ebene (Bildtafel) verwendet, benutzt man bei der Zentralprojektion Strahlen (Geraden) durch einen festen Punkt , den Augpunkt. Die Zentralprojektion erzeugt Bilder, wie sie auch beim Sehen mit einem Auge im Augpunkt entstehen. Während bei der Parallelprojektion parallele Geraden auf ebensolche abgebildet werden, werden bei der Zentralprojektion parallele Geraden, die nicht parallel zur Bildtafel verlaufen, auf Geraden abgebildet, die sich in einem Punkt, dem Fluchtpunkt, schneiden. Zentralprojektionen geben den räumlichen Eindruck eines Objektes viel besser wieder als eine Parallelprojektion (s. Häuserreihe). Die Zentralprojektion entspricht der Abbildung der Umwelt durch das menschliche Auge und ergibt somit einen natürlichen Bildeindruck. Sie wird in Technik und Architektur, in der Kartografie, in der Malerei und beim Zeichnen, sowie in der Computergrafik angewendet.
- ---
- Bezeichungen:
- ---

Zentralprojektion: Bezeichnungen 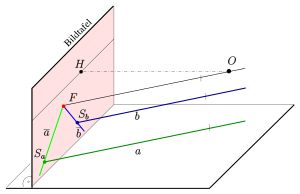
Flucht- und Spurpunkte von Geraden 
Haus mit zwei Fluchtpunkten bzw. einem Fluchtpunkt 
Beispiel mit Sehkreis 
Variation von Bildtafel und Augpunkt 
Funktionsweise einer Lochkamera - Den Augpunkt, das Zentrum der Projektionsstrahlen einer Zentralprojektion, bezeichnet man üblicherweise mit O, womit eine Beziehung zum Auge (lat.: oculus = Auge) hergestellt wird. Den Lotfußpunkt vom Augpunkt auf die Bildtafel nennt man Hauptpunkt, da er bei der Herstellung einer Zentralprojektion und beim anschließenden Betrachten eine wichtige Rolle spielt. Der Hauptpunkt ist sozusagen der Mittelpunkt des Bildes. Der Abstand des Augpunktes von der Bildtafel heißt Distanz (der aktuellen Zentralprojektion). Ist der Hauptpunkt im Bild gekennzeichnet und die Distanz bekannt, so weiß man, wo man beim Betrachten des Bildes das Auge positionieren muss, um einen perfekten Eindruck zu erhalten. Der Fluchtpunkt eines parallelen Geradenbüschels, das nicht zur Bildtafel parallel ist, ist der gemeinsame Schnittpunkt der zugehörigen Bildgeraden und ist immer der Schnittpunkt mit der Bildtafel (Spurpunkt) derjenigen Gerade des Büschels, die den Augpunkt enthält (s. Bild). Geraden, die zur Bildtafel parallel sind, haben also keine Fluchtpunkte oder man sagt, der zugehörige Fluchtpunkt liegt im „Unendlichen“. Eine Gerade, die senkrecht zur Bildtafel verläuft nennt man Tiefenlinie. Der Fluchtpunkt aller Tiefenlinien ist der Hauptpunkt. Bei vielen Objekten spielen horizontale Geraden und damit deren Fluchtpunkte eine wichtige Rolle. Die Fluchtpunkte aller horizontalen Richtungen bilden zusammen den Horizont h, eine horizontale Gerade. Falls die Bildtafel senkrecht steht, liegt der Hauptpunkt immer auf dem Horizont. Quaderförmige Objekte haben a) drei natürliche Fluchtpunkte, wenn keine der Kanten parallel zur Bildtafel ist (s. Bild des Würfels im ersten Bild), b) zwei Fluchtpunkte, wenn eine Kante parallel zur Bildtafel ist (s. 1. Haus), c) einen Fluchtpunkt, wenn zwei Richtungen parallel zur Bildtafel verlaufen (s. 2. Haus). Den letzten Fall nennt man Frontalperspektive. Meistens werden Zentralprojektionen von Objekten mit Hilfe von Auf- und Grundrissen hergestellt. Die Grundrissebene wird in Anlehnung an das Fotografieren als die Standebene (des Betrachters) bezeichnet. Die Schnittgerade (Spurgerade) s der Grundrissebene (Standebene) mit der Bildtafel wird oft aus technischen Gründen mit in das Bild eingezeichnet und Standlinie genannt. Standlinie und Horizont sind immer parallel zueinander. Mit Hilfe von Strahlen durch den Augpunkt O lassen sich alle Punkte des Raumes außer den Punkten in der zur Bildtafel parallelen Ebene durch den Augpunkt abbilden. Die Punkte dieser Ebene nennt man Verschwindungspunkte und die Ebene Verschwindungsebene. Beim Betrachten einer Zentralprojektion hat man oft den Eindruck, dass Randbereiche verzerrt erscheinen. Dies liegt immer daran, dass man sein Auge nicht im Augpunkt positioniert hat. Den Bereich des Bildes, den man nämlich bei Positionierung des Auges im Augpunkt und Fixierung des Hauptpunktes noch überblicken kann, ist erfahrungsgemäß kegelförmig eingeschränkt. Den Schnitt dieses Sehkegels mit der Bildtafel ist der Sehkreis (s. Bild einer Brücke). Sein Radius beträgt ungefähr 0.58*Distanz. Dies entspricht einem halben Öffnungswinkel des Sehkegels von 30°.
- In der darstellenden Geometrie bildet man immer Objekte ab „vor“ der Verschwindungsebene ab, d. h. Objekt und Bildtafel befinden sich auf derselben Seite der Verschwindungsebene. Bei der Fotografie liegen Objekt und Bild immer auf verschiedenen Seiten von . Dadurch stehen fotografische Bilder in der Kamera immer „auf dem Kopf“, was auf das Betrachten später keinen Einfluss hat, da man das Bild dann einfach „richtig herum“ hält.
- Der Vorteil einer Zentralprojektion ist, dass sie sehr anschauliche Bilder liefert, nämlich Bilder, die das Sehen (mit einem Auge) oder das Fotografieren nachahmen. Allerdings lassen sich Längen aus einer Zentralprojektion oder auch nur Verhältnisse von Längen nicht ablesen. Denn im Gegensatz zur Parallelprojektion, die verhältnistreu ist, bleibt bei einer Zentralprojektion nur das Doppelverhältnis (Verhältnis von Verhältnissen) invariant.
- Die Zentralprojektion stellt Objekte im Randbereich zu groß dar. So werden die Felder eines Schachbretts, welches zur Bildtafel parallel liegt, alle gleich groß und quadratisch abgebildet. Tatsächlich sind die weiter vom Hauptpunkt entfernt liegenden Felder auch weiter vom Betrachter entfernt und müssten auf der Bildtafel kleiner dargestellt werden, um eine natürliche Abbildung zu erhalten. In der Tat wird dieser Effekt bei Abbildungen mit Fischaugenobjektiven sichtbar. Der menschliche Sehapparat korrigiert jedoch die entstehenden verkrümmten Kanten bei der Betrachtung großer, naher Objekte, so dass die Fischaugenperspektive gerade nicht natürlich erscheint.
BM2166

Bild 1 - Zentralprojektion
- ---
- Zur Bedeutung von Hauptpunkt, Distanz und Augpunkt
- ---
- Das Bild mit Variationen eines Hauses zeigt die Bedeutung der wesentlichen Parameter Hauptpunkt, Distanz und Augpunkt. Hält man den Augpunkt fest und schiebt die Bildtafel auf den Augpunkt zu, d. h. man verkürzt die Distanz, so wird das Bild lediglich verkleinert auf ein zum ersten Bild ähnliches Bild. Winkel bleiben dabei erhalten. Hält man dagegen die Bildtafel fest und schiebt den Augpunkt auf den Hauptpunkt zu, d. h. auch hier wird die Distanz verkürzt, so entsteht ein Bild mit einer neuen Bildwirkung. Das Bild ist nicht mehr ähnlich zum ersten Bild. Entsprechende Winkel sind nicht mehr gleich. Eine Verschiebung des Hauptpunktes entlang der Gerade bewirkt lediglich eine Verkleinerung oder Vergrößerung des Bildes. Eine Verschiebung des Augpunktes entlang bewirkt eine wesentliche Veränderung des Bildes.
- ---
- Konstruktion der Zentralprojektion eines Objektes
- ---
- Die Konstruktion einer Zentralprojektion eines Objektes ist deutlich aufwendiger als eine Parallelprojektion. Hierzu gibt es ein dem Einschneideverfahren für Parallelprojektionen ähnliches Verfahren: die Architektenanordnung. Wie beim Einschneideverfahren müssen Grund- und Aufriss besonders positioniert werden. Für die Konstruktion des Bildes werden nur Punkte verbunden und Geraden geschnitten. Parallelen spielen bei der Parallelprojektion eine wichtige erleichternde Rolle. Auch bei Zentralprojektion sind sie durch ihre Fluchtpunkte eine große Hilfe. Eine weitere relativ einfache Methode ist die Frontalperspektive. Sie ähnelt der Kavaliersperspektive für eine Parallelprojektion. Bei der Frontalperspektive ist die Bildtafel zu einer wesentlichen Ebene des Objekts, z. B. einer Hausfront, parallel oder die Bildtafel und diese wesentliche Ebene sind identisch. Letzteres hat den großen Vorteil, dass man einfach den Aufriss des Objektes zur Frontalperspektive ausbauen kann. Ein weiterer wichtiger Vorteil einer Frontalperspektive ist, dass Kreise in der wesentlichen Ebene wieder auf Kreise abgebildet werden (s. Beispiel in Frontalperspektive). Allerdings gibt es auch einen Nachteil: Die Frontebene des Objektes wird stark betont. Bei einer Zentralprojektion mit zwei wesentlichen Fluchtpunkten ist dies meistens nicht der Fall.
BM2167

- Anwendungen der Zentralprojektion
- ---
- Typische Anwendungen der Zentralprojektion finden sich:
- in der darstellenden Geometrie
- in der Architektur bei der perspektivischen zeichnerischen Darstellung von Objekten,
- in Malerei und Zeichnen
- in der Computergrafik
- in der Fotografie z. B. bei der Rekonstruktion von Gebäuden aus Fotografien
- in der Photogrammetrie z. B bei der Auswertung und Ausmessung von (Luft-)Bildern, beim Entzerren von Schrägaufnahmen,
- in der Kartografie für Kartennetzentwürfe (gnomonische Projektion; stereografische Projektion),
- in der Gnomonik der Lehre von der Sonnenuhr zur Abbildung der Sonne auf ein Zifferblatt.
BM2168
- Was ist der Unterschied zwischen der Zentralprojektion und der Parallelprojektion?
Lösung BM2168 - Zentralprojektion: Die Projektionsgeraden gehen alle durch einen Punkt.
- Parallelprojektion: Die Projektionsgeraden liegen alle parallel zueinander.
BM2169

Funktionsweise einer Camera obscura Projektion von Dächern und Baumkronen gegenüber einer Mauer mit Schießscharten auf eine Wand 
Kastenförmige
Camera obscura
Zeltförmige
Camera obscura
Hüttenförmige
Camera obscura
Camera obscura. Federzeichnung; 17. Jahrhundert - Camera obscura
- ---
- Eine Camera obscura (lat. camera „Kammer“; obscura „dunkel“) ist ein dunkler Raum mit einem Loch in der Wand, die als Metapher für die menschliche Wahrnehmung und für die Herstellung von Bildern verwendet wird. Hat der dunkle Raum die Größe einer Schachtel, spricht man auch von einer Lochkamera.
- Während die technischen Prinzipien der Lochkamera bereits in der Antike bekannt waren, wurde die Nutzung des technischen Konzepts zur Herstellung von Bildern mit einer linearen Perspektive in Gemälden, Zeichnungen, Karten, architektonischen Umsetzungen und später auch Fotografien erst in der (bzw., vgl. Erwin Panofsky, den) Renaissance(n) der europäischen Kunst und der wissenschaftlichen Revolution der Neuzeit angewendet. Unter anderem nutzte Leonardo da Vinci die Camera obscura als Ebenbild des Auges, René Descartes für das Zusammenspiel von Auge und Bewusstsein und John Locke begann das Prinzip als Metapher des menschlichen Bewusstseins an sich zu benutzen. Diese moderne Verwendung der Camera Obscura als "epistemische Maschine" hatte wichtige Auswirkungen auf die Entwicklung des wissenschaftlichen Denkens. Nicht zuletzt benutzt Karl Marx Dialektischer Materialismus und dessen berühmter Anspruch, die hegelsche Dialektik vom Kopf auf die Füße stellen zu wollen (vgl. Die deutsche Ideologie 1845-46), den optischen Effekt als zentrale Metapher.
- ---
- Aufbau
- ---
- Eine Camera obscura besteht aus einem lichtdichten Kasten oder Raum, in den durch ein schmales Loch das Licht einer beleuchteten Szene auf die gegenüberliegende Rückwand trifft. Auf der Rückwand entsteht dabei ein auf dem Kopf stehendes und seitenverkehrtes Bild dieser Szene. Das Bild ist lichtschwach und nur bei ausreichender Abdunklung gut zu sehen. Bei transparenter Rückwand kann man das Bild auch von außen betrachten, wenn man für ausreichende Abdunklung sorgt, indem man beispielsweise ein lichtundurchlässiges Tuch verwendet, das die Rückseite der Rückwand und den Kopf des Betrachters bedeckt.
- ---
- Funktionsweise der Camera obscura
- ---
- Fällt Licht durch eine Sammellinse oder ein kleines Loch in einen ansonsten lichtdichten Hohlkörper, so wird in ihm ein spiegelverkehrtes und auf dem Kopf stehendes Bild, eine Projektion des Außenraumes erzeugt. Die Schemazeichnung rechts oben zeigt exemplarisch zwei Strahlenbündel, die von zwei Punkten eines Gegenstands in das Loch eintreten. Der kleine Durchmesser der Blende beschränkt die Bündel auf einen kleinen Öffnungswinkel und verhindert die vollständige Überlappung der Lichtstrahlen. Strahlen vom oberen Bereich eines Gegenstands fallen auf den unteren Rand der Projektionsfläche, Strahlen vom unteren Bereich werden nach oben weitergeleitet. Jeder Punkt des Gegenstands wird als Scheibchen auf der Projektionsfläche abgebildet. Die Überlagerung der Scheibchenbilder erzeugt ein verzeichnungsfreies Bild. Mathematisch ausgedrückt ist das Bild das Ergebnis einer Faltung aus idealer Abbildung des Gegenstands mit der Blendenfläche.
BM2170

Funktionsweise einer Lochkamera - Lochkamera
- ---
- Eine Lochkamera ist eine einfache Kamera. Licht, welches durch eine kleine Öffnung (dem Loch) in einen sonst lichtdichten und verhältnismäßig kleinen schachtelförmigen Hohlkörper fällt, ergibt auf dessen Rückseite ein auf dem Kopf stehendes Bild. Weil das Loch meist mit einer Stecknadel gestochen wird, heißt der englische Terminus pinhole camera. Das auf der gegenüberliegenden Innenseite entstehende reelle Bild lässt sich auf lichtempfindlichem Material (Fotopapier oder Film) oder über einen elektronischen Bildwandler (Bildsensor) festhalten. Besteht die Bildseite aus transparentem Material, kann man das Bild von außen betrachten. Technische Anwendungen ergeben sich im Bereich der Röntgenstrahlung, Gammastrahlung sowie von Partikelstrahlung, da hier Lochblenden eine (manchmal die einzige) Möglichkeit darstellen, Abbildungen zu erzeugen. Linsenfreie Lochaugen finden sich in der Natur unter anderem bei den Perlbooten (wasserbewohnende Kopffüßer).
- Der Begriff ist deutlich spezieller und jünger als der gelegentlich synonym gebrauchte Begriff camera obscura, mit der sowohl das grundlegende technische Konzept, großdimensionierte und etwa mit Linsen erweiterte komplexere Ausführungen als auch metaphorische Verwendungen bezeichnet werden.
- ---
- Funktionsweise:
- Das Abbildungsprinzip einer Lochkamera besteht darin, dass durch eine Lochblende nahezu alle Lichtstrahlen, bis auf ein möglichst kleines Bündel in gerader Verbindung zwischen Objekt- und Bildpunkt, ausgeblendet werden. Da im Gegensatz zu einer fokussierenden Kamera mit Objektiv keine weitere Bündelung des Lichts vorgenommen wird, bestimmt allein der Durchmesser der Lochblende die Bildschärfe und die Helligkeit des Bildes. In der Strahlenoptik gilt: Je kleiner die Lochblende, desto schärfer die Abbildung, aber desto geringer die Lichtstärke.
- Die Lichtstärke realer Lochkameras ist 10- bis 500-mal kleiner als die von fokussierenden Kameras (damit fangen sie nur 1/100sten bis 1/250.000sten Teil des Lichts ein), die Schärfentiefe ist dadurch aber um den Faktor 10 bis 500 größer. Allerdings ist diese Schärfentiefe nur in seltenen Fällen nutzbar, da sie unmittelbar hinter der Lochblende beginnt (was man selten braucht) und das Bild nirgends wirklich scharf ist.
- ---
- Lochkameras in der Technik:
- Im Bereich von Röntgenstrahlung, Gammastrahlung sowie von Partikelstrahlung stellen Lochblenden eine (manchmal die einzige) Möglichkeit dar, um Abbildungen zu erzeugen, da sich für diese Strahlungsarten keine klassischen Linsen herstellen lassen.
BM2171 - BM2180
[editar]BM2171
- Normalprojektion
- ---
- Die Normalprojektion oder Dreitafelprojektion und in Österreich der Kreuzriss ist ein Verfahren zur zeichnerischen Darstellung eines räumlichen Objekts in verschiedenen Ebenen Ansichten.
- ---
- Verwendung:
- Die Zeichnungen der Normalprojektion finden häufig Verwendung in der Architektur und im Bauwesen. Präsentationszeichnungen dienen vor allem der Darstellung eines Konzeptes oder Entwurfes. Grundrisse, Schnitte und Ansichten dagegen sind messbare Zeichnungen. Diese „Bauzeichnungen“ dienen den Planern dazu, die Dimensionen eines Bauwerkes genau zu definieren. Die Ausführenden können anhand dieser Zeichnungen das Bauwerk realisieren.
- Auch bei technischen Zeichnungen, zum Beispiel im Maschinenbau sind die Zeichnungen der Normalprojektion die wichtigste Form der Darstellung und essentiell für die Planung und Ausführung.
- ---

Projektionssymbole nach DIN 6
links: europäische Darstellung
rechts: amerikanische Darstellung- Ansichten:
- Zu den drei orthogonalen Projektionsflächen gibt es jeweils zwei Seiten und folglich sechs Ansichten. Bei der Anordnung der Ansichten auf dem Papier gibt es zwei Systeme:
- Projektionsmethode 1, auch europäische Darstellung oder First Angle Projection genannt und gekennzeichnet mit FR (für französisch, vgl. auch Schaubild rechts) und
- Projektionsmethode 3, auch amerikanische Darstellung oder Third Angle Projection genannt (Kz. US), die allerdings neben U.S.A. auch in Australien vorherrschend.
- Die nebenstehende Symbolik ermöglicht anhand eines abgeschnittenen Kegels und dem Trapez als Vorderansicht die Kennzeichnung der gewählten Methode. Die Entfaltung des Projektionsquaders verdeutlicht die jeweils zugrunde liegende Logik.
- Drei der Projektionen dienen als Hauptansicht für die Dreitafelprojektion. Bei der Wahl der Vorderansicht hat die aussagekräftigste Seite den Vorzug. Bei unübersichtlichen Objekten können zusätzliche Ansichten ergänzt werden. Manchmal wird auch auf eine der drei Ansichten verzichtet und man erhält eine Zweitafelprojektion.
- Projektionsmethode 1
-
Darzustellender Körper im Projektionsquader
-
Projektion nach hinten auf den Quader
-
Entfaltung nach hinten
-
Die sechs Ansichten
- Projektionsmethode 3
-
Körper im Projektionsquader
-
Projektion nach vorne auf den Quader
-
Entfaltung nach vorne
-
Die sechs Ansichten
| Bezeichnung | alte Bezeichnung | Position nach Projektionsmethode 1 | Position nach Projektionsmethode 3 |
|---|---|---|---|
| Vorderansicht | Aufriss | Mitte | Mitte |
| Seitenansicht von links | Seitenriss oder Kreuzriss | rechts von der Mitte | ganz links |
| Draufsicht oder Aufsicht | Grundriss | unten | oben |
| Rückansicht | ganz rechts | ganz rechts | |
| Seitenansicht von rechts | ganz links | rechts der Mitte | |
| Untersicht | oben | unten |
- ---
- Erläuterung
- ---
- Geometrisch betrachtet wird jeder Punkt des Objektes zunächst in einem räumlichen Koordinatensystem als P(x|y|z) beschrieben. Dann wird jeweils eine der Koordinaten auf einen festen Wert (z. B. auf null) gesetzt, um eine ebene Darstellung zu ermöglichen. Dies entspricht einer Projektion in jeweils einer der Grundebenen.
| Sicht | Koordinaten | Ebene |
|---|---|---|
| Vorderansicht | = P(0|y|z) | = yz-Ebene |
| Draufsicht | = P(x|y|0) | = xy-Ebene |
| Seitenansicht | = P(x|0|z) | = xz-Ebene |
- Ein Gebäude (Abbildung unten links) soll in Dreitafelprojektion dargestellt werden.
- Seine Eckpunkte werden in die Grundebenen projiziert und wieder miteinander verbunden (unten mittig). Verdeckte Kanten werden dabei gestrichelt eingetragen.
- Die drei Projektionen werden nun in einer Ebene gezeichnet, indem man die räumliche Anordnung der drei Ebenen längs der x-Achse aufschneidet und in die yz-Ebene umklappt. Die x-Achse tritt in der Zeichnung dann zweimal auf.
-
3D-Zeichnung
-
Projektion der Ansichten in der 3D-Zeichnung
BM2172
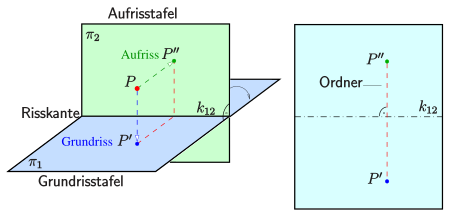
Bild 1: Grund- und Aufriss in Zweitafelprojektion 
Bild 2 
Bild 3 - Zweitafelprojektion
- ---
- Die Zweitafelprojektion ist eine grundlegende Methode der Darstellenden Geometrie. Dabei wird ein Punkt des Anschauungsraums mit Hilfe zweier senkrechter Parallelprojektionen auf zwei zueinander senkrechte Ebenen (Bildtafel) projiziert. Üblicherweise ist die Ebene
- horizontal und heißt Grundrisstafel und
- vertikal, die Aufrisstafel.
- Die Schnittgerade
- heißt Risskante.
- Die entstehenden
- Bilder sind Grundriss bzw. Aufriss von .
- Stellt man sich als x-y-Ebene und als y-z-Ebene vor, die sich in der y-Achse schneiden, so erkennt man, dass in beiden Projektionen (Rissen) alle räumlichen Informationen (Koordinaten) des Punktes enthalten sind.
- Solche Risse waren schon den Griechen und Römern bekannt.
- Man klappte die Aufrisstafel um die Risskante in die Grundrisstafel und benutzte die Grundrisstafel als Zeichenebene.
- Man sagt, Grundriss und Aufriss sind in der Zeichenebene einander zugeordnet.
- ---

Bild 4: Zweitafelprojektion: verschiedene Lagen von Punkten - Grund- und Aufrisse verschiedener Punkte
- ---
- Da die Anschaulichkeit der Lage von Punkten in der Zweitafelprojektion deutlich geringer ist als in einem räumlich wirkenden Bild (Axonometrie), bedarf es einiger Übung, um sich die räumliche Lage eines konkreten Punktes anhand seines Grund- und Aufrisses vorzustellen. Normalerweise erwartet man, dass bei einer Zweitafelprojektion der Grundriss eines Punktes unterhalb und der Aufriss eines Punktes oberhalb der Risskante sich befindet. Wie Beispiele in dem Bild zeigen, muss das nicht der Fall sein. Allerdings ist man immer bemüht, Grund- und Aufriss eines Objektes in der Zweitafelprojektion optisch zu trennen (Grundriss „unten“, Aufriss „oben“).
BM2173

- Eintafelprojektion
- ---
- Unter Eintafelprojektion versteht man eine senkrechte Parallelprojektion auf eine horizontale Ebene mit weiteren Informationen (z. B. Höhen in Landkarten oder Traufkantenhöhen und Neigungswinkel von Dachflächen).
- In der Darstellenden Geometrie wird eine Eintafelprojektion oft als kotierte Projektion bezeichnet (von franz. coter = notieren) und ist der Oberbegriff für die Darstellung von Böschungsflächen und der Dachausmittlung. Das wichtigste Hilfsmittel beim Arbeiten mit kotierten Projektionen sind Höhenlinien.
- Anwendung finden Eintafelprojektionen
- in der Kartografie für topografische Karten zur Beschreibung von unebenem Gelände und im Straßenbau zur Darstellung von Böschungsflächen (Schüttflächen an Straßenrändern) und
- bei Dachausmittlungen zur Ermittlung von Grat-, Kehl- und Firstlinien (Schnittgeraden benachbarter Dachflächen) in Form des Grundrisses des Traufkantenpolygons zusammen mit Angaben über Traufkantenhöhen und Dachneigungen.
- Die Bezeichnung Eintafelprojektion wurde bewusst in Anlehnung an Zweitafelprojektion gewählt. Bei einer Zweitafelprojektion stecken alle räumlichen Informationen (z.B. Koordinaten) in zwei zugeordneten senkrechten Parallelprojektionen (Grundriss und Aufriss). Bei einer Eintafelprojektion spielt der Grundriss eine dominierende Rolle. Die fehlenden räumlichen Informationen werden in der Regel durch Zahlen (Höhen, Neigungswinkel,...) oder Farben ergänzt. Bei irgendeiner senkrechten oder schiefen Parallelprojektion spricht man nicht von einer Eintafelprojektion.
-
Wanderkarte mit Höhenlinien
-
Straße mit einem Teil einer Böschungsfläche (Die Zahlen geben Höhen an.)
-
Dachausmittlung: Grat-Kehl- und Firstlinien (Die Zahlen geben Dachneigungen an.)
BM2174

Grund- und Aufriss in Zwei-Tafel-Projektion 
oben der Aufriss,
unten der Grundriss eines Hauses- Aufriss
- ---
- Der Aufriss eines räumlichen Objektes (z. B. eines Hauses, einer Brücke usw.) ist eine orthogonale Parallelprojektion auf eine senkrecht stehende Zeichenebene (s. Zweitafelprojektion). Zusammen mit dem Grundriss (eine orthogonale Parallelprojektion auf eine horizontal liegende Zeichenebene) wird das räumliche Objekt eindeutig beschrieben. Daneben existieren noch Kreuzrisse, Ansichten und Schnitte. Die theoretische Grundlage liefert die Zweitafelprojektion. Zum Anfertigen des Aufrisses bedient man sich eines Reißzeugs. Bauleute wie Zimmerer fertigen Aufrisse oftmals in großem Maßstab direkt auf dem Reißboden.
- Grund- und Aufrisse von realen Objekten wie Haus, Brücke usw. sind immer skalierte (verkleinerte) orthogonale Parallelprojektionen des Objektes. In Bauplänen wird oft auf 1:100 oder 1:50 oder 1:10 verkleinert (siehe Plan).
BM2175

Ansichtszeichnung eines Hauses in Venedig - Ansicht
- ---
- Als Ansicht werden bei einer Architekturzeichnung oder technischen Zeichnung die zweidimensionalen Darstellungen eines dreidimensionalen Körpers von verschiedenen Seiten aus bezeichnet.
- Im Maschinenbau kann es sich bei dem Körper zum Beispiel um ein Bauteil handeln, in Architektur und Bauwesen zum Beispiel um ein Bauwerk.
- ---
- Ansichten in der Dreitafelprojektion:
- In der Dreitafelprojektion werden die Ansichten aus drei rechtwinklig zueinander stehenden Blickwinkeln ausgeführt.
- Generell kann man aus zwei bekannten Ansichten jede weitere Betrachtungsweise sprich Ansicht konstruieren, auch nichtorthogonale. Voraussetzung dafür ist allerdings, dass es sich nicht um die Konterposition handelt, z.B. Ansicht von Rechts und Ansicht von Links. Ansichten werden häufig als: „Draufsicht“ DS, „Vorderseite“ VS, „Seitelinks“ SL, „Seiterechts“ SR, „Rückansicht“ RA, oder „Ansicht von Unten“ AU, definiert. Ansichten können mit und ohne unsichtbare Kanten dargestellt werden. Häufig gegebene Ansichten sind die Draufsicht und Ansicht von Vorne. Aus diesen Beiden lassen sich unmittelbar die Ansichten von Rechts und Links konstruieren.
- Die Auswahl der dargestellten Ansichten ist wichtig, da man daraus unmissverständlich die Form des dargestellten Körpers ablesen können muss.
-
Darzustellender Körper im Projektionsquader
-
Projektion auf den Quader
-
Entfaltung des Quaders
-
Die sechs Ansichten
BM2176

Grundrisse und Aufsicht eines Gebäudes - Aufsicht
- ---
- Eine Aufsicht oder auch Draufsicht ist eine zeichnerisch dargestellte, zweidimensionale orthogonale Projektion einer räumlichen Gegebenheit. Aufsichten werden nach den Regeln der Dreitafelprojektion erstellt. Das Objekt wird dabei von oben betrachtet.
- Im Gegensatz zur Vogelperspektive handelt es sich bei der Aufsicht um eine planare Darstellung, aus der man (bei maßstäblicher Darstellung) die Dimensionen des Objektes abmessen kann.
- Aufsichtsdarstellungen finden sich in Technischen Zeichnungen, insbesondere jedoch in Bauzeichnungen. Im Bauwesen dienen Aufsichten dazu, eine bereits vorhandene Gegebenheit zu dokumentieren (Bestandsplan) oder werden im Rahmen einer Bauplanung erstellt. Sie stellen die Geometrie der Dachlandschaft eines Bauwerkes dar. Häufig findet man Dachaufsichten in Lageplänen.
- Aufsichten können in unterschiedlichsten zeichnerischen Maßstäben vorliegen. In CAD-Programmen wird die Aufsicht häufig mit den englischen Begriffen „Top“ oder „TopView“ bezeichnet.
- Das Gegenteil der Aufsicht ist die Untersicht, bei der das Objekt von unten betrachtet wird.
BM2177
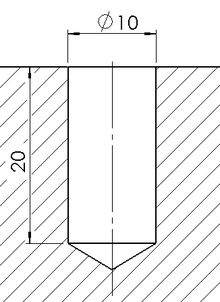
Schnittzeichnung im Maschinenbau (Bohrung) - Schnitt
- ---
- Eine Schnittzeichnung, Schnittdarstellung oder auch kurz ein Schnitt ist eine Darstellungsform in Zeichnungen. Sie wird (vor allem im Baugewerbe) auch Risszeichnung oder kurz Riss genannt, wovon sich auch die Begriffe Grundriss und Aufriss (die Ansicht) ableiten. Je nach Schnittebene bezeichnet man die Zeichnungen als Längsschnitt oder Querschnitt (seltener auch den Grundriss als Grundrissschnitt).
- Eine Schnittzeichnung dient dazu, verdeckte innenliegende Konturen, Materialien und Strukturen eines Körpers zu zeigen. Gegebenenfalls müssen unterschiedliche Schnitte durch einen Körper gelegt werden, um alle relevanten Einzelheiten in mehreren Schnittflächen darstellen zu können.
- ---
- Einsatzbereiche:
- Schnittzeichnungen und -darstellungen kommen in vielen Bereichen zum Einsatz. Beim technischen Zeichnen bei der Darstellung von Bauelementen und Bauteilen im Maschinenbau oder im Bauwesen (Hochbau, Tiefbau); bei der Darstellung von Gebäuden in der Architektur; bei der anschaulichen Darstellung von Geräten und Maschinen für Laien; in der Science-Fiction-Szene, wo Fans oder Autoren fiktive Raumschiffe und Raumstationen darstellen; in der Biologie bei der Darstellung des Aufbaus von Flora und Fauna; bei der Darstellungen der Schichten im Boden in Geologie und Archäologie; in der Medizin zur tomographischen Bildgebung des menschlichen Körpers und so weiter.
- ---

Klassische Schnittdarstellung eines Gebäudes - Darstellung
- Bei klassischen Schnittzeichnungen werden die Schnittkanten dicker dargestellt als die Konturen der Elemente, die man in der Ansicht sieht. Die Schnittflächen werden oft flächig oder mit Schraffuren gefüllt. Je nach Einsatzbereich gibt es verschiedene Regeln für Schnittzeichnungen.
- Im Maschinenbau zum Beispiel gelten für die Darstellung von geschnittenen Gewinden, Bohrungen und Passungen genauso wie für deren Bemaßung besondere Regeln.
- Konventionen gelten ebenso im Bauwesen. Für die Darstellung der Bauzeichnungen im amtlichen Bauantragsverfahren gelten Vorschriften (Bauvorlagenverordnung)
- Wenn die Schnittebene durch mehrere Körper verläuft, sind die Schnittflächen durch Schraffuren unterschiedlicher Richtung darzustellen. Zur Kennzeichnung verschiedener Materialien (Metall, Beton, Mauerwerk, Holz, Textilien, Kunststoff u. a.) werden Schraffuren unterschiedlicher Art verwendet (z. B. Linien-, Kreuzlinien-, Strichlinien-, Punktschraffur u. a. in verschiedenen Linienweiten und -abständen sowie Raster und Flächen in unterschiedlichen Grau- oder Farbtönen).
- Neben den klassischen, zweidimensionalen Schnittzeichnungen gibt es auch perspektivische Zeichnungen, die häufig aus im Computer generierten Modellen heraus erzeugt werden. Sie sind für Laien oft einfacher verständlich. Gelegentlich werden Schnittzeichnungen auch gesprengt, indem einzelne Bereiche zur besseren Übersicht versetzt dargestellt werden und sich damit nicht verdecken. Man spricht dann von Explosionszeichnungen.
- Beispiele:
-
Schnittmodell eines Porsche 987c Cayman S
-
Perspektivische Schnittzeichnung
-
Schnittdarstellung eines Zahnes in der Biologie
-
Dreidimensionale Schnittzeichnung in der Biologie
-
Sagittales Schnittbild eines Kniegelenks durch MRT (Magnetresonanztomographie)
BM2178

Fadengitter, Vorrichtung zum perspektivischen Zeichnen (1710) - Perspektive
- ---
- Perspektive (von lateinisch perspicere‚ hindurchsehen, hindurchblicken) bezeichnet die räumlichen, insbesondere linearen Verhältnisse von Objekten im Raum: das Abstandsverhältnis von Objekten im Raum in Bezug auf den Standort des Betrachters. Damit ist die Perspektive stets an den Ort des Betrachters gebunden und kann nur durch Veränderung der Orte der Objekte und des Betrachters im Raum verändert werden.
- Diese Feststellung ist dahingehend wichtig, dass eine andere Perspektive nicht durch bloße Veränderung des Betrachtungsausschnitts ohne Ortswechsel (z. B. durch Verwendung eines Zoom-Objektivs in der Fotografie) herbeigeführt werden kann.
- Die perspektivische Darstellung fasst die Möglichkeiten zusammen, dreidimensionale Objekte auf einer zweidimensionalen Fläche so abzubilden, dass dennoch ein räumlicher Eindruck entsteht.
- ---

Chauvet-Höhle, perspektivenartige Einzeldarstellungen von Tiergruppen (ca. 31.000 B.P. - before present - geologische Altersangaben werden vom Jahre 1950 rückgerechnet) 
Fresko aus einem ägyptischen Grab (um 1500 v. Chr.; Darstellungen sowohl in normal seitlicher wie in verdrehter Perspektive kommen vor.) 
Zentralperspektive; perspektivische Tiefenwirkung als städtebauliches Gestaltungsmittel - Arten perspektivischer Darstellung
- ---
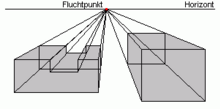
Fluchtpunktperspektive 
3-Punkt-Perspektive - Geometrische Projektionsverfahren.
- Zentralprojektion: Sehstrahlen gehen von einem Augpunkt aus, raumparallele Kanten scheinen in der Projektion in einen Punkt zu flüchten – den sogenannten Fluchtpunkt.
- Zentralperspektive (Frontalperspektive): Zentralprojektion mit einem Fluchtpunkt, eine Raumfläche liegt parallel zur Bildebene, diese wird bildparallel abgebildet, die andere orthogonal dazu – deren Raumflächen fluchten in einem Punkt
- 2-Punkt-Perspektive (Übereckperspektive): Zentralprojektion mit zwei Fluchtpunkten, die horizontparallelen Raumkanten sind nicht bildebenenparallel und flüchten in ihrem jeweiligen Fluchtpunkt, die Vertikalen werden bildparallel abgebildet.
- Froschperspektive: Zentralprojektion mit drei Fluchtpunkten, es gibt keine bildebenenparallelen Raumkanten, der Augpunkt liegt unter dem abgebildeten Gegenstand.
- Vogelperspektive: Zentralprojektion mit drei Fluchtpunkten, es gibt keine bildebenenparallelen Raumkanten, der Augpunkt liegt über dem abgebildeten Gegenstand.
- Fischaugenprojektion: sphärische Projektion. Linien, die nicht durch das Zentrum gehen, werden gekrümmt, Flächen am Rand kleiner abgebildet, als in Bildmitte, der Blickwinkel erreicht 180 Grad und mehr.
- Parallelprojektion: Sehstrahlen verlaufen parallel, raumparallele Kanten werden in der Projektion ebenfalls parallel abgebildet. Es gibt keine Fluchtpunkte.
- Orthogonalprojektion: Sehstrahlen treffen rechtwinklig auf die Projektionsfläche.
- Hauptriss (Dreitafelprojektion)
- Axonometrie
- isometrisch
- dimetrisch (Dimetrie)
- trimetrisch
- schiefwinklig: Sehstrahlen treffen in einem schrägen Winkel auf die Projektionsfläche.
- Kavalier (Kavalierperspektive)
- Kabinett
- Militär
- Orthogonalprojektion: Sehstrahlen treffen rechtwinklig auf die Projektionsfläche.
- Panoramabild: Beim Panoramabild erfolgt die Abbildung zunächst auf eine zylinderförmige Fläche, die dann in eine Ebene aufgerollt werden kann. Es gibt aber auch große Panoramen, die als Zylinder aufgestellt sind. Parallele Linien werden nur im Sonderfall parallel abgebildet. Man erreicht einen Blickwinkel von 180 Grad und mehr (bis 360 Grad).
- Zentralprojektion: Sehstrahlen gehen von einem Augpunkt aus, raumparallele Kanten scheinen in der Projektion in einen Punkt zu flüchten – den sogenannten Fluchtpunkt.
- Bedeutungsperspektive: Begriff in der Malerei. Die Größe der dargestellten Figuren und Gegenstände hängt von deren Bildbedeutung ab, nicht von den räumlich-geometrischen Gegebenheiten.
- Luft- und Farbperspektive: Die Farb- und Helligkeitskontraste nehmen in die Ferne ab – Farben erscheinen matter, meistens heller und ins Blau verschoben
- Verdrehte Perspektive: zuerst in den europäischen Höhlenbildern, später besonders auffallend in der altägyptischen Kunst, noch später häufig in der Moderne, etwa bei Pablo Picasso.
- Geometrische Projektionsverfahren.
-
Zentralperspektive
-
2-Punkt-Perspektive
-
Froschperspektive
-
Fischaugenprojektion
-
Panoramabild
- ---
- Beispiele für perspektivische Darstellungen:
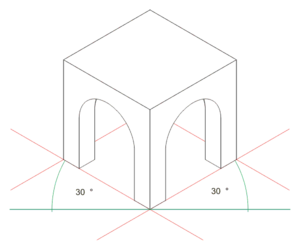
Isometrische Darstellung Schrägprojektion, sog. „Militärperspektive“ 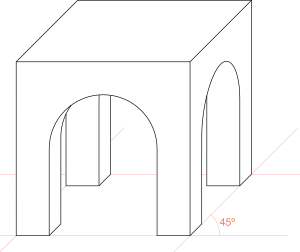
Schrägprojektion, sog. „Kabinettperspektive“ (auch „Kavalierperspektive“) 
Zentralperspektive (mit einem Fluchtpunkt)
BM2179

Isometrische Perspektive in einem Computerspiel, hier Studie mit Figuren aus The Battle for Wesnoth - Parallelperspektivische Darstellung
- ---
- Linien, die in der Wirklichkeit parallel verlaufen, werden bei der parallelperspektivischen Abbildung gleichfalls parallel dargestellt. Dadurch wird ein Zusammenlaufen der Linien in Richtung der Fluchtpunkte vermieden, sodass die abgebildeten Flächen gut erkennbar bleiben. Dieser Effekt ist z. B. von Architekten erwünscht, die bezwecken, dass die Ansichten von Häusern unabhängig vom Blickwinkel immer gleich deutlich sind. Architekten sprechen hier von „Parallelperspektive“.
- ---
- Axonometrische Darstellung
- ---
- Axonometrische Darstellungen sind parallelperspektivische Darstellungen. Der Fluchtpunkt ist ins Unendliche gerückt. Zu den axonometrischen Projektionen zählen die isometrische und die dimetrische Darstellung.
- ---

Isometrische Axonometrie - Isometrische Axonometrie, nach DIN 5
- Wird der darzustellende Körper in der Draufsicht um 45° gedreht und in der Seitenansicht hinten so gehoben, dass seine Fläche unter ca. 35° zur Grundfläche steht, wird ein räumliches Bild projiziert, bei dem die Höhe (H) senkrecht, die Längen (L) und Tiefen (T) im Winkel von 30° zur Grundlinie erscheinen. Die Richtungen der Breiten- (Längen-), Höhen- und Tiefenausdehnung (beim rechtwinkligen Körper die Richtungen der Kanten) erscheinen in verschiedenen Winkeln, aber nicht rechtwinklig zueinander. Alle drei Richtungen sind gleichmäßig verkürzt, verhalten sich zueinander wie 1:1:1, haben also einen gemeinsamen Maßstab (Isometrie). Ausgehend von einer senkrechten Raumkoordinate (Achse, daher „Axonometrie“) werden alle Kanten bzw. Punkte eines Körpers nur über die, in Wirklichkeit rechtwinklig zueinander stehenden, Raumkoordinaten senkrecht bzw. im Winkel von 30° zur Grundlinie konstruiert. Linien oder Kanten, die nicht die Richtung einer Raumkoordinate haben (z. B. die schräge Giebelkante eines Hauses, die Diagonalen eines Würfels), werden nicht maßstäblich wiedergegeben, können also auch nicht direkt konstruiert werden. Die Endpunkte solcher Linien müssen über einen Umweg mittels der Raumkoordinaten ermittelt werden. Zweckmäßig ist es, in eine solche Darstellung drei Linienmaßstäbe in Richtung der Raumkoordinaten einzuzeichnen, um zu verdeutlichen, dass nur in diesen Richtungen die Maße stimmen. Diese räumliche Darstellungsart ist vorzuziehen bei Körpern mit gleichwertigen Ansichten. Man nennt sie nach DIN 5 Isometrische Axonometrie (s. Abb).
- ---

Dimetrische Axonometrie - Dimetrische Axonometrie, nach DIN 5
- Wird der darzustellende Körper in der Draufsicht und in der Seitenansicht um nur 20° gedreht, entsteht ein räumliches Bild, bei dem die Längen im Winkel von 7°, die Tiefen im Winkel von 42° zur Grundlinie dargestellt werden. Die Tiefen erscheinen gegenüber den Höhen und Längen um die Hälfte verkürzt. Das räumliche Bild ist also zweimaßstäblich (dimetrisch, z. B. H u. L 1:5, T 1:10). Diese Darstellung wird bei einer gegenüber den anderen Ansichten besonders wichtigen Vorderansicht verwendet. Unter Beachtung der verschiedenen Winkel und Maßstäbe wird der Körper sonst wie bei der isometrischen Axonometrie gezeichnet. Zur Verdeutlichung sollten hier unbedingt entsprechende Linienmaßstäbe in Form eines Raumachsenkreuzes eingezeichnet werden. Man nennt diese Darstellungsweise nach DIN 5 Dimetrische Axonometrie (s. Abb.).
BM2180

Zentralperspektive in einem Zimmerbild von Johann Erdmann Hummel (um 1820) - Zentralperspektivische Darstellung
- ---
- Die einfachste Form der Perspektive bildet die Zentralperspektive. Sie wird vor allem in der Architektur und zur Veranschaulichung benutzt. Raumparallele Kanten werden nicht abbildungsparallel dargestellt, sondern vereinigen sich optisch in einem scheinbaren, gedachten Punkt, dem sog. Fluchtpunkt. Dieser auf der Horizontlinie liegende Fluchtpunkt lässt sich über die Schnittstelle finden, die durch die Verlängerung der in der Realität parallel liegenden Objektkanten entsteht.
- Die Zentralperspektive ist eine besondere Form der Fluchtpunktperspektive, bei der sich der Fluchtpunkt in der Bildmitte befindet. Dadurch erhält man meist eine Frontalansicht des Objektes. Es gibt keine Verschiebungen nach rechts oder links, aber nach oben oder unten. Auch wenn durch unterschiedlich verlaufende Objektkanten mehrere Fluchtpunkte entstehen, wie etwa bei der Darstellung eines Hauses, liegen diese alle auf der Horizontlinie. Die dem Betrachter zugewandten Flächen des Objektes sind bildparallel, während die in die Tiefe des Raumes führenden Objektkanten sich scheinbar in einem Fluchtpunkt am Horizont vereinigen.
- Weitere Varianten stellen die Perspektiven mit zwei – auch Über-Eck-Perspektiven genannt – oder drei Fluchtpunkten dar. Da bei einer Perspektive mit drei Fluchtpunkten der Horizont notwendigerweise nach oben, bzw. unten wandert, nennt man die jeweiligen Abbildungen auch Froschperspektive oder Vogelperspektive.
 |
 |
 |
BM2181 - BM2190
[editar]BM2181

[1] Aufnahme mit Fluchtpunkt 
Duisburg Hbf: Blick vom Bahnsteig in nördliche Richtung 
- Fluchtpunkt
- ---
- In einer perspektivischen Abbildung (Zentralprojektion) schneiden sich die Bilder aller Geraden, die im Original zueinander parallel verlaufen aber nicht zur Bildebene parallel sind, in einem gemeinsamen Fluchtpunkt.
- Bei der perspektivischen Abbildung werden räumliche Objekte auf eine ebene Fläche, die Bildebene, projiziert. Das ist zum Beispiel bei der fotografischen Aufnahme der Fall. Im Bildoriginal [1] sind unter anderem die Straßenränder, Dachfluchten und Fensterfluchten der bebauten Straße parallele Geraden: Sie alle laufen auf einen gemeinsamen Fluchtpunkt zu.
- Auch die senkrechten Hauskanten sind parallele Geraden. Allerdings liegt deren Fluchtpunkt weit außerhalb des Bildes, im "Unendlichen".
- Alle parallelen Ebenen schneiden sich in einer gemeinsamen Fluchtgeraden. Für die waagerechten Ebenen des Bildes [1], wie zum Beispiel die Straßenfläche und die Stockwerksdecken, ist das der Horizont. Die Fluchtpunkte aller Parallelen in einer solchen Ebene liegen auf dieser Fluchtgeraden.
-
Abbildung mit einem Fluchtpunkt
-
[2] Abbildung mit zwei Fluchtpunkten
-
Abbildung mit drei Fluchtpunkten (Vogelperspektive)
- Vor allem bei Gebäuden gibt es zueinander senkrecht stehende Linien in drei Richtungen: Höhe, Breite, Tiefe. Die Blickrichtung (Aufnahmerichtung der Kamera, Perspektive) für eine Abbildung kann dabei so gewählt werden, dass ein, zwei oder drei Fluchtpunkte entstehen. Dies wird als Fluchtpunktperspektive bezeichnet.
- Die Perspektive eines Bildes führt den Blick des Betrachters auf den Fluchtpunkt. Die Wahl der Lage und der Anzahl der Fluchtpunkte eines Bildes sind daher eine wesentliche Aufgabe der Bildgestaltung. Fluchtpunkte schaffen Dynamik und Raumtiefe. Sie setzen Akzente und bringen Objekte in den Blickpunkt des Betrachters.
- ---
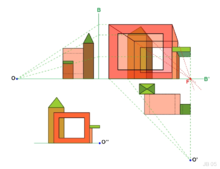
Bild 3: Konstruktionsbeispiel einer Zentralprojektion mit einem Fluchtpunkt - Geometrische Konstruktion
- Die Abbildung 3 zeigt den geometrischen Zusammenhang zwischen der Fluchtpunktperspektive und der Parallelprojektion. Letztere wird für ausmessbare Karten und Pläne verwendet. Die Projektion aller Objektpunkte von einem Augenpunkt O auf eine Bildfläche B sowohl für Grundriss (O', B') als auch für den Aufriss (O, B) ergeben senkrechte und waagerechte Schnittgeraden zu den entsprechenden Bildpunkten in der Projektion. Das Bild zeigt, dass die Dynamik umso stärker wird, je näher der Augenpunkt an das Objekt rückt. Die Lage des Augenpunktes entscheidet nicht nur über den Aspektwinkel, sondern auch über die Sichtbarkeit von Objektdetails.
- Ist die Bildebene parallel zu einer Objektfläche, hier der Gebäudefront, so hat diese Fläche (ebenso wie alle dazu parallelen Flächen) ihre Fluchtpunkte im Unendlichen. Insbesondere werden alle parallelen Geraden, die in einer parallelen Ebene zur Bildebene liegen, weiterhin parallel abgebildet. Wird die Bildebene B' (Grundriss) gedreht, so entsteht für diese Flächen ebenfalls ein Fluchtpunkt im Endlichen. Es entsteht ein Bild analog zu Bild 2. Eine Kippung der Bildebene B im Aufriss führt entweder zur Vogel- oder zur Froschperspektive.
BM2182

Grundriss der Kathedrale von Amiens - Grundriss
- ---
- Der Grundriss (griechisch: Ichnographie) ist eine abstrahierte, zeichnerisch dargestellte, zweidimensionale Abbildung einer räumlichen Gegebenheit. Grundrissdarstellungen finden sich in technischen Zeichnungen, insbesondere jedoch in Bauzeichnungen. In der darstellenden Geometrie existieren neben Grundrissen zusätzlich Aufrisse, Kreuzrisse, Ansichten und Schnitte. Die theoretische Grundlage liefert die Zweitafelprojektion.
- Die Bezeichnung Grundriss wird allerdings nicht nur für eine zeichnerische Darstellung, sondern auch für die räumlichen Verhältnisse als solche verwendet. So kann damit auch die Anordnung, Lage und Größe der Räume innerhalb eines Gebäudes gemeint sein. In diesem Zusammenhang existieren Begriffe wie Freier Grundriss und Offener Grundriss.
- Historisch lässt sich Grund-Riss mit „Boden-Zeichnung“ übersetzen. Die Grundrissdarstellung ist dementsprechend eine zeichnerische Abbildung der Bodenfläche. In der Architektur ist es allerdings üblich, den Grundriss als gedachten waagerechten Schnitt in zirka einem Meter Höhe anzulegen, beispielsweise um Fensteröffnungen darzustellen, die in der Regel nicht bis zum Boden reichen. Dinge unterhalb dieser Schnittebene, wie Fensterbrüstungen, erscheinen dann in ihrer Aufsicht.
- Grundrissdarstellungen dienen beispielsweise dazu, eine bereits vorhandene Gegebenheit zu dokumentieren (Bestandsplan). Häufig jedoch werden sie im Rahmen einer Konstruktionsphase oder Bauplanung erstellt. Grundrisse können in unterschiedlichsten zeichnerischen Maßstäben vorliegen. Je nach Verwendungszweck und Lage der waagerechten Schnittebene sind sie oft nicht eindeutig von Aufsichten beziehungsweise Draufsichten abzugrenzen.
- ---
- Sprachliche Übertragungen
- Auch ein kurzgefasstes Lehrbuch, ein Leitfaden oder eine Abhandlung, die eine Orientierung oder einen Überblick über ein bestimmtes Thema vermittelt, werden mitunter als Grundriss bezeichnet.
BM2183

Bauzeichner am Reißbrett 
Ingenieure an Reißbrettern 
Ingenieur am Reißbrett - Reißbrett
- ---
- Das Reißbrett (eigentlich Zeichenbrett genannt, gelegentlich auch Zeichenplatte oder Zeichenmaschine) dient technischen Zeichnern, Konstrukteuren und Architekten zum Erstellen technischer Zeichnungen und Bauzeichnungen, also zum Anfertigen von Grundrissen, Aufrissen, Schnitten und Perspektivdarstellungen. Der Name stammt noch aus der Zeit vor der Erfindung des Bleistiftes, als mit einem harten „Reißbley“ mehr geritzt als gezeichnet wurde. Ein Merkmal des Reißbrettes ist, dass die richtige Winkligkeit der Linien zueinander über eine Mechanik sichergestellt wird.
- Als Hilfsmittel zur Erstellung technischer Zeichnungen wurde das Reißbrett in den 1990er-Jahren durch den Einsatz von Computern mit entsprechender Software und häufig speziell angepassten Eingabegeräten Computer Aided Design (CAD) weitgehend verdrängt. Es findet nur noch in wenigen Nischenbereichen Anwendung, in denen das Zeichnen per Hand noch betrieben wird. Oft dient ein letztes verbliebenes Exemplar in Konstruktionsbüros noch als Pinnwand für geplottete Zeichnungen.
- ---
- Vorteile:
- Die Technik des Reißbrettes kann wesentlich preiswerter als 2D-CAD-Technik sein. Es gab auch Untersuchungen, die zeigten, dass in der Entwurfsphase jene auf Papierbasis erstellten technischen Lösungen funktional besser und kreativer waren als solche, die am Computer entstanden. Gründe dafür mögen sein, dass man sich auf das Wesentliche einer Konstruktion konzentrieren kann, im Maßstab ein besseres Größengefühl hat und auf einem A0-Blatt einen besseren Überblick auf das Ganze haben kann als auf einem dazu relativ kleinen Ausschnitt auf einem Monitor.
- Ein eminenter Vorteil der Zeichenmaschine im Zeitalter sonst bewegungsarmer Computerarbeit ist außerdem die körperliche Bewegung in der Arbeit am „Brett“ sowie die Möglichkeit, gleichzeitig und effektiv an einer Zeichnung zu arbeiten, bzw. diese zu begutachten und mit anderen zu diskutieren.
- ---
- Nachteile:
- Nachteile der papiergebundenen Arbeitsweise liegen unbestreitbar in der schlechteren Genauigkeit und Reproduzierbarkeit, der geringeren Effizienz und der Unflexibilität, auf komplexe Änderungen schnell reagieren zu können. Zudem sind keine Automatisierungen oder sofortige digitale Zeichnungsverteilungen wie bei CAD-Systemen möglich.
- Ein Nachteil der Zeichenmaschine ist ihr Platzverbrauch von etwa zwei Metern Breite mitsamt der Beweglichkeit eines Storchenschnabels und einer Tiefe von meist deutlich über einem Meter, um den Tisch auch in die Waagerechte bringen zu können.
BM2184

Reißzeug, um 1750 - Reißzeug
- ---
- Reißzeug ist eine Zusammenstellung von Zeichengeräten für technische Zeichnungen, die daher auch Risse genannt werden. Um eine hohe Zeichnungsgenauigkeit zu erreichen, sind besonders dünne Linien erforderlich, die mit dem messerscharfen oder nadelspitzen Zeichengerät geritzt (gerissen) und erst bei Bedarf mit Tusche ausgezogen werden.
- Zum Reißzeug gehören in der Regel verschiedene Zirkel zum Abtragen von Kreisen und Ellipsen und die Reiß- oder Ziehfeder zum Ausziehen der Zeichnung mit feinstem Tuschestrich. Maßstab, Lineal, Dreiecke, ein meißelförmig angeschliffener harter Bleistift und die Kopiernadel zum Übertragen von bemaßten Punkten und Linien auf die Zeichnung ergänzen das Reißzeug.
- Ziehfeder und Ziehfedereinsätze für Zirkel wurden in den 1970er Jahren durch die Einführung von Tuschestiften verdrängt. Heute werden technische Zeichnungen am Computer erstellt. Das Reißzeug hat damit in diesem Bereich außer zur Bearbeitung sehr alter Zeichnungen keine Bedeutung mehr.
BM2185

Darstellung des Anreißens mittels eines Parallelreißers auf einer Anreißplatte 
Mehrere Reißnadeln 
Reißzirkel 
Anreißplatte 
Anreißwinkel - Anreißen
- ---
- Als Anreißen wird das Anbringen von Maßlinien oder Bohrpunkten auf einer Werkstückoberfläche durch Einritzen oder Zeichnen genannt.
- ---
- Prinzip:
- Maße für Bohrungen, Schnitte und andere Bearbeitungen werden in Form von Gravuren oder gezeichneten Linien auf das Werkstück aus Holz, Metall oder Stein aufgebracht. Genauso dient es der „Vermittlung“ von Formenumrissen bei gröberen Guss- und Schmiedeteilen und bei manuellen Brennschneideverfahren. Das Anreißen wird mit einem Stift, Kreide, einer Reißnadel oder einem Reißzirkel ausgeführt.
- Stifte und Kreide werden unter anderem benutzt, wenn ein Anritzen der Oberfläche vermieden werden muss (Schädigung der Fläche oder Rissbildung durch Kerbwirkung). Empfindliche Oberflächen oder solche, die keine Beschädigung erleiden sollen, können mit leicht lösbarem Papier beklebt werden, auf dem der Bleistiftriss erfolgt.
- Manchmal werden die angebrachten Reisslinien durch Körnerpunkte ergänzt, um sie nach diversen Bearbeitungsvorgängen, bei denen die Linien zunehmend undeutlich werden, noch sicher identifizieren zu können. Große Werkstückumrisse werden mit einem Doppelkörner (zwei dicht nebeneinanderliegende Spitzen) entlang der Anreißlinie markiert.
- Um den Riss auf metallischen Oberflächen besser sichtbar zu machen, werden spezielle dunkle, kupfersulfathaltige Lacke vor dem Anreißen auf das Werkstück aufgebracht und so die metallisch blanken Anrisse hervorgehoben. In der Praxis wird anstatt einer Anreißfarbe oft ein wasserfester Stift eingesetzt. Auch ist nass aufgetragene Schlämmkreide möglich, wenn grobe Teile mit größerer Ungenauigkeit verwendet werden.
- Das Anreißen durch das Nachziehen einer aufgelegten Kontur (Schablone) auf das Arbeitswerkstück erfolgt wie zuvor beschrieben. Ein bereits hoher Fertigungszustand kann durch eine Schablone auf das Werkstück projiziert werden. Gelegentlich werden dazu Pantografen zum Übertragen der Konturen im gleichen, größeren oder kleineren Maßstab verwendet.
- Das Anreißen hat auch unter Berücksichtigung des nachfolgenden Fertigungsverfahrens zu erfolgen. So ist festzulegen, ob beispielsweise beim Sägen der Anriss am fertigen Teil noch vorhanden sein muss oder nicht.
- Die erreichbare Genauigkeit des Anreißens beträgt ungefähr 0,1 mm.
- ---
- Werkzeuge:
- Alle Anreißwerkzeuge sind Bestandteil der Metalltechnik. Sie finden sich vor allem in Werkstätten mit Kleinstserien- und Einzelfertigung, aber auch im Werkzeugbau von Großbetrieben. Um eine sinnvolle Haltbarkeit (Metalltechnik: Standzeit) und eine erkennbare Ritzwirkung am Werkstück zu erreichen, sind diese Werkzeuge gehärtet oder tragen eine Spitze aus Hartmetall.
- ---
- Reißnadel
- Sie ist aus Stahl, Stahl mit Hartmetallspitze oder aus Messing. Typische Reißnadeln sind circa 20 bis 30 cm lang und haben einen Durchmesser von etwa 3 bis 4 mm. Meist sind sie beidseitig sehr lang angespitzt, wobei ein Ende nach circa 3 cm um 90 Grad abgewinkelt ist. Der Spitzenwinkel beträgt ungefähr 15 Grad. Typische Modelle haben in der Mitte als Griff eine Umhüllung aus einem zirka 10 cm langen, gerändelten Rohrstück. Andere Varianten sind wie Kugelschreiber mit Hartmetallspitze oder als einfache, längliche Nadel ausgeführt.
- Der Reißzirkel ist ein Zirkel, der wie eine Reißnadel Metallspitzen besitzt.
- Höhenreißer oder Parallelreißer dienen dem Anreißen von Hilfslinien, die parallel zur Auflagefläche des Höhenreißers verlaufen. Höhenreißer bestehen aus einem schweren Standfuß, auf dem vertikal ein Ständer mit Skala angebracht ist. Den Ständer umschließt eine mit Nonius oder digital arbeitende, vertikal bewegliche Einheit, dessen Reißnadel sich weiterhin mittels zweier Schrauben horizontal verstellen lässt.
- ---
- Anreißtisch bzw. Anreißplatte:
- Damit die Anreißlinie absolut gerade verläuft, werden Höhenreißer auf einer Anreißplatte oder einem Anreißtisch geführt, die aus Grauguss oder Granit bestehen. Sie weisen bei Beschädigungen keine Aufwölbungen auf und behalten somit eine hohe Ebenheit. Diese Tische stehen mitunter auf drei Beinen, um bei unebenem Boden nicht zu wackeln.
- Um das Führen des Parallelreißers zu erleichtern, wird Graphit in Flockenform auf den Anreißtisch gestreut.
- Es dürfen auf der Anreißplatte keine anderweitigen Werkzeuge oder Werkstücke abgelegt werden, da diese die Anreißplatte beschädigen könnten.
- ---
- Anreißwinkel:
- Anreißwinkel sind Vorrichtungen, die es gestatten, vorhandene Winkelmaße an Bauteilen zu ermitteln und diese Winkel an anderen Bauteilen zum Anreißen mittels Reißnadel zu übertragen.
- ---
- Nachteile:
- Reißnadeln und Anreißmesser können auf der Werkstoffoberfläche eine Kerbe erzeugen, die trotz ihrer geringen Ausdehnung Kerbeffekte/Kerbwirkungen auslösen können, die das Bauteil durch schwingende Belastung zerstören können. Dies gilt besonders für weiche Werkstoffe wie Aluminium und seine Legierungen. Im Flugzeugbau sind Reißnadeln daher nicht zulässig und werden durch spezielle Stifte ersetzt, die die Werkstoffoberfläche nicht einritzen oder einkerben können.
BM2186

Bild 1: Kavalierperspektive: Gartenmöbel 
Bild 2: Kavalierperspektive: Torbogen - in der Ansichtsebene (x-z-Ebene) nicht verzerrt 
Bild 3 
Bild 4: Kavalierperspektive eines runden Teils 
Bild 5: Explosionszeichnung in Kavalierperspektive 
Bild 6: Kavalierperspektive (von links unten) 
Bild 7: Würfel in Kavalierperspektive - mit verschiedenen Winkeln (Vielfache von 30° und 45° und ihre Kombination - Kavalierpespektive
- ---
- Die Kavalierperspektive wurde ursprünglich für Militärfestungen verwendet. Im Französischen ist ein „cavalier“ (Reiter; vgl. Kavallerie) ein künstlich angelegter Hügel hinter der Festungsmauer, der den Verteidigern erlaubt den Feind, der außerhalb der Mauern ist, zu beobachten. Die Kavalierperspektive war die Perspektive von diesem erhöhten Punkt.
- Eine andere Erklärung für den Namen „Kavalierperspektive“ ist, dass das die Perspektive ist, aus der ein Reiter vom Rücken eines Pferdes die Objekte am Boden sieht.
- ---
- Bei der Kavalierperspektive wird ein Punkt durch die drei Koordinaten x, y und z repräsentiert. In der Zeichnung wird ein Punkt dagegen nur durch zwei Koordinaten x und y repräsentiert. Auf der flachen Zeichenebene, stehen die beiden Achsen, x und z in der Zeichnung, senkrecht aufeinander. Und die Länge der Achsen in der Zeichnung sind im Verhältnis 1:1 (Maßstab 1:1). Die dritte Achse, die y-Achse, liegt diagonal, in einem bestimmten Winkel, gewöhnlich 30° oder 45°. Die Länge der dritten Achse hat einen anderen Maßstab.
- Die Kavalierperspektive ist sehr leicht auf mit dem Stift auf Papier zu zeichnen. Die Kavalierperspektive wird deshalb oft verwendet, wenn ein Körper mit der Hand gezeichnet werden soll.
- Die Kavalierperspektive ist eine Abart der Parallelprojektion, eine schräge Parallelprojektion. Dabei liegt die Ansichtsfläche rechtwinklig (frontal) zum Betrachter. Deshalb haben die beiden Dimensionen der Ansichtfläche (x- und z-Dimension) den gleichen Maßstab. Dageben wird die Tiefendimension (y-Dimension), die auf der Ansichtsfläche nicht dargestellt ist, verkürzt dargestellt.
- In der Höhe und Breite kann man die echte Höhe und Breite direkt aus der Zeichnung ablesen, währen nach hinten, ein anderer Maßstab gilt, gewöhnlich 1:2; 2:3 oder 3:4. Gewöhnlich wird mit einem Winkle von 45° nach hinten rechts in die Tiefe gezeichnet.
- Die x-Achse bildet mit der z-Achse einen Winkle von 90°. Die x-Achse bildet mit der y-Achse einen Winkel von 45°.
- In der Kavalierperspektive kann man sehr leicht einen Körper zeichnen. Dabei geht mon von seiner Vorderansicht aus und zeichnet zuerst alle Linien in x- und z-Richtung. Um die Tiefe darzustellen zeichnet man zum Schluss die Kanten in y-Richtung, ausgehend von den Eckpunkten der Vorderansicht.
- Weil sie leicht zu zeichnen ist, wird die Kavalierperspektive gerne in Darstellungen verwendet, obwohl diese Darstellungsart das tatsächliche Aussehen der Dinge nicht ganz genau widergibt. Die Kavalierperspektive verzichtet auf eine perspektivische Verkleinerung der Dinge in der Tiefe, also die Zentralprojektion, was dem wahren Sehen entsprechen würde.
- ---
- Vorgehen beim Zeichnen der Kavalierperspektive
- Um ein Objekt in der Kavalierperspektive zu zeichnen, verwendet man ein Geodreieck (Zeichendreieck), an das man ein LIneal im Winkel von 45° anlegt. Das Lineal dient als Stützlinie (Referenz) für das Geodreieck. Je nachdem, ob man die senkrechten oder wagerechten Linien der Vorderansicht zeichnet, wird das Geodreieck quer oder hochkant an das Lineal angelegt. Das Lineal wird wärend des gesamten Zeichenvorgangs nicht bewegt und fest auf die Unterlage angepresst. Lediglich das Zeichendreieck wird zum Zeichnen verschoben bzw. umgedreht.
- Die Linien für die Tiefe, die 45° nach hinten verlaufen, stehen senkrecht auf dem Lineal.
 |
 |
 |
 |
- ---

Bild 12 - Beispiel für die Kavalierperspektive:
- Als Beispiel für die Kavalierperspektive nehmen wir einen Würfel mit einem Kreis auf jeder Fläche. Die Kreise füllen die Fläche jeweils ganz aus, sie berühren also die Würfelkanten tangential.
- Wir legen für unsere Zeichnung fest, dass die y-Achse horizontal liegt, die z-Achse vertikal steht und die x-Achse mit der Horizontalen einen Winkel von 45° bildet. Der maßstab für die y- und z-Achsen soll 1:1 betragen, also den realen Maßen entspechen. In der x-Achse verringern wir den Maßstab um 50 %. Das Ergebnis ist Bild 12: Die Vorderseite (y- und z-Achse) ist in der Abbildung ein Quadrat und der Kreis ist ohne Verzerrung kreisrund dargestellt. Die verkürzt dargestellte Oberseite sowie die rechte Seite wird als Parallelogramm abgebildet, und die auf ihnen befindlichen Kreise werden als Ellipsen gezeichnet.
- Das ist die übliche Darstellung in der Kavalierperspektive: 45° Winkel für die Tiefe und ein um 50 % verkleinerter Maßstab für die Tiefe.
- Insgesamt gibt es aber 4 Möglichkeiten einen Körper in der Kavalierperspektive darzustellen:
- 1.) von rechts oben betrachtet (Bild 13),
- 2.) von links oben betrachtet (Bild 14),
- 3.) von links unten betrachtet (Bild 15),
- 4.) von rechts unten betrachtet (Bild 16).
 |
 |
 |
 |
BM2187

Bild 1 - Gegeben ist Punkt in der Dreitafelprojektion.
- Bild ein zeigt, wie man einen Punkt in der Kavalierperspektive darstellt. Erläutere die einzelnen Arbeitsschritte!
1. Lösung BM2187 - Aus den drei Abbildungen der Dreitafelprojektion entnehmen wir die drei Koordinaten des Punktes . Für die drei Koordinaten () würde uns eigentlich schon die Zweitafelprojektion reichen.
- ---
- Wir zeichnen ein Koordinatensystem in der Kavalierperspektive und tragen auf den drei Achsen die Einheiten an.
- Die y-Achse zeichnen wir im 45°-Winkel schräg nach oben links. Die Einheiten auf der y-Achse sind um die Hälfte Kürzer.
- Auf den drei Achsen markieren wir den x-, y- und z-Wert. Von diesen Punkten aus zeichnen wir jeweils parallel zu einer anderen Achse eine Hilfslinie (hier im Bild rot gestrichelt).
- Der Schnittpunkt der Hilfslinien ist unser gesuchter Punkt .
- ---
- In der Abbildung sind mehr Hilfslinien eingezeichnet, als erforderlich wären um einzuzeichnen.
- Wie viel mal mehr Hilfslinien sind eingezeichnet, als erforderlich wären?
- Wie viel verschieden Varianten gibt es, um die Lage von zu ermitteln?
BM2188

Bild 1: Axonometrie eines Hauses auf Karo-Papier 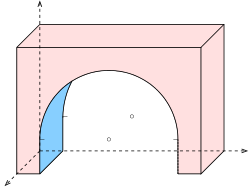
Bild 2: Torbogen (Kreise) in Kavalierprojektion - Axonometrie
- ---
- Die Axonometrie ist ein Verfahren in der darstellenden Geometrie, um relativ einfach räumliche Objekte in einer Zeichenebene darzustellen.
- Hierbei verwendet man die Koordinaten wesentlicher Punkte und die Bilder der drei Koordinatenachsen in einer Zeichenebene. Das Resultat ist für jede Wahl der Bildachsen bis auf eine Skalierung eine Parallelprojektion. Im Allgemeinen ergibt sich eine schiefe (oder schräge) Parallelprojektion. Nur bei besonderer Wahl der Bildachsen und der Verzerrungsverhältnisse ergibt sich eine orthogonale (oder senkrechte) Parallelprojektion, das heißt die Abbildungsstrahlen stehen senkrecht auf der Bildebene (s. orthogonale Axonometrie).
- ---

Bild 3: verschiedene Verzerrungen eines Einheitswürfels
(Bildebene parallel zur yz-Ebene)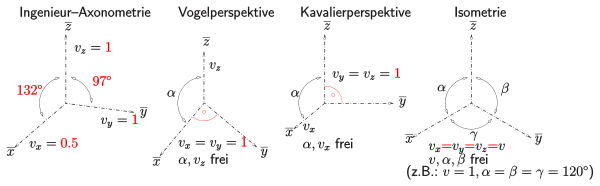
Bild 4: Parameter spezieller Axonometrien (die Militärprojektion ist eine Vogelperspektive) 
Bild 5: Parameter einer allgemeinen Axonometrie - Bildachsen und Verzerrungen
- ---
- Nur bei geeigneter Wahl von Bildachsen und Verzerrungen ist der Bildeindruck gut. Eine gute Bildwirkung erzielt man, wenn man die Bildachsen und die Verzerrungsverhältnisse so wählt, dass das Ergebnis eine senkrechte Parallelprojektion ist. Da man mit möglichst einfachen Verzerrungsverhältnissen (z. B.: 1 oder 0,5) arbeiten möchte, kann man sich bei der Wahl der Bildachsen und Verzerrungen an folgenden Beispielen (siehe Bild) orientieren. Hat man Karo-Papier zur Verfügung, so bietet sich die folgende Wahl für Achsen und Verzerrungen an: Zwei Koordinatenachsen fallen mit den Hauptrichtungen des Karo-Papiers zusammen, die dritte Achse verläuft in Richtung der Karo-Diagonalen (siehe Eingangsbild). Um die Konstruktion einfach zu halten, sollte man die Einheiten auf der waagrechten und senkrechten Achse zwei Kästchen und auf der Diagonalrichtung eine Kästchendiagonale als Einheit wählen. Das ergibt dann folgende Verzerrungen: gleich ≈ 0,7:1:1.

Bild 6: trimetrisch, dimetrisch, isometrisch - Axonometrien mit zwei gleichen Verzerrungen heißen dimetrisch, mit drei gleichen Verzerrungen isometrisch, ansonsten trimetrisch.
- ---
- Kavalierprojektion, Kabinettprojektion
- ---
- Bildebene parallel zur yz-Ebene
- Bemerkung: In der Literatur werden die Begriffe Kavalierperspektive und Kabinettperspektive nicht einheitlich definiert. Die obige Definition ist die allgemeinste. Oft werden weitere Beschränkungen gefordert: z. B.:
- Kabinettprojektion: zusätzlich und (Dimetrie),
- Kavalierprojektion: zusätzlich und (Isometrie),
- ---
- Isometrische Axonometrie
- ---

Bild 7: Beispiele in Standard-Isometrie: Würfel, Quader, Haus und Kugel - Bei der isometrischen Axonometrie, kurz: Isometrie, sind die Verzerrungen alle gleich. Die Winkel zwischen den Achsen-Bildern können noch frei gewählt werden.
- Bei der als Standard-Isometrie bezeichneten Darstellung gilt folgendes:
- (alle Achsen unverzerrt)
- , wobei die -Achse senkrecht ist
- Die Vorteile dieser Parameterwahl sind:
- Die Koordinaten können unverändert übernommen werden,
- Das axonometrische Bild ist eine um den Faktor skalierte Orthogonalprojektion (senkrechte Parallelprojektion). Daraus resultiert eine gute Bildwirkung und der Umriss einer Kugel ist ein Kreis.
- Zeichensysteme, wie z. B. xfig, bieten ein Dreiecksraster, um das Zeichnen von Objekten mit achsenparallelen Kanten zu erleichtern.
- Die „Nachteile“ sind:
- Ein Schönheitsfehler aufgrund der Symmetrie ist, dass zwei der 8 Eckpunkte eines achsenparallelen Würfels zusammenfallen (siehe Bild).
BM2189
Bild 1 - Auch in der der Dreitafelprojektion sind die Zeichnungen nicht immer eindeutig. (Bild 1)
- ---

Bild 2 
Bild 3 - 1.) Ein Körper zeigt in der Zweitafelprojektion den in Bild 2 dargestellten Umriss.
- Ist so ein Körper überhaupt möglich?
- Wie sieht dieser Körper aus?
- ---
- 2.) Ein Körper zeigt in der Dreitafelprojektion den in Bild 3 dargestellten Umriss.
- Ist so ein Körper überhaupt möglich?
- Wie sieht dieser Körper aus?
Lösung BM2189
- BM2190

Bild 1 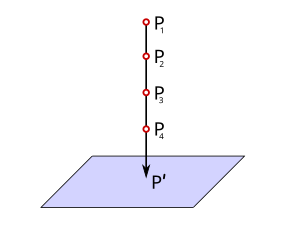
Bild 2 
Bild 3 - Projektion eines Punktes
- ---
- Projeziert man einen geometrischen Körper senkrecht auf eine Bildebene, so spricht man von senkrechter Eintafelprojektion.
- Das Bild nennt man Riss.
- Zur Unterscheidung von Bild und Original versehen wir die Bezeichnung des zum neuen Punkt gehörenden Bildes mit einem Strich .
- Den Riss erhalten wir, indem wir von jedem Eckpunkt des Körpers das Lot auf die Grundrissebene fällen. (Bild 4)
- Die Fußpunkte der Lote ergeben die Bildpunkte. Dabei können mehrere Eckpunkte denselben Bildpunkt haben.
- ---
- SATZ: Bei senkrechter Eintafelprojektion ist jedem Punkt des Raumes ein und nur ein (genau ein) Bildpunkt zugeordnet.
- ---
- Umgekehrt gilt jedoch:
- Bei senkrechter Eintafelprojektion kann jeder Bildpunkt unendlich viele Originalpunkte haben. (Bild 1 und 2)
- Das heißt: Die senkrechte Eintafelprojektion ist im Gegensatz zur Verschiebung, Dreheung oder Spiegelung nur eine eindeutige, aber keine eineindeutige (umkehrbar eindeutige) Abbildung.
- (eindeutige Abbildung; aber NICHT eineindeutige Abbildung)
- (Bild 3: eineindeutige Abbildung; umkehrbar eindeutige Abbildung; in beide Richtungen eindeutig)

Bild 4
BM2191 - BM2200
[editar]BM2191

Bild 1 
Bild 2 
Bild 3 - Projektion einer Strecke
- Projektion einer Geraden
- ---
- Betrachten wir die Lage einer Strecke bezüglich der Bildebene, so können wir drei Fälle unterscheiden:
- 1. Fall: Die Strecke liegt parallel zur Bildebenen. Der Riss ist kongruent zum Original. (Bild 1)
- 2. Fall: Die Strecke liegt geneigt zur Bildebenen. Der Riss ist kleiner als das Original. (Bild 2)
- 3. Fall: Die Strecke liegt senkrecht zur Bildebenen. Der Riss ist ein Punkt. (Bild 3)
- ---
- SATZ: Das Bild einer Strecke, die nicht senkrecht zur Bildebene liegt, ist bei senkrechter Eintafelprojektion wieder eine Strecke.
- ---
- Die Länge der Originalstrecke nennt man wahre Länge der Strecke.
- Unter dem Neigungswinkel einer Strecke versteht man den Winkel, den die Gerade mit der Bildebene einschließt.
BM2192

Bild 1 
Bild 2 - Höhenlinien und Falllinien
- ---
- Da die Bilder der Punkte einer geneigten Ebene die gesamte Bildebene ausfüllen. benutzt man zur Darstellung einer Ebene besondere Linien.
- Jede Gerade, auf der nur Punkte gleicher Höhe über der Bildebene liegen, heißt Höhenlinie. Jede Gerade in einer geneigten Ebene, die senkrecht zu den Höhenlinien dieser Ebene liegt, heißt Falllinie. Sie stellt den WEg dar, den eine Kugel auf einer geneigten Ebene zurücklegt, wenn man sie von einem Punkt der Ebene aus rollen lässt.
- Die Bilder der Höhenlinie einer geneigten Ebene liegen parallel zueinander. Diese Tatsache beruht auf dem Satz: Zueinander parallele Geraden, die nicht in Projektionsrichtung liegen, haben bei Parallelprojektion zueinander parallele Bilder.
- Das Bild einer Falllinie einer geneigten Ebene verläuft senkrecht zu den Bildern der Höhenlinie dieser Ebene.
- ---
- SATZ: Das Bild eines rechten Winkles ist bei senkrechter Parallelprojektion wieder ein rechter Winkel, wenn
- 1.) Wenigstens ein Schenkel parallel zur Bildebene verläuft und
- 2.) der andere Schenkel nicht senkrecht auf der Bildebene steht.
 |
 |
 |
 |
 |
 |
 |
 |
BM2193
- Grund- und Aufriss eines Punktes
- ---
- Wir haben in den meisten Fällen die Bildebene in horizontaler Lage angenommen, obwohl das nicht nötig ist. Eine Ausnahme bildet z. B. die Kavalierperspektive, wo die Bildebenen vertikal angenommen wurde.
- In dem speziellen Fall, in dem die Bildebene horizontal liegt, wollen wir künftig den Riss als Grundriss und die Bildebene als Grundrissebene bezeichnen.
- Wie wir wissen, liefert die Projektion eines Punktes ein eindeutiges Bild:
- Jedem Originalpunkt ist genau ein Bildpunkt zugeordnet.
- aber:
- Einem Bildpunkt können viele Originalpunkte zugeordnet sein.
- In der Eintafelprojektion erzielen wir Eindeutigkeit durch Beifügen eines Höhenmaßstabes. Für die Eintafelprojektion mit Höhenmaßstab gilt:
- Jedem Originalpunkt ist genau ein Bildpunkt zugeordnet.
- und:
- Jedem Bildpunkt ist genau ein Originalpunkt zugeordnet.
- ---
- Wir können auch Eindeutigkeiten erzielen, indem wir dem Grundriss an Stelle eines Höhenmaßstabs einen zweiten Riss auf einer Bildebene beifügen, die zur ersten Bildebene senkrecht steht. Dieses Verfahren heißt senkrechte Zweitafelprojektion.

Bild 1 - Im Bild 1 wird dieses Verfahren am Modell einer Pyramide veranschaulicht.
BM2194
- Logarithmus
- ---
- Die Umkehroperation der Addition ist die Subtraktion:
- ---
- Die Umkehroperation der Multiplikation ist die Division:
- ---

Logarithmentafel 
Rechenschieber 
Logarithmus-Taste am wiss. Taschenrechner
- Die Umkehroperation des Potenzierens - einer Variablen - ist das Wurzelziehen:
- ---
- Die Umkehroperation des Potenzierens - mit einer Variablen - ist das Logarithmieren:
- ---
- Das Wurzelziehen und Logarithmieren wird in späteren Lektionen noch sehr ausführlich erläutert und geübt werden.
- Hier erfolgt erst mal nur eine erste Einführung in das Logarithmieren.
- ---
- Wie für das Wurzelziehen, so gibt es auch für das Logarithmieren keine einfachen Rechenverfahren, wie wir sie von den vier Grundrechenarten () kennen.
- Heute erfolgt das Logarithmieren mit dem Taschenrechner.
- Früher gab es dafür Tabellen. Später auch den Rechenschieber.
BM2195
- (lies: Logarithmus zur Basis ist gleich )
- ---
- (lies: Logarithmus zur Basis ist gleich )
- ---
- (lies: Logarithmus zur Basis ist gleich )
- ---
- Als Logarithmus (Plural: Logarithmen; von altgriech. „Verständnis, Lehre, Verhältnis“, und arithmós, „Zahl“) einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl zu erhalten. Logarithmen sind nur für positive reelle Zahlen definiert, auch die Basis muss positiv sein.
- Der Logarithmus einer positiven reellen Zahl zur Basis ist also der Wert des Exponenten, wenn als Potenz zur Basis dargestellt wird, also diejenige Zahl , welche die Gleichung
- löst.
- Man schreibt .
- ---
- Das Logarithmieren, d. h. der Übergang von zu , ist damit eine Umkehroperation des Potenzierens.
- ---
- Mit Logarithmen lassen sich sehr stark wachsende Zahlenreihen übersichtlich darstellen, da der Logarithmus für große Zahlen viel langsamer steigt als die Zahlen selbst.
- ---
- Wegen der Rechenregel kann man durch Logarithmieren eine Multiplikation durch die viel weniger rechenintensive Addition ersetzen.
- Auch beschreiben Logarithmen auf mathematisch elegante Weise viele technische Prozesse sowie Phänomene der Natur wie etwa das Verhalten einer Halbleiter-Diode, die Spirale eines Schneckenhauses oder die Wahrnehmung unterschiedlicher Lautstärken durch das menschliche Ohr.
- ---
- Der Logarithmus wurden in Tabellenwerken, den Logarithmentafeln, erfasst, um sie nachschlagen zu können und nicht immer neu berechnen zu müssen. Diese Tabellen wurden schließlich durch Rechenschieber und später durch Taschenrechner verdrängt. Der Wechsel von den Tabellen zum Rechenschieber erfolgte in deutschen Schulen in den 1960er Jahren, der Wechsel zu Taschenrechnern ab den 1970er Jahren.
- ---
- Logarithmen erlangten ihre historische Bedeutung durch den Zusammenhang
- der es erlaubt, eine Multiplikation durch eine Addition auszudrücken.
- Formal sind Logarithmen alle Lösungen der Gleichung
- zu vorgegebenen Größen und .
- Je nachdem, über welchem Zahlenbereich und für welche Größen diese Gleichung betrachtet wird, hat sie keine, mehrere oder genau eine Lösung. Ist die Lösung eindeutig, dann wird sie als der Logarithmus von zur Basis bezeichnet und man schreibt
- Beispielsweise ist der Logarithmus von 8 zur Basis 2 gleich 3, geschrieben , denn es ist .
BM2196
- Logarithmus:
- zur Basis 10 (Zehnerlogarithmus)
- zur Basis 2 (Zweierlogarithmus)
- mit der Basis (natürlicher Logarithmus)
- (Die Eulersche Zahl ).
- (Viele Taschenrechner haben für die Zahl eine eigene Taste.)
- ---

Bild 1 - Der Logarithmus von zu Basis 10 ist gleich .
- ---
- Der Logarithmus von zu Basis 2 ist gleich .
- ---
- Der Logarithmus von zu Basis ist gleich .
- ---
- Wird die Eulersche Zahl – die im Jahre 1728 von Leonhard Euler (1707–1783) bestimmt und erstmals 1742 veröffentlicht wurde – als Basis des Logarithmus verwendet, so nennt man ihn den natürlichen Logarithmus. Der natürliche Logarithmus wird dabei durch „ln“ abgekürzt.
- ist das Gleiche wie
- ---
- Beispiele:
- , denn
- , denn
- , denn
- , denn
- ---
- , denn
- , denn
- , denn
- , denn
- , denn
BM2197
- Bezeichnungen
- ---
- Man schreibt für den Logarithmus von zur Basis
- und sagt: „x ist der Logarithmus von a zur Basis b.“ heißt Numerus oder veraltet auch Logarithmand.
- Das Ergebnis des Logarithmierens gibt also an, mit welchem Exponenten man die Basis potenzieren muss, um den Numerus zu erhalten.
- Für die Vorkommastellen des Logarithmus wird meist der Begriff Charakteristik (manchmal auch Kennzahl) verwendet, seine Nachkommastellen werden Mantisse genannt.
- Das allgemeine mathematische Zeichen für den Logarithmus gemäß DIN 1302. Seltener findet man auch davon abweichende Schreibweisen, wie zum Beispiel .
- Das Zeichen ohne eine angegebene Basis wird verwendet, wenn die verwendete Basis keine Rolle spielt, wenn diese getrennt vereinbart wird, aus dem Zusammenhang ersichtlich ist oder aufgrund einer Konvention festgelegt ist. In technischen Anwendungen (so z. B. auf den meisten Taschenrechnern) steht oft für den dekadischen Logarithmus. In theoretischen Abhandlungen, insbesondere zu zahlentheoretischen Themen, steht oft für den natürlichen Logarithmus.
- Darüber hinaus sind für den Logarithmus in DIN 1302 je nach Anwendung spezielle Schreibweisen festgelegt:
- Natürlicher Logarithmus (lat. logarithmus naturalis), der Logarithmus zur Basis , der Eulerschen Zahl 2,7182818… Er wird im Zusammenhang mit Exponentialfunktionen verwendet.
- Dekadischer Logarithmus, auch als Zehnerlogarithmus oder Briggsscher Logarithmus bezeichnet, der Logarithmus zur Basis 10. Er wird bei numerischen Rechnungen im Dezimalsystem verwendet.
- Binärer Logarithmus, auch als Zweierlogarithmus bezeichnet, der Logarithmus zur Basis 2. Er wird in der Informatik bei Rechnungen im Binärsystem verwendet. Außerhalb der Norm wird mit gleicher Bedeutung auch – logarithmus dualis – verwendet.

Bedienelemente an einem Taschenrechner. Die Taste LOG steht herstellerübergreifend für den Logarithmus zur Basis 10, LN berechnet den natürlichen Logarithmus zur Basis e. Darüber hinaus ist als zweite Belegung der jeweiligen Tasten die entsprechende Umkehrfunktion vorgesehen (gelbe Beschriftung jeweils oberhalb), die Exponentialfunktion zur Basis 10 oder e.
BM2198
- Definition des Logarithmus als Umkehrfunktion der Exponentialfunktion
- ---
- Der Logarithmus zur Basis ist die Umkehrfunktion der allgemeinen Exponentialfunktion zur positiven Basis :
- Die Funktionen und sind also Umkehrfunktionen voneinander, d. h. Logarithmieren macht Exponenzieren rückgängig und umgekehrt:
- Der natürliche Logarithmus ergibt sich mit der Basis , wobei
- die Eulersche Zahl ist.
BM2199
- Logarithmengesetze
- ---
- Im Folgenden wird stets vorausgesetzt, dass die Variablen von Null verschieden sind; im Falle des reellen Logarithmus werden die Zahlen sogar als positiv vorausgesetzt. Die Basen des Logarithmus dürfen ferner nicht 1 sein.
- ---
- Produkte:
- Für das Rechnen mit Logarithmen von Produkten steht die hilfreiche Rechenregel
- zur Verfügung;
- Der Logarithmus eines Produkts ist die Summe der Logarithmen der Faktoren.
- ---
- Quotienten:
- Die Quotienten leiten sich direkt aus den Logarithmen von Produkten ab. Hier sei nur der einfache Fall
- angegeben. Der Logarithmus eines Quotienten ist der Logarithmus des Zählers minus den Logarithmus des Nenners .
- Insbesondere ergibt sich daraus (da ):
- Allgemeiner ergibt sich direkt aus der obigen Quotientenregel das Reziprozitätsgesetz:
- ---
- Potenzen:
- Für Potenzen mit reellem Exponent gilt die Regel
- Der Logarithmus einer Potenz ist also das Produkt aus dem Exponenten mit dem Logarithmus der Basis.
- Auch daraus lässt sich für
- ermitteln.
- Der Logarithmus eines Stammbruchs ist der negative Logarithmus des Nenners .
- Diese Rechenregeln lassen sich von den Potenzgesetzen ableiten.
- ---
- Wurzeln:
- Da Wurzeln nichts anderes als Potenzen mit gebrochenem Exponenten sind, ergibt sich nach der oben angegebenen Potenzregel des Logarithmus die Rechenregel
- ---

Bild 1 
Bild 2 
Bild 3: Lies die Zahlenwerte ab!
BM2199a
- Basisumrechnung von Logarithmen
- ---
- Um Logarithmen zur Basis mithilfe von Logarithmen einer beliebigen Basis zu berechnen, verwendet man den Zusammenhang
- denn mit gelten die Umformungen
- Damit sieht man, dass sich Logarithmen zu verschiedenen Basen nur um einen konstanten Faktor voneinander unterscheiden. Die meisten Tabellenwerke stellen Logarithmen nur zur Basis 10 zur Verfügung, Taschenrechner auch zur Basis e (den natürlichen Logarithmus). Mit obiger Formel lassen sich daraus Logarithmen zu einer beliebigen Basis berechnen.
- Ein prominenter Spezialfall, der sich aus obiger Formel ergibt, lautet:
- oder
- Beispiel:
BM2199b
- Logarithmenpapier
- ---

- Logarithmenpapier (auch logarithmisches Papier) gehört zu den mathematischen Papieren (auch: Netzpapier) und ist mit einem Koordinatennetz überzogen, so dass auf ihm Koordinaten auf einfache Weise dargestellt werden können.
- Es kann entweder für eine oder beide Achsen die logarithmische Achseinteilung verwendet werden.
- Durch die Möglichkeit, grafische Darstellungen auch aus Computerprogrammen heraus zu erzeugen, nimmt die Bedeutung solcher Spezialpapiere ab.
- ---
- Einfachlogarithmisches Papier:
- Einfachlogarithmisches Papier oder auch halblogarithmisches Papier ist mit einem speziellen Koordinatennetz versehen, das entweder waagerecht oder senkrecht logarithmisch geteilt ist. Das bedeutet, die tatsächliche Abmessung ist der Logarithmus der angeschriebenen Zahl.
 |
 |
- ---
- Doppeltlogarithmisches Papier:
- Doppeltlogarithmisches Papier ist mit einem speziellen Koordinatennetz versehen, das sowohl waagerecht als auch senkrecht logarithmisch geteilt ist. Das bedeutet, die tatsächliche Abmessung ist der Logarithmus der angeschriebenen Zahl.
BM2199c
- Logarithmen
- ---
- Bisher stellten wir uns die Frage, was ist ? Nämlich 100!
- Ebenfalls fragten wir uns, was ist ? In diesem Fall die 10!
- ---
- Welcher Exponent gehört zur Basis, in unserem Fall der 10, damit 100 rauskommt?
- Dieses mathematische Problem ist mit dem Logarithmus zu lösen. Mathematisch geschrieben, sähe die Fragestellung so aus:
- ?
- Wenn man statt des Fragezeichens wie üblich ein x schreibt , dann lautet die Frage : Was ist x in der folgenden Gleichung:
- 10x = 100
- oder
- x =
- Allgemein :
- mit x: Logarithmus , a: Basis, b: Numerus
- Man liest : x ist gleich der Logarithmus der Zahl b zur Basis a
- Eine andere oft benutzte Darstellung von a log b ist logab.
- Aus
- 10x = 100
- wird dann
- x = log10100 = 2
- ---
- Beispiele:
- Am einfachsten zu verstehen ist der Logarithmus zu Basis 10, wenn man die Zahlen 10, 100, 1000, 10000 etc betrachtet. Der Logarithmus ist dann einfach die Anzahl der Nullen hinter der 1.
- ,
- denn 101 = 10
- ,
- denn 102 = 100
- ,
- denn 103 = 1000
- ,
- denn 104 = 10000
- ---
- Nicht viel schwieriger ist der duale oder binäre Logarithmus:
- ,
- denn 21 = 2
- ,
- denn 22 = 4
- ,
- denn 23 = 8
- Hat man das Prinzip einmal begriffen, dann kann man auch den Logarithmus zu einer anderen Basis leicht verstehen:
- ,
- denn 42 = 16
- ,
- denn 34 = 81
- Man sieht das allgemeine Prinzip des Logarithmus: Große Zahlen kann man mit seiner Hilfe in kleine Zahlen umwandeln.
- ---
- Logarithmensysteme:
- Es gibt gewisse Regeln, die man sich einfach merken sollte, um sich das Leben mit den Logarithmen zu vereinfachen. So können wir immer sagen, dass der Logarithmus von 1 für jede Basis 0 ist. Denn wir wissen ja, dass eine Basis hoch 0 immer 1 ergibt.
- Der Logarithmus mit gleicher Basis und gleichem Numerus ist immer 1
- Der Logarithmus von Null ist eine Ausnahme, sein Grenzwert strebt ins negativ Unendliche.
- , denn
- Logarithmen mit gleicher Basis bilden ein Logarithmensystem
- , denn ax = ax.
- ---
- Basis:
- Als Basis werden am häufigsten folgende Zahlen verwendet: 2,e,10
- dualer oder binärer Logarithmus
- Basis b = 2
- (2er Logarithmus) abgekürzt als ld oder lb
- natürlicher Logarithmus
- Basis b = e = 2,718281828459...
- abgekürzt als ln
- dekadischer oder zehner Logarithmus
- Basis b = 10
- abgekürzt als lg
- ---
- Basisumwandlung:
- Viele Taschenrechner können nur den Logarithmus zur Basis 10 bestimmen (dekadischer Logarithmus).
- Oftmals ist es daher nützlich, verschiedene Basen ineinander umzuwandeln.
- Dies geschieht nach folgendem Gesetz:
- logna=logma/logmn
- ---
- Dekadischer Logarithmus zur Basis 10:
- Um die Rechnung zu vereinfachen, wählte man per Definition die Basis 10. Man nennt diese Logarithmen Briggsche, dekadische oder gewöhnliche Logarithmen.
- Die Basis 10 muss an diese Logarithmen nicht dran geschrieben werden. Allerdings
- schreibt man nun statt log nur noch lg
- ---
- Logarithmengesetze
- ---
- Produkt innerhalb des Logarithmus:
- Wenn wir ein Produkt logarithmieren, so dürfen wir es auch als Summe zweier Logarithmen beschreiben.
Ein kleines Beispiel :-
- , denn 103 = 1000
-
- ---
- Brüche innerhalb des Logarithmus:
- Man glaubt es kaum, aber ein Bruch wird nun, statt wie bei der Multiplikation addiert, nun voneinander
subtrahiert. - ---
- Potenzen innerhalb Logarithmen:
- Wird der Numerus potenziert, so darf man die Potenz mit der Basis multiplizieren.
- ---
- Wurzeln innerhalb Logarithmen:
- Eine Wurzel wird logarithmiert, indem man den Logarithmus der Basis durch den Wurzelexponenten
- dividiert.
BM2199d
- (mit )
- ---
- = Basis
- = Numerus (oder Logarithmand)
- = Logarithmus von a zur Basis b
- ---
- Rechenregeln:
- 1.)
- 2.) , denn
- 3.) , denn
- 4.) , denn
- 5.) , denn
- 6.)
- 7.)
- 8.)
- 9.)
- 10.)
BM2199e
- 1.)
- 2.)
- 3.)
- 4.)
- 5.)
- 6.)
- 7.)
BM2199f
- Binärer Logarithmus; Binäre Logarithmen;
- ---
- Natürlicher Logarithmus; Natürliche Logarithmen;
- ---
- Dekadischer Logarithmus; Dekadische Logarithmen;
BM2199g
- Mantisse
- ---
- Als Mantisse bezeichnet man die Ziffernstellen einer Gleitkommazahl vor der Potenz.
- Beispiel: Bei der Zahl 2,9979 · 108 ist 2,9979 die Mantisse.
- ---
- Mantisse bei Logarithmen:
- Bei der Arbeit mit dekadischen Logarithmen ist es auch üblich, nur die Nachkommastellen als Mantisse zu bezeichnen. Der Grund dafür ist, dass sie es sind, die die Folge der Ziffern der logarithmierten Zahl bestimmen, während die Stellen vor dem Komma für ihren Exponenten stehen.
- Beispiel: Der dekadische Logarithmus von 2,9979 · 108 ist gleich log(2,9979) + log(108) = 0,4768 + 8 = 8,4768. Der auf seine Nachkommastellen reduzierte Logarithmus 0,4768 ist der Logarithmus der Mantisse 2,9979. Die Vorkommastellen des Logarithmus ergeben die ganze Zahl 8, den Exponenten von 108.
BM2199h
- Dekadischer Logarithmus
- ---
- Der dekadische Logarithmus oder Zehnerlogarithmus ist der Logarithmus zur Basis 10. Die mathematische Schreibweise für den dekadischen Logarithmus einer Zahl ist gemäß DIN 1302.
- oder
- Seine Umkehrfunktion ist , das heißt ist gleichbedeutend mit
- Die Schreibweise (ohne Basis) ist mit widersprüchlichen Bedeutungen belegt, wird in der Praxis aber dennoch mitunter für den dekadischen Logarithmus verwendet.
- Logarithmentabellen erleichterten das Rechnen, bevor in den 1970er Jahren Taschenrechner zu einem weitverbreiteten Hilfsmittel wurden. In den Anhängen vieler Bücher fanden sich Logarithmentafeln, die für alle Zahlen von 1 bis 10 in Schritten von beispielsweise 0,01 oder 0,001 den Wert des dekadischen Logarithmus auflisteten. Es mussten nur die Werte für Zahlen von 1 bis 10 gedruckt werden, da sich die Werte für andere Zahlen wie im folgenden Beispiel berechnen lassen. Liest man etwa in der Tabelle ab, dass gilt, so folgt
- .
- Der dekadische Logarithmus wird nach Henry Briggs auch Briggsscher Logarithmus genannt.
BM2199i
- Antilogarithmus
- ---
- Antilogarithmus ist eine englische umgangssprachliche Bezeichnung für die Exponentialfunktion zur Basis 10.
- Wird mit Hilfe von Logarithmentafeln eine Multiplikation oder Division durchgeführt, werden die Logarithmen der Faktoren addiert bzw. die Logarithmen von Dividend und Divisor subtrahiert. Das Ergebnis erhält man dann durch "antilogarithmieren". Andere Bezeichnungen für "antilogarithmieren" sind "delogarithmieren", "entlogarithmieren" und "exponenzieren".
- Auf diesem Prinzip beruht der Rechenschieber.
- ---
- Beispielrechnung:
- Die Division 12345678 durch 23456 soll ausgeführt werden. Zuerst wird zur Basis 10 logarithmiert, wodurch wir 7,0915 und 4,3703 erhalten. Die Subtraktion ergibt 2,7212, durch den Antilogarithmus erhalten wir das Ergebnis 526,3.
- ---
- Herleitung
- Multiplikation:
- Division:
BM2200
- ---
- ---
- Beispiele:
- und , also ist
- Kontrolle:
- ---
- , wegen :
- ---
- Beispiel:
- und
- índice
- Lección 093b ← Lección 094b → Lección 095b
- Lección 094






























































































































![[2] Abbildung mit zwei Fluchtpunkten](http://upload.wikimedia.org/wikipedia/commons/thumb/1/18/2-punktperspektive.svg/180px-2-punktperspektive.svg.png)
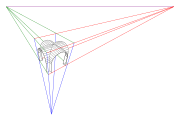

















































































































































![{\displaystyle \log _{b}{\sqrt[{n}]{x}}=\log _{b}\left(x^{\frac {1}{n}}\right)={\frac {1}{n}}\log _{b}x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67539e2acb1a493452d8ddd9912c8b2631d8b0d2)


































![{\displaystyle \lg \left({\sqrt[{a}]{b}}\right)={\frac {\lg b}{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb88dba3e9b503ee764fc8eb46052805ebb8de24)















![{\displaystyle log_{b}{\sqrt[{n}]{a}}=log_{b}{(a^{\tfrac {1}{n}})}={\tfrac {1}{n}}\cdot log_{b}{a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beaa0a5613e93282cb34e639176d7298c596a698)






![{\displaystyle log_{2}{\sqrt[{4}]{\tfrac {1}{16}}}={\tfrac {1}{4}}\cdot log_{2}{\tfrac {1}{16}}={\tfrac {1}{4}}(-4)=-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7ac00924cdfab209141422841e500005c50b090)





























