Curso de alemán para principiantes con audio/Lección 060b
Apariencia
- índice
- Lección 059b ← Lección 060b → Lección 061b
- Lección 060
- Mathematik auf Deutsch - 10
BM451 - BM460
[editar]BM451
- Dividiere durch 10!
- ---
- 90
- 160
- 560
- 800
- 1.500
- 10.000
BM452
- Berechne das Doppelte der Zahlen 16.420
- 600
- 2.400
- ---
- Dividiere durch 100!
- 800
- 2.300
- 6.000
- 7.500
- 10.000
- ---
- Berechne die Hälfte der Zahlen
- 80
- 460
- 5.200
- 10.000
BM453
- 1 km = 1.000 m = 10.000 dm = 100.000 cm = 1.000.000 mm
- 1 m = 100 cm = 1.000 mm
- 10 cm = 100 mm
- 1 cm = 10 mm
- ---
- Treten in Längenangaben zwei Einheiten auf, kann man auch die größere von beiden Einheiten in die kleinere umrechnen.
- ---
- 7 m 80 cm oder 7,80 m
- 7 km 850 m oder 7,850 km
- ---
- Rechne in die jeweils kleiner Einheit um!
- 3 cm 7 mm
- 7 m 80 cm
- 5 m 40 cm
- 6 m 5 cm
BM454
- Rechne in Zentimeter um!
- 2 m
- 20 m
- 5 m
- 9 m
- 10 m
- 8 m
- ---
- Rechne in Meter um!
- 3 km
- 8 km
- 10 km
- 30 km
- 4 km
- 17 km
- ---
- Rechne in Zentimeter um!
- 4 m
- 9 m
- 6 m
- 5 m
- 10 m
- 14 m
BM455
- Gib in Zentimeter an!
- 80 m
- 76 m
- 3 m 70 cm
- 8 m 5 cm
- 9 m 20 cm
- 4 m 90 cm
- 4 m 5 cm
- --
- Rechne folgende Längenangaben jeweils in die kleinere Einheiten um!
- 3 cm 7 mm
- 8 cm 4 mm
- 1 cm 8 mm
- 9 cm 1 mm
- 4 m 35 cm
- 12 m 75
- 26 m 18 cm
- 5 km 350 m
- 7 km 240 m
- 9 km 75 m
- 2 km 55 m
- 5 m 5 cm
- 5 m 8 cm
- 10 m 5 cm
BM456
- Gib den 100. Teil an!
- 5 Euro
- 3 kg
- 8 t
- 40 cm
- 8 g
- 6 m
- 4 km
- ---
- viestellige Zahlen
- Die Zahlen von 1.000 bis 9.999 nennt man vierstellig Zahlen.
- ---
- fünfstellige Zahlen
- 46.304
- --
- sechsstelligen Zahlen
- 375.084
BM457
- Stellentafel
- ---
- Die Zahlen 2.000; 300; 40, 5 und 2.379 sind in einer Stellentafel eingetragen.
- ---
103 102 101 100 1000 100 10 1 2 0 0 0 3 0 0 4 0 5 2 3 7 9
- Die Stellentafel enthält für jede Zehnerpotenz eine Spalte. Es werden nur die Faktoren der Zehnerpotenzen eingetragen:
- 2.379
- 2 * 103 + 3 * 102 + 7 * 10 + 5 * 1
- Die Summanden sind Produkte aus einstelligen Zahlen und 103, 102, 10 und 1.
- ---
- Wenn in einer Zahl ein Faktor mit einer Zehnerpotenz Null ist, so wird in der Zifferndarstellung an dieser Stelle die Ziffer „0“ geschrieben.
BM458
- Bestimme jeweils den Vorgänger und den Nachfolger!
- ---
- 9.999
- 4.001
- 10.000
- 79.000
- 80.100
- 8.089
- 90.001
BM459
- Sechsstellige Zahlen
- Die Zahlen von 100.000 bis 999.999 sind sechsstellig
- ---
- 3 * 100.000 + 45.789 = 300.000 + 45.789
- 3 * 100.000 + 45.789 = 345.789
- ---
- Zerlege 873.568 in Summanden!
- 873.568 = 800.000 + 70.000 + 3.000 + 500 + 60 + 8
- ---
- Zerlege 873.568 in Summanden von Produkten!
- 873.568 = 8 * 100.000 + 7 * 10.000 + 3 * 1.000 + 5 * 100 + 6 * 10 + 1 * 8
- 873.568 = 8 * 105 + 7 * 104 + 3 * 103 + 5 * 102 + 6 * 101 + 1 * 100
BM460
- Bestimme jeweils den Vorgänger und den Nachfolger!
- ---
- 500.000
- 700.000
- 456.999
- 347.999
- 915.999
- 706.201
- 880.900
- 240.000
- 500.190
- 589.989
- dreizehnhundert
- dreizehntausenddreizehnhundertdreizehn
- ---
- Wie viel ist die Hälfte von siebzehntausendelfhundertfünfzehn?
BM461 - BM470
[editar]BM461
- Ermittle jeweils die kleinste und die größte Zahl, die folgende Ungleichungen erfüllen!
- ---
- 100.000 < x < 1.000.000
- 345.000 < x < 445.000
- 200.000 < x < 900.000
- 270.000 < x < 720.000
BM462
- Einheiten der Masse
- ---
- 1 g = 1.000 mg
- 1 kg = 1.000 g
- 100 kg = 100.000 g
- 1 t = 1.000 kg = 1.000.000 g
- ---
- 7 kg und 500 g
- 7,5 kg (rechts neben dem Komma steht jeweils die Angabe in der nächstkleineren Einheit)
- ---
- 12,500 t bedeutet 12 t und 500 kg.
- Für 12,500 t schreibt man oft 12,5 t
- ---
- 12 t = 12,000 t
- Nullen hinter dem Komma (Rechts vom Komma können weggelassen werden, wenn danach keine andere Ziffer mehr folgt.)
- Aber 4,005 t ist NICHT gleich 4,5 t.
- ---
- 7,500 g bedeutet 7 g 500 mg
- Für 7,500 g schreibt man 7,5 g.
BM463
- Rechne in Milligramm um!
- 3g
- 10 g
- 6 g
- 50 g
- 8 g
- 100 g
- ---
- Rechne in Gramm um!
- 7.000 mg
- 7,000 mg
- 53.000 mg
- 10.000 mg
- 65.540 mg
- ---
- Rechne in Milligramm um!
- 2 g 300 mg
- 3 g 50 mg
- 5 g 750 mg
- 7 g 5 mg
- ---
- Rechne in Milligramm um!
- 3 g 200 mg
- 6 g 89 mg
- 12 g 530 mg
- 2 g 9 mg
BM464
- 100 g Weißkohl enthalten 40 mg Vitamin C.
- Eine Vitamintablette enthält 50 mg Vitamin C.
- Wie viele Tabletten entsprechen dem Vitamingehalt von einem Kilogramm Weißkohl?
- ---
- 100 g Hagebutten enthalten 400 mg Vitamin C.
- Es gibt Dragees mit je 200 mg Vitamin C.
- Wie viel Dragees entsprechen dem Vitamingehalt von einem Kilogramm Hagebutten?
- ---
- Wie viel Tüten mit 10 g „Heroin“ kann man aus 1 kg, aus 10 kg, aus 100 kg, aus einer Tonne Heroin füllen, wenn das Heroin beim Abpacken zur Hälfte mit Milchpulver gestreckt wird?
BM465
- Schreibe 102, 103, 104, 105, 106 als Produkte mit den Faktoren 10.
- Beispiel: 102 = 10 * 10
- ---
- 106 = 1.000.000 (eine Million)
- 107 = 10.000.000 (zehn Millionen)
- 108 = 100.000.000 (einhundert Millionen)
- 109 = 1.000.000.000 (eine Milliarde)
- 1010 = 10.000.000.000 (zehnMilliarden)
- ---
- Eine Milliarde = 1.000 Millionen
- ---
- Wenn man die Zahl 1 mit 10 multipliziert (1 * 10), dann das Produkt wieder mit 10 und so fort multipliziert (1 * 10 * 10 * 10 * ...), dann erhält man nacheinander alle zehnerpotenzen.
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- ---
- 101 = 10
BM466
- Die Stellentafel wird erweitert:
Milliarden Millionen Tausend 1011 1010 109 108 107 106 105 104 103 102 101 100 ... ... 1 Mrd. ... ... 1 Mill. ... ... 1.000 100 10 1
BM467
- 109 = 1.000.000.000 (eine Milliarde hat 9 Nullen)
- 1010
- 1011
- 1012 = 1.000.000.000.000 (eine Billion hat 12 Nullen)
- ---
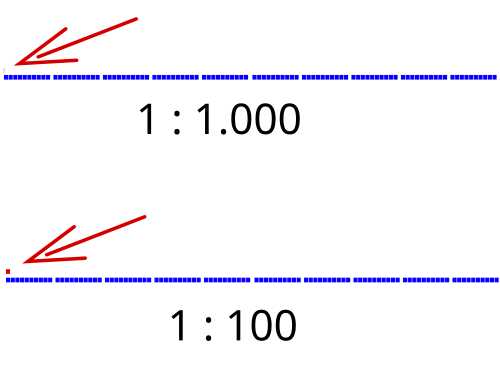
- Viele Menschen denken im ersten Moment, dass eine Milliarde gleich 100 Millionen ist. (also: 100 : 1)
- Aber eine Milliard ist gleich 1.000 Millionen. (also: 1.000 : 1)

BM468
- Gib die Differenz zur nächstgrößere Einheit an!
- ---
- 50 kg
- 80 kg
- 99 kg
- 500 g
- 560 g
- 780 mg
- 890 m
- 5 cm
- 3 mm
BM469
- Wie heißen die Zahlen?
- --
- 4 * 105 + 5 * 104 + 7 * 103 + 3 * 102 + 6 * 101 + 7 * 100
- --
- 9 * 104 + 0 * 103 + 6 * 102 + 3 * 101 + 4 * 100
- --
- 9 * 108 + 3 * 107 + 0 * 106 + 4 * 105 + 5 * 104 + 8 * 103 + 0 * 102 + 0 * 101 + 5 * 100
BM470
- Dividiere durch 10!
- 50
- 7.000
- 35.000
- 892.000
- ---
- Dividiere durch 100!
- 800
- 9.000
- 23.500
- 360.000
- ---
- Dividiere durch 1.000!
- 7.000
- 60.000
- 836.000
- 780.000
BM471 - BM480
[editar]BM471
- Subtrahiere von 100.000!
- 25.000
- 85.000
- 60.500
- ---
- Schreibe die Zahl auf, die um 52.900 größer ist als 500.000!
- ---
- Schreibe die Zahl auf, die um 125.000 größer ist als 3.000.000!
BM472
- Zu jeder Zahl kann man eine um 1 größere Zahl bestimmen.
- Es gibt keine größte natürliche Zahl.
- jede natürliche Zahl a hat einen Nachfolger a + 1.
- Die Zahl a + 1 ist die nächstgrößere natürliche Zahl nach a.
- ---
- 0 (Null) ist die kleinste natürliche Zahl.
- Jede von Null verschiedene natürliche Zahl b hat einen Vorgänger b-1.
- Die Zahl b - 1 ist die zu b nächstkleinste natürliche Zahl.
- ---
- Von 0 (Null) ausgehend kann man durch die fortlaufende Addition von 1 jede beliebige natürliche Zahl bilden.
- ---
- Warum stellt man natürliche Zahlen mit Hilfe eines Zahlenstrahls dar?
- Warum verwendet man hierfür keine Strecke oder Gerade?
BM473
- Dekadisches Positionssystem
- ---
- Alle Zahlen kann man durch fortlaufende Addition von 1 oder durch Addition der Vielfachen von Zehnerpotenzen bilden.
- 7.346 = 7 * 103 + 3 * 102 + 4 * 101 + 7 * 100
- ---
- Man spricht bei diesem Zahlensystem von einem Zehnersystem oder dekadischen System.
- „Deka“ bedeutet „zehn“, das Wort kommt aus der griechischen Sprache.
- Im Zehnersystem verwendet man zehn Grundziffern.
- Das sind die Zeichen: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- In den arabischen Ländern (besonders in den östlichen arabischen Ländern) werden folgende Ziffern verwendet: ٠ ,١ ,٢ ,٣ ,٤ ,٥ ,٦ ,٧ ,٨ ,٩,
- Zahlen schreibt man mit Hilfe dieser Grundziffern.
- Dabei ordnet man den Grundziffern bestimmte Stellenwerte zu.
- Die Stellentafel verdeutlicht das:
- ---
105 104 103 102 101 100 7 3 0 4 6 6
- ---
- Es ist von Bedeutung, welcher Stelle eine Grundziffer zugeordnet ist.
- Das System wird deshalb als dekadisches Stellenwertsystem oder dekadisches Positionssystem genannt.
BM474
- Es gibt auch andere Positionssysteme
- ---
- Im Zweiersystem (= Binärsystem) ist jede Stelle in der Zifferndarsellung einer Zahl eine Potenz von 2 zugeordnet.
- In der Stellentafel ist das in der oberen Zeile entsprechend dargestellt.
- Die nächste Zeile enthält dann die Zahlen 1, 2, 4, 8, ... ;
- denn 22 = 2 * 2 = 4
- denn 23 = 2 * 2 * 2 = 8
- denn 24 = 2 * 2 * 2 * 2 = 16
- ---
27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1
- ---
- Im Zehnersystem benötigt man zur Darstellung der Zahl zehn Grundziffern.
- Im Zweiersystem sind dagegen nur zwei Grundziffern erforderlich. Dies können die Grundziffern 0 und 1 sein.
BM475
- Die Zahl 13 wird im Zehnersystem und im Zweiersystem dargestellt.
- ---
- Im Zehnersystem:
103 102 101 100 1.000 100 10 1 0 0 1 3
- 13 (lies: dreizehn)
- Man kann ohne Stellentafel schreiben:
- 0 * 103 + 0 * 102 + 1 * 101 + 3 * 1
- ---
- Im Zweiersystem
23 22 21 20 8 4 2 1 1 1 0 1
- 1101 (Lies: eins eins null, eins)
- Man kann ohen Stellentafel schreiben:
- 1 * 23 + 1 * 22 + 0 * 21 + 1 * 1
BM476
- Im Zweiersystem ist jeder Stelle eine Zweierpotenz zugeordnet.
- ---
- Beispiele:
- 101
- 1 * 22 + 0 * 21 + 1 * 1
- = 4 +1 = 5
- ---
- 1001
- 1 * 23 + 0 * 22 + 0 * 21 + 1 * 1
- = 8 * 1 = 9
- ---
- 1010
- 1 * 23 + 0 * 22 + 1 * 21 + 0 * 1
- = 8 + 2 = 10
- ---
- 11001
- 1 * 24 + 1 * 23 + 0 * 22 + 0 * 21 + 1 * 1
- = 16 + 8 + 1 = 25
- ---
- 101100
- 1 * 25 + 0 * 24 + 1 * 23 + 1 * 22 + 0 * 21 + 0 * 1
- = 32 + 8 = + 4 = 44
BM477
- Achtersystem
- ---
- Das Zehnersystem hat sich weltweit verbreitet, weil der Mensch zehn Finger hat und damit zählt.
- Das Zweiersystem wird für Computer verwendet, weil der PC „zwei Finger“ hat: ein Schalter im Computer kann an oder aus sein. Der Strom kann fließen oder nicht fließen.
- Im Film „ALF“ hat der Außerirdische 4 Finger an jeder Hand, also insgesamt 8 Finger.
- Er rechnet sicher im Achtersystem (= Oktalsystem). Spaß beiseite: In Computers wird das Oktalsystem sehr oft verwendet.
- ---
84 83 82 81 80 4096 512 64 8 1 6 2 7 0 7
- 6 * 84 + 2 * 83 + 7 * 82 + 0 * 81 + 7 * 8
- = 6 * 4096 + 2 * 512 + 7 * 64 + 0 * 8 + 7 * 1
- = 24.576 + 1.024 + 448 + 0 + 7
- = 26.055
BM478
- Sechzehnersystem
- ---
- Das Sechzehnersystem, bekannter ist der Name Hexadezimalsystem ist die Darstelung von Zahlen in einem Stellenwertsystem zur Basis 16.
7-Segment-Anzeige mit Ziffern und Buchstaben - Das Zehnersystem hat 10 Ziffern: 0 bis 9
- Das Hexadezimalsystem hat 16 Ziffern: 0 bis 9 und zusätzlich noch die 6 Buchstaben A, B, C, D, E, F und G
- Die 6 zusätzlichen Ziffern werden also durch Buchstaben dargestellt.
- Als Zahlzeichen auch manchmal die Kleinbuchstaben a bis e verwendet.
- Auf Taschenrechnern mit 7-Segment-Anzeige werden die Buchstaben A, C, E, F, G als Großbuchstaben dargestellt und b, d als Kleinbuchstaben.
-
A
-
b
-
C
-
d
-
E
-
F
-
G
BM479
- Gezählt wird im Hexadezimalsystem wie folgt:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | G |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E | 1F | |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 2A | 2B | 2C | 2D | 2E | 2F | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | FA | FB | FC | FD | FE | FF | |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 10A | 10B | 10C | 10D | 10E | 10F | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| FF0 | FF1 | FF2 | FF3 | FF4 | FF5 | FF6 | FF7 | FF8 | FF9 | FFA | FFB | FFC | FFD | FFE | FFF | |
| 1000 | 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 | 100A | 100B | 100C | 100D | 100E | 100F | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| FFF0 | FFF1 | FFF2 | FFF3 | FFF4 | FFF5 | FFF6 | FFF7 | FFF8 | FFF9 | FFFA | FFFB | FFFC | FFFD | FFFE | FFFF | |
| 10000 | 10001 | 10002 | 10003 | 10004 | 10005 | 10006 | 10007 | 10008 | 10009 | 1000A | 1000B | 1000C | 1000D | 1000E | 1000F | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
BM480
164 163 162 161 160 65.536 4.096 256 16 1 7 3 1 4 8
- 73148
- = 7 * 164 + 3 * 163 + 1 * 162 + 4 * 161 + 8 * 160
- = 458.752 + 12.288 + 256 + 64 + 8
- = 471.368
- ---
- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15
- ---
- 3F4B
- (lies: 3, f, 4, b)
- = 3 * 163 + F * 162 + 4 * 161 + B * 160
- = 3 * 4.096 + 15 * 256 + 4 * 16 + 11 * 1
- = 12.288 + 3.840 + 64 + 11
- = 16.203
- ---
- AB4CDF
- (lies: a, b, 4, c, d, f)
- = A * 165 + B * 164 + 4 * 163 + C * 162 + D * 161 + F * 160
- = 10 * 1.048.576 + 11 * 65.536 + 4 * 4.096 + 12 * 256 + 13 * 16 + 15 * 1
- = 10.485.760 + 720.896 + 16.384 + 3.072 + 208 + 15
- = 11.226.335
BM481 - BM490
[editar]BM481
- Damit man bei der Umrechnung zwischen verschieden Zahlensystemen nicht durcheinander kommt werden die Zahlen durch eine tiefergestellte Zahl markiert, die anzeigt auf welche Basis sich die Zahl bezieht.
- Binärsystem: 1001102 = 3810
- Oktalsystem: 1001108 = 3284010
- Dezimalsstem: 10011010
- Hexadezimalsstem: 10011016 = 104884810
- ---
- 6B16 = 1538 = 10710 = 011010112
- ---
- Auch die Schreibweise mit Klammern und Basis ist üblich:
- (6B)16 = (153)8 = (107)10 = (01101011)2
- ---
- Auch eine Basis mit anderen Zahlen ist möglich, aber in der Praxis nicht verbreitet.
BM482
- Schreibe die ersten 30 Zahlen, beginnend bei Eins:
- a) im Binärsystem
- b) im Hex-System
- c) im Oktalsystem
- ---
- Schreibe die Zahl 100 und ihren Vorgänger und Nachfolger:
- d) im Binärsystem
- e) im Hex-System
- f) im Oktalsystem
BM483
- Römische Zahlen
- Richtig müsste es heißen: Römische Zahlzeichen, denn die Zahlen sind die gleichen.
I V X L C D M 1 5 10 50 100 500 1.000
BM484
I 1 II 1 + 1 III 1 + 1 + 1 IV 5 - 1 V 5 VI 5 + 1 VII 5 + 1 + 1 VIII 5 + 1 + 1 + 1 IX 10 - 1 X 10 XI 10 + 1 XII 10 + 1 + 1 XIII 10 + 1 + 1 + 1 XIV 10 + 5 - 1 XV 10 + 5
- Beim Zusammenstellen mehrerer Zeichen muss addiert werden.
- In manchen Fällen wird auch subtrahiert.
- Dieses System ist ein Additionssystem.
- Im Gegensatz zum Positionssystem hat beispielsweise das Zeichen „I“ (römische Eins) stets die Bedeutung 1, ganz gleich wo es auch steht.
- Diese 1 kann zu einer anderen Zahl addiert oder von einer anderen Zahl subtrahiert werden.
- Vergleiche dazu z. B. die Zeichen für die Zahlen 9 und 11.
BM485
| 1 × 1000 | + | (−1 × 100 + 1 × 1000) | + | 1 × 50 | + | 3 × 10 | + | (−1 × 1 + 1 × 5) | = | 1984 |
| M | + | CM | + | L | + | XXX | + | IV | = | MCMLXXXIV |
- MDLVI = 1.000 + 500 + 50 + 5 + 1 = 1.556
- DCCCXXIII = 500 + 100 + 100 + 100 + 10 + 10 + 1 + 1 + 1 = 823
- CMLXXIV = 1.000 - 100 + 50 + 10 + 10 + 5 - 1 = 974
BM486
- Gib die folgenden römischen Zahlen im Dezimalsystem an und im Dualsystem und im Hexadezimalsystem! Überprüfe dein Ergebnis mit einem Zahlenkonverter, den du im Internet finden kannst! („converter roman to decimal“; „converter decimal to binary“; „converter decimal to hex“)
- ---
- LII
- MMXVI
- MDCLXXII
- MMMCMXCIX
- MCMXVI
- MDCCCCX
- MCMXXIII
BM487
- Näherungswert
- ---
- Ein Näherungswert ist in der Mathematik ein angenähertes Ergebnis für einen exakten Wert, zum Beispiel eine Dezimalzahl als Näherung für die Kreiszahl (sprich: pi). Näherungswerte werden häufig verwendet, wenn die exakte Berechnung sehr aufwendig oder nicht möglich ist oder nur eine bestimmte Genauigkeit benötigt wird.
- Die Kreiszahl hat den Wert 3,14159 26535 89793 23846 26433 ... (Beachte, dass bei solchen langen Zahlen die Nachkommastellen in Fünferblöcken und nicht in Dreierblöcken geschriben werden!)
- Pi hat den Näherungswert 3,14
- 3,14
- Dieses Zeichen (), das einem Gleichheitszeichen in Wellenform ähnelt, steht für „ungefähr“; „rund“ oder angenähert gleich
BM489
- Wenn verschiedene Leute einen Messung durchführren,, sind bei den Messergebnissen häufig kleine Abweichungen festzustellen. Das gleiche passiert, wenn ein und die selbe Person mehrere Messungen duchführt.
- Es ist zum Beispiel nicht sinnvoll die Länge eines Fußballfeldes in Millimeter anzugeben, da es bei mehreren Messungen immer wieder unterschiedliche Ergebnisse geben würde.
- Da es bei wiederholten Messungen immer zu Abweichungen kommt, wird die Länge einer Strecke angenähert angegeben.
- ---
- Man benötigt nicht immer Messergebnisse, die auf den Millimeter genau angegeben werden.
- Je nach Kontext rundet man auf ganze Zahlen (also 732 statt 732,1) oder auf ganze Zehner (also 730 statt 732,1) oder auf ganze Hunderter (also 700 statt 732,1).
- Manchmal braucht man nur auf einen Meter genau zu messen (z. B. die Länge eines Fußballfeldes).
- Manchmal braucht man nur auf einen Kilometer genau zu messen (z. B. der Abstand zwischen Berlin und Hamburg).
- Längen weden oft mit Näherungswerten angegeben.
BM490
- Die folgenden Städte hatten am 31. Dezember die angegebenen Einwohnerzahlen:
- Berlin: 3.520.031
- Frankfurt: 732.688
- Hamburg: 1.787.408
- Hannover: 532.163
- Leipzig: 560.472
- München: 1.450.381
- Rostock: 206.011
- ---
- Bei Vergleichen ist das Arbeiten mit Näherungswerten oft einfacher.
- Berlin: 3.500.000
- Frankfurt: 700.000
- Hamburg: 1.800.000
- Hannover: 500.000
- Leipzig: 600.000
- München: 1.500.000
- Rostock: 200.000
BM491 - BM500
[editar]BM491
- Führe eine Überschlagsrechnung durch!
- ---
- 3.426 : 6 ≈ 3.000 : 6
- 3.426 : 6 ≈ 500
- ---
- 3.148 : 7 ≈ 2.800 : 7
- 3.148 : 7 ≈ 400
- ---
- Bei der Überschlagsrechnung sucht man eine Zahl, die ungefähr so groß ist wie der Dividend und die sich leicht durch den Disvisor teilen lässt. Man rechnet also mit Näherungswerten.
- ---
- a : b = c
- Dividend duch Divisor ist gleich Quotient
BM492
- Führe erst eine Überschlagsrechnung durch, dann dividiere! (überschlagen)
- ---
- 5.541 : 3
- 8.154 : 6
- 984 : 6
- 4.830 : 7
BM493
- Bilde die Näherungswerte! Nimm nur Vielfache von Tausend!
- ---
- 658
- 17.329
- 380.325
- 526.272
- 138.569
BM494
- Führe nur eine Überschlagsrechnung durch!
- ---
- 268 : 5
- 786 : 8
- 1.456 : 7
- 3.532 : 9
- 13.456 : 6
- 45.702 : 5
- 351.476 : 8
- 177.823 : 6
BM495
- Runden
- ---
- Rundung ist eine arithmetische Operation, bei der eine Zahl in Stellenschreibweise, meist eine Dezimalzahl, durch eine Zahl mit einer geringeren Anzahl signifikanter (bedeutungstragender) Stellen ersetzt wird. Dabei wird der Unterschied zwischen ursprünglicher und gerundeter Zahl, der Rundungsfehler, so gering wie möglich gehalten.
- ---
- Zweck einer Rundung ist:
- Platz für die Darstellung zu sparen
- die Anzahl der Ziffern der Genauigkeit eines Rechenergebnisses anzupassen
- die Genauigkeit des Ergebnisses der darstellbaren bzw. messbaren Einheit anzupassen (kleinste mögliche Währungseinheit z. B. Cent, ganze Gramm bei Küchenwaagen, ...)
- ---
- Meist verringert man die Anzahl der Dezimalstellen und damit die Anzahl der dargestellten Ziffern. Doch werden auch große Ganzzahlen gerundet. Zum Beispiel rundet die Bundesagentur für Arbeit die errechnete Anzahl der Arbeitslosen auf volle 100. Hier bleibt die Anzahl der dargestellten Ziffern unverändert, aber die letzten zwei Stellen werden als nicht signifikant gekennzeichnet.
BM495
- aufrunden
- abrunden
- ---
- Wird eine positive Zahl vergrößert, so spricht man von „aufrunden“; wird sie verkleinert, von „abrunden“.
- Werden Nachkommastellen nur weggelassen, spricht man von „abschneiden“. Beim Runden von Zahlen ändert sich im Allgemeinen deren Wert.
- ---
- Gängige Rundungsverfahren lassen sich gemäß der Richtung einteilen:
- aufwärts
- abwärts
- Richtung null
BM496
- Kaufmännisches Runden
- ---
- Kaufmann
- Kauffrau
- Kaufleute
- ---
- Das Kaufmännische Runden geschieht wie folgt:
- Ist die Ziffer an der ersten wegfallenden Dezimalstelle eine 0, 1, 2, 3 oder 4, dann wird abgerundet.
- Ist die Ziffer an der ersten wegfallenden Dezimalstelle eine 5, 6, 7, 8 oder 9, dann wird aufgerundet.
- ---
- Beispiele (jeweils Rundung auf zwei Nachkommastellen):
- 13,3749 ... € ≈ 13,37 €
- 13,3750 ... € ≈ 13,38 €
BM497
- Mathematisches Runden
- ---
- Die Mathematische Rundung ist wie folgt definiert:
- 1.) Folgt auf die letzte beizubehaltende Ziffer eine 0, 1, 2, 3 oder 4, so wird abgerundet.
- 2.) Folgt auf die letzte beizubehaltende Ziffer eine 5 (gefolgt von weiteren Ziffern, die nicht alle null sind), 6, 7, 8 oder eine 9, so wird aufgerundet.
- 3.) Folgt auf die letzte beizubehaltende Ziffer lediglich eine 5 (oder eine 5, auf die nur Nullen folgen), so wird derart gerundet, dass die letzte beizubehaltende Ziffer gerade wird.
- ---
- Diese Art der Rundung wird in der Mathematik und Ingenieurwissenschaften verwendet.
- ---
- Beispiele (Rundung auf eine Nachkommastelle):
- 2,2499 ≈ 2,2 (nach Regel 1)
- 2,2501 ≈ 2,3 (nach Regel 2)
- 2,2500 ≈ 2,2 (nach Regel 3 zur geraden Ziffer hin gerundet)
- 2,3500 ≈ 2,4 (nach Regel 3 zur geraden Ziffer hin gerundet)
- ---
- Kaufmännisches und mathematisches Runden unterscheiden sich nur darin, wohin eine Zahl genau in der Mitte zwischen zwei Zahlen mit der gewählten Anzahl von Dezimalziffern gerundet wird.
- ---
- Das kaufmännische Runden erzeugt kleine systematische Fehler, da das Aufrunden um 0,5 vorkommt, das Abrunden um 0,5 jedoch nie; das kann Statistiken geringfügig verzerren. Die mathematische Rundung rundet von der genauen Mitte zwischen zwei Ziffern immer zur nächsten geraden Ziffer auf oder ab. Dadurch wird im Mittel genauso oft auf- wie abgerundet und der oben angesprochene systematische Fehler vermieden.
BM498
- Mathematisches Runden (nach der „gerade-Zahl-Regel“)
- ---
- Wenn die letzte Grundziffer eine 1, 2, 3 oder 4 ist, wird diese beim Runden durch 0 ersetzt und die vorletzte Grundziffer bleibt unverändert. Man erhält in diesen Fällen beim Runden stets kleinere Zahlen.
- Man sagt hierzu abrunden.
- 12.311 ≈ 12.310
- 12.312 ≈ 12.310
- 12.313 ≈ 12.310
- 12.314 ≈ 12.310
- ---
- 12.316 ≈ 12.320
- 12.317 ≈ 12.320
- 12.318 ≈ 12.320
- 12.319 ≈ 12.320
- Wenn die letzte Grundziffer eine 6, 7, 8 oder 9 ist, wird diese beim Runden durch 0 ersetzt und die vorletzte Grundziffer durch die für die nächstgrößere Zahl ersetzt. Man erhält in diesen Fällen beim Runden stets größere Zahlen.
- Man sagt hierzu aufrunden.
- ---
- Wenn die letzte Grundziffer eine 5 ist, rundet man nach folgender Regel:
- Man rundet so, dass die vorletzte Grundziffer der gerundeten Zahl eine gerade Zahl bezeichnet.
- Diese Regel heißt „gerade-Zahl-Regel“.
BM499
- Mathematisches Runden
- ----
- Runde auf Vielfache von 10!
- Beispiel:
- 14.735 ≈ 14.740
- 14.725 ≈ 14.720
- ---
- 375
- 165
- 845
- 985
- 10.624
- 996.553
- 374.781
- 808.711
BM500
- Beim Aufrunden ist folgender Sonderfall zu beachten:
- Es soll 408.697 auf ein Vielfaches von 10 gerundet werden.
- Weil die letzte Ziffer von 408.697 eine 7 ist, muss man aufrunden. Zur 9 ist 1 zu addieren. Dadurch muss zu 6 (an der Hunderterstelle) auch 1 addiert werden:
- 408.697 ≈ 408.700
- ---
- Runde 23.997 auf ein Vielfaches von 10!
- ---
- Runde auf ein Vielfaches von 100!
- 6.340
- 3.170
- 4.750
- índice
- Lección 059b ← Lección 060b → Lección 061b
- Lección 060















