In der klassischen Geometrie wird NICHT mit Zahlen gemessen.
Das Lineal hat keine Skale und keine Zahlen.
Das Zeichendreieck hat keine Skale und keine Zahlen - und auch keinen Winkelmesser.
Längen und Abstände werden mit einem Zirkel übertragen.
---
In der klassischen Geometrie wird nur mit Lineal und Zirkel gezeichnet (ohne Zeichendreieck), aber nicht gemessen. Mit diesen drei Arbeitsgeräten müssen z. B. verschieden Figuren konstruiert werden - ohne rechnen, abmessen oder Taschenrechner.) Natürlich ist ein Bleistift erlaubt und mit dem Zirkel kann man nicht nur abmessen, sondern auch Kreise zeichnen.
--
Der Zirkel (= Zeichenzirkel) ist mit einer montierbaren Spitze bzw. Bleistiftmine.
Wenn der Zirkel nur zwei Spitzen hat, dann kann man damit nur Längen übertragen, aber nicht zeichnen.
Solch ein Zirkel heißt Stechzirktel.
---
Das Lineal wird nur zum Zeichen von Geraden verwendet, nicht aber zum Abmessen.
Gerade = Linie
Bild 1
Bild 2
Bild 3
Bild 4
Bild 1: Mit dem Lineal eine Linie zwischen den Punkten A und B zeichnen. Eine Gerade zeichnen, die durch die Punkte A und B geht.
Bild 2: Mit dem Zirkel einen Kreis zeichnen, der den Radius der Streck AB hat.
Bild 3: Konstruktion eines 7-Ecks mit Zirkel und Lineal.
Bild 4: einen Winkel halbieren
BM408
Geometrieaufgabe:
Gegeben ist die Gerade g und der Punkt P.
Aufgabe: Zeichne durch den Punkt P eine Gerade k parallel zur Geraden g.
Erkläre die einzelnen Schritte -s o wie sie auf dem animierten Bild gezeigt werden.
Zeichnen der zu g parallelen Geraden k durch P (3 Sekunden Pause zwischen 2 Bildern)
Lösung BM408
Erklärung der Konstruktion
---
Man legt das Dreieck so an die gegebene Gerade g, dass der rechte Winkel des Dreiecks die Gerade berührt.
Senkrecht zu g legt man das Lineal an die andere Seite des Dreiecks, so dass es den rechten Winkel des Dreiecks berührt.
Nun verschiebt man das Dreieck entlang des Lineals, bis die Seite, die vorher an der Geraden g anlag, durch den Punkt P geht.
Nun zeichnet man entlang dieser Dreiecksseite die Parallele zu g, die durch den Punkt P geht.
Die Bezeichnung der neu gezeichneten Geraden k mit dem Buchstaben "k" wurde im Bild vergessen.
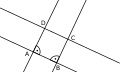
BM409
Gegeben ist die Gerade g und der Punkt P.
Aufgabe: Zeichen durch den Punkt P eine Gerade k parallel zur Geaden g. Dieses mal aber ohne Verwendung des rechten Winkles vom Dreieck.
Erkläre die einzelnen Schritte -s o wie sie auf dem animierten Bild gezeigt werden.
Was ist der Unterschied zur Konstruktion in der vorherigen Übung (Übung BM208).
Zeichnen der zu g parallelen Geraden k durch P (3 Sekunden Pause zwischen 2 Bildern)
Lösung BM409
Erklärung der Konstruktion
---
Da für die Aufgabe kein Drieck mit einem "garantiert rechen Winkel" zur Verfügugn steht, können wir nicht mit dem "rechten Winkel" des Dreieck arbeiten.
Wir legen das Dreieck mit seiner langen Seite an die Gerade g an.
Dann legen wir das Lineal an eine kurze Seite des Dreiecks.
Nun verschieben wir das Dreieck entlang des Lineals, bis die lange Seite des Dreiecks durch den Punkt P geht.
Zum Schluss können wir entlang des langen Seite des Dreieck die Gerade durch den Punkt P zeichnen, die parallel zu g verläuft.
Zum Schluss bezeichnen wird die neue Gerade mit dem Kleinbuchstaben "k".
BM410
Die Gerade g schneidet die Gerade h so, dass vier gleich große Winkel entstehen.
Zeichne eine Gerade d und einen Punkt P auf der Geraden d! Durch den Punkt P zeichne die Gerade c, die senkrecht auf der Geraden d steht!
Lösung BM411
Bild 1
Bild 2
Bild 3
BM412
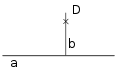
Zeichne eine Gerade a und einen Punkt D, der nicht auf der Gerade a liegt! Durch den Punkt D zeichne eine Gerade b, die senkrecht auf der Geraden a steht!
Lösung BM412
Bild 1
Bild 2
Bild 3
BM413
Zeichne eine Gerade f, und auf dieser Geraden kennzeichne vier Punkte A, B, C und D! Zeichne durch diese Punkte vier Geraden a, b, c und d, die auf der Geraden f senkrecht stehen!
Lösung BM413
Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
BM414
Die Gerade r schneidet die beiden Geraden m und n in den Punkten A und B. Wie kannst du überprüfen, ob die Geraden m und n parallel sind?
BM415
Die Gerade k schneidet die Geraden g und h rechtwinklig. (Der rechte Winkel wird durch einen Kreisbogen mit einem Punkt drin angezeigt.)
Es entstehen die Schnittpunkte A und B.
Die Länge der Strecke ist der Abstand der parallelen Geraden g und h.
BM416
In Bild 1 sehen wir ein beliebiges Viereck. Alle 4 Seiten sind schief zueinander. Das Viereck ist schief.
In Bild 2 sehen wir ein Parallelogramm. Die gegenüberliegenden Seiten sind parallel zueinander.
In Bild 3 sehen wir ein Rechteck.
In Bild 4 sehen wir ein Quadrat..
Bild 1: Viereck ABCD
Bild 2: Parallelogramm ABCD
Bild 3: Rechteck ABCD
Bild 4: Quadrat ABCD
Parallelogramme entstehen, wenn sich zwei Streifen schneiden.
Parallelogramme entstehen, wenn sich zwei Paar parallele Geraden schneiden.
Ein Rechteck ist ein Parallelogramm, bei dem alle Winkel rechte Winkel sind.
Parallelogramm die nur rechte Winkel haben sind Rechtecke.
Jedes Rechteck ist auch ein Parallelogramm, aber nicht jedes Parallelogramm ist ein Rechteck.
Rechtecke sind spezielle Parallelogramme.
Ein Rechteck, bei dem alle Seiten gleich lang sind, ist ein Quadrat.
Jedes Quadrat ist auch ein Rechteck, aber nicht jedes Rechteck ist ein Quadrat. Ein Quadrat ist ein spezielles Rechteck.
Außerdem ist jedes Quadrat auch ein Parallelogramm.
Jedes Parallelogramm, dass rechts Winkel hat und gleich lange Seiten ist ein Quadrat.
Ein Parallelogramm, dass aber nur gleich lange Seiten hat und keine rechten Winkel ist weder ein Rechteck noch ein Quadrat.
BM417
Gegeben sind die Punkte A und B.
Zeichne eine Strecke g, die fünf mal so lang ist wie der Abstand der Punkte A und B.
Zeichne zuerst eine Gerade. Kennzeichne auf ihr einen Punkt C! Greife mit dem Zirkel den Abstand zwischenden Punkten A und B ab und trage diese Länge mit Hilfe des Zirkels auf der Geraden von C aus ab! Du erhälst den Punkt D.
Die Strecke ist fünf mal so lang, wie der Abstand zwischen den Punkten A und B.
---
Beschreibe wie du das zeichnest! Halte dich an die Arbeitsschritte, die du auf dem Bild siehst.
BM418
Trapez
Zwei Geraden g und h schneiden einen Streifen in den Punkten A, B, C und D. Es entstehen die Strecken , , und . Sie sind die Seiten des Trapezes ABCD.
Trapez
Das ist eine Trapezfläche
BM419
Die parallelen Geraden a und b werden durch die Geraden c und d geschnitten. Es entsteht ein Trapez ABCD.
Trapez
Die parallelen Geraden e und f weden durch die Geraden g und h geschnitten. Es entsteht ein Trapez EFGH.
g und h sind parallel. Es entsteht ein Parallelogramm.
Ein Parallelogramm ist ein spezielles Trapez.
Ein Parallelogramm ist ein besonderes Trapez.
Jedes Parallelogramm ist auch ein Trapez. Aber nicht jedes Trapez ist ein Parallelogramm.
Bei einem Parallelogramm sind die gegenüberliegenden Seiten jeweils parallel zueinander.
Bei einem Trapez sind mindestens zwei gegenüberliegende parallel zueinander
Bei einem Parallelogramm sind die gegenüberliegenden Seiten gleich lang.
Parallelogramm
BM420
Zeichne zwei parallele Geraden! Lege auf einer Geraden eine Strecke fest und auf der zweiten Geraden eine genauso lange Strecke! Vervollständige die Figur so, dass ein Trapez entsteht!
Stelle bei jedem dieser Vierecke die besonderen Merkmale fest und entscheide danach, was es für ein Viereck ist!
Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
BM422
der Radius
Die Strecke, die den Mittelpunkt des Kreises mit einem beliebigen Punkt des Kreises verbindet, heißt Radius.
BM423
Sehne
Sehne
die Sehne
Dieser Kreis mit dem Mittelpunkt M wird von den Geraden (g, h, m, n) geschnitten. Dabei entstehen die Schnittpunkte A, B, C, D, E, F, G und H und die Strecken , , und .
Eine Strecke, die zwei Punkte des Kreises verbindet, heißt Sehne.
BM424
Durchmesser
der Durchmesser
Jede Sehne, die durch den Mittelpunkt M des Kreises geht, heißt Durchmesser des Kreises.
BM425
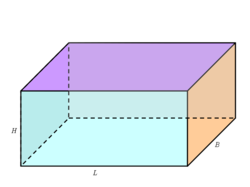
Quader
Würfel
die Grundfläche
die Deckfläche
---
Bei einem Quader sind Grund- und Deckfläche gleich.
Bei einem Quader sind gegenüberliegende Fläche gleich.
Bei einem Würfel sind alle gegenüberliegenden Flächen gleich.
BM426
Auseinander geklapptes Netz eines Quaders
Auseinander geklapptes Netz eines Würfels
Netz eines Würfels
Netz eines Quaders
---
Wie viel Möglichkeiten gibt es einen Würfel aufzufalten? Zeichne alle Möglichkeiten auf!
Lösung BM426
Es gibt 11 Möglichkeiten einen Würfel aufzufalten.
BM427
Zylinder; h = Höhe; r = Radius
der Zylinder
Grund- und Deckfläche sind eine Kreisfläche.
Bei Zylindern sind Grund- und Deckfläche gleich große Kreisflächen.
Bei Zylindern sind nur die Kreisflächen ebene Flächen.
Die Mantelfläche ist gekrümmt.
BM428
die Pyramide
der Kegel
Die Grundfläche dieser Pyramide ist ein Quadrat.
Diese Pyramide hat eine quadratische Grundfläche.
Die Seitenflächen einer Pyramide sind Dreiecke.
Die Grundfläche bei einem Kegel ist eine Kreisfläche.
BM429
Von zwei verschiedenen Zahlen kann man stets sagen, dass die eine Zahl größer oder kleiner ist als die andere.
---
Das klingt trivial, aber es gibt Zahlen (komplexe Zahlen), bei denen man das nicht sagen kann. So wie man auch nicht sagen kann, welche Farbe größer ode kleiner ist.
---
38 > 20
38 ist größer als 20
---
14 < 30
14 ist kleiner als 30
---
Beim Vergleich der Zahlen erhält man Ungleichungen. Jeden derartigen Vergleich von Zahlen kann man mit Hilfe der Addition begründen
38 > 20 denn 38 = 20 + 18
14 < 30 denn 14 + 16 = 30
---
542 ist der Nachfolger der Zahl 541
541 ist der Vorgänger der Zahl 542
BM430
Die Folge der natürlichen Zahlen
---
Jede Zahl hat genau einen Nachfolger.
Die Zahl a hat als Nachfolger die Zahl a + 1.
Die Zahl a + 1 ist um 1 größer als die Zahl a.
Wenn die Zahl b der Nachfolger der Zahl a ist, so gilt:
a < b und a + 1 = b
z. B. 5 < 6 und 5 + 1 = 6
Jede Zahl außer der Zahl Null hat genau einen Vorgänger.
Man kann Zahlen auf verschiedene Arten darstellen-
---
Beispiel:
vierhundertfünfzehn
415
400 + 10 + 5
---
siebenhundertachtundfünfzig
fünfhundertsiebenunddreißig
sechshundertachtunddreißig
BM432
Stellentafel
---
Wenn man Zahlen mit Ziffern darstellt, wird jeder Stelle eine bestimmte Zehnerpotenz zugeordnet. Darum schreibt man nur die Faktoren der Zehnerpotenzen. Die Ziffer 415 wird mit den Grundziffern „4“, „1“ und „5“ geschrieben.
---
Zehnerpotenzen
100 = 1 (Null Nullen)
101 = 10 (eine Null)
102 = 100 (zwei Nullen)
103 = 1000 (drei Nullen)
104 = 10000 (vier Nullen)
---
102
10
1
5
1
5
7
5
8
5
3
7
6
3
8
---
100
10
1
5
1
5
7
5
8
5
3
7
6
3
8
BM433
Zehnerpotenzen
100 = 1 (Null Nullen)
101 = 10 (eine Null)
102 = 100 (zwei Nullen)
---
Die folgenden Geldbeträge sollen in Hundert-Euro-Scheinen; zehn-Euro-Scheinen und in Ein-Euro-Münzen ausgezahlt werden. (100; 10; 1) Wie viel Scheine bzw. Münzen von jeder Sorte sind jeweil erforderlich?
263 Euro
506 Euro
872 Euro
811 Euro
904 Euro
BM434
Von einer Drahtrolle mit 150 m Draht werden 5 Stück von je 17 m Länge abgeschnitten. Wie viel Meter bleiben auf der Drahtrolle übrig?
BM435
Für alle natürlichen Zahlen a, b und c gilt:
a + b = b + a
(a + b) + c = a + (b + c)
a + 0 = a
---
Wenn a - b = c gilt, so gilt auch c + b = a.
Dabei kann c auch gleich Null sein.
Beispiel: 8 - 5 = 3 3 + 5 = 8
---
heißt: „ausfolgt“
heißt: „ist äquivalent zu“ oder auch „genau dann, wenn“
---
Beispiel: 8 - 5 = 3 3 + 5 = 8
Beispiel: 9 - 9 = 0 0 + 9 = 9
BM436
Addition
Subtraktion
Multiplikation
Division
---
Für alle natürlichen Zahlen a gilt:
a - 0 = a
a - a = 0
---
a + b = c
Summand + Summand = Summe
---
a - b = c
Minuend - Subtrahend = Differenz
---
a * b = c
Faktor * Faktor = Produkt
---
Für alle natürlichen Zahlen a, b und c gilt:
a * b = b * a
(a * b) * c = a * (b * c)
(a + b) * c = a * c + b * c
a * 1 = a
a * 0 = 0
BM437
Division
a : b = c
Dividend : Divisor = Quotient
Die Division ist im Bereich der natürlichen Zahlen nur dann ausfürhbar, wenn der Dividend a ein Vielfaches des Divisors b ist und wenn der Divisor größer als Null ist.
Die Division durch Null ist NICHT möglich.
---
36 : 7 = n.l.
36 : 7 = 5 (Rest 1)
---
Wenn a : b = c gilt, so gilt auch c * b = a.
Beispiel:
---
Die Division ist die Umkehroperation der Multiplikation.
Die Subtraktion ist die Umkehroperation der Addition; und umgekehrt.
---
Wenn a und b Vielfache von c sind und wenn c größer als Null ist, so gilt für die natürlichen Zahlen a, b und c:
(a + b) : c = a : c * b : c
(a + b) : c = (a : c) * (b : c)
---
Für alle natürlichen Zahlen a gilt:
a : 1 = a
---
Wenn a größer als Null ist, gilt für die natürlichen Zahlen a:
a : a = 1
---
Wenn a größer als Null ist, gilt für die natürlichen Zahlen a:
0 : a = 0
BM438
Zehnerpotenzen
---
100 = 10 * 10
(zwei Nullen; eine Null; eine Null)
---
Für 10 * 10 kann man die Potenz 10 2 schreiben.
100 = 2
---
1000 = 10 * 10 * 10
(drei Nullen; eine Null; eine Null; eine Mull)
Für 10 * 10 * 10 kann man die Potenz 10 3 schreiben.
1000 = 10 3
---
Entsprechend bildet man:
10000 = 10 4
10000 = 10 * 10 * 10 * 10
(vier Nullen)
---
einhunderttausend
100000 = 10 * 10 * 10 * 10 * 10
(fünf Nullen)
100000 = 10 5
---
Die Potenz 10 5 hat fünf Nullen.
---
eine Million
10 * 10 * 10 * 10 * 10 * 10 = 1 000 000
1 Mill. = 10 6
BM439
Zifferngruppierung
Trennzeichen für Tausender
22 465 (mit Leerzeichen; in Dreierblöcken; zweiundzwanzig-tausend- vierhundertfünfundsiebzig)
6 392 845
22.475 (mit Punkt)
345.941
6.392.845
---
In den USA und in England wird der Punkt als Dezimaltrennzeichen verwendet.
z. B.: 2.5
In Deutschland 2,5
Deshalb wird in den USA und in England als Trennezichen für Tausender NICHT ein Punkt verwendet, sondern ein Komma:
USA; z.B. :22,465 (= Deutschland; 22.465)
USA; z.B. :4,803.5 (= Deutschland; 4.803,5)
---
Wenn man also eine Zahl liest, dann kann man sie nicht korrekt interpretiert, wenn man nicht weiß, ob sie in einem deutschen oder englischen Buch steht:
345,941
---
Manchmal (z. B. in der Schweiz) werden die Ziffern auch mit einem Hochstrich voneinander getrennt, um die genannten Probleme mit Komma und Punkt auszuschließen:
Beispiel: 123'456'789.123 bzw. 123'456'789,123
---
Bei den meisten Taschenrechner werden Hochstriche als Tausender- und Punkte als Dezimaltrennzeichen verwendet. Hierbei haben Punkt und Komma je eine eindeutige Bedeutung.
BM440
Multipliziere
---
10 * 10
10 * 100
10 * 1.000
10 * 10.000
10 * 100.000
---
Die Zahlen 1, 10, 100, 1.000, 10.000, 100.000, 1.000.000 sind Zehnerpotenzen
Das Zehnfache einer Zehnerpotenz ist gleich der nächstgrößeren Zehnerpotenz.
.png)
