Álgebra Abstracta/Divisibilidad

Introducción

En este capítulo, estudiaremos abstracciones de la teoría de la divisibilidad de los Enteros. Aunque muchas de las nociones relevantes pueden extenderse a anillos cualesquiera, la extensión natural es a dominios de integridad (o sea anillos conmutativos con unidad y sin divisores de cero). En este capítulo, y en los siguientes, dominio será sinónimo de dominio de integridad.

Los Enteros están contenidos en los Racionales, que son un cuerpo formado por las fracciones de números enteros. En total analogía, veremos que cada dominio tiene asociado un cuerpo de fracciones de elementos del dominio.

Convenio. Todos nuestros anillos serán conmutativos con identidad, a menos se diga explícitamente lo contrario.

La Divisibilidad

En primer lugar, extenderemos la divisibilidad y nociones asociadas de los Enteros a anillos conmutativos generales.

Definición. (Divisores, Unidades, Asociados) Sea $A$ un anillo conmutativo con identidad.

• Decimos que un elemento no nulo $a$ divide a $b,$ ssi, hay un elemento $x$ tal que $ax=b.$ Simbólicamente $a|b.$
• Decimos que un elemento $u$ de $D$ es una unidad, ssi, $u$ es un divisor de la identidad.
• Decimos que los elementos $a$ y $b$ son asociados, ssi, hay una unidad $u$ tal que $a=bu.$

Observaciones.

1. Cuando $a$ divide a $b,$ podemos también decir alguna de las siguientes expresiones.
   • $a$ es un factor de $b.$
   • $a$ des un divisor de $b.$
   • $b$ es un múltiplo de $a.$
   • $b$ es divisible por $a.$
2. Las unidades ya habían sido definidas anteriormente como los elementos invertibles del dominio. Claramente, ambas nociones coinciden.
3. Un divisor de cero es cualquier elemento no nulo que divide (en el sentido de la definición) al 0, o que es un factor no nulo del 0.

---

La siguiente proposición resume las principales propiedades de la divisibilidad.

Proposición 1. Sea $A$ un anillo conmutativo con identidad. Para todo $a,$ $b,$ $c$ en $A$ se cumple que

1. Cualquier elemento $a$ es divisible por 1, $1|a.$
2. Cualquier elemento es divisible por sí mismo, $a|a.$
3. Cero es divisible por cualquier elemento, $a|0.$
4. La relación de divisibilidad es transitiva. Es decir, si $a|b$ y $b|c$ entonces $a|c.$
5. Si $a|b$ y $a|c$ entonces $a|(b+c).$
6. Si $a|b$ entonces $a|cb.$

Demostración: Ejercicio.

---

Unidades

Como observamos anteriormente, la noción de unidad en un anillo es lo mismo que invertible respecto a la multiplicación, pero la tradición es usar el nombre unidad en el contexto de divisibilidad.

Observemos que cuando $u$ es una unidad, como $u|1,$ $u$ es un divisor de cualquier elemento del anillo. Claramente, en cualquier anillo, $1$ y $-1$ son divisores de 1 y son, por lo tanto, unidades. El siguiente ejemplo muestra que, en general, puede haber otras unidades en un anillo. Además, en cualquier cuerpo, cualquier elemento no nulo es una unidad.

Ejemplo (Enteros de Gauss).

Sea $A=\mathbb {Z} [i]=\{a+bi:a,b\in \mathbb {Z} ,i^{2}=-1\}.$ Sabemos de ejemplos anteriores que $A$ es un anillo respecto a las operaciones usuales. Además, como es un subconjunto de $\mathbb {C} ,$ es un dominio de integridad.

Además de $1$ y $-1,$ también son unidades $i$ y $-i,$ ya que $i(-i)=1.$ Se puede verificar que esas son las únicas unidades de ese anillo.

---

Simbolizamos el conjunto de las unidades de un anillo por $A^{*}$ o $U(A).$ Como las unidades son los elementos invertibles, $U(A)$ es cerrado respecto a la multiplicación, contiene al 1 y es cerrado respecto a tomar inversos. Es decir que $U(A)$ tiene una estructura de grupo, que es un subgrupo del semigrupo multiplicativo del anillo.

Asociados

Sea $a$ un asociado de $b$ , digamos que $a=bu,$ donde $u$ es una unidad. Sea $v$ tal que $uv=1.$ Entonces,

$a=bu\implies av=(bu)v=b(uv)=b.$

lo que prueba que $b$ está asociado con $a.$ Es decir que la relación "estar asociado con" es una relación simétrica. De hecho, puede probarse que es una relación de equivalencia.

La siguiente proposición es básica para entender el rol de las unidades en la divisibilidad y las nociones asociadas con ella.

Proposición 2. Sea $A$ un anillo conmutativo con Identidad. Sean $a$ y $b$ elementos de $A$ tales que $a|b.$

1. Cualquier asociado de $a$ divide a $b.$
2. Cualquier asociado de $b$ es divisible por $a.$

Demostración: Supongamos que $x$ es tal $ax=b$ Sea $a=cu,$ con $u$ unidad. Entonces, $b=ax=(cu)x=c(ux),$ lo que prueba que $c$ divide a $b.$ Sea $d=bu$ con $u$ unidad. Entonces, $d=bu=(ax)u=a(xu),$ lo que prueba que $a$ divide a $d.$

---

Los resultados de la proposición muestran los roles de las unidades en un anillo, y los problemas que ocasionan. Supongamos que queremos definir máximo común divisor (MCD) de dos elementos de un anillo. Nos gustaría tener una definición que leyera como sigue:

Sean $a$ y $b$ dos elementos de un anillo $A$ (conmutativo con identidad). Un elemento $d$ es un MCD de $a$ y $b,$ ssi,
1. $d$ es un divisor común de $a$ y $b,$ y
2. $d$ es divisible por cualquier otro divisor común.

Esta definición tiene dos variaciones con respecto a la definición usual para los enteros. En la definición para números enteros se pide que el MCD sea un número positivo. Como en general, no tenemos orden, no podemos hablar de elementos positivos. Sigue de la definición, que si hay un MCD de dos números, por la proposición anterior, cualquier asociado con él, también será un MCD. Por eso es que hablamos de un MCD y no de el MCD.

Ejemplo.

En los Enteros, de acuerdo a la definición anterior de $MCD,$ se tiene que 4 y 6 tiene como MCD a 2 y a $-2$ (el asociado a 2).

---

La consecuencia de lo anterior es que cualquier definición que use divisibilidad, por ejemplo, elemento primo, no determinará un único elemento, sino que al elemento y a todos sus asociados. Por lo que algunas veces hablaremos de unicidad, excepto por asociados o modulo asociados.

En el caso de los Enteros como $a$ y $-a$ son los únicos asociados con $a,$ podemos, usando el orden, escoger el positivo.

Algunos elementos importantes en un anillo conmutativo son los elementos irreducibles y los elementos primos, que definiremos a continuación. En el anillo de los Enteros, los números primos tienen dos propiedades básicas:

• (Irreducibilidad). Cada número primo es divisible solamente por si mismo (o un asociado) o por una unidad.
• (Primacidad) Cuando un número primo divide al producto de dos números, divide al menos a uno de ellos.

Generalizaremos esas dos nociones para anillos conmutativos cualesquiera como nociones separadas, ya que en general no coincidirán.

Definición. (Elementos Irreducibles, Primos) Sea $A$ un anillo conmutativo con identidad.

1. Un elemento $a$ de $A$ es irreducible (en $A$), ssi, $a$ no es nulo ni es una unidad y $a=xy$ implica que $x$ o $y$ es una unidad.
2. Un elemento $p$ de $A$ es primo (en $A$), ssi, no es nulo, no es una unidad y cuando $p|ab$ entonces $p|a$ o $p|b.$

Claramente, los asociados de irreducibles son irreducibles y los asociados de elementos primos son primos. La definición dice que un irreducible solamente tiene como factores a un asociado con él o a una unidad.

Observaciones.

1. En el anillo de los números enteros, los números primos son irreducibles y primos de acuerdo a las definiciones anteriores.
2. En un cuerpo, no hay elementos irreducibles ni primos, ya que todos los elementos no nulos son unidades. Desde el punto de vista de la divisibilidad, los cuerpos son triviales.
3. Puede haber dominios donde haya elementos irreducibles que no son primos. Ver ejemplo más adelante.

---

La Aritmética en un Dominio

La divisibilidad puede definirse sobre cualquier anillo con identidad, tomando precauciones acerca del lado adonde estamos multiplicando. Para los efectos de nuestro estudio, sin embargo, las propiedades más interesantes se presentan cuando trabajamos sobre un dominio de integridad. La divisibilidad en un dominio tiene las siguientes propiedades adicionales.

Proposición 3. Sea $D$ un dominio, entonces

1. Si $a|b$ y $b|a$ entonces $a$ y $b$ son asociados.
2. Si $a|b$ hay un único elemento $c$ tal que $b=ac.$ Escribiremos que $c=b/a.$

Demostración:
1. Como $a|b$ hay un $x$ tal que $ax=b.$ Análogamente, $b|a$ implica que hay un $y$ tal que $a=by.$ Luego, como $a=by\implies a=axy,$ se tiene que $a1=axy,$ cancelando $a$ se tiene que $xy=1,$ por lo que $x$ y $y$ son unidades. De donde el resultado.
2. Si $b=ac=ac',$ por cancelación $c=c'.$

---

Proposición 4. (Primos son Irreducibles) Si $p$ es un elemento primo de un dominio $D,$ $p$ es irreducible.

Demostración: Sea $p$ un elemento primo de $D.$ Supongamos que $p=ab.$ Luego, por definición de elemento primos se tiene que $p|a$ o $p|b.$ Luego para $a$ o $b,$ digamos $a$ se cumple que $a|p$ y que $p|a.$ Por lo que, por la proposición anterior, se tiene que $p$ y $a$ son asociados. Luego hay una unidad $u$ tal que $p=au.$ Como $p=ab,$ por cancelación se tiene que $b=u,$ o sea que $b$ es una unidad.

---

Ejemplo (Un dominio donde hay un irreducible que no es primo).

Sea $D=\mathbb {Z} [{\sqrt {-5}}]=\{a+bi{\sqrt {5}}:a,b\in \mathbb {Z} ,\quad i^{2}=-1\}.$ Sabemos que $D$ es un dominio, ya que es un subanillo de $\mathbb {C} .$

Primeramente, determinaremos las unidades de $D.$ Para $z$ en $D,$ recordemos que llamamos norma de $z,$ al número denotado por $N(z)$ y definido como $N(z):=z\,{\overline {z}},$ donde ${\bar {z}}$ es el conjugado de $z$ como número complejo. Observemos que, en este caso, para cada $a+bi{\sqrt {5}}$ en $D,$ se cumple que $N(a+bi{\sqrt {5}})=(a+bi{\sqrt {5}}){\overline {(}}a-bi{\sqrt {5}})=a^{2}+5b^{2}.$ Por lo que la norma de un elemento de $D$ es un número entero. Se cumple, además, que

$N(zw)=(zw){\overline {(zw)}}=zw{\overline {z}}\,{\overline {w}}=z{\bar {z}}\,w{\bar {w}}=N(z)N(w).$

Supongamos que $u=a+bi{\sqrt {5}}$ fuera una unidad de $D.$ Se tendría, entonces, que hay un $v$ tal que $uv=1.$ Por lo que $N(u)N(v)=N(uv)=N(1)=1.$ Como los valores de la norma son enteros positivos o cero, tenemos que la norma de una unidad debe ser igual a 1. Luego, cuando $u=a+bi$ es una unidad, tenemos que $N(u)=u{\bar {u}}=a^{2}+5b^{2}=1,$ por lo que se cumplirá que $a^{2}=1$ y $b^{2}=0.$ Luego, $1$ y $-1$ son las únicas unidades de $D.$

Probaremos ahora que $3$ es irreducible. Suponiendo que $3=zw,$ tomando conjugados tenemos que $3={\bar {z}}{\bar {w}}.$ Multiplicando las relaciones anteriores, obtenemos que

$9=z{\bar {z}}w{\bar {w}}=N(z)N(w).$

Luego $N(z)=z{\bar {z}}=a^{2}+5b^{2}$ es igual a 1 o 3 o 9. Como es imposible $a^{2}=3$ con $a$ entero y $b>0$ implica que $N(z)\geq 5,$ la alternativa $N(z)=3$ es imposible. Luego $N(z)=1$ o $N(z)=9.$ Claramente, $N(z)=1$ implica $z{\bar {z}}=1,$ lo que dice que $z$ es un unidad. Si $N(z)=9,$ $z$ no es unidad, pero entonces $N(w)=1,$ por que $w$ una unidad. En consecuencia, 3 es irreducible.

Observemos ahora que $(1+2{\sqrt {-5}})(1-2{\sqrt {5}})=21=3*7.$ Como, obviamente $3$ no divide a $1+2{\sqrt {-5}}$ o a su conjugado, $3$ no puede ser primo.

---

Máximo Común Divisor y Mínimo Común Múltiplo

Las definiciones de los conceptos son totalmente análogas a los correspondientes conceptos para con los números enteros, excepto que no hay unicidad.

Definición. (MCD, MCM) Sea $D$ un dominio y sean $a,$ $b$ elementos de $D$ y al menos uno de ellos no es nulo.

1. Un elemento $d$ es un mcd (máximo común divisor) de $a$ y $b,$ ssi, es un divisor común de $a$ y $b,$ y es divisible por cualquier otro factor común. Notación ${\text{mcd}}\{a,b\}.$
2. Un elemento $d$ es un mcm (mínimo común múltiplo) de $a$ y $b,$ ssi, es un múltiplo común de $a$ y $b,$ y divide a cualquier otro múltiplo común. Notación ${\text{mcm}}\{a,b\}.$

Observaciones.

1. Cuando existen, dos mcd (resp. mcm) son asociados. Por lo que, cuando existen mcds, hay tantos mcd (resp. mcm) como unidades.
2. Es posible tener dominios donde haya mcd, pero no mcm.

---

Se tiene la siguiente proposición.

Proposición 5. Sea $D$ un dominio y sean $a,$ $b$ elementos no nulos de $D.$

1. Si $a$ y $b$ tienen mcd y mcm, entonces, excepto por un asociado, se cumple que $ab={\text{mcd}}\{a,b\}{\text{mcm}}\{a,b\}.$
2. Si existe ${\text{mcm}}$ entonces ${\text{mcd}}=ab/{\text{mcm}}.$

Demostración: Ejercicio.

---

Ejercicios

1. Probar la proposición 1.
2. Sean $a,b,d$ elementos de un anillo $A.$ Sea $d$ tal que $d|a$ y $d|b$ Probar que para todo $x,$ $y$ en $A,$ $d|(ax+by).$
3. Sean $(x_{i})$ $1\leq i\leq r$ una familia de elementos de un anillo $A$ y $d$ un divisor común de los elementos de la familia. Probar que $d$ divide cualquier combinación lineal de los $a_{i}$'s con coeficientes en $a,$ o sea que $d$ es un divisor de $\sum _{i-1}^{n}a_{i}x_{i},$ para todo $a_{i}$'s en $A.$
4. Probar que si $a$ y $b$ son elementos de un dominio de integridad y ${\text{mcd}}(a,b)=d,$ entonces ${\text{mcd}}(a/d,b/d)=1.$
5. Probar la proposición 5.
6. Sea $D=\mathbb {Z} [{\sqrt {-m}}]$ donde $m$ es un entero positivo. Probar que si $u$ es una unidad, entonces su conjugado ${\overline {z}}$ también lo es.
7. Sea $\mathbb {Z} [i]$ el dominio de los Enteros de Gauss.
   1. Probar que $(1+i)$ es un factor de $2,$ de $1+3i$ y de $7-3i.$
   2. Hallar otros tres factores de 2 en $\mathbb {Z} [i].$
8. Sea $p$ un entero primo y sea $D_{p}=\{a/b\in \mathbb {Q} :{\text{mcd}}(a,b)=1,\ b=p^{k}{\text{ para algún }}k\geq 0\}.$ Probar que $D_{p}$ es un dominio de integridad. Hallar las unidades y primos de $D_{p}.$ Probar que cada primo en $D_{p}$ es irreducible.
9. Sea $D=\{a+b{\sqrt {5}}\in \mathbb {C} :a,b\in \mathbb {Z} \}.$ Sea $J=\langle 2\rangle .$ Construir la tabla de la adición y multiplicación de $D/J.$ Hallar ideales de $D/J.$
10. Sea $D=\{a+b{\sqrt {7}}:a,b\in \mathbb {Z} \}$ y sea $N(a+b{\sqrt {7}})=a^{2}-7b^{2}.$ Verificar que;
    1. $a+b{\sqrt {7}}=c+d{\sqrt {7}},$ ssi, $a=b$ y $c=d.$
    2. $a+b{\sqrt {7}}$ es una unidad, ssi, $a^{2}-7b^{2}=1.$
    3. $8\pm 3{\sqrt {7}}$ y $-8\pm 3{\sqrt {7}}$ son unidades de $D.$
    4. $127-48{\sqrt {7}}$ es una unidad.
    5. $1+{\sqrt {7}}$ es asociado de $29+11{\sqrt {7}}.$
    6. $(11+4{\sqrt {7}})(11-4{\sqrt {7}})=9=3*3.$ (¿Qué pasa con la factorización única?)
11. Sea $D=\{a+b{\sqrt {7}}:a,b\in \mathbb {Z} \}$ y sea $N(a+b{\sqrt {7}})=a^{2}-7b^{2}.$
    1. Si $x,$ $y$ están en $D,$ $N(x,y)=N(x)N(y).$
    2. La ecuación $x^{2}-7y^{2}=3$ no tiene soluciones enteras.
    3. No hay elemento $x$ de $D$ tal que $N(x)=3.$
    4. Un entero no nulo $m$ divide a $x=a+b{\sqrt {7}},$ ssi, $n$ divide a $a$ y a $b.$

Ideales Principales

En el capítulo anterior vimos dos tipos especiales de ideales: primos y maximales. Recordemos que ideal es maximal, cuando no hay otro idel propio diferente de el que lo contenga. Caracterizamos a los ideales maximales I de A, como aquellos idelaes cuyo anillo cociente es un cuerpo. Un ideal J es primo cuando su anillo cociente es un dominio, o equivalentemente, cuando para todo x, y se cumple que xy en J implica que x está en J o y está en J. posteriores:ideales primos e ideales maximales.

A continuación, veremos una relación entre elementos primos e ideales principales (o sea generados por un elemento) primos.

Proposición 8. Sea $A$ un anillo conmutativo con identidad y sea $I$ un ideal principal no nulo, digamos que $I=\langle a\rangle ,$ $a\neq 0.$ El ideal $I$ es un ideal primo en $A,$ ssi, $a$ es un elemento primo de $A.$

Demostración: ($\Rightarrow$) Supongamos que $\langle a\rangle$ es un ideal primo. Si $a|bc$ se tiene que $bc,$ por ser un múltiplo de $a,$ es un elemento de $\langle a\rangle .$ Por ser primo el ideal, tenemos que $b$ o $c$ están en $\langle a\rangle .$ Es decir que al menos uno de ellos es un múltiplo de $a,$ o sea que $a$ divide a uno de ellos. Pero eso, es precisamente la definición de elemento primo. ($\Leftarrow$) Sea $a$ primo y sean $bc$ en $\langle a\rangle .$ Eso implica que $a|bc,$ por lo que $a|b$ o $b|c.$ Es decir que $b$ está en $\langle a\rangle$ o $c$ está en $\langle a\rangle .$ Lo que prueba que $\langle a\rangle$ es un ideal primo.

---

Ejemplo.
Los ideales $pZ$ de $\mathbb {Z}$ con $p$ primo, son ideales primos.

---




La Estructura de los Zm

Convenio. Con el fin de simplificar la notación, de ahora en adelante, usaremos los representantes canónicos para denotar los elementos del anillo $\mathbb {Z} _{m}$. Así, $x$ en $\mathbb {Z} _{m}$ denotará la clase de $x$ ($[x]$) .

Los anillos $\mathbb {Z} _{m}$ proveen interesantes ejemplos de anillos. Sabemos que si $m$ es primo, $\mathbb {Z} _{m}$ es un cuerpo y que, en caso contrario, contiene divisores de 0.

Sabemos, también, que cuando $m=rs$ con ${\text{mcd}}(r,s)=1$ entonces

$\mathbb {Z} _{m}\cong \mathbb {Z} _{r}\oplus \mathbb {Z} _{s}.$

Por inducción, cuando $m=p_{1}^{r_{1}}\cdots p_{k}^{r_{k}}$ entonces

$\mathbb {Z} _{m}\cong \mathbb {Z} _{p_{1}^{r_{1}}}\oplus \dots \oplus \mathbb {Z} _{p_{k}^{r+k}}.$

Las Unidades de $\mathbb {Z} _{m}.$ Recordemos que vimos anteriormente que un elemento $[a]$ es invertible, ssi, ${\text{mcd}}(a,m)=1.$ El cardinal de $\mathbb {Z} _{m}^{*}=U(\mathbb {Z} _{m})$ es $\varphi (m),$ donde $\varphi$ es la función de Euler. Vimos también que, con $m$ como en la discusión anterior que

$\mathbb {Z} _{m}^{*}=\mathbb {Z} _{p_{1}^{r_{1}}}^{*}\oplus \dots \oplus \mathbb {Z} _{p_{k}^{r+k}}^{*}.$

La discusión anterior reduce el problema de la estructura de $\mathbb {Z} _{m}$ a considerar el caso donde $m$ es una potencia de un primo.

Ejemplo.


Sea $m=p^{3}$ donde $p$ es un número primo. Consideremos el anillo cociente $A=\mathbb {Z} /\langle p^{3}\rangle =\mathbb {Z} _{p^{3}}.$

Observemos que ${\text{mcd}}(a,p^{3})=1$ implica que ${\text{mcd}}(a,p)=1.$ Por lo que las unidades de $A$ corresponden a números que no son divisibles por $p.$ Luego, un elemento $x$ de $A$ es un divisor de cero, ssi, $p|x.$ Luego, los divisores de cero en $A$ son:

$p,2p,,\dots ,(p-1)p,[p*p,(p+1)p,\ldots ,(p^{2}-1)].$

Luego, hay $p^{2}-1$ divisores de cero. El resto, son unidades, por lo que $\varphi (p^{3})=(p^{3}-1)-(p^{2}-1)=p^{3}-p^{2}=p^{2}(p-1).$

Sea $J$ un ideal propio de $A.$ Como $J$ no puede contener unidades, los elementos de $J$ serán múltiplos de $[p].$ Observemos que si $J=\langle p\rangle$ se tiene que $J$ es maximal, ya que fuera de $J$ todos los elementos son unidades. Además, ese razonamiento muestra, junto con la observación anterior, que $\langle p\rangle$ es el único ideal maximal de $A.$ Sea $K$ un ideal propiamente contenido en $J.$ Sea $r,$ $1<r<p^{2}$ tal que $r$ es minimal respecto a que $[rp]$ está contenido en $K.$ Si $1<r<p$ o $p<r<p^{2}$ , se tiene que $r$ es una unidad, por lo que $r^{-1}rpp=p$ y $K$ coincidiría con $J.$ Luego, $K=\langle pp\rangle =\langle p^{2}\rangle .$ Es decir que, tenemos una cadena de ideales,

$\{0\}\subset K=\langle p^{2}\rangle \subset J=\langle p\rangle \subset A=\mathbb {Z} _{p^{3}}.$

---

Proposición 9. Sea $m=p^{k},$ $k\leq 1$ y $p$ es un entero primo. Si $k=1,$ $\mathbb {Z} _{p}$ es un cuerpo. Las unidades de $\mathbb {Z} _{m}$ forman un grupo de orden $p^{k-1}(p-1)$ y los divisores de cero forman un ideal de cardinalidad $p^{k-1}$ que está generado por $p.$ Dicho ideal es maximal y es el único ideal maximal. Todos los otros ideales son de la forma $\langle p^{s}\rangle ,$ $s>1.$

Demostración: Ejercicio

---

Ejercicios

1. Hallar los ideales maximales y primos de $\mathbb {Z} _{12}$
2. Hallar los ideales maximales y primos de $\mathbb {Z} _{27},$
3. Hallar un ideal primo de $\mathbb {Z} _{20}$ que no sea maximal.
4. Hallar un ideal primo de $\mathbb {Z} \times \mathbb {Z}$ que no sea maximal.
5. Hallar un ideal propio de $\mathbb {Z} \times \mathbb {Z}$ que no sea primo.
6. ¿Cierto o falso?
   1. Cada ideal primo de un anillo (conmutativo con identidad) es un ideal maximal.
   2. Cada ideal maximal de un anillo (conmutativo con identidad) es un ideal primo.
   3. La intersección de dos ideales primos es un ideal primo.
7. Sea $p$ un entero primo y sea $A=\{a/b\in \mathbb {Q} :a,b\in \mathbb {Z} ,\quad p\nmid b\}.$
   1. Probar que $A$ es un subanillo de $\mathbb {Q} ,$ pero no es un subcuerpo de $\mathbb {Q} .$
   2. Hallar las unidades de $A,$
   3. Probar que todos los ideales de $A$ son principales y de la forma $\langle p^{k}\rangle ,$ $k\geq 1.$
   4. Describir $A/\langle p\rangle .$
8. Dar un ejemplo de un anillo donde hay un ideal primo que no es maximal.
9. Probar la proposición 9. .
10. Probar que cada elemento de $\mathbb {Z} _{p^{r}}$ que no es unidad es nilpotente (tiene una potencia igual a cero).
11. Verificar que $\mathbb {Z} _{10}/2\mathbb {Z}$ es un cuerpo.
12. Verificar que $\mathbb {Z} _{20}/2\mathbb {Z}$ no es un cuerpo.
13. ¿Cuáles son todos los ideales de $\mathbb {Z} _{m},$ $m$ cualquiera? (Sug. Probar que si $J$ es un ideal $\mathbb {Z} _{m}$ entonces $I=\{x:[x]\in J\}$ es un ideal de $\mathbb {Z}$ que contiene a $\langle m\rangle =m\mathbb {Z} .$) Aplicar lo anterior para hallar todos los ideales de $\mathbb {Z} _{12}.$ Buscar los ideales primos y maximales entre ellos.
14. Probar que cada ideal primo de un anillo finito (conmutativo con identidad) es maximal.
15. Probar que un ideal $M$ en un anillo $A$ es maximal, ssi, $A/M$ es simple (no tiene ideales propios).
16. Sean $I,$ $J$ ideales de un anillo $A$ y sea $P$ un ideal primo de $A.$ Probar que $IJ\subset P$ implica que $I\subset P$ o $J\subset P.$

El Cuerpo de Fracciones de un Dominio

Recordemos que los números racionales se construyen a partir de los enteros, como un conjunto de fracciones de números enteros.

Como veremos en esta sección, hay una construcción análoga de un cuerpo a partir de cualquier dominio. Es decir que dado un dominio $D,$ es posible hallar un cuerpo $K$ que estará formado por las fracciones de elementos de $D,$ que se llamará, por lo tanto, el cuerpo de fracciones de $D.$ Recordemos para efectos posteriores que los anillos sin divisores de cero tienen todos sus elementos cancelables. Técnicamente, el problema es cómo inventar fracciones cuando no hay división.

El problema es como inventar fracciones cuando no hay división.

Sea ${\mathcal {D}}=D\times D^{*}$ , el conjunto formado por todas las posibles parejas ordenadas de elementos de $D,$ donde el segundo elemento no puede ser nulo. Intuitivamente, podemos imaginar a cada una de esas parejas como representando una fracción.

Introduciremos una relación $\sim$ en $D\times D^{*},$ que resultará ser de equivalencia.

Sean $(x,y),$ $(x',y')$ elementos de $D\times D^{*}.$ $(x,y)\sim (x',y')\iff xy'=yx'.$


Lema A.


La relación $\sim$ es una relación de equivalencia en $D\times D^{*}.$

Demostración:
1. Reflexividad. Como $xy=yx,$ se tiene que $(x,y)\sim (x,y).$
2. Simetría. Supongamos que $(x,y)\sim (x',y')<math>.Entonces,<math>xy'=yx',$ de donde $x'y=y'x.$ Es decir, $(x',y')\sim (x,y).$
3. Transitividad. Supongamos que $(x,y)\sim (x',y')$ y $(x',y')\sim (x'',y'').$ Entonces, se cumple que $xy'=yx',\qquad x'y''=y'x''.$

   Multiplicando término a término de las ecuaciones anteriores, obtenemos:

   $xy'x'y''=yx'y'x''.$

   Es decir, $x'y'xy''=x'y'yx'',$ de donde cancelando $x'y'$ en ambos lados, obtendremos que $xy''=yx''.$ Lo que es equivalente a afirmar que

   $(x,y)\sim (x'',y'').$

---

La proposición anterior implica que $\sim$ divide $D\times D^{*}$ en una colección de clases disjuntas: las clases de equivalencia de $\sim .$

Notación. Sea $k:=(D\times D^{*})/\sim ,$ el conjunto formado por todas las clases de equivalencia de $\sim .$

Simbolizaremos por $[a,b]$ la clase de equivalencia de $(a,b),$ o sea al conjunto formado por todos los elementos de ${\mathcal {A}}$ equivalentes con $(a,b).$ Recordemos que las clases de equivalencias son disjuntas entre sí y que su reunión es todo el conjunto $D\times D^{*}.$

Los resultados del siguiente lema se usarán sistemáticamente más adelante, en especial la parte a.

Lema B. Sean $a,b,c$ elementos de $D$ tales que $ab\neq 0.$ Entonces, ${\begin{matrix}{\text{a. }}&[ca,cb]=[a,b]\quad &\quad &{\text{b. }}&[0,b]=[0,1].\quad &\quad &{\text{c. }}&[a,a]=[1,1].\end{matrix}}$

Demostración:
1. $(ca)n=(cb)a.$
2. $[0,b]=[0\cdot b,1\cdot b]=[0,1].$
3. $[a,a]=[1\cdot a,1\cdot a]=[1,1].$

---

Introduciremos operaciones en $k$ mediante las siguientes definiciones.

$\quad [a,b]+[c,d]=[ad+bc,bd].$
$\quad [a,b]\cdot [c,d]=[ac,bd].$

Lema C.
Las operaciones anteriores están bien definidas, o sea, no dependen de los representantes escogidos.

Demostración: Supongamos que $(a,b)\sim (a',b')$ y que $(c,d)\sim (c',d').$ Debemos verificar que $[a,b]+[c,d]=[a',b']+[c',d']$ y que $[a,b]\cdot [c,d]=[a',b']\cdot [c',d'].$ Es decir que, para la adición, se cumple que $[ad+bc,bd]=[a'd'+b'c',b'd'].$ Como $(ad+bc)b'd'=adb'd'+bcb'd'=ab'dd'+cd'bb'=a'bdd'+c'dbb'=(a'd'+b'c')bd,$ obtenemos el resultado deseado.

Análogamente, para la multiplicación, deberemos probar que $[ac,bd]=[a'c',b'd'].$ Como $acb'd'=a'bc'd=a'bc'd=bda'c',$ se tiene el resultado.

---


Proposición 10. (Estructura de Cuerpo de $k$)
$<k,+,\cdot >$ tiene una estructura de cuerpo.

Demostración: ($<k,+>$ es un grupo abeliano.) Sigue inmediato de la definición que la adición es conmutativa en $k.$ Como $[a,b]+[0,1]=[a\cdot 1+b\cdot 0,b\cdot 1]=[a,b]$ se concluye que $[0,1]$ es un neutro respecto a la adición. Como $[a,b]+[-a,b]=[ab+b(-a),b^{2}]=[0,b^{2}]=[0,1],$ concluimos que cada elemento tiene opuesto aditivo. Finalmente probaremos que la operación es asociativa. Sean $\alpha =[a,b],$ $\beta =[c,d]$ y $\gamma =[e,f]$ elementos de $k.$ Entonces, ${\begin{array}{rcl}\alpha +(\beta +\gamma )&=&[a,b]+[cf+de,df]\\&=&[adf+bcf+bde,bdf]\quad {\text{y}}\\(\alpha +\beta )+\gamma &=&[ad+bc,bd]+[e,f]\\&=&[adf+bcf+bde,bdf]\end{array}}$ Lo que prueba la asociatividad.
• $<k,\cdot >$ es un semigrupo con identidad, cuyos elementos no nulos son todos invertibles. Iniciaremos la demostración con la prueba de la asociatividad. Usaremos la notación empleada en la demostración de la asociatividad de la suma. ${\begin{array}{rcl}\alpha \cdot (\beta \cdot \gamma )&=&[a,b]\cdot [ce,df]=[ace,bdf]\quad {\text{y,}}\\(\alpha \cdot \beta )\cdot \gamma &=&[ac,bd]+[e,f]=[ace,bdf],\end{array}}$

  lo que prueba la asociatividad.

  La conmutatividad sigue directamente de la definición.

  Como $[a,b]\cdot [1,1]=[a,b],$ concluimos que $[1,1]$ es una identidad.

  Como $[a,b]=[0,1],$ ssi, $a=0.$ Sigue que cuando $[a,b]\neq [0,1],$ se tiene que $a\neq 0,$ y por lo tanto, que $[b,a]$ es un elemento de $k.$ Además se cumple que

  $[a,b]\cdot [b,a]=[ab,ab]=[1,1].$

  Es decir que cada elemento no nulo tiene inverso multiplicativo.

  (Distributividad.) Notación como en las pruebas de asociatividad.

  ${\begin{array}{rcl}\alpha \cdot (\beta +\gamma )&=&[a,b]\cdot [cf+de,df]=[acf+ade,bdf]\quad {\text{y,}}\\\alpha \cdot \beta +\alpha \cdot \gamma &=&[ac,bd]+[ae,bf]=[abcf+abde,b^{2}df]\\&=&[b(acf+aed),b(bdf)]=[acf+aed,bdf]\end{array}}$ lo que prueba la distributividad.

---

Veremos, ahora, que hay un subanillo de $k$ que es isomorfo a $A.$ Identificando $A$ con ese subanillo de $k,$ consideraremos a $A$ un subconjunto de $k.$

Sea $f:A\longrightarrow k$ tal que envía cada elemento $a$ de $A$ en el elemento $[a,1]$ de $k.$ Tenemos, en primer lugar que, cuando $[a,1]=[b,1],$ se cumple que $a\cdot 1=1\cdot b,$ o sea que $a=b.$ Es decir que se trata de una función inyectiva.

Además, tenemos que

${\begin{array}{rcl}f(a)+f(b)&=&[a,1]+[b,1]=[a\cdot 1+1\cdot b,1\cdot 1]=[a+b,1]=f(a+b)\quad y\\f(a)f(b)&=&[a,1]\cdot [b,1]=[ab,1]=f(ab).\end{array}}$

Lo que prueba que $f$ es un homomorfismo inyectivo de $D,$ cuya imagen (que será un subanillo de $k$ es, por lo tanto, isomorfa a $D$ como anillos con identidad, ya que $f(1)=[1,1].$ Identificaremos a $D$ con su imagen, es decir con las fracciones con ``denominador 1.

La identificación anterior nos permitirá escribir los elementos de $k$ de manera más simple. Como, de lo anterior, resulta que $[a,b]=[a,1][1,b]=a[1,b]$ y como $[1,b]=[b,1]^{-1}=b^{-1},$ tenemos que

$[a,b]=ab^{-1}={\frac {a}{b}}.$

Los elementos de $D$ se identifican con las fracciones de denominador 1.

Definición. (Cuerpo de Fracciones) Llamaremos cuerpo de fracciones de un dominio $D$ al cuerpo $k$ construido arriba. El elemento $[a,b]$ se escribirá siempre como una fracción

${\frac {a}{b}}\quad {\text{ o }}\quad a/b.$

Los elementos de $D$ son las fracciones con denominador 1, que se escriben usualmente sin usar fracciones.


El cuerpo de fracciones de un dominio tiene la siguiente propiedad universal.


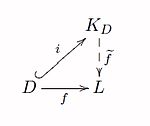
Proposición 11. (Propiedad Universal del cuerpo de Fracciones) Sea $D$ un dominio de integridad y sea $K_{D}$ su cuerpo de fracciones. Sea $L$ un cuerpo cualquiera y sea $f:D\longrightarrow L$ un homomorfismo inyectivo de anillos con identidad. Entonces, hay un único homomorfismo de cuerpos ${\widetilde {f}}:K_{D}\longrightarrow L$ que coincide con $f$ para los elementos de $D.$ Es decir, que hace conmutativo el siguiente diagrama.



Demostración: Recordemos que en un cuerpo, la fracción $a/b$ está definida como $ab^{-1}.$ Sean $a,$ $b$ elementos de $D.$ Si queremos que se cumpla la conmutatividad del diagrama debemos tener que ${\widetilde {f}}(a/b)={\widetilde {f}}(ab^{-1})={\widetilde {f}}(a){\widetilde {f}}(b)^{-1}=f(a)f(b)^{-1}=f(a)/f(b).$

Usando la última relación, ${\widetilde {f}}(a/b)=f(a)/f(b)$ como definición para ${\widetilde {f}},$ donde la primer fracción es en $K_{D}$ y la segunda en $L,$ se ve la unicidad si esa función está bien definida y es un homomorfismo de cuerpos.

Sea $c/d=a/b,$ entonces $ad=bc,$ por lo que $f(a)f(d)=f(b)f(c).$ Por lo tanto, $f(a)/f(b)=f(c)/f(d)$; lo que implica que ${\widetilde {f}}$ está bien definida, su valor no depende del representante usado de una fracción. El resto de la demostración queda de ejercicio.

---

Corolario 11.1. Sea $D$ un dominio y $K_{D}$ su cuerpo de fracciones. Sea $L$ un cuerpo cualquiera que contiene a $D,$ entonces $K_{D}$ es isomorfo a un subcuerpo de $L$ que contiene a $D,$

Demostración: Aplicar la proposición a la inclusión canónica $D\hookrightarrow L.$

---

En la situación del corolario, es usual identificar el cuerpo de fracciones con el subcuerpo isomorfo.

Cualquier cuerpo $L$ de característica cero tiene un anillo primo isomorfo a los Enteros, por lo que contienen un subcuerpo identificable con los racionales, $\mathbb {Q} ,$ que es obviamente el cuerpo primo del cuerpo.




Ejercicios

1. Completar la demostración de la proposición 11.
2. Probar que el cuerpo de fracciones de $\mathbb {Z} [{\sqrt {13}}]=\{a+b{\sqrt {13}}:a,b\in \mathbb {Z} \}$ es $K=\mathbb {Q} [{\sqrt {13}}]=\{x+y{\sqrt {13}}:x,y\in \mathbb {Q} \}.$ Determinar cuáles de los siguientes números están en $K.$ En caso afirmativo expresarlos en la forma $a+b{\sqrt {13}},$ $a$ y $b$ racionales.
   ${\begin{matrix}a.&{\dfrac {1}{1-{\sqrt {13}}}}.&b.&{\sqrt {53}}.\\c.&{\dfrac {5-{\sqrt {13}}}{2+{\sqrt {13}}}}.&d.&(2+{\sqrt {3}})^{-2}.\\\end{matrix}}$
3. Sea $D=\mathbb {Z} [{\sqrt {m}}]=\{x+y{\sqrt {m}}:x,y\in \mathbb {Z} \},$ $m$ entero que no es un cuadrado perfecto. Probar que $D$ es un dominio y describir a su cuerpo de fracciones.
4. Probar que los Racionales son el cuerpo de fracciones de los Enteros.
5. Probar que no hay un número racional $x$ tal que $x^{2}=2.$ (Suponer que lo hay, y usar que 2 es primo en el anillo $\mathbb {Z} .$)
6. ¿Cuál es el cuerpo de fracciones de un cuerpo?

Ejercicios del Capítulo

1. Sean $a,$ $b$ elementos de un dominio. Probar que $\langle a\rangle =\langle b\rangle ,$ ssi, $a$ y $b$ son asociados.
2. Probar que la relación de "ser asociado con" es una relación de equivalencia.
3. Sea $D=\mathbb {Z} [i]$ el dominio de los enteros de Gauss y sea $N(z)=z{\overline {z}}$ la norma de $D$.
   1. Probar que 5 no es irreducible en $D.$ Sugerencia $5=(2+i)(2-i),$ por lo que no puede ser un elemento primo de $D.$
   2. Probar que 3 es irreducible en $D.$
   3. Probar que un número entero primo $p$ que puede escribirse como la suma de dos cuadrados, digamos $p=a^{2}+b^{2}$ no puede ser irreducible en $D.$
   4. Sea $\pi$ un elemento primo de $D.$ Probar que su conjugado también es primo.
4. Sea $D=\mathbb {Z} [{\sqrt {2}}],$ probar que ${\sqrt {3}}$ no está en $D.$ Sea $E=D[{\sqrt {3}}]=\{\alpha +\beta {\sqrt {3}}:\alpha ,\beta \in D\}.$ Probar que $E$ es un dominio de integridad, que cada elemento de $E$ puede escribirse de una única manera como $a+b{\sqrt {2}}+c{\sqrt {3}}+d{\sqrt {6}},\quad a,b,c,d,\in \mathbb {Z} .$

   Hallar una descripción el cuerpo de fracciones de $E.$

5. Sea $\langle M,\cdot ,e\rangle$ un monoide cancelativo, es decir que $ax=ay\implies x=y.$ Imitar la construcción del cuerpo de fracciones, para construir un grupo $G$ que contiene una copia de $M$ y donde cada elemento de $M$ es invertible. (Por ejemplo, si el monomio es $\langle \mathbb {N} ,+,0\rangle ,$ el grupo será $\mathbb {Z}$)

Comentarios

Como hemos mencionado antes, los intentos de prueba del Último teorema de Fermat, condujeron a la creación de nuevas matemáticas. Varios matemáticos intentaron conseguir una solución en dominios de números complejos que incluían radicales. Parecía que la divisibilidad en esos dominios era semejante a aquella de los Enteros. Muchas pruebas erróneas tuvieron origen en esta creencia que siempre la semejanza era perfecta. Al descubrir situaciones donde irreducibles no eran primos llevo a profundizar el estudio de esos dominios, lo que nosotros haremos en el capítulo sobre Álgebra/Álgebra Abstracta (Primer Curso)/Contenidos/Tipos de Dominio|Tipos de dominios]].