En esta sección añadimos problemas de convolución
Para el circuito RLC que se muestra en la figura, determine (R=3,L=2,C=K=2):
- La respuesta al escalón
- La respuesta al impulso
- La respuesta a

Considere un sistema LTI cuya respuesta al impulso es la función  . ¿Es este sistema causal?. Justifique su respuesta.
. ¿Es este sistema causal?. Justifique su respuesta.
Calcule y grafique la salida del sistema a las señales:


El sistema de la pregunta anterior se coloca en cascada con un segundo sistema cuya respuesta al impulso es  , donde
, donde  . ¿Es este segundo un sistema causal?
. ¿Es este segundo un sistema causal?
Determine y grafique la respuesta de la cascada de sistemas a las entradas del problema anterior
Considere la cascada de dos sistemas. El primero, que llamaremos S1, comprime (operación sobre el tiempo) la señal de entrada por un factor de 2, i.e.,  . El segundo (S2) es un circuito RC (filtro pasabajos) con RC=1. Si la señal de entrada es
. El segundo (S2) es un circuito RC (filtro pasabajos) con RC=1. Si la señal de entrada es  calcule la salida de la cascada de ambos si:
calcule la salida de la cascada de ambos si:


¿Serán idénticas las salidas?, ¿deberían serlo?.
Considere la señal  y tengamos un sistema cuya respuesta al impulso es
y tengamos un sistema cuya respuesta al impulso es  . Calcule y grafique la respuesta a las siguientes señales:
. Calcule y grafique la respuesta a las siguientes señales:
 . T>1
. T>1 .
. .
.- ¿Puede generalizar su resultado a cualquier h(t)y x(t)?
Grafique cada una de las señales y realice las siguientes convoluciones:
 .
. .
. .
. .
. .
.
Resuelto por Ender Valdivieso Carnet 06-40411
Ejercicio 1
 .
.
 .
.
Gráfica de  .
.

Gráfica de  .
.
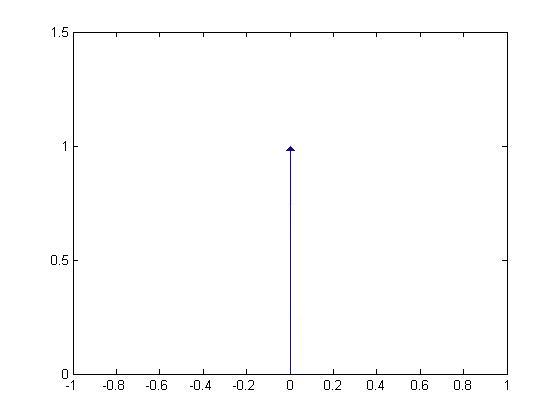
A priori conocemos que la función delta  es el elemento neutro en la convolución. Por ende, debemos obtener la misma señal como salida. Al realizar los cálculos tenemos:
es el elemento neutro en la convolución. Por ende, debemos obtener la misma señal como salida. Al realizar los cálculos tenemos:

Para 



Gráfica de #  .
.

Ejercicio 2
 .
.
 .
.
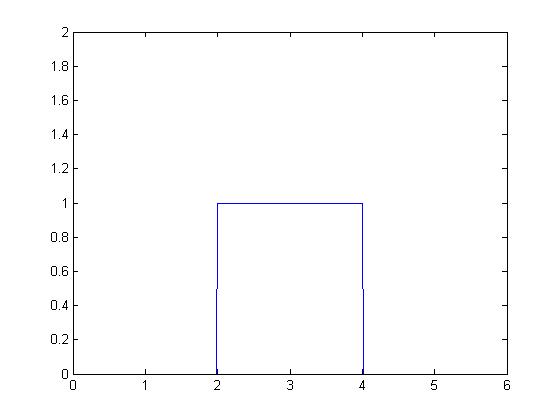
Gráfica de  .
.

Gráfica de  .
.


Para 


Para 


Para 


Enotonces la función  quedaría de la forma
quedaría de la forma

Gráfica de #  .
.

Ejercicio 3
 .
.
 .
.
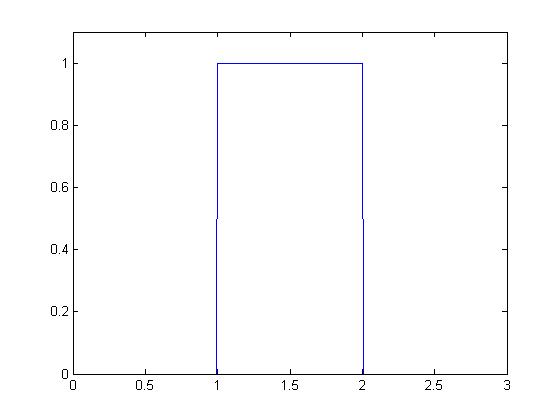
Gráfica de  .
.

Gráfica de  .
.


Para 


Para 


Para 


Para 


Para 


La función sería  para cualquiero otro valor de
para cualquiero otro valor de 
En síntesis, la función sería de la forma

Gráfica de #  .
.

Ejercicio 4
 .
.
 .
.
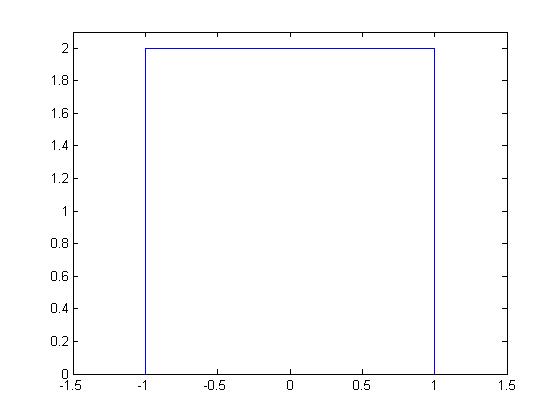
Gráfica de  .
.

Gráfica de  .
.


Para 


Para 


Para 


En síntesis, la función sería de la forma

Gráfica de #  .
.

Ejercicio 5
 .
.
 .
.
Gráfica de  .
.
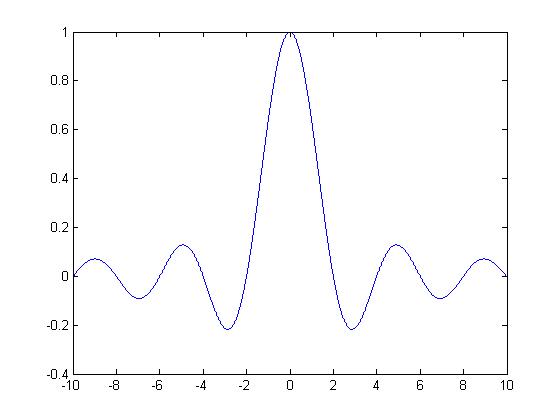
Gráfica de  .
.



Para todo tiempo se cumple que

Una versión imprimible se encuntra en el siguiente archivoArchivo
Sean,



Determine:


Subsección 1 Problema 1
[editar]Realizado Por: Jesús Querales #05-38758
1. 
Haciendo,


Por definición tenemos que la convolución esta dada por:

Estableciendo,


Entonces resulta,


Usando la propiedad de filtrado del impulso,

Subsección 2 Problema 1
[editar]Realizado Por: Alexander Gamero #05-38196
En el intervalo donde esta definido  ,
, ![{\displaystyle [0,2]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c930c6b148a1afeee1a559f22d76ee3262a73a56) ,
, 
Por lo que se puede reescribir 
Al ser  una señal periódica (
una señal periódica ( ), se puede convolucionar
), se puede convolucionar  con un período de
con un período de 
Para  ,
,

Entonces, utilizando la definición de convolución;

Esta convolución se calcula graficamente de la siguiente manera:






 para todo lo demás
para todo lo demás
Para hallar la señal periódica  reemplazamos
reemplazamos  , resultando:
, resultando:
 '
'


























































































































![{\displaystyle [0,2]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c930c6b148a1afeee1a559f22d76ee3262a73a56)
















