Fundamentos de la Matemática/Texto completo

Fundamentos de la Matemática

Los fundamentos de las matemáticas, independientemente de las divisiones y subdivisiones de esta materia, e independientemente de la evolución histórica que ha tenido, se fundamenta claramente en la intuición, definiendo intuición como la capacidad para entender conceptos.

El concepto más básico en matemáticas es el concepto de conjunto, y entendido este concepto, es la relación y particularmente la relación binaria, lo que define la base de las matemáticas, las matemáticas no tiene que hablar de números necesariamente, si bien los números son una parte importante.

Teoría intuitiva de conjuntos

La teoría intuitiva de conjuntos, se basa en la capacidad intuitiva, innata, para poder entender esta parte de las matemáticas, según unos conceptos básicos sin una base teórica previa. La teoría de conjuntos se atribuye a Georg Cantor entre otros autores, aquí no plantearemos teoría de ningún tipo, sino conceptos intuitivos.

Definiciones

Que es un conjunto: un conjunto es una agrupación de elementos hecho con cualquier criterio, por ejemplo: las cosas que hay encima de una mesa en un momento dado, los coches de una ciudad, las letras del alfabeto, las piezas de un motor, etc. son conjuntos.

Los conjuntos suelen representarse con letra mayúscula: A, B, C, ...

Que es un elemento: un elemento de un conjunto tiene carácter único, que tiene propiedades que lo hace diferénciale de los demás elementos del conjunto, puede haber propiedades que varios elementos de un mismo conjunto puede cumplir o no.

Los elementos suelen representarse con letras minúsculas: a, b, c ...

Que es el conjunto universal: el conjunto universal o de referencia es el conjunto que abarca todos los elementos que en cada caso podamos tratar, todos los conjuntos que en cada caso estemos tratando son subconjuntos de ese conjunto universal.

El conjunto universal suele representarse con la letra: U

Que es el conjunto vacío: el conjunto vacío es el que no tiene ningún elemento, suele representarse así: $\varnothing$

Definición por extensión

Un conjunto se define por extensión cuando se enumeran todos sus elementos, por ejemplo, podemos definir el conjunto de las vocales V:

$V=\{a,e,i,o,u\}$

o de días de la semana S:

$S=\{lunes,martes,mi{\acute {e}}rcoles,jueves,viernes,s{\acute {a}}bado,domingo\}$

Definición por comprensión

Cuando el conjunto se define por una o más propiedades o condiciones que los elementos del conjunto cumplen, el conjunto de las vocales V:

$V=\{x|x\;es\;una\;vocal\}$

El conjunto V se define como el conjuntos x tal que x sea una vocal. El conjunto de días de la semana S:

$S=\{x|x\;es\;un\;d{\acute {\imath }}a\;de\;la\;semana\}$

El conjunto S se define como el de los elementos x, tal que x sea un día de la semana.

Diagramas de Venn

Un diagrama de Venn es una representación grafica plana en la cual define un conjunto por una superficie cerrada, un circulo, un ovalo, un rectángulo etc, que delimita el conjunto y la relación entre varios conjuntos.

Se define el conjunto universal U y los conjuntos A y B:

$U=\{a,b,c,d,e,f\}$

El conjunto A:

$A=\{b,c,d\}$

El conjunto B:

$B=\{d,e\}$

---

Con el conjunto universal U y los conjuntos A y B:

$U=\{a,b,c,d,e,f\}$

El conjunto A:

$A=\{b,c\}$

El conjunto B:

$B=\{e,f\}$

---

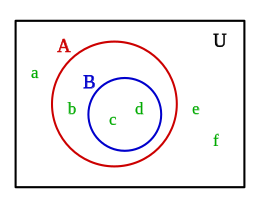
Otro ejemplo con el conjunto universal U y los conjuntos A y B:

$U=\{a,b,c,d,e,f\}$

El conjunto A:

$A=\{b,c,d\}$

El conjunto B:

$B=\{c,d\}$

---

Relaciones de conjuntos

Dado el conjunto universal U:

$U=\{a,b,c,d,e,f\}$

Que señala que el conjunto esta formado por los elementos: a, b, c, d, e, f. Los elementos del conjunto se representan ente llaves y se separan por comas.

Los conjuntos A y B se representan:

$A=\{b,c\}$

$B=\{a,b,c,f\}$

$\varnothing =\{\}$

Un elemento pertenece a un conjunto si forma parte de él y se representa:

$f\in U\;,\quad f\notin A\;,\quad f\in B$

Que se puede leer: f es un elemento de U, f no es un elemento de A, f es un elemento de B.

Subconjunto, un conjunto A es subconjunto de otro B si todos los elementos de A pertenecen también a B. Todo conjunto es subconjunto de si mismo, el conjunto vacío es subconjunto de todo conjunto.

$U\subseteq U\;,\quad A\subseteq U\;,\quad B\subseteq U\;,\quad \varnothing \subseteq U\;,\quad B\nsubseteq A$

Que se puede leer: U es un subconjunto de U, A es un subconjunto de U, B es un subconjunto de U, el conjunto vació es un subconjunto de U, B no es un subconjunto de A.

Dos conjuntos son iguales si tienen los mismos elementos.

$A\subseteq B\quad \land \quad B\subseteq A\quad \longleftrightarrow \quad A=B$

Si A es subconjunto de B y B es subconjunto de A, es equivalente a que A y B son iguales.

Operaciones entre conjuntos

Dados unos conjuntos se pueden definir algunas operaciones:

Complemento de un conjunto: Dado un conjunto universal U y un conjunto A de U, el complemento de A es el formado por los elementos de U que no perteneces a A. Que se representa:

$A^{C}$

Se puede ver también que:

${A^{C}}^{C}=A$

El complemento del complemento de un conjunto es el mismo conjunto.

$U^{C}=\varnothing$

El complemento del conjunto universal es el conjunto vacío.

Del mismo modo:

$\varnothing ^{C}=U$

El complemento del conjunto vacío es el conjunto universal.

---

La unión de dos conjuntos: A y B es el conjunto formado por los elementos que pertenecen a A o a B. y se representa:

$A\cup B$

La operación unión es conmutativa:

$A\cup B=B\cup A$

La unión de A con B es igual a la unión de B con A.

La unión del conjunto universal con otro conjunto da como resultado el conjunto universal:

$U\cup A=U$

La unión de un conjunto con el conjunto vacío da como resultado el mismo conjunto:

$A\cup \varnothing =A$

---

La intersección de dos conjuntos: A y B es el conjunto formado por los elementos que pertenecen a A y a B. y se representa:

$A\cap B$

La operación intersección es conmutativa:

$A\cap B=B\cap A$

La intersección de A con B es igual a la intersección de B con A.

La intersección del conjunto universal con otro conjunto da como resultado ese conjunto:

$U\cap A=A$

La intersección de un conjunto con el conjunto vacío da como resultado el conjunto vacío:

$A\cap \varnothing =\varnothing$

Producto cartesiano

El producto cartesiano de dos conjuntos: A y B es una operación, que da como resultado otro conjunto: A*B, cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto.

Por ejemplo, dados los conjuntos:

$A=\{1,2,3\}$

y

$B=\{a,b,c\}$

su producto cartesiano es:

${\begin{array}{r|ccc}c&(1,c)&(2,c)&(3,c)\\b&(1,b)&(2,b)&(3,b)\\a&(1,a)&(2,a)&(3,a)\\\hline A\times B&1&2&3\\\end{array}}$

Que se expresa:

$A\times B=\{(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),(3,a),(3,b),(3,c)\}$

Cada uno de los elementos:

$(x,y)\in A\times B\;:\quad x\in A\;\land \;y\in B$

Un par ordenado: (x,y) de A*B, cumple que x pertenece a A e y pertenece a B.

El producto cartesiano no es conmutativo:

$A\times B\neq B\times A$

Y por tanto:

$(a,b)\neq (b,a)$

El par ordenado (a,b) es distinto del par ordenado (b,a).

Producto cartesiano, caso general

El caso general de producto cartesiano con n conjuntos, que designaremos como:

$A_{1},\;A_{2},\;A_{3},\;\ldots ,\;A_{n}$

Cada uno de los elementos del producto cartesiano de n conjuntos se denomina tupla:

$(a_{1},a_{2},a_{3},\ldots ,a_{n})\in A_{1}\times A_{2}\times A_{3}\times \ldots \times A_{n}$

Bibliografía

1. Dávila Cervantes, Claudio Alberto; Pardo Montaño, Ana Melisa (2016) (en español). Teoría de conjuntos (1 edición). FLACSO. 

Enlaces externos

1. Teoría de Conjuntos
2. Capítulo 7: TEORIA DE CONJUNTOS

Relación matemática

Una relación matemática entre los elementos, de uno o más conjuntos, es el conjunto de las tuplas de elementos de esos conjuntos que cumplen una determinada condición.

El caso más general de relaciones matemáticas es el de relaciones binarias, donde intervienen dos elementos en la relación:

${\mathcal {R}}=\left\{\left(a,b\right)\in A\times B\mid {\mathcal {P}}\left(a,b\right)\right\}$

La relación ${\mathcal {R}}$ es el conjunto de pares ordenados (a,b) que pertenecen al producto $A\times B$ que cumplen la propiedad ${\mathcal {P}}(a,b)$

Claramente:

${\mathcal {R}}\subseteq A\times B$

La relación ${\mathcal {R}}$ es un subconjunto de $A\times B$

Notación caso general

Dada una relación entre los elementos de n conjuntos:

${\mathcal {R}}=\left\{(a_{1},a_{2},a_{3},\ldots ,a_{n})\in A_{1}\times A_{2}\times A_{3}\times \ldots \times A_{n}\mid {\mathcal {P}}(a_{1},a_{2},a_{3},\ldots ,a_{n})\right\}$

La relación: ${\mathcal {R}}$ se define como las tuplas: $(a_{1},a_{2},a_{3},\ldots ,a_{n})$, del producto de conjuntos: $A_{1}\times A_{2}\times A_{3}\times \ldots \times A_{n}$, que cumplen la condición: ${\mathcal {P}}(a_{1},a_{2},a_{3},\ldots ,a_{n})$.

Si una tupla es de la relación se expresa:

${\mathcal {R}}(a_{1},a_{2},a_{3},\ldots ,a_{n})\quad o\quad (a_{1},a_{2},a_{3},\ldots ,a_{n})\in {\mathcal {R}}$

Si la tupla no es de la relación:

${\cancel {\mathcal {R}}}(a_{1},a_{2},a_{3},\ldots ,a_{n})\quad o\quad \lnot {\mathcal {R}}(a_{1},a_{2},a_{3},\ldots ,a_{n})\quad o\quad (a_{1},a_{2},a_{3},\ldots ,a_{n})\notin {\mathcal {R}}$

Tipos de relaciones por el número de elementos

En las relaciones se diferencian los tipos según el número de conjuntos en el producto cartesiano, que es el número de términos de la relación:

Relación unaria: un solo conjunto $R\subseteq A\times 1,\;R(a)$

Relación binaria: con dos conjuntos $R\subseteq A_{1}\times A_{2},\;R(a_{1},a_{2})$

Relación ternaria: con tres conjuntos $R\subseteq A_{1}\times A_{2}\times A_{3},\;R(a_{1},a_{2},a_{3})$

Relación cuaternaria: con cuatro conjuntos $R\subseteq A_{1}\times A_{2}\times A_{3}\times A_{4},\;R(a_{1},a_{2},a_{3},a_{4})$

Relación n-aria: caso general con n conjuntos $R\subseteq A_{1}\times A_{2}\ldots \times A_{n},\;R(a_{1},a_{2},\ldots ,a_{n})$

Tipos de relaciones por la igualdad de los conjuntos

Si el producto cartesiano es del mismo conjunto:

$A\times A\times A\times \ldots \times A=A^{n}$

La relación se denomina relación homogénea y se representa:

${\mathcal {R}}=\left\{(a_{1},a_{2},a_{3},\ldots ,a_{n})\in A^{n}\mid {\mathcal {P}}(a_{1},a_{2},a_{3},\ldots ,a_{n})\right\}$

Si no todos los conjuntos son iguales, se denomina: relación heterogénea y se representa:

${\mathcal {R}}=\left\{(a_{1},a_{2},a_{3},\ldots ,a_{n})\in A_{1}\times A_{2}\times A_{3}\times \ldots \times A_{n}\mid {\mathcal {P}}(a_{1},a_{2},a_{3},\ldots ,a_{n})\right\}$

Relación binaria

Un caso particular de relación matemática, y el más ampliamente estudiado y de mayor interés matemático en cuanto a su interés generalizado, el la relación binaria.

Una relación matemática es binaria si la relación es entre dos elementos, del mismo o de distintos conjuntos, si los dos elementos de la relación son del mismo conjunto se dice homogénea, si los dos conjuntos son distintos o los tomamos como distintos la relación se dice heterogénea, que comúnmente se denomina correspondencia

Dado el conjunto A:

$A=\{a,b,c,d\}$

y la relación binaria homogénea definida entre sus elementos:

${\mathcal {R}}=\{(a,b),(b,a),(b,c),(c,d),(d,d),(d,b)\}$

Que se representa en la figura de la derecha.

Esta misma relación puede representarse como heterogénea o correspondencia:

${\begin{array}{rrcl}{\mathcal {R}}:&A&\longrightarrow &A\\\end{array}}$

La relación R definida de A sobre A.

${\begin{array}{r|cccc}d&&&+&+\\c&&+&&\\b&+&&&+\\a&&+\\\hline A\times A&a&b&c&d\end{array}}$

El producto cartesiano se puede representar como un cuadrante, y la relación se señala con un signo: +, y en blanco si no existe relación. Los elementos del primer conjunto se ponen en el eje horizontal y los elementos del segundo conjunto en el vertical.

Los conjuntos de una correspondencia no tienen que ser iguales, como se indica en la definición de relación binaria heterogénea, sino que pueden ser de distinto tipo, a la derecha se puede ver una correspondencia entre un conjunto de pinceles: P, con otro de caras pintadas: C, asociando cada pincel de P, con la cara de C, que esta pintada del mismo color.

Relación binaria homogénea

En matemáticas, una relación binaria homogénea es una relación matemática $R$ entre dos elementos que pertenecen al mismo conjunto. Una relación $R$ de $A^{2}$ se puede representar mediante pares ordenados $(a,b)$ para los cuales se cumple una propiedad ${\mathcal {P}}(a,b)$, de forma que $(a,b)\in A^{2}$, y se anota:

$R=\left\{\left(a,b\right)\in A^{2}\mid {\mathcal {P}}\left(a,b\right)\right\}$

Que se lee: la relación binaria $R$ es el conjunto de pares ordenados $(a,b)$ pertenecientes al producto cartesiano $A^{2}$, y para los cuales se cumple la propiedad ${\mathcal {P}}$ que los relaciona.

Por oposición a la relación binaria heterogenia, o correspondencia matemática donde los dos elementos de la relación binaria son de conjuntos diferentes.

Propiedades de las relaciones binarias homogéneas

Una relaciones binarias homogéneas, puede cumplir o no una determinada propiedad de la relación binaria homogénea según estas propiedades se determina una determinada estructura en el conjunto respecto a la relación binaria definida.

Dada la definición de relación binaria homogénea de un conjunto A y una propiedad P como el conjunto de pares ordenado R de A que cumple la propiedad P, ha de tenerse en cuenta que la relación binaria es ese conjunto de pares ordenados, que además puede cumplir otras propiedades, reflexiva, simétrica, transitiva, etc, normalmente se dice relación reflexiva, relación simétrica, etc.

Aquí diferenciaremos la relación de sus propiedades, y llamaremos relación al conjunto de pares ordenados de forma general o a sus subtipos, y llamaremos como propiedades a las que una relación puede o no cumplir, por lo tanto diremos: propiedad reflexiva, propiedad simétrica, propiedad transitiva, etc. Ayudando a diferenciar de este modo lo que una relación y sus subtipos de lo que son propiedades de una relación

Reflexividad

En una relación binaria homogénea la reflexividad determina la posible relación de un elemento con sigo mismo, en todos los casos, nunca o a veces.

Propiedad reflexiva

Una relación es reflexiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}$

Se dice que esta relación binaria homogénea es relación reflexiva, si cumple:

• Relación reflexiva: la relación R es reflexiva si todo elemento a de A está relacionado con sigo mismo.

$\forall a\in A:\;(a,a)\in R$

Para todo a de A se cumple que (a,a) pertenece a R

Propiedad no reflexiva

Una relación es no reflexiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}$

Se dice que esta relación binaria homogénea es relación no reflexiva, si cumple:

• Relación no reflexiva: la relación R es no reflexiva si existen elementos a de A que no está relacionados con sigo mismo.

$\exists a\in A:\;(a,a)\notin R$

Existe a de A que cumple que (a,a) no pertenece a R

Propiedad irreflexiva

Una relación es irreflexiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}$

Se dice que esta relación binaria homogénea es relación irreflexiva, si cumple:

• Relación irreflexiva: la relación R es irreflexiva si ningún elemento a de A está relacionado con sigo mismo.

$\forall a\in A:\;(a,a)\notin R$

Para todo a de A se cumple que (a,a) no pertenece a R

Propiedad no irreflexiva

Una relación es no irreflexiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}$

Se dice que esta relación binaria homogénea es relación no irreflexiva, si cumple:

• Relación no irreflexiva: la relación R es no irreflexiva si existen elementos a de A que están relacionados con sigo mismo.

$\exists a\in A:\;(a,a)\in R$

Existen elementos a de A que cumplen que (a,a) pertenece a R

Propiedad arreflexiva

Una relación es arreflexiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}$

Se dice que esta relación binaria homogénea es relación arreflexiva, si cumple:

• Relación arreflexiva: la relación R es arreflexiva si existen elementos a de A que están relacionados con sigo mismo y existen elementos b de A que no están relacionados con sigo mismo.

${\Bigg \{}{\begin{array}{l}\exists a\in A\;:\;(a,a)\in R\\\exists b\in A\;:\;(b,b)\notin R\end{array}}$

Existen elementos a de A que cumplen que (a,a) pertenece a R y existen elementos b de A que cumplen que (b,b) no pertenece a R

Simetría

En una relación binaria homogénea la simetría determina la posible de que si un elemento a esta relacionado con otro b el b este relacionado con el a, en todos los casos, nunca o a veces.

Propiedad simétrica

Una relación es simétrica si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación simética, si cumple:

• Relación simétrica: la relación R es simétrica si el elemento a esta relacionado con b, entonces b esta relacionado con a.

$\forall a,b\in A\;:\;(a,b)\in R\quad \longrightarrow \quad (b,a)\in R$

Para todo a, b de A si cumple que (a,b) pertenece a R, entonces (b,a) también pertenece a R.

Propiedad no simétrica

Una relación es no simétrica si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación no simética, si cumple:

• Relación no simétrica: la relación R es no simétrica si existe el elemento a que esta relacionado con b y b no esta relacionado con a.

$\exists a,b\in A\;:\;(a,b)\in R\quad \land \quad (b,a)\notin R$

Existen a, b de A que cumple que (a,b) pertenece a R y (b,a) no pertenece a R.

Propiedad antisimétrica

Una relación es antisimétrica si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación antisimética, si cumple:

• Relación antesimétrica: la relación R es antisimetrica si el elemento a esta relacionado con b, entonces b no esta relacionado con a.

$\forall a,b\in A\;:\;(a,b)\in R\quad \longrightarrow \quad (b,a)\notin R$

Para todo a, b de A si cumple que (a,b) pertenece a R, entonces (b,a) no pertenece a R.

Propiedad no antisimétrica

Una relación es no antisimétrica si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación no antisimética, si cumple:

• Relación no antesimétrica: la relación R es no antisimetrica si existe el elemento a esta relacionado con b y b esta relacionado con a.

$\exists a,b\in A\;:\;(a,b)\in R\quad \land \quad (b,a)\in R$

Existe a, b de A que cumple que (a,b) pertenece a R y (b,a) pertenece a R.

Propiedad asimétrica

Una relación es asimétrica si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación asimética, si cumple:

• Relación asimétrica: la relación R es asimetrica si existe el elemento a que esta relacionado con b y b esta relacionado con a y existe el elemento c que esta relacionado con d y d no esta relacionado con c.

${\Bigg \{}{\begin{array}{l}\exists a,b\in A\;:\;(a,b)\in R\;\land \;(b,a)\in R\\\exists c,d\in A\;:\;(c,d)\in R\;\land \;(d,c)\notin R\end{array}}$

Existe a, b de A que cumple que (a,b) pertenece a R y (b,a) pertenece a R y existe c, d de A que cumple que (c,d) pertenece a R y (d,c) no pertenece a R.

Transitividad

En una relación binaria homogénea, la transitividad, determina la posible relación de un elemento con un segundo, la de este segundo con un tercero y la del primero con el tercero, en todos los casos, nunca o a veces.

Propiedad transitiva

Una relación es transitiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación transitiva, si cumple:

• Relación transitiva: la relación R es transitiva si el elemento a esta relacionado con b y b esta relacionad con c, entonces a esta relacionado con c.

$\forall a,b,c\in A\;:\;(a,b)\in R\;\land \;(b,c)\in R\quad \longrightarrow \quad (a,c)\in R$

Para todo a, b, c de A si se cumple que (a,b) pertenece a R y (b,c) pertecece a R, entonces (a,c) pertenece a R.

Propiedad no transitiva

Una relación es no transitiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación no transitiva, si cumple:

• Relación no transitiva: la relación R es no transitiva si existen los elementos a que esta relacionado con b y b que esta relacionad con c y a no esta relacionado con c.

$\exists a,b,c\in A\;:\;(a,b)\in R\quad \land \quad (b,c)\in R\quad \land \quad (a,c)\notin R$

Existen a, b, c de A que cumple que (a,b) pertenece a R y (b,c) pertecece a R y (a,c) no pertenece a R.

Propiedad intransitiva

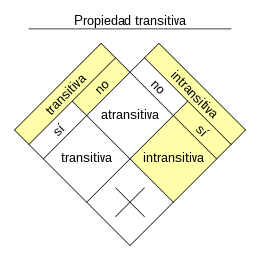
Una relación es intransitiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación intransitiva, si cumple:

• Relación intransitiva: la relación R es intransitiva si el elemento a esta relacionado con b y b esta relacionad con c, entonces a no esta relacionado con c.

$\forall a,b,c\in A\;:\;(a,b)\in R\;\land \;(b,c)\in R\quad \longrightarrow \quad (a,c)\notin R$

Para todo a, b, c de A si se cumple que (a,b) pertenece a R y (b,c) pertecece a R, entonces (a,c) no pertenece a R.

Propiedad no intransitiva

Una relación es no intransitiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación no intransitiva, si cumple:

• Relación no intransitiva: la relación R es no intransitiva si existen los elementos a que esta relacionado con b y b que esta relacionad con c y a esta relacionado con c.

$\exists a,b,c\in A\;:\;(a,b)\in R\quad \land \quad (b,c)\in R\quad \land \quad (a,c)\in R$

Existen a, b, c de A que cumple que (a,b) pertenece a R y (b,c) pertecece a R y (a,c) pertenece a R.

Propiedad atransitiva

Una relación es atransitiva si:

Dado un conjunto A, y una relación binaria homogénea: R entre sus elementos

$R=\{(a,b)\in \;A^{2}:\quad R(b,a)\}$

Se dice que una relación binaria homogénea es relación atransitiva, si cumple:

• Relación atransitiva: la relación R es atransitiva si existen los elementos: a que esta relacionado con b y b que esta relacionado con c y a esta relacionado con c, y existen los elementos d que esta relacionado con e y e esta relacionado con f y d no esta relacionado con f.

${\Bigg \{}{\begin{array}{l}\exists a,b,c\in A\;:\;(a,b)\in R\;\land \;(b,c)\in R\;\land \;(a,c)\in R\\\exists d,e,f\in A\;:\;(d,e)\in R\;\land \;(e,f)\in R\;\land \;(d,f)\notin R\end{array}}$

Existen a, b, c de A que cumplen que (a,b) pertenece a R y (b,c) pertenece a R y (a,c) pertenece a R y existen d, e , f de A que cumplen que (d,e) pertenece a R y (e,f) pertenece a R y (d,f) no pertenece a R.

Relación parcial o total

Una relación binaria homogénea es parcial si existen un par de elementoa: a, b del conjnto A: a esta relacionado con b, o b esta relacionado con a.

La relación es total si todo par de elementos: a, b del conjunto A: a esta relacionado con b o b esta relacionado con a.

Relación parcial

Una relación binaria R en el conjunto A es una relación parcial cuando se cumple que existen al menos dos elementos a, b que estan relacionado:

$\exists a,b\in A:\quad aRb\quad \lor \quad bRa$

Existen a, b de A que cumplen que a esta relacionada con b o b esta relacionada con a.

Los elementos a, b del conjunto A, que estan relacionados a con b o b con a se dicen comparables.

Los elementos a, b del conjunto A, que no estan relacionados ni a con b ni b con a se dicen no comparables.

Relación total

Una relación binaria R en un conjunto A es una relación total (o relación conexa) cuando se cumple que para cada dos elementos a y b de A, o a está relacionado con b o b está relacionado con a, esto es:

$\forall a,b\in A:\quad aRb\quad \lor \quad bRa$

Para todo a, b de A, se cumple que a esta relacionado con b o b esta relacionado con a.

Tenga en cuenta que esto implica una relación reflexiva.

Si relación binaria R en un conjunto A es de orden total, todos los elementos a, b de A son comparables.

Relación parcial y total

Una relación binaria R en un conjunto A es parcial si existen un par de elementos a, b de A y a esta relacionado con b.

Una relación binaria R en un conjunto A es total si para todo par de elementos a, b de A y a esta relacionado con b.

Toda relación total es parcial, dado que la relación total es un caso particular de relación parcial.

Relación parcial y no total

Una relación binaria R en un conjunto A es parcial si existen un par de elementos a, b de A y a esta relacionado con b.

Una relación binaria R en un conjunto A es no total si no para todo par de elementos a, b de A y a esta relacionado con b.

Toda relación es solo parcial, al ser no total.

Conjunto parcialmente ordenado y acotado

Es necesario que $(A,\precsim )$ cumpla las propiedades: reflexiva, antisimétrica y transitiva, por lo tanto un conjunto parcialmente ordenado, para que el conjunto pueda estar acotado.

Dado un conjunto A y una relación binaria $\precsim$ definida entre el conjunto A, que expresaremos $(A,\precsim )$ y la relación se representa:

$x,y\in A\;,\quad x\precsim y$

que se lee: siendo x e y elementos de A, x antecede a y.

La no relación se representa:

$x,y\in A\;,\quad x\not \precsim y$

que se lee: siendo x e y elementos de A, x no antecede a y

Conjunto acotado inferior

Diremos que el conjunto A está acotado inferiormente respecto a $\precsim$ si:

$\exists z\in A\;/\quad z\precsim x\quad \forall x\in A$

se cumple que existe un z de A tal que z antecede a x para todo x de A.

A los elementos z del conjunto se les denomina minimales.

Conjunto no acotado inferior

Diremos que el conjunto A no está acotado inferiormente respecto a $\precsim$ si:

$\neg \exists z\in A\;/\quad z\precsim x\quad \forall x\in A$

se cumple que no existe un z de A tal que z antecede a x para todo x de A.

Conjunto acotado superior

Diremos que el conjunto A está acotado superiormente respecto a $\precsim$ si:

$\exists y\in A\;/\quad x\precsim y\quad \forall x\in A$

se cumple que existe un y de A tal que x antecede a y para todo x de A.

A los elementos y del conjunto se les denomina maximales.

Conjunto no acotado superior

Diremos que el conjunto A no está acotado superiormente respecto a $\precsim$ si:

$\neg \exists y\in A\;/\quad x\precsim y\quad \forall x\in A$

se cumple que no existe un y de A tal que x antecede a y para todo x de A.

Conjunto acotado

Diremos que un conjunto está acotado, si está acotado superior e inferiormente.

Comjunto no acotado

Diremos que un conjunto es no acotado, si no está acotado superior ni inferiormente.

Elemento maximal y minimal

Dado el conjunto A formado por los elementos:

$A=\{a,b,c,d,e,f,g,h\}$

en el que se ha definido una relación binaria $\precsim$ representada en la figura, siendo $(A,\precsim )$ un conjunto parcialmente ordenado, los elementos y de A que cumplen:

$y\in A\;es\;maximal\;si:\quad \forall x\in A\;:\quad y\precsim x\quad \longrightarrow \quad y=x$

y de A es maximal si para todo x de A que cumple que y anteceda a x entonces y es igual a x.

Los elementos y de A se denominan maximales y definen una cuota superior en A, los elementos maximales no tiene porque ser únicos, en el ejemplo a, c y g son maximales de A.

Del mismo modo los elementos z de A que cumplen:

$z\in A\;es\;minimal\;si:\quad \forall x\in A\;:\quad x\precsim z\quad \longrightarrow \quad z=x$

z de A es minimal si para todo x de A que cumpla que x anteceda a z entonces z es igual a x.

se denominan minimales y definen una cuota inferior en A, los elementos minimales no tiene porque ser únicos, en el ejemplo d, g y h son minimales de A.

Se puede ver que el elemento g es maximal y minimal en A. Un elemento que es maximal y minimal al mismo tiempo se un elemento aislado.

Elemento máximo y mínimo

Dado el conjunto A formado por los elementos:

$A=\{a,b,c,d,e,f,g\}$

en el que se ha definido una relación binaria $\precsim$ representada en la figura, siendo $(A,\precsim )$ un conjunto parcialmente ordenado.

El elemento y de A que cumple:

$y\in A\;es\;m{\acute {a}}ximo\;si:\quad \forall x\in A\;/\quad x\precsim y$

se denomina máximo y define una cuota superior en A, el elemento máximo es único, en el ejemplo c es el máximo de A. El elemento máximo de un conjunto es el maximal unico en ese conjunto.

Del mismo modo el elemento z de A que cumple:

$z\in A\;es\;m{\acute {\imath }}nimo\;si:\quad \forall x\in A\;/\quad z\precsim x$

se denomina mínimo y define una cuota inferior en A, el elemento mínimo es único, en el ejemplo g es mínimo de A. El elemento mínimo de un conjunto es el minimal unico en ese conjunto.

Tipos de las relaciones binarias homogéneas

Una relación binaria homogéneas puede cumplir o no una serie de propiedades:

reflexiva o no reflexiva

simétrica o antisimétrica

transitiva

acotada

total

Esto da lugar a que se pueda clasificar por tipos según las propiedades que cumpla. Normalmente desde un punto de vista matemático se estudian unos tipos de relaciones binarias homogéneas muy concretas que podemos ver en el esquema.

Relaciones binarias homogéneas

Dado un conjunto A y una relación R entre los elementos de ese conjunto, dado que el conjunto inicial y final de esa relación es el mismo conjunto, esta relación se dice homogénea, a diferencia de la correspondencia (o relación binaria heterogenia) en las que los conjuntos inicial y final son diferentes o los consideramos como diferentes.

Partiendo de este tipo de relación matemática podemos considerar los siguientes casos:

Relación reflexiva

Una relación binaria homogénea, que cumple la propiedad reflexiva, se dice relación reflexiva.

Dado un conjunto A en el que se ha definido una relación binaria R, si se cumple que:

$\forall x\in A:(x,x)\in R$

Para todo elemento x de A, se cumple que el par ordenado (x,x) pertenece a la relación, esta relación es reflexiva.

En el ejemplo, representado en el diagrama sagital de la derecha, tenemos el conjunto:

$A=\{a,b,c,d\}$

Y la relación:

$R=\{(a,a),(a,d),(b,b),(c,a),(c,c),(d,a),(d,d)\}$

Su representación cartesiana seria:

${\begin{array}{c|cccc}d&\star &\cdot &\cdot &\star \\c&\cdot &\cdot &\star &\cdot \\b&\cdot &\star &\cdot &\cdot \\a&\star &\cdot &\star &\star \\\hline R&a&b&c&d\\\end{array}}$

Donde puede verse la relación R, entre los elementos del conjunto A, en el eje horizontal el conjunto A como conjunto inicial (de donde salen las flechas) y en el eje vertical el conjunto A como conjunto final (donde llegan las flechas). Representando con una estrella si esa relación se cumple y con un punto si no se cumple, puede verse que la diagonal todo son estrellas, lo que indica que la relación es reflexiva, cada elemento está relacionado consigo mismo.

Relación no reflexiva

Una relación binaria homogénea, que no cumple la propiedad reflexiva, se dice relación no reflexiva.

$\lnot \forall x\in A:(x,x)\in R$

No para todo elemento x del conjunto A, se cumple que el par ordenado (x,x) pertenece a la relación R.

Lo que es lo mismo que: Dado un conjunto A en el que se ha definido una relación binaria R, si se cumple que:

$\exists x\in A:(x,x)\notin R$

Si existe x de A, y se cumple que el par ordenado (x,x) no pertenece a la relación, esta relación es no reflexiva.

Dado el conjunto:

$A=\{a,b,c,d\}$

Y la relación representada en el diagrama de la derecha:

$R=\{(a,a),(a,d),(b,b),(c,a),(d,a),(d,d)\}$

Su representación cartesiana seria:

${\begin{array}{c|cccc}d&\star &\cdot &\cdot &\star \\c&\cdot &\cdot &\cdot &\cdot \\b&\cdot &\star &\cdot &\cdot \\a&\star &\cdot &\star &\star \\\hline R&a&b&c&d\\\end{array}}$

Se puede ver que el elemento c no está relacionado con sigo mismo, y por tanto no se cumple la propiedad reflexiva. Es suficiente con que un único elemento del conjunto no cumpla la propiedad reflexiva para que la relación sea no reflexiva.

---

La relación representada en el diagrama de la derecha:

$R=\{(a,d),(b,b),(c,a),(d,a),(d,d)\}$

Su representación cartesiana seria:

${\begin{array}{c|cccc}d&\star &\cdot &\cdot &\star \\c&\cdot &\cdot &\cdot &\cdot \\b&\cdot &\star &\cdot &\cdot \\a&\cdot &\cdot &\star &\star \\\hline R&a&b&c&d\\\end{array}}$

Los elementos a y c no cumplen la relación reflexiva.

---

La relación representada en el diagrama de la derecha:

$R=\{(a,d),(b,b),(c,a),(d,a)\}$

Su representación cartesiana seria:

${\begin{array}{c|cccc}d&\star &\cdot &\cdot &\cdot \\c&\cdot &\cdot &\cdot &\cdot \\b&\cdot &\star &\cdot &\cdot \\a&\cdot &\cdot &\star &\star \\\hline R&a&b&c&d\\\end{array}}$

Los elementos a, c y d no cumplen la relación reflexiva.

---

La relación representada en el diagrama de la derecha:

$R=\{(a,d),(c,a),(d,a)\}$

Su representación cartesiana seria:

${\begin{array}{c|cccc}d&\star &\cdot &\cdot &\cdot \\c&\cdot &\cdot &\cdot &\cdot \\b&\cdot &\cdot &\cdot &\cdot \\a&\cdot &\cdot &\star &\star \\\hline R&a&b&c&d\\\end{array}}$

Los elementos a, b, c y d no cumplen la relación reflexiva. que son todos los elementos del conjunto A.

Dado un conjunto A en el que se ha definido una relación binaria R, se cumple que:

$\forall x\in A:(x,x)\notin R$

Para todo elemento x del conjunto A, se cumple que el par ordenado (x,x) no pertenece a R. Esto es la relación R definida en A cumple la propiedad irreflexiva, que es un caso particular de las relaciones no reflexivas en la que ningún elemento del conjunto está relacionado con sigo mismo.

Las relaciones que son no reflexivas y no irreflexivas simultáneamente se dicen arreflexivas.

Galería de relación binaria homogénea

Fundamentos de la Matemática/Galería de relación binaria homogénea

Correspondencia

Dado un conjunto A y otro B y una relación donde algunos elementos de A están asociados con algunos elementos de B, es una correspondencia .

En la figúra de la derecha se puede ver una correspondencia de A sobre B, donda a los elementos a de A se le asocia los elementos b de B de modo que b sea multiplo de a.

Definiciones

En una correspondencia de A sobre B donde el elemento a de A esta relacionado con el elemneto b de B, al elemento a se le llama origen de b y al elemento b se le llama imagen de a.

En una correspondencia podemos distinguir cuatro conjuntos:

Conjunto inicial: es el conjunto desde el que se define la correspondencia. En la figura el conjunto inicial es el conjunto A, siendo A el formado por los siguientes elementos:

$A=\{e,f,g\}$

Conjunto final: es el conjunto sobre el que esta definida la correspondencia. El la figura es el conjunto B, formado por los siguientes elementos:

$B=\{i,j,k\}$

Conjunto origen: o conjunto de origenes, es el formado por los elemento de conjunto inicial que tienen imagen, los que son origen de la relación, en la figura es el formado por los siguientes elementos:

$O=\{e,f\}$

Conjunto imagen: o conjunto de imagenes, es el formado por los elementos del conjunto final que tienen origen, los que son imagenes de la relación. En la figura es el formado por los siguientes conjuntos:

$I=\{i,j\}$

Propiedades de las correspondencias

Una correspondencia puede tener cuatro propiedades:

Unicidad de imagen, ui: si se cumple que los elementos del cinjunto inicial que tienen imagen tienen una sola imagen.

Unicidad de origen, uo: si se cumple que los elementos del conjumto final que tienen origen tienen un solo origen.

Existencia de imagen, ei: si se cumple que todos los elementos del conjunto inicial tienen imagen.

Existencia de origen, eo: si se cumple que todos los elementos del conjunto final tienen origen.

Estas propiedades son independientes entre si, de modo que el cumplimiento de una de ellas no implica el complimiento o no de las otra, de modo que entre dos conjuntos A y B según cumplan o no estas propiedades se pueden dar dieciseis casos diferentes.

$2^{4}=16$

Fijando una de las propiedades en verdadero, se pueden formar con las otras tres, ocho casos distintos.

$2^{3}=8$

Correspondencia que cumplen la unicidad de imagen

Los elementos del conjunto A que tienen imagen tienen una unica imagen, esto no significa que todos los elementos de A tengan que tener imagen, pero los que la tienen tienen una unica imagen.

ui-1	ui-2	ui-3	ui-4

ui-5	ui-6	ui-7	ui-8

Correspondencia que cumplen la unicidad de origen

Los elementos del conjunto B que tienen origen, tienen un unico origen, esto no quiere decir que todos los elementos de B tengan que tener origen, pero los que si lo tienen, tienen un unico origen.

uo-1	uo-2	uo-3	uo-4

uo-5	uo-6	uo-7	uo-8

Correspondencia que cumplen la existencia de imagen

Todos los elementos del conjunto A tienen imagen, una o más, pero todos sin excepción tienen alguna imagen en B.

ei-1	ei-2	ei-3	ei-4

ei-5	ei-6	ei-7	ei-8

Correspondencia que cumplen la existencia de origen

Todos los elementos del conjunto B tienen un origen en A, uno o más, pero todos sin escepción tienen origen.

eo-1	eo-2	eo-3	eo-4

eo-5	eo-6	eo-7	eo-8

Tipos de correspondencias

Los tipos de correspondencia

Como ya se ha dicho una correspondencia puede tener cuatro propiedades:

Unicidad de imagen:	ui
Unicidad de origen:	uo
Existencia de imagen:	ei
Existencia de origen:	eo

Estas propiedades son independientes, el cumplimiento de una de ellas no implica el cumplimiento o no cumplimiento de las demás, esto da lugar a 16 casos tipo de correspondencia, pero no todas tienen importancia matemática, estos 16 casos se agrupan en 7 que tienen nombre propio y se estudian por separado.

Se pueden diferenciar los siguientes casos.

Dados dos conjuntos A y B, donde algunos elementos de A esta asociados con algunos elementos de B, esta relación es una correspondencia.

Una correspondencia que cumple la unicidad de imagen, se denomina correspondencia unívoca.

Una correspondencia que cumple la unicidad de imagen y la unicidad de origen, se denomina correspondencia biunívoca. Una correspondencia biunívoca es previamente correspondencia unívoca.

Una correspondencia que cumple la unicidad de imagen y existencia de imagen se llama aplicación matemático.

Una aplicación matemática que cumple la existencia de origen se denomina aplicación sobreyectiva.

Una aplicación matemática que cumple la unicidad de origen se denomina aplicación inyectiva.

Una aplicación matemática que cumple la unicidad de origen y la existencia de origen se denomina aplicación biyectiva.

Correspondencias

correspondencia-1	correspondencia-2	correspondencia-3	correspondencia-4

correspondencia-5	correspondencia-6	correspondencia-7	correspondencia-8

correspondencia-9	correspondencia-10	correspondencia-11	correspondencia-12

correspondencia-13	correspondencia-14	correspondencia-15	correspondencia-16

Correspondencia unívoca

unívoca-1	unívoca-2	unívoca-3	unívoca-4

unívoca-5	unívoca-6	unívoca-7	unívoca-8

Correspondencia biunívoca

biunívoca-1	biunívoca-2	biunívoca-3	biunívoca-4

Aplicación matemático

aplicación-1	aplicación-2	aplicación-3	aplicación-4

Aplicación sobreyectiva

sobreyectiva-1	sobreyectiva-2

Aplicación inyectiva

inyectiva-1	inyectiva-2

Aplicación biyectiva

biyectiva-1

Galería de ejemplos

A fin de ilustrar lo anterior podemos ver una galería de ejemplos de los tipos de correspondencia que pueden darse.

Habiendo cuatro propiedades independientes: unicidad de imagen, ui; unicidad de origen, uo; existencia de imagen, ei; existencia de origen, eo, se pueden dar 16 posibles combinaciones.

---

1 Unicidad de imagen: no Unicidad de origen: no Existencia de imagen: no Existencia de origen: no

2 Unicidad de imagen: si Unicidad de origen: no Existencia de imagen: no Existencia de origen: no

3 Unicidad de imagen: no Unicidad de origen: si Existencia de imagen: no Existencia de origen: no

4 Unicidad de imagen: si Unicidad de origen: si Existencia de imagen: no Existencia de origen: no

---

5 Unicidad de imagen: no Unicidad de origen: no Existencia de imagen: si Existencia de origen: no

6 Unicidad de imagen: si Unicidad de origen: no Existencia de imagen: si Existencia de origen: no

7 Unicidad de imagen: no Unicidad de origen: si Existencia de imagen: si Existencia de origen: no

8 Unicidad de imagen: si Unicidad de origen: si Existencia de imagen: si Existencia de origen: no

---

9 Unicidad de imagen: no Unicidad de origen: no Existencia de imagen: no Existencia de origen: si

10 Unicidad de imagen: si Unicidad de origen: no Existencia de imagen: no Existencia de origen: si

11 Unicidad de imagen: no Unicidad de origen: si Existencia de imagen: no Existencia de origen: si

12 Unicidad de imagen: si Unicidad de origen: si Existencia de imagen: no Existencia de origen: si

---

13 Unicidad de imagen: no Unicidad de origen: no Existencia de imagen: si Existencia de origen: si

14 Unicidad de imagen: si Unicidad de origen: no Existencia de imagen: si Existencia de origen: si

15 Unicidad de imagen: no Unicidad de origen: si Existencia de imagen: si Existencia de origen: si

16 Unicidad de imagen: si Unicidad de origen: si Existencia de imagen: si Existencia de origen: si

Tipos de correspondencias

Para centrar ideas, veremos un caso con valores numéricos concreto, así definiremos una correspondencia entre dos conjuntos de números naturales A y B de modo que los elementos a de A están asociados con elementos b de B de modo que b sea un múltiplo de a.

${\mathcal {R}}=\left\{(a,b)\in A\times B\;:\quad b={\dot {a}}\right\}$

R es la relación de pares ordenados (a,b) del producto cartesiano de A por B, que cumple, que b sea un múltiplo de a.

---

Caso: 1

En la figura de la derecha tenemos que:

$A=\{2,3,5\}$

$B=\{4,6,7\}$

${\mathcal {R}}=\{(2,4),(2,6),(3,6)\}$

La correspondencia se define asociando el elemento a de A con el elemento b de b si b es múltiplo de a, su representación cartesiana seria la siguiente.

${\begin{array}{r|ccc}7&\cdot &\cdot &\cdot \\6&\star &\star &\cdot \\4&\star &\cdot &\cdot \\\hline A\times B&2&3&5\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	no
Existencia de imagen:	no
Existencia de origen:	no

---

Caso: 2

En la figura de la derecha tenemos que:

$A=\{2,3,5\}$

$B=\{6,7\}$

${\mathcal {R}}=\{(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}7&\cdot &\cdot &\cdot \\6&\star &\star &\cdot \\\hline A\times B&2&3&5\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	no
Existencia de imagen:	no
Existencia de origen:	no

---

Caso: 3

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{2,4,7\}$

${\mathcal {R}}=\{(2,2),(2,4),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}7&\cdot &\cdot \\4&\star &\cdot \\2&\star &\cdot \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	si
Existencia de imagen:	no
Existencia de origen:	no

---

Caso: 4

En la figura de la derecha tenemos que:

$A=\{2,3,5\}$

$B=\{4,9,11\}$

${\mathcal {R}}=\{(2,4),(2,9)\}$

Representación cartesiana:

${\begin{array}{r|ccc}11&\cdot &\cdot &\cdot \\9&\cdot &\star &\cdot \\4&\star &\cdot &\cdot \\\hline A\times B&2&3&5\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	si
Existencia de imagen:	no
Existencia de origen:	no

---

Caso: 5

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{4,6,7\}$

${\mathcal {R}}=\{(2,4),(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}7&\cdot &\cdot \\6&\star &\star \\4&\star &\cdot \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	no
Existencia de imagen:	si
Existencia de origen:	no

---

Caso: 6

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{6,7\}$

${\mathcal {R}}=\{(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}7&\cdot &\cdot \\6&\star &\star \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	no
Existencia de imagen:	si
Existencia de origen:	no

---

Caso: 7

En la figura de la derecha tenemos que:

$A=\{2\}$

$B=\{2,4,7\}$

${\mathcal {R}}=\{(2,2),(2,4)\}$

Representación cartesiana:

${\begin{array}{r|ccc}7&\cdot \\4&\star \\2&\star \\\hline A\times B&2\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	si
Existencia de imagen:	si
Existencia de origen:	no

---

Caso: 8

En la figura de la derecha tenemos que:

$A=\{2,3,5\}$

$B=\{4,6\}$

${\mathcal {R}}=\{(2,4),(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}6&\star &\star &\cdot \\4&\star &\cdot &\cdot \\\hline A\times B&2&3&5\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	no
Existencia de imagen:	no
Existencia de origen:	si

---

Caso: 9

En la figura de la derecha tenemos que:

$A=\{2,3,5\}$

$B=\{6\}$

${\mathcal {R}}=\{(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}6&\star &\star &\cdot \\\hline A\times B&2&3&5\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	no
Existencia de imagen:	no
Existencia de origen:	si

---

Caso: 10

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{2,4\}$

${\mathcal {R}}=\{(2,2),(2,4)\}$

Representación cartesiana:

${\begin{array}{r|ccc}4&\star &\cdot \\2&\star &\cdot \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	si
Existencia de imagen:	no
Existencia de origen:	si

---

Caso: 11

En la figura de la derecha tenemos que:

$A=\{2,3,5\}$

$B=\{4,9\}$

${\mathcal {R}}=\{(2,4),(3,9)\}$

Representación cartesiana:

${\begin{array}{r|ccc}9&\cdot &\star &\cdot \\4&\star &\cdot &\cdot \\\hline A\times B&2&3&5\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	si
Existencia de imagen:	no
Existencia de origen:	si

---

Caso: 12

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{4,6\}$

${\mathcal {R}}=\{(2,4),(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}6&\star &\star \\4&\star &\cdot \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	no
Existencia de imagen:	si
Existencia de origen:	si

---

Caso: 13

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{6\}$

${\mathcal {R}}=\{(2,6),(3,6)\}$

Representación cartesiana:

${\begin{array}{r|ccc}6&\star &\star \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	no
Existencia de imagen:	si
Existencia de origen:	si

---

Caso: 14

En la figura de la derecha tenemos que:

$A=\{2\}$

$B=\{2,4\}$

${\mathcal {R}}=\{(2,2),(2,4)\}$

Representación cartesiana:

${\begin{array}{r|ccc}4&\star \\2&\star \\\hline A\times B&2\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	si
Existencia de imagen:	si
Existencia de origen:	si

---

Caso: 15

En la figura de la derecha tenemos que:

$A=\{2\}$

$B=\{2,4\}$

${\mathcal {R}}=\{(2,2),(2,4)\}$

Representación cartesiana:

${\begin{array}{r|ccc}4&\star \\2&\star \\\hline A\times B&2\\\end{array}}$

Unicidad de imagen:	no
Unicidad de origen:	si
Existencia de imagen:	si
Existencia de origen:	si

---

Caso: 16

En la figura de la derecha tenemos que:

$A=\{2,3\}$

$B=\{4,9\}$

${\mathcal {R}}=\{(2,4),(3,9)\}$

Representación cartesiana:

${\begin{array}{r|ccc}9&\cdot &\star \\4&\star &\cdot \\\hline A\times B&2&3\\\end{array}}$

Unicidad de imagen:	si
Unicidad de origen:	si
Existencia de imagen:	si
Existencia de origen:	si

Aplicación matemática

Una aplicación matemática: (f), es un caso particular de correspondencia, entre dos conjuntos, que cumple la unicidad de imagen y la existencia de imagen, eso es: para cada elemento del conjunto inicial: (A), existe un único elemento de conjunto imagen: (B), que es su imagen.

Una aplicación matemática: (f), se representa:

${\begin{array}{rccl}f:&A&\longrightarrow &B\\&a&\longmapsto &b=f(a)\end{array}}$

Los siguientes ejemplos de correspondencia son aplicaciones matemáticas:

Una aplicación matemática que cumple la unicidad de origen se dice: aplicación inyectiva. Los siguientes ejemplos son aplicaciones inyectivas:

Una aplicación matemática que cumple la existencia de origen se dice: aplicación sobreyectiva. Los siguientes ejemplos son aplicaciones sobreyectivas:

Una aplicación matemática que cumple la unicidad y la existencia de origen se dice: aplicación biyectiva. El siguiente ejemplo es aplicacion biyectivas:

Una aplicación es biyectiva si es inyectiva y sobreyectiva simultáneamente.

Operación binaria

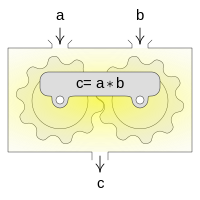
Se define como operación binaria aquella operación matemática, que necesita el dos operandos (argumentos) para que se calcule un valor.

Dados tres conjuntos A, B y C una operación binaria, representando la operación por el signo $\circ$, es una aplicación que asigna a cada par de valores a de A y b de B un solo valor c de C, que podemos representar:

${\begin{array}{rccl}\circ :&A\times B&\longrightarrow &C\\&(a,b)&\longmapsto &c=\circ (a,b)\end{array}}$

Podemos expresar la operación:

$\circ (a,b)=c\;,\quad a\circ b=c\;,\quad (a,b)\xrightarrow {\circ } c$

Tipos de operaciones binarias

Según los conjuntos que intervienen en la operación binaria podemos diferenciar los siguientes casos:

Si solo interviene un conjunto la operación de dice interna, si interviene más de uno se dice externa.

Las operaciones internas las representaremos con los signos:

$\circledcirc \;,\quad \odot \;,\quad \circledast \;,\quad \oplus \;,\quad \ominus \;,\quad \otimes \;,\quad \oslash \;.$

y las externas:

$\circ \;,\quad \cdot \;,\quad \ast \;,\quad +\;,\quad -\;,\quad \times \;,\quad \diagup \;.$

ejemplo de operación interna:

${\begin{array}{rccl}\circledast :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=\circledast (a,b)\quad \equiv \quad c=a\circledast b\end{array}}$

ejemplo de operación externa:

${\begin{array}{rccl}\ast :&B\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=\ast (a,b)\quad \equiv \quad c=a\ast b\end{array}}$

Ley de composición

Un ley de composición es un tipo de operación binaria que define una estructura algebraica, si la ley de composición relaciona dos elementos de un mismo conjunto y el resultado es de ese mismo conjunto la ley de composición se denomina interna, si la ley de composición relaciona dos elementos de dos conjuntos distintos se denomina externa.

Convenio de representación

Adoptaremos como convenio de representación para expresar, las cuestiones relacionadas con las estructuras algebraicas, lo siguiente:

Los conjuntos los llamaremos con letras mayúsculas:

$A,B,C,\dots$

Los elementos los representaremos con letras minúsculas:

$a,b,c,\dots$

Las leyes de composición internas las representaremos:

$\circledcirc ,\odot ,\circledast ,\oplus ,\ominus ,\otimes ,\oslash ,\dots$

Las leyes de composición externas las representaremos:

$\circ ,\cdot ,\ast ,+,-,\times ,\diagup ,\dots$

Ley de composición interna

Dado un conjunto A y una operación $\odot$, que representaremos como el par $(A,\odot )$, se dice que $\odot$ es una ley de composición interna u operación interna en A cuando es una aplicación de la forma siguiente.

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

Una ley de composición interna asigna a cada par ordenado (a, b), cuyas componentes pertenecen ambas al conjunto A, un tercer elemento c, también contenido en A. Este elemento c es único para cada par (a, b) determinado, lo cual se expresa en símbolos de la siguiente manera.

$\forall (a,b)\in A\times A\;,\quad \exists !c\in A\;:\quad c=a\odot b$

Ley de composición externa

Si los dos elementos operados no pertenecen al mismo conjunto la ley de composición es externa, pudiendo diferenciar:

Ley de composición externa por la derecha

Dado dos conjunto A y B, y una operación: $\cdot$, que representaremos $(A,B,\cdot )$:

${\begin{array}{rccl}\cdot :&A\times B&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\cdot b\end{array}}$

por la que definimos una aplicación que, a cada par ordenado (a, b) de A por B, le asigna un c de A.

$\forall (a,b)\in A\times B\,,\quad \exists !c\in A\;:\quad c=a\cdot b$

Para todo par ordenado (a,b) en A por B, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

Se denomina ley de composición externa por la derecha.

Ley de composición externa por la izquierda

Del mismo modo también se considera ley de composición externa, que se denota: $(A,B,\circ )$:

${\begin{array}{rccl}\circ :&A\times B&\longrightarrow &B\\&(a,b)&\longmapsto &c=a\circ b\end{array}}$

Donde a cada par de valores (a, b) de A por B se le asigna un valor c de B.

$\forall (a,b)\in A\times B\,,\quad \exists !c\in B\;:\quad c=a\circ b$

Para todo par ordenado (a,b) en A por B, se cumple que existe un único c en B, tal que c es el resultado de operar a con b.

Se denomina ley de composición externa por la izquierda.

Cualquier operación distinta de las anteriores no se considera ley de composición.

Enlaces externos

• w:Ley de composición
• Ley de composición
• LEYES DE COMPOSICION INTERNAS

Propiedades de las leyes de composición internas

Véase también: w:Propiedades de las operaciones binarias

En álgebra las operaciones binarias internas en el conjunto A, o bien las aplicaciones de A x A en A:

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

son las de mayor interés, porque se utilizan tanto en los sistemas numéricos como en relaciones binarias en los sistemas algebraicos. Las operaciones gozan de ciertas propiedades, usadas con frecuencia en la axiomatización de los diversos sistemas matemáticos, en palabras de George David Birkhoff.

Propiedades de una ley de composición interna

Dado un conjunto A no vacío y definida una aplicación de $A\times A$ sobre A, donde a cada par ordenado (a,b) se le asigna un valor c de A, que representamos: $(A,\odot )$

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

La ley de composición: $(A,\odot )$ es interna dado que se cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\odot b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

Pueden tener las siguientes propiedades:

Propiedad conmutativa

Véase también: w:Propiedad conmutativa

Dado un conjunto no vacío A, en el que se ha definido una ley de composición interna $\odot$, que se representa: $(A,\odot )$, se dice que $\odot$ tiene la propiedad conmutativa en A si se cumple:

$\forall a,b\in A\;:\quad a\odot b=b\odot a$

Para todo a, b de A, se cumple que el resultado de operar a con b es igual al de operar b con a.

Del mismo modo podemos decir que la ley de composición interna $\odot$, no es conmutativa en A si:

$\exists a,b\in A\;:\quad a\odot b\neq b\odot a$

Si existe algún a, b en A, que cumple que el resultado de operar a con b es distinto de operar b con a.

Propiedad anticonmutativa

La operación $\odot$ en A es anticonmutativa si:

$\forall a,b\in A\;:\quad a\odot b=-(b\odot a)$

Para todo a, b de A, se cumple que el resultado de operar a con b es igual al opuesto de operar b con a.

en general, para cualquier par de vectores a, b:

$\mathbf {a} \land \mathbf {b} =-(\mathbf {b} \land \mathbf {a} )$

Propiedad asociativa

Véase también: w:Propiedad asociativa

Sea A un conjunto no vacío y $\odot$ una operación binaria en A, se dice que $(A,\odot )$ es asociativa si, solo si:

$\forall a,b,c\in A\;:\quad (a\odot b)\odot c=a\odot (b\odot c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

También se puede decir que la operación $\odot$ no es asociativa si se cumple:

$\exists a,b,c\in A\;:\quad (a\odot b)\odot c\neq a\odot (b\odot c)$

Existen a, b, c en A que cumplen que operando a con b y el resultado con c es distinto de operar a con el resultado de operar b con c.

Propiedades con dos leyes de composición interna

Dado un conjunto A no vacío y definidas dos aplicación de A por A sobre A, donde a cada par ordenado (a,b) se le asigna con la operación $\odot$ un valor c de A y con la operación $\circledcirc$ el valor d de A que representamos: $(A,\odot ,\circledcirc )$.

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}\quad \quad {\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &d=a\circledcirc b\end{array}}$

Pueden tener las siguientes propiedades:

Propiedad distributiva

Véase también: w:Propiedad distributiva

Dado un conjunto A no vacío en el que se han definidos dos operaciones internas, que expresaremos $(A,\odot ,\circledcirc )$, se dice que la operación $\odot$ es distributiva por la izquierda de $\circledcirc$ si se cumple:

$\forall a,b,c\in A\;:\quad a\odot (b\circledcirc c)=(a\odot b)\circledcirc (a\odot c)$

Del mismo modo se dice que la operación $\odot$ es distributiva por la derecha de $\circledcirc$ si se cumple:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\odot c=(a\odot c)\circledcirc (b\odot c)$

Una operación $\odot$ es distributiva sobre otra $\circledcirc$ si es distributiva por la derecha y por la izquierda.

Elementos distinguidos

Elemento neutro

Véase también: w:Elemento neutro

Si se tiene el conjunto A, no vacío, provisto de una operación binaria $\odot$, que indicaremos: $(A,\odot )$,

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

Diremos que el elemento e, es el elemento neutro por la derecha si:

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad e\odot a=a$

Para todo a de A, se cumple que existe e de A, tal que operando e con a el resultado es a.

Se demuestra que si hay otro elemento neutro por la derecha: $e^{,}\,$, tal que: $e^{,}\odot a=a$, entonces: $e=e^{,}$; hecho que se conoce como unicidad del elemento neutro.

Diremos que el elemento e, es el elemento neutro por la izquierda si:

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad a\odot e=a$

Para todo a de A, se cumple que existe e de A, tal que operando a con e el resultado es a.

Se demuestra que si hay otro elemento neutro por la izquierda: $e^{,}\,$, tal que: $a\odot e^{,}=a$, entonces: $e=e^{,}$; hecho que se conoce como unicidad del elemento neutro.

Un elemento e es elemento neutro en $(A,\odot )$ si es elemento neutro por la derecha y por la izquierda.

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad e\odot a=a\odot e=a$

Para todo a de A, se cumple que existe e de A, tal que el resultado de operar e con a es igual a operar a con e y es igual a a.

Elemento simétrico

Véase también: w:Elemento simétrico

Sea A un conjunto no vacío y $\odot$ una operación binaria:

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

Se dice que un elemento $a\in A$ tiene:

El elemento simétrico por la izquierda respecto de la operación $\odot$ si:

$a\in A\;:\quad \exists {\overrightarrow {a}}\in A\;\vert \quad {\overrightarrow {a}}\odot a=e$

El elemento simétrico por la derecha respecto de la operación $\odot$ si:

$a\in A\;:\quad \exists {\overleftarrow {a}}\in A\;\vert \quad a\odot {\overleftarrow {a}}=e$

El elemento simétrico respecto de la operación $\odot$, si existe, es elemento simétrico por la izquierda y por la derecha, esto es:

$a\in A\;:\quad \exists {\bar {a}}\in A\;\vert \quad {\bar {a}}\odot a=a\odot {\bar {a}}=e$

Un elemento simétrico ${\bar {a}}$ de $A\,$ es simétrico por la derecha del elemento $a\,$ y simétrico por la izquierda del elemento $a\,$. Donde e es el elemento neutro.

• En la operación suma, el elemento simétrico, se suele denominas opuesto o inverso aditivo.
• En la operación multiplicación, el elemento simétrico, se suele denominar inverso o inverso multiplicativo.

Elemento involutivo

Sea A un conjunto no vacío y $\odot$ una operación binaria:

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

Diremos que $d\in A$ es elemento involutivo si:

$d\odot d=d$

• El 0 es elemento involutivo respecto a la suma en el conjunto Z de los números enteros:

$0+0=0$

• el 0 y 1 son elementos involutivos respecto de la multiplicación en el conjunto Z de los enteros:

$0\cdot 0=0\;,\quad 1\cdot 1=1$

Elemento absorbente

Véase también: w:Elemento absorbente

Sea A un conjunto no vacío y $\odot$ una operación binaria:

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

Diremos que $s\in A$ es Elemento absorbente si:

$\forall a\in A\;:\quad \exists s\in A\;\vert \quad s\odot a=a\odot s=s$

Se denomina así al elemento s de A, tal que para todo a de A se cumple que operado s con a es igual que operas a con s y el resultado es s.

• 0 es elemento absorbente un sistema numérico multiplicativo.

$\forall x\in \mathbb {R} \;,\;\exists 0\in \mathbb {R} \;:\quad 0\cdot x=x\cdot 0=0$

• El conjunto vacío Ø es elemento absorbente para la intersección definida en el conjunto de partes de U.

$\forall A\subseteq U\;,\;\exists \varnothing \subseteq U\;:\quad \varnothing \cap A=A\cap \varnothing =\varnothing$

• El conjunto universal U es elemento absorbente para la unión definida en el conjunto de partes de U.

$\forall A\subseteq U\;,\;\exists U\subseteq U\;:\quad U\cup A=A\cup U=U$

Operación simétrica

Sea A un conjunto con una operación binaria $(A,\odot )$:

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\odot b\end{array}}$

por lo que cabe la ecuación:

$\forall a,b\in A\,,\quad \exists !c\in A\;:\quad a\odot b=c$

Si:

$a\odot b=c$

Si $(A,\odot )$ admite elementos simétricos, se define:

$a\odot b\odot {\overline {b}}=c\odot {\overline {b}}$

Agrupando:

$a\odot (b\odot {\overline {b}})=c\odot {\overline {b}}$

donde e es el elemento neutro:

$a\odot e=c\odot {\overline {b}}$

simplificando:

$a=c\odot {\overline {b}}$

La operación simétrica seria ${\overline {\odot }}$

$a=c\,{\overline {\odot }}\,b$

Que se definiria:

${\begin{array}{rccl}{\overline {\odot }}:&A\times A&\longrightarrow &A\\&(c,b)&\longmapsto &a=c{\overline {\odot }}b\end{array}}$

Estructura algebráica de un conjunto y una ley de composición interna

Sea un conjunto: A y una ley de composición: $\circledcirc$, definida:

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Dado que se cumple:

$\forall (a,b)\in A\times A\,,\quad \exists !c\in A\;:\quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

El par $(A,\circledcirc )$ es una estructura definida en un unico conjunto con una sola ley de composición, que puede dar lugar a las estructuras algebráicas: magma, semigrupo, monoide o grupo, según las propiedades que cumpla.

grupo monoide semigrupo magma conjunto ley de composición interna asociativa elemento neutro elemento simétrico

Magma

Véase también: w:Magma (álgebra)

Un Magma es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

El término magma se debe a la asociación de matemáticos franceses que se hace llamar Nicolás Bourbaki. Durante algún tiempo compitió, para reflejar el mismo concepto, con la palabra grupoide, que tiene otros sentidos en matemática (ver grupoide), por lo que no es aconsejable su uso como sinónimo de magma.

Magma conmutativo

Un Magma conmutativo o abeliano es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna y conmutativa:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad conmutativa: Dado un conjunto no vacío A, en el que se ha definido una ley de composición interna $\circledcirc$, que se representa: $(A,\circledcirc )$, se dice que $\circledcirc$ tiene la propiedad conmutativa en A si se cumple:

$\forall a,b\in A\;:\quad a\circledcirc b=b\circledcirc a$

Para todo a, b de A, se cumple que el resultado de operar a con b es igual al de operar b con a.

Semigrupo

Véase también: w:Semigrupo

Un Semigrupo es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna y asociativa:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad asociativa: La ley de composición: $(A,\circledcirc )$ cumple la propiedad asociativa si:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\circledcirc c=a\circledcirc (b\circledcirc c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

Semigrupo conmutativo

Un Semigrupo conmutativo o abeliano es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna, asociativa y conmutativa:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad asociativa: La ley de composición: $(A,\circledcirc )$ cumple la propiedad asociativa si:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\circledcirc c=a\circledcirc (b\circledcirc c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

3.- Propiedad conmutativa: Dado un conjunto no vacío A, en el que se ha definido una ley de composición interna $\circledcirc$, que se representa: $(A,\circledcirc )$, se dice que $\circledcirc$ tiene la propiedad conmutativa en A si se cumple:

$\forall a,b\in A\;:\quad a\circledcirc b=b\circledcirc a$

Para todo a, b de A, se cumple que el resultado de operar a con b es igual al de operar b con a.

Monoide

Véase también: w:Monoide

Un Monoide es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna, asociativa y elemento neutro:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad asociativa: La ley de composición: $(A,\circledcirc )$ cumple la propiedad asociativa si:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\circledcirc c=a\circledcirc (b\circledcirc c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

3.- Elemento neutro: Un elemento e es elemento neutro en $(A,\circledcirc )$ si es elemento neutro por la derecha y por la izquierda.

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad e\circledcirc a=a\circledcirc e=a$

Para todo a de A, se cumple que existe e de A, tal que el resultado de operar e con a es igual a operar a con e y es igual a a.

Monoide conmutativo

Un Monoide conmutativo o abeliano es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna, asociativa, elemento neutro y conmutativa:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad asociativa: La ley de composición: $(A,\circledcirc )$ cumple la propiedad asociativa si:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\circledcirc c=a\circledcirc (b\circledcirc c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

3.- Elemento neutro: Un elemento e es elemento neutro en $(A,\circledcirc )$ si es elemento neutro por la derecha y por la izquierda.

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad e\circledcirc a=a\circledcirc e=a$

Para todo a de A, se cumple que existe e de A, tal que el resultado de operar e con a es igual a operar a con e y es igual a a.

4.- Propiedad conmutativa: Dado un conjunto no vacío A, en el que se ha definido una ley de composición interna $\circledcirc$, que se representa: $(A,\circledcirc )$, se dice que $\circledcirc$ tiene la propiedad conmutativa en A si se cumple:

$\forall a,b\in A\;:\quad a\circledcirc b=b\circledcirc a$

Para todo a, b de A, se cumple que el resultado de operar a con b es igual al de operar b con a.

Grupo

Véase también: w:Grupo (matemática)

Un Grupo es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna, asociativa, con elemento neutro y elemento simétrico:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad asociativa: La ley de composición: $(A,\circledcirc )$ cumple la propiedad asociativa si:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\circledcirc c=a\circledcirc (b\circledcirc c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

3.- Elemento neutro: Un elemento e es elemento neutro en $(A,\circledcirc )$ si es elemento neutro por la derecha y por la izquierda.

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad e\circledcirc a=a\circledcirc e=a$

Para todo a de A, se cumple que existe e de A, tal que el resultado de operar e con a es igual a operar a con e y es igual a a.

4.- Elemento simétrico: El elemento simétrico en el conjunto A respecto de la operación $\circledcirc$, si es elemento simétrico por la izquierda y por la derecha, esto es:

$\forall a\in A\;:\quad \exists {\bar {a}}\in A\;\vert \quad {\bar {a}}\circledcirc a=a\circledcirc {\bar {a}}=e$

Un elemento simétrico ${\bar {a}}$ de $a\,$ en $(A,\circledcirc )$ es simétrico por la derecha del elemento $a\,$ y simétrico por la izquierda del elemento $a\,$. Donde e es el elemento neutro.

Grupo conmutativo

Véase también: w:Grupo abeliano

Un Grupo conmutativo o abeliano es una estructura algebraica de la forma $(A,\circledcirc )$ donde A es un conjunto en el que se ha definido una ley de composición interna: $\circledcirc$.

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Siendo esta ley de composición una operación interna, asociativa, con elemento neutro, elemento simétrico y conmutativa:

1.- Operación interna: La ley de composición: $(A,\circledcirc )$ es interna si cumple:

$\forall (a,b)\in A\times A\,:\quad \exists !c\in A\;\vert \quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b.

2.- Propiedad asociativa: La ley de composición: $(A,\circledcirc )$ cumple la propiedad asociativa si:

$\forall a,b,c\in A\;:\quad (a\circledcirc b)\circledcirc c=a\circledcirc (b\circledcirc c)$

Para todo a, b, c de A se cumple que operando a con b y el resultado con c es igual a operar a con el resultado de operar b con c.

3.- Elemento neutro: Un elemento e es elemento neutro en $(A,\circledcirc )$ si es elemento neutro por la derecha y por la izquierda.

$\forall a\in A\;:\quad \exists e\in A\;\vert \quad e\circledcirc a=a\circledcirc e=a$

Para todo a de A, se cumple que existe e de A, tal que el resultado de operar e con a es igual a operar a con e y es igual a a.

4.- Elemento simétrico: El elemento simétrico en el conjunto A respecto de la operación $\circledcirc$, si es elemento simétrico por la izquierda y por la derecha, esto es:

$\forall a\in A\;:\quad \exists {\bar {a}}\in A\;\vert \quad {\bar {a}}\circledcirc a=a\circledcirc {\bar {a}}=e$

Un elemento simétrico ${\bar {a}}$ de $a\,$ en $(A,\circledcirc )$ es simétrico por la derecha del elemento $a\,$ y simétrico por la izquierda del elemento $a\,$. Donde e es el elemento neutro.

5.- Propiedad conmutativa: Dado un conjunto no vacío A, en el que se ha definido una ley de composición interna $\circledcirc$, que se representa: $(A,\circledcirc )$, se dice que $\circledcirc$ tiene la propiedad conmutativa en A si se cumple:

$\forall a,b\in A\;:\quad a\circledcirc b=b\circledcirc a$

Para todo a, b de A, se cumple que el resultado de operar a con b es igual al de operar b con a.

Estructura algebráica de un conjunto y dos leyes de composición internas

En este capitulo veremos las estructuras algebraicas en un conjunto y con dos leyes de composición internas.

Sea un conjunto: A y dos leyes de composición: $\circledcirc ,\odot$, definida:

- 1º ley:

${\begin{array}{rccl}\circledcirc :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &c=a\circledcirc b\end{array}}$

Dado que se cumple:

$\forall (a,b)\in A\times A\,,\quad \exists !c\in A\;:\quad c=a\circledcirc b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único c en A, tal que c es el resultado de operar a con b con esta 1º ley.

- 2º ley:

${\begin{array}{rccl}\odot :&A\times A&\longrightarrow &A\\&(a,b)&\longmapsto &d=a\odot b\end{array}}$

Dado que se cumple:

$\forall (a,b)\in A\times A\,,\quad \exists !d\in A\;:\quad d=a\odot b$

Para todo par ordenado (a,b) en A por A, se cumple que existe un único d en A, tal que d es el resultado de operar a con b con esta 2º ley.

La terna $(A,\circledcirc ,\odot )$ es una estructura definida en un unico conjunto: A, con dos leyes de composición, que puede dar lugar a las estructuras algebráicas: semianillo, semianillo unitario, anillo, anillo unitari o cuerpo, entre otras estructuras según las propiedades que cumplan.

Semianillo

Véase también: w:Semianillo

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de semianillo si se cumple que:

1. $(A,\circledcirc )$ es semigrupo conmutativo.
2. $(A,\odot )$ es semigrupo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Senianillo conmutativo

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de semianillo conmutativo si se cumple que:

1. $(A,\circledcirc )$ es semigrupo conmutativo.
2. $(A,\odot )$ es semigrupo conmutativo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Semianillo unitario

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de semianillo unitario si se cumple que:

1. $(A,\circledcirc )$ es semigrupo conmutativo.
2. $(A,\odot )$ es monoide.
3. $\odot$ es distributiva sobre $\circledcirc$.

Senianillo unitario conmutativo

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de semianillo unitario conmutativo si se cumple que:

1. $(A,\circledcirc )$ es semigrupo conmutativo.
2. $(A,\odot )$ es monoide conmutativo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Anillo

Véase también: w:Anillo (matemática)

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de anillo si se cumple que:

1. $(A,\circledcirc )$ es grupo conmutativo.
2. $(A,\odot )$ es semigrupo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Anillo conmutativo

Véase también: w:Anillo conmutativo

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de anillo conmutativo si se cumple que:

1. $(A,\circledcirc )$ es grupo conmutativo.
2. $(A,\odot )$ es semigrupo conmutativo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Anillo unitario

Véase también: w:Anillo unitario

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de anillo unitario si se cumple que:

1. $(A,\circledcirc )$ es grupo conmutativo.
2. $(A,\odot )$ es monoide.
3. $\odot$ es distributiva sobre $\circledcirc$.

Anillo unitario conmutativo

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de anillo unitario conmutativo si se cumple que:

1. $(A,\circledcirc )$ es grupo conmutativo.
2. $(A,\odot )$ es monoide conmutativo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Cuerpo

Véase también: w:Cuerpo (matemáticas)

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de cuerpo si se cumple que:

1. $(A,\circledcirc )$ es grupo conmutativo.
2. $(A,\odot )$ es grupo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Cuerpo conmutativo

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de cuerpo conmutativo si se cumple que:

1. $(A,\circledcirc )$ es grupo conmutativo.
2. $(A,\odot )$ es grupo conmutativo.
3. $\odot$ es distributiva sobre $\circledcirc$.

Álgebra de Boole

Véase también: w:Álgebra de Boole

Véase también: w:Álgebra de Heyting

Véase también: w:Retículo distributivo

Véase también: w:Conjunto parcialmente ordenado

Dado un conjunto: A y dos leyes de composición internas: 1ª ley: $\circledcirc$, 2ª ley: $\odot$, definidas en A, la terna $(A,\circledcirc ,\odot )$ es una estructura álgebraica de álgebra de Boole si se cumple que:

1. $(A,\circledcirc )$ es monoide conmutativo.
2. $(A,\odot )$ es monoide conmutativo.
3. $\circledcirc$ es distributiva sobre $\odot$.
4. $\odot$ es distributiva sobre $\circledcirc$.

Propiedades de las leyes de composición externas

Fundamentos de la Matemática/Propiedades de las leyes de composición externas