Curso de alemán para principiantes con audio/Lección 105b
Apariencia
- índice
- Lección 104b ← Lección 105b → Lección 106b
- Lección 105
- Mathematik auf Deutsch - 55
BM2701 - BM2710
[editar]BM2701
- Die Steigung einer Linie findet man
- a) grafisch (also Linie zeichnen und abzäheln)
- b) mit der Steigungsgleichung (also die zahlen in die Steigungsformel einsetzen)
- ---

Bild 1 - Bild 1: Gegeben ist eine Gerade die durch die Punkte A () und B () geht.
- ---
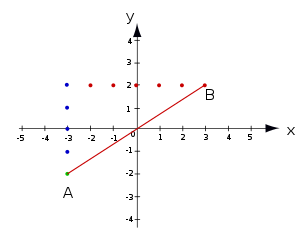
Bild 2 - Bild 2: Um die Steigung zu ermitteln zählen wir von Punkt A nach oben bis zur Höhe von Punkt B und kommen auf 4 Einheiten (blaue Punkte). Dann zählen wir nach rechts bis Punkt B und kommen auf 6 Einheiten (rote Punkte).
- Die Steigung ist also . Nach dem Kürzen erhalten wir
- .
- Man kann jeden beliebigen Punkt auf der Geraden nehmen und kommt auf einen zweiten Punkt auf der Geraden, indem man vom 1. Punkt aus 2 Schritte hoch geht und 3 Schritte nach rechts.
- ---
- Die andere Methode zur Ermittlung der Steigung ist das Einsetzen der Koordinaten in die Steigungsformel.
- (Tipp: Beim Einsetzen der x- und y-Werte in die Formel lieber nicht im Kopf rechnen, sondern erst einmal die Werte alle stumpf eintragen, denn sonst kommt es sehr häufig zu Flüchtigkeitsfehlern. Am besten schreibt man beim Einsetzen alles in Klammern.)
- (Hinweis: Ein möglicher Fehler ist das Einsetzen der Koordinaten in folgender falscher „gekreuzter“ Anordnung
- Richtig muss es natürlich lauten:
- oder auch
BM2702
- Gegeben sind die Punkte P1 () und P2 () einer Geraden.
- Ermittle die Steigung grafisch und rechnerisch!
Lösung BM2702 - Wir schreiben erst mal das Gerüst der Steigungsformel mit Klammern und ohne Werte hin.
- (Achtung: Kopfrechnen beim Einsetzen führt oft zu Flüchtigkeitsfehlern.)
BM2703
- Gegeben sind die Punkte A () und B () einer Geraden.
- Ermittle die Steigung grafisch und rechnerisch!
Lösung BM2703 - Wir schreiben erst mal das Gerüst der Steigungsformel mit Klammern und ohne Werte hin.
- m = 0 (Die Steigung ist Null, also keine Steigung bei der Bewegung von li. nach re.)
BM2704
- Gegeben sind die Punkte A () und B () einer Geraden.
- Ermittle die Steigung grafisch und rechnerisch!
BM2705


- Warum ist die Division durch Null nicht definiert?
- ---
- Beispiel: Pizza
- ---
- Eine Pizza hat 8 Stücke.
- Er hat davon 0 Stücke gegessen. (Er hat Null Pizza gegessen.)
- Der Nenner gibt an der wievielte Teil der Pizza es ist.
- Der Zähler gibt an wie viel Stücke davon.
- ---
- (zwei Stück von einer ganzen Pizza)
- ---
- Die Division durch Null ist nicht definiert.
- Ein Beispiel:
- Ich habe KEINE Pizza. (0; Null)
- Davon habe ich 4 Stücke gegessen.
- Geht das überhaupt? Nein, das ist Nonsens! Nur kleine Mädchen füttern ihre Puppen mit nicht vorhandenen Pizzastücken.
- Man kann nicht 4 Stücke von Null Pizza essen. Deshalb bezeichnet man das als „undefiniert“.
- Die Division durch Null ist nicht definiert!
BM2706
- Die Steigung algebraisch berechnen
- ---
- Um eine Steigung zu ermitteln muss man den Graphen nicht zeichnen.
- Ob man erst die Koordinaten von Punkt A oder Punkt B einsetzt ist egal.
- Ob man zuerst die Koordinaten des ersten Punktes oder des zweiten Punktes einsetzt ist egal.
- Aber die x- und y-Werte von Punkt A müssen genau untereinander stehen. Ebenso die x- und y-Werte von Punkt B.
- ---
- Gegeben ist Punkt A () und Punkt B ()
Lösung BM2706
BM2707
- Warum wird bei der Berechnung der Steigung subtrahiert?
Lösung BM2707 - Weil man für die Ermittlung der Steigung die zurückgelegte Höhe bzw. Strecke braucht und das ist die Differenz zwischen Start- und Endpunkt.
BM2708
- Gibt die Steigung an!
- A ()
- B ()
Lösung BM2708
BM2709
- Gibt die Steigung an!
- A ()
- B ()
Lösung BM2709 - Die Steigung ist nicht definiert.
- Die Gerade ist also vertikal.
BM2710
- Gibt die Steigung an!
- A ()
- B ()
Lösung BM2710 - Die Gerade ist also waagerecht.
BM2711 - BM2720
[editar]BM2711
- Graphen zeichnen mit einem Punkt und der Steigung
- ---
- Es gibt mehrere Möglichkeiten um einen Graphen zu zeichnen.
- a) Man braucht zwei Punkte
- b) Man braucht einen Punkt und die Steigung
- ---
- Zeichne die Gerade, die durch den Pkt. () geht und eine Steigung von hat!
Lösung BM2711 - Wir tragen den Punkt () ein und gehen von diesem Punkt vier Einheiten nach rechts und eine Einheit nach oben. Das ist dann Punkt (). So haben wir einen zweiten Punkt gefunden und können den Graphen zeichnen.
BM2712
- Zeichne die Gerade, die durch den Pkt. () geht und eine Steigung von hat!
Lösung BM2711 - Wir tragen den Punkt () ein und gehen von diesem Punkt zwei Einheiten nach rechts und eine Einheit nach unten. Das ist dann Punkt (). So haben wir einen zweiten Punkt gefunden und können den Graphen zeichnen.
BM2713
- Ordne richtig zu!
- a)
- b)
- c)
- d)
- e)
- f)
-
Bild 1
-
Bild 2
-
Bild 3
-
Bild 4
-
Bild 5
-
Bild 6
Lösung BM2713 - a) Bild: 1
- b) Bild: 4
- c) Bild: 2
- d) Bild: 3
- e) Bild: 6
- f) Bild: 5
BM2714
- Zeichne die Gerade, die durch den Pkt. () geht und eine Steigung von hat!
BM2715
- Zeichne die Gerade, die durch den Pkt. () geht und eine Steigung von hat!
BM2716
- Wenn statt eines Punktes der y-Achsenabschnitt und die Steigung gegeben ist, dann ist es nichts anderes, als wenn ein Punkt außerhalb der y-Achse gegeben ist.
- Wir haben jetzt nicht einen Pkt. mit Zahlenwerten gegeben, sondern in einer anderen Form: als y-Achsenabschnitt, also der Schnittpunkt der Geraden mit der y-Achse. Das ist schließlich auch nichts anderes als ein Punkt mit x- und y-Koordinaten.
- ---
- geg.: y-Achsenabschnitt 4 und Steigung
- Um den linearen Graphen zu zeichnen benötigen wir zwei Punkte. Der y-Achsenabschnitt 4 hat die Koordinaten ()
- Die Steigung entspricht .
- Wir gehen also vom Punkt () 5 Einheiten nach rechts und 3 Einheiten nach oben und kommen so zu Punkt (). Das ist der zweite Punkt. Und schon können wir unseren Graphen zeichnen.

- Zur Kontrolle sollte man am gezeichneten Graphen nochmals kurz überprüfen, ob die gegebenen Steigung ungefähr mit der Linie übereinstimmt.
- In unserem Fall ist die Steigung ein flache negative Steigung, die leider nicht mit dem Graphen übereinstimmt, denn dieser steigt leicht an.
- Wo ist uns ein Fehler unterlaufen? Kannst du ihn finden?
Lösung BM2716 - Vorzeichenfehler!
- Die Steigung entspricht .
- Wir gehen also vom Punkt () 5 Einheiten nach rechts und 3 Einheiten nach unten (wir waren fälschlicherweise nach oben gegangen) und kommen so zu Punkt (). Das ist der zweite Punkt.
BM2717
- Gegeben ist der y-Achsenabschnitt -3 und Steigung .
- Zeichne den Graphen!
Lösung BM2717 - Der y-Achsenabschnitt -3 hat die Koordinaten ()
- Wir gehen also vom Punkt () 2 Einheiten nach rechts und 5 Einheiten nach oben und kommen so zu Punkt (). Das ist der zweite Punkt. Und schon können wir unseren Graphen zeichnen.
BM2718
- Eine Firma verkauft
- 40 Adapter für insgesamt 70 €
- und
- 75 Adapter für insgesamt 131,25 €
- Diese Zahlenangaben sind Zahlenpaare.
- Was ist die abhängige Variable und was ist die unabhängige?
- Gewöhnlich bestimmt die gekauft Menge (z. B. 40 Stk.) den Kaufpreis (z. B. 70 EUR)
- ---
- Finde m und stelle die Gerade, die die beiden Zahlenpaare verbindet grafisch dar!
1. Lösung BM2718 - (Stückzahl; Preis)
- (40; 70) (x1; y1)
- (75; 131,25) (x2; y2)
- m = Delta y / Delta x
- Wir schreiben erst mal das Gerüst der Steigungsformel mit Klammern und ohne Werte hin.
- (Achtung: Kopfrechnen beim Einsetzen führt oft zu Flüchtigkeitsfehlern.)
- Irgendwas stimmt nicht mit dem Graphen? Fällt dir ein Fehler auf?
2. Lösung BM2718 - Es gibt keine negativen Preise. Jedenfalls nicht im Rahmen der Aufgabenstellung. Auch negative Stückzahlen machen keinen Sinn. Es ist also unzulässig die Gerade außerhalb des 1. Quadranten weiter zu verlängern. Das würde für diese Aufgabe keinen Sinn machen.
BM2719
- Lineare Funktionen in Normalform
- mit Steigung und Achsenabschnitt
- ---
- Die Steigung für jede beliebige Gerade kann in der Form geschrieben werden.
- ---
- Gegeben ist die Gleichung
- Um den Graphen zu zeichnen setzen wir einige Werte für x ein, um den jeweils dazugehörigen y-Wert zu ermitteln.

Bild 1 - Wir nehmen 3 verschiedene x-Werte. Meist lässt sich mit den Werten 0; 1 und 2 einfach rechnen.
x y 0 1 2
- Nun setzen wir die x-Werte nacheinander in die gegebenen Gleichung ein und rechnen so die dazugehörigen y-Werte aus.
- ⇒ ⇒
- ⇒ ⇒
- ⇒ ⇒
- Mit den so ermittelten y-Wert vervollständigen wir unsere Wertetabelle.
x y 0 1 1 3 2 5
- Mit diesen 3 Punkten können wir unseren Graphen zeichnen.
- Wir haben zur Sicherheit 3 Punkte genommen. Das ist einer mehr, als die zwei erforderlichen, um eine Gerade zu zeichnen. So können wir unserer Flüchtigkeitsfehler beim Rechnen eventuelle noch erkennen und korrigieren. Denn bei einem Fehler würden die 3 Punkte nicht auf einer Geraden liegen.
- Diese Methode mit der Wertetabelle ist aber zeitraubend und fehleranfällig.
BM2720
- Es ist viel schneller und einfacher aus der Gleichung einer linearen Funktionen in Normalform die Steigung und den Achsenabschnitt direkt abzulesen.
- ---
- Beispiel:
- Die beiden Zahlen 2 und 1 geben uns direkt die Steigung und den Achsenabschnitt an.
- m = 2
- b = 1
- (In manchen Schreibweisen wird der Achsenabschnitt auch mit a oder n bezeichnet.)
- Mit Achsenabschnitt ist immer der y-Achsenabschnitt gemeint, also der Schnittpunkt der Geraden mit der y-Achse.
- Diese beiden Zahlen für m und b zeigen uns also direkt, wie die Gerade aussieht.
- ---
- Nenne für die folgenden Gleichungen jeweils m und b!
- 1.)
- 2.)
- 3.)
- 4.)
- 5.)
- 6.)
- 7.)
Lösung BM2720 - 1.)
- ---
- 2.)
- ---
- 3.)
- ---
- 4.)
- ---
- 5.)
- 6.)
- ---
- 7.)
- Wenn bei einer Aufgabenstellung die Steigung gesucht ist, muss immer in die Normalform umgestellt werden, falls diese noch nicht vorliegt.
BM2721 - BM2730
[editar]BM2721
- Wir setzen Null als Wert für x ein, um den zugehörigen y-Wert zu erhalten.
- Dadurch wird der Term zu also zu Null.
- Es bleibt also übrig
- ---
- Jedes mal, wenn wir in eine lineare Gleichung der Form für x den Wert Null einsetzen, dann verschwindet der Term , denn ergibt immer Null.
- Das funktioniert natürlich nur, wenn y auf der linken Seite isoliert steht.
- ---
- Für erhalten wir .
- Das entspricht also dem Punkt (0; b)
- Genau deshalb können wir aus der Normalform den Achsenabschnitt b direkt ablesen.
- Denn dort wo die Gerade die y-Achse schneidet haben wir den x-Wert 0.
- „b“ ist die y-Koordinate des Schnittpunktes mit der y-Achse (also des y-Achsenabschnitts). Dieser Punkt hat wie gesagt als x-Wert immer Null-
- Also schneidet die Gerade die y-Achse im Punkt (0; b).
- Wenn man also ganz korrekt ist, dann ist „b“ nicht der Schnittpunkt (Achsenabschnitt), sondern nur die y-Koordinate des y-Achsenabschnitts.
- ---
- Steigung
- Die Steigung „m“ ist immer die Zahl vor dem „x“.
- Der Koeffizient vor dem „x“ ist unser Steigung „m“.
- oder
- 1 Schritt nach rechts, 2 Schritte hoch
- ---
- Wenn man mit dem y-Achsenabschnitt den ersten Punkt hat (0; b), dann kann man mit Hilfe der Steigung m einen zweiten Punkt ermitteln.
- Wenn wir also die Steigung oder haben, dann gehen wir mit dem x-Wert einen Schritt nach rechts. Also . Die Null ist die x-Koordinate des y-Achsenabschnitts.
- Und den y-Wert erhöhen wir um den Wert des Zählers von der Steigung.
- Also
- Nochmals zusammengefasst: Wir rechnen und erhalten
- ---
- Den Graphen mittels Achsenabschnitt und Steigung zu zeichnen ist wesentlich schneller, als eine Punktwerttabelle zu erstellen.
BM2722
- Neutrales Element:
- Ein neutrales Element ist dadurch gekennzeichnet, dass jedes Element durch die Verknüpfung mit dem neutralen Element auf sich selbst abgebildet wird.
- Das neutrale Element für Multiplikation ist 1.
- Wenn man eine Zahl mit mit Eins multipliziert, dann erhält man genau die gleiche Zahl wieder.
- ---
- Die Null ist das neutrale Element der Addition.
- denn
BM2723
- Bestimme zwei Punkte des Graphen: den y-Achsenabschnitt und den zweiten Punkt mittels der Steigung
Lösung BM2723 - 1. Punkt y-Achsenabschnitt (grün): (0; b) also (0; 1)
- 2. Punkt mit Hilfe der Steigung (blau): (0; 1) + (2; -1) also (2; 0)
- bei einer negativen Steigung nehmen wir das Minus üblicherweise immer zum Zähler
- also für
- Wenn wir das Minus einer negativen Steigung zum Nenner nehmen würden, dann würden wir einen anderen Punkt bekommen, aber genau die gleiche Gerade.
- also für
- ergibt als 2. Punkt (rot): (0; 1) + (-2; 1) also (-2; 2)
- Warum nehmen wir das Minus bei einer negativen Steigung üblicherweise zum Zähler und nicht zum Nenner?
2. Lösung BM2723 - Weil das der allgemeinen Richtung zur Beurteilung der Steigung entspricht: von rechts nach links
- Bei einer pos. Steigung von re. nach li.
- und auch bei einer neg. Steigung von re. nach li.
- ---
- pos. Steigung
- z. B.
- oder oder
- Steigung: ein Schritt nach rechts (IMMER NACH RECHTS); zwei Schritt hoch (weil Plus)
- ---
- neg. Steigung
- z. B.
- oder
- Steigung: zwei Schritt nach rechts (IMMER NACH RECHTS); einen Schritt runter (weil Minus)
- ---
- 2. Beispiel
- neg. Steigung
- oder
- Steigung: 8 Schritt nach rechts (IMMER NACH RECHTS); 3 Schritte nach unten (weil Minus 3)
- ---
- 3. Beispiel
- pos. Steigung
- oder
- Steigung: 4 Schritte nach rechts (IMMER NACH RECHTS); zwei Schritt hoch (weil Plus 4)
BM2724
- ---
- Das können wir auch als schreiben
- Also:
- m = 0
- b = 4
- Egal welches x wir einsetzen (-2; - 1; 0; 1; 2; ...), unser y-Wert ist immer 4.
- Also ist der dazugehörige Graph eine Parallele zur x-Achse, die die y-Achse bei +4 schneidet.
- Wir können oder auch als schreiben.
- Also einen Schritt nach rechts (IMMER NACH RECHTS); Null Schritte hoch oder runter.
- Der y-Achsenabschnitt ist natürlich (0; 4)

BM2725
- ---
- Das können wir auch als oder als schreiben
- Also:
- m = 1
- b = 0
- Wenn b = 0 ist, dann geht der Graph durch den Koordinatenursprung (0; 0)
- Wenn m = 1 ist, dann steigt die Gerade mit 45° an, weil immer genau ein Schritt nach rechts und ein Schritt hoch.

BM2726
BM2727
Lösung BM2727 - 1. Punkt y-Achsenabschnitt: (0; -2) also b = -2
- 2. Punkt: Steigung vom 1. Punkt aus bestimmen
- also:
BM2728
Lösung BM2728 - 1. Punkt y-Achsenabschnitt: (0; 0) also b = 0
- 2. Punkt: Steigung vom 1. Punkt aus bestimmen
- also:
- oder kürzer und besser
BM2729
- Die Methode mit Steigung und y-Achsenabschnitt funktioniert nur, wenn die lineare Gleichung nach y aufgelöst ist, also in der Normalform vorliegt.
- m = Steigung
- b ergibt den y-Achsenabschnitt mit den Koordinaten
- ---
- also ist und .
- Daraus ergibt sich der y-Achsenabschnitt
- ---
- also ist und .
- Daraus ergibt sich der y-Achsenabschnitt
- ---
- also ist und .
- Daraus ergibt sich der y-Achsenabschnitt
- ---
- also ist und .
- Daraus ergibt sich der y-Achsenabschnitt
- ---
- Um eine Gerade zu zeichnen benötigt man 2 Punkte oder
- einen Punkt und eine Vorschrift um einen 2. Punkt zu ermitteln. Diese Vorschrift ergibt sich aus der STeigung.
BM2730
- Aus dieser Form kann man die Steigung nicht unmittelbar und schnell ablesen. Man muss erst nach y umstellen, was manchmal mühsam ist.
- ---
- Stelle nach y um!
Lösung BM2730
BM2731 - BM2740
[editar]BM2731
- ---
- Bei Gleichungen der Form (Koordinatenform) ist es einfacher den y-Achsenabschnitt und den x-Achsenabschnitt zu berechnen und mit diesen beiden Punkten die Gerade zu zeichnen.
- ---
- Berechne für die Gleichung den y-Achsenabschnitt und den x-Achsenabschnitt und zeichne damit den Graphen!
- Wenn wir allerdings die Steigung der Gleichung ermitteltn sollen, dann müssen wir wohl oder übel nach y umstellen. (Das haben wir bereits in der Übung BM2730 getan.)
- Dort hatten wir nach der Umstellung
- erhalten, also
- ---
- Interessierten sei verraten, dass es mit etwas Kopfrechnen sehr wohl einen Weg gibt, um die Steigung aus einer Gleichung der Form (Koordinatenform) direkt zu ermitteln.
- ---
- Also ist
- ---
- Konkret bedeutet dass, dass unsere Gleichung die Steigung
- hat.
- ---

- Aus dem fertigen Graphen der Gleichung könnte man nachträglich auch die Steigung ablesen. Aber das ist manchmal auch kompliziert.
BM2732
- Die Normalform einer linearen Gleichung () ist wie gesagt nicht immer die effektivste Form einer linearen Gleichung, um ihren Graphen zu zeichnen.
- Wenn x und y auf der gleichen Seite der Gleichung stehen und die Konstante auf der anderen Seite (), dann ist die Methode mit der Berechnung der Achsenabschnitte meist am effektivsten.
- ---
- Berechne für die Gleichung den Graphen...
- 1.) ... indem Du die Gleichung in die Normalform umstellst!
- 2.) ... indem Du die Gleichung in die Koordinatenform umstellst!
3. Lösung BM2732 - Diese Steigung haben wir auch schon in der 1. Lösung erhalten:
BM2733
- Berechne für die Gleichung den Graphen...
- 1.) ... indem Du die Gleichung in die Normalform umstellst!
- 2.) ... indem Du die Gleichung in die Koordinatenform umstellst!
2. Lösung BM2733 - Koordinatenform:
- Da müssen wir nichts mehr umstellen, denn die Koordinatenform liegt bereits vor.
- für folgt also ()
- für folgt also ()
- Natürlich sind die Graphen der 1. und 2. Lösung identisch. Sie haben lediglich unterschiedliche Punkte, um sie zu zeichnen.
- Kannst du die Steigung aus der Gleichung direkt im Kopf ausrechnen? Die Lösung steht unter „3. Lösung“.
3. Lösung BM2733 - ---
- Die Steigung können wir natürlich auch aus der Normalform ablesen, wie wir sie in der 1. Lösung ermittelt hatten.
BM2734
- Berechne für die Gleichung den Graphen...
- 1.) ... indem Du die Gleichung in die Normalform umstellst!
- 2.) ... indem Du die Gleichung in die Koordinatenform umstellst!
2. Lösung BM2734 - Koordinatenform:
- Da müssen wir nichts mehr umstellen, denn die Koordinatenform liegt bereits vor.
- für folgt
- also ()
- ---
- für folgt
- also ()
- Wir haben jetzt 2 Punkte (den y-Achsenabschnitt und den x-Achsenabschnitt) und könnten jetzt eigentlich unseren Graphen damit zeichnen.
- Dummerweise sind diese beiden Punkte identisch (0; 0). Beide Punkte liegen im Koordinatenursprung. Wir können also keinen Graphen zeichnen.
- Die Methode versagt immer dann wenn in der Koordinatenform die Konstante eine Null ist, also immer dann, wenn der Graph durch den Nullpunkt des Koordinatenkreuzes geht.
- ---
- Aus der Gleichung können wir also nicht direkt die Achsenabschnitte berechnen. Eigentlich können wir sie schon berechnen, da sie aber identische Punkte sind hilft uns das nicht den Graphen zu zeichnen. Wir müssen also die Gleichung in die Normalform umwandeln (nach y umstellen), um zusätzlich noch die Steigung zu erhalten, so wie wir das in der 1. Lösung getan haben.
BM2735
- Berechne für die Gleichung den Graphen...
- 1.) ... indem Du die Gleichung in die Normalform umstellst!
- 2.) ... indem Du die Gleichung in die Koordinatenform umstellst!
1. Lösung BM2735 - Normalform:
- Ee ist nicht ratsam als erstes die Brücke zu beseitigen, indem man sie mit dem kgV erweitert.
- Die Brüche werden wir hier erst ganz zum Schluss versuchen aufzulösen.
2. Lösung BM2735 - Koordinatenform:
- Da müssen wir nichts mehr umstellen, denn die Koordinatenform liegt bereits vor.
- für folgt
- also ()
- ---
- für folgt
- also ()
- Eigentlich sollten die die Graphen der 1. und 2. Lösung identisch sein - sind sie aber nicht.
- Wo liegt der Fehler? Kannst du ihn finden?
3. Lösung BM2735 - In der 1. Lösung hat der y-Axhsenabschnitt die Koordinaten und in der 2. Lösung . Es sieht also nach einem Vorzeichenfehler aus. Wo hat er sich eingeschlichen?
- Der zweite Punkt (der x-Achsenabschnitt) scheint in beiden Graphen identisch zu sein.
- ---
- In der 2. Lösung hat sich sowohl für als auch für auf der rechten Seite der Gleichung ein Minuszeichen zu viel eingeschlichen.
- Deshalb haben wir für das falsche Ergebnis statt
- Aber warum haben wir für trotz des eingeschlichenen Minuszeichens das richtiges Ergebnis ?
- Weil von der erten Zeile zur zweiten Zeile zusätzlich noch ein Fehler gemacht wurde. Statt die Minuszeichen auf beiden Seiten gegeneinander aufzuheben, ist auf der rechten Seite das Minuszeichen rechts stehen geblieben, während nur das Minuszeichen auf der linken Seite verschwunden ist. So sind wir durch zwei Vorzeichenfehler zufällig trotzdem auf das richtige Ergebnis gekommen. Aber der Rechenweg war nichtsdestotrotz falsch.
BM2736
- Berechne für die Gleichung den Graphen...
- 1.) ... indem Du die Gleichung in die Normalform umstellst!
- 2.) ... indem Du die Gleichung in die Koordinatenform umstellst!
2. Lösung BM2736 - Koordinatenform:
- Da müssen wir nichts mehr umstellen, denn die Koordinatenform liegt bereits vor.
- Wie wir bereits wissen sind liegen der y-Achsenabschnitt als auch der x-Achsenabschnitt im Koordinatenursprung. Wir können also mit der Koordinatenform nicht direkt einen Graphen zeichnen.
- Die Methode versagt immer dann wenn in der Koordinatenform die Konstante eine Null ist, also immer dann, wenn der Graph durch den Nullpunkt des Koordinatenkreuzes geht.
BM2737
- Geraden und Parallelen
- Geraden und Senkrechte
- ---
- Parallelität:
- In der euklidischen Geometrie definiert man: Zwei Geraden sind parallel, wenn sie in einer Ebene liegen und einander nicht schneiden. Außerdem setzt man fest, dass jede Gerade zu sich selbst parallel sein soll.
- Zu jeder Geraden und jedem Punkt, der nicht auf der Geraden liegt, gibt es genau eine Gerade, die zur gegebenen Geraden parallel ist und durch den gegebenen Punkt geht (die Parallele durch diesen Punkt).
- ---
- Parallele Geraden schneiden sich nie.
- Parallelen schneiden sich nie.
- ---
- Eine Linie, die senkrecht auf einer anderen Linie steht schneidet diese in einem rechten Winkel.
- Eine Senkrechte schneidet die Gerade, auf der sie senkrecht steht in einem Winkel von 90°.
- ---
- Parallelen haben die gleiche Steigung. Deshalb schneiden sie sich nicht.
- ---
- Zwei Geraden, die senkrecht zueinander stehen haben jeweils eine Steigung mit unterschiedlichem Vorzeichen.
- Sonderfall: senkrecht (also Steigung Null); vertikal (also Steigung nicht definiert). Und anders rum.
- rechtwinklig = orthogonal
BM2738
- Finde die Gleichung der Geraden, die parallel zu verläuft und durch den Punkt geht!
1. Lösung BM2738 - Um die Steigung zu ermitteln stellen wir die gegebenen Gleichung erst mal in die Normalform um.
- ---
- Als zweiten Schritt suchen wir die Gleichung für die Gerade, die
- 1.) durch den Punkt geht und
- 2.) parallel zur Steigung verläuft, also auch genau diese Steigung hat.
- Dazu nehmen wir uns die allgemeine Gleichung der Normalform
- Diese Gleichung hat vier Unbekannte: y; m ; x und b.
- Wenn wir konkrete Zahlenwerte für 3 dieser Unbekannten einsetzen, dann können wir den Wert für die 4. Unbekannte ausrechnen.
- Uns sind die Werte für y; m und x bekannt. Also können wir b ausrechnen.
- Und der Punkt bedeutet nichts anderes als und .
- Das setzen wir jetzt ein und rechnen b aus.
- Warum haben wir das gemacht? Warum haben wir x und y eingesetzt?
- Sonst machen wir das meist anders rum. Wir haben eine Gleichung, z. B. und setzen nacheinander viele verschiedene Werte für x ein, rechnen so die dazugehörigen y-Werte aus und zeichnen dann die Gerade. Jedes x-y-Zahlenpaar ist ein Punkt der Geraden. Es reichen uns zwar zwei Punkte, um eine Gerade zu zeichnen, aber trotzdem hat die Gerade unendlich viele Punkte, die alle x-y-Zahlenpaare sind, für die die Gleichung wahr ist - also auf beiden Seiten die gleichen Ergebnisse gibt.
- Hier haben wir es jetzt anders rum gemacht. Wir haben aus dem fertigen Graphen einen Punkt genommen - P - um mit seinen Werten die Gleichung zu ermitteln.
- ---
- Noch sind wir nicht ganz fertig.
- Wir wissen, dass die gesucht parallele Linie die Steigung hat und den y-Achsenabschnitt .
- Das müssen wir jetzt nur noch ordentlich in einer linearen Gleichung in Normalform aufschreiben:
- Kontrolliere dein Ergebnis!
2. Lösung BM2738 - Um das Ergebnis zu kontrollieren setzen wir den gegebenen Punkt in die Gleichung ein, denn dieser soll ja auf der Geraden liegen, also die Gleichung erfüllen.
- Beide Seiten der Gleichung sind identisch. Also ist die Gleichung erfüllt. Die Gleichung ist wahr.
- Der Punkt liegt wir gefordert auf der Geraden. Oder wie es in der Aufgabenstellung formuliert ist: Die Gerade geht durch den Punkt.
- ---
- Nun vergleichen wir noch die Steigung unserer gefundenen Geradengleichung () mit der Steigung der vorgegebenen Geraden ().
- Beide Steigungen sind identisch.
- unsere Probe hat also ergeben, dass wir die richtige Gleichung gefunden haben.
- ---
- Etwas später (Übunf BM2740) werden wir solche Aufgaben mit der Punktsteigungsform der Geradengleichung wesentlich effektiver und schneller lösen.
BM2739
- Finde die Gleichung der Geraden, die senkrecht auf steht und durch den Punkt geht!
- Das ist fast die gleiche Aufgabe, wie in der vorherigen Übung, nur dass dieses mal die gesuchte Gerade nicht parallel sondern senkrecht verläuft.
- ---
- Dazu müssen wir noch kurz lernen, wie man die Steigung einer Senkrechten ermittelt.
- Wir nehmen den NEGATIVEN REZIPROKEN WERT
- Beispiel:
- ganz allgemein:
- ---
- Jetzt aber los!
- Finde die Gleichung der Geraden, die senkrecht auf steht und durch den Punkt geht!
Lösung BM2739 - Um die Steigung zu ermitteln stellen wir die gegebenen Gleichung erst mal in die Normalform um.
- Bis hier war alles wo wie auch bei der vorhergehenden Aufgabe, denn wir brauchn so oder so die Steigung der gegebenen Geraden.
- ---
- Als zweiten Schritt suchen wir die Gleichung für die Gerade, die
- 1.) durch den Punkt geht und
- 2.) senkrecht auf der Geraden mit der Steigung steht, also die folgende Steigung hat:
- Unsere gesuchte Senkrechte hat die Steigung .
- ---
- Der nächste Schritt ist bereit aus der vorherigen Aufgabe bekannt: Um das b für unsere Gesucht Senkrechts zu ermitteln setzen wir den x- und y-Wert des gegebenen Punktes ein und die Steigung, die unsere Senkrechte haben soll.
- Und der Punkt bedeutet nichts anderes als und .
- Das setzen wir jetzt ein und rechnen b aus.
- Warum haben wir das gemacht? Warum haben wir x und y eingesetzt? Wir haben aus dem fertigen Graphen einen Punkt genommen - P - um mit seinen Werten die Gleichung zu ermitteln.
- ---
- Noch sind wir nicht ganz fertig.
- Wir wissen, dass die gesucht parallele Linie die Steigung hat und den y-Achsenabschnitt .
- Das müssen wir jetzt nur noch ordentlich in einer linearen Gleichung in Normalform aufschreiben:
- Die Null können wir weglassen.
- Kontrolliere dein Ergebnis!
2. Lösung BM2739 - Um das Ergebnis zu kontrollieren setzen wir den gegebenen Punkt in die Gleichung ein, denn dieser soll ja auf der Geraden liegen, also die Gleichung erfüllen.
- ; Punkt ; ;
- Die Gleichung stimmt für diesen Punkt.
- ---
- Dann vergleichen wir noch die Steigung (gegebene Gerade) und (Senkrechte dazu).
- ist die negative Inverse von
- Das ist also die gesuchte Senkrechte zur gegebenen Geraden.
BM2740
- Punktsteigungsform der Geradengleichung
- ---
- Wie wir bereits wissen ist die Steigung
- Das ist die Steigung, wenn die Punkte und gegeben sind.
- ---
- Wenn wir aber nicht zwei Punkte gegeben haben, sondern nur einen Punkt und die Steigung, dann müssen wir unser Vorgehen etwas ändern.
- Gegeben sind ein Punkt und die Steigung m. Erst diese Steigung hilft uns irgendeinen zweiten Punkt zu finden.
- Dieser zweite Punkt ist irgendein Punkt auf der Geraden, also ein variabler Punkt.
- Da wir nur einen konkreten Punkt haben, aber keinen konkreten Punkt , verwenden wir ganz allgemein und für den variablen Punkt , der jeder Punkt auf der Geraden sein kann.
- Der zweite Punkt gibt uns also ganz allgemein ein und statt die konkreten Koordinaten .
- Wir haben jetzt also statt
- die leicht abgeänderte Gleichung
- .
- Da wir nur einen einzigen Punkt und die Steigung m gegeben haben, haben wir auch noch keinen konkreten Punkt (also auch noch kein und ).
- Für diesen Punkt können wir jeden beleibigen Punkt der Geraden nehmen. Deshalb nehmen wir nur ganz allgemein und statt des konkreten und .
- Durch Umstellen dieser Gleichung wollen wir den Bruch loswerden, denn mit Brüchen lässt sich meist schlechter rechnen.
- Wir tauschen noch die Seiten, damit unser y auf der linken Seite steht, so wie auch bei der Normalform .
- Diese Gleichung prägen wir uns bitte ein als Punktsteigungsform der Geradengleichung.
- ---
- Normals zur Erklärung woher die Gleichung in der Punktsteigungsform kommt:
- Wir haben mit der Steigung m begonnen.
- Wenn wir aber einen dieser Punkte nicht kennen, sonder nnur den Punkt und die Steigung m, dann setzen wir in dieser Gleichung statt und die Variablen für irgendeinen Punkt ein.
- Das ist ja gerade der Zweck von Variablen.
- Und so kommen wir auf
- .
- ---
- Diese Form der lin. Gleichung heißt Punktsteigungsform. Der Name ist offensichtlich, denn mit Hilfe eines Punktes und der Steigung ermitteln wir den Graphen.
BM2741 - BM2750
[editar]BM2741
- Finde die Gerade, die durch den Pkt. geht und die Steigung 3 hat!
1. Lösung BM2741 - geg.:
- Wir setzen diese Werte in die Punktsteigungsform der linearen Gleichung ein.
- Aus lesen wir ab: und .
- x und y sind Variablen, dort setzen wir nichts ein.
- und (mit tiefergestelltem Index) sind Platzhalter für konkrete Zahlenwerte, für einen festen Punkt.
- (Ebenso sind in der Normalform die Buchstaben m und b Platzhalter für konkrete Zahlen, während x und y Variablen sind.)
- Und schon sind wir fertig.
- ---
- Wir können nacheinander viele verschieden Werte für x einsetzen und dafür jeweils die entsprechenden dazugehörigen y-Werte einsetzen.
- Aber mit dieser Gleichung können wir keinen Graphen zeichnen. Dafür müssen wir die Punktsteigungsform in die Normalform umstellen.
- Damit können wir nur einen Graphen zeichnen.
- Kontrolliere Dein Ergebnis!
2. Lösung BM2741 - Gegeben war die Steigung 3 und unsere gefundene Gleichung hat ebenfalls die Steigung 3.
- ---
- Nun kontrollieren wir noch, ob der gegebene Punkt auf der gefunden Gleichung liegt:
- Gleichung erfüllt.
BM2742
- Finde die Gerade, die durch den Pkt. geht und die Steigung hat!
1. Lösung BM2742 - geg.:
- ges.: Gleichung der Geraden
- Wir setzen diese Werte in die Punktsteigungsform der linearen Gleichung ein.
- Aus lesen wir ab: und .
- x und y sind Variablen, dort setzen wir nichts ein.
- Achtung: Doppelte Minuszeichen müssen in Klammern gesetzt werden.
- Um einen Graphen zeichnen zu können müssen wir die Punktsteigungsform in die Normalform umstellen.
- Damit können wir nur einen Graphen zeichnen.
- Kontrolliere Dein Ergebnis!
2. Lösung BM2742 - Gegeben war die Steigung 0,5 und unsere gefundene Gleichung hat die Steigung , was nichts anderes ist als 0,5.
- ---
- Nun kontrollieren wir noch, ob der gegebene Punkt auf der gefunden Gleichung liegt:
- Gleichung erfüllt.
BM2743
Lösung BM2743 - Dafür sollte jetzt aber wirklich keine Hilfe mehr erforderlich sein, nachdem wir das zur Genüge geübt haben.
- Viele Wege führen nach Rom.
- Vergiss die Probe nicht!
- ---
- Wir haben die Punkte und
- Daraus ergibt sich
- Jedenfalls beauptet das www.wolframalpha.com
- wenn wir
- (3; 8) and (-32/21; 0)
- eingeben.
BM2744
- Punktsteigungsform
- ---
- Für die Verwendung der Punktsteigungsform gbit es drei mögliche Fälle:
- 1.) Gegeben sind die Steigung m und ein Punkt mit seinen x- und y-Koordinaten. Das ist die einfachste Version, denn wir müssen nur noch die Werte in die Punktsteigungsform einsetzen.
- 2.) Gegeben sind 2 Punkte. Nun müssen wir mit Hilfe dieser Punkte erst die Steigung ermitteln ( ). Erst dann können wir wie bereits in der 1. Version die Steigung und einen Punkt in die Punktsteigungsform einsetzen.
- 3.) Gegeben ist eine Gleichung, also die Gleichung einer Linie, und ein Punkt. Weiterhin ist vorgegeben, dass gesuchte Linie parallel bzw. rechtwinklig zur gegebenen Gleichung verlaufen soll.
- parallel:
- rechtwinklig:
BM2745
- geg.: Punkt und Steigung
- ges.: Gleichung und die dazugehörige Gerade
- Bitte das Ergebnis auch überprüfen!
Lösung BM2745 - einsetzen also und
- ---
- ---
- Ergebnis überprüfen:
- Wir setzen die Koordinaten des gegebenen Punktes in das Ergebnis ein und überprüfen ob die Gleichung korrekt ist.
- Die Gleichung ist wahr. Also war unser Ergebnis korrekt.
BM2746
- geg.: Punkt und Steigung
- ges.: Gleichung und die dazugehörige Gerade
- Bitte das Ergebnis auch überprüfen!
Lösung BM2746 - einsetzen also und
- ---
- ---
- Ergebnis überprüfen:
- Wir setzen die Koordinaten des gegebenen Punktes in das Ergebnis ein und überprüfen ob die Gleichung korrekt ist.
- Die Gleichung ist wahr. Also war unser Ergebnis korrekt.
BM2747
- Gesucht ist die Gerade, die Parallel zur Geraden verläuft und durch den Punkt und geht.
- Bitte das Ergebnis auch überprüfen!
Lösung BM2747 - Da die gesucht Gerade parallel zur gegebenen Geraden verläuft, sind die Steigungen identisch.
- Dann: einsetzen also und
- ---
- Ergebnis überprüfen:
- Wir setzen die Koordinaten des gegebenen Punktes in das Ergebnis ein und überprüfen ob die Gleichung korrekt ist.
- Die Gleichung ist wahr. Also war unser Ergebnis korrekt.
BM2748
- Gesucht ist die Gerade, die senkrecht zur Geraden liegt und durch den Punkt und geht.
- Bitte das Ergebnis auch überprüfen!
Lösung BM2748 - Da die gesucht Gerade SENKRECHT (rechtwinklig) zur gegebenen Geraden verläuft, sind die Steigungen identisch.
- Dann setzen wir den also und in die Gleichung der Punktsteigungsform ein.
- ---
- Ergebnis überprüfen:
- Wir setzen die Koordinaten des gegebenen Punktes in das Ergebnis ein und überprüfen ob die Gleichung korrekt ist.
- Die Gleichung ist wahr. Also war unser Ergebnis korrekt.
BM2749
- Gesucht ist die Gerade, die durch zwei gegebene Punkte verläuft.
- In der Standardversion brauchen wir für eine Gerade einen Punkt und die Steigung (m):
- Nun sind aber nur die zwei Punkte und gegeben. Aus diesen können wir uns aber die Steigung (m) errechnen.
- Um die Steigung zu errechnen setzen wir erst mal in die obige Formel unsere beiden Punkte ein.
- genauer
- .
- Durch Umstellen kommen wir dann auf die Steigung, die wir ausrechnen.
- Es ist VÖLLIG EGAL, ob wir den einen oder den anderen Punkt in 1 oder 2 einsetzen, das Ergebnis ist das gleiche.
- Trotzdem wäre es cleverer, wenn wir in
- unsere beiden gegebenen Punkt so einsetzen, dass wir uns - wenn möglich - die Rechnung erleichtern. Sollte also einer der beiden gegebenen Punkt ein oder zwei Nullen als Koordinaten enthalten, dann wäre es geschickter diesen in einzusetzen.
- ---
- Fangen wir an zu rechnen!
- Gegeben sind die beiden Punkte: (-1; -7) und (2; 5).
- Berechne daraus die Steigung und gib dann die Gleichung für die Gerade an, die durch beide Punkte geht!
1. Lösung BM2749 - Unsere Steigung ermitteln wir mit
- Umgestellt nach m ist das:
- Wir wählen Punkt (2; 5) als und setzen ein:
- Nun müssen wir nur noch die Linearengleichung aufschreiben.
2. Lösung BM2749 - m = 4
- Als Punkt setzen wir (2; 5) ein. Wir könnten auch den anderen Punkt nehmen, das gibt zum Schluss das gleiche Ergebnis.
- ausmultiplizieren:
- nach y umstellen:
- Wir könnten auch den anderen Punkt nehmen, das gibt zum Schluss das gleiche Ergebnis. Wetten?
- Punkt: (-1; -7)
- m = 4
- ausmultiplizieren:
- nach y umstellen:
- Wette gewonnen!
Kontrolle BM2749 - Einsetzen in
- 1. Test: Punkte: (-1; -7) einsetzen:
- Stimmt!
- 2. Test: Punkte: (2; 5) einsetzen:
- Stimmt!
BM2750
- Gegeben sind die beiden Punkte: (1; -4) und (-2; 5).
- Wie lautet die Geradengleichung?
1. Lösung BM2750 Wir entscheiden uns z. B. für
- (1; -4) als Punkt und
- (-2; 5) als Punkt
- Nun die Formel!
2. Lösung BM2750 - m = - 3
- Wir nehmen willkürlich den Punkt (1; -4)
Kontrolle BM2750 - 1. Test: Punkt (1; -4) einsetzen:
- Da stimmt irgendwas NICHT!
- 2. Test: Punkt (-2; 5) einsetzen:
- Auch falsch! Das stinkt gewaltig.
- Das Ergebnis ist FALSCH!
- Findest du den Fehler?
3. Lösung BM2750 - In der 2. Lösung stand der Fehler:
- Für hatten wir fälschlicherweise "-1" eingesetzt, statt "+1".
- So ist es jetzt richtig!
- Frage: Kann man eigentlich mit dem ersten Punkt die Steigung berechnen und dann für die endgültige Geradenformel den zweiten Punkt einsetzen?
4. Lösung BM2750 - JA!
- Das Ergebnis ist das gleiche.
- Man führe die Kontrolle des gefundenen Ergebnisses immer mit beiden Punkten durch. Es könnte ja sein, dass einer der beiden Punkte auf der Geraden liegt, nicht aber der andere Punkt-
- índice
- Lección 104b ← Lección 105b → Lección 106b
- Lección 105




























































































































































































































































































































































































































