Curso de alemán para principiantes con audio/Lección 103b
Apariencia
- índice
- Lección 102b ← Lección 103b → Lección 104b
- Lección 103
- Mathematik auf Deutsch - 53
BM2601 - BM2610
[editar]BM2601

Bild 1 
Bild 2: 1. - 4. Quadrant - Wenn sowohl der x-Wert als auch der y-Wert des Koordinatenpaares positiv ist, dann liegt der Punkt im oberen rechten Viertel des Koordinatenkreuzes.
- Dieses obere, rechte Viertel nennt man 1. Quadrant.
- Ausgehend vom 1. Quadranten wird die Nummerierung der Quadranten entgegen dem Uhrzeigersinn fortgesetzt.
- entgegen dem Uhrzeigersinn = gegen den Uhrzeigersinn (Gegenteil: im Uhrzeigersinn)
- Der 4. Quadrant liegt also rechts unten.
BM2602
- Setze die folgenden Sätze fort:
- Beispiel:
- 1.Quadrant
- ⇒ Im 1. Quadranten sind die x-Werte positiv und die y-Werte positiv.
- ---
- 2.Quadrant
- 3.Quadrant
- 4.Quadrant
Lösung BM2602 - Im 1. Quadranten sind die x-Werte positiv und die y-Werte positiv.
- Im 2. Quadranten sind die x-Werte negativ und die y-Werte positiv.
- Im 3. Quadranten sind die x-Werte negativ und die y-Werte negativ.
- Im 4. Quadranten sind die x-Werte positiv und die y-Werte negativ.
BM2603
- In welchem Quadranten liegt der Punkt:
- A (3; 5)
- B (2; -3)
- C (-3; -5)
- D (0; 0)
- E (-5; a)
- F (3; 2)
- G (- 3; 1)
- H (1; -3)
- I (- 1,5; - 2,5)
- J (a; b)
- K (-0,3; )
- L (b; -10)
- M (8; )
- N (-9; -4,2)
BM2604
- Ordne die folgenden Punkte den Punkten in der Abbildung zu!

- A (- 1,5; - 2,5)
- B (a; b)
- C (3; 5)
- D (8; )
- E (2; -3)
- F (-3; -5)
- G (- 3; 1)
- H (0; 0)
- I (b; -10)
- J (1; -3)
- K (-5; a)
- L (-9; -4,2)
- M (3; 2)
- N (-0,3; )
Lösung BM2604 - A-i (- 1,5; - 2,5)
- B- (a; b)
- C-a (3; 5)
- D- (8; )
- E-b (2; -3)
- F-c (-3; -5)
- G-g (- 3; 1)
- H-d (0; 0)
- I- (b; -10)
- J-h (1; -3)
- K-e (-5; a)
- L-n (-9; -4,2)
- M-f (3; 2)
- N-k (-0,3; )
BM2605

- Unterschied zwischen geordneten Zahlenpaaren (x-y-Koordinaten) und Mengen
- Bei geordneten Zahlenpaaren spielt die Reihenfolge eine Rolle
- , denn hat die Werte x=2 und y=3.
- Dagegen hat die Werte x=3 und y=2.
- Bei geeorneten Zahlenpaaren für Koordinaten wird als 1. Zahl immer der Wert der Abszisse und als 2. Zahl der Wert der Ordinate angegeben. Das ist meist x und y.
- Aber auch andere Variablen sind möglich.
- (siehe Abbildung)
- ---
- Dagegen ist bei Mengen die Reihenfolge egal
-
BM2606
Bild 1: Piktogramm - Diagramm
- ---
- Ein Diagramm (von altgriechisch diágramma „geometrische Figur, Umriss“) ist eine grafische Darstellung von Daten, Sachverhalten oder Informationen. Je nach der Zielsetzung des Diagramms werden höchst unterschiedliche Typen eingesetzt. Die Bandbreite von bildhaften Elementen bis rein abstrakten Gebilden ist dabei sehr groß.
- Im Unterschied zum Piktogramm (oder Bildsymbol) wird mit Hilfe eines Diagramms vor allem versucht, einen Zusammenhang zu verdeutlichen, während ein Piktogramm nur für eine gezielte Information steht. Diagramme sind zudem oft codiert, was bedeutet, dass man mit Hilfe seines Vorwissens ein Diagramm analysieren muss, um es verstehen zu können, während ein Piktogramm durch seinen ikonischen (bildlichen) Charakter unmittelbar verständlich ist. Allerdings können Diagramme durchaus Piktogramme enthalten.
- ---
- Achsendiagramme
- Achsendiagramme dienen zur Veranschaulichung der Zusammenhänge zwischen voneinander abhängigen Werten oder Messgrößen in einem Koordinatensystem.

Bild 2: Punktdiagramm - Bild 2: Bei einem Punktdiagramm spannen zwei aufeinander senkrecht stehende Koordinatenachsen eine Fläche auf, in die die Wertepaare als Punkte (Kreuze, Kreise) eingetragen werden: Allgemeiner und in der Statistik werden Punktdiagramme auch als Streudiagramm bezeichnet.
- Ein Punktdiagramm oder Streudiagramm (engl. scatter plot) ist die graphische Darstellung von beobachteten Wertepaaren zweier statistischer Merkmale. Diese Wertepaare werden in ein kartesisches Koordinatensystem eingetragen, wodurch sich eine Punktwolke ergibt. Die Darstellung der Punkte kann durch verschiedene kleine Symbole erfolgen.
- ---

Bild 3: Liniendiagramm - Bild 3: Bei einem Liniendiagramm werden die Punkte miteinander durch Linien (Geraden, Kurven) verbunden. Ist die Fläche zwischen Achse und Linie ausgefüllt, spricht man von einem Flächendiagramm.
- Ein Liniendiagramm (auch Kurvendiagramm) ist die graphische Darstellung des funktionellen Zusammenhangs zweier (bei 2D-Darstellung) oder dreier (bei 3D-Darstellung) Merkmale in Linienform. Im Gegensatz zum Streudiagramm kann es jeweils nur ein Wertepaar bzw. Wertetrio geben.
- ---

Bild 4: Säulendiagramm - Bild 4: Bei Säulendiagrammen wird der Abstand zwischen Abszissenachse und Datenpunkt mit einer senkrecht auf der Achse stehenden Linie oder rechteckigen Fläche dargestellt.
- Das Säulendiagramm, bei sehr schmalen Säulen auch Stabdiagramm genannt, ist ein Diagramm, das durch auf der x-Achse senkrecht stehende, nicht aneinandergrenzende Säulen (Rechtecke mit bedeutungsloser Breite) die Häufigkeitsverteilung einer diskreten (Zufalls-)Variablen veranschaulicht.
- ---
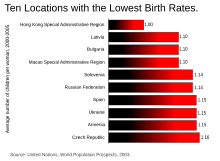
Bild 5: Balkendiagramm - Bild 5: Ein Balkendiagramm ist dem Säulendiagramm ähnlich, allerdings mit waagerechter Darstellung.
- Das Balkendiagramm ist einer der häufigsten Diagrammtypen. Es ist dem Säulendiagramm sehr ähnlich, stellt die Datenreihen allerdings durch waagerecht liegende Balken dar. Es eignet sich sehr gut zur Veranschaulichung von Rangfolgen.
BM2607
- Anfertigung eines Punktdiagramms
- (anfertigen)
- ---
- Gegeben ist eine Tabelle mit Werten
- Beispiel: Anzahl der Unfälle je Jahr
Jahr 2010 2011 2012 2013 2014 Anzahl 220 228 236 243 251
- Daraus soll ein Punktdiagramm erstellt werden.
- Die Jahreszahlen fassen wir als x-Wert auf. Denn das Jahr bestimmt wie viel Unfälle es gab.
- Nicht anders rum: Die Anzahl der Unfälle bestimmt nicht welches Jahr es ist. Es könnte ja in verschiedenen Jahren die gleiche Anzahl von Unfällen geben.
- ---

Bild 1 
Bild 2 - Da die Jahreszahlen nicht beim Jahr Null anfangen (dafür haben wir keine Unfallzahlen) sollte man die Aufteilung der x-Achse etwas modifizieren und nicht bei Null anfangen.
- Würde die x-Achse bei Null anfangen, dann wäre der darzustellende Bereich von 2ß10-2014 nur ein klitzkleiner Abschnitt ganz rechts auf der Abszisse. Den ganzen übrigen Wertebereich der x-Achse brauchen wir eigentlich nicht.
- ---

Bild 3 
Bild 4 - Also können wir den Bereich der x-Achse, der uns interessiert weiter nach links rücken und über die gesamte Länge der x-Achse ausdehnen.
- Die Unterbrechung der x-Achse wird hier durch zwei Schrägstriche hervorgehoben.
- Es ist aber nicht zwingend erforderlich die x-Achse in der Zeichnung überhaupt zu unterbrechen, denn schon allein aus den Zahlenwerten an der x-Achse ergibt sich das.
- ---

Bild 5 - Auch die senkrechte Achse haben wir unterbrochen, da nur der Zahlenbereich für y-Werte zwischen 220 und 250 von Interesse ist.
- So wird der uns interessierende Bereich in unserem Koordinatensystem wesentlich größer dargestellt.
- ---

Bild 6 - Nun übetragen wir die Werte aus der gegebenen Tabelle in das Koordinatensystem:
- Hier nochmals die Wertetabelle:
Jahr 2010 2011 2012 2013 2014 Anzahl 220 228 236 243 251
- ---

Bild 7 - Abschließend verbinden wir die Punkte mit einer Geraden.
- Diese Gerade können wir aber nicht durch den Nullpunkt verlängern, denn die Achsen wurden in diesem Bereich beschnitten. Außerdem gibt es gar keine x-Werte, die kleiner als 2010 sind.
- Weil hier unsauber gezeichnet wurde liegen die Puntke hier nicht genau auf der Verbindungsgeraden.
BM2608

Bild 8 - Nicht immer ergibt sich bei Messwerten eine eindeutige Linie. Es gibt immer Abweichungen einiger Messwerte, wobei die große Frage bleibt was Abweichungen sind. Deshalb kann man oft dieselben Messpunkte mit zwei verschiedenen Ausgleichslinien verbinden: In Bild 8 oben als Kurve und unten als gerade Linie (also lineare Gleichung).
- ---

Bild 9: Liniendiagramm (bei streuenden Werten; Steuung) - In einem Liniendiagramm gibt es nicht eine einzige gerade Linie, sondern alle Punkte werden mit einer entsprechenden Zickzack-Linie verbunden, da man gar nicht erwartet, dass die Punkte eine gerade oder gekrümmte Linie formen.
- Diese Messwerte streuen, das heißt sie liegen auseinander.
BM2609
- Das Jahr Null
- ---
- Ein Jahr Null gibt es in der von den Historikern angewendeten traditionellen christlichen Zeitrechnung NICHT, wohl aber in der modernen Jahreszählung der Astronomen.
- Im traditionellen System werden die Jahre mit Ordinalzahlen vor und nach der Geburt Christi gezählt: Das Jahr 1 vor Christi Geburt endet am 31. Dezember (1 v. Chr.), am nächsten Tag, dem 1. Januar, beginnt das Jahr 1 nach Christi Geburt (1 n. Chr.).
- Die astronomische Jahreszählung verwendet hingegen die um die Null und die negativen Zahlen erweiterten natürlichen Zahlen, die sogenannten ganzen Zahlen. Die in dieser Zahlenreihe enthaltene 0 wird dem Jahr „1 v. Chr.“, die Zahl −1 dem Jahr „2 v. Chr.“ zugeordnet.
BM2610
x (Jahr) 2010 2011 2012 2013 2014 y (Anzahl) 220 228 236 243 251
- Zuerst wird die Variable „x“ auf der x-Achse gesucht und dazu die zugehörige Variable „y“ auf der y-Achse gesucht.
- Zuerst ist die Variable „x“ gegeben und daraus folgt dann die Variable „y“.
- „x“ ist die unabhängige Variable und „y“ ist die abhängige Variable. („y“ ist von „x“ abhängig.)
- ---
- Beispiel 1:

unabhängige Variable: Zeit (t); abhängige Variable: Strecke (s). In Abhängigkeit von der Zeit wird eine bestimmte Strecke zurückgelegt. - In einer Gleichung, zum Beispiel einer physikalischen Formel, betrachtet man oft, wie sich eine Variable verändern muss (die abhängige Variable), um die Gleichung zu erfüllen, wenn man eine andere Variable ändert (die unabhängige Variable).
- ---
- Beispiel 2:
- Erhöhung der Werbeausgaben, um den Absatz eines Produktes zu steigern.
- unabhängige Variable: Werbeausgaben (immer auf der Abszisse; x-Achse)
- abhängige Variable: Absatz (immer auf der Ordinate; y-Achse)
- ---
- Beispiel 3:
- Erhöhung der Qualität eines Produktes (Produktionskosten), um den Absatz eines Produktes zu steigern.
- ---
- Beispiel 4: Man will wissen, ob die Farbe einen Einfluss auf den Absatz eines Autos hat. Dann ist die Farbe die unabhängige Variable und der Absatz die abhängige Variable.
- Will man hingegen wissen, ob der Absatz die Farbe beeinflusst, dann ist der Absatz die unabhängige Variable und die Farbe die abhängige Variable.
- ---
- Allgemein: x beeinflusst y
- x = unabhängige Variable
- y = abhängige Variable
- ---
- y = 2x + 3
- ---
- In einem wissenschaftlichen Experiment wird eine willkürlich veränderliche Stellgröße, die unabhängige Variable (meist als „x“ bezeichnet), vom Versuchsleiter gezielt verändert und die Auswirkungen dieser Manipulationen auf eine Messgröße, die abhängige Variable (meist als „y“ bezeichnet), gemessen.
- ---
- Die unabhängige Variable kann aktiv verändert werden. Die abhängige Variable dagegen ist nicht veränderbar - sie hängt nur indirekt von der Veränderung der unabhängigen Varible ab.
- ---
- Die Werte, den man erändern kann, nennt man unabhängige Variable. Jene Variable, die man beobachtet bzw. aufzeichnest, nennt man abhängige Variablen.
- ---
- unabhängige Variable: immer auf der Abszisse; x-Achse
- abhängige Variable: immer auf der Ordinate; y-Achse
BM2611 - BM2620
[editar]BM2611
- y = x + 3
- Was ist die unabhängige Variable?
Lösung BM2611 - „x“ ist die unabhängige Variable.
- Zuerst geben wir „x“ ein. Dann erhalten wir das Ergebis „y“, die abhängige Variable.
BM2612
x (Jahr) 2010 2011 2012 2013 2014 y (Bevölkerung) 28.112 30.056 33.217 34.9978 36.300

Bild 1 
Bild 2 - Die Bevölkerungszahl häng vom Jahr ab, und nicht anders rum.
- Es wäre komisch, wenn man sagt: „Wir haben eine Bevölkerung von 33.217. Also ist es das Jahr 2012.“
- ---
- Die unabhängige Variable folgt aus der abhängigen Variable.
- ---
- Mit Graphen können wir den Zusammenhang zwischen der unabhängigen und der abhängigen Varible veranschaulichen (visualisieren) und so einen Trend erkennen (Bild 1). So ein Graph hilft bei der Auswertung von Daten.
- Die Zahlenpaare (x;y) geben uns mehrere Punkte im Koordinatensystem. Durch diese Punkte (Punktewolke) können wir dann eine Linie ziehen. Aber nicht immer ergibt sich bei Messwerten eine eindeutige Linie. (Bild 2).
BM2613
- Graphen von linearen Gleichungen mit zwei Variablen
- ---
- Lineare Gleichungen haben 2 Variablen mit dem Exponenten 1.
- x1 (sprich: „x“ hoch Eins) (Die Eins nennt man „Exponent“.)
- x1 = x
- x1 oder kurz und einfach „x“
- y1 oder kurz und einfach „y“
- Dagegen sind Gleichungen mit der Variablen x2 KEINE linearen Gleichungen.
- y = 3x + 2 ist eine lineare Gleichung.
- Diese linearen Gleichungen haben als Graphen eine Gerade.
- Diese linearen Gleichungen haben als Graphen eine gerade Linie.
- ---
- Sind die folgenden Ausdrücke lineare Gleichungen? Warum?
- a) y = 4 - 5x
- b) 2y + 3x
- c) z = 3x - 5y
- d) 4t + 5b = 7
- e) y = 4x2 - 3
- f) 4x0 + 6y = 8
Lösung BM2613 - Eine lineare Gleichung hat genau zwei Variablen mit dem Exponenten Eins.
- ---
- a) y = 4 - 5x (JA. Zwei Variablen mit dem Exponenten Eins.)
- b) 2y + 3x (NEIN. Das ist keine Gleichung, denn es gibt kein Gleichheitszeichen.)
- c) z = 3x - 5y (NEIN. Es gibt drei Variablen. Es dürften nur zwei sein für eine lineare Gleichung.)
- d) 4t + 5b = 7 (JA. Zwei Variablen mit dem Exponenten Eins. Die Variablen müssen nicht unbedingt „x“ und „y“ heißen.)
- e) y = 4x2 - 3 (NEIN. Eine der Variablen hat den Exponenten Zwei.)
- f) 4x0 + 6y = 8 (NEIN. Eine der Variablen hat den Exponenten Null.)
BM2614

Black Box: Chiffriermaschine „Enigma“ - Eingabe (engl. Input)
- Ausgabe (engl. Output)
- Black Box (schwarzer Kasten)
- ---
- Als Black Box bezeichnet man ein (möglicherweise sehr komplexes) System, von welchem (im gegebenen Zusammenhang) nur das äußere Verhalten betrachtet werden soll. Die innere Struktur mag bekannt sein; solche Kenntnis darf aber nicht benutzt werden (etwa weil ein Nachfolgemodell innen anders gebaut sein darf).
- Man beschränkt sich bei der Untersuchung und Beschreibung auf die Messung der Input-Output-Beziehungen (Eingabe-Ausgabe-Beziehung).
- Wortherkunft:
- Der Begriff Black Box (engl. für schwarze Kiste) stammt ursprünglich aus der militärischen Fernmeldetechnik und bezeichnete erbeutetes Feindgerät, das wegen der möglicherweise darin enthaltenen Sprengladung nicht geöffnet werden durfte.
- ---
- Allgemein ist eine Black Box ein Objekt, dessen innerer Aufbau und innere Funktionsweise unbekannt sind oder als nicht von Bedeutung erachtet werden. Von Interesse ist vielmehr nur das Verhalten der Black Box, die über definierte Schnittstellen (Verbindungsstellen; Verbindungspunkt; die Grenze der Black Box) eine bestimmte Funktionalität sicherstellt.
- Die Motivation bei der Verwendung des Begriffs tendiert zu „das Innere interessiert (jetzt) nicht“, auch wenn er manchmal im Sinn von „wir wissen es (sowieso) nicht“ verwendet wird.
- Diese Herangehensweise wird oft verwendet, um die Komplexität des Beobachtungsgegenstandes zu reduzieren. Das bewusste Weglassen von detaillierterer Information wird auch als Geheimnisprinzip bezeichnet.
- ---
- Eingabe ⇒ Verarbeitung ⇒ Ausgabe
- Eingabe ⇒ Black Box ⇒ Ausgabe
- ---
- Eingabe („x“) ⇒ Gleichung (y = 7x - 3) ⇒ Ausgabe („y“)
x (Jahr) 2010 2011 2012 2013 2014 y (Bevölkerung) 28.112 30.056 33.217 34.9978 36.300
- Wir kennen nicht die genaue Formel, die für diese Tabelle gilt. Aber das Modell der Black Box trifft auch für die Beziehung der „x-“ und „y-Wert“ in dieser Tabelle zu.
- Eingabe ⇒ Gleichung ⇒ Ausgabe
- Eingabe x=1 ⇒ Ausgabe y=5
- Eingabe x=2 ⇒ Ausgabe y=8
- Eingabe x=3; 4; 5;... ⇒ Ausgabe y=11; 14;...
- Wie lautet die Gleichung in der Black Box?
Lösung BM2614 - Eingabe ⇒ Gleichung (y = 3x + 2) ⇒ Ausgabe
BM2615
- Zeichne den Graphen der Gleichung y = 3x + 2
x 1 2 3 4 5 y
- Wir gehen immer von „x“ nach „y“.
- Nun ersetzen wir paarweise die Variablen durch Zahlenwerte für „y“.
x 1 2 3 4 5 y 5 8
- So erhalten wir Zahlenpaare (Koordinaten), die eine Lösung der Gleichung sind.
x 1 2 3 4 5 y 5 8 11 14 17
- Das sind natürlich nur einige Punkte der Linie. Dazwischen gibt es unendlich viele weitere Punkte.
- ---
- Liegt der Punkt (2,5; 9,5) auf der Linie des Graphen der Gleichung y = 3x + 2?
Lösung BM2616-1 - (2,5; 9,5)
- x=2,5; y=9,5
- Eingabe:
- x=2,5 in die Gleichung y = 3x + 2
- y = 3*2,5 + 2
- y = 9,5
- Ja, der Punnkt (2,5; 9,5) gehört zum Graphen.
- Zum Graphen gehören alle Punkte, die die Gleichung erfüllen
- Gehört der Punkt (-2; -4) zum Graphen y = 3x + 2?
Lösung BM2616-2 - (-2; -4)
- x = -2
- y = - 4
- Ja, der Punkt (-2; -4) gehört zum Graphen y = 3x + 2?
BM2617

Bild 1 
Bild 2 - Gegeben sind die beiden Punkte A (1; 5) und B (-2: -4). Diese Punkte haben wir oben aus der Gleichung
- errechnet.
- Zwei Punkte reichen um eine Gerade zu zeichnen.
- So reichen auch diese zwei Punkte, um eindeutig eine Gerade zu zeichnen. Es gibt in der x-y-Ebene nur eine einzige Gerade, die durch diese Punkte A und B geht.
BM2618

- A) Diagonale Geraden haben eine Gleichung mit genau zwei Variablen.
- B) Horizontel Geraden haben ein Gleichung mit genau einer Variablen, die nur die Variable der Ordinate enthält (meist y). Beispiel: y=2
- C) Vertikale Geraden haben ein Gleichung mit geanu einer Variablen, die nur die Variable der Abszisse enthält (meist x). Beispiel: x=2
BM2619
- Gegeben ist wieder unser Gleichung
- Liegen die folgenden Punkte auf der Geraden?
- A (-2; -3)
- B (5; 19)
- C (0; 2)
- D ()
Lösung BM2619 - Punkt A (-2; -3)
- Also: FALSCH, denn
- ist keine wahre Aussage. Das ist eine falsche Aussage. Das ist keine Lösung.
- Es ist falsch, dass der Punkt (-2; -3) auf der Linie liegt.
- ---
- Punkt B (5; 19)
- Keine Lösung. Der Punkt B (5; 19) gehört nicht zur Linie.
- ---
- Punkt C (0; 2)
- Ja, der Punkt C gehört zur Linie.
- ---
- Punkt D ()
- Ja, der Punkt D gehört zur Linie.
BM2620

- Graphen, Linien und Geraden bestehen aus unendlich vielen Punkten, sie sind kontinuierlich.
- Sie sind nicht unterbrochen. Sie haben keine Unterbrechung.
- Wenn unsere Eingabewerte für „x“ aus der Menge der natürlichen Zahlen sind (), dann erhalten wir keine durchgehende Linie, sondern nur eine Reihe von Punkten.
x () 1 2 3 4 5 y
- Eine durchgehende Linie erhalten wir nur, wenn „x“ aus der Menge der reellen Zahlen ist ().
- Geraden bestehen nicht nur aus 2 Punkten, aber 2 Punkte reichen, um eine Gerade zu definieren.
- ---

Kurve - Kurve:
- In der Mathematik ist eine Kurve (von lat. curvus „gebogen, gekrümmt“) ein eindimensionales Objekt.
- Eindimensional bedeutet dabei informell, dass man sich auf der Kurve nur in einer Richtung (bzw. der Gegenrichtung) bewegen kann. Ob die Kurve in der zweidimensionalen Ebene liegt („ebene Kurve“) oder in einem höherdimensionalen Raum (siehe Raumkurve), ist in diesem begrifflichen Zusammenhang unerheblich.
- Eine Kurve ist in der Mathematik eine durch eine Gleichung definierte Linie.
- ---
- Diagramm:
- Ein Diagramm (von altgriechisch diágramma „geometrische Figur, Umriss“) ist eine grafische Darstellung von Daten, Sachverhalten oder Informationen. Je nach der Zielsetzung des Diagramms werden höchst unterschiedliche Typen eingesetzt. Die Bandbreite von bildhaften Elementen bis rein abstrakten Gebilden ist dabei sehr groß.
- Ein Diagramm ist eine grafische Darstellung eines Sachverhalts, der zahlenmäßig erfasst ist.
- ---
- Gerade:
- Eine gerade Linie oder kurz Gerade ist ein Element der Geometrie. Die kürzeste Verbindung zweier Punkte ist gerade und wird als Strecke bezeichnet. Eine gerade, unendlich lange, unendlich dünne und in beide Richtungen unbegrenzte Linie nennt man eine Gerade.
- Eine Gerade ist in der Geometrie eine gerade Linie, die durch zwei Punkte definiert ist.
- ---
- Linie:
- Eine Linie ist in der Geometrie eine (gedachte) gerade oder gekrümmte Verbindung zwischen zwei Punkten.
BM2621 - BM2630
[editar]BM2621
- Geraden bestehen nicht nur aus 2 Punkten, aber 2 Punkte reichen aus, um eine Gerade zu definieren.
- Wichtige Punkte zur Definition der Geraden sind der Ursprung des Koordinatensystems und Schnittpunkte der Geraden mit der x-Achse oder der y-Achse.
- ---
- Der Nullpunkt (Ursprung) hat die Koordinaten (0; 0).
- ---
- Der Punkt (0; 2) liegt auf der Linie der Gleichung .
- Weil 2 = 2 wahr ist.

Punkt (0; 2) - Der Punkt (0; 2) liegt nicht nur auf dem Graphen , sondern auch auf der y-Achse. Alle Punkte auf der y-Achse haben den X-Wert Null.
- Der Schnittpunkt mit der y-Achse liegt bei 2. Wegen der Koodinaten (0; 2) für (x; y).
- ---
- Der y-Achsenabschnitt oder Ordinatenabschnitt bezeichnet die -Koordinate des Schnittpunktes eines Funktionsgraphen mit der y-Achse oder Ordinate. Er entspricht dem Funktionswert an der Stelle .
- Achsenabschnitt
- x-Achsenabschnitt
- y-Achsenabschnitt
BM2622
x () -2 0 y -4 2 3
- Zwei Punkt würden zum Zeichnen der Geraden reichen. Mit drei Punkten sind wir aber auf der sicheren Seite, denn falls wir uns verrechnen würde die Linie einen Knick haben und uns auf einen Rechenfehler hinweisen.
- Der Graph der Gleichung muss eine Linie sein. Deshalb heißen Gleichungen mit dem Exponenten 1 lineare Gleichungen.
- Die Linie hat nicht nur 3 Punkte, sondern unendlich viele und sie geht in beide Richtungen unendlich weiter.
BM2623

Punkt (0; 2) - Ein effektives Vorgehen zum Ermitteln der Punkte für einen Graphen ist die Bestimmung der Schnittpunkte mit der x-Achse und der y-Achse.
- Wo kreuzt der die y-Achse?
- Im Punkt
- Das funktioniert aber nur, wenn die Gleichung exakt in der Form
- vorliegt oder erst mal in diese Form umgewandelt wird.
- Meist wird diese allgemeine Form nicht sondern statt „a“ ein „m“ geschrieben, also in der Form
- . Diese Form nennt man Normalform der linearen Gleichung (egal ob mit „a“ oder „m“.
- Auch die Schreibweise ist verbreitet.
- Wenn die Gleichung in dieser Form vorliegt, dann kann man den y-Achsenabschnitt direkt aus der Gleichung ablesen:
- n = 2
- Der Graph schneidet also die y-Achse im Punkt „+2“.
- Dieser Punkt hat die x-y-Koordinaten .
BM2624
Lösung BM2624 - a) : Punkt
- b) : Punkt
BM2625

Bild 1: m = 3 - Welchen Einfluss hat der Faktor auf den Graphen?
- Die sagt uns, wie wir von Punkt zu Punkt auf dem Graphen kommen.
- Wir können die auch als betrachten. Den Zähler nehmen wir als y-Wert und den Nenner nehmen wir als x-Wert.
- Das bedeutet: einen Schritt nach rechts () und drei Schritte nach oben ().
- ---

Bild 2: m=3; n=2; y=3x+2 - Man nehme einen Punkt der Geraden , z. B. den y-Achsenabschnitt (den Kreuzungspunkt mit der y-Achse), den wir bereits ermittelt hatten: (0; 2)
- Jetzt gehen wir einen Schritt nach rechts, also von x=0 nach x=1 und dann noch 3 Schritte nach oben: Also von y=2 nach y=5.
- Und schon haben wir mit x=1 und y=5 den Punkt (1; 5) und damit haben wir einen 2. Punkt für unsere Gerade.
-
BM2626
- Wenn die lineare Gleichung in der Normalform (oder Abschnitts-Steiguns-Form) vorliegt, dann kann man die Steigung und den y-Abschnitt direkt aus dieser Gleichung ablesen.
- ---
- Nenne von den folgenden Gleichungen den y-Achsenabschnitt und einen 2. Punkt, der sich aus der Steigung „m“ ergibt!
- a)
- b)
BM2626
- Graphen von linearen Gleichungen zeichnen
- Die Punkte auf der Linie sind die Lösung.
x y
- Wähle willkürlich mehrere Zahlen für „x“!
x -3 0 1 2 3 y
- Wir nehmen ganze Zahlen, weil mit diesen einfacher zu rechnen ist als mit Kommazahlen (Dezimalzahlen). Eine neg. Zahl für „x“ ist auch immer gut. Null und Eins sind meist auch gut zu rechnen.
- Zur Sicherheit nehmen wir mindestens 3 Punkte (Zahlenpaare), obwohl man für das Zeichnen einer Linie nur 2 Punkte bräuchte. Wir rechnen mit 3 Punkten, denn falls sich ein Fehler in unsere Rechnung einschleichen sollte, dann ist der Graph keine Gerade. Das kann aber bei einer linearen Gleichung nicht sein.
- Mit diesen gewählten Werten für „x“ rechnen wir damit den jeweiligen y-Wert aus.
- „x“ ist unsere unabhängige Variable. Nach der „Verarbeitung“ in der Gleichung erhalten wir unsere abhängige Variable „y“.
- Die Zahlenpaare ergeben sich aus der Eingabe-Ausgabe-Beziehung
- Eingabe ⇒ Gleichung ⇒ Ausgabe
- input ⇒ Gleichung ⇒ output
- x ⇒ Gleichung ⇒ y
- Wie lauten die zugehörigen y-Werte? Nenne die Zahlenpaare! Zeichne die Punkte in ein Koordinatensystem ein, verbinde sie mit einer Linie! Falls die Linie einen Knick hat, dann hast Du falsch gerechnet.
x -3 0 1 2 3 y
- An welcher Stelle schneidet der Graph die y-Achse?
Lösung BM2626-2 - (Wir stellen die Gleichung etwas um.)
- So hat sie exakt die Normalform und wir brauchen nur noch „n“ ablesen und haben damit unseren y-Achsenabschnitt - den Schnittpunkt mit der y-Achse.
- ---
- Wie kommt das, dass „n“ uns den y-Achsenabschnitt liefert?
- Na, wenn man für „x“ eine Null einsetzt, dann wird daraus immer eine Null und dieser Teil der Gleichung vershwindet somit immer.
BM2627
BM2628
- Wie zeichnet man diesen Graphen?
Lösung BM2628
BM2629
- Wir rechnen uns mit einigen willkürllich gewählten x-Werten einige y-Werte aus und tragen sie als Zahlenpaare in eine Tabelle ein.
x 0 1 2 4 y
- Der x-Wert Null ist immer gut.
- x=1 ist hier nicht so clever, weil dann „y“ keine ganze Zahl ist. Besser sind x-Werte, die identisch mit dem Nenner sind, denn so kürzt sich der Nenner weg. In unserem Beispiel nehmen wir deshalb x=2. Genauso gut ist ein Vielfaches des Nenners, denn dann kürzt sich der Nenner auch weg. In unserem Beispiel 4 oder 6.
- Die Tabelle für die x-y-Zahlenpaare kann man auch senkrecht anlegen. So sind die x-y-Zahlenpaare ganz einfach zeilenweise abzulesen.
- Rechne die y-Werte der folgenden Tabelle aus!
x y 0 1 2 4
Lösung BM2629 x y 0 3 1 3,5 2 4 4 5
BM2630
- Wähle für die folgenden Gleichungen jeweils mindestens drei passende Punkte und ermittle die Koordinatenpaare dazu! Zeichne den Graphen der Gleichung!
- a)
- b)
BM2631 - BM2640
[editar]BM2631
- ---

fallende Gerade; m < 0 - Die Steigung „m“ kann negativ sein, dann ist die Linie fallend. Wobei wir den Verlauf immer von links nach rechts betrachten.
- Beispiele:
-
- ---

steigende Gerade; m > 0 - Die Steigung „m“ kann positiv sein, dann ist die Linie steigend - immer von links nach rechts betrachtet.
- Beispiele:
-
BM2632
- Um den Graphen einer linearen Gleichung zu zeichnen gibt es zwei mögliche Methoden:
- 1.(Eine Punktetabelle ausrechnen und diese Punkte in das Koordinatensystem eintragen.
- 2. Methode: Die Schnittpunkte mit der x- und y-Achse ausrechnen indem man einmals x=0 setzt und zum zweiten y=0 setzt.
- 3.) Man wandelt die Gleichung in die Form y=mx+b um und ließt direkt den Schnittpunkt mit der y-Achse ab (0; b) und die Steigung.
BM2633
- Versuche alle 3 Methoden mit der folgenden Gleichung und zeichne den Graphen!
Lösung BM2633 - 1. Methode:
- Wertetabelle
- Wir nehmen willkürlich die x-Werte 0; 1; 2 und 4.
x y 0 -1 1 1 2 3 4 7
- ---
- 2. Methode:
- x=0 ⇒ ⇒
- (0; -1)
- ---
- y=0 ⇒ ⇒
- also: x=0,5
- (0,5; 0)
- Da die beiden Schnittpunkte sehr dicht beieinander liegen is der Graph damit sehr schwer, genauer gesagt nur sehr ungenau, zu zeichnen.
- ---
- 3. Methode: umstellen
- m=2
- b= -1 ⇒ 1. Punkt (0; -1)
- 2. Punkt:
- (0+1; -1+2) (Hier werden die Koordinaten des 1. Punkte mit m bzw 1 addiert)
- (1; 1) (2. Punkt)
- ---
- Natürlich führen alle drei Methoden zum gleichen Ergebnis.
BM2634
- Je nach Art der linearen Gleichung ist die eine oder andere Methode effektiver.
- Beispielsweise funktioniert die Methode mit der Bestimmung der x-Achsen- und y-Achsen-Schnittpunkte nicht, wenn der Graph durch den Ursprung des Koordinatensystems nicht.
- Das ist der Fall, wenn auf der einen Seite eine Null steht und auf der aderen Seite unser x und y.
- ---
- Beispiel: Die Gleichung würde nicht gehen, wenn rechts eine Null stehen würde:
- Zeichne den Graphen der Gleichung !
Lösung BM2634 - 1. Methode: Wertetabelle
x y 0 0 1 2 2 4 4 8
- ---
- 2. Methode: (Funktioniert NICHT!)
- x=0 ⇒ ⇒
- (0; 0)
- ---
- y=0 ⇒ ⇒
- also: x=0
- (0; 0)
- Wir haben also zwei mal den Punkt (0;0). Deshalb können wir damit keinen Graphen zeichnen, denn uns fehlt ein zweiter Punkt.
- ---
- 3. Methode: umstellen
- m=2
- b= 0 ⇒ 1. Punkt (0; 0)
- 2. Punkt:
- (0+1; 1+2) (Hier werden die Koordinaten des 1. Punkte mit m bzw 1 addiert)
- (1; 3) (2. Punkt)
- KOMISCH: Bei der ersten Methode haben wir Punkt (1; 2) aber mit der 3. Methode Punkt (1; 3)
- Das kann nicht sein! Wo liegt der Fehler?
Fehler-Korrektur BM2634 - Der Fehler lag bei der 3. Methode
- m=2
- b= 0 ⇒ 1. Punkt (0; 0)
- 2. Punkt:
- (0+1; 1+2) (Hier liegt de Fehler.)
- Es muss natürlich heißen:
- (0+1; 0+2)
- (1; 2) (2. Punkt)
- Und schon stimmt das Ergebnis mit der 1. Methode überein.
BM2635
- Zeichne den Graphen der Gleichung!
Lösung BM2635 - 1. Methode: Wertetabelle
- x=1 ist hier nicht angebracht, da dadurch nicht der Bruch mittels Kürzen beseitigt werden kann. Besser ist ein x-Wert, der dem Nenner entspricht oder einem Vielfachen des Nenners, also 4 und 8.
x y 0 -5 4 0 8 5
- ---
- 2. Methode:
- x=0 ⇒ ⇒
- (0; -5)
- ---
- y=0 ⇒ ⇒
- (4; 0)
- ---
- 3. Methode: umstellen
- ⇒ 1. Punkt (0; -5)
- 2. Punkt:
- (1; -3,75)
BM2636
- Zeichne den Graphen der Gleichung!
Lösung BM2636 - 1. Methode: Wertetabelle
x y 0 2 1 4/3 2 2/3 4 - 2/3
- ---
- 2. Methode:
- x=0 ⇒ ⇒
- (0; 2)
- ---
- y=0 ⇒ ⇒
- (3; 0)
- ---
- 3. Methode: umstellen
- ⇒ 1. Punkt (0; 2)
- 2. Punkt:
- (1; 1,33)
BM2637
- In der vorhergehenden Übung hatten wir diese Gleichung nach y umgestellt.
- Man könnte die Gleichung auch nach x umstellen.
- Stelle die Gleichung nach x um!
Lösung BM2637-1
- Nun könnte man die y-Werte in die gefundene Gleichung einsetzen und die dazugehörigen x-Werte mit Hilfe der umgestellten Gleichung ausrechnen.
y x 0 1 2 4
- Das große Problem ist , dass dann die x-y-Paare umgekehrt sind. So entstehen oft Verwechslungen bei der Anordnung der x-y-Werte in den Zahlenpaaren. Wir sollten also zum Lösen linearer Gleichungen besser NICHT nach x umstellen.
- ---
- Die horizontale Achse (Abszisse) wird immer zum Eintragen der ersten Zahl im Zahlenpaar genommen.
- Die zweite Zahl des Zahlenpaares wird auf der vertikalen Achse eingetragen. Wie heißt die vertikale Achse? (Meistens ist das die y-Achse, aber dieser Name ist nicht gemeint.)
- Wie heißen die Synonyme für horizontal und vertikal?
Lösung BM2637-2 - Abszisse (= x-Achse)
- Ordinate (= y-Achse)
- waagerecht = horizontal
- senkrecht = vertikal
BM2638

- Steigung
- Die Steigung wir immer von links nach rechts betrachtet, so wie die Radfahrer auf der Abbildung fahren.
- ---
- Wenn es aufwärts geht dann ist die Steigung positiv.
- Wenn es berghoch geht, dann haben wir eine pos. Steigung.
- Wenn es steil hoch geht, dann haben wir eine große pos. Steigung.
- Wenn es nur leicht aufwärts geht, dann haben wir eine kleine pos. Steigung.
- Wenn es weder hoch noch runter geht, dann haben wir keine Steigung, dann ist die Steigung Null.
- Wenn es runter geht, dann ist die Steigung negativ
- Wenn es abwärts geht, dann haben wir eine neg. Steigung.
- Wenn es stark bergab geht, dann haben wir eine starke neg. Steigung.
- Wenn es leicht nach unten geht, dann ist die Steigung neg.
- ---
- Eine ansteigende Gerade hat eine pos. Steigung.
- Eine abfallende Gerade hat eine neg. Steigung.
- ---
- Welche Steigung haben die Geraden a, b, c, d und e?
Lösung BM2638 - a) Steigung Null, (m = 0)
- b) Steigung schwach positiv (m > 0)
- c) Steigung stark positiv (m > 0)
- d) Steigung schwach negativ (m < 0)
- e) Steigung stark negativ (m < 0)
BM2639
- Bild: 1
- Die eine Diagonale in einem Quadrat hat die Steigung 1 (m = 1).
- In einem Quadrat sind alle Seiten Gleich lang. Der Anstieg der Diagonalen entspricht also einer Einheit (Schritt) nach rechts und einem Schritt nach oben.
- ---

Bild 2
- Bild 2:
- Die andere Diagonale des Quadrats hat folglich die Steigung minus Eins. (Eine Längeneinheit nach rechts und eine Längeneinheit nach unten.
- ---

Bild 3 - Bild 3:
- Die Gerade a hat die Steigung minus Drei. (m = -3)
- Die Gerade b hat die Steigung minus Eins. (m = -1)
- Die Gerade c hat die Steigung minus ein Halb. (m = -1/2)
- Die Gerade d hat die Steigung Null. (m = 0)
- Die Gerade e hat die Steigung zwei Drittel. (m = 2/3)
- Die Gerade f hat die Steigung Eins. (m = 1)
- Die Gerade g hat die Steigung Zwei. (m = 2)
- Die Gerade h hat die Steigung Fünf. (m = 5)
BM2640

Bild 1 - Mathematischer Drehsinn:
- a)
- b)
- c)
- d)
- e)
- f)
- g)
- h)
- ---
- Wenn wir eine Gerade links fixieren und rechts immer weiter anheben, also um den linken Fixpunkt drehen, dann wird die Steigung immer größer. Deshalb ist in der Mathematik die Drehrichtung als Drehung gegen den Uhrzeigersinn definiert.
- Drehrichtung = mathematische Drehsinn
- Drehung gegen den Uhrzeigersinn = andersrum als die Uhrzeiger sich bewegen
- Drehung im Uhrzeigersinn = Drehung in die gleiche Richtung, wie die Uhrzeiger sich bewegen
- Bei einer Drehung im math. pos. Drehsinn wird also die Steigung immer größer:
- von nach bis und weiter mit der pos. Steigung
- von über und nach
- und so weiter, bis m ganz groß wird. Die Steigung kann aber nie plus unendlich werden und auch nie minus unendlich.
- Durch die Drehung um den Fixpunkt wird ein Bereich von 180° abgedeckt.
- ---

Bild 2 - Im Bild 2 gehen alle Geraden durch den Ursprung (also b = 0). Die Geraden mit positiver Steigung (m>0) sind rot markiert. Die Geraden mit negativer Steigung (m<0) sind grün markiert.
BM2641 - BM2650
[editar]BM2641
- Rechne und zeichne den Graphen! Stelle dazu die Gleichung nach y um!
- Ja, diese Gleichung hatten wir schon mal. Das sollte jetzt also ruckzuck gehen.
- (ruckzuck = ratzfatz)
BM2642

Bild 1 - Bild 1:
- Wenn wir in einer Gleichung x=0 setzen und dafür die y-Koordinate ausrechnen, dann liegt dieser Punkt unbedingt irgendwo auf der y-Achse.
- Jeder Punkt (0;a) liegt auf der y-Achse.
- (0; y)
- ---

Bild 2 - Bild 2:
- Analog zu Bild 1 gilt, dass alle Punkte auf der x-Achse immer die y-Koordinate Null haben.
- (x; 0)
- Um also den Punkt zu finden, an dem eine Gerade die x-Achse schneidet, muss man y gleich Null setzen und die Gleichung ausrechnen. Das Koordinatenpaar (x; 0) gibt den Punkt auf der x-Achse an, an dem der Graph die x-Achse schneidet.
- ---
- Hier nochmals das Beispiel von weiter oben:
- x=0 ⇒ ⇒
- (0; 2)
- y-Achsen-Schnittpunkt. bei y=2
- ---
- y=0 ⇒ ⇒
- (3; 0)
- x-Achsen-Schnittpunkt. bei x=3

Bild 3
BM2643
- Der Schnittpunkt des Graphen mit der x-Achse hat die Koordinaten (x;0)
- und er Schnittpunkt mit der y-Achse die Koordinaten (0;y)
- ---
- Achsenabschnitt oder Achsenschnittpunkt
- y-Achsenabschnitt
- Der y-Achsenabschnitt oder Ordinatenabschnitt bezeichnet die y-Koordinate des Schnittpunktes eines Funktionsgraphen mit der y-Achse oder Ordinate. Er entspricht dem Funktionswert an der Stelle x=0.
- ---
- Bei linearen Funktionen, also y=mx+b, gibt das absolute (= konstante) Glied des Funktionsterms den y-Achsenabschnitt an.
- Beispiel: y = 3 ⋅ x + 7; der y-Achsenabschnitt beträgt 7.
- Ein Spezialfall davon ist y = m ⋅ x
- Der Graph dieser Funktion verläuft durch den Ursprung des Koordinatensystems, der y-Achsenabschnitt ist daher 0.
- ---
- Nullstelle
- Nullstellen von Funktionen sind Argumente („x-Werte“), die eingesetzt den Funktionswert („y-Wert“) null liefern.
- Die Nullstelle ist genau die Stellen der x-Achse, an denen der Graph einer Funktion x-Achse schneidet.
- ---

- Welche Nullstelle hat der nebenstehende Graph
Lösung BM2643 - Die Nullstelle ist 3.
BM2644
Lösung BM2644-1 - Bei Punkt B.
Lösung BM2644-2 - Der y-Achsenabschnitt liegt nicht bei 8 und auch nicht bei 4, sondern bei Punkt (4;0)
- Das ist ein kleiner aber feiner Unterschied!
BM2645
- Für den y-Achsenabschnitt müssen wir nur die y-Koordinate bestimmen, denn die x-Koordinate ist am y-Achsenschnittpunkt immer Null.
- Für den x-Achsenabschnitt müssen wir nur die x-Koordinate bestimmen, denn die y-Koordinate ist am x-Achsenschnittpunkt immer Null.
- ---
- Graphen von linearen Gleichungen haben immer einen x-Achsenabschnitt. Sie haben immer genau einen x-Achsenabschnitt.
- Sonderfall: Wenn der Graph keine Steigung hat, also parallel zur x-Achse liegt, dann gibt es keinen Schnittpunkt mit der x-Achse.
- Beispiel: y = 5
- Beispiel: y = 0 * x + 5
- ---
- Graphen von linearen Gleichungen haben immer einen y-Achsenabschnitt. Sie haben immer genau eineny-Achsenabschnitt.
- Sonderfall: Wenn der Graph vertikal verläuft, also parallel zur y-Achse liegt, dann gibt es keinen Schnittpunkt mit der y-Achse.
- Beispiel: x = 3 (Das ist allerdings keine lineare Gleichung.)
- ---
- Graphen von quadratischen Gleichungen (x2) haben eine Parabel als Graphen.
- Die Parabel der Gleichung x = (x - 3)2 - 5 hat drei Schnittpunkte, weil sie keine lineare Gleichung ist.

Bild 1
- Welche Koordinaten haben diese drei Schnittpunkte (x-Achsenabschnitt, y-Achsenabschnitt)?
Lösung BM2645 - (0,73; 0) (x-Achsenabschnitt; 1. Nullstelle)
- (5,23; 0) (x-Achsenabschnitt; 2. Nullstelle)
- (0; 4) (x-Achsenabschnitt)
- Nicht-lineare Gleichungen (z. B. quadratische Gleichungen) können mehr als einen Schnittpunkt mit der x-Achse haben, aber nie mehr als einen Schnittpunkt mit der y-Achse.
BM2646
- Intervall
- ---
- Als Intervall wird in der Mathematik eine „zusammenhängende“ Teilmenge einer Gesamtmenge (zum Beispiel der Menge der reellen Zahlen bezeichnet. Das Intervall besteht aus allen Elementen , die man mit zwei begrenzenden Elementen des Intervalls, der unteren Grenze und der oberen Grenze des Intervalls, der Größe nach vergleichen kann und die im Sinne dieses Vergleichs zwischen den Grenzen liegen.
- Dabei können die Grenzen des Intervalls dem Intervall angehören (abgeschlossenes Intervall, ), nicht angehören (offenes Intervall ) oder teilweise angehören (halboffenes Intervall, ; ).
- ---
- Zusammenhängend bedeutet hier: Wenn zwei Objekte in der Teilmenge enthalten sind, dann sind auch alle Objekte, die (in der Gesamtmenge) dazwischen liegen, darin enthalten. Die wichtigsten Beispiele für Gesamtmengen sind die Mengen der reellen, der rationalen, der ganzen und der natürlichen Zahlen. In den genannten Fällen und allgemeiner immer dann, wenn eine Differenz zwischen zwei Elementen der Gesamtmenge erklärt ist, bezeichnet man die Differenz zwischen der oberen und unteren Grenze des Intervalls () als Länge des Intervalls oder kurz Intervalllänge.
- ---
- Beispiele:
- In der Menge der natürlichen Zahlen
- In diesem Fall einer diskreten Menge sind die Elemente des Intervalls benachbart.
- In der Menge der reellen Zahlen
- ,
- die Menge aller Zahlen zwischen 0 und 1, wobei die Endpunkte 0 und 1 mit eingeschlossen sind.
- Triviale Beispiele von Intervallen sind die leere Menge und Mengen, die genau ein Element besitzen. Wenn man diese nicht einschließen möchte, dann spricht man von echten Intervallen.
- Die Menge kann auch als Teilmenge der Gesamtmenge der reellen Zahlen betrachtet werden. In diesem Fall handelt es sich nicht um ein Intervall, da die Menge zum Beispiel die zwischen 6 und 7 liegenden nichtnatürlichen Zahlen nicht enthält.
BM2647
- Intervalle
- Bezeichnungs- und Schreibweisen
- ---
- Ein Intervall kann (beidseitig) beschränkt oder – auch einseitig – unbeschränkt sein. Es ist durch seine untere und seine obere Intervallgrenze eindeutig bestimmt, wenn zusätzlich angegeben wird, ob diese Grenzen im Intervall enthalten sind.
- ---
- Es gibt zwei verschiedene häufig verwendete Intervallschreibweisen:
- Bei der häufigeren der beiden verwendet man für Grenzen, die zum Intervall gehören, eckige Klammern und runde für Grenzen, die nicht zum Intervall gehören. Die eckigen Klammern entsprechen einem schwachen Ungleichheitszeichen ≤.
- Bei der anderen Schreibweise werden statt der runden Klammern nach außen gewendete (gespiegelte) eckige verwendet.
- ---
- Beschränkte Intervalle
- Ein beschränktes Intervall ist abgeschlossen, wenn es beide Grenzen enthält, und 'offen wenn beide Grenzen nicht enthalten sind. Ein beschränktes Intervall heißt halboffen, wenn es genau eine der beiden Intervallgrenzen enthält.
- ---
- Abgeschlossenes Intervall (Kompaktes Intervall)
- Das Intervall enthält sowohl als auch .
- ---
- Ein Intervall ist genau dann kompakt, wenn es abgeschlossen und beschränkt ist.
- ---
- Offenes Intervall
- Das Intervall enthält weder noch . Die Notation ist die traditionell verwendete, während auf Bourbaki zurückgeht.
- ---
- halboffenes (genauer rechtsoffenes) Intervall
- Das Intervall enthält , aber nicht .
- ---
- halboffenes (genauer linksoffenes) Intervall
- Das Intervall enthält nicht , wohl aber .
- ---
- Im Fall von und ist das offene Einheitsintervall und das abgeschlossene Einheitsintervall.
BM2648
- Intervalle
- Bezeichnungs- und Schreibweisen
- ---
- Unbeschränkte Intervalle
- Wenn auf einer Seite die Intervallgrenze fehlt, es dort also keine Schranke geben soll, spricht man von einem (auf dieser Seite) unbeschränkten Intervall. Meist werden hierfür die bekannten Symbole und als „Ersatz“-Intervallgrenzen verwendet, die selbst nie zum Intervall gehören (deshalb die Schreibung mit runder Klammer). In mancher Literatur werden beschränkte Intervalle auch als eigentlich, unbeschränkte als uneigentlich bezeichnet.
- ---
- linksseitig unendliches abgeschlossenes Intervall
- Es enthält alle Zahlen, die kleiner oder gleich sind.
- ---
- linksseitig unendliches offenes Intervall
- Es enthält alle Zahlen, die kleiner als sind.
- ---
- rechtsseitig unendliches abgeschlossenes Intervall
- .
- Es enthält alle Zahlen, die größer oder gleich sind.
- ---
- rechtsseitig unendliches offenes Intervall
- .
- Es enthält alle Zahlen, die größer als sind.
- ---
- beidseitig unendliches offenes (und zugleich abgeschlossenes) Intervall
- Es enthält alle Zahlen zwischen und . Dies entspricht der gesamten Menge der reellen Zahlen ().
- ---
- Bei obiger Definition wird übrigens nicht gefordert, sodass für jedes Intervall leer ist. Daneben existieren auch je nach Anwendung Definitionen, die solche Intervalle nicht erlauben oder im Falle einfach die Grenzen vertauschen.
- ---
- Zur Vermeidung von Verwechslungen mit dem Dezimalkomma wird als Trennzeichen auch das Semikolon (;), selten auch ein senkrechter Strich (|) verwendet, z. B.
BM2649

Steigungsdreiecke am Graph der linearen Funktion - Graph einer linearen Funktion
- ---
- Der Graph einer linearen Funktion ist eine Gerade. In kartesischen Koordinaten gilt
- mit reellen Zahlen und wobei (die Abszisse) eine unabhängige und (die Ordinate) die abhängige Variable ist.
- Es gibt zahlreiche andere Bezeichnungskonventionen für den Funktionsterm, z. B. oder In Österreich wird häufig verwendet, in der Schweiz hingegen In Belgien findet man auch oder
- Diese Darstellung bezeichnet man auch als die Normalform einer linearen Funktion. Ihre zwei Parameter lassen sich wie folgt interpretieren:
- Die Zahl m gibt die Steigung der Geraden an.
- Die Zahl n ist der y-Achsen- oder Ordinatenabschnitt, die Inhomogenität oder die Verschiebungskonstante.
- Der Graph einer linearen Funktion verläuft nie parallel zur y-Achse, da damit einem x mehr als ein y zugeordnet wäre, was in Widerspruch zur definitorisch geforderten (Rechts-) Eindeutigkeit einer Funktion stünde.
BM2650

Ursprungsgeraden in der euklidischen Ebene - Ursprungsgerade
- ---
- Eine Ursprungsgerade ist in der Mathematik eine Gerade, die durch den Koordinatenursprung eines gegebenen kartesischen Koordinatensystems verläuft. Daher werden Ursprungsgeraden durch besonders einfache Geradengleichungen beschrieben.
- ---
- Ursprungsgeraden in der Ebene
- Definition
- Eine Ursprungsgerade in der euklidischen Ebene ist eine Gerade, die durch den Ursprung des Koordinatensystems verläuft. In der Koordinatenform (s. nächste Lektion) besteht eine Ursprungsgerade damit aus denjenigen Punkten der Ebene, deren Koordinaten die Geradengleichung
- erfüllen, wobei und Parameter sind, die nicht beide gleich null sein dürfen. Durch Auflösen dieser Gleichung nach erhält man, sofern ist, die einfachere Form
- mit der Steigung . In dieser Form kann eine Ursprungsgerade allerdings nicht senkrecht zur x-Achse verlaufen.
- ---
- Beispiele
- Wichtige Beispiele für Ursprungsgeraden sind die beiden Koordinatenachsen mit den Geradengleichungen
- und .
- Weitere wichtige Beispiele für Ursprungsgeraden sind die Winkelhalbierenden des I. und III. sowie des II. und IV. Quadranten mit den Geradengleichungen
- und .
- índice
- Lección 102b ← Lección 103b → Lección 104b
- Lección 103















































































































































































![{\displaystyle [0,1]=\{x\in \mathbb {R} \mid 0\leq x\leq 1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59720e37aef81554e89f04b735e17071dc1c0ec)
![{\displaystyle [a,b]:=\{x\in \mathbb {R} \mid a\leq x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/602ac1258fbfd33508ed394aaa45b93bf4f91cf7)
![{\displaystyle (a,b)={]a,b[}:=\{x\in \mathbb {R} \mid a<x<b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d09b46c9ddf51c14f8f7e9c54705ca44f5dfb92)

![{\displaystyle {]a,b[}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db32da0a1eb3aab2b111c28c26604501b45ca8b)

![{\displaystyle (a,b]={]a,b]}:=\{x\in \mathbb {R} \mid a<x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c60402015ad73e30ce797a3c69c16208d93809df)


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle (-\infty ,b]={]{-\infty ,b}]}:=\{x\in \mathbb {R} \mid x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66acfdf806380321d3a865eaf94c861c055166db)
![{\displaystyle (-\infty ,b)={]{-\infty ,b}[}:=\{x\in \mathbb {R} \mid x<b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30616ceebc6e515924f437a9c2925d6bdcc306f)

![{\displaystyle (a,\infty )={]{a,\infty }[}:=\{x\in \mathbb {R} \mid a<x\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d646bf86a5cf1b1b5caf9974f246b7be8b84c70f)
![{\displaystyle (-\infty ,\infty )={]{-\infty ,\infty }[}:=\mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d35dc86aacaaea8659a0f07fc9c1ae6200f0d932)




![{\displaystyle (0,2{,}5]=(0;2{,}5]=(0|2{,}5].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40896aeece549b21b60cfe36f03d74ae0aac59ed)






















