Algoritmia/Algoritmo de Dijkstra

El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto, dado un vértice origen, hacia el resto de los vértices en un grafo que tiene pesos en cada arista. Su nombre alude a Edsger Dijkstra, científico de la computación de los Países Bajos que lo describió por primera vez en 1959.

Ejemplo

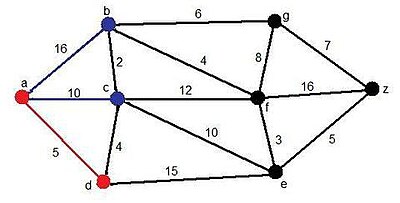
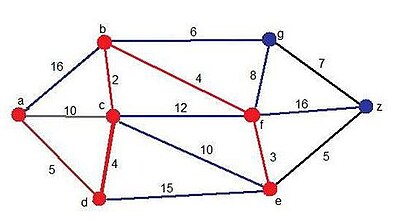
El siguiente ejemplo se mostrara como se desarrollará con el fin de encontrar el camino más corto desde a hasta z:

Leyenda:

• Rojo: Aristas y vértices pertenecientes a la solución momentánea.
• Azul: Aristas y vértices candidatos.

Paso 1

Se escoge de los nodos adyacentes aquel que tiene un menor peso en la arista, en este caso, el nodo d. En d

• Distancia:5

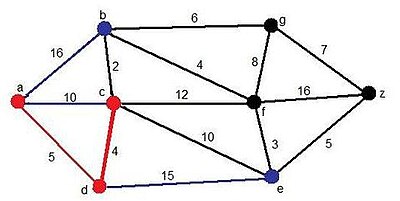
Paso 2

Ahora, vemos que se añade un nuevo candidato, el vértice e, y el vértice c, pero esta vez a través del d. Pero el camino mínimo surge al añadir el vértice c.

Solución momentánea:

• Camino: ADC
• Distancia:9

Paso 3

Solución momentánea:

• Camino: ADCB
• Distancia:11

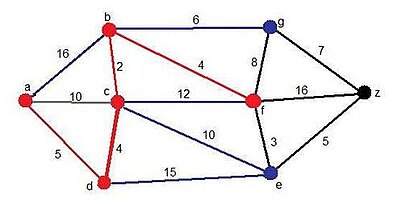
Paso 4

Como podemos comprobar, se han añadido un candidato nuevo, el vértice g, a través del vértice b. El mínimo camino hallado en todo el grafo hasta ahora es el siguiente:

Solución momentánea:

• Camino: ADCBF
• Distancia:15

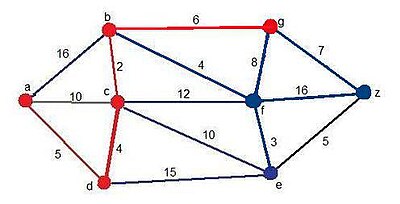
Paso 5

En este antepenúltimo paso, se añaden tres vértices candidatos, los vértices g, z y e. Este último ya estaba pero en esta ocasión aparece a través del vértice f. En este caso el camino mínimo, que cambia un poco con respecto al anterior, es:

Solución momentánea:

• Camino: ADCBG
• Distancia:17

Paso 6

En el penúltimo paso, vuelve a aparecer otro candidato: el vértice e, pero esta vez a través del vértice f. De todas formas, el camino mínimo vuelve a cambiar para retomar el camino que venía siguiendo en los pasos anteriores:

Solución momentánea:

• Camino: ADCBFE
• Distancia:18

Paso 7

Por fin, llegamos al último paso, en el que sólo se añade un candidato, el vértice z a través del vértice e. El camino mínimo y final obtenido es:

Solución Final:

• Camino: ADCBFEZ
• Distancia:23

Implementación en Java

	/**
	 * Realizar el algoritmo de Dijkstra sobre el grafo
	 * @param origen nodo inicial
	 * @param destino nodo destino
	 * @return camino ArrayList con el camino a seguir.
	 */
	  public ArrayList<Integer> dijkstra(int origen, int destino) {
		  ArrayList<Integer> camino= new ArrayList<Integer>();
		  int distancia=Grafo.INFINITO;
		  int nodo=origen;
		  boolean fin=true;
		  camino.add(nodo);
		  while(fin) 
		  
		      
			  if(this.floydC[nodo][destino]<distancia) {
			      /*El metodo siguiente(nodo, destino), nos devuelve
			      el siguiente nodo a visitar*/
				  nodo=this.siguiente(nodo, destino);
				  camino.add(nodo);
			  }
			  
			  if(nodo==destino) {
				  fin=false;
			  }
		  }
		  
		  return camino;
	  }

Otra versión en C++ del algoritmo de Dijkstra

//Declarando variables
#define MAX_NODOS 1024 /* número máximo de nodos */
#define INFINITO 1000000000 /* un número mayor que cualquier ruta máxima */
#include<iostream>
using namespace std;
int n,i,k,minimo, dist[MAX_NODOS][MAX_NODOS]; /* dist[i][j] es la distancia de i a j */

struct nodo { /* Indica eL estado del nodo,la ruta y quien lo precede a dicho nodo */
	int predecesor; /* nodo previo */
	int longitud; /* longitud del origen a este nodo */
	bool etiqueta;	/*verdadero para un nodo permanente y falso para nodo tentativo*/
} nodo[MAX_NODOS];

void inicializacion(){
	for (auto p = &nodo[0]; p < &nodo[n]; p++) { /* estado de inicialización*/
		p->predecesor = -1;
		p->longitud = INFINITO;
		p->etiqueta = false;
	}
}
void relajar(){
	for (int i = 0; i <n; i++){ /* este grafo tiene n nodos */		
		if (dist[k][i] != 0 && nodo[i].etiqueta == false) { 
			if (nodo[k].longitud + dist[k][i] < nodo[i].longitud) {
				nodo[i].predecesor = k;
				nodo[i].longitud = nodo[k].longitud + dist[k][i];
			}
		}
	}
}
void extraer_minimo(){ 	/* Encuentra los nodo etiquetados tentativamente y determina el menor entre estos nodos tentativos. */ 
	k = 0; 
	minimo = INFINITO;
	for (i = 0; i < n; i++){
		if (nodo[i].etiqueta == false && nodo[i].longitud < minimo) {
			minimo = nodo[i].longitud;
			k = i;
		}
	}
}	
void camino_corto(int s, int t, int camino[]) { 
	inicializacion();
	nodo[t].longitud = 0; nodo[t].etiqueta = true;
	k = t; /* k es el nodo de trabajo inicial */
	do{ /* ¿hay una ruta mejor desde k? */			
		relajar();
		extraer_minimo();
		nodo[k].etiqueta = true;
	} while (k != s);
	/* Copia la ruta en el arreglo de salida y procede a ir imprimiendolo. */
	i = 0; k = s;
	cout<< "La ruta es: ";
	do {
		cout<< k<< " ";
		camino[i] = k; 
		k = nodo[k].predecesor; 
		i++;
	} while (k >= 0);
		cout <<"La ruta minima es: "<<minimo<<endl ;
}
int main(){
	int nodo_final,nodo_inicial,arista;
	//solicita o ingresa directamente los valores de nodo_final,nodo_inicial
	//Llenar de 0 la matriz
	for (int i=0; i<n; i++){
		for( int j=0; j<n; j++){
			dist[i][j]=0;
		}
	}	
	// Llenar la matriz dist[i][j]
	/*............................
	............................*/
	//Por ultimo llamar a la función camino corto
	//camino_corto(nodo_final,nodo_inicial,arista);
	
	return 0;
}