Administración de empresas/Estadística para los negocios/Regresión y correlación/Herramientas/Diagrama de dispersión
AMA DE DISPERSIÓN
|
|
|
Los principios tratados en este recuadro representan a los principios por los cuales se guía el libro. Aunque no se mencionen explícitamente en cada parte, se encuentran, aún así, ímplicitos.
- La administración depende del contexto.
- El recurso más valioso es el tiempo.
- Las personas no son un recurso.
- El éxito no es alcanzable directamente, o sea, no se puede pretender alcanzarlo mediante un plan de acción o la consecución de esfuerzos; sino que puede nacer o no como consecuencia de los resultados hechos o nuestras acciones.
Es una herramienta estadística que permite demostrar gráficamente la existencia o no de una relación entre la cantidad de datos de dos variables y cuantificar la intensidad de dicha magnitud; así como también de qué tipo es su correlación (positiva, negativa o nula).
Su diagramación es a través de un plano cartesiano.
Representación
[editar]Diagrama de dispersión simple
[editar]Para realizar esta clase de diagrama se siguen los siguientes pasos:
- 1. Determinar qué variable depende de la otra variable.
- Se puede usar la pregunta "¿Si Variable 1 aumenta, Variable 2 también lo hace?", si es correcto entonces Variable 1 es la variable independiente o la variable X.
- 2. Se dibuja la escala de representación del plano cartesiano teniendo en cuenta los valores máximos y míninos de los valores de cada variable (x ; y).
- 3. Se representan los puntos a través de las intersecciones de pares de cada grupo de datos (horizontal x ; vertical y)
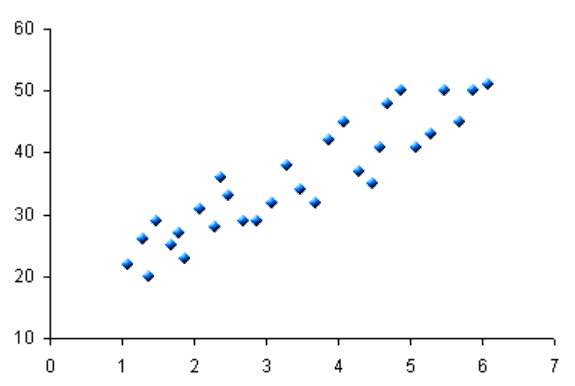
Diagrama de dispersión con regresión
[editar]Esta clase de diagramas tiene como objetivo trazar una línea a través de los puntos dibujados para representar la intensidad de la relación de dos variables.

Se usan dos fórmulas para determinar su pendiente:
Coeficiente de Correlación Lineal
[editar]- Transcluido de Regresión y Correlación
Para determinar el grado de relación entre variables, se usa la siguiente fórmula (coeficiente de Pearson):
Donde:
= Suma total de los valores multiplicados entre X e Y
= Suma total de solamente los valores de X
= Suma total de los valores de X al cuadrado
= Suma total de solamente los valores de Y
= Suma total de los valores de Y al cuadrado
= Número de valores tomados (en pares). Se puede determinar mediante
el número de filas cuando los datos se ordenan verticalmente y en pares.
- Dependiendo del resultado obtenido a través de la fórmula, se le asigna un grado de relación:
| Valores | Relación |
|---|---|
| de ± 0.80 a ± 0.99 | Muy alta |
| de ± 0.60 a ± 0.79 | Alta |
| de ± 0.40 a ± 0.59 | Moderada |
| de ± 0.20 a ± 0.39 | Baja |
| de ± 0.01 a ± 0.19 | Muy baja |
Regresión lineal simple
[editar]- Transcluido de Regresión y Correlación
Esta fórmula se utiliza para determinar la pendiente del gráfico.
Modelo de estimación:
| Donde:
= Suma total de los valores multiplicados entre X e Y |
Donde:
= Valor obtenido en la fórmula B1 |
Tipos de diagrama
[editar]Dispersión positiva o creciente
[editar]
Dispersión positiva débil
[editar]
Dispersión negativa o decreciente
[editar]
Dispersión negativa débil
[editar]
Dispersión nula
[editar]
Ejemplo
[editar]Un establecimiento desea ampliar el número de cajas que posee.
Se ha recolectado información del tiempo de espera de sus clientes y el número de cajas, los datos se muestran a continuación:
| Tiempo de espera | Número de cajas |
|---|---|
| 17.1 | 5 |
| 21.3 | 4 |
| 10.2 | 8 |
| 19.4 | 4 |
Desarrollo
[editar]- 1. Se determina qué variable depende de otra.
- Se puede usar la pregunta "¿Si Variable 1 aumenta, Variable 2 también lo hace?", si es correcto entonces Variable 1 es la variable independiente o la variable X.
- 2. Se realiza un cuadro para determinar los valores que se usarán en la fórmula.
| Tiempo de espera (Y) | Número de cajas (X) | XY | X² | Y² |
|---|---|---|---|---|
| 17.1 | 5 | 85.5 | 25 | 292.41 |
| 21.3 | 4 | 63.9 | 9 | 453.69 |
| 10.2 | 8 | 81.6 | 64 | 104.04 |
| 19.4 | 4 | 77.6 | 16 | 376.36 |
| _____________ | _____________ | _____________ | _____________ | _____________ |
| 68 | 20 | 308.6 | 114 | 1226.5 |
- 3. Con los datos, reemplazar en la fórmula y determinar la correlación.
- 4. Con los datos, se procede a diagramar el gráfico.

- 5. Ahora, determinamos el modelo de regresión lineal y le añadimos la línea de regresión para determinar su correlación gráficamente.
|
|
|
- Por lo que se tiene que el modelo de estimación es...




![{\displaystyle r={\frac {{\color {Melon}n}({\color {BrickRed}\Sigma xy})-({\color {Blue}\Sigma x})({\color {BurntOrange}\Sigma y})}{\sqrt {[{\color {Melon}n}({\color {Fuchsia}\Sigma x^{2}})-({\color {Blue}\Sigma x})^{2}][{\color {Melon}n}({\color {Mahogany}\Sigma y^{2}})-({\color {BurntOrange}\Sigma y})^{2}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bca3cb29e2bc924cc465577fb2d0244451a69d58)







![{\displaystyle {\color {OliveGreen}B_{1}}={\frac {{\color {Melon}n}({\color {BrickRed}\Sigma xy})-({\color {Blue}\Sigma x})({\color {BurntOrange}\Sigma y})}{[{\color {Melon}n}({\color {Fuchsia}\Sigma x^{2}})-({\color {Blue}\Sigma x})^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b3174a7ac64a46fbef1c25151b9f3b2b84691f4)




![{\displaystyle r={\frac {{\color {Melon}4}({\color {BrickRed}308.6})-({\color {Blue}20})({\color {BurntOrange}68})}{\sqrt {[{\color {Melon}4}({\color {Fuchsia}114})-({\color {Blue}20})^{2}][{\color {Melon}4}({\color {Mahogany}1226.5})-({\color {BurntOrange}68})^{2}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ecd9eee15355bc68db867c1bb87c27365fd8fc1)

![{\displaystyle {\color {OliveGreen}B_{1}}={\frac {{\color {Melon}4}({\color {BrickRed}308.6})-({\color {Blue}20})({\color {BurntOrange}68})}{[{\color {Melon}4}({\color {Fuchsia}114})-({\color {Blue}20})^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6b2a4c0ba85683430aa7f283631b21c85ca5779)



