Álgebra Abstracta/Grupos Cíclicos
Introducción
[editar]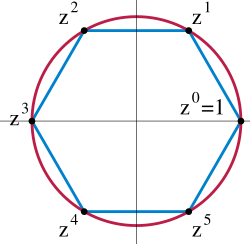
Los grupos cíclicos han aparecido varias veces anteriormente. Tales grupos son muy importantes en la teoría de los grupos, especialmente de los grupos abelianos. Dedicaremos este capítulo a establecer la estructura interna de los grupos cíclicos y algunas propiedades no vistas anteriormente.
Resumimos, a continuación, nuestro conocimiento de grupos cíclicos
- Un grupo (o subgrupo) cíclico consiste de todas las potencias enteras de uno de sus elementos, llamado generador del grupo.
- Los grupos cíclicos son abelianos.
- Dos grupos cíclicos finitos de igual orden, son isomorfos. Denotamos a un grupo cíclico de orden n por Cn .
- Hay grupos cíclicos finitos (Enteros módulo m) e infinitos (los Enteros).
- Cada elemento de un grupo cualquiera genera un subgrupo cíclico, denotado por .
¿Qué más nos interesaría conocer?
¿Cuántos subgrupos tiene el grupo cíclico
Hay grupos cíclicos finitos de cualquier orden, ¿pasa lo mismo con los sugrupos de un grupo ciclíco? ¿Cómo es el grupo de automorfimos de un grupo ciclíco?
Clasificación de los Grupos Cíclicos
[editar]En esta sección produciremos un listado completo de todos los posibles grupos cíclicos.
Sea G un grupo cíclico, digamos que . Entonces, para cada entero n, an es un elemento de G, por lo que podemos definir una función f desde los Enteros en G por f(m) = am. Claramente, f es suprayectiva y, por las propiedades de las potencias, tenemos que:
Es decir, que f es un homomorfismo (suprayectivo) de en G. Por los resultados sobre homomorfismos, tendremos que el núcleo de este homomorfismo, o sea el conjunto de todos los enteros n tales que f(n) = an = e, es un subgrupo de . De acuerdo a los resultados de un capítulo anterior, sabemos que los únicos subgrupos aditivos de los Enteros son los (múltiplos enteros de un número positivo o cero m). Por lo que el núcleo de f será uno de esos subgrupos. Tenemos varias posibilidades para ese núcleo, dependiendo de su generador.
- . En este caso, . Esto implica que f es inyectiva. Como f es, además, suprayectiva, tendremos que f establece un isomorfismo entre el grupo aditivo y el grupo .
- . En este caso, se cumple que para todo n, . En particular con n = 1, tenemos que a = e. Por lo tanto, ,el subgrupo nulo.
- donde d es un entero positivo mayor que 1. El número d es el menor entero positivo tal que ad = e. Para cualquier otro entero m tendremos entonces que, m=qd+r, con y, por lo tanto, Es decir que
un grupo cíclico con d elementos.
Proposición 1. (Clasificación de los Grupos Cíclicos) Sea . Tenemos tres posibilidades para G.
- G es isomorfo al grupo de los Enteros, por lo que es un grupo infinito, o
- G es el subgrupo trivial integrado únicamente por el elemento neutro, o
- G es isomorfo a .
Observaciones.
- Sigue de la proposición que grupos cíclicos de orden infinito son isomorfos.
- Los Enteros módulo m, la raíces n--ésimas de la unidad caen en la tercera categoría anterior.
- En el grupo aditivo de los Enteros, cualquier elemento diferente de 0 tiene orden infinito, pero no son necesariamente generadores del grupo.
Orden de Elementos
[editar]Ejemplo.
Sea G= . La tabla siguiente presenta los ordenes de cada uno de sus elementos.
Ejemplo de verificación: o([3]) = 4 ya que 4[3] = [12] = [0] y, 1[3] = [3] [0], 2 [3] = [6] [0] y 3[3] = [9] [0]. Notemos que cualquier elemento cuyo orden sea 12 es un generador del grupo, es decir, es posible que haya más de un generador de un grupo cíclico.
Proposición 2. (Caracterización del Orden por Divisibilidad) Sea G un grupo y g un elemento de G con orden finito d. Entonces, cuando , se cumple que d es un divisor de n.
-
Demostración: Se tiene que n = qd + r con . Si r fuera positivo, como r = n - dq, se tendría que ar = an-dq = an(ad)-q = e, por lo que ar=e; pero como r < d, esto es imposible. Luego, r = 0, por lo que se tiene el resultado.
Subgrupos de Grupos Cíclicos
[editar]Describiremos, a continuación, las posibilidades para los subgrupos de un grupo cíclico.
Proposición 3. (Subgrupos de un Grupo Cíclico)
- Cada subgrupo de un grupo cíclico es cíclico.
- Sea G un grupo cíclico de orden n. Entonces, para cada divisor del orden de G, hay exactamente un subgrupo con ese orden. En forma más precisa, si n=qd y , el subgrupo de orden d es ,
- Sea de orden n. El orden de es n/mcd(k,n).
-
Demostración:
- Sea G un grupo cíclico. Si G es infinito, el resultado sigue del resultado acerca de los subgrupos del grupo . Si G es nulo, el resultado es trivial. Supongamos entonces que y que el orden de a fuera d>1. Es decir, d sería el menor entero positivo tal que ad=e. Sea H un subgrupo no trivial de G, entonces habrá algún ak en H con . Sea s el entero positivo minimal con la propiedad que as \in H. Afirmamos que H = <as>. Sea ap un elemento cualquiera de H, entonces por el algoritmo de la división de Euclides, aplicado a p y s, nos proveerá enteros q y r tales que: . Notemos que
, lo que muestra que ar es un elemento de H. Por la minimalidad de s, tendremos que r = 0, lo que implica que cada elemento de H es una potencia de as. Es decir que, H = < as es un subconjunto de <as>; como la inclusión inversa es trivial, tendremos que H = <as>, de donde, concluimos que H es cíclico. - Sea G un grupo cíclico de orden n y sea d un divisor de n, digamos que n = qd. Probaremos que <aq> tiene orden d. En efecto, se tiene que (aq)d = aqd = an = e, o sea que d debe ser un múltiplo del orden de aq. Supongamos que k fuera el orden de aq, si k fuera menor que d, se tendría que aqk} = (aq)k = e. Como qk < qd = n, lo anterior es imposible, ya que n es el menor entero positivo p tal que ap=e. Luego, k debe ser igual a d. Probaremos ahora la unicidad, sean d y q como antes y sea H un subgrupo de orden d de G, queremos probar que H= q. Sabemos que H es cíclico y que, por lo tanto, existe un s tal que H = s>; como an = e, se tiene que s es un divisor de n y, por los argumentos anteriores, el orden de a debe ser igual a n/s. Pero ese orden es d = n/q. Luego n/s=n/q, de donde s=q y queda probada la unicidad.
- Sea d= mcd(k,n). Entonces k=k1d y n=n1d. Luego,
Pero, , por lo que . Sigue de la caracterización del orden por divisibilidad que o
Orden de los Elementos
[editar]¿Cuáles son los posibles ordenes de los elementos de un grupo cíclico?
Notemos que el orden de un grupo cíclico coincide con el orden de su generador . Si entonces el orden es infinito, mientras que si , , entonces .
Ejemplo.
En el grupo aditivo de los Enteros, cualquier elemento diferente de 0 tiene orden infinito.
Ejemplo.
Sea . La tabla siguiente presenta los ordenes de cada elemento.
Ejemplo de verificación: ya que y, , y . Notemos que cualquier elemento cuyo orden sea 12 es un generador del grupo, es decir, es posible que haya más de un generador de un grupo cíclico.
Proposición 4. (Caracterización del Orden por Divisibilidad) Sea un elemento con orden finito . Entonces, cuando , se cumple que es un divisor de .
-
Demostración: Tenemos, por división, que con . Si fuera positivo, como , se tendría que , por lo que ; pero como , esto es imposible. Luego, , y se tiene el resultado.
La función de Euler.
Sea un grupo de orden . Sigue de la parte c) de la proposición anterior que los elementos de orden de son los tales que . Es decir, todos los , que son relativamente primos con . La cantidad de esos elementos se llama la función de Euler de y se denota por .
Ejemplo.
Si es primo, . Por lo que los generadores de son todos los elementos, excepto el neutro.
La tabla siguiente muestra los valores de para valores pequeños de ,
Homomorfismos y Grupos Cíclicos
[editar]Proposición 5. (Homomorfismos y Cíclicos) Sea G un grupo cíclico y un homomorfismo de grupos. Entonces, la imagen es un subgrupo cíclico.
-
Demostración: Sea un generador de . Entonces, para cada de hay un , para algún , tal que . Lo que implica que ; lo que muestra que es cíclico con generador .
Los Automorfismos de los Enteros Módulo m
[editar]Recordemos que un automorfismo de un grupo es un isomorfismo (homomorfismo biyectivo) del grupo en si mismo. Todos los automorfismo de un grupo determinan, a su vez, un grupo simbolizado por (G). Sea G=, el grupo cíclico con m elementos y sea f: G \flecha G un automorfismo, entonces la imagen de [1] debe ser un generador de G, ya que . Luego, hay posibles selecciones para la imagen de G. Por lo que se tiene que .
Los Grupos Simétricos
[editar]Recordemos que llamamos grupo simétrico de un conjunto al grupo determinado por todas las biyecciones del conjunto en si mismo, con la composición de funciones como operación. Dos conjuntos con igual cardinal tienen grupos simétricos isomorfos.
Cuando el conjunto es finito, es tradicional llamar \textbf{permutaciones} a los elementos del grupo simétrico.
Advertencia. Para simplicidad de la exposición, supondremos que nuestro grupo simétrico de símbolos actúa en . Esto no es realmente una gran restricción, ya que los grupos simétricos de conjuntos con elementos son, siempre, isomorfos entre si. Como la intuición de permutaciones es reordenación, el conjunto donde actúan las permutaciones debe estar ordenado, lo que se traducer en una enumeración como
y al restringirnos a es como que estuviéramos trabajando cono los índices.
Recordemos que denotamos por al grupo simétrico de y llamamos permutaciones (de símbolos) a sus elementos.
Intuitivamente, una permutación de una cierta cantidad de objetos es un (re)ordenamiento de los mismos.
Los Ciclos
[editar]Ejemplo A.
Sea una permutación de .
Notemos que la (función) es tal que y .
Es decir que mueve el , y de manera cíclica, mientras que deja fijos a y . Tales permutaciones se llaman \textit{ciclos}, que definiremos de manera general más adelante.
Ejemplo B.
Sea una permutación de . En este caso, los puntos que no se mueven son 3 y 7. ¿Qué pasa con aplicaciones sucesivas de a puntos que no quedan fijos?
En este caso tenemos dos puntos fijos y dos ciclos.
Sea una permutación de un conjunto finito con elementos. Sea un elemento cualquiera de . Consideremos la sucesión obtenida por aplicaciones sucesivas de a un punto de y a sus imágenes.
Como es un conjunto finito, los términos de la sucesión
no pueden ser todos diferentes. Por lo que hay y , con , tales que . Si , entonces , lo que implica que , o sea , lo que es una contradicción ya que . Luego , o sea .
Introduciremos una terminología que nos ayudará a estudiar los ``ciclos de una permutación.
Definición. (Ciclos) Sea un conjunto con elementos. Sea una sucesión de elementos diferentes de , . Llamaremos ciclo (de largo ) o k--ciclo a la permutación de que deja fijo a todos los elementos de que no aparecen en la sucesión y tal que
Es decir que
Simbolizamos por a ese ciclo.
Llamamos transposición a un ciclo de largo 2.
Veremos, más adelante, que cada permutación puede expresarse como un producto de ciclos. Antes, presentaremos algunas nociones que nos ayudarán en el estudio de los ciclos de una permutación.
- (Puntos fijos de una permutación) Llamamos punto fijo o elemento fijo por (o de) una permutación en a un punto de tal que . Hay ejemplos de permutaciones y de transformaciones que no tienen puntos fijos, mientras que la identidad deja a todos los puntos fijos. En el ejemplo A, los puntos fijos son 3 y 5.
- (Soporte de una permutación.) Llamamos soporte de la permutación al subconjunto de formado por todos los elementos de que no quedan fijos por .
En otras palabras, el soporte de una biyección es el complemento (como conjunto) del conjunto de elementos fijos por . Coloquialmente, decimos que la permutación \textit{mueve} a los puntos de su soporte.
El soporte del permutación del ejemplo B es .
Observaciones.
- Un ciclo de largo 1 indica que todos los elemento de quedan fijo por la permutación, o sea que se trata de la identidad.
- Una permutación puede dar origen a uno o más ciclos.
- Si , entonces el soporte de es precisamente .
- Llamamos \textit{permutación cíclica} de al ciclo de . \index{permutación!cíclica}
- Sea un --ciclo. Se tiene que
Observemos que .
Permutaciones disjuntas.
Decimos que dos permutaciones son disjuntas cuando sus soportes lo sean.
Observemos que cuando dos permutaciones son disjuntas, los puntos que una mueva, la otra los deja fijos. Esto implica que el producto de las dos biyecciones es independiente del orden del producto.
|
Permutaciones disjuntas conmutan. |
Observemos que una biyección y su inversa tienen igual soporte. También si y son disjuntas se tiene que
Veremos, a continuación, lo anunciado más arriba.
Proposición 6. Cada permutación de es un ciclo o un producto único de ciclos disjuntos, excepto por el orden y 1--ciclos.
-
Demostración: (Por inducción sobre la cantidad de elementos en .)
Si , entonces que es un producto de ciclos disjuntos de largo 1.
Sea y sea en tal que . Sea el menor entero positivo tal que . Sea el ciclo . Sea en , entonces, razonado con el prueba del inverso, . Por lo que fija cada elemento de . Si no está en , entonces , por lo que . Luego, , ssi, . Esto implica que . Por la hipótesis de inducción, tenemos que debe ser igual a un producto de ciclos disjuntos, , que como fijan deben ser disjuntos de . Luego
Veamos ahora la unicidad. Supongamos que . Entonces, . Además, implica que . Cada en pertenece por lo tanto a un único , . Por lo que ya que coincide con en . Es decir que los ciclos quedan únicamente determinados por .
Transitividad de la acción
[editar]Sea un conjunto finito tal que . Dados dos puntos , , sea definida por
Claramente es una permutación de , cuando . Cuando un grupo de permutaciones, tiene la propiedad de que dado , hay un elemento del grupo que envía un punto en el otro, decimos que el grupo \textit{actúa transitivamente} sobre el conjunto.
Veremos, a continuación, que actúa transitivamente en el conjunto de sucesiones de --elementos diferentes de , clásicamente llamadas las --permutaciones de un conjunto con elementos.
Sean y dos sucesiones de elementos diferentes. Sea una sucesión formada por los elementos del complemento de . Sea la sucesión análoga para . Entonces, definimos una función que asigna a cada , el correspondiente . Claramente, tal función es la permutación deseada.
Ejemplo.
Sean , y , entonces una permutación satisfaciendo lo indicado arriba es
Esta construcción será usada más adelante para obtener permutaciones con una asignación parcial de sus valores.
Ejercicios
[editar]- Sean , y permutaciones de , con , y . Expresar cada una de esas permutaciones como un producto de permutaciones disjuntas.
- Sean , , y permutaciones de . Expresar cada uno de esos ciclos en la forma matricial.
- Sean , , y permutaciones de . Realizar las operaciones indicadas.
- Suponer que las permutaciones son de . Sea . Hallar , , , , y . Probar, además, que .
- Suponer que las permutaciones son de . Sean , y .
- Probar que los cuadrados de esas transposiciones son la identidad.
- Probar que cada una de esas transposiciones tiene un inverso igual a ellas mismas.
- Simplificar .
- Simplificar .
-
- Sea una transposición de . Probar que y que .
- Sea un 3--ciclo de . Probar que y que .
- ¿Cómo se podrían generalizar lo anterior a --ciclos de ? Conjeturar y tratar de probar.
- Probar que en , se tiene las siguientes relaciones:
- .
- .
- .
¿Qué se puede conjeturar?
- Construir la tabla de , el grupo simétrico del conjunto . Comparar la tabla del grupo con la tabla de la multiplicación de .
- Verificar la tabla de . Determinar todos los subconjuntos cerrados de . Comparar la tabla de con la tabla de las simetrías de un triángulo equilátero .
- Sea un subgrupo de un grupo simétrico y sean . Probar que el conjunto de permutaciones en que fijan , es un subgrupo de denotado por .
Propiedades de los Ciclos de Permutaciones
[editar]Sea un ciclo de largo en , digamos que
Mostraremos que cualquier punto que aparece en el ciclo, definen al mismo ciclo. Es decir que un ciclo no tiene una representación única, ya que cualquiera de los siguientes representa el mismo ciclo.
En efecto, tomemos como punto inicial a , entonces por sucesivas aplicaciones de obtenemos la sucesión
Como , tenemos que la sucesión anterior es
Es decir una sucesión de puntos que aparecen en el ciclo que se inicia en . Además, . Si hubiera un tal que , tendríamos que , de donde , lo que no puede ser. Sea el ciclo de largo que se inicia en . Claramente, el soporte de es igual al soporte de . Además, para cada tenemos que . Es decir que .
Cantidad de -ciclos.
¿Cuántos ciclos hay en de largo , ?
Las posiciones en un --ciclo, pueden llenarse de
diferentes maneras. Como cada -ciclo puede escribirse de diferentes maneras, tenemos que
Cantidad de k--ciclos =
Orden de Ciclos.
Sea . Los cómputos anteriores muestran que para todo se cumple que . Si no está en , es fijo por luego . Lo anterior prueba la siguiente proposición.
Proposición 7. Un --ciclo tiene orden como elemento del grupo .
En la terminología de la teoría de grupos, el subgrupo generado por un --ciclo es un subgrupo cíclico de orden . Como hay ciclos de largo , para todo . , tenemos que contiene subgrupos ciclos de orden . La siguiente proposición sigue directamente de la teoría de grupos cíclicos, pero, daremos también una demostración directa
Proposición 8. Sea un --ciclo de . Se cumple que
- es un ciclo tal que (subíndices computado los índices mayores que módulo ) .
- Si entonces es un -ciclo.
- Si entonces es un producto de ciclos de largo
-
Demostración:
- Como , tenemos la parte a).
- Cuando , entonces para todo , , los enteros
son enteros diferentes módulo .
En efecto, si , se tendría que . Como no divide a , se tiene que .
- Cuando , se tiene que . Lo que prueba la afirmación sobre el orden de . El resto sigue de forma inmediata.
Ejemplo.
Sea . Entonces,
Inversa de un ciclo.
La permutación inversa de un ciclo es un ciclo que hace un recorrido inverso de los puntos del ciclo original.
Notemos que se tiene
Observemos también que la inversa de una permutación tiene el mismo orden y soporte que la permutación. Tales resultados siguen en forma inmediata de la proposición anterior aplicada a .
Conjugado de un Ciclo.
Lema de Conjugación Sea un ciclo de y sea una permutación cualquiera de . Entonces, el conjugado de por , , es el ciclo de igual largo
-
Demostración: Sea . Entonces
Además,
Lo que prueba que
Ejemplo.
Sea en . Sea . Entonces, .
Ejemplo.
Sea un transposición de , . Sea una permutación tal que y . Entonces,\
Esto muestra que todos los 2--ciclos son conjugados con el ciclo . Como la relación de conjugación es de equivalencia, sigue que dos transposiciones cualesquiera son siempre conjugadas entre si.
Proposición 9. (Orden de un producto de ciclos disjuntos) Sean y ciclos disjuntos. Entonces, es igual mínimo común múltiplo de y .
-
Demostración: Como y son disjuntos, conmutan entre si. Luego, para cualquier se cumple que . Sea . Supongamos que , que y que . Sea . Entonces,
ya que es un múltiplo de los ordenes de y . Luego .
Si está en , . Luego, ; lo que implica que . Análogamente ,
Luego . Lo que prueba que .
Corolario 9.1. Sea . Entonces el orden de es el mínimo común múltiplo de los ordenes de los factores.
-
Demostración: Inducción sobre .
Ejemplo.
En la permutación tiene orden 6.
Ejemplo.
En hay un elemento de orden 30.
- El orden de es 30.
Clases de Conjugación
[editar]Sea una permutación de y sea la descomposición en ciclos disjuntos de incluyendo los 1--ciclos y tal que
( es el largo del ciclo ).
Llamamos tipo de a la sucesión . Notemos que
Luego, cada tipo de una permutación define una partición de .
Como cada conjugado de un ciclo tiene igual largo que el ciclo, sigue que los conjugados de una permutación tienen igual tipo que la permutación. Sean y dos permutaciones de igual tipo con las descomposiciones normalizadas como arriba.
Observemos que el soporte es la reunión disjunta de los soportes de los , . Análogamente para el soporte de . Supongamos que donde . Sea el ciclo correspondiente de . Sea la permutación tal que sobre el soporte de es tal que . Luego, por el lema de conjugación, . Se tiene entonces que
Proposición 10. Dos permutaciones son conjugadas, ssi, tienen igual tipo. Hay tantas clases de conjugación de como tipos, o sea como particiones de .
Ejercicios
[editar]- Expandir como una permutación completa de cinco elementos, cada uno de los siguientes ciclos de .
- Probar que en , se tiene las siguientes relaciones:
- .
- .
- .
¿Qué se puede conjeturar?
- Hallar todos los ciclos de largo 3 en y en .
- Probar que y que .
- Sea un producto de transposiciones disjuntas. Probar que .
- Sea . Probar que donde los subíndices mayores que se computan módulo . Por ejemplo, Usar lo anterior, para computar rápidamente los siguientes cuadrados: , , , . Observar que no siempre el cuadrado de un ciclo produce un ciclo del mismo largo. Inventar un método para calcular cubos de permutaciones rápidamente.
- Sean y permutaciones disjuntas de . Probar que
- y son permutaciones disjuntas, y que
- .
- \label{exDCT} Probar que . Es decir que todo ciclo es un producto de transposiciones.
- Probar que en , Si y son ciclos disjuntos, entonces .
- Sean , , , y . Verificar que
- Sea donde es un producto de ciclos disjuntos de . Sea . Probar que y que .
- Sea donde es tal que . Sea . Probar que y que .
- Hallar la cantidad de 2--ciclos en .
- Probar que el soporte de un ciclo es la órbita de cualquiera de los elementos del ciclo por .
Ejercicios del Capítulo
[editar]- Para cada grupo indicado, hallar el subgrupo cíclico generado por el elemento indicado
- Describir al subgrupo cíclico de generado por las matrices siguientes.
- Sea .
- ¿Por qué este grupo es cíclico?
- Hallar todos los posibles ordenes de elementos de G.
- Para cada divisor d de 12, hallar un elemento de G con orden igual a d.
- ¿Cuáles son todos los generadores de ?
- Hallar los automorfismos de .
- Sea G un grupo finito. Sean a y b elementos de G. Probar las siguientes relaciones acerca de sus ordenes.
- o(a-1)= o(a).
- o(bab-1) = o(a).
- Si ab=ba entonces o(ab) = mcm(o(a), o(b)).
- Si mcd(o(a),o(b)) = 1 y ab =ba entonces o(ab)=o(a)o(b).
- Hallar la cantidad de generadores de para
- Probar que el grupo multiplicativo para m=5 y 7 es cíclico, pero que no es cíclico.
- Sea de orden Probar que , ssi, .
- Sea f: G --> H un homomorfismo de grupos con G = <g> y H = <h>. Probar que o(h) es un divisor de o(g).
- Probar que la imagen por un homomorfismo de un grupo cíclico es un grupo cíclico. ¿Cuál es uno de los generadores de este grupo cíclico? ¿Puede pasar que el grupo original sea infinito, pero que su imagen sea un grupo finito?
- Sea G un grupo cíclico infinito. Probar que si G es un generador del grupo, hay solamente otro generador, que es el inverso de G. ¿Será cierto que un grupo cíclico con exactamente dos generadores es infinito?
- Sea G un grupo cíclico que tiene un único generador. Probar que G tiene solamente dos elementos.
- (Producto de Grupos Cíclicos)
- Sea H el grupo cíclico de orden 5 generado por a y sea K el grupo cíclico de orden 3 generado por b. Probar que el producto es un grupo cíclico generado por (a,b). Concluir que .
- Sea H el grupo cíclico de orden 4 generado por a y sea K el grupo cíclico de orden 2 generado por b. Probar que el producto no es un grupo cíclico.
- ¿Cuándo el producto de grupos cíclicos es cíclico?
- Sea p un número primo. Probar que f(pn)=pn-1(p-1), donde f es la función de Euler. (Sugerencia. mcd(a,pn=1, ssi, mcd(a,p)=1.)
- (La función f de Euler). Probar que para cada entero positivo n se cumple que . (Sugerencia: considerar el grupo cíclico con n elementos y la cantidad de generadores de cada uno de sus subgrupos.)
- Probar que Un (raíces enésimas de la unidad) es un grupo cíclico de orden n respecto a la multiplicación de números complejos.
- Marcar cada uno de los siguientes enunciados como válido o falso.
- Un grupo abeliano es un grupo cíclico.
- Un grupo cíclico de orden 30 tiene un subgrupo de orden 12.
- Un elemento x de un grupo G tiene orden n, ssi,
- Los Racionales positivos con la multiplicación forman un grupo cíclico infinito.
- Cada elemento diferente del neutro es un posible generador de un grupo cíclico.
- ¿Cuáles grupos cíclicos tiene la propiedad que cualquier elemento diferente del neutro es un generador del grupo?
- (Monoides) Un monoide es cíclico cuando todos sus elementos son potencias naturales de un elemento m, y . ¿Cuáles resultados de grupos cíclicos se podrían extender a monoides cíclicos?
- (*) Se prueba en el texto que para cada divisor del orden de un grupo cíclico, hay exactamente un subgrupo de ese orden. ¿Caracteriza esta propiedad a los grupos cíclicos? Es decir, si sabemos que un grupo finito tiene para cada uno de los divisores de su orden exactamente un subgrupo de orden dicho divisor, ¿podremos concluir que el grupo es cíclico?
Comentarios
[editar]Los grupos cíclicos son los bloques para la construcción de grupos abelianos. Se tiene los siguientes resultados:
- Cada grupo abeliano finito es un producto de grupos cíclicos.
- Sea G un grupo abeliano de orden . Entonces, hay una sucesión de enteros positivos mayores de 1 tales que cada número de la sucesión es un divisor del próximo y cuyo producto es , tal que G es el producto de los . Además dicha sucesión es única. [1]
La demostración de esos resultados requiere otros resultados que no están cubiertos en este texto. Sin embargo, resulta interesante sus aplicaciones para la clasificación de grupos abelianos finitos.
- Grupos abelianos de orden 8.
Los divisores positivos de 8 (mayores que 1) son 2, 4, 8. Por lo que tenemos las siguientes sucesiones posibles:(2,2,2), (2,4) y (8). Luego hay tres tipos posibles de grupos abelianos de orden 8.
- Grupos abelianos de orden 10. Los divisores positivos de 10 (mayores que 1) son 2, 5 y 10. Por lo que la única sucesión posible satisfaciendo las condiciones de divisibilidad es 10. Es decir que hay solamente un grupo abeliano de orden 10, el grupo cíclico de orden 10.
- Grupos abelianos de orden 20. Los divisores positivos de 20 (mayores que 1) son 2, 4, 5, 10 y 20. Luego, las únicas sucesiones satisfaciendo las condiciones de divisibilidad son 20 y 2, 10. Es decir que los únicos grupos abelianos de orden 20 son el grupo cíclico de orden 20 y el producto
Lecturas Adicionales
[editar]Véase también
- Wikipedia: Grupo Cíclico
- Wikipedia: Aritmética Modular
- Weisstein, Eric W. "Cyclic Group." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CyclicGroup.html
Notas
[editar]- ↑ Ver, por ejemplo (BB) Dean pag. 152.




















![{\displaystyle {\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c|c|}{\text{elemento}}&[0]&[1]&[2]&[3]&[4]&[5]&[6]&[7]&[8]&[9]&[10]&[11]\\\hline {\text{orden}}&1&12&6&4&3&12&2&12&3&4&6&12\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1e618804d2e6947d364c71dd582847c799c021f)


















![{\displaystyle o([3])=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4768d713b53174175eeffdefb21c145d6b231365)
![{\displaystyle 4\cdot [3]=[12]=[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b51985aa448022d54c82f69c7a9391f84f2aac)
![{\displaystyle 1[3]=[3]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47b7644bd0e907ada9e3f8c766538fb288dc3a6b)
![{\displaystyle 2[3]=[6]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3455755a0b4f4956eaafe2fe9bab3b04b9f84de)
![{\displaystyle 3[3]=[9]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/975a6feecf4bba1d93dd074cfbc3eea28925c33f)












































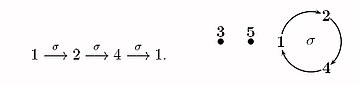


















































































































































































































































![{\displaystyle \mathbb {Z} _{30},\quad [10].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f006f9104a286d8aca01551fdefdcc69207a566)
![{\displaystyle \mathbb {Z} _{50},\quad [12].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1620c9561924c7811d9024d33a7596a485547685)
![{\displaystyle \mathbb {Z} _{50},\quad [11].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a547ec964e18ec6f03b6c1f38bf9c6a877b8b46)
















