Es la primera de las fórmulas de integración cerrada de Newton–Cotes.
Corresponde al caso donde el polinomio en la ecuación de integración es de primer orden:
La integral se representa como:
I ≈ ancho x altura promedio
I
=
∫
a
b
[
f
(
a
)
+
f
(
b
)
−
f
(
a
)
b
−
a
(
x
−
a
)
]
d
x
=
(
b
−
a
)
f
(
a
)
+
f
(
b
)
2
{\displaystyle I=\int _{a}^{b}{\left[{f(a)+{{f(b)-f(a)} \over {b-a}}(x-a)}\right]}dx=(b-a){{f(a)+f(b)} \over 2}}
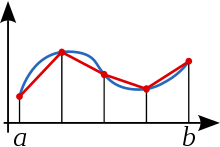
Ilustración de la regla del trapecio compuesta La regla del trapecio compuesta o regla de los trapecios es una forma de aproximar una integral definida utilizando n trapecios. En la formulación de este método se supone que f es continua y positiva en el intervalo [a ,b ]. De tal modo la integral definida
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx}
f y el eje x , desde x =a hasta x =b . Primero se divide el intervalo [a ,b ] en n subintervalos, cada uno de ancho
Δ
x
=
(
b
−
a
)
/
n
{\displaystyle \Delta x=(b-a)/n}
Después de realizar todo el proceso matemático se llega a la siguiente fórmula:
∫
a
b
f
(
x
)
d
x
∼
h
2
[
f
(
a
)
+
2
f
(
a
+
h
)
+
2
f
(
a
+
2
h
)
+
.
.
.
+
f
(
b
)
]
{\displaystyle \int _{a}^{b}f(x)\,dx\sim {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}
Donde
h
=
b
−
a
n
{\displaystyle \textstyle h={\frac {b-a}{n}}}
n es el número de divisiones.
La expresión anterior también se puede escribir como:
∫
a
b
f
(
x
)
d
x
∼
b
−
a
n
[
f
(
a
)
+
f
(
b
)
2
+
∑
k
=
1
n
−
1
f
(
a
+
k
b
−
a
n
)
]
{\displaystyle \int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left[{\frac {f(a)+f(b)}{2}}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right]}
El error en esta aproximación se corresponde con :
−
(
b
−
a
)
3
12
n
2
f
(
2
)
(
ξ
)
{\displaystyle -{\frac {(b-a)^{3}}{12n^{2}}}\,f^{(2)}(\xi )}
Siendo n el número de subintervalos
∫
1
2
3
x
d
x
{\displaystyle \int _{1}^{2}3x\,dx}
Primero se obtiene h , de los límites de la integral que representan a y b y para n =6 queda:
h
=
b
−
a
n
{\displaystyle h={\frac {b-a}{n}}}
=
2
−
1
6
=
1
6
{\displaystyle ={\frac {2-1}{6}}={\frac {1}{6}}}
Y ahora se sustituye en la fórmula
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx}
h
2
[
f
(
a
)
+
2
f
(
a
+
h
)
+
2
f
(
a
+
2
h
)
+
.
.
.
+
f
(
b
)
]
{\displaystyle {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}
y queda:
∫
1
2
3
x
d
x
{\displaystyle \int _{1}^{2}3x\,dx}
1
2
⋅
1
6
[
3
(
1
)
+
2
[
3
(
1
+
1
⋅
1
6
)
]
+
2
[
3
(
1
+
2
⋅
1
6
)
]
+
2
[
3
(
1
+
3
⋅
1
6
)
]
+
2
[
3
(
1
+
4
⋅
1
6
)
]
+
2
[
3
(
1
+
5
⋅
1
6
)
]
+
3
(
2
)
]
=
4.5
{\displaystyle {\frac {1}{2}}\cdot {\frac {1}{6}}[3(1)+2[3(1+1\cdot {\frac {1}{6}})]+2[3(1+2\cdot {\frac {1}{6}})]+2[3(1+3\cdot {\frac {1}{6}})]+2[3(1+4\cdot {\frac {1}{6}})]+2[3(1+5\cdot {\frac {1}{6}})]+3(2)]=4.5}

![{\displaystyle I=\int _{a}^{b}{\left[{f(a)+{{f(b)-f(a)} \over {b-a}}(x-a)}\right]}dx=(b-a){{f(a)+f(b)} \over 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e704b1adf18875e7673cfc6d19f2b95baa4b9345)


![{\displaystyle \int _{a}^{b}f(x)\,dx\sim {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f1b5c6a7245887f1241f8a623edf4c3975c1ec2)

![{\displaystyle \int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left[{\frac {f(a)+f(b)}{2}}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed95b3abd58bd3f419658c546afcd7b1fd48ca24)




![{\displaystyle {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/118092dfd0e9a60f55b8c1a5529fafc8d4651909)
![{\displaystyle {\frac {1}{2}}\cdot {\frac {1}{6}}[3(1)+2[3(1+1\cdot {\frac {1}{6}})]+2[3(1+2\cdot {\frac {1}{6}})]+2[3(1+3\cdot {\frac {1}{6}})]+2[3(1+4\cdot {\frac {1}{6}})]+2[3(1+5\cdot {\frac {1}{6}})]+3(2)]=4.5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5503eaf0747fe771b29973292d3b8a5e11d63012)