Matemáticas Universitarias/Espacios Métricos/Texto Completo
Introducción
[editar]El objetivo de este capítulo es presentar algunos resultados “intuitivos”, cuya formalización condujo al desarrollo de los Espacios Métricos Y la Topología.
Generalidades
[editar]Recordemos que, en los cursos de Cálculo, se define la noción de derivada de una función como un cierto límite; donde por límite de los valores de una función se entiende un cierto número al que se aproximan dichos valores cuando el argumento de la función se restringe adecuadamente.
¿Qué significa exactamente lo anterior? En la mayoría de los textos de Cálculo no se desarrolla una teoría profunda acerca de los límites, ya que el interés primario está en la manipulación de funciones derivables e integrables: cómo “calcular” una derivada o hallar una integral, así como en sus aplicaciones (máximos y mínimos, por ejemplo).
Tras bastidores, por así decirlo, están las funciones continuas, que para nosotros serán las más importantes. Generalmente, tales funciones aparecen definidas en términos de límites, diciendo que el limite de los valores de la función en un cierto número es precisamente el valor de la función en ese número. Intuitivamente, se dice que una función es continua en un punto de su dominio cuando su gráfica no tiene “saltos” en dicho punto. Si la función está definida sobre un intervalo, continuidad en el intervalo significa, intuitivamente, que podemos dibujar la gráfica de la función sin necesidad de tener que levantar el lápiz.
Cuando examinamos un texto de Cálculo, especialmente en el área de aplicaciones de las derivadas, usualmente hallamos los enunciados de algunos teoremas, con las pruebas omitidas por pertenecer a matemáticas más avanzadas. Este texto provee esas "matemáticas más avanzadas". Una notable excepción a lo anterior es el texto de Cálculo de Spivak [16].
Examinaremos, a continuación, algunos de esos teoremas.
Teorema A. (Teorema del Valor Intermedio) Sea f : [a, b] → R una función continua tal que f(a) y f(b) tienen signos opuestos. Entonces, hay un c tal que a < c < b y f(c) = 0.
Teorema B.) (Acotamiento de Funciones) Sea f : [a, b] → R una función continua, entonces hay un real positivo M tal que para todo x en [a, b] se cumple que −M ≤ f(x) ≤ M. En palabras, la función f es acotada.
Teorema C. (Existencia de Máximos y Mínimos Absolutos) Sea f : [a, b] → R una función continua, entonces hay números c y d tales que a ≤ c, d ≤ b con f(c) ≤ f(x) ≤ f(d), para todo x en [a, b]. En palabras, la función f alcanza máximos y mínimos absolutos.

Examinemos tales teoremas. Veamos primeramente su plausibilidad, o sea ¿por qué creemos que pueden ser válidos? Mirando a la parte (a) de la figura 1.1, y usando la intuición de que la gráfica no tiene saltos, vemos que yendo de (a, f(a)) (que está por debajo del eje X) a (b, f(b)) (que está por encima del eje X) tenemos que cruzar al menos una vez el eje, que es precisamente lo que dice el teorema A.
Igualmente, mirando a la parte (b) de la figura, podemos razonar que por mucho que suba o baje la gráfica, debe finalmente llegar al punto (b, f(b)), que nos dice lo que enuncia el teorema B. Dicha figura también ilustra lo indicado por el teorema C.
La discusión heurística anterior, puede conducirnos a una serie de preguntas interesantes. ¿Por qué no aparece una demostración de esos teoremas, que parecen tan obvios? Inicialmente, los matemáticos tomaron a esos resultados como “evidentes”, razonando gráficamente como arriba. Varios tropiezos posteriores con tales argumentos gráficos, llevó a los matemáticos del siglo XIX a estudiar seriamente como probar lógicamente dichos teoremas. Fue solamente en las décadas finales de ese siglo que se obtuvo una teoría que permitió tales demostraciones.
Volviendo a los teoremas, notemos que los tres tienen una hipótesis común: “sea f : [a, b] → R una función continua.” ¿Por qué el dominio de la función tiene que ser un intervalo cerrado y acotado? ¿Qué pasa si tomamos un intervalo que no sea cerrado o acotado o un dominio que no sea un intervalo?
(♠) Usaremos, en algunos de los ejemplos posteriores, el teorema que establece que cuando una función tiene derivada, la función es continua.
Ejemplo 1.1.1. Sea A =]0, 1] = {x ∈ R : 0 < x ≤ 1}. Notemos que la única diferencia con el intervalo [0, 1] es que A no contiene el punto 0, o sea que es un intervalo abierto en 0.
Sea f : A → R tal que f(x) = 1/x. Esta función es continua en A (porque tiene derivada, f′(x) = −1/x2) Tal función no es acotada superiormente, ya que si x = 1/n, n entero positivo, f(x) = n, o sea que alcanza valores tan grande como queramos. Por la misma razón, no alcanza un valor máximo.
El ejemplo anterior ilustra que la ausencia de un punto del dominio hace que los teoremas B y C no sean válidos.
Moraleja: un sólo punto puede hacer una gran diferencia!!!!
Ejemplo 1.1.2. Sea B =]0, 1[= {x ∈ R : 0 < x < 1}. Sea f : B → R tal que f(x) = x. Esta función es continua en A (porque tiene derivada, f′(x) = 1). Es fácil ver que esa función es acotada, ya que para todo x en B se cumple que, digamos −2 < f(x) < 2; sin embargo, la función no alcanza valor máximo ni mínimo. (Los valores candidatos están fuera del dominio de la función.)
Ejemplo 1.1.3. En los ejemplos anteriores, hemos quitado un punto del extremo de un intervalo cerrado, ¿qué pasará si quitamos un punto dentro del intervalo?

Sea C = {x ∈ R : −1 ≤ x < 0 o 0 < x ≤ 1, o sea el intervalo [−1, 1] menos el 0. Sea f : C → R tal que f(x) = 1 cuando x > 0 y, en caso contrario, f(x) = −1.
Mirar la gráfica en la figura 1.2. Claramente la función tiene derivada en todo su dominio, derivada que es nula. Notemos que f(−1) = −1 < 0 y f(1) = 1 > 0, pero no hay un número c entre −1 y 1 donde f(x) = 0. (Ver el teorema A).
Recordemos, también que hay un teorema de Cálculo que dice que una función con derivada nula es constante. Nuestra función tiene derivada nula en todo su dominio, pero no es constante.
¿Qué sucede?
Simplemente, que el teorema que la derivada nula implica función constante requiere en su hipótesis que el dominio sea un intervalo, o sea que no puede haber un punto faltante entre los extremos. En este caso el dominio está desconectado (consiste de dos partes que no tienen punto común) y como consecuencia, su
gráfica también.
Los ejemplos anteriores muestran que la conducta de una función (es o no acotada, alcanza un cierto valor o tiene máximos o mínimos, etc.) depende no solamente de la regla o fórmula de la función, sino que también es muy importante el conjunto donde está definida la función.
Los ejemplos anteriores, y muchos otros más, condujeron a un estudio matemático formal de las situaciones envueltas. Nuevas teorías fueron creadas: Análisis para formalizar los procesos de derivación e integración, Geometría Multidimensional
(geometría y Cálculo de varias variables), Espacios Métricos, la teoría
de Conjuntos y finalmente la Topología.
Los Espacios Métricos y la Topología estudian la noción de proximidad, ¿qué quiere decir estar cerca de un punto o de un conjunto? ¿Cuándo un conjunto tiene partes separadas? ¿Cuál es la diferencia entre intervalos cerrados y abiertos? Los espacios métricos lo hacen usando una noción de distancia entre puntos, los espacios topológicos lo hacen sin recurrir a la noción de distancia. Hay situaciones donde no hay una métrica o distancia posible o donde la métrica no es lo más natural, por lo que se recurre a la noción de “vecindad” (espacios topológicos). Dos puntos de la misma vecindad están “cercanos”, puntos pertenecientes a diferentes vecindades estarán más separados. La habilidad de los matemáticos ha sido crear un lenguaje formal para estudiar adecuadamente dichas intuiciones. Para entender un poco los problemas que trata la teoría de los espacios métricos y la topología, veamos la siguiente situación.
Consideremos el círculo unitario del plano cartesiano, o sea al conjunto
Sea p = (a, b) un punto del plano. Tratar de responder a las siguientes preguntas sin mirar a un dibujo de la situación, o sea solamente usando la definición de C.
- ¿Qué condiciones deben satisfacer a y b para que p sea un punto en el interior de C? ¿en el borde de C? ¿en el exterior de C?
- ¿Cómo definir que p es un punto en el interior (resp. borde, exterior) de C sin usar las ecuaciones? (Sug. Mirar que pasa con los vecinos de p (los puntos suficientemente cercanos a p.)
|
No olvidar de leer la sección Convenios del Prefacio |
Los Números Reales
[editar]Introducción
[editar]La historia de los espacios métricos empieza con los (números) Reales. Representamos intuitivamente a los Reales mediante la llamada línea numérica, equipada con la distancia entre números definida como el valor absoluto desu diferencia. Informalmente hablando, un espacio métrico será un conjunto provisto con una noción de distancia; los Reales con la distancia mencionada seránn el ejmeplo básico de espacio métrico (las definirionaes formales aparecerán en capítulos posteriores). Las propiedades de subconjuntos de los Reales y de las funciones definidas sobre ellos fueron generalizadas o abstraídas a las teorías de los espacios métricos y de los espacios topológicos.
En este capítulo revisaremos las propiedades relevantes de los Reales. Recomendamos a los lectores que revisen lo expuesto, aunque será muy probable que lo hayan visto con anterioridad. Es muy importante que revisen las secciones dedicadas a la completitud, el axioma del supremo y sus consecuencias, especialmente cuando la palabra "supremo" les sea deconocida. El énfasis de la exposición será en aquellos aspectos útiles para el resto del texto.
La segunda sección es un resumen muy breve de las propiedades generales de los Reales. La tercera sección presenta las consideraciones métricas de los Reales. En la cuarta sección, presentamos/revisamos la noción de supremo, que completa la presentación de la estructura de los Reales y que será muy importante en nuestro estudio. En las últimas secciones, veremos relaciones entre los Racionales y los Reales.
Los Números Reales
[editar]Formalmente, los Reales están caracterizados por las propiedades de sus operaciones, las propiedades del orden y la completitud. Revisaremos primeramente lo referente a las operaciones y al orden.
La Estructura de Cuerpo
[editar]En los Reales, R, hay definidas dos operaciones a las que llamamos adición () y multiplicación (*). Tales operaciones satisfacen los siguientes axiomas o postulados.[1]
- (Axiomas de la Adición) La adición es asociativa, conmutativa, tiene un neutro 0 (a+0=a) y cada número a tiene un opuesto aditivo -a tal que a + (-a) = 0.
- (Axiomas de la Multiplicación) La multiplicación es asociativa, conmutativa, tiene neutro 1 (a*1=a) y cada número a ≠ 0 tiene un recíproco 1/a tal que a * (1/a) = 1).
- (Axiomas MIxtos) La multiplicación es distributiva respecto a la adición. Los neutros 0 y 1 son diferentes.
- Cuando en un conjunto cualquiera K haya definidas operaciones con las propiedades anteriores, decimos que K tiene o posee con dichas operaciones una estructura de cuerpo o simplemente que K es un cuerpo. Por lo que, los postulados anteriores dicen que R es un cuerpo.
- Cuando en un conjunto cualquiera K haya definidas operaciones con las propiedades anteriores, decimos que K tiene o posee con dichas operaciones una estructura de cuerpo o simplemente que K es un cuerpo. Por lo que, los postulados anteriores dicen que R es un cuerpo.
- Otros cuerpos importantes que seguramente el lector conoce son los Racionales, Q, que es un subconjunto de los Reales y los Complejos, C, que contienen a los Reales.
- Otros cuerpos importantes que seguramente el lector conoce son los Racionales, Q, que es un subconjunto de los Reales y los Complejos, C, que contienen a los Reales.
En un cuerpo, se definen dos operaciones auxiliares: substracción y división.
Como es costumbre, escribiremos xy en lugar de x * y.
Los Reales contienen algunos subconjuntos especiales que recordamos a continuación.
- Los Naturales, N, caracterizado por ser el subconjunto más pequeño de los Reales que satisface las siguientes propiedades
- (i) 0 es un número natural; [2]
- (ii) Si k es un número natural, también lo es k+1.
- Los Enteros, Z, que está formado por los naturales y sus opuestos aditivos.
- Los Racionales, Q, cuyos elementos son fracciones de enteros.
La Estructura de Cuerpo Ordenado
[editar]Tenemos para el orden los siguientes axiomas.
Axiomas del Orden. Hay una relación "≤" entre números reales, tal que
- (i) Si (x ≤ y) y (y ≤ z) entonces (x ≤ z) (transitividad).
- (ii) (x ≤ y) y (y ≤ x) <==> x=y.
- (iii) para todo x, y se cumple que (x ≤ y) o que (y ≤ x).
- (iv) si (x ≤ y) entonces (x + z ≤ y + z).
- (v) si (0 ≤ x) y (0 ≤ y) entonces (0 ≤ xy).
Cuando en un cuerpo hay una relación como la anterior, (llamada relación de orden), se dice que se trata de un cuerpo ordenado. Los Reales y los Racionales forman un cuerpo ordenado, mientras que los Complejos no.
(Relaciones de orden asociadas) Asociada con la relación ≤ tenemos "x < y" que quiere decir que (x ≤ y) pero que (x ≠ y). Suponemos conocido por los lectores los significados de "x > y" y de "x ≥ y", así como la terminología acerca de positivos y negativos.
Notación de Intervalos. Simbolizaremos los extremos abiertos de intervalos usando "]" para el extremo inferior y "[" para el extremo superior. Así, por ejemplo, ]3, 6[ = {x ∈ R: 3 < x < 6}. Usamos esta notación, para distinguir intervalos abiertos de pares ordenados.
Hay una propiedad muy importante que aparecerá frecuentemente en nuestras discusiones.
Principio del Buen Orden (PBO) Esta es una propiedad del orden referentes a los Enteros que establece que:
- Cualquier subconjunto de enteros no-negativos tiene un primer elemento, o sea un elemento que es menor o igual que cualquier otro elemento del conjunto.
Ejercicios 2.2.
[editar]- Sean x, y tales que x < y, sea z = (x+y)/2. Probar que x < z < y.
- (Demostraciones de que un número es igual a 0)
- Si x + y = x entonces y = 0.
- Si x + x = x entonces x = 0.
- a ∗ 0 = 0. (aplicar lo anterior).
- (Opuestos aditivos).
- Si x + y = 0 entonces y = −x.
- −(−x) = x (evaluar −x + x).
- −(a + b) = −a + (−b.1
- (−a)b = −ab (evaluar ab + (−a)b).
- (−a)(−b) = ab.
- Hallar el conjunto solución de la siguientes inecuaciones.
- 2x − 3 < 5.
- x2 + 12 ≤ 7x.
- Probar que todo número natural se cumple que n ≥ 0 y si n 6= 0, n > 0.
- Probar que para todo número natural n se cumple que n < 2n.
Nociones Métricas en los Reales
[editar]Llamaremos nociones métricas a nociones asociadas al valor absoluto, ya que dicho valor absoluto nos permite definir una distancia entre puntos de R. Recordemos, primeramente, la definición de valor absoluto.
Definición. (Valor Absoluto) Llamamos valor absoluto de un número real x, al número real tal que , cuando ; e igual a , en caso contrario.
Notemos que para todo a, se cumple que -|a| ≤ a ≤ |a|.
Lema Sea a un número real positivo. Entonces,
- |x|<a, ssi, -a < x < a.
- |x|=a, ssi, x = a.
- |x|>a, ssi, x < -a o x > a.
Demostración.
- Probaremos (a) y el resto queda de ejercicio. Por tricotomía se tiene que x>0 o x=0 o x<0.
- Supongamos que |x|< a (*). Si x es positivo, (*) es equivalente a x<a; si x=0, (*) es equivalente a 0<a; finalmente, si x es negativo, (*) es equivalente a -x<a, o sea que x>-a. Por lo tanto, (*) es equivalente a -a < x < a.
Proposición 2.3.2. (Propiedades Básicas del Valor Absoluto) Para todo a, b reales se cumple:
- (VA1) |a| ≥ 0.
- (VA2) |a|=0, ssi, a=0.
- (VA3) |-a| = |a|.
- (VA4) |a+b| ≤ |a|+|b|.
- (VA5) |ab| = |a| |b|.
-
Demostración.
(VA1), (VA2) y (VA3) siguen en forma directa de la definición.
(VA4) Sigue de la definición que (1) -|a| ≤ a < |a| y que (2) -|b| ≤ b ≤ |b|. Sumando miembro a miembro en las desigualdades anteriores, obtenemos que
- -(|a|+|b|) ≤ a + b ≤ |a| + |b|.
- (VA5) sigue de un análisis de casos de los signos de a y b.
- Si a, b>0 entonces |ab| = ab = |a| |b|.
- Si a= o b=0 el resultado es trivial.
- Si a < 0 y b >0 entonces, |ab| = -a *b = |a| \, |b|.
- Si a <0 y b<0 entonces |ab| = ab = (-a)(-b) = |a|\,|b|.
La noción de valor absoluto se usa en los cursos básicos para definir una distancia entre números reales a y b, por
|
|
Proposición 2.3.3 (Propiedades de la Distancia). Sean a,b,c reales. Se cumple:
- (D1) d(a,b) ≥ 0.
- (D2) d(a,b) = 0, ssi, a=b.
- (D3) d(b,a) = d(a,b). (Simetría)
- (D4) d(a,b) ≤ d(a,c) + d(c,b). (Desigualdad Triangular)
- Demostración. Las demostraciones siguen directamente de las propiedades correspondientes del valor absoluto.
- (D1) d(a,b) = |a-b| ≥ 0. (VA1)
- (D2) d(a,b)=0 ,ssi, ax-b|=0, ssi, a-b=0, ssi, a=b. (VA2)
- (D3) d(b,a) = |b-a| = |-(a-b)| = |a-b| = d(a,b). (VA3)
- (D4) d(a,b) = |a-b| = |(a-c) + (c-a)| ≤ |a-c|+|c-b|=d(a,c) + d(c,b). (VA4)
Lo que es importante es mirar siempre a |a-b| como indicando distancia del punto a al punto b. Esto permite visualizar expresiones que contienen valor absoluto.
Ejemplo 2.3.1.
- Hallar todos los x tales que |x-3| = |x + 5|.
Resolución: Reescribiendo la ecuación como |x-3| = |x -(-5)|, vemos que se trata de hallar un punto o puntos cuya distancia a 3 sea igual a su distancia a -5. Es fácil, entonces ver que la única solución posible es x=-1. - Hallar todos los x tales que |x-5| < 3.
Resolución. Buscamos x cuya distancia a 5 sea inferior a 3. Fácil de ver que se trata de los x tales que 2=5-3< x < 5+3= 8, o sea que el conjunto solución es el intervalo abierto ]2,8[.
Ejercicios 2.3
[editar]- (Desigualdades)
- Probar que para todo número real a, a2 ≥ 0 y que a2 = 0, ssi, a = 0.
- Usar lo anterior para probar que |a| = √(a2).
- Cuando a y b son números positivos o cero, entonces 2ab ≤ a2 + b2.
(Sug: Usar que (a − b)2 ≥ 0) ¿Cuándo la desigualdad es igualdad? - Cuando a y b son números positivos o cero, entonces
- √ab ≤ (a + b)/2.
- Sabemos que |a + b| ≤ |a| + |b|. Investigar cuando se tiene la igualdad.
- Probar que ||a| − |b|| ≤ |a − b|. (Sug. Usar que x = y + (x − y) y que y = x + (y − x).)
Completitud
[editar]Esta sección está dedicada al actor principal en el drama de los Reales: el supremo, Si la lectora o lector sabe lo que supremo e ínfimo significan, puede ir a mirar el Postulado del Supremo en la sección 2.4.2, el teorema 2.4.4 y sus corolarios. Si siente que está suficientemente familiarizada o familiarizado con esas nociones puede saltarse esta sección e ir al próximo capítulo. Siempre será posible volver a consultarlo.
Suponemos conocido por los lectores que además de los números racionales (iguales a una fracción de enteros) hay otros que no lo son, los irracionales. Algunos irracionales famosos: , , , etc.
Observamos anteriormente que tanto los Racionales como los Reales son cuerpos ordenados, lo que implica que los axiomas de cuerpo ordenado no pueden dar cuenta de los irracionales. Necesitaremos axioma o axiomas adicionales. Tales axiomas se llaman axiomas de completitud. Hay varias versiones posibles para lograr ese objetivo, como veremos más adelante.
Revisaremos, primeramente, las bases intuitivas de la completación.
Suponemos conocido que cada número real tiene una expansión decimal. Es decir, suponiendo que , podemos hallar un entero positivo y una sucesión infinita de dígitos (decimales)------tales que
| (1) |
lo que usualmente se escribe abreviadamente como
| (2) |
donde llamamos numeral decima} a la expresión de la derecha.
Lo anterior es más fácil escribirlo que explicarlo lógicamente, ¿cuál es el significado de un numeral decimal? La notación en (2) oculta el hecho de que se trata de una suma infinita.
Podemos, además, preguntarnos, ¿cómo se obtiene el numeral digital asociado a un número real? ¿será siempre posible esa asociación? ¿dada una expansión decimal cualquiera hay un número real asociado?
La búsqueda de una respuesta a esas preguntas, fue el origen de la teoría de los espacios métricos.
Hemos intencionalmente llamado "numeral decimal" a la expresión en (2), para insinuar que no estamos seguro de que se trate de un número real.
Ejemplo 2.4.1.. Antes de pasar adelante, para ilustrar que las consideraciones anteriores no son una cosa trivial, consideremos los numerales decimales siguientes:
Las expresiones anteriores se han construido no--periódicas, porque se sabe que cuando tales expansiones son periódicas representan a números racionales.
Si alguien supone que las consideraciones anteriores y otras posteriores son triviales, suponga que y representan números reales, y calcule y . \end{ejemplo}
Supondremos conocido que cuando el numeral decimal es finito (a partir de un cierto subíndice todos los son nulos), entonces el numeral decimal representa a un número racional, ya que
| (3) |
Sea un numeral decimal como en (2) y sea la truncación (eliminar la cola) del numeral después de la posición ), o sea que es lo que aparece en (3). Si ponemos que , vemos que el numeral da origen a una sucesión , , , \ldots de números racionales tales que
| (4) |
Se puede, además, verificar que para todo se cumple que .
¿Define el numeral decimal o equivalentemente la sucesión en (4), a un número real?
Si se piensa en la expansión decimal de un irracional, por ejemplo , vemos que no podemos obtener una respuesta lógicamente válida usando solamente los postulados de cuerpo ordenado. Este razonamiento heurístico muestra que necesitamos algo más: postulados de completitud.
\medskip Una solución simple es postular que "cada numeral decimal define a un número real, lo que llamaremos la ""completitud ingenua. Tal completitud es la que se usa en cursos primeros de matemáticas/ Una solución más formal requiere (entre otras opciones) la introducción de la noción de supremo.
Supremos, Ínfimos, Axioma del Supremo
[editar]Sea A un subconjunto de los Reales.
Cota Superior, Cota Inferior. Decimos que un número real M es una cota superior del conjunto A, ssi, para todo x se cumple que
Tenemos un concepto dual.
Decimos que un número real m es una cota inferior del conjunto A, ssi, para todo x se cumple que
Ejemplo 2.4.2.
Sea A=]0,1]. Entonces 1, 2, 100, etc. son cotas superiores de A, mientras que 0, -1, -5 son cotas inferiores de A.
Notemos que cuando un conjunto tiene una cota , digamos superior, cualquier número mayor que es también una cota superior, por lo que cuando un conjunto tiene una cota superior, tiene infinitas cotas superiores. Dualmente, cuando un conjunto tiene una cota inferior, cualquier número inferior a esa cota, es también una cota inferior. Notemos, también, que las cotas pueden o no pertenecer al conjunto.
Conjunto Acotado. Decimos que un subconjunto está acotado superiormente (resp. inferiormente) cuando haya una cota superior (resp. inferior) del conjunto. Un conjunto es acotado, ssi, es acotado superior e inferiormente.
Usando la noción de cota definiremos supremo e ínfimo.
Definición. (Supremo, Ínfimo) Sea A un subconjunto de los Reales.
- Llamamos supremo de A a una cota superior que sea menor o igual que cualquier otra cota superior.
- Llamamos ínfimo de A a una cota inferior que sea mayor o igual que cualquier otra cota inferior.
Proposición 2.4.1. Cuando un conjunto tiene un supremo (resp. ínfimo) dicho supremo es único.
- Demostración. Sea S y S' supremos de un conjunto A. Aplicando la definición de supremo a S y viendo a S' como una cota superior, tenemos que S ≤ S'. Invirtiendo los roles, se tiene que S' ≤ S. Por lo que se concluye que S=S'.
La parte del ínfimo queda de ejercicio.
El supremo de un conjunto es la menor de sus cotas superiores, mientras que el ínfimo es la mayor de sus coptas inferiores.
Notación. Denotaremos el supremo de A (cuando exista) por sup(A) o
sup{x ∈ A}. Por su parte, inf(A) será el ínfimo de A.
Postulado del Supremo
[editar]Nuestro postulado simplemente asegura la existencia de supremos para ciertos conjuntos.
|
Todo subconjunto de los Reales no vacío y acotado superiormente tiene un supremo. |
Sigue de forma inmediata que dado un numera decimal α el conjunto de las truncaciones
es acotado superiormente (por α0+1), por lo que tiene un supremo; que será el número real representado por ese numeral. En breve, cada numeral decimal produce un número real.
Para finalizar, digamos que se puede probar que hay a lo más un cuerpo ordenado completo (que cumpla con el axioma del supremo) y que hay una construcción comenzando con los llamados axiomas de Peano para los Naturales para construir desde cero a un cuerpo ordenado completo. Ver un desarrollo completo en WEB [3].
Finalmente, podemos resumir nuestras suposiciones sobre los Reales en el siguiente enunciado
|
Los Reales son un cuerpo ordenado completo. |
El siguiente resultado será usado frecuentemente.
Proposición 2.4.2. Sea S = sup(A), A un conjunto no vacío. Entonces, para todo número real positivo ε hay un x de A tal que S-ε < x ≤ S.
-
Demostración. En caso contrario, S-ε sería una cota superior de A menor que el supremo; lo que es imposible.
Proposición 2.4.3. Sean A, B subconjuntos de R tales que A ⊂ B y B es acotado superiormente. Entonces, el supremo de A existe y es menor o igual que el supremo de B.
-
Demostración. Por la hipótesis, cualquier cota superior de B es una cota superior de A, por lo que A es acotado superiormente; de donde sabemos, por el postulado del supremo, que A tiene un supremo. Como sup(B) es una cota superior de B, también lo es de A. Luego, sup(A) ≤ sup(B), ya que sup(A) es la menor cota superior de A.
Ejemplo 2.4.3. Este ejercicio servirá para mostrar que hay un número real positivo cuyo cuadrado es igual a 2. Es decir probaremos que √2 es un número real.
Sea A = {x ∈ Q: x ≥ 0, x2 < 2}, es decir el conjunto de los racionales no negativos cuyo cuadrado es menor que 2. Probaremos que A tiene un supremo tal que su cuadrado es 2.
Resolución. Como 1 es un racional positivo tal que 12<2, tenemos que A no es vacío. Notemos que todo x en A debe ser menor que 2, ya que en caso contrario, x ≥ 2 implica que x2 ≥ 4. Por lo que 2, es una cota superior del conjunto A. Por el axioma del supremo, A tiene un supremo, digamos S. Probaremos que S2=2.
Supongamos que S2 < 2. Buscaremos un número 0<h<1 tal que (S+h)2 < 2. La suposición de que h<1 implica que h2<h. Tenemos, entonces que
| (*) |
Resolviendo S2 + (2S+1)h < 2, obtenemos que h < (2-S2)/(2S+1) Por lo que tomando un h satisfaciendo la última desigualdad y que, a la vez, sea menor que 1, obtendremos que (S+h)2 < 2. Luego, S+h sería un elemento de A. Como S+h >S, esto es imposible, porque S es una cota superior de A. Por lo tanto, .
Supongamos, ahora, que S2 > 2. Buscaremos un k>0 tal que S-k sea cota superior de A. Si probamos lo anterior, tendríamos la contradicción de que habría una cota superior menor que el supremo. Por lo que S2 ≯ 2. Por tricotomía, se concluye que S2=2 (ya que no puede ser ni menor ni mayor que 2).
Buscaremos un k > 0 tal que (S-k)2 > 2.
Tomando, k < (S2 -2)/(2S), se tiene que (S - k)2 >2. Si hubiera un x en A tal que x > S-k, entonces x2>(S-k)2 >2, lo que no puede ser. Luego, para todo x en A, x ≤ S-k, o sea S-k es una cota superior de A. Como esto es absurdo, concluimos que .
Consecuencias del Axioma del Supremo
[editar]Consideremos al conjunto de los Naturales, N, como subconjunto de los Reales.
Teorema 2.4.4. Los Naturales no están acotados superiormente.
- Demostración. Supongamos que lo estuvieran. Como el conjunto no es vacío, tendría un supremo, digamos S. Consideremos al número S-1. Debe haber al menos un natural n tal que S-1< n ≤ S, si no S no será la menor cota superior. Pero, S-1< n implica que S < n+1 y, como n+1 es un número natural, esto es imposible ya que S es una cota superior de N. Como hemos llegado a una contradicción, nuestra suposición inicial era falsa, por lo que se tiene lo dicho en la proposición.
Corolario 2.4.5 (Propiedad Arquimediana I). Sea a un número real positivo.
Hay un número natural n tal que a < n.
- Demostración.
Si no lo hubiera, a sería una cota superior de los naturales.
Corolario 2.4.6 (Propiedad Arquimediana II). Sea a un número real positivo.
Hay un número natural n tal que 1/n < a.
- Demostración.
Si no lo hubiera, para todo n>0, se tendría que a≤1/n, de donde n ≤ 1/a, y 1/a sería una cota superior de los Naturales.
Nos referiremos a los resultados de los corolarios como las propiedades arquimedianas.
Proposición 2.4.7. Sea x un número real no negativo tal que para todo n en N+ (Naturales positivos)se cumple que 0 ≤ x < 1/n.
Entonces, x = 0.
- Demostración. Si x > 0, por la propiedad arquimediana habría un natural tal que 1/n < x.
Ejemplo 2.4.4. Probar que el conjunto A = {2n : n natural positivo} no es acotado superiormente.
- Resolución. Probaremos que para todo n ≥ 1, 2n > n. Por lo que si hubiera una cota superior para A, dicha cota sería una cota de los Naturales.
Si n = 1 entonces 21 = 2 > 1. Suponer que tenemos para un k ≥ 1 que se cumple 2k ≥ k.
Entonces, 2k+1 = 2 ∗ 2k > 2k = k +k ≥ k +1. El resultado sigue por inducción.
Ejercicios 2.4
[editar]- Probar los enunciados siguientes.
- Sean A, B subconjuntos de R tales que A ⊂ B y B es acotado, entonces A es acotado.
- Los intervalos con extremos finitos son acotados.
- Un conjunto de números reales es acotado, ssi, está contenido en un intervalo cerrado acotado.
- Hallar el supremo e ínfimo de cada conjunto, cuando existan. Probar sus
afirmaciones.
- A = {x ∈ R : 0 ≤ x < 1}.
- B = N.
- C = {1/n :n natural positivo}.
- D = {x2 − 4x + 7 : x ∈ R}.
- E = {x2 − 4x + 7 : −5 < x < 5}.
- Hallar el supremos e ínfimo (cuando existan) de los siguientes conjuntos.
- {x ∈ R : x2 < 5}.
- {x ∈ R : x2 > 11},
- {0.3, 0.33, 0.333, . . .}.
- Probar que todo subconjunto de los Reales no vacío y acotado inferiormente tiene un ínfimo.
- Sean A y B subconjuntos no vacíos de los Reales disjuntos y cuya reunión es R. Si para todo a en A y b en B se cumple que a ≤ b. Entonces, sup(A) = ínf(B)
- Sea a < 0. Probar que hay un natural n tal que −n < a.
- Sea a < 0. Probar que hay un natural n tal que a < −1/n.
- Sean x, y números reales tales que para todo real positivo r se cumple que
x ≥ y + r.
Entonces, x = y. - Sean A, B subconjuntos de R. Examinar la validez de los siguientes enunciados.
- sup(A ∩ B) ≤ mín{sup(A), sup(B)}.
- sup(A ∩ B) = mín{sup(A), sup(B)}.
- sup(A ∪ B) ≥ máx{sup(A), sup(B)}.
- sup(A ∪ B) ≥ máx{sup(A), sup(B)}.
- Sea In =]- 1/n, 1/n[, n ≥ 0. Sea I la intersección de todos los In. Describir al conjunto I.
- Sea An =]0, n[, n ≥ 1 natural. ¿Cuál es la reunion de todos los An?
- Probar que el conjunto {10n : n ∈ N}, no es acotado superiormente. Hallar conclusiones semejantes a las propiedades arquimedianas para este conjunto.
- Probar que la reunión de los intervalos ]−n, n[, n natural es igual a todo R.
Aproximaciones Racionales de Números Reales
[editar]Parte Entera. Sea a un número real positivo cualquiera. Como los Naturales no están acotados superiormente, habrá un número entero n tal que a < n. Por el Principio del Buen Orden, hay un menor entero positivo con esa propiedad. Llamando m+1 a ese entero, tendremos que se cumple que m ≤ a < m+1. Llamamos parte entera del número a al entero m.
La noción se puede extender a los números negativos y al cero, como lo haremos en la siguiente definición.
Definición. (Parte Entera) Llamamos parte entera de un número real a, al mayor entero que es menor o igual que el número. Notación: .
Observemos que se cumple que . La desigualdad de la izquierda es igualdad, ssi, a es un número entero.
Ejemplo 2.5.1. ⌊5⌋ = 5, ⌊π = 3⌋, ⌊-3.5⌋ = −4.
La noción es bastante clara, solamente para mantener la logicidad de esta exposición,
debemos probar que cada número real a tiene una parte entera. Sea a un número real positivo cualquiera. Como los Naturales no están acotados superiormente, habrá un número entero positivo n tal que a < n. Por el Principio del Buen Orden habrá un menor entero positivo con esa propiedad. Llamando m+1 a ese entero, tendremos que m ≤ a < m+1. Tal m es precisamente la parte entera de a.
Cuando a = 0 su parte entera es 0. ¿Qué pasa cuando a es negativo? Si a es entero, coincide con su parte entera. Si a no es entero es fácil verificar (ejercicio) que su parte entera es igual a -⌊-a⌋ -1.
Densidad de los Racionales
[editar]Sea un número real cualquiera y sea un número entero positivo. Sea la parte entera de . Por lo que tenemos que , de donde
Sigue de lo anterior que
Es decir que la distancia de a es inferior a , por lo que decimos que es una aproximación raciona} al número real con un error de a lo más ( . Lo anterior tiene la siguiente importante consecuencia.
Proposición 2.5.1 (Densidad de los Racionales).
Sea a un número real. Entonces, para todo r>0, hay un racional q tal que
|a-q|<r.
-
Demostración.
Sea r >0 dado. Por la propiedad arquimediana, podemos hallar un n tal que 1/n <r y, en consecuencia, tal que
|a-m/n|<1/n < r.
En otras palabras, dado un número real a, podemos hallar un número racional q que está tan cerca de a como queramos. “Como queramos” quiere decir que podemos escoger r > 0 arbitrariamente pequeño. Este es un resultado de tipo topológico, ya que nos habla de proximidad de puntos de un conjunto. Esta propiedad se conoce como la densidad de los Racionales en los Reales.
La densidad de los Racionales en los Reales tiene una gran cantidad de aplicaciones, entre ellas la posibilidad de computar con los Reales aproximándolos por Racionales. Otra interesante aplicación está contenida en la siguiente proposición.
Proposición 2.5.2. Entre dos números reales, siempre hay un número racional.
- Demostración. Sean a, b números reales tales que a < b. Sea c = (a+b)/2, el punto medio entre a y b.
Sea r = (b-a)/2 (= |c-a| =|c-b|). Entonces, en ]c-r,c+r[, hay un racional q. Luego
Los Reales Extendidos
[editar]Los lectores seguramente habrán encontrado, anteriormente, los símbolos ±∞ de manera informal. Algunas veces, especialmente calculando límites en infinito, podía ser conveniente tratar a ±∞ como “números”. Mostraremos en esta sección como formalmente hacer lo anterior, mediante la introducción de los Reales Extendidos. Se trata de un conjunto denotado por R# y que estará formado por todos los reales (ordinarios) y los símbolos +∞ y −∞. Para nosotros, los Reales Extendidos nos servirán para ilustrar nociones métricas y topológicas que veremos más adelante. A continuación, extenderemos (aunque sea parcialmente) las operaciones de R y el orden de R, a R#.
R# := R ∪ {+∞,-∞}.
Extensión de las Operaciones
[editar]Suponemos válidas para R# la asociatividad y la conmutatividad de la suma y la multiplicación. Igualmente, la distributividad de la multiplicación. Supondremos, además, lo siguiente: para cada número real a se cumple:
| +∞ ± a = +∞ | +∞∗ a = +∞, a > 0 |
| -∞ ± a = −∞ | +∞∗ a = +∞, a < 0 |
| −∞∗ a = −∞, a > 0 | |
| −∞∗ a = +∞, a < 0 | |
| +∞+∞ = +∞ | +∞∗ +∞ = +∞ |
| −∞−∞ = −∞ | −∞∗ −∞ = +∞ |
Además, −∞ < a < +∞. El resto de las combinaciones psobles queda indefinido.
Definiremos también que |+∞| = |-∞| = +∞; y, agregaremos el siguiente convenio
sup(∅) := +-∞, ınf(∅) = +∞.
Cualquier subconjunto no vacío de R# tiene como cota superior a +∞; además cuando se trate de un subconjunto no acotado en R, esa sera su única cota superior, es decir que será su supremo. Análogas observaciones para −∞. Cuando A sea vacío, su supremo será −∞ (Notemos que cuando A es vacío, para todo real a se cumple que x ∈ A =⇒ x ≤ a (Un condicional es siempre válido cuando su antecedente es falso). Análogamente,ınf(∅) = +∞. Sigue de lo anterior, que cualquier subconjunto de R# tiene supremo e ínfimo.
Proposición 2.6.1. Sean A y B subconjuntos no vacíos de R# tales que A ⊂ B. Entonces
ınf(B) ≤ inf(A) ≤ sup(A) ≤ sup(B).
- Demostración. Ejercicio.
Ejercicios 2.6.
[editar]- Probar la proposición 2.6.1.
- Hallar en R# el conjunto solución de
- |x| < 5.
- |x| > 5.
- |x| < +∞.
- |x| > +∞.
Ejercicios del Capítulo 2
[editar]- Sea α un número real cualquiera y sea A =]-∞, α[= {x ∈ R : x < α}.
Probar que
-
a) Si x está en A y y < x entonces y está en A.
b) El conjunto A no es ni vacío ni igual a R.
c) Si x está en A hay un y en A que es mayor que x. - Hallar sup(A) e ínf(A) para cada uno de los siguientes conjuntos.
- A = {x ∈ R : x2 - 4x < 21}.
- A = {x ∈ R : x2 < 5}.
- A = {x ∈ R : x2 > 11}.
- A = {2 + 1/n : n ∈ N}.
- A = {x ∈ R : x2 - 4x < 21}.
- Sea A ⊂ R. s es un supremo de A, ssi, s es una cota superior de A y para todo ε > 0 hay x en A tal que x > s - ε.
- Sea A ⊂ R. m es un ínfimo de A, ssi, s es una cota inferior de A y para todo ε > 0 hay x en A tal que x − ε < m.
- Investigar la validez de los siguientes enunciados.
- Para todo número real x > 0 hay un número irracional y tal que 0 <
y < x.
- Para todo número real x > 0 hay un número irracional y tal que y < x.
- Para todo número real x > 0 hay un número irracional y tal que 0 <
y < x.
- Sea A un conjunto no vacío acotado superiormente de los Reales. ¿Cuáles
de los conjuntos siguientes son acotados superiormente? En caso afirmativo,
cuál es la relación entre su supremo y el supremo de A.
- 5A = {5a : a ∈ A}.
- A + b = {a + b : a ∈ A}, b número real cualquiera.
- A2 = {a2 : a ∈ A}.
- Sean A y B subconjuntos acotados superiormente de los Reales. ¿Cuáles
de los conjuntos siguientes son acotados superiormente. En caso afirmativo,
cuál es la relación entre su supremo y los supremos de A y de B. Repetir
para los ínfimos.
- A ∗ B = {ab : a ∈ A, b ∈ B}.
- −A = {-a : a ∈ A}.
- A ∪ B.
- A ∩ B.
- A ∗ B = {ab : a ∈ A, b ∈ B}.
- Sea f : [0, 1] → [a, b], a < b, tal que f(t) = (b − a)t + a. Probar que
- f es biyectiva con imagen [a, b].
- La restricción de f a ]0, 1[ tiene como imagen a ]a, b[.
- f es biyectiva con imagen [a, b].
- (Biyecciones entre intervalos reales)
- Probar que si A = [a, b] y B = [c, d], a < b y c < d, hay una función
biyectiva de A en B. Además, dicha función se puede escoger de modo
que preserve el orden (s, t ⇒ f(s) < f(t)).
- (♠) Sea f : R → R tal que f(t) = arctan(t). Probar que f es biyectiva con imagen ]-π/2, π/2[.a) 5A = {5a : a ∈ A}.
- Probar que si A = [a, b] y B = [c, d], a < b y c < d, hay una función
biyectiva de A en B. Además, dicha función se puede escoger de modo
que preserve el orden (s, t ⇒ f(s) < f(t)).
Referencias
[editar]
Los Espacios Normados
[editar]En este capítulo presentamos varios ejemplos de espacios provistos de una noción de distancia. Uno de los ejemplos más importantes es toda una familia de espacios que nos acompañará a lo largo de este texto: los espacios Euclídeos n--dimensionales, . Además de la métrica o distancia euclídea tradicional, veremos que hay otras posibles distancias en esos conjunto.
Usaremos la noción de norma (generalización del valor absoluto de los Reales) para definir la noción abstracta de espacios normados, que incluirán como ejemplos a los , y a algunos espacios de funciones. La distancia en esos espacios está definida en total analogía a la distancia en los Reales a partir del valor absoluto.
Nuestro principal interés reside en los espacios vectoriales $\Rn$ con la norma euclídea, pero también exploraremos otros espacios, especialmente algunos espacios de funciones.
Los Espacios Rn
[editar]Los espacios Rn aparecen inicialmente en los cursos de Cálculo Vectorial (o de varias variables) y en los cursos de Álgebra Lineal.
El conjunto Rn está formado por todas las n--uplas ordenadas de números reales, a las que, usualmente representaremos como (x1,x2, ... , xn), o simplemente por (xi), o cuando necesitemos especificar el valor de n.
Cuando x = (xi), los números que aparecen en la n--upla se llaman las coordenadas de x, recibiendo los nombres de primera, segunda, ... , i--ésima, ... , n--ésima coordenada para x1, x2, ... , xi, ... , xn respectivamente.
El caso más simple es R1, que identificaremos con los Reales. Por su parte, R2 se puede identificar con el plano cartesiano usual; etc.
- La regla de oro en el trabajo con los espacios Rn es considerar el caso n = 2. Si uno entiende lo que pasa en ese caso, resultará, a menudo, fácil de entender el caso general.

Observemos, de partida, que las n--uplas presentan una doble personalidad: puntos y vectores. Consideremos el caso de R2; allí un par ordenado representa,
por una parte, a un punto del plano y, por la otra, a la punta de una flecha que comienza en el origen, en cuyo caso hablamos de vector. Los vectores a diferencias de los puntos tiene largos asociados (el largo de la flecha). Normalmente, hablamos de puntos cuando se trata de nociones geométricas, mientras que hablamos de vectores para consideraciones algebraicas. En consecuencia, en este texto la mayoría del tiempo hablaremos de puntos.
La Estructura de Espacio Vectorial
[editar]Podemos proveer a los conjuntos Rn con dos operaciones algebraicas: la suma de vectores y la multiplicación por un escalar (en este contexto, se llama escalares a los números reales). Las operaciones se definen como operaiones en las coordenadas.
Recordemos que cuando x=(xi), y=(yi) son vectores de Rn, decimos que x=y, cuando se cumple que xi=yi, para todo i=1, ... , n.
Sean x=(xi), y=(yi) dos vectores de Rn, a un escalar.
Ejemplo 3.1.1. En R3 tenemos que:
- (3,-2,0,1) + (4,3,-2,5) = (7,1,-2,6).
- 4(3,-2,0,1) = (12,-8,0,4).
Propiedades Básicas de la Suma. La suma es asociativa, conmutativa, tiene neutro al vector nulo o cero u origen (el vector cuyas coordenadas son todas cero), y para cada vector x = (xi) hay un opuesto aditivo, -x=(-xi) tal que x + (-x) =0.
Propiedades básicas de la multiplicación por escalar. Sean x, y vectores, a y b escalares. Se cumple que:
- (a+b)x = ax +bx.
- (ab)x = a(bx)
- 1x = x.
- a(x+y) = ax + ay.
Las propiedades son fáciles de recordar y de aplicar, ya que semejan a las propiedades usuales de la suma y la multiplicación. En los ejercicios, al final de la sección, se pide probar formalmente dichas propiedades. Para ilustrar como proceder, probaremos la asociatividad de la suma de vectores.
Para todo x=(xi), y=(yi) y z=(zi) se cumple que (x + y) + z = x + (y + z).
- Demostración. (Idea: Evaluar ambos lados y comparar)
Por la asociatividad de la suma de los números reales, los dos vectores al final de las líneas son iguales—ya que tienen iguales coordenadas, lo que prueba que los vectores al comienzo de las líneas son iguales. Lo que concluye la prueba de la asociatividad de la suma
Las propiedades indicadas de suma y multiplicación en Rn se abstraen en la siguiente definición.
Definición. (Espacio Vectoriales) Llamamos espacio vectorial a un trio donde E es un conjunto, + es una suma en E, y es una multiplicación por escalares, tales que satisfacen las propiedades básicas de la suma y de la multiplicación por escalar dadas más arriba.
- Los espacios Rn con las operaciones definidas arriba son espacios vectoriales.
- Sea el conjunto de todas las matrices de tamaño m x n con entradas números reales. La suma de matrices junto con la multiplicación por constante (escalar) proveen a dicho conjunto con una estructura de espacio vectorial. Poniendo las filas una tras otra, vemos que podemos considerar a como Cuando m = n (matrices cuadradas) hay definida, además, una multiplicación que es distributiva respecto a la suma; por lo que hablamos de una álgebra de las matrices. (álgebra = espacio vectorial + multiplicación distributiva)
El Álgebra Lineal es el área de las matemáticas que estudia a los espacios vectoriales. En este texto, necesitaremos solamente algunas propiedades elementales que recordaremos oportunamente, aunque es recomendable tener un texto de Álgebra Lineal a mano, para consultas.
Definición. (Subespacio vectorial) Sea E un espacio vectorial. Un subconjunto no vacío H de E determina un subespacio de E cuando con las operaciones restringidas a H tiene una estructura de espacio vectorial. Tal evento pasa cuando H es cerrado respecto a la suma (suma de vectores en H están en H) y a los múltiplos por escalares ( producto de cualquier escalar por elementos de H) están en H. Notación: H < E.
Ejemplo 3.1.2. Sea E = R3 y H = {(x1,x2,x3) : x3 = 2x1 + 3x2 }. Probar que H es un subespacio vectorial de R3.
Resolución. El subconjunto H no es vacío porque (0,0,0) es claramente un elemento de H. Sean x = (x1,x2,x3) y y=(y1,y2,y3) elementos de H, o sea que x3 =2x1+3x2, y y3=2y1+3y2. Entonces, x + y = (x1 +y1, x2 + y2, x3 + y3) y x3 + y3 = 2x1+3x2 + 2y1+3y2 = 2(x1+y1) + 3(x2+y1), lo que prueba que x + y está en H. Análogamente, como ax3 = a(2x1+3x2) = 2(ax1)+3(ax2), tenemos que ax está en H. Conclusión: H < R3.
Ejemplo Trabajaremos en R3. Sean e1 := (1,0,0), e2:=(0,1,0) y e3:=(0,0,1). Sea x=(x1,x2,x3) un vector cualquiera de R3, entonces,
El resultado del cómputo anterior se expresa diciendo que cualquier vector de R3 es una combinación lineal de e1, e2, e3.
El ejemplo anterior se generaliza de la siguiente manera.
Combinaciones lineales, Bases. Sea E un espacio vectorial cualquiera. Sea {f1, f2, ... , f_k} una familia finita de vectores.
- Decimos que un vector x de E es una combinación lineal de los
fi's, cuando hay escalares ai, con 1 ≤ i ≤ k, tales que:
- Decimos que la familia f1, ... , f_k es una base del espacio E, ssi, cada vector del espacio puede representarse como una combinación lineal de los f_k's, de una única manera.
El ejemplo anterior muestra que {e1, e2, e3} es una base de R3.
Resultados del Álgebra Lineal
- Cada espacio vectorial tiene una base.
- Dos bases de un mismo espacio tienen igual cantidad de elementos. Dicha cantidad se llama la dimensión del espacio.
- Los espacios Rn tienen a los vectores e1, ... , ei, ... en como una base, donde ei es un vector cuyas coordenadas son todas nulas, excepto la i--ésima que es 1. Luego, la dimensión de Rn es n.
- Nuestro interés principal reside en los espacios vectoriales Rn, que son el modelo de todos los espacios cuya dimensión es finita. Hay, sin embargo, espacios vectoriales que no tienen dimensión finita, por lo que decimos que tiene dimensión infinita. Más adelante encontraremos ejemplos de tales espacios.
Transformaciones Lineales. Una transformación lineal de un espacio vectorial E en un espacio vectorial F es una función L : E → F tal que
- (i) L(x + y) = L(x) + L(y)
- (ii) L(αx) = αL(x),
para todo x, y en E, y escalares α, β.
Cuando una transformación lineal es biyectiva como función, se verifica que su inversa es lineal. En tal situacíón, llamamos isomorfismo lineal a la transformación.
Resultados del Álgebra Lineal
- La imagen por una transformación lineal de un subespacio es un subespacio,
- La preimagen por una transformación lineal de un subespacio es un subespacio.
- La preimagen de {0} se llama el núcleo de la transformación. Notación: ker(L).
- La composición de transformaciones lineales es una transformación lineal .
- La imagen por un isomorfismo de la base de un espacio es una base de la imagen del espacio.
- Cualquier espacio de dimensión n es isomórfico a Rn.
Teorema 3.1.1 (Teorema Fundamental del Álgebra Lineal). Sea L : E → F lineal. Entonces,
Ejercicios 3.1.
[editar]- Probar las propiedades básicas de la suma de vectores en Rn
- Probar las propiedades básicas de la multiplicación por escalar en Rn.
- Sea H = {(x,y) ∈ R2 : y=x}. Probar que H es un subespacio de R2.
- Sea E un espacio vectorial cualquiera. Usar las propiedades básicas de
espacio vectorial para probar los enunciados siguientes.
- Si x + x = x entonces x = 0 (vector nulo).
- Si a = 0 entonces ax = 0.
- Si ax = 0 entonces a = 0 o x = 0.
- Si x + y = 0 entonces y = -x.
- a(-x) = -ax.
- Probar que los ei's forman una base de Rn.
- Sean f1 = (1, 1, 0), f2 = (1, 0, 1) y f3 = (0, 1, 1). Sea v = (−1, 6, 1). Hallar escalares t1, t2, t3 tales que v = t1f1 + t2f2 + t3f3.
- Probar que L : R2{s,t} → R3 tal que L(s, t) = (3s−2t, 2s+t, 5s−t) es una transformación lineal.
- La imagen de una combinación lineal por una transformación lineal es una combinación lineal.
Los Espacios Euclídeos
[editar]Los espacios euclídeos son las generalizaciones n–dimensionales del plano y Del espacio tridimensional de la Geometría Clásica. Las nociones principales son: norma, distancia y producto interior.
La Norma Euclídea
[editar]
Consideremos el plano R2 y un vector v = (a,b) del plano. Mirando a la figura, vemos que podemos computar el "largo" de la flecha usando el teorema clásico de Pitágoras. Así, obtendremos que
Inspirados en la relación anterior definiremos "largo" para vectores en Rn.
Definición. (Norma de un Vector) Sea x=(xi) un vector de Rn. Llamamos norma de x o largo del vector x al número real denotado por y definido como
Claramente, la definición es una generalización de lo que obtuvimos para R2. Notemos, además, que si aplicamos la definición con n=1, o sea a los Reales, obtenemos que
Es decir que podemos considerar a la norma como una generalización del valor absoluto usual. Dicha consideración se ve reforzada por las siguientes propiedades, que se cumplen para todo vector x y escalar a:
Proposición 3.2.1. (Propiedades de la Norma)
- N1. , para todo vector x.
- N2. , ssi, x=0.
- N3. .
- N4. .
Las propiedades siguen de forma inmediata de la definición. Por ejemplo para N3 tenemos que
Para completar el parecido con el valor absoluto necesitamos que se cumpla la desigualdad en N4 , llamada desigualdad de Minkowski.
Verificaremos que esa desigualdad es válida. Una demostración usará la noción de producto interior que veremos en la próxima sección.
El Producto Interior
[editar]Introduciremos la noción de producto interior que nos ayudará a desarrollar una variedad de cosas interesantes.
Definición. (Producto Interior) Sea E un espacio vectorial. Un producto interior en E es una función que envía el par (x,y) en el número real simbolizado por que es bilineal, simétrica y positivamente definida. Es decir que
- PI1.
- PI2.
- PI3. (Simetría)
- PI4. , cuando (Definición positiva)
Las condiciones PI1 y PI2 especifican la linealidad en el primer argumento; por la simetría se tiene la linealidad en la segunda variable; de donde lo bilineal.
Producto Interior Canónico
[editar]Es posible definir varios productos interiores para Rn, sin embargo para nuestos propósitos bastará con aquel llamado producto interior canónico que definiremos a continuación. Además, en los cursos de Álgebra Lineal se prueba que todos los productos interiores son, en un cierto sentido, equivalentes a dicho producto interior.
|
|
(Tradicionalmente, se usa en vez de para el producto interior canónico, por lo que algunas veces se le llama también el "producto punto".)
Notemos inmediatamente que coincide con el cuadrado de la norma de x definida arriba.
Para probar la desigualdad de Minkowski, desarrollaremos algunos resultados previos.
3.2.2 (Cuadrado del Binomio). Sean x, y vectores de Rn,
- Demostración.
Corolario 3.2.3. El producto interior puede expresase en términos de los largos.
Proposición 3.3.4 (Desigualdad de Cauchy—Schwarz). Sean x, y vectores de Rn.
-
Demostración.
Sea w = tx + y, t un número real. Usando el tenemos que
Observemos que la expresión de la derecha se puede considerar como una expresión cuadrática en t. Como las normas nunca son negativas, tal expresión cuadrática nunca es negativa, lo que implica que su discriminante nunca es positivo, es decir que
de donde, .
Dividiendo por 4 y tomando raíz cuadrada en ambos lados de la desigualdad, obtenemos el resultado deseado.
Proposición 3.2.5 (Desigualdad de Minkowski).
Sean x, y vectores de Rn.
-
Demostración.
Tomando raíz cuadrada en ambos lados, obtenemos el resultado deseado.
Norma y Distancia Euclídea
[editar]Norma Euclídea. Llamamos norma euclídea de Rn a la norma estudiada arriba, esto es
La distancia Euclídea en Rn
Usando la norma euclídea, podemos definir "distancia"" entre puntos x, y en total analogía a la distancia en R , o sea como la norma de la diferencia entre x y y. Es decir que la distancia euclídea entre x y y será
- Geométricamente, la distancia de x a y es el largo de x-y, o sea el largo del segmento que une x con y.
Usando las propiedades de norma, se verifica que la definición anterior tiene
formalmente las propiedades de la distancia en los Reales ( la demostración de lo anterior es totalmente análoga a la proposición 2.3.3, reemplazando valor absoluto por norma).
Propiedades de la Base Canónica.
Notemos que los vectores de la base canónica de Rn, {e_1, e2, ... , en}, satisfacen lo siguiente:
- cada ei es un vector unitario, o sea .
- el producto interior entre dos vectores diferentes es 0.
Bases con esas propiedades se llaman bases ortonormales.
Algunos nociones de la Geometría Euclídea
[editar]Revisaremos brevemente algunas nociones de la Geometría Euclídea. Sea E = Rn (se prueba que cualquier espacio vectorial de dimensión n es esencialmente (isomórfico) a Rn).
Sea L : E → F una trasformación lineal. Sea b un elemento de F, se prueba en cursos de Álgebra Lineal que la ecuación L(x) = b tiene como conjunto solución, cuando hay al menos una solución xp a un conjunto de la forma
| x_p + ker(L). |
La solución xp es una solució particular y los elementos del núcleo son las soluciones de la ecuación homogénea asociada L(x) = 0. Tales conjuntos soluciones son llamados variedades (afines).
Variedades. Una variedad lineal de dimensión r de E es un subconjunto V de la forma
a + H, donde H es un subespacio vectorial de E de dimensión r. Esto equivale a decir que hay una base {v1, ... , vr} de H, tal que que cada elemento x de V = a + H puede escribirse de la forma
para escalares únicos α1, ... , αr.
Cuando V = a + H decimos que H es la dirección de V y a es un punto por donde pasa la variedad.
Paralelismo, Dos variedades son paralelas cuando la dirección de una está contenida en la otra.
Variedades especiales. Una variedad de dimensión 1 (resp.2) se llama línea (resp. plano).
Sea L una línea, digamos que L = {x ∈ E : x = a + αv, v ≠ 0,α en R }. Entonces,
una línea M := {x ∈ E : x = b + βw,w ≠ 0} es paralela a L, ssi, w es un
múltiplo escalar de v. Simbolizaremos a la línea L superior como L : a + αv.
Notemos que cuando b es un punto de L diferente de a, b = a + αv, para algún vector no nulo v. Entonces, b−a = αv, lo que nos dice que la línea L′ : a+β(b−a) es paralela a L y pasa por a, lo que implica que L = L′. Es decir que la única línea que pasa por a y b es La,b : a + α(b − a).
Notemos que z ∈ La,b ⇐⇒ z = a + t(b − a), para un cierto escalar t, o sea, ssi, z = (1 − t)a + tb.
Observemos que si ponemos x(t) = (1−t)a+tb podemos pensar la ecuación de definición de La, b como especificando la trayectoria de un móvil que está al tiempo t en x(t). Notemos que x(0) = a y x(1) = b. Por lo que a tiempos 0 < t < 1, x(t) está entre a y b. El segmento que une a con b es
Perpendicularidad.
Decimos que dos vectores son ortogonales o perpendiculares cuando su producto interior es nulo.
Dos variedades son ortogonales, cuando cada vector de la dirección de una es perpendicular a un vector de la dirección de la otra.
Por ejemplo, los vectores de la base canónica de Rn son mutuamente ortogonales
Ángulo entre vectores
Sigue de la desigualdad de Cauchy, ver 3.2.2. que
−||x|| ||y|| ≤ x · y ≤ ||x|| ||y||.
De donde, cuando x y y no son nulos se tiene que
Luego, podemos definir el ángulo entre el vector x y el vector y como
|
|
Finalmente, revisemoos un resultado clásico.
Proposición 3.2.6 (Teorema de Pítágoras). Sean A, B y C los vértices de un triángulo tal que los lados B-A y C-B son ortogonales. Entonces,
- Demostración.
Aplicando el teorema del binomio, tenemos que
Ejercicios 3.2
[editar]- Hallar la distancia (en R3 del punto (1, 1, 1) a (3, 4, 5).
- Mostrar que si y = tx, t escalar no nulo (o sea geométricamente, ambos son vectores en una línea que pasa por el origen), entonces ||x+y|| = ||x||+||y||. ¿Es válido el recíproco?
- Probar que | ||a|| − ||b|| ≤ | ≤ ||a − b||.
- Probar, usando cuadrado del binomio, que en Rn se cumple que
- (Ley del Paralelogramo)
- .
- Sea d la distancia euclídea de Rn. Probar las siguiente afirmaciones usando
solamente las propiedades de la norma euclídea. Para todo x, y y z.
- (D1) d(x, y) ≥ 0.
- (D2) d(x, y) = 0, ssi, x = y.
- (D3) d(y, x) = d(y, x).
- (D4) d(x, y) ≤ d(x, z) + d(z, y). Desigualdad Triangular.
- Sean sucesiones finitas de números
- .
- .
- .
(Sug: Después de lo hecho en esta sección, los resultados deben ser fáciles de probar.)
Los Espacios Normados
[editar]Generalizaremos la noción de norma vista para Rn, usando como base las propiedades de la prroposición 3.2.1
Definición. (Espacio Normado) Llamamos espacio normado a un espacio vectorial E provisto de una función de E en los Reales, tal que para todo x, y vectores, a escalar, se cumple que
- N1.
- N2. , ssi, x=0.
- N3. .
- N4. .
Asociamos con cada norma, una distancia .
Proposición 3.3.1. Sea E un espacio normado. La distancia tiene las siguientes propiedades, para todo x, y se cumple que:
- D1. .
- D2. , ssi, a=b.
- D3. . (Simetría)
- D4: . (Desigualdad Triangular)
- Demostración. Ejercicio.
El ejemplo básico de espacio normado es Rn con la norma euclídea. Sin embargo, como veremos más adelante hay otros espacios normados. A continuación, veremos otras normas posibles para Rn.
Es posible que, por nuestra experiencia con la geometría elemental, nos parezca que la norma y la distancia euclídea son la manera más natural de definir esas nociones. Sin embargo, como veremos en esta sección, es posible definir otras normas y distancias asociadas con ellas, que son diferentes del caso euclídeo, pero que son útiles en algunas consideraciones.
La Norma--ciudad
[editar]
Consideremos la situación ilustrada en la figura lateral, que Consideraremos como la representación del plano de una ciudad. ¿Cuál es la distancia entre el punto A y el punto B? Computando la distancia euclídea obtenemos una posible respuesta, que es correcta desde el punto de vista de la geometría euclídea; pero, si preguntáramos cuántos bloques debo caminar para ir de A hasta B, la distancia euclídea no sería la respuesta correcta. Una mejor respuesta consistiría en sumar la cantidad de bloques caminando (en la dirección horizontal del mapa) más la cantidad de bloques caminando verticalmente. Es decir,
Inspirados en estas consideraciones, definiremos una nueva norma en Rn, a la que nos referiremos como norma--ciudad.
Es fácil probar que se cumplen las propiedades N-1 a N-4 de normas. La desigualdad de Minkowski proviene de la desigualdad triangular del valor absoluto. Asociada con esa norma, tendremos una distancia
La Norma--maxima
[editar]Pensemos en un rectángulo y los vértices de una de sus diagonales. La distancia euclídea es el largo de esa diagonal. La distancia--ciudad (d_c) es la suma del largo más el ancho. Ahora introduciremos una distancia a la que solamente le interesa cuál es es el lado más largo. Comenzamos con la definición de una norma, para luego pasar a la distancia asociada.
Sean x, y vectores de Rn.
Nuevamente, tenemos que se cumplen trivialmente las propiedades N-1 a N-3 de normas. Para N4, tenemos que
de donde obtenemos que
Como consecuencia, tenemos también una distancia (máxima)
Notación. En este contexto, cuando estemos considerando varias normas o
distancias en Rn, denotaremos por ||*||_e a la norma
euclídea definida anteriormente, d_e será la correspondiente distancia.
Ejemplo 3.1.3. Sean x = (1,2,3), y = (3,-2,4). Entonces,
- .
- .
- .
Ejercicios 3.3
[editar]- Sean x1, x2, ... , xn, y1, y2, ... , yn, z1, z2 , ... ,.
zn sucesiones finitas de números reales. Probar que
- .
- Sea E = Rn. Probar que para todo x en Rn se cumple que:
- a) ||x||max ≤ ||x||ciudad ≤ n||x||max.
- b) ||x||max ≤ ||x||euclídea ≤ √n||x||max.
- (La distancia dp) Se puede verificar que la siguiente definición provee a Rn con una norma. Sea p un entero positivo,
Verificar que cuando p=1 (resp. p=2) obtenemos la norma--ciudad (resp. norma euclídea) vista anteriormente. Los detalles (para la desigualdad de Minkowski) son eleborados, por lo que no los incluimos aquí. Ver Kolmogoroff [7].
Espacios de Funciones
[editar]El objetivo de esta sección es mostrar que además de los Rn, hay otros espacios normados. En cursos de Cálculo y otros previos, considerábamos funciones desde un intervalo [a,b] en los Reales. Para tales funciones había definidas sumas, productos y multiplicación por constantes; tales operaciones aparecían en teoremas tales como "la derivada de la suma de dos funciones es igual a ... ",.
Generalizaremos esas consideraciones a funciones con valores reales, pero con un dominio cualquiera.
Sea X un conjunto no vacío. Simbolizaremos por F(X,R ) al conjunto formado por todas las funciones de X en R . Se definen operaciones de suma, multiplicación y multiplicación por constantes (números reales) punto a punto. Es decir tales que
F(X,R ) con las operaciones indicadas tiene una estructura de espacio vectorial con multiplicación (álgebra de funciones).
Una función f: X → R es acotada cuando hay un número M (cota) tal que para todo x en X se cumple que |f(x)| ≤ M. Las funciones constantes siempre son acotadas. Simbolizaremos por B(X,R ) el subconjunto de F(X,R) formada por las funciones acotadas. Sean f y g funciones acotadas con cotas M_f y M_g respectivamente. Entonces, para todo x en X se cumple que
- , lo que muestra que f+g es acotada.
- , lo que prueba que af es acotada.
Los resultados anteriores implican que B(X,R) es un espacio vectorial, subespacio de F(X,R).
Una propiedad fundamental de los Reales es que cada conjunto no vacío acotado superiormente tiene un supremo (= cota superior estricta o menor cota superior). Definiremos, para f en B(X,R),
Proposición 3.4.1.
La función es una norma en B(X,R).
- Demostración.
Sean f y g funciones en B(X,R).
(N1)Como tomamos supremos de un conjunto de números no negativos, dicho supremo nunca negativo, por lo que se cumple N-1, ||f|| ≥ 0.
(N2)Si ||f||= 0, quiere decir que todos los |f(x)| son nulos, es decir que f(x) \equiv 0. o sea que f=0. La otra mitad de N-2, es trivial.
(N3) |af(x)| = |a| |f(x)| ≤ |a| ||f(x)|| y |a| |f(x) = |af(x)| ≤ ||af|| implican que ||af|| = |a| ||f(x)||.
(N4) |f(x) + g(x)| ≤ |f(x)|+ |g(x)| ≤ ||f|| + ||g||, luego ||f+g|| ≤ ||f|| + ||g||.
Sucesiones. Una sucesión (de números reales) es una familia de números reales con conjunto de índices igual a los Naturales. Una sucesión es, por lo tanto, una función de N en R tal que tradicionalmente, escribimos en lugar de s(n). Luego, el conjunto de todas las sucesiones de números reales es F(N,R).
sigue de lo anterior que las sucesiones acotadas determinan un subespacio que es un espacio normado para la norma ||(s_n)|| := sup{|sn|:n \in R}.
Se puede verificar qu el espacio de las sucesiones no tiene una base finita., por lo que es un espacio de dimensión infinita.
Ejercicios 3.4
[editar]- Verificar que F(X,R ) es un espacio vectorial con una multiplicación distributiva con respecto a la suma.
- Hallar la norma de las siguientes funciones en F([0,1],R ).
- .
- Sea X = R, ¿cuáles de las siguientes funciones son acotadas sobre
X? En caso afirmativo, ¿cuál es su norma?
- .
- Hallar la norma de las siguientes sucesiones, cuando sean acotadas.
- 1/2, 2/3, 3/4, 4/5, ....
- 1/2, 1/4, 1/8, 1/16, ....
- 1, 2, 4, 8, 16, ....
- 0.9, 0.99, 0.999, ...
Los Números Complejos
[editar]Los números complejos son expresiones de la forma donde y son reales, el número es tal que (la unidad imaginaria). La correspondencia permite identificar al conjunto de los complejos, , con , lo que será útil para muchas consideraciones acerca de los complejos.
Hay definidas operaciones de suma y multiplicación en que lo proveen con una estructura de cuerpo; pero tal cuerpo no es ordenado, ya que hay cuadrados de complejos que son negativos.
Se define una valor absoluto en los complejos, también llamado \textit{módulo} en este contexto, por
Notemos que usando la identificación anteriormente mencionada, dicho valor absoluto coincide con la norma euclídea en .
Hay toda una teoría de espacios vectoriales con escalares complejos cuyos prototipos de dimensión finita son los espacios , -uplas de números complejos. Dichos espacios pueden identificarse de manera natural con
Cada número complejo , tiene asociado un conjugado, .
Se cumple, para todo par de complejos , que
- a)\
- b)\
- c)\
Notemos que cuando es real, o sea cuando , se cumple que , por lo que se puede eliminar el subíndice , sin problemas.
Hay un producto "interior" definido en llamado producto hermitiano,
cuyos valores son números complejos y tiene propiedades básicas análogas al producto interior de los espacios reales, excepto que
Cada , , es un espacio normado con norma . Cuando identificamos con dicha norma coincide con la norma euclídea de .
Ejercicios del Capítulo 3
[editar]- Sea E un espacio normado para todo a en E, sea τa la
función de E en si mismo que envía x en a+x (traslación por a).
Probar que τa preserva distancia entre puntos,
- Sea E=R2. La línea que pasa por p y q es el
conjunto de puntos x tales que x = p + t(p-q), t \in R . Esta es la trayectoria de un móvil que al tiempo t=0 está en p y que se mueve con velocidad dada por q-p.
El punto x está entre p y q cuando 0 < t < 1.
- Probar que cuando x está entre p y q se cumple que d(p,q) = d(p,x) + d(x,q), para cualquier norma de R2.
- Cuando la norma es euclídea, si x no está entre p y q, la desigualdad triangular con punto intermedio x es estricta, d(p,q) < d(p,x) + d(x,q). (Sug. Usar teorema de Pitágoras.)
- (Norma--ciudad) Sean A=(0,0) y B=(4,3). Probar que si C=(x,y) tal que 0 ≤ x ≤ 4 y 0 ≤ y ≤ 3, entonces dc(A,B) = dc(A,C) + dc(C,B).
- (Norma--max) Sean A=(0,0) y B=(4,3). Hallar puntos C tales que . Verificar que (2,1) es uno de esos puntos.
- ¿Qué pasa si reemplazamos R2 por Rn o por un espacio normado cualquiera?
- Probar la identidad de Lagrange
(Sug: la prueba es puramente algebraica,tratar primero el caso n = 2.) - Sean a1 ≥ a2 ≥ ··· ≥ an y b1 ≥ b2 ≥ ··· ≥ bn. Probar que
Los Espacios Métricos
[editar]Introducción
[editar]Un espacio métrico es básicamente un conjunto provisto con una (noción de) distancia, formalmente semejante a aquella de los espacios normados vistos en el capítulo anterior. Los espacios métricos son una abstracción de dichos espacios y de otras situaciones que irán apareciendo en este capítulo y los siguientes.
Daremos primeramente una definición abstracta de espacio métrico, para luego examinar algunas de sus propiedades básicas.
Las Definiciones Básicas
[editar]Definición. (Métrica, Distancia}) Una métrica o distancia en un conjunto E es una función d:E x E → R tal que para todo x, y, z en E se cumple que
- D1 d(x,y) ≥ 0. (la distancia entre dos puntos nunca es negativa).
- D2 d(x,y) = 0, ssi, x=y.
- D3 d(x,y) = d(y,x). (simetría)
- D4 d(x,y) ≤ d(x,z) + d(z,x). (desigualdad triangular)
Definición. (Espacio Métrico) Un espacio métrico es un par <E,d> donde E es un conjunto no vacío y d es una distancia (métrica) en E.
Cuando no haya riesgo de confusión sobre la distancia envuelta, podremos hablar simplemente del espacio métrico E, en vez de <E,d>.
Ejemplos de Espacios Métricos
[editar]- Los Reales, ℝ con la distancia definida a partir del valor absoluto, d(s,t) := |s -t| . Nos referiremos a este espacio como la línea real.
- Los diferentes espacios normados en Rn con la distancia asociada con la norma. Este ejemplo muestra la necesidad de, algunas veces, de usar el par <E,d>, ya que puede haber diferentes métricas en un mismo conjunto. (Convenio.) Cuando no especifiquemos la norma o distancia de Rn, siempre supondremos que se trata del espacio Euclídeo .</math>
- Los Complejos y los con la métrica deducida de su norma hermitania.
- En general, cualquier espacio normado tiene asociada una distancia que los hace un espacio métrico
- (Espacio Discreto) Cualquier conjunto no vacío admite trivialmente una métrica, definiendo para todo , Llamaremos espacio discreto a este espacio métrico. Los espacios discretos tienen importantes aplicaciones a pesar de su aparente carácter artificial. Algunas veces nos referiremos a este espacio como el espacio con la métrica 0--1. Notemos que esta métrica, en el caso de , no puede provenir de una norma, ya que tal norma no cumpliría la propiedad N3,
Subespacios.
[editar]Sea <E,d> un espacio métrico y sea X un subconjunto no vacío de E . Si restringimos la metrica a X obtenemos un espacio métrico <X, d'>, donde d' es la restricción de d a X x X. Diremos que ese espacio es un subespacio (métrico) de E .
- Cada intervalo (abierto, cerrado, acotado o no acotado) de la línea real es un espacio métrico que es un subespacio de la línea real
- Los Racionales, Q, determinan un subespacio de los Reales.
Notemos que estos ejemplos, aunque corresponden a subconjuntos de un espacio normado, no determinan un espacio normado. En ambos casos, la multiplicación de un escalar por un elemento del espacio puede acabar fuera del espacio.
En general, las propiedades métricas o topológicas de subespacios pueden ser bastante diferentes de aquellas del espacio total. Por ejemplo, un intervalo [a,b] de los Reales es un espacio métrico acotado, mientras que el conjunto de los reales no lo es.
Veamos, a continuación, una proposición simple, pero con una importante propiedad de las métricas. Proposición 4.2.1. Sean x, y, z, w en E, entonces
Demostración.
- Aplicando la desigualdad triangular, tenemos que
- (1) d(x, y) ≤ d(x, z) + d(z, y), y
- (2) d(z,w) ≤ d(z, y) + d(y,w).
- (1) y (2) ⇒ d(x, y) − d(z,w) ≤ d(x, z) + d(y,w) (*)
- (3) d(z,w) ≤ d(z, y) + d(y,w) ⇒ d(z,w) − d(z, y) ≤ d(y,w).
- (4) d(x, y) ≤ d(x, z) + d(z,w) ⇒ d(x, y) = d(z,w) ≤ d(x, z).
- (3) y (4) ⇒ d(z,w) − d(x, y) ≤ d(x, z) + d(y,w). (**)
- De (*) y (**), concluimos que
- −d(x, z) − d(y,w) ≤ d(x, y) − d(z,w) ≤ d(x, z) + d(y,w).
- Lo que implica el resultado.
Corolario 4.2.2. Sean x, y, z puntos de un espacio métrico E. Entonces,
|d(x, z) − d(y, z)| ≤ d(x, y).
Demostración. Ejercicio.
Isometrías
[editar]Definición. (Isometría) Sean <E,d> y <E',d'> espacios métricos. Llamamos isometría de E en E' a una función biyectiva f de E en E' que preserva la distancia entre puntos. Esto es, para todo x, y en E, se cumple que:
Ejemplo 4.2.1. Cuando d es una métrica en un espacio, k veces d es también una
métrica. Ver ejercicio 2 al final de la sección.
Sean E = R2, d la métrica euclídea y d′ = 6d. La función f :< E, d′ > → < E, d > tal que f(x, y) = (6x, 6y) es una isometría.
- d(f(x, y), f(u, v)) = d((6x, 6y), (6u, 6v)) = ||(6x − 6u, 6y − 6v)||
- = 6||(x − u, y − v)|| = 6d((x, y), (u, v)) = d′((x, y), (u, v)).
- d(f(x, y), f(u, v)) = d((6x, 6y), (6u, 6v)) = ||(6x − 6u, 6y − 6v)||
Proposición 4.2.3. La composición de isometrías es una isometría. La inversa de una isometría es una isometría. Demostración.
- Sean f : E → E′ y g : E′ → E′′ isometrías. Entonces, para
todo x, y en E se cumple que
- d(g(f(x)), g(f(y))) = d(f(x), f(y)) ya que g es isometría
- = d(x, y) ya que f es isometría
- d(g(f(x)), g(f(y))) = d(f(x), f(y)) ya que g es isometría
- Lo que prueba que la composición de una isometría.
- Sea h la función inversa de f, entonces
- d(h(x′), h(y′)) = d′(f(h(x′)), f(h(y′)) = d′(x′, y′).
- Lo que prueba que h es una isometría.
Observación 4.1. (♠) En Geometría se denomina grupo de transformaciones de un espacio X a un subconjunto no vacío G de biyecciones del conjunto que es cerrado respecto a la composición (la composición de dos funciones de G está en G) y cerrado respecto a tomar inversos (la inversa de una función de G está en G). La proposición anterior aplicada al conjunto de isometrías de un espacio métrico E en si mismo, Iso(E), muestra que forman un grupo de transformaciones de E. Cuando E = R2, dicho grupo es el grupo de las congruencias o grupo Euclídeo de la Geometría plana clásica.
Traslaciones en un Espacio Normado. Sean un espacio normado y un elemento de . Llamamos traslación por a, a la función de en si mismo que envía cada punto en <m>a+x</math>.
Proposición 4.2.4.
Las traslaciones son isometrías en cualquier espacio normado.
-
Demostración. Sea ta(x) = a + x, Entonces
d(ta(x), ta(y)) = ||ta(x) − ta(y)|| = ||(a + x) − (a + y)||= ||x − y|| = d(x, y).
Ejercicios 4.2
[editar]- Sea <E,d> un espacio métrico. Sea d'(x,y) := kd(x,y) donde k es un número real positivo. Probar que d' es una métrica en E .
- Sea x1, x2, ..., xn una sucesión finita de puntos de un espacio métrico. Probar que
d(x1,xn) ≤ d(x1,x2) + ... + d(xn-1,xn). - Probar que la inversa de una isometría es una isometría.
- (Geometría de R2) Probar que las funciones siguientes determinan isometrías del plano.
- f(x,y) = (x+3, y-5) .
- f(x,y) = (ax -by, ax+by) con a2 + b2 = 1 .
- (Transporte de Estructura) Sea < E, d > un espacio métrico y sea f : X → E una función biyectiva. Para todo x, y en X definir
d′(x, y) := d(f(x), f(y)). ¿Es d′ una métrica en X? En caso afirmativo, ¿qué tendría de especial la función F?
- Sea h(x) = sen(x) + 2. La gráfica de g es el conjunto
X = {(x, y) ∈ R2 : y = h(x)}. 
Sea f : X → R :: f(x, h(x)) = x. Probar que f es biyectiva. Definir una distancia en X, por d((x, h(x)), (y, h(y)) = |x − y|. ¿Es d una métrica en X?
- Una semejanza lineal del plano R2 de razón r es una transformación hr del plano en si mismo, tal que hr(x) = rx.
- Si r ≠ 0, hr es biyectiva.
- d(hr(x), hr(y)) = |r|d(x, y).
- Sea f : E → E′ una isometría.
- La imagen por f de una bola abierta (resp. cerrada) es una bola del mismo typo y de igual radio.
- La imagen de un conjunto de diámetro D tiene el mismo diámetro. La imagen de un conjunto acotado es acotado.
- ¿Qué otras çosas"son preservadas por las isometrías?
Las Funciones Continuas
[editar]Las funciones continuas entre espacios métricos (y, posteriormente, entre espacios topológicos) constituyen la familia más importante de funciones a considerar desde el punto de vista de la proximidad. Una función continua será una función que preserva la proximidad.
Los lectores deben haber encontrado esta noción en sus cursos de Cálculo, donde muchas veces es opacada por las nociones de funciones diferenciables o integrables. Se dice usualmente en los textos de Cálculo que una función de un subconjunto de los Reales en R, es continua en un número a, ssi, para todo ε > 0 hay un δ >0 tal que
|x-a| < δ ==> |f(x) - f(a)| < ε (*)
Digamos, en primer lugar que la notación ε---δ es tradicional, se trata de un par de números reales denominados de esa manera por uso y costumbre. Cualquier otro par de símbolos serviría igual.
Algunas veces la definición no aparece explícitamente de esa forma, sino que se dice que . La transcripción a símbolos de la expresión con límites, es precisamente la ecuación (*).
Lo que nos interesa aquí, es entender por qué esa ecuación representa una preservación de cercanía o proximidad de puntos. En primer lugar, y para conectarla con los espacios métricos, la escribiremos usando la noción de distancia en los Reales.
Tenemos entonces que f es continua en a, ssi, para todo ε >0 hay un δ >0 tal que
| (**) |
Decimos de manera más o menos informal que la ecuación anterior establece que podemos hacer la distancia entre f(x) y f(a) tan pequeña como queramos (menor que ε ), siempre y cuando tomemos la distancia entre x y a lo suficientemente pequeña (menor que δ) .
La proximidad entre f(x) y f(a) está determinada por la distancia usada (espacio métrico) y por la elección de ε. La función será continua en el punto a, cuando no importa que ε escojamos, siempre podremos hallar un valor δ tal que tomando los valores de x adecuados (con distancia a a menor que δ) podremos lograr que d(f(x), f(a)) sea menor que ε;.
Ejemplo 4.3.1.
Mostraremos el significado operacional de la definición de continuidad
indicada, probando que la función f : R → R tal que f(x) = 3x + 4 es
continua en x = 5.
Resolución. Comenzaremos evaluando |f(x) − f(5)|.
|f(x) = f(5)| = |(3x + 4) − (3 ∗ 5 + 4)| = |3x − 3 ∗ 5| = 3|x − 5|.
La expresión a la derecha es la clave para la demostración, ya que nos dice que si queremos que |f(x) − f(5)| < ε, bastará con hacer 3|x − 5| < ε, lo qual se logra tomando |x − 5| < ε/3. De esta manera, podemos hallar el valor adecuado de δ, que en este caso será cualquier número menor o igual a ε/3. En efecto, cuando |x − 5| < δ se cumplirá que |f(x) = f(5)| = 3|x − 5| < 3δ = 3 ∗ ε/3 = ε. Como el valor de ǫ era arbitrario, concluimos que f es continua en 5.
Ejemplo 4.3.2.
Probaremos, para tener un ejemplo más elaborado, que la función
f(t) = t2 es continua en 3.
Resolución. Nuevamente empezamos acotando |f(x) − f(3)|. Tenemos que
| ( 1) |
No podemos proceder, sin embargo, de una manera tan simple como en el ejemplo anterior, debido al factor
|x + 3|. Como interesa que pasa cerca de 3, limitaremos los valores de x a que
|x − 3| < 1(Cualquier otro valor positivo serviría), o sea que 2 < x < 4. Usando la última relación, concluimos que 5 < x + 3 < 7, De donde,
| (2) |
Luego, si queremos que |f(x) − f(3)| < ε, bastará con que |x − 3| < ε/7,
lo cual nos da una pista sobre el valor adecuado para δ, ε/7. Una vez obtenido
lo anterior, procedemos a la demostración formal. Sea ǫ > 0 dado. Escojamos
δ = mín{ε/7, 1} (debemos asegurarnos que el valor de δ sea menor que 1, en
caso que ε/7 sea mayor que 1.
Sigue entonces de la ecuación (2) que |f(x) - f(3)| < ε, lo que prueba la
continuidad de f en 3.
Ejemplo 4.3.3. Veamos ahora una función discontinua. Sea f : R → R tal que f(x) = 1, cuando x > 0, y f(x) = 0, cuando x ≤ 0.
Veremos que f no puede ser continua en 0. Cualquier bola abierta con centro en 0 contiene números positivos, sea x0 uno de ellos, entonces f(x0)−f(0) = 1−0 = 1. Por lo que no importa que δ escojamos la distancia entre esas imágenes será igual a 1, por lo que no puede hacerse tan pequeña como queramos (por ejemplo 1/2).
En el último ejemplo, la gráfica de la función tiene un “salto” en 0. El salto mide 1. Cualquier salto impide, por las mismas razones del ejemplo, la continuidad de la función. Por eso, a veces, hay quienes dicen que una función continua es aquella cuya gráfica puede dibujarse sin tener que levantar el lápiz del papel
Extenderemos la definición de función continua a una función entre espacios
métricos.
Daremos, a continuación, una definición formal de continuidad para completar nuestra discusión.
Definición. (Continuidad) Sea f :< E, d > → < E′,d′ > una función.
- (Local) f es continua en un punto p de E, ssi, para todo ǫ > 0, podemos
hallar un δ > 0 tal que
- d(x, p) < δ ⇒ d′(f(x), f(p)).
- (Global) f es continua en (el espacio) E, ssi, es continua en cada punto de E.
Siempre hay funciones continuas entre dos espacios métricos: las funciones constantes.
Proposición 4.3.1. Cada función constante de un espacio métrico en otro es continua en todo el espacio.
Demostración.
- Sea f : E → E′ tal que para todo x en E, f(x) = b. Sea p un punto cualquiera de E. Como para todo x, se cumple que d(f(x), f(p)) = d′(b, b) = 0, vemos que para cualquier ε > 0, podemos usar cualquier δ > 0 y se tendrá que
- d(x, p) < δ ⇒ d′(f(x), f(p)) = 0 < ε.
Proposición 4.3.2.
Las isometrías son funciones continuas en todo el dominio.
Demostración.
- Sea f : E → E′ una isometría. Como d′(f(x), f(a)) = d(x, a), dado un ε > 0, basta tomar δ = ε para que se cumpla la definición de continuidad en a.
Dejaremos aquí, nuestra excursión a las funciones continuas, a las que dedicaremos un capítulo completo. (Cap 6. Continuidad.) Lo que más nos interesa de la definición, por ahora, es que nos servirá para motivar los conceptos de la próxima sección.
Ejercicios 4.3
[editar]- Probar que en R las funciones siguientes son biyectivas y continuas.
- f : t ↦ t + a.
- g : t ↦ at, a ≠ 0.
- h : t ↦ mt + n, m ≠ 0.
- Sea f : E → E′ continua en p y g : E′ → E′′ continua en f(p). Probar que la composición g ◦ f es continua en p.
- Sean a, b, c y d números reales tales que a < b y c < d. Probar que la
función f : [a, b] → [c, d] tal que
es biyectiva y continua.
- Sea f: E → E' una función continua. Sea A un subconjunto no vacío de E. Proanr que la restricción de f a A es continua.
- Sean E un espacio métrico y 1E la función identidad, 1E(x) = x; probar que se trata de una función continua.
Bolas Abiertas, Cerradas y Esferas
[editar]Comenzamos en esta sección el estudio de la topología de un espacios métrico. Como parte de la definición de continuidad aparecen x tales que d(x,a) < δ . Por lo que interesa estudiar conjuntos que tienen esa propiedad. Si pensamos geométricamente, tal conjunto será semejante al "interior" de una circunferencia (en un plano) con centro a y radio δ. Generalizaremos las nociones anteriores a espacios métricos cualesquiera.

Definición. (Bolas y Esferas) Sea E un espacio métrico, p un punto de E y r un número real positivo.
- Llamamos bola abierta con centro p y radio r al subconjunto de E denotado por Br(p) (o B(p:r)) y que está formado por todos los puntos de E cuya distancia a p es menor que r .
- Llamamos bola cerrada con centro p y radio r al subconjunto de E denotado por Br[p](o B[p;r]) y que está formado por todos los puntos de E cuya distancia a p es menor o igual que r .
- Llamamos esfera de centro p y radio r al subconjunto de E denotado por Srr(p) (o S(p;r)) y que está formado por todos los puntos de E cuya distancia a p es igual a r .
Claramente, Br[p] = Br(p) ∪ Sr(p).
-
(☩) Intuitivamente, una bola abierta contiene a todos los puntos vecinos próximos a su centro. ¿Cuán próximos?... depende del valor del radio.
Cuando decimos que podemos escoger puntos "tan cerca como queramos" de un cierto punto, estamos hablando de los puntos de un bola abierta con centro en el
punto y con un radio tan pequeño como queramos.
Observación 4.2. La terminología no es estándar. Algunos autores usan esferas en lugar de bolas. En situaciones planas, se usa también discos (abiertos y cerrados). Nosostros hablaremos, también, de la r–vecindad de un punto p, para referirnos a la bola de radio r y centro p.
Ejemplos 4.4.1.
- En el espacio euclídeo R2, las bolas abiertas son los interiores de los círculos con igual centro y radio. Por su parte, las bolas cerradas corresponden al círculo anterior, pero agregando la circunferencia correspondiente, que es la correspondiente esfera. En la geometría plana hablamos de círculo y circunferencia en vez de bola cerrada y esfera (que son más propios de espacios tridimensionales).
- En la línea real, la bola abierta Br(a) coincide con el intervalo abierto ]a-r,a+r[. Mientras que la bola cerrada de igual centro y radios es el intervalo cerrado [a-r,a+r]. La esfera Sr(a) es igual al conjunto {a-r, a+r}.
Ejemplo 4.4.2 (Propiedad de Hausdorff) .
Sean x, y puntos diferentes de un espacio métrico. Probar que hay bolas abiertas B1 y B2 que contienen a x y a y respectivamente y que son disjuntas entre si.
Resolución. Un dibujo puede inspirarnos en la solución.

Vemos que parece que tomando como r=d(x,y)/3, las bolas de radio r y centros en x y y serán disjuntas.
- Demostración.
Como x ≠ y , d(x,y) es un número positivo, por lo que r= d(x,y)/3 también es un número positivo. Sean B1=Br(x) y B2=Br(y). Claramente, x ∈ B1 , y ∈ B2. Falta, tan solo, probar que dichas bolas son disjuntas. Supongamos que no y sea z un punto común a ambas bolas. Entonces,
3r =d(x,y) ≤ d(x,z) + d(z,y) < r + r = 2r.
Como es imposible que 3r < 2r , hemos obtenido una contradicción. Luego, nuestras bolas deben ser disjuntas.
El último ejemplo muestra que buenos dibujos pueden ayudarnos a comprender la situación o a inspirarnos en las demostraciones. Sin embargo, solamente una demostración es la única garantía de que andamos pisando terreno firme.
Ejemplo 4.4.3.
Supongamos que X es un espacio discreto (métrica 0--1). ¿Cómo son las bolas abiertas o cerradas en X? La siguiente tabla muestra algunos resultados.
Bolas y Esferas en Subespacios
[editar]Usualmente, las "formas" más extrañas de bolas y esferas aparecen en los subespacios, aunque esperamos que el lector o lectora descubra que sus dibujos intuitivos son suficientemente buenos para guiar en una demostración.
Sea E un espacio métrico y sea F un subespacio de E. Para precisión en la exposición, simbolizaremos por dE y dF a las distancias en E y F respectivamente, aunque si x,y están en F se cumple que dF(x,y) = dE(x,y), por definición de subespacio. Análogamente, simbolizaremos por BE(p;r) y BF(p;r) a las bolas abiertas en E y F respectivamente.
Sea p un punto de F. Notemos que un punto x está en BF(p;r), ssi, x está en F y dF(p,r) < r, ssi, x está en F y dE(x,p)<r. Es decir que
BF(p;r) = BE(p;r) ∩ F.
El razonamiento es general, por lo que hemos probado que las bolas abiertas de F son la intersección de una bola abierta de E (con igual centro y radio) con el subespacio F. Análogamente, para bolas cerradas y esferas,
Ejemplo 4.4.4.
Sea E = [0,2[ = {x ∈ R: 0 ≤ x < 2}.
Notemos que en el espacio métrico E con la distancia inducida de la distancia usual en los Reales, tenemos que
- B1(0) = [0,1) (bola abierta).
- B1[1] = [0,2[ (bola cerrada)
- S3(1) = ∅.
Ejemplo 4.4.5.
La métrica usada también afecta a las figuras, como se ilustra a continuación; donde podemos ver esferas de igual radio con igual centro, pero para diferentes métricas de R2.

Observación. El lenguaje de bolas y esferas proviene de la geometría de los espacios euclídeos usuales (Rn con la métrica euclídea). Tal préstamo puede ayudar a desarrollar nuestra intuición de situaciones más abstractas. Sin embargo, cabe advertir que la situación no es tan simple, como se pudo apreciar en el ejemplo 4.4.3 anterior. Situaciones semejantes se hallarán en la próxima sección y en la sección sobre espacios ultramétricos.
Moraleja: es conveniente visualizar las relaciones y propiedades en el modelo euclídeo; pero, es absolutamente necesario probar la validez general de dichas visualizaciones.
Los Espacios de Funciones
[editar]Sea E el espacio de funciones reales acotadas definidas en el intervalo [a,b], o sea el espacio normado B([a,b], R) definido en la sección el espacio normado de todas las funciones acotadas definidas sobre el intervalo [a,b]. Ver la sección 4 del capítulo 3. Basado en dicha norma, tenemos una distancia definida por
Dada una función f por su gráfica, ¿cómo se ve gráficamente una bola de radio r con centro en la función f?

Mirando a la figura vemos un dibujo de tal bola abierta. La linea continua es el centro de la bola y las líneas entrecortadas son la esfera. Una función está en la bola abierta, cuando su gráfica se ubique entre las dos líneas entrecortadas.
Ejercicios 4.4
[editar]- Sean r1, r2 números reales tales que 0 < r1< r2. Probar que la bola abierta (resp. cerrada) de radio r1 está contenida en la bola abierta (resp. cerrada) de radio r2.
- La distancia entre dos elementos de una misma bola abierta (resp. cerrada) de radio r es menor (resp. menor o igual) que 2r.
- Sea B = Br(a) . Probar que para todo punto p de B , hay una bola abierta con centro en p , totalmente contenida en B.
- Sean B1, B2 bolas abiertas con intersección no vacía. Probar que dicha intersección contiene a una bola abierta.
- Verificar las afirmaciones del ejemplo 4.4.3.
Productos de Espacios Métricos
[editar]Sean <Ei, di>, para i=1, ... , n, una familia de espacios métricos. Sea E el producto cartesiano de los Ei's. Los elementos de E son n-uplas (x1, ... , xi, ... , xn) con xi en Ei.
¿Podremos definir una estructura métrica en E relacionada con los factores?
La respuesta es afirmativa, y daremos dos posibles definiciones.
Definiciones de métricas productos.
| (MP-1) |
| (MP-2) |
Queda de ejercicio, verificar que tenemos métricas.
Ejercicios 4.5.
[editar]- Verificar que las funciones MP--1 y MP--2 definidas en el texto, efectivamente proveen métricas al espacio producto. Discutir la relación entre esas definiciones y las métricas ciudad y máxima de Rn. ¿Podría proveerse al espacio producto con una métrica análoga a la euclidiana?
- Suponer que E es un espacio métrico con métrica , que es la métrica discreta 0--1. Sea SE el conjunto formado por todas las sucesiones de elementos de E. Definir para dos sucesiones (xn), (yn),
Verificar que es una métrica en SE. ¿Es d discreta?
Algunas Nociones Métricas
[editar]Veremos, en esta sección, diversas nociones asociadas a subconjuntos de un espacio métrico. (Esta sección hace uso de las nociones de supremo e ínfimo, para un repaso ver la sección correpondiente del Capítulo 2 (Números Reales)..
Diámetro de un Conjunto
[editar]Llamamos diámetro de un subconjunto A de un espacio métrico E al número real
δ(A) := sup{ d(x, y): x, y ∈ A}.
Cuando A no sea vacío y el supremo anterior no exista, diremos que el conjunto tiene un diámetro infinito (+∞).
(☩) El diámetro de un conjunto mide lo más "ancho" del conjunto.
Conjunto Acotado. Decimos que un subconjunto A de un espacio métrico es acotado, cuando su diámetro es finito.
Ejemplo 4.6.1.
Hallar el diámetro de A= ]0,1].
Resolución. Intuitivamente ese diámetro (que aquí coincidirá con el largo intuitivo del intervalo) debe ser 1. Daremos, sin embargo, una demostración formal de ese resultado, para ilustrar como trabajamos con las definiciones. Notemos que cuando x, y son elementos de A, se tiene que
0 < x < y ≤ 1 implica que d(x,y)= |x-y| = y-x < 1-x. Considerando x=1/n, n > 1, vemos que d(x,y) = 1-1/n. Tales valores tienen supremo 1; lo que implica que el diámetro es 1.
Ejemplo 4.6.2.
Sea A igual la cinta {(x,y) ∈ R2: 1 < x ≤ 5}. Hallar el diámetro de A .
Resolución. Notemos que para todo número natural a = (3,0) y b=(3,n) son puntos de A y que . Como los naturales no son acotados superiormente, no hay un supremo finito para las distancias, luego tendremos que δ(A) = +∞ .
Lema 4.6.1. Sean A,B subconjuntos de un espacio métrico.
Cuando A es un subconjunto de B se cumple que δ(A) ≤ δ(B) .
Demostración.
- Sean x, y puntos de A y, por lo tanto, de B . Luego, para todo x, y en A , d(x,y) ≤ δ(B) --ya que δ(B) es una cota superior de esos valores. De donde, sup{d(x,y): x,y ∈ A} ≤ δ(B) ---supremo es la menor cota superior.
Ejemplo 4.6.3.
Sean B = Br(a) y B'=Br[a]. Entonces, δ(B) ≤ δ(B') ≤ 2r.
Resolución. Sean x , y en B', entonces
d(x,y) ≤ d(x,a)+d(a,y) ≤ r + r = 2r.
Luego, δ(B') ≤ 2r. La otra desigualdad sigue del lema anterior.
Notemos que, al pasar, hemos probado que bolas, ya sean abiertas o cerradas son conjuntos acotados.
Lema 4.6.2. Un conjunto no vacío es acotado, ssi, está contenido en una bola (ya sea abierta o cerrada) Demostración.
- Supongamos que el conjunto X fuera acotado, digamos que su diámetro fuera igual a m. Entonces, cuando a es un punto de X , se tiene para todo x en X que d(x,a) ≤ m. Luego, X está contenido en Bm[a] ⊂ B2m(a).
- El recíproco sigue del lema anterior y de que las bolas son conjuntos acotados.
Distancia entre conjuntos
[editar]Llamamos distancia entre subconjuntos A y B de un espacio métrico al número
d(A,B) := inf {d(x,y) : x ∈ A, y ∈ B}.
Cuando A = {a} escribimos d(a,B) y hablamos de distancia del punto a al conjunto B.
Ejemplo 4.6.4.
Hallar la distancia euclídea del punto p=(1,1) a la línea L con ecuación cartesiana x+y=1.
Resolución. Sea s la distancia del punto p a un punto (x,y) de la línea L. Tenemos que
- m2 = d((x,y), (1,1)))2= (x-1)2 + (y-1)2 = (x-1)2 + (1-x-1)2
- = x2 - 2x + 1 + x2 = 2x2 - 2x + 1 = 2(x2 - x + 1/4 + 1/2.
- = 2(x - 1/2)2 + 1/2
- m2 = d((x,y), (1,1)))2= (x-1)2 + (y-1)2 = (x-1)2 + (1-x-1)2
Por lo que, m2 tiene como valor mínimo 1/2, luego la distancia buscada es .
Ejercicios 4.6
[editar]- Probar los siguientes enunciados.
- δ(A) = 0, ssi, A consiste de un único punto.
- Hallar el diámetro de los siguientes conjuntos de la línea real. Después de intuir el resultado dar una prueba formal.
- ]a,b[),
- [a,b],
- {números primos}.
- ¿Será cierto que δ(A ∩ B) ≤ δ(A) + δ B ? En caso afirmativo, dar una prueba. En caso negativo, dar un contraejemplo. Cuando puede que pase en algunas situaciones, indicar las condiciones con prueba.
- (Conjuntos Acotados) Probar lo siguiente:
- Un conjunto contenido en un conjunto acotado, es un conjunto acotado.
- La reunión de dos conjuntos acotados es un conjunto acotado.
- (Rn con la métrica euclídea)
- Sea B (resp. B' ) la bola abierta (resp. cerrada) con centro en a y radio r . Probar que cuando la distancia de un punto a B' es s , entonces la distancia del punto a B también es s .
- Hallar una fórmula para la distancia entre una bola de radio r1 y una bola de radio r2 . Analizar las posibles posiciones de los centros y valores de los radios.
- (*) ¿Son válidos los resultados anteriores en un espacio discreto?
- ¿Cierto o falso? Si cierto, dar una demostración o un ejemplo; en caso contrario, dar un contraejemplo?
- Un espacio métrico puede consistir de un único punto.
- Las bolas abiertas siempre son distintas de las bolas cerradas.
- Sea r < ρ. La bola abierta (resp. cerrada) de radio r es diferente a la bola abierta (resp. cerrada) de radio ρ.
- Una esfera de radio positivo nunca es vacía.
Los Reales Extendidos, R#
[editar]Definiremos una estructura de espacio métrico en los Reales extendidos, R# = R ∪ {+∞,−∞}.
Sea f : R → ]-1,1[ tal que
y sea g :]-1,1[ → tal que
g(x) = x/(1 - |x|). Se tiene que
Análogamente, g(f(x)) = x, lo que prueba que f y g son biyectivas. Extendamos f a F : R → [-1,1], poniendo F(x) = f(x) cuando x es un número real, F(+∞) = 1, y ¯ F(−∞) = −1. Claramente, F es también biyectiva. Por lo que la usaremos para definir una métrica d* en R# por d(x, y) := |F(x) − F(y)|. La verificación de que d* es una métrica queda de ejercicio. Con respecto a esta métrica, la función F es una isometría. Notemos que, por ejemplo, d*(1,+∞) = |f(1)−f(+∞)| = 1/2 y que d*(−∞,+∞) = 2. Como [−1, 1] es acotado, tendremos que R# es también acotado y que el subconjunto de los Reales también lo será.
Naturalmente, la restricción de esta métrica a R es bastante diferente a la métrica usual, definida por su valor absoluto, de la línea real.
¿Cuáles son las vecindades de +∞ en R#? Consideremos por ejemplo la bola abierta de radio 1/2 con centro en +∞. Tenemos que
| . |
Ejercicios 4.6
[editar]- Probar que una bola cerrada con radio mayor que 2 es igual a todos los Reales extendidos.
- Describir las bolas abiertas centradas en +∞.
- Idem. para las bolas centradas en −∞.
Espacios Ultramétricos
[editar]Describiremos, en esta sección, a unos espacios métricos cuya métrica satisface una condición más estricta que la desigualdad triangular. Dichos espacios tienen interesantes aplicaciones en diversas áreas de matemáticas. Para nosotros servirán de ejemplos de espacios métricos con unas propiedades ``extrañas, lo que quiere decir bastante diferente de lo que pasa en espacios euclídeos.Una ultramétrica en un conjunto E es una métrica que satisface una condición más estricta que la desigualdad triangular.
Claramente, cada ultramétrica es una métrica. Un espacio ultramétrico es un espacio provisto de una ultramétrica.
Antes de dar ejemplos, veremos algunas de las propiedades ``extrañas de los espacios ultramétricos.
Ejemplo 4.8.1. Todos los triángulos en un espacio ultramétrico son isósceles. Es decir que dados tres puntos x, y, z, al menos dos de las distancias entre esos puntos son iguales.
Resolución. Supongamos que hay al menos dosdistancias desiguales (el caso contrario es trivial), digamos que d(x, y) < d(x, z). Entonces, como d(y, z) ≤ máx{d(y, x), d(z, x)} concluimos que d(y, z) ≤ d(x, z). Por su parte, d(x, z) ≤ máx{d(x, y), d(y, z)} implica que d(x, z) ≤ d(y, z) (ya que es mayor que la otra alternativa). Luego, d(y, z) = d(x, z).
Ejemplo 4.8.2. En un espacio ultramétrico, cualquier punto de una bola abierta es centro de la bola.
Resolución. Sean B = Br(x), y ∈ B. Probaremos que Br(x) = Br(y). Sea z ∈ B. Entonces, d(z, y) ≤ máx{d(z, x), d(x, y)} < r. Es decir que z ∈ Br(y). Lo que prueba que Br(x) ⊂ Br(y). Comenzando con un punto en Br(y) obtenemos la inclusión inversa.
Los valores absolutos p-ádicos en los Racionales
[editar]En esta sección veremos una familia de valores absolutos para los Racionales que tienen las mismas propiedades formales que el valor absoluto usual, pero con la propiedad adicional de que
la distancia deducida de tal valor absoluto es una ultramétrica.
Sea p un número primo. Es sabido que dado un número primo cualquiera p, cada número entero z no nulo puede representarse como el producto una potencia del primo p con un número relativamente primo con p.
con r ≥ 0 y m no divisble por p.
Diremos que el entero no negativo r de la relación anterior es la p--ponderación de m y la denotaremos por ordp(m). Extenderemos la p--ponderación a los racionales de la manera siguiente: si q=z/w, con z, w tales que ordp(z) = m y ordp(w) = n, entonces
Notemos que si z = pmx y w = pnx , el racional z/w = pm-n (x/y) con x, y no divisibles por p.
Valor absoluto p--ádico. Sea p un número primo y sea | |p definido para un racional x como
cuando x ≠ 0, y |0|p = 0.
Ejemplos 4.8.3. Consideremos el caso cuando p = 5.
- 35 = 51 * 7, luego, ord_p(35)=1, por lo que |35|5 = 5-1.
- 1/25 = 5-2, luego |1/25|5 = 5\sup2.
- 9 = 5^0 , luego |9|5= 1.
- 35/100 = (5 * 7)/ (52 * 4) = 5-1 )7/4) , luego |35/100|,sub>5 = 51.
Notemos que para todo x, |x|_p es un número entero, que es una potencia de p cuando x no es nulo. Llamaremos a |x|_p , el valor absoluto p --ádico de >Q. El nombre de valor absoluto proviene de las propiedades mostradas en la siguiente proposición. Comparar con la propiedades del valor absoluto usual---que en este contexto llamaremos el valor absoluto proveniente del orden.
Proposición 4.8.1.(Propiedades del Valor Absoluto p --ádico) Sean x, y números racionales.
- |x|_p ≥ 0.
- |x|_p = 0 \iff x =0.
- |-x|_p = |x|_p.
- |x+y|_p ≤ max{|x|_p, |y|_p }.
- |xy|_p = |x|_p |y_p|.
-
Demostración. Los enunciados UVA1 al UVA3 son triviales. Las propiedades UVA4 y UVA5 ameritan demostraciones explícitas.
Sean x, y racionales; si uno de ellos es nulo, los resultados son triviales. Supongamos que ordp(x) = r y ordp(y) = s , o sea que x=p^{r} (z/w) , y = p^s(u/v) con z , w , u , v , enteros no divisibles por p. Luego, |x|_p = p^{-r} y |y|_p = p^{-s}.
(UV4) Sin perdida de generalidad, podemos suponer que r ≤ s. Entonces,
Entonces,
Claramente, p no divide a vw. Supongamos que ordp(q) = e , con e ≥ 0. Entonces, ordp(x+y) = r+e. Por lo que,
Lo que prueba la afirmación.(UV5) Como
con zu y wu no son divisibles por p , se tiene que |xy|_p= p^{-(r+s)} ; lo que prueba el resultado.
Notemos que la propiedad UV4 implica inmediatamente una desigualdad triangular, ya que
Lo que justifica la nomenclatura de valor absoluto. Asociaremos con este valor absoluto, la distancia p --ádica en Q , definida como d_{(p)}(x,y) = |x-y|_p. Como
vemos que se trata de una ultramétrica.
Observación 8.4. Si llamamos valor absoluto en \Q a cualquier función que asigna a cada racional un número real que cumple las propiedades formales del valor absoluto, se sabe,por un teorema de Ostrowski, que los únicos valores absolutos en Q son esencialmente el valor absoluto usual (asociado al orden) y los p-ádicos de esta sección.
Los Racionales provistos de un valor absoluto p--ádico son ejemplos de cuerpos llamados no arquimedianos, ya que se tiene la siguiente proposición.
Proposición 4.8.2. Sea p un número primo. Los Naturales como subconjunto de los Racionales no son acotados respecto al valor absoluto asociado al orden, pero son acotados respecto a las normas p--ádicas, ya que se cumple para todo n en N que |n|_p ≤ 1.
-
Demostración. Notemos que |0|_p= 0 y que |1|_p = 1. Supongamos que k ≥ 1 y que |k|p ≤ 1. Entonces,
El resultado sigue por inducción.
Se puede hallar, además de los Racionales con los valores absolutos p--ádicos, otros espacios ultramétricos, pero nuestra exploración de tales espacios acaba, por ahora, aquí, ya que nos interesaban principalmente como ejemplo de las consecuencias posibles de los axiomas de espacio métrico.
Ejercicios 4.8
[editar]A. Suponer que el primo p es igual a 5.
- Evaluar ord5(100) , ord5(-10!) , ord5(20) , ord5(15/23) .
- Evaluar |100|5 , |7-3|5 , |750-625|5 , |1/9 - (-1/6)|5 .
- Probar que un número entero z tiene |x|5=1 , ssi, z no es divisible por 5.
- Probar que un número entero z tiene |x|5<1 , ssi, z es divisible por 5.
- Probar que q=m/n , m y n relativamente primos, tiene |q|5 >1 , ssi, n es divisible por 5 .
- Si |x-a|5 < |a|5 entonces |x|5 = |a|5 .
B. Bolas abiertas, cerradas y esferas en Q con el valor absoluto 5 --ádico.
- Verificar que los valores posibles del valor absoluto 5 --ádico son las potencias enteras de 5 o 0.
- Probar que B(0;8) = B(0,5) = B[0;1] .
- Probar que S(0;8) es vacío.
- Probar que el diámetro de B(0;1) es 1.
C. Suponer que E es un espacio ultramétrico.
- El diámetro de una bola es menor o igual que su radio.
- Cuando dos bolas (abiertas o cerradas) tienen un punto en común, entonces una de ellas está contenida en la otra.
- Cualquier punto de una bola cerrada es centro de la bola.
Ejercicios del Capítulo 4
[editar]- Cuando un punto p pertenece a un conjunto A, entonces d(p,A) = 0. ¿Es válido el recíproco?
- . Sea < E, d > un espacio métrico. Sea Probar que d′ es una distancia en E. (Sug. Para la desigualdad triangular, escriba lo que desea probar, luego expanda y simplifique.) Probar, además, que para todo x, y en E, d′(x, y) < 1.
- Sea BS(R) el conjunto formado por todas las sucesiones acotadas en E.
- Probar que la suma término a término y el producto de constante por cada término proveen a BS(R) de una estructura de espacio vectorial (ver definición en el capítulo 3).
- Definir d((xn), (yn)) := sup{d(xn, yn) : n ∈ N}. d en una métrica en BS(R).
- Sea X un espacio métrico discreto y E un espacio métrico cualquiera, ¿cuándo una función f : X → E es continua?
- Sea f : E → R una función continua en un punto p de E.
- f es acotada en una vecindad de p.
- Si f(p) ≠ 0, hay una vecindad V de p tal que x en V implica que f(x) tiene igual signo que f(p).
- Sea f: E → E' una isometría.
- La imagen por f de una bola abierto (resp. cerrada) es una bola del mismo typo y de igual radio.
- La imagen de un conjunto de diámetro D tiene el mismo diámetro.
- La imagen de un conjunto acotado es acotado.
- ¿Qué otras "cosas" son preservadas por las isometrías?
Los Conjuntos Abiertos y Cerrados
[editar]Introducción
[editar]Este capítulo estará dedicado completamente a la topología de los subconjuntos de un espacio métrico. Veremos como formalizar algunas de las principales nociones asociadas a “proximidad” entre puntos (o entre conjuntos, o entre puntos y conjuntos).
Cuando pensamos en una figura plana, podemos intuitivamente considerar puntos que están ya sea dentro de la figura, en el borde de la figura, o en el exterior de la figura. Aquí formalizaremos esas nociones. Introduciremos el cómodo lenguaje de vecindades y clasificaremos a los puntos por la cantidad de vecinos en un vecindario próximo.
Los lectores deberán seguir cuidadosamente las argumentaciones de las demostraciones y ejemplos, porque son básicas en el razonamiento topológico. Una mayoría de las demostraciones se basan en propiedades de conjuntos y sus operaciones, por lo que resultará conveniente echar un vistazo a las sección A.1 del apéndice A, donde se resumen las propiedades de las operaciones. También, usaremos propiedades de familias de conjuntos que aparecen en la sección B.5 del apéndice B.
En los ejemplos, proposiciones, etc. sugerimos hacer un dibujo de la situación. Un dibujo apropiado puede ayudar a la intuición y guiar en la formalización de la misma.
Los Conjuntos Abiertos
[editar]La primera noción que estudiaremos, conjunto abierto, representa la formalización de la intuición de puntos próximos o cercanos.
Definición. (Conjunto Abierto) Sea E un espacio métrico. Decimos que un subconjunto A de E es abierto, si y solo si, para cada punto x de A podemos hallar un número real r > 0 tal que la bola abierta de centro x y radio r está contenida en A.
(☩) Informalmente, un conjunto es abierto cuando contiene todos los vecinos
suficientemente próximos a cada uno de sus puntos
Ejemplo 5.2.1. El semiplano H = {(x, y) ∈ R2 : y > 0} es un conjunto abierto.
Resolución. Sea p = (x0, y0) un punto cualquiera del semiplano H. Debemos probar que hay un disco abierto con centro en p totalmente contenido en H. Sea r = y0/2 y B = Br(p). Entonces, para todo (x, y) en B, se tiene que
de donde
Como |y − y0| < r es equivalente a y0 − r < y < y0 + r y y0 − r = y0 − y0/2 = y0/2 > 0, tenemos que (x, y) está en H. Lo que prueba que H es un abierto.
Proposición 5.2.1.
En cualquier espacio métrico, las bolas abiertas son conjuntos
abiertos..
-
Demostración.

Sea B la bola abierta con centro a y radio r y sea x un punto cualquiera de B. Sea ρ = r − d(x, a) y sea V = B_ρ(x). Entonces, para todo z en V tenemos que
Lo que prueba que V está contenido en B; o sea que x es un punto interior de B.
Ejemplo 5.2.2.
Sigue de la proposición que los intervalos abiertos acotados de la
línea real son abiertos, ya que son bolas abiertas.
Introduciremos dos nociones auxiliares: vecindad y punto interior. Tales nociones nos ayudarán a expresar más significativamente algunas propiedades.
Definición. (Vecindad) Sea E un espacio métrico y sea A un subconjunto de E. Llamamos vecindad de A a cualquier conjunto V que contenga a un abierto que contiene a A. Cuando A = {p}, decimos que V es una vecindad de p.
Una vecindad abierta es una vecindad que como subconjunto del espacio es un conjunto abierto.
Definición. (Punto Interior) Sea E un espacio métrico y sea A un subconjunto de E. Decimos que un punto p es un punto interior de A, ssi, A es una veceidad de p; o sea, cuando haya un abierto U que contenga a p y que esté contenido en A.
Sigue de lo anterior que cada conjunto abierto, en particular, una bola abierta, es una vecindad abierta de cada uno de sus puntos y que, por lo tanto, cada uno de sus puntos es interior.
Vecindad es una noción auxiliar que simplifica la expresión, ya que decir “vecindad de p” es más simple que decir “un conjunto que contiene a un abierto que contiene a p” y nos da, además, la idea de proximidad o cercanía.
Algunas veces, por simplicidad de la expresión, hablaremos de una r–vecindad de un punto para referirnos a una vecindad que es una bola abierta de radio r con centro en el punto.
¿Cuándo no es abierto un conjunto A? Cuando haya, al menos, un punto p del conjunto tal que todas las bolas abiertas con centro en el punto p, contienen al menos un punto que no está en A. Es decir que cada bola abierta con centro en p interseca en forma no vacía al complemento de A.
Sigue de la observación anterior que cuando no hay tal punto, el conjunto es abierto. Un conjunto, en particular que no tiene ese tipo de puntos es el conjunto vacío, es decir que:
|
El conjunto vacío es un conjunto abierto. |
Propiedades de Vecindades y Conjuntos Abiertos
[editar]Veremos algunas de las propiedades de los conjuntos abiertos y dejaremos como ejercicios las propiedades análogas para las vecindades (que se deducen casi en forma inmediata de las propiedades de los abiertos.
Supongamos que A y B fueran abiertos en un espacio métrico. ¿Que podríamos decir de A ∪ B? Supongamos que p fuera un punto de la reunión que, por definición de reunión, estaría tanto en A como en B. Si estuviera en A, habría una r–vecindad V de p totalmente contenida en A. Como V ⊂ A implica que V ⊂ A∪B, concluiríamos que A ∪ B es abierto. Un razonamiento análogo funciona para p en B. Revisando el argumento, vemos que si consideramos la reunión de más de dos abiertos, el mismo argumento es válido, inclusive para la reunión de una familia cualquiera de abiertos.
Sea (Ai), i ∈ I, una familia de abiertos y sea A = {Ai: i∈I}. Probaremos que A es abierto, razonando como arriba. Sea p un punto de A. Entonces (paso clave) hay al menos un i en I tal que p ∈ Ai. Como Ai es abierto, hay una r–vecindad V de
p totalmente contenida en Ai. Luego, como V ⊂ Ai ⊂ A, concluimos que A es
abierto.
¿Qué pasa con A ∩ B cuando A y B son abiertos? Primeramente, observemos que si la intersección es vacía, entonces se trata de un conjunto abierto. Supongamos que los conjuntos no fueran disjuntos y que p fuera un punto de la intersección. Como A es abierto, hay una r1–vecindad de p totalmente contenida en A; análogamente, hay una r2–vecindad de p totalmente contenida en B. Sea r el menor valor entre r1 y r2 y sea V = Br(p), como r ≤ ri, i = 1, 2, V ⊂ B(p;r1) ⊂ A y V ⊂ B(p;r2) ⊂ B. Como V está contenida tanto en A como en B, está contenida en A ∩ B, lo que prueba que dicho conjunto es abierto.
El argumento anterior se puede extender a una familia finita de abiertos, razonando por inducción (ver más abajo la demostración). Sin embargo, el argumento no vale necesariamente para familias infinitas, ya que puede que no haya valor mínimo de los radios y que el ínfimo de los mismos sea 0.
Ejemplo 5.2.3.
Consideremos la familia de abiertos (An), An =] - 1/n, 1/n[, donde n es un natural positivo.
Veremos que A = ∩{An : n∈N } = {0}, que es un conjunto que será, claramente, un conjunto que no es abierto ya que cualquier vecindad abierta con centro en 0 contiene números diferentes de 0.
Veamos una demostración formal de lo anterior. Suponer que hubiera un número real x que perteneciera a A. Sin perdida de generalidad, por la simetría de la situación, podemos suponer que x > 0. Por el principio arquimediano, siempre podremos hallar un n tal que 1/n < x. Pero esto implica que x no está en ]−1/n, 1/n[, por lo que no puede estar en A (que consiste de los elementos comunes a todos los An). Luego A = {0}. Resumimos las consideraciones anteriores en la siguiente importante proposición.
Proposición 5.2.2 (Propiedades de los Abiertos). Sea E un espacio métrico.
- El conjunto vacío y todo el espacio E son abiertos.
- La reunión de una familia cualquiera de abiertos es un abierto.
- La intersección de una familia finita de abiertos es un abierto.
-
Demostración.
- Trivialmente cada punto de E es interior a E. El resultado sobre el conjunto vacío sigue de una observación anterior
- Probado arriba.
- Sea A = A1 ∩ A2 ∩· · ·∩ An. Probaremos que A es abierto por inducción sobre n. Cuando n = 2 el resultado sigue de lo hecho arriba. Supongamos que la intersección de k conjuntos abiertos, k ≥ 2, fuera abierto. Consideremos la intersección de k + 1 abiertos
A = A1 ∩ A2 ∩ · · · ∩ Ak ∩ Ak+1 = (A1 ∩ A2</> ∩ · · · ∩ Ak) ∩ Ak+1.
Por la hipótesis de inducción, la intersección de los k primeros es un conjunto abierto cuya intersección con otro abierto es un abierto, por lo hecho arriba. Por inducción se tiene el resultado.
Proposición 5.2.3 (Propiedades de las Vecindades).
Sea A un subconjunto de un espacio métrico E. Entonces,
- El espacio E es una vecindad de A.
- La intersección de dos vecindades de A es una vecindad de A.
- La reunión de una familia cualquiera de vecindades de A es una vecindad de A.
- Cualquier conjunto que contiene a una vecindad de A es una vecindad de A.
-
Demostración. Probaremos (c) y dejaremos el resto de ejercicio. Sean y vecindades del conjunto . Entonces, hay abiertos y tales que , .
Luego, , lo que prueba la afirmación.
Ejemplo 5.2.4. El intervalo abierto I =]a,+∞[ es un conjunto abierto en R, ya que es una reunión de abiertos.
Sea x un número cualquiera que sea mayor que a. Entonces, x − a es positivo y hay, por lo tanto, un natural n mayor que x−a (PropiedadAarquimediana). Como x − a < n implica que x < a + n, tenemos que x está en ]a, a + n[ y, por lo tanto, en la reunión indicada. Esto prueba que el intervalo está contenido en la reunión de los ]a, a + n[’s. La inclusión inversa es trivial; de donde la igualdad.
Ejemplo 5.2.5.
El intervalo (semiabierto) A = [0, 1[ no es abierto.
Consideremos al punto 0 de A. Cualquier bola abierta con centro en 0 contiene números negativos que no están, por lo tanto, en A; por lo que 0 no es un punto interior de A, lo que implica que A no puede ser abierto.
Proposición 5.2.4.
Sea E un espacio métrico. Cualquier conjunto abierto A es
igual a una reunión de bolas abiertas.
-
Demostración.
Sigue de la definición de conjunto abierto que para cada x en A hay una bola abierta con centro en x, digamos B(x) totalmente contenida en A.
Sea G la reunion de todas esas bolas abiertas. Como para todo x en A, se tiene que x ∈ B(x) ⊂ G, concluimos que A está contenido en G.
Sea y un punto cualquiera de G, entonces hay al menos un x en
A tal que y está en B(x). Por lo que y está en A. Luego, G está contenido en A.
Es decir que A = G.
Base de los Abiertos. Cuando una familia de abiertos tiene la propiedad que cualquier abierto es una reunión de abiertos de la familia, se dice que familia es una base para los abiertos. El resultado de la proposición anterior expresa que las bolas abiertas son una base para los abiertos del espacio.
Ejemplo 5.2.6. Sea E un espacio métrico discreto con métrica 0–1. Entonces, para cada x de E, la (1/2)-vecindad de x contiene solamente a x. Por lo que deducimos que cada conjunto con un único punto es abierto. Como cualquier subconjunto de E es una reunión de conjuntos con un único elemento, concluimos que cada subconjunto de E es un abierto.
La siguiente proposición muestra un resultado casi trivial, pero muy importante
más adelante.
Proposición 5.2.6 (Propiedad de Hausdorff).
- Sean x, y puntos diferentes de un espacio métrico. Hay abiertos U y V tales que (i) x ∈ U, (ii) y ∈ V, y (iii) U ∩ V = ∅. (Decimos que dos puntos diferentes están separados por abiertos disjuntos.)
-
Demostración.
Sea r = (1/3)d(x, y). Por hipótesis r > 0. Sean U = Br(x) y V = Br(y). U y V son abiertos que satisfacen (i) y (ii). Probemos que son disjuntos, por contradicción. Supongamos que hubiera un z en A ∩ B entonces,
Lo que es imposible, luego los conjuntos son disjuntos.
Los Abiertos en Rn
[editar]Sabemos, del capítulo anterior, que hay varias métricas posibles en Rn. Veremos, relaciones entre algunas de esas métricas. Como siempre, cuando no especificamos la métrica es porque se trata de la métrica euclidiana.
Ejemplo 5.2.7. Llamamos celda o caja abierta de R2 a un conjunto de la forma ]a, b[×]c, d[. Probaremos que dicha celda abierta es un conjunto abierto.
Resolución. Sea C la celda indicada. Sea (x0, y0) en C. Observemos que a < x0 < b y c < y0 < d. Sea r = mín{x0 − a, b − x0, y0 − c, d − y0}. Luego, r ≤ x0 −a ≤ ⇒ a ≤ x0−r. Análogamente, tenemos que x0 +r ≤ b, c ≤ y0−r y y0 + r < d. Sea B = B((x0, y0); r), y sea (x, y) un punto de B. Se tiene entonces que |x − x0| ≤ d((x, y), (x0, y0)) < r. De donde, r < x − x0 < r, o sea que x0 − r < x < x0 + r. Por las observaciones anteriores tenemos que a ≤ x0 − r < x < x0 + r ≤ b. Análogamente se verifica que c ≤ y0 − r < y < y0 + r ≤ d. Lo que prueba que (x, y) está en C. Por lo que B ⊂ C, o sea que C es abierto.
Ejemplo 5.2.8. Probaremos que los conjuntos abiertos respecto a la métrica--máxima son abiertos respecto a la métrica euclídea.
Sea C(p;r) la celda ]xp − r, xp + r[ × ]yp − r, yp + r[, donde
(xp, yp ) = p. De acuerdo al ejemplo anterior, dicha celda es un abierto de R2 respecto a la métrica euclídea.
Lo que implica que cualquier bola abierta respecto a la métrica--máxima, es un abierto respecto a la métrica euclidiana.
Sea un abierto respecto a la distancia máxima. Por definición de abierto, esto quiere decir que para cada punto en , hay una celda contenida en . Como contiene a , concluimos que es un abierto euclídeo. Resumiendo,
Proposición 5.2.6. Cada abierto respecto a la métrica máxima es un abierto respecto a la métrica euclídea.
Observación 5.1. El resultado del ejemplo anterior no es trivial, ya que puede haber conjuntos con diferentes métricas y que los abiertos respecto a una de las métricas no sean necesariamente abiertos respecto a la otra métrica. Por ejemplo, con respecto a la métrica discreta cualquier subconjunto de los Reales es abierto, lo que no pasa con respecto a la métrica usual de los Reales. El resultado de ejemplo también sugiere investigar el converso, ¿son los abiertos euclidianos abiertos respecto a la métrica máxima?
Ejercicios 5.2
[editar]- Decidir la validez o falsedad de cada uno de los siguientes enunciados. Explicar su respuesta.
- 1/2 es un punto interior del intervalo abierto ]0,1[.
- 1/2 es un punto interior del intervalo cerrado [0,1].
- El intervalo cerrado [0,1] es una vecindad de 1/2.
- El intervalo [0,1] es abierto.
- ¿Cuáles de los conjuntos siguientes son conjuntos abiertos en la línea real?
- El intervalo semiabierto ]a, b].
- El intervalo ]a,+∞[.
- El intervalo [a,+∞].
- {t ∈ R : t ≠ 0}.
- El complemento del conjunto ]a, b[.
- El complemento del conjunto [a, b].
- El complemento de los Naturales.
- El complemento de los Enteros.
- El complemento de los Racionales.
- ¿Cuáles de los siguientes conjuntos son conjuntos abiertos en R2 ?
- A = {(x, y) ∈ R2 : y < 2}.
- B = {(x, y) ∈ R2 : 2 < x < 5}.
- C = {(x, y) ∈ R2 : y = 5}.
- Probar que R2 \ {(0, 0)} es abierto.
- Probar que el conjunto {(x, y) ∈ R2 : x + y < 1} es abierto en R2.
- (♠) Probar que el conjunto {t ∈ R : sen(t) > 0} es abierto.
- Un conjunto es acotado, ssi, hay una bola abierta que lo contiene.
- El subconjunto de un conjunto formado por todos sus puntos interiores es un conjunto abierto.
- Cuando en un conjunto todos los puntos son interiores, el conjunto es abierto
- Probar que cuando V es una vecindad cualquiera de un punto p, hay una r–vecindad de p, contenida en V.
- (Propiedad de Separación de Hausdorff) Sean x, y puntos diferentes de un espacio métrico. Probar que hay vecindades V, W de x y y, respectivamente, que son disjuntas.
- Sea f : E → E′ una isometría de espacios métricos. La imagen de cualquier bola abierta B de E por f es una bola abierta B’de E′ de igual radio y cuyo centro es la imagen del centro de B. Usar lo anterior para probar que las imagen por una isometría de un abierto, es un conjunto abierto abierto.
- Probar la proposición 5.2.3.
- (Relaciones entre la métricas euclidiana y máxima del plano) En el ejemplo
5.2.5 se vió que cada abierto respecto a la métrica máximal es abierto
respecto a la métrica euclidiana. Se trata ahora de probar el recíproco.
- Probar que cada bola euclidiana contiene una celda C(p;r).
- Concluir que cada abierto euclidiano es un abierto respecto a la métrica máxima
- Un subconjunto V de R2 es una vecindad de un punto p, ssi, contiene una caja ]a, b[×]c, d[ que contiene a p. (Este resultado ayuda a probar que ciertos subconjuntos de R2 son abiertos, porque es más fácil, a veces, trabajar con cajas, que con bolas.) d) Generalizar los resultados del ejemplo citado y los de este ejercicios a R3.
- Idem para Rn.
Los Conjuntos Cerrados
[editar]En esta sección, introduciremos un concepto dual al de conjunto abierto: conjunto cerrado. Los intervalos cerrados de la línea real serán los ejemplos iniciales de la noción. La definición inicial no será muy ilustrativa desde el punto de vista topogeométrico, pero la presentamos de esta manera porque queremos, por razones que quedarán claras más adelante, usar abiertos en las definiciones de los conceptos importantes. Cuando veamos la noción de \textit{puntos de acumulación}, tendremos una imagen topogeométrica más clara del significado de cerrado. [4]
Definición. (Conjunto Cerrado) Sea E un espacio métrico. Decimos que un subconjunto F de E es un conjunto cerrado, ssi, su complemento es abierto.
Ejemplos 5.3.1. Cuando A es un subconjunto de otro X, su complemento en X se denota por X \ A. Cuando el conjunto X es el conjunto universal de la discusión, entonces podremos simbolizar el complemento de A por Ac.
- Un intervalo cerrado de la línea real es un conjunto cerrado.
[a, b]c = ]−∞, a[ ∪ ]b,+∞[ (abierto) y ] −∞, a]c = ]a,+∞[ (abierto)
- El conjunto vacío y todo el espacio son cerrados, ya que sus complementos son abiertos.
- Los Naturales son cerrados, porque su complemento es abierto
Nc = ]-∞, 0[ ∪ {]n, n + 1[: n ∈ N}. - El intervalo ]0, 1] no es cerrado, ya que su complemento es la reunion de ]−∞, 0] con ]1,+∞[. El primer conjunto no es abierto, porque 0 no es un punto interior del conjunto, por lo que la reunión no es un abierto.
Ejemplo 5.3.2. Sea E un espacio discreto. Vimos en el ejemplo 5.2.6 que cada subconjunto de E es abierto, por lo que su complemento es cerrado, Luego, todos sus subconjuntos son cerrados, ya que sus complementos son abiertos.
Conclusión: en un espacio discreto los subconjuntos son abiertos y cerrados a la vez.
☞ Notemos los ejemplos muestran que hay conjuntos abiertos---pero no abiertos, conjuntos cerrados---pero no abiertos, conjuntos que no son ni abiertos ni cerrados, y otros que son abiertos y cerrados a la vez (el conjunto vacío y todo el espacio).
Puntos Aislados, Puntos de Acumulación
[editar]Para entender el significado topológico de la noción de cerrado, introduciremos dos conceptos: punto aislado y punto de acumulación, que se referirán a la cantidad de vecinos que puede tener un punto.
Veamos las posibilidades. Supongamos que tenemos un punto p de un espacio métrico y un conjunto A. Si tomamos una vecindad V de p ¿cuántos vecinos de V V están en A? Si hubiera una cantidad finitas de vecinos diferentes de p en A, tomando como r a la menor de las distancias entre esos vecinos y p, tendríamos que la r–vecindad de p no contendría puntos de A diferentes de p. →Tal punro será un punto aislado en A; algo opuesto serán los puntos de acumulación.
Definición. (Puntos Aislados, Puntos de Acumulación) Sea < E, d > un espacio métrico. Sea A un subconjunto de A y p un punto de E.
- Decimos que un punto p de A es un punto aislado de A, ssi, hay una vecindad del punto que no contiene otro punto de A.
- Decimos que un punto p (no necesariamente en A) es un punto de acumulación de A, ssi, cada vecindad del punto contiene al menos un punto de A diferente del punto p.
Ejemplo 5.3.3. Sea X = {a1,..., an} un espacio métrico finito (por ejemplo un subconjunto finito de un espacio métrico). Sea p un punto cualquiera de X. El conjunto {d(p, ai) : ai ≠ p} es un conjunto finito. Si r es el menor de esos
números, entonces la bola abierta con centro p y radio r no contiene otro punto de A, luego p es aislado.
|
Cada espacio métrico finito consiste solamente de puntos aislados. |
Nuestro próximo ejemplo muestra que hay conjuntos infinitos tales que cada uno de sus puntos es aislado.
Ejemplo 5.3.4. Los Naturales en los Reales son un subconjunto infinito tal que todos sus puntos son aislados. En efecto, para cada número natural m, la bola abierta de centro m y radio 1/2 solamente contiene a un número natural m.
Ejemplo 5.3.5. Consideremos al subconjunto A = [0, 1] de los Reales.
Cualquier punto p en A=]0, 1[ es interior y la bola abierta con centro en p y contenida en A contiene puntos de A diferentes de p; es decir que p es un punto de acumulación de A.
Consideremos ahora a p = 0. Entonces, cualquier intervalo abierto centrado en 0, contiene números positivos que son elementos de A por lo que 0 es un punto de acumulación de A. Análogamente, se verifica que 1 es un punto de acumulación de A. Es decir que todos los puntos de [0, 1] son puntos de acumulación.
Consideremos al subconjunto B=]0, 1] de los Reales. Razonando como arriba, vemos que 0 es un punto de acumulación de B, aunque no pertenece a B.
Ejemplo 5.3.6. Sea A = {1/n : n es un natural positivo}∪{0}. Notemos que por la propiedad arquimediana de los Reales (ver sección 2.4.3) se tiene que para todo r > 0 hay un n tal que 1/n < r. Es decir que cualquier bola abierta con centro en 0 contiene puntos del conjunto diferentes del 0. Es decir que 0 es un punto de acumulación de A. Consideremos ahora al punto p = 1/n. Como los “vecinos” de p son 1/(n + 1) y 1/(n − 1) y como
tomando r = (1/2)|(1/n) − (1/(n + 1)) es fácil verificar que la bola con centro 1/n y radio r contiene solamente al punto 1/n del conjunto. Es decir, que excepto por el 0 todos los puntos de A son puntos aislados.
Ejemplo 5.3.7. Los ejes de coordenadas del plano cartesiano son un conjunto cerrado porque su complemento es la reunión de los cuadrantes que son conjuntos abiertos.
La siguiente proposición caracteriza topogeométricamente a los conjuntos cerrados.
Proposición 5.3.1. Un conjunto F es cerrado, ssi, contiene a todos sus puntos de acumulación.
- Demostración. Si F es el conjunto vacío o todo el espacio, el resultado es trivial. (Como el conjunto vacío no tiene puntos de acumulación, los contiene a todos)
- Supongamos que F fuera un conjunto que contiene a todos sus puntos de acumulación y sea x un punto cualquiera del complemento de F. Como x no está en F, no puede ser un punto de acumulación de F. Por lo tanto, hay una bola abierta con centro en x que no contiene puntos de F, es decir que está contenida en Fc. Lo que prueba que Fc es un conjunto abierto y, por lo tanto, que F es cerrado.
- Supongamos ahora que F fuera cerrado. Necesitamos probar que F contiene a todos sus puntos de acumulación. Si hubiera un punto de acumulación x de F que no estuviera en F, estaría en Fc. Pero, al ser Fc abierto, habría una bola abierta con centro en x totalmente contenida en Fc lo que implicaría que no puede contener punto alguno de F; o sea que no puede ser punto de acumulación. Luego, F debe contener a todos sus puntos de acumulación.
La siguiente proposición muestra que un punto de acumulación tiene muchos vecinos.
Proposición 5.3.2. Sea p un punto de acumulación de un conjunto A en un espacio métrico E. Cada vecindad de p tiene infinitos puntos de A.
- Demostración. Sea V una vecindad de p Mostraremos que podemos hallar una sucesión x1,..., xn,... de puntos de V ∩ A, que son diferentes entre si y diferentes de p. Por definición de vecindad, hay una r1–vecindad de p totalmente contenida en V. Por definición de punto de acumulación, hay un punto x1 ≠ p de A contenido en la r1–vecindad. Sea r2 = d(x1, p), por la definición r2 es un número positivo menor que r1. En la r2–vecindad hay un punto x2 de A que es diferente tanto de p como de x1 (ya que r2 < r1). Supongamos que hemos construido una sucesión de puntos de V ∩ A: x1,..., xk tales que todos ellos son diferentes de p y tales que d(x1, p) > d(x2, p) > ··· > d(xk, p). Razonando como arriba, poniendo r{k+1} = d(xk, p), podemos hallar en la r{k+1}–vecindad un nuevo punto x{k+1} en V ∩A tal que es diferente de p y de los puntos anteriormente seleccionados. Por inducción, obtenemos una sucesión infinita de puntos (xn) en V ∩ A, todos diferentes entre si y diferentes de p. Lo que prueba nuestra proposición.
- Demostración.
- (⇒) Supongamos que d(p,A) = 0. Si p está en A no hay nada más que probar.
- Supongamos que p no está en A y que no fuera un punto de acumulación de A.
- Entonces, podríamos hallar un r > 0 tal que la r–vecindad de p fuera disjunta de A. Pero, eso implicaría que para todo a en A, d(p, a) ≥ r, de donde d(p,A) ≥ r, lo que contradice la hipótesis. Por lo tanto, si p no está en A debe ser un punto de acumulación de A.
- (⇐) Si p está en A, se cumple que d(p,A) = 0. Supongamos que p fuera un punto de acumulación de A y que d(p,A) = d > 0. Entonces, habría un n tal que 1/n < d.
- Por definición de punto de acumulación, la 1/n–vecindad de p contiene al menos un punto de A, digamos a, diferente de p. Luego,
- lo que es absurdo. Luego, d(p,A) = 0.
- En R2, una bola cerrada es un círculo de igual centro y radio; mientras que la esfera es la circunferencia correspondiente.
- En la línea real, la bola cerrada Br[a] es el intervalo cerrado [a − r, a+ r] y la correspondiente esfera es el conjunto {a − r, a + r}.
- Demostración. Sea F = Br[a]. Probaremos que el complemento de F es un conjunto abierto. Si dicho complemento es vacío no hay nada que probar. :Supongamos que x es un punto de Fc. Entonces, se tiene que d(x, a) > r. Sea r′ = d(z, a) − r. r′ es un número positivo. Sea y un punto de Br'(x).. :Entonces,d(x, a) ≤ d(x, y) + d(y, a), lo que implica que
- lo que muestra que y está en Fc. Es decir que Fc es abierto. Luego F es cerrado.
- Sea S = Sr(a). Notemos que Sc es la reunion de los x tales que d(x, a) < r con los x tales que d(x, a) > r. Es decir que
- Por lo tanto, Sc es abierto (reunión de abiertos) y, en consecuencia, S es cerrado.
- El conjunto vacío y todo el espacio son conjuntos cerrados.
- La reunión de una familia finita de cerrados es un conjunto cerrado.
- La intersección de una familia cualquiera de cerrados es un cerrado.
- ¿Cuándo un conjunto no es cerrado?
- ¿Cuando un punto no es punto de acumulación de un cierto conjunto?
- ¿Cuáles de los siguientes subconjuntos de la línea real son cerrados?
- El conjunto Z de los enteros.
- El conjunto Q de los racionales.
- Un conjunto que contiene exactamente dos puntos.
- Un intervalo de la forma [a, b[.
- {x ∈ R : x = 1/n, n ∈ N+ }.
- {x ∈ R : x ≠ 1/n, n ∈ N+ }.
4. ¿Cuáles de los conjuntos siguientes son abiertos? ¿cuáles son cerrados?
- {x ∈ R : |x − 5| ≤ 3}.
- {x ∈ R : |x − 2| > 5}.
- ∩n ∈ N[−1, 1/n[ en R.
- A line in the plane R2.
- {(x, y) ∈ R2 : |x − 3| < 2, |y − 5| > 1}.
5. ¿Cuándo un punto p NO es un punto de acumulación de un conjunto A?
6. ¿Cuáles son los puntos de acumulación del conjunto de los racionales positivos en R?
7. Sea A un subconjunto de R. ¿Es necesariamente el supremo de A un punto de acumulación de A?
8. Sea A un subconjunto no vacío, cerrado y acotado de la línea real. Probar que el supremo de A está en A. Enunciar y probar un teorema análogo para ínfimos.
9. Sea A un conjunto de números reales abierto, no vacío y acotado superior e inferiormente. Probar que el supremo y el ínfimo del conjunto no pertenecen al conjunto.
10. Sean A y B subconjuntos de la línea real. Cuando p es un punto de acumulación de A ∪ B, ¿necesariamente p es un punto de acumulación de A o de B?
11. Cada conjunto con exactamente un elemento es cerrado.
12. Probar que R2 \ {0, 0)} es abierto. (Este ejercicio apareció en la sección anterior, pero ahora hay una respuesta más fácil)
13. Sea Z2 = {(x, y) ∈ R2 : x, y son números enteros}. Probar que Z2 es un conjunto cerrado.
14. ¿Cuáles son los puntos de acumulación del conjunto {(x, y) ∈ R2 : 3x2 + 2y2 = 1}?
15. Probar que en un espacio discreto (con métrica 0–1) todos los subconjuntos son abiertos y cerrados.
16. Suponer que para toda r–vecindad del punto p hay un punto de A diferente de p. Probar que p es un punto de acumulación de A.
17. El punto a es un punto de acumulación de A, ssi, es un punto de acumulación de A \ {a}.
18. En un espacio métrico < E, d > sean p un punto de E y r > 0. Probar que
- {x ∈ E : d(x, p) > r} es abierto, y
- {x ∈ E : d(x, p) ≥ r} es cerrado.
19. Sea A un subconjunto de R.
- Cuando A es un conjunto abierto y B = {(x, y) ∈ R2 : x ∈ A}, entonces B es abierto.
- Cuando A es un conjunto cerrado y B = {(x, y) ∈ R2 : x ∈ A}, entonces B es cerrado
20. Explicar de dos manera diferentes (obviamente lógicamente equivalentes) por qué un conjunto finito de un espacio métrico tiene que ser cerrado.
21. Si d(x,A) > 0 hay una vecindad V de x tal que V ∩ A = ∅.
22. Dar ejemplos en la línea real de
- un subconjunto infinito que no tiene punto de acumulación en R.
- un subconjunto no vacío contenido en el conjunto de sus puntos de acumulación.
- un subconjunto que tiene infinitos puntos de acumulación, pero que no contiene a ninguno de ellos.
23. Sea f : E → E′ una isometría de espacios métricos, probar que f envía conjuntos cerrados en conjuntos cerrados.
Interior, Borde, Exterior y Clausura
[editar]
- (☩) Consideremos una figura plana, por ejemplo un cuadrado. Intuitivamente podemos reconocer puntos que están en el interior de la figura en su borde o en su exterior. En esta sección formalizaremos dichas nociones.
Interior, Exterior
[editar]Recordemos que llamamos punto interior de un conjunto A a un punto que está contenido en un abierto que, a su vez, está contenido en A, o sea tal que A es una vecindad de p. Un punto es interior de un conjunto, cuando todos los vecinos son puntos del conjunto.
¿Cuándo un punto estará en el exterior de un conjunto? Intuitivamente tal punto deberá de estar en el complemento del conjunto, pero un punto en el borde del conjunto (pensemos en una bola cerrada de R2), no está totalmente afuera del conjunto.
Definición. (Interior, Exterior)
Sea X un espacio métrico y A un subconjunto de X Llamamos interior del conjunto A al subconjunto de A formado por todos sus puntos interiores. Simbolizaremos al interior de A por Ao o por Int(A).
Llamamos exterior del conjunto A al interior de su complemento.Ext(A) := (Ac)o = Int(Ac). La siguiente proposición resume las propiedades básicas del interior de un conjunto.
Proposición 5.4.1 (Propiedades del Interior de un Conjunto). Sean A y B subconjuntos de un espacio métrico. Se cumple lo siguiente.
- El interior del conjunto A es un conjunto abierto que contiene a cualquier otro conjunto abierto contenido en A.
- A es abierto, ssi, Ao = A.
- (Ao)o =Ao.
- Si A ⊂ B entonces Ao ⊂ Bo.
- Ao ∪ Bo ⊂ (A ∪ B)o.
- (A ∩ B)o = Ao ∩ Bo.
-
Demostración.
- Sea A un conjunto. Si el interior de A es vacío entonces no hay nada más que probar. Supongamos que el interior de A no fuera vacío. Si A contiene a un abierto U, por definición de punto interior, cada punto de U es un punto interior de A, por lo que U está contenido en el Int(A). Como para cada punto de p del interior, hay una vecindad abierta Vp que lo contiene y está contenida en A. Sigue de lo anterior que la reunión V de todos los Vp es un abierto contenido en A y, por lo tanto, en Int(A). Como cada punto del interior está contenido en algún Vp y, por lo tanto, en V, ya que Int(A) es la reunión de las puntos interiores, concluimos que Int(A) un subconjunto de V. Luego, Int(A) = V, lo que prueba que el interior es abierto.
- Si A es abierto, A es un abierto contenido en A, por lo que A ⊂ Ao. Como siempre el interior es un subconjunto del conjunto, tenemos la afirmación.
- El interior es un conjunto abierto.
- Si A ⊂ B entonces Ao ⊂ A implica que Ao ⊂ B. El resultado sigue de la parte (a).
- Como Ao ⊂ A y Bo ⊂ B, tenemos que Ao ∩ Bo ⊂ A ∩ B, de donde el resultado.
- Como A ∩ B ⊂ A,B se concluye que (A ∩ B)o ⊂ Ao,Bo. De donde, (A ∩ B)o ⊂ Ao ∩ Bo. Lo que concluye la demostración.
Corolario 5.4.2. El exterior de un conjunto es un conjunto abierto.
Clausura y Frontera
[editar]-
(☩) ¿Cómo definir el borde o frontera de un conjunto? Pensemos en un
círculo abierto del plano, su borde es la circunferencia, que son los puntos
del plano pegados al círculo. Formalmente, puntos de acumulación. Pudiéramos
pensar que el borde consiste de los puntos de acumulación que no están
en el conjunto, pero si a nuestro círculo abierto le agregamos inicialmente
una semicircunferencia; intuitivamente, los puntos de la semicircunferencia
son puntos de acumulación que están en el conjunto.
Veamos que tiene de especial un punto p del exterior de un conjunto A. Por definición, ese punto es interior al complemento de A. Por lo que hay una vecindad V del punto que está totalmente contenida en Ac. Luego, V ∩ A = ∅. Es decir que el punto p no es ni punto de A ni punto de acumulación de A. Cuando un punto no esté en el exterior de A, entonces deberá ser un punto de A o un punto de acumulación de A. Tales puntos recibirán un nombre especial: puntos de la clausura de A.
Definición. (Clausura). Sea A un subconjunto de un espacio métrico E. Llamamos clausura de A al conjunto denotado por Cl(A) o A-- y que está formado por los puntos que están en A o que son puntos de acumulación de A. Un punto de clausura de un conjunto es un punto de la clausura del conjunto.
Notemos que un punto p está en la clausura de A, ssi, para cada vecindad V de p, V ∩ A ≠ ∅. Algunos autores llaman adherencia a la clausura.Usando la noción de clausura, definiremos la noción de frontera de un conjunto.
Definición. (Frontera) La frontera o borde de un conjunto A en un espacio métrico es el conjunto formado por los puntos comunes a las clausuras de A y de su complemento.
Fr(A) := Cl(A) ∩ Cl(Ac). Ejemplo 5.4.1. Sea A =]a, b[⊂ R. La clausura de A es el intervalo cerrado [a, b]. El exterior de A es
]−∞,a[ ∪ ]b,+∞[ con clausura ]−∞,a] ∪ [b,+∞[. Luego, la frontera de ]a, b[ es el conjunto{a, b}, o sea el conjunto formado por sus extremos.
La notación usual para la clausura del conjunto A es . Por razones tipográficas, no es fácil escribir lo anterior, por lo que usaremos Cl(A) o A--.
Sigue de la definición de clausura que los puntos de la clausura de un conjunto son o puntos del conjunto o puntos de acumulación del conjunto. Notemos que cuando un conjunto A es cerrado, coincide con su clausura.
Ejemplos 5.5.1.
- Un conjunto cuyos puntos son todos aislados es un conjunto cerrado, por lo tanto es igual a su clausura.
- La clausura de un intervalo real cualquiera con extremos a y b es el intervalo cerrado[a, b].
- La clausura del conjunto vacío es el conjunto vacío.
Sigue, también, de la definición de clausura que cuando un punto p no está la
clausura de un conjunto, está en el exterior de ese conjunto, que es un conjunto
abierto; es decir que el complemento de la clausura es abierto, lo que implica que
la clausura es un conjunto cerrado. En símbolos,
A-- = Cl(A) = (Ext(A))c = (Ac)o)c = Acoc.
Como veremos, en la siguiente proposición, se trata del cerrado más pequeño que contiene al conjunto. La proposición muestra las propiedades básicas de la clausura de un conjunto. Por comparación con la proposición 5.4.1 podemos afirmar que “clausura” e "interior” son nociones duales.
Proposición 5.4.3 (Propiedades de la Clausura de un conjunto). Sean A y B subconjuntos de un espacio métrico. Se cumple que
- La clausura de un conjunto A es un conjunto cerrado que contiene a A y que está contenido en cualquier conjunto cerrado que contenga a A.
- A es cerrado, ssi, Cl(A) = A.
- Cl(Cl(A))= Cl(A).
- Si A ⊂ B entonces Cl(A) ⊂ Cl(B).
- La clausura de la union de A con B es igual a la reunión de la clausura de A con la clausura de B. Cl(A ∪ B) = Cl(A) ∪ Cl(B).
- La clausura de la intersección de dos conjuntos está contenida en la intersección de la clausura de dichos conjuntos. Cl(A ∩ B) ⊂ Cl(A) ∩ Cl(B).
-
Demostración.
- Sabemos que la clausura de A es el complemento del exterior de A, que es abierto, por lo que la clausura es cerrado. Si F es un conjunto cerrado que contiene a A, todos los puntos de A están en F. Por lo que cualquier punto de acumulación p de A también está en F, ya que cualquier vecindad de p contiene puntos de A y, por lo tanto, de F diferentes a p. Luego, F contiene a Cl(A).
- Trivial.
- La clausura es un conjunto cerrado.
- Si A ⊂ B, como B ⊂ Cl(B), A está contenida en el cerrado Cl(B). De donde el resultado.
- Como A ⊂ Cl(A) y B ⊂ Cl(B), tenemos que A ∪ B es un subconjunto de Cl(A ∪ B)— que es un conjunto cerrado, por lo tanto, Cl(A ∪ B) ⊂ Cl(A) ∪ Cl(B). Como A y B son subconjuntos de A ∪ B ⊂ Cl(A ∪ B), tenemos que A y B son subconjuntos de Cl(A ∪ B). Luego, Cl(A) ∪ Cl(B) ⊂ Cl(A ∪ B). Lo que prueba la igualdad indicada.
- A ∩ B ⊂ A,B ⇒ Cl(A ∩ B) ⊂ Cl(A), Cl(B). De donde el resultado.
Conjuntos Densos
[editar]Sabemos de las propiedades de los números reales que en cada vecindad de un número real siempre hay al menos un número racional. Ver la sección 2.5.
En términos de lo visto en este capítulo, podemos expresar lo anterior diciendo que los Reales son la clausura de los Racionales. Generalizamos esa relación con la siguiente definición.
Definición. (Subconjunto Denso)
Sea E un espacio métrico. Decimos que un subconjunto A de E es denso en E, ssi, la clausura de A es igual a E (o sea que E = Cl(A)).
La observación anterior muestra que los Racionales son densos en los Reales. Opuesto a este concepto, tenemos lo siguiente: un conjunto es nunca denso en E, ssi, su clausura tiene interior vacío. Por ejemplo, los Naturales son un conjunto nunca denso de la línea real.
Ejercicios 5.4
[editar]- Hallar el interior, exterior, frontera y clausura de cada uno de los siguientes
conjuntos en la línea real.
- [0, 1[.
- {t ∈ R : |t − 5| < 3}.
- {2n : n ∈ N}.
- {1/(2n) : n ∈ N}
- Los Racionales.
- Q ∩ [0, 1].
- Probar que
- (Ao)o = Ao.
- (A--)-- = A --.
- Probar las afirmaciones de la proposición 5.4.3 usando la relación A-- = Acoc
- Probar que el exterior de A es el complemento de la clausura de A.
- Hallar el interior, exterior, frontera y clausura de cada uno de los siguientes
conjuntos del plano R2.
- {(x, y) ∈ R2 : y ≥ x2}.
- El círculo unitario, {(x, y) : x2 + y2 ≤ 1}
- {(x, y); |x| > 1, |y| ≥ 1}.
- {(x, y) ∈ R2 : x > 0, xy < 1.}.
- . Hallar la frontera de cada uno de los conjuntos siguientes:
- A = {x, y) ∈ R2 : xy > 1}.
- B = {(x, y) ∈ R2 : x2 < y}.
- C = A ∩ B.
- (Cubo Unitario) Llamamos cubo unitario al subconjunto de Rn denotado por In y definido por
Hallar el interior, la clausura y la frontera del cubo unitario.
- Demostrar que, en Rn, la clausura de una bola abierta es la bola cerrada del mismo centro y radio y su frontera es la esfera correspondiente. ¿Es lo anterior válido para cualquier espacio métrico?
- Dar un ejemplo de un conjunto infinito que no tenga puntos interiores.
- Hallar conjuntos A, B, C y D de la línea real tales que
- Int(A) ∩ Int(B) = Int(A ∩ B).
- Int(C) ∪ Int(D) Int(C ∪ D).
- Hallar conjuntos A, B, C y D de la línea real tales que
- Cl(A ∪ B) = Cl(A) ∪ Cl(B).
- Cl(C ∩ D) ⊂ Cl(C) ∩ Cl(D, sin igualdad.
- Investigar la validez total o parcial de los siguientes enunciados
- Int(Cl(A)) = A.
- Cl(A) ∩ A = A.
- Cl(Int(A)) = A.
- Fr(Cl(A)) = Fr(A)
- (Clausura y Bolas Abiertas) Sea A un subconjunto de un espacio métrico.
- Probar que cuando toda bola abierta de centro p contiene un punto de A diferente de p, entonces p es un punto de acumulación de A.
- Probar que cuando toda bola abierta de centro p y radio 1/n, n natural, contiene un punto de A diferente de p, entonces p es un punto de acumulación de A.
- Sea A un conjunto no vacío. Probar que x está en A cuando, y solo cuando, d(x,A) = 0.
- Sea A un conjunto no vacío cualquiera en un espacio métrico < E, d >,
A ≠ E. Demostrar las siguientes afirmaciones.
- x ∈ Aco, ssi, d(x,A) > 0.
- x ∈ Ao, ssi, d(x,Ac) > 0.
- Si A y B son conjuntos no vacíos de < E, d >. Probar que d(Cl(A),Cl(B)) = d(A,B).
- Probar que para cualquier conjunto A, la frontera de A coincide con la frontera del complemento de A.
- Sean A y B son conjuntos cualesquiera de <E,d>, si Cl(A) ∩ Cl(B) = &empty: entonces Fr(A ∪ B) = Fr(A) ∪ Fr(B).
- Probar que la frontera de la frontera de un conjunto está contenida en la frontera del conjunto.
- Sea F un subespacio de < E, d > y A ⊂ F. Hallar relaciones entre el interior y la clausura de A en F con respecto al interior y la clausura en E.
- Probar que los siguientes enunciados son equivalentes para un subconjunto
A de un espacio métrico E.
- A es denso en E.
- Para todo x en E, d(x,A) = 0.
- Para todo abierto no vacío U de E, U ∩ A ≠ ∅.
- Sea A un subconjunto cualquiera de un espacio métrico E. B = Ac ∪ A es denso en E.
- Demostrar que si A y B son abiertos y densos en un espacio métrico E, entonces A ∩ B también es denso.
- Si A y B son conjuntos en un espacio métrico E tales que A ∪ B es denso en E y B es nunca–denso, entonces A es denso en E.
- Dar un ejemplo de una sucesión de conjuntos densos cuya intersección no sea densa.
- Demostrar que un conjunto A de un espacio métrico E es nunca–denso, ssi, para todo abierto U hay un abierto no vacío V contenido en U y tal que V ∩ A = ∅.
- Sea f : E → E′ una isometría. Sea B = f(A), ¿qué podemos decir de la imagen del interior (resp. exterior, clausura, frontera) de A?
Espacios Ultramétricos
[editar]Los espacios ultramétricos se caracterizan por ser espacios métricos donde la métrica satisface la propiedad adicional
Vimos en el capítulo anterior que los Racionales con el valor absoluto p--ádico
cuando x &neq; 0,y |0|,sub>p = 0; donde si x = m/n, vp(m) (resp. vp(n)) es el exponente de la mayor potencia de p que divide a m (resp. a n). Por su parte, vp_p(x) = vp(m) - vp(n). Vimos, también, que en cualquier espacio ultramétrico se cumple lo siguiente.
- Cada punto de una bola, sea abierta o cerrada, es un centro de la bola.
- Cuando dos bolas tienen intersección no vacía, aquella cuyo radio es menor o igual que el radio de la otra, está contenida en la otra bola.
Proposición 5.5.1. En un espacio ultramétrico se cumple que las bolas abiertas, las bolas cerradas y las esferas son conjuntos abiertos y cerrados a la vez.
- Demostración. Probaremos lo afirmado acerca de las bolas abiertas y dejaremos el resto como ejercicio.
Las bolas abiertas son siempre conjuntos abiertos, luego solamente tenemos que probar que son cerrados. Sea B=B(x;r). Si B no tiene puntos de acumulación, B es trivialmente un conjunto cerrado. Sea p un punto de acumulación de B, entonces cada bola abierta con centro en p tiene intersección no vacía con B \ {p}$; en particular B(p;r). Sigue de lo anterior que $B(p;r)=B$; lo que implica que p está en
B. Como B contiene a todos sus puntos de acumulación es un conjunto cerrado.
Ejercicios 5.5
[editar]- Probar lo que falta de la demostración de la proposición~ 8.5.1..
- Sea Q con el valor absoluto 5--ádico.
- Los únicos valores del valor absoluto p--ádico son potencias enteras de 5 o 0.
- Si r no es una potencia de 5, entonces la esfera S(0;r) es vacía.
- Verificar que la bola abierta con centro en 0 y radio 5 es diferente de la bola cerrada con igual centro y radio. Usar lo anterior para concluir que en un espacio ultramétrico no se cumple necesariamente que: (i) la clausura de una bola abierta, es la bola cerrada de igual centro y radio; (ii) el interior de una bola cerrada, es la bola abierta de igual centro y radio (iii) las bolas abiertas tienen frontera no vacía. Todas las afirmaciones anteriores son válidas en espacios euclídeos.
- Hallar ejemplos de bolas concéntricas de distinto radio que son iguales.
\end{enumerate}
Ejercicios del Capítulo 5
[editar]A. Cierto o Falso
- Cada espacio métrico discreto es finito.
- En un espacio métrico, cada conjunto con un único punto es cerrado.
- Hay conjuntos abiertos cuya frontera es vacía.
- Hay conjuntos cerrados que no contienen puntos de acumulación.
- Un punto es de acumulación de un conjunto cuando cada abierto que contiene al punto tiene intersección no vacía con el conjunto.
- Una bola abierta nunca es un conjunto cerrado
- La frontera de un conjunto está contenida en el conjunto.
- Un punto que no es punto de acumulación de un conjunto es un punto asilado del conjunto.
B. Hacer lo indicado o probar las afirmaciones.
- Sea A un conjunto no vacío de números reales acotado superiormente. Si s = sup(A) no es elemento de A, entonces s es un punto de acumulación de A.
- Hallar una familia infinita de subconjuntos cerrados de R cuya reunión no sea cerrada.
- Hallar una familia infinita de subconjuntos abiertos de R cuya intersección no sea abierta.
- Dar ejemplos en la línea real de:
- un subconjunto infinito que no tiene puntos de acumulación,
- un subconjunto no vacío contenido en el conjunto de sus puntos de acumulación,
- un subconjunto que tiene infinitos puntos de acumulación, pero que no contiene a ninguno de ellos.
- Todo conjunto abierto y no vacío en R contiene números racionales e irracionales.
- Todo intervalo cerrado en R es intersección de una sucesión de abiertos.
- Cada vecindad V de un punto de la frontera del conjunto A es tal que
V ∩ A ≠ ∅ y V ∩ Ac ≠ &empty:. - A abierto implica que Int(A) = Cl(A) \ Fr(A). ¿Vale lo anterior para un conjunto cualquiera?
- Sea A un subconjunto no vacío de un espacio métrico E. Sean Vr(A) = {x ∈ E : d(x,A) < r} y Wr(A) = {x ∈ E : d(x,A) ≤ r}. Entonces,
- Vr(A) es una vecindad abierta de A.
- Wr(A) es un conjunto cerrado.
- La intersección de todos los Vr(A), r > 0, es la clausura de A.
- Si A y B son conjuntos en un espacio métrico < E, d >, probar que
(A ∩ B)′ ⊂ A′ ∩ B′, y (A ∪ B)′ = A′ ∪ B′. (donde X’ es el conjunto derivado de X, o sea aquel subconjunto formado por los puntos de acumulación de X). Dar un ejemplo donde la primera relación es una inclusión propia.
- A es abierto y B cualquiera en un espacio < E, d >. Probar que
A ∩ Cl(B) ⊂ Cl(A ∩ B), y Cl(A ∩ Cl(B)) ⊂ Cl(A ∩ B). - Si A es abierto y B cualquiera en un espacio < E, d >, probar que <centger> A ∩ B = ∅ ⇒ A ∩ B = ∅.
- Sea A un subconjunto de Rn y p un vector cualquiera. Sea p+A = {p+x : x ∈ A}. la traslación de A por p.
- Si A es abierto, p + A, también es abierto.
- ¿Qué se puede decir de p + F, cuando F es cerrado?
- . Sean A, B subconjuntos de Rn. Sea A + B = {a + b : a ∈ A, b ∈ B}.
-
a) Investigar si A + B es abierto, cuando al menos uno de los conjuntos
(A, B) lo es, o cuando ambos lo son.
- Investigar si A + B es cerrado, cuando al menos uno de los conjuntos (A, B) lo es, o cuando ambos lo son.
- Investigar la relación entre A, B, y A + B.
- Investigar la relación entre Int(A + B) e Int(A), Int(B).
- Sea A un subconjunto de Rn. Sea −A = {−a : a ∈ A}.
- Investigar si −A es abierto (resp. cerrado) cuando A lo es.
- Investigar la relación entre Cl(−A) y Cl(A).
- Investigar la relación entre Int(−A) e Int(A).
16. (Espacios Ultramétrico) Ver definición en la sección 4.7. Sea E un espacio ultramétrico. Probar las siguientes afirmaciones.
- Cuando dos bolas (abiertas o cerradas ambas) tienen un punto en común, las bolas coinciden.
- Probar que las bolas abiertas son conjuntos cerrados.
- Probar que las bolas cerradas son conjuntos abiertos.
- Dos bolas abiertas diferentes de radio r contenidas en una bola cerrada de radio r tienen una distancia igual a r.
Referencias
[editar]
La Continuidad
[editar]Introducción
[editar]Las funciones continuas aparecen en cursos de Cálculo, donde son informalmente descritas como aquellas funciones cuyas gráficas no presentan "saltos". Más formalmente, se dice que una función f es continua en un punto p de su dominio cuando, y solo cuando, lim{x \to p}f(x) = f(p). Aquí, límite significa que dado un valor numérico ε, podemos hallar un número δ > 0 tal que la distancia de f(x) a f(a) se puede hacer menor que ε, cuando se cumple que la distancia de x a p es menor que δ. Es decir que para todo ε >0, podemos hallar un δ >0, tal que
(*)
- La terminología epsilon--delta es tradicional. Matemáticamente hablando, podríamos usar cualquier otro nombre para esos números, por ejemplo r y s.
En este capítulo, estudiaremos la continuidad para funciones entre dos espacios métricos cualesquiera.
Definiciones de Continuidad
[editar]La noción de continuidad es central en nuestros estudios topogeométricos, por lo que empezaremos viendo varias versiones (lógicamente equivalentes) para su definición. Recordemos, primeramente, la definición de continuidad que dimos en el capítulo 4.
Sean E, F espacios métricos y f una función de E en F. Dijimos que la función f era continua en un punto p de E, ssi,
-
(I) para todo ε > 0, podemos hallar un δ > 0 tal que
Esta definición es la generalización directa de la definición formal de los cursos de Cálculo. Diremos que una función es discontinua en un punto de su dominio, cuando no sea continua en ese punto.
Veremos a continuación, algunas versiones equivalentes a la definición anterior, pero usando el lenguaje de bolas abiertas---que fue introducido posterior a la definición anterior.
- f es continua en p, ssi,
(II) para toda ε--vecindad de f(p) hay una δ--vecindad de p tal que
(III) para toda ε-- vecindad de p hay una δ--vecindad de p tal que
Los lectores deberán revisar los enunciados anteriores hasta entender plenamente por qué esos dos enunciados dicen lo mismo que la definición original. A continuación, expresaremos la definición en término de vecindades.
- f es continua en p, ssi,
(IV) para toda vecindad V de f(p), hay una vecindad U de p tal que para todo x se cumple que
(V) para toda vecindad V de f(p) hay una vecindad U de p tal que
Claramente, (IV) y (V) son equivalentes. Probaremos que (III) y (V) también lo son.
-
Demostración.
Supongamos (III). Sea V una vecindad de f(p). Entonces, hay una ε--vecindad B' de f(p) contenida en V. Por la suposición, hay una δ--vecindad B de p, tal que f(B) ⊂ B'. Poniendo U = B, tenemos que f(U) = f(B) ⊂ B' ⊂ V.
Supongamos ahora (V). Sea ε >0 dado y sea V la ε--vecindad de f(p). Por la suposición, hay una vecindad U de p tal que f(U) ⊂ V. Como U es vecindad de p, hay una bola abierta B_\delta(p) contenida en U. Luego,
- Explicar lo que significa que una función sea discontinua en un punto, usando cada una de las alternativas (I al VI) de la definición de continuidad.
- Sea E un espacio discreto con métrica 0-1 y sea F un espacio métrico cualquiera. Probar que cualquier función de E en F es continua.
- Sea E el espacio métrico definida en R por la métrica discreta 0--1. Cualquier función de E en R (con la métrica usual) es continua, pero id: R → E tal que id(x) = x no lo es. Explicar.
- Si f es continua en p y g es continua en f(p) entonces g o f es continua en p.
- Si f y g son continuas (en todo su dominio), su composición es continua.
- Sea W una vecindad de g(f(p)). Por definición de continuidad aplicada a g en f(p), tenemos que hay una vecindad V de f(p) tal que g(V) está contenida en W. Por definición de continuidad de f en p, tenemos que hay una vecindad U de p tal que f(U) está contenida en V. Luego, g(f(U)) ⊂ g(V), lo que implica que g(f(U)) ⊂ W. Esto prueba la afirmación.
- Directo de la parte anterior.
- Suponer que f es continua en p, es suponer que para un ε cualquiera se cumple que d(f(x),f(p))< ε, siempre que restrinjamos los valores de x a una vecindad adecuada (por ejemplo, una bola abierta de centro p y de radio un cierto δ). Coloquialmente, decimos que "podemos hacer d(f(x),f(p)) tan pequeña como queramos" ---a veces, agregando la condición de "cuando d(x,p) sea lo suficientemente adecuada o pequeña".
- Probar que una función es continua puede resultar complicado usando directamente la definición (en cualquiera de sus alternativas), por lo que usaremos teoremas tales como que la composición de funciones continuas es continua y otros que veremos más adelante.
- Una estrategia útil---cuando usamos directamente la definición---consiste en acotar superiormente a d(f(x), f(p)) en una vecindad de p, mediante una expresión que contenga d(x,p). Cuando podamos lograr que tal acotamiento se exprese como una constante veces d(x,p), la continuidad sera inmediata. Ver los ejemplos 4.3.1 y 3.3.2 del capitulo 4, y, más adelante, el lema 5.3.5.
- (♠) Para poder dar ejemplos significativos usaremos un resultado de Cálculo que establece que "toda función derivable en un punto es continua en ese punto." En particular, son continuas, en sus dominios, las funciones potencias, trigonométricas, exponenciales y logarítmicas. Usando lo anterior, por ejemplo, podemos afirmar que la función f tal que f(x) = sen(ex) es continua, ya que es una composición de funciones continuas: x ↦ e^x ↦ sen(ex).
- a. x ↦ sen(x) + ex cos(x) (producto y suma de funciones continuas).
- b. g(x) = 1/(1 + x2) (cociente de funciones continuas, además el denominador nunca es nulo).
- c. h : R2 → R, h(x, y) = x2 + y2. (proyecciones son continuas).
- Sea f : [−2,−1]∪[1, 2] tal que f(x) = −1 cuando x es negativo y f(x) = 1 cuando x > 0. ¿Es f continua?
- Sea f : <>b>R → <>b>R tal que f(x) = | sen(x)|. Trazar la gráfica de f. ¿Es f continua?
- Sea f : E → R continua, ¿es |f| continua? (|f|(x) := |f(x)|)
- Sean f, g funciones continuas de E en R. Probar lo siguiente.
- {x ∈ E: f(x) = g(x) } es cerrado en E.
- {x ∈ E: f(x) < g(x) } es abierto en E.
- Sean E un espacio métrico, A un subconjunto de E y f: E → F continua. Si x es un punto de la clausura de A, entonces f(x) es un punto de la clausura de f(A).
- (Principio de Extensión de Identidades) Sean f y g funciones continuas de un espacio métrico E en un espacio métrico F. Si f(x) = g(x) para todo x en un subespacio A denso en E, entonces f = g.
- (Principio de Extensión de Desigualdades) Sean f y g funciones continuas de un espacio métrico E en R. Si f(x) ≤ g(x) para todo x en un subespacio A denso en E, entonces f(x) ≤ g(x), para todo x en E.
- |(x-p)(x-q)| < δ2.
- |(x-p)q| < | δ.
- |p(y-q)| < |p| δ.
-
Supongamos δ escogido de manera que δ ≤1, para que δ2 ≤ δ. Entonces, usando (**) y los estimados anteriores, tenemos que
Luego, para que |xy-pq| sea menor que ε es suficiente con escoger
Como para todo (x,y) en Bδ(p,q), |x-p|,|y-q| ≤ ||(x,y)-(p,q)||<δ, vemos que la función multiplicación es continua. - La suma y la resta de las funciones f y g son funciones continuas.
- El producto de f y g es continuo.
- El producto af es continuo, a real.
- Si g no toma el valor 0, g(x) ≠ 0 para todo x en X, 1/g es continua.
- Si g no toma el valor 0, g(x) ≠ 0 para todo x en X, f/g es continua.
- La función x ↦ f(x) + g(x) puede descomponerse como
Es decir, como la composición de dos continuas, por lo que es continua. - La función x → f(x) g(x) puede descomponerse como
- Sigue de (b), tomando g(x) = a.
- La función x → 1/g(x) puede descomponerse como Es decir como la composición de dos continuas, por lo que es continua.
- Como , el resultado sigue de (b) y (d).
- f(x,y,z) = x2 + y2.
- g(x,y,z) = 2x - 3y + z2 - 8.
- f(x,y) = sen(x2+y2);
- g(x,y,z) = e-z sen(xy).
- Cuando f1, ... , fn : E → R son continuas, entonces su suma y su producto también lo son.
- Probar que la función x ↦ |x| de R en R es continua.
- Probar que la función x ↦ ||x|| de \R^n en R es continua.
- Probar que la función (x,y) ↦ d(x,y) es continua.
- Probar que la elipse con ecuación 9x2+4y2 = 36 es un subconjunto cerrado de R2.
- (i) f y g coinciden en U ∩ A, con la posible excepción de p, y
- (ii) g(p) = L.
- (Límites y Operaciones)
Sean f y g funciones con codominio un subconjunto de ;los Reales y tales que limx → p f(x) = L y limx → p g(x) = M. Entonces,
- limx → p (f(x) + g(x)) = L + M.
- limx → p (f(x) - g(x)) = L - M.
- limx → p (f(x) g(x)) = L M.
- limx → p , siempre que M ≠ 0.
- Sean g y f funciones con g continua.
Entonces,
- Sea f una función con valores reales. Suponer que hay una vecindad V de p tal que para todo x en V, x ≠ p se cumple que f(x) ≥ 0. Entonces, cuando el límite existe, se tiene que limx → p f(x) ≥
- (Teorema del Sandwich])Sean f, g y h funciones reales tales que en una vecindad U de p se cumple para todo x, x ≠ p, que
Si \limx → p f(x) y limx → p g(x) existen y son iguales, digamos a L, entonces limx → p g(x) existe y es igual a L. - Sea f una función real definida en una vecindad V de p con la posible excepción de p.
Si limx → p |f(x)| = 0 entonces, limx → p f(x) = 0. - límn sn = p (el limite de la sucesión (sn) es p);
- límn → ∞ sn = p;
- sn → p (sn converge a p).
- (a) Cuando {xn} es finito la sucesión converge, ssi, hay un único término cuyo valor se repite infinitas veces.
- (b) Cuando {xn} es infinito la sucesión converge, ssi, el conjunto {xn} tiene un único punto de acumulación. En tal caso, dicho punto de acumulación es el límite de la sucesión.
- (a) f es continua en p.
- (b) Para cada sucesión (xn) en E, xn → p ⇒ f(xn) → f(p).
- Probar que las diferentes versiones de límite (vecindad, métrica y cardinal) son equivalentes.
- Sea (sn) una sucesión convergente de un espacio métrico. Probar que para todo ε > 0 hay un n0 tal que m, n ≥ n0 implica que d(xm, xn) < ε.
- Probar que la sucesión en R, sn = (n−1)/n converge.
- Probar que la sucesión en R, sn = 1/n2 converge. (no hay mucho que calcular, basta con mencionar un ejemplo y una proposición).
- (a) La sucesión x + y converge a a + b.
- (b) La sucesión xy converge a ab,
- (c) La sucesión αx converge a αa, α número real.
- (1) n ≥ n1 ⇒ |xn − a| < ε/2,
- (2) n ≥ n2 ⇒ |yn − b| < ε/2.
- Sea n0 = m´ax{n1, n2}. Entonces, n ≥ n0 ⇒ |(xn − yn) − (a + b)| = |(xn − a) + (yn − b)| ≤ |xn − a| + |yn − b| < ε/2 + e/2 = ε.
- Debemos probar que hay un natural n0 tal que para todo m,m ≥ n0 se cumple que |xmym − ab| < ε.
Sea δ un número positivo, cuyo valor específico determinaremos más adelante;
por ahora simplemente supondremos que es menor o igual a 1. Se tiene la
siguiente identidad (que los lectores deberán verificar)
|xnyn − ab| = |xn − a| |yn − b| + |a| |yn − b| + |b| |xn − a|. (*) Veremos a continuación, como acotar cada sumando en el lado derecho de (*) en términos de δ, para finalmente expresar δ en términos de ε.
Procediendo como en la parte (a) podemos hallar un n0 tal que
Luego, cuando m ≥ n0 se tiene que
Por lo tanto, si escojemos a δ = mín {jε/(1 + |a| + |b|), 1} obtendremos que
m ≥ n0 ⇒ |xnyn − ab| < ε.(c) Sigue de (b),
- Cuando y entonces y el producto , real.
- Cuando la sucesión es convergente, también lo es la sucesión de normas, .
- Cuando , una sucesión en es convergente, ssi, las sucesiones de sus componentes lo son.
- cuando ,
- cuando
- Cuando S converge, su termino enésimo an tiende a 0;
- La serie geométrica a + ar + · · · + arn + ... , a ≠ 0, converge cuando |r| < 1, diverge si r ≥ 1. Cuando converge su límite es a/(1 − r).
- La serie de potencias ∑n anxn converge cuando ρ = límn |an+1/an| < 1, diverge cuando ρ > 1. El caso ρ = 1 es ambiguo.
- Sea f : R→ R continua. Sea (xn) una sucesión convergente. Entonces (f(xn)) l es una sucesión convergente y límn f(xn) = f(límn xn).
- Probar la proposición 7.3.2.
- Probar la proposición 7.3.3.
- Si (an) es una sucesión de números reales que es creciente (an ≤ an+1) y acotada superiormente, entonces (an) es convergente.
- La suma y el producto de sucesiones reales acotadas son sucesiones acotadas.
- Considerar las sucesiones reales cuyos términos se indican a continuación.
¿Cuáles de esas sucesiones reales son acotadas?¿Cuáles son convergentes?
En caso de convergencia, si fuera posible hallar el límite. Indicar los teoremas
o proposiciones usadas para obtener la respuesta.
a) b) c) d) e) f) g) h) i)
j) k) l) - Probar la proposición 7.3.4.
- Probar que cada expansión decimal de un número real positivo define una sucesión de números racionales, la sucesión de las truncaciones, que es acotada superiormente. Aplicar el postulado del supremo para concluir que dicha expansión tiene un límite.
- Sea u una sucesión en R2 tal que un = (xn, yn), Entonces, la sucesión
(un) es acotada (resp. convergente), ssi, las sucesiones (xn) y (yn) lo son.
Usar ese resultado para evaluar
límn (3 + 1/n, 2+1/n) en R2. Generalizar para sucesiones en Rn. - Sea E un espacio normado cualquiera.
- Las sucesiones en E convergentes son acotadas.
- La suma y el producto de sucesiones acotadas (resp.convergentes) es una sucesión acotada (resp. convergente).
- Sean (xn), (yn) y (zn) sucesiones de un espacio métrico E. Suponer que hay un n0 tal que yn = zn cuando n < n0, y yn = xn cuando n ≥ n0. Las sucesiones (xn), (yn) convergen o divergen simultáneamente. Es decir que podemos alterar una cantidad finita de términos de una sucesión sin afectar su convergencia o divergencia.
- Sea E un espacio métrico con métrica discreta. Probar que cuando una sucesión (xn) es convergente, hay un n0 tal que m ≥ n0 implica que xm = xn0.
- Sea E un espacio métrico. Probar que la suma, resta, multiplicación y cociente de sucesiones de Cauchy son sucesiones de Cauchy.
- y , cuando i ≠ j.
- y , cuando i ≠ j.
- ¿Cuándo un espacio métrico no es completo? Dar un ejemplo de un espacio métrico que no sea completo.
- Suponer que R es un espacio completo. Probar que R2 es completo. Generalizar a Rn.
- Probar que un espacio métrico E es completo, ssi, cada sucesión decreciente de bolas cerradas cuyos radios tienden a cero tiene intersección no vacía.
- Formar un conjunto con todas las sucesiones de Cauchy en X al que denotaremos por SCy(X).
- Definir una relación ∼ entre las sucesiones de Cauchy, por (xn) ∼ (yn) ⇐⇒ límn d(xn, yn) = 0. La relación así definida es de equivalencia.
- Simbolizar por X* al conjunto cociente SCy(X)/ ∼, es decir al conjunto formado por las clases de equivalencia de la relación anterior, Simbolizar por [xn] a la clase de equivalencia de la sucesión (xn).
- Definir una distancia d*([xn], [yn]) = límn d(xn, yn). Probar que la sucesión (d(x_n,y_n))esuna sucesión de Cauchy.
- <X*, d*> es un espacio métrico completo que contiene un subconjunto identificable con X (las sucesiones constantes) y tal que la clausura de X es X*. Tal construcción es total análogo a una de la construcciones de los Reales a partir de los Racionales. Ver por ejemplo Fundamentos del Análisis en el sitio [1].
- Para cada uno de los siguientes enunciados decidir si son válidos o falsos.
En caso de válidos dar una demostración, en caso contrario producir un
contraejemplo.
- Cuando una sucesión converge, cualquier subsucesión converge al mismo límite.
- Cuando una sucesión tiene dos subsucesiones que convergen a límites diferentes la sucesión no tiene límite.
- Cuando una sucesión tiene dos subsucesiones convergentes es convergente.
- Cada sucesión tiene una subsucesión acotada.
- Sea (xn) una sucesión acotada. Entonces, para todo número real a, (xn−a) y (axn) son sucesiones acotadas.
- Sea (xn) una sucesión de números reales. Decimos que diverge a infinito, xn → +∞, ssí, para todo número real positivo a, el intervalo ]a,+∞[ contiene a casi todos los elementos de la sucesión (es decir todos, excepto por una cantidad finita). Enunciar y probar teoremas con respecto a esta noción,
- Sea E un espacio métrico y E′ un subespacio de E. Probar que cada sucesión convergente en E′ es convergente en E al mismo límite. Dar un ejemplo de una sucesión convergente en un espacio, pero que no es convergente en un subespacio.
- Probar que de(x,y) := |ex - ey| es una métrica en R y que respecto a esta métrica R ni es completo. ðescribir la completación de este espacio.
- (I) El conjunto vacío y el conjunto X están en T ;
- (II) La reunión de una familia cualquiera de conjuntos en T está en T ;
- (III) La intersección de dos conjuntos de T está en T .
- Los espacios métricos son espacios topológicos cuya su topología está determinada por los abiertos definidos a partir de las bolas abiertas. Mirar la proposición 5.2.4. Llamamos a esta topología la topología inducida por la métrica. En particular, llamamos línea real a los Reales R con la métrica usual.
- Llamamos espacio topológico discreto a cualquier espacio donde cualquier subconjunto es abierto.
- Llamamos espacio topológico indiscreto aun espacio donde los únicos abiertos son todo el espacio y el subconjunto vacío.
- Sea X = {a, b, c} y sea T = {X, ∅, {a}, {a, b}, {a, c}}. Es fácil verificar que T es una topología de X. Notemos que no hay abiertos que separen a b y c (la propiedad de Hausdorff). Por lo que el espacio X no puede tener una métrica cuyos abiertos coincidan con los elementos de T . Aunque, por ahora, parezcan una curiosidad, estos espacios topológicos finitos pueden tener algunas aplicaciones interesantes.
- El punto p es interior de A, ssi, hay un abierto U que contiene a p y está contenido en A.
- El punto p es exterior a A, ssi, es interior al complemento de A.
- El punto p es de clausura de A, ssi, cada vecindad abierta de p tiene intersección no vacía con A.
- El punto p es de frontera de A,ssi, es de clausura de A y de su complemento.
- El punto p es de acumulación de A, ssi, cada vecindad de p contiene un punto de A diferente de p.
- El punto p de A es aislado en A, ssi, hay una vecindad de p donde el único punto de A es p.
- El interior de A (Int(A) o Ao) es el conjunto de puntos interiores de A.
- El exterior de A (Ext(A) ) es el conjunto de puntos exteriores de A.
- La clausura de A (Cl(A) o A--) es el conjunto de puntos de la clausura de A.
- La frontera de A (Fr(A)) es el conjunto de puntos de la frontera de A.
- a) revisar las propiedades enunciadas en el capítulo 5 que no hagan referencias a nociones dependientes de distancias tales como diámetro, distancia entre conjuntos,etc.
- b) verificar su validez en el contexto de espacios topológicos. Ver también los ejercicios
- (i) el conjunto vacío y el conjunto X están en ,
- (ii) la intersección de cualquier familia de conjuntos de está en , y
- (iii) la reunión de dos conjuntos en está en ;
- Sea X un espacio topológico y sean A y B subconjuntos cualesquiera de
X. Probar que
- a) El interior de A ∩ B es igual a Int(A) ∩ Int(B)
- b) El interior de A es igual a la reunión de todos los abiertos contenidos en A.
- c) La clausura de A ∪ B es igual a la reunión de las clausuras de A y B.
- d) La clausura de A es igual a la intersección de todos los cerrados que contienen a A.
- e) Si A ⊂ B entonces Int(A) ⊂ Int(B) y Cl(A) ⊂ Cl(B).
- f) El interior del complemento de A es igual al complemento de la clausura de A.
- g) La clausura de A es la reunión de A con su frontera.
- h) El interior de A es A \ Fr(A).
- i) Fr(Cl(A)) ⊂ Fr(A) y Fr(Int A) ⊂ Fr(A).
- j) Fr(A ∪B) ⊂ Fr(A) ∪ Fr(B).
- Sea X = [0,∞[ ⊂ R. Sea T = {∅,X} ∪ {[a,+∞]: a ≥ 0}. Probar que T es una topología de X.
- (Topología del punto especial) Sea X cualquier conjunto no vacío y sea p
un punto de X.
Probar que Tp = {∅} ∪ {A ⊂ X : p ∈ A} es una topología de X. - (Topología del punto excluido) Sea X cualquier conjunto no vacío y sea p un punto de X. Probar que T = {X} ∪ {A ⊂ X : p ∉ A} es una topología de X.
- (Topología de los complementos finitos) Sea X cualquier conjunto infinito. Probar que T = {∅} ∪ {A ⊂ X : X \ A es finito } es una topología de X.
- Sea X un espacio con la topología del punto especial p. ¿Cuál es la clausura de {p}? Probar que cuando F es un subconjunto cerrado propio de X, su interior es vacío.
- (Espacio de Sierpinski) Sea X = {a, b} y sea T = {∅,X, {a}}.
- a) Verificar que T es una topología en X que coincide con la topología del punto especial para a y con la topología del punto excluido para b.
- b) Hallar el interior, el exterior, la clausura y la frontera de los conjuntos {a} y {b}.
- ¿Cuáles de los siguientes espacios topológicos son Hausdorff?
- a) Los Reales.
- b) Un espacio discreto.
- c) Un espacio indiscreto.
- d) Un espacio con la topología de complementos finitos (ver definición en un ejercicio anterior).
- e) Un espacio métrico cualquiera.
- Sean X un espacio y Y, Z subespacios de X con Z ⊂ Y . Probar que la topología relativa de Z como subespacio de Y coincide con la topología relativa de Z como subespacio de X.
- Sean X un espacio, A y B subespacios de X y C un subconjunto de A ∩ B. Si C es abierto respecto a las topologías relativas de A y B, C es abierto en X.
- Probar que un subespacio de un espacio Hausdorff es un espacio Hausdorff.
- Sea X un espacio Hausdorff. Para todo p en X, {p} es cerrado.
- Probar que la topología usual de R coincide con la topología relativa como subespacio de R2 con su topología usual.
- Un subconjunto F de un subespacio Y de X es cerrado, ssi, es la intersección de Y con un cerrado de X.
- Sea +∞ un símbolo que no está en N y sea N♯ = N ∪ {+∞}. Sea T el conjunto formado por los subconjuntos de <N♯ cuyo complemento es finito.Probar que:
- a) T es una topología en N♯, y que
- b) la topología de N como subespacio de N♯ es diferente de la topología de N como subespacio de la línea real.
Funciones Continuas y Homeomorfismos
[editar]Funciones Continuas
[editar]La definición de función continua entre espacios topológicos será formalmente igual a la versión de continuidad global en espacios métricos contenida en la proposición 6.4.1. A nivel de topología, lo interesante es la continuidad global.
Definición. (Función Continua en Espacios Topológicos) Sean X y Y espacios topológicos. Sea f : X → Y una función cualquiera. Decimos que la función f es continua, ssi, para cada abierto V de Y, su preimagen, f-1(V), es un abierto en X.
Notemos que si TX y TY son las topologías de X y Y respectivamente, entonces una función continua de X en Y induce una función , ; por lo que decimos que la función inversa de una función continua preserva (a los conjuntos) abiertos.- Las funciones constantes son continuas.
- Sea Y un subespacio de X. La inyección canónica i (deducida de la inclusión) es continua. (i-1(V ) = V ∩ Y.)
- Cualquier función continua entre espacios métricos es continua para los espacios topológicos inducidos por las métricas (ver la proposición citada arriba). Por lo que no haremos distinción entre ambas nociones.
Proposición 8.3.1 (Composición de Continuas). La composición de funciones continuas es continua.- Demostración. Sean f : X → Y y g : Y → Z funciones continuas. Sea W un abierto de Z, entonces g-1(W) es un abierto en Y. Por lo que (g o f)-1(W) = f-1(g-1(W)) es un abierto de X, lo que prueba la proposición.
(Comparar con la demostración de la proposición 6.3.3 referente a la composición de funciones continuas en espacios métricos.)
Veremos, a continuación, una condición equivalente a la definición de continuidad, pero en términos de vecindades.
Lema 8.3.2. Sea f : X → Y una función entre espacios. Entonces, los enunciados siguientes son equivalentes.- (a) La función f es continua.
- (b) Para cada punto p de X y cada vecindad W de f(p) se cumple que f-1(W) es una vecindad de p.
- Demostración.
[(a) ⇒ (b)] Sea p un punto de X y sea W una vecindad de f(p), entonces hay un abierto V de Y tal que f(p) ∈ V ⊂ W. Luego, f-1(W) contiene a f-1(V) que es un abierto de X que contiene a p. Lo que muestra que f-1(W) es una vecindad de p.
[(b) ⇒ (a)] Sea V un abierto de Y. Si V es vacío, entonces f-1(V) es vacío, por lo que es abierto. Supongamos entonces que hay un y = f(x) en V. Como V es una vecindad de f(x), hay por hipótesis una vecindad U de x tal que U ⊂ f-1(V ). Por definición de vecindad hay un abierto U0 tal que x ∈ U0 ⊂ U ⊂ f-1(V ). Lo que prueba que f es continua.
Lema 8.3.3. Sean f : X → Y una función continua y A un subconjunto de X. Entonces, f(Cl(A)) ⊂ Cl(f(A)).-
Demostración. Sea p un punto de la clausura de A. Sean V un abierto de Y que
contiene a f(p), entonces hay una vecindad U de p tal que f(U) está contenida
en V. Como p es punto de la clausura de A, tenemos que U ∩ A ≠ ∅. Luego, f(U n A) ≠ ∅. Como,
tenemos que f(p) es un punto de la clausura de f(A).
Proposición 8.3.4. Sea f : X → Y una función, X, Y espacios topológicos. Los enunciados siguientes son equivalentes.- (a) f es continua.
- (b) Para todo abierto V de Y , su imagen inversa por f, f-1(V ), es abierto en X.
- (c) Para todo cerrado W de Y , su imagen inversa por f, f-1(W), es cerrado en X.
- (d) Para todo subconjunto A de X, f(Cl(A)) ⊂ Cl(f(A)).
-
Demostración. La definición de continuidad da la equivalencia (a) ⇐⇒ (b). La equivalencia (b) ⇔ (c) sigue de que la preimagen (o imagen inversa) del complemento de un conjunto es igual al complemento de la preimagen del conjunto.
[(d) ⇒ (c)] Sea W cerrado en F y sea W0 = f-1(W). Entonces, f(Cl(W0)) ⊂ Cl(f(W0) )= Cl(f(f-1(W) ) ⊂ Cl(W) = W. Lo que implica que Cl(W0) ⊂ f-1(W) = W0, lo que implica que W0 es cerrado.
[(a) ⇒ (d)] El resultado sigue del lema previo.
Observación 8.2. Notemos que, en general, imágenes de abiertos no son abiertos. Por ejemplo, las funciones numéricas constantes, que son continuas, envían cualquier conjunto en un conjunto con un único punto, que no es abierto (es cerrado).
Para otro ejemplo consideremos la función f : R → R tal que f(t) = sen(t). Entonces, f(] - p, 3p[) = [-1, 1].
Dualmente, las imágenes de cerrados no son necesariamente cerrados. La función t ↦ 1/t de X = R \ 0 en Y = R envía todo el espacio X (que es cerrado, ya que es todo el espacio) en ]-∞ 0[ ∪ ]0,+∞[ que no es cerrado en R.
Los Homeomorfismos
[editar]Las funciones continuas, aunque sean biyectivas, no proporcionan necesariamente “isomorfismos” de espacios topológicos. Necesitaremos algo más.
Ejemplo 8.3.1. Sea Rdiscreto el espacio discreto sobre los Reales. Entonces, se tiene que la función identidad de Rdiscreto en R, t ↦ t, es claramente biyectiva. Además, es continua ya que la preimagen de cada abierto en R es un abierto en Rdiscreto—todos los subconjuntos son abiertos. La función inversa no es continua por la misma razón, no todos los subconjuntos de R son abiertos.
Definición. (Homeomorfismo) Llamamos homeomorfismo de un espacio X en un espacio Y a una función continua biyectiva f : X → Y tal que su inversa también es continua.
Cuando haya un homeomorfismo de un espacio X en un espacio Y , diremos que los espacios X y Y son homeomorfos y escribiremos que X ≅ Y.
Sigue de la definición que la composición de homeomorfismo es un homeomorfismo y que la inversa de un homeomorfismo es un homeomorfismo. Algunas veces,en la literatura (especialmente antigua), aparece la expresión “función bicontinua” para referirse a los homeomorfismos.Ejemplo 8.3.2. Vimos en la proposición 6.5.1, que las funciones t ↦ t + a y t ↦ bt, b ≠ 0 son funciones de R en R continuas, invertibles, y con inversas continuas, por lo que son homeomorfismos
Ejemplo 8.3.3 (♠ Cálculo ). Sea f : R → R tal que f : t ↦ t3, f es biyectiva con inversa . Como ambas funciones son continuas, f y su inversa son homeomorfismos.
Ejemplo 8.3.4. Las isometrías entre espacios métricos son homeomorfismos. Basta con observar que cuando f : E → F es una isometría, las imágenes directas e inversas de bolas abiertas son bolas abiertas de igual radio.
Significado de los Homeomorfismos
[editar]La noción de homeomorfismo es central en el estudio de los espacios topológicos, ya que un homeomorfismo entre dos espacios induce una correspondencia biyectiva entre sus topologías. Como todas las nociones topológicas dependen de la topología, todas las propiedades topológicas de uno, serán propiedades topológicas del otro. También, la correspondencia biyectiva entre los abiertos induce una correspondencia entre sus complementos: los cerrados. Igualmente, para cada noción que dependa de los abiertos: clausura, exterior, punto de acumulación, etc.
Dos espacios homeomórficos son, por lo tanto, indistinguibles para la topología. Desde el punto de vista de la topología, ambos espacios son, esencialmente, el mismo espacio, solamente hay un cambio de nombre de sus elementos.
Propiedad Topológica. Decimos que una propiedad de un espacio es una propiedad topológica, cuando cada espacio homeomórfico al espacio tiene la misma propiedad.
Cada propiedad o noción cuya definición dependa solamente de los abiertos es, por lo tanto, una propiedad topológica. Por ejemplo, abiertos, cerrados, interior, etc. son nociones topológicas. Aunque la métrica de un espacio define una topología, nociones que dependen especialmente de la distancia (y no de los abiertos), [por jemplo conjunto acotado, no serán nociones topológicas, como veremos en ejemplos posteriores.
Propiedad Hereditaria. Decimos que una propiedad P es hereditaria, si cuando un espacio tiene la propiedad, entonces la tienen todos sus subespacios no vacíos.Cuando en el futuro estudiemos propiedades de espacios topológicos, una pregunta natural será acerca de si es heredada por subespacios. Por ejemplo, un subespacio es un espacio Hausdorff es Hausdorff (ver ejercicios de la sección anterior.)
Propiedad Invariante. Sea f : X → Y una función (no necesariamente continua) entre espacios. Diremos que f preserva una propiedad de X o de un subconjunto de X, cuando su imagen por f tiene la propiedad.
Notemos que propiedades invariantes de funciones continuas son propiedades topológicas. La afirmación recíproca no es válida, ya que hay ejemplos de espacios uno de ellos imagen del otro por una función continua, pero tales que uno de ellos es Hausdorff y el otro no.
Proposición 8.3.5. (Propiedades de "es homemorfo con") Sean X, Y y Z espacios topológicos.
Se cumple que:
- (a) X ≅ X.
- (b) X ≅ Y implica que Y ≅ X.
- (c) X ≅ Y y Y ≅ Z entonces X ≅ Z.
-
Demostración. Ejercicio.
Veremos, a continuación, algunos ejemplos no triviales de conjuntos homeomórficos.
Proposición 8.3.6. Dos intervalos abiertos acotados de la línea real son homeomórficos.
-
Demostración. Basta con probar que ]a, b[ ≅ ]0, 1[. Sea f :]0, 1[ → ]a, b[ tal que f(t) = (b - a)t + a. Claramente f es continua y biyectiva. Su inversa es: s : t ↦ (t - a)/(b - a) que también es continua.
Es decir que para un topólogo no hay diferencia entre ambos intervalos. Lo cual es una ventaja, por ejemplo, si queremos estudiar topológicamente a las funciones continuas de ]a, b[ en los Reales, basta considerar el caso a = 0, b = 1.
Sigue, en forma inmediata, de la proposición anterior que diámetro de un conjunto no es una propiedad topológica, ya que, si b-a ≠ 1, se tiene que el diámetro de ]0, 1[ es 1, mientras que aquel de ]a, b[ es b - a. Más espectacular, lo anterior implica que distancia entre puntos no es una propiedad topológica.
El siguiente ejemplo muestra otro aspecto interesante.
Ejemplo 8.3.5 (♠ Cálculo). La función f : R → (-1, 1) tal que f(t) =(2/π) arctan(t) es biyectiva y continua (es derivable) y su inversa g(t) = (π/2) tan(t) también es continua, Luego, la línea real y el intervalo abierto ]-1, 1[ son homeomórficos.
Notemos que mientras que R es un espacio métrico completo, el intervalo abierto no es completo. Completitud es, por lo tanto, una propiedad métrica que no es topológica.
Ejemplo 8.3.6. Sean E = {(x, y, z) : x2+y2+z2 = 1, z ≥ 0} y F = {(x, y, z) ∈ R3 : x2 + y2 = 1, z = 0}.
E es el hemisferio superior de la esfera unitaria de R3 y F es su proyección en el plano z = 0. Claramente, la proyección (x, y, z) ↦ (x, y, 0) es biyectiva con inversa . Se puede verificar que ambas funciones son continuas, por lo que se trata de homeomorfismos.
Notemos que tales homeomorfismos no son isometrías. En general, la distancia euclídea entre dos puntos de la semiesfera es mayor que la distancia de sus proyecciones. Además, la distancia euclídea en E heredada de R3 (distancia por el interior de la Tierra) no es aquella más natural en E. El homeomorfismo nos dice, en cambio, que topológicamente se tratan del mismo espacio, lo que resulta conveniente para muchos estudios.
Proposición 8.3.7. Dos bolas cerradas cualesquiera de Rn son homeomorfas.
-
Demostración. Sea X = B[a; r] una bola cualquiera y sea B la bola con centro el origen y radio 1. Cuando ta es la traslación que envía cada punto p en p + a, tenemos que t-a(B[a; r]) = B[0; r]. Como traslaciones son homeomorfismos, ya que son isometrías, se tiene que una esfera cualquiera es homeomorfa a una esfera del mismo radio, pero con centro en el origen. Sea hr, r > 0, la función que envía cada punto p en rp. Como
||hr(p) - hr(q)|| = r||p - q||, vemos que hr es continua. Además es obviamente biyectiva, con inversa h1/r. Luego se trata de un homeomorfismo. Como hr(B) = B[0; r], se concluye que cualquier bola cerrada es homeomorfa a B.
Análogamente, se verifica que cualquier esfera de Rn es homeomorfa a la esfera unitaria –centro el origen y radio 1. Ver los ejercicios.
Convenio. Denotaremos por Bn a la bola cerrada de centro el origen y radio 1 de Rn. Topológicamente, Bn representa a todas las bolas cerradas de Rn. Por su parte, denotaremos por Sn la esfera unitaria de Rn+1 (que es homeomorfa a todas las esferas en Rn+1).
Funciones Abiertas y Cerradas
[editar]Un homeomorfismo de X en Y envía abiertos en abiertos y cerrados en cerrados. Funciones que tienen esas propiedades reciben nombres especiales.
Definición. (Funciones Abiertas, Cerradas) Una función abierta (resp. cerrada) f de un espacio topológico X en un espacio topológico Y es una función que envía abiertos de X en abiertos de Y (resp. cerrados de X en cerrados de Y ).
Un homeomorfismo es una función biyectiva que es continua, abierta y cerrada.Las nociones son, sin embargo, independientes. Sea A un subconjunto de un espacio topológico X. Entonces, la inclusión i : A ⇒ X es abierta (resp. cerrada), ssi, A es un conjunto abierto (resp. cerrado).
Notamos, anteriormente, que funciones numéricas constantes son continuas, pero no abiertas.
Ejercicios 8.3
[editar]- Explicar cuando una función entre dos espacios topológicos no es continua.
- Explicar por qué una función de un espacio discreto en cualquier espacio es continua.
- Probar que una función cualquiera de un espacio topológico cualquiera en un espacio discreto es una función abierta, que no necesariamente es continua. Probar que dicha función también es cerrada. Si la función fuera biyectiva, ¿debe necesariamente ser un homeomorfismo?
- Probar que la composición de homeomorfismos es un homeomorfismo y que la función inversa de un homeomorfismo es un homeomorfismo.
- (R2) Probar que el cuadrado con vértices (1, 0), (0, 1), (-1, 0) y (0,-1) es homeomórfico a la circunferencia unitaria {(x, y) : x2 + y2 = 1}.
- (R2) Probar que cada celda cerrada [a, b] × [c, d] es homeomórfica al cuadrado unitario I2 = {(x, y) : 0 ≤ x , y \le 1}.
- Sea Sn-1 la esfera unitaria de Rn (todos los puntos que distan 1 del origen). Probar que cualquier esfera de Rn es homeomorfa a Sn-1.
- Sea Sn, n > 0, la esfera unitaria de Rn+1. Se tiene (con respecto a la métrica euclídea) que
Sean
Probar las afirmaciones siguientes.
- Sean X = [0, 1] y Y = {0, 1} con la topología de Sierpinski (topología = {∅, Y, {0}}. Probar que f : X → Y tal que f(x) = 0 si 0 = x < 1/2, y f(x) = 1 en caso contrario, es continua. X es Hausdorff, pero Y no lo es.
- Probar que una función biyectiva es continua, ssi, su inversa es abierta.
- Probar que una función biyectiva continua y abierta es un homeomorfismo.
- Una función f : X → Y es continua, ssi, para todo subconjunto A de X se cumple que f(Int(A)) ⊂ Int(f(A)).
- Probar que si X es un espacio Hausdorff y f : X → Y es un homeomorfismo, entonces Y es un espacio Hausdorff. Es decir que Hausdorff es una propiedad topológica.
- En un espacio normado son homeomorfismos
- a) las traslaciones (x ↦ a + x);
- b) las multiplicaciones por escalar no nulo (x ↦ α x).
- c) las simetrías alrededor de un punto c (x ↦ 2c - x).
- Probar que en un espacio normado todas las bolas abiertas son homeomorfas entre si. Lo mismo pasa con las bolas cerradas y con las esferas.
- (♠) Probar que dos parabolas del plano son siempre homeomórficas. Usar que rotaciones y reflexiones alrededor de líneas son isometrías.
Topologías de un Conjunto
[editar]Sea X un conjunto. Vimos, anteriormente que es posible proveer a X con diferentes métricas. Algo semejante sucede con las topologías. Más adelante, necesitaremos tener topologías especialmente adaptadas a ciertas propiedades. Como las topologías son conjuntos (de conjuntos), podremos comparar a dos topologías mediante la inclusión. En esta sección, introduciremos la nomenclatura usada al respecto y algunas propiedades de la comparación.
Definición. (Comparación de Topologías) Sea T1 y T2 topologías de un mismo conjunto X. Decimos que la topología T1 es menos fina que T2, cuando cada abierto de T1 sea un abierto de T2 (o sea cuando T1 ⊂ T2).
Nomenclatura. Cuando T1 es menos fina que T2, también se dice que:- T2 es más fina que T1;
- T1 es más débil que T2;
- T2 es más fuerte que T1.
En cada conjunto X tenemos una topología discreta—donde cada subconjunto es abierto (y, por lo tanto, cerrado). Esta es la topología más fina posible sobre X. Opuesta a esa topología, está la topología indiscreta que tiene como abiertos solamente al conjunto vacío y a todo el espacio, que es la menos fina de todas las topologías posibles en un conjunto.
Sean T1, T2 dos topologías de un mismo conjunto, probaremos que su intersección, digamos T = T1 n T2 es una topología (menos fina que las topologías originales). Dicha topología consiste de todos los conjuntos que son abiertos en ambas topologías.
Claramente el conjunto vacío y todo el espacio están en T. Sea U = (Ui)i ∈ I, una familia de abiertos de T . Entonces U es una familia de abiertos tanto en T1 como en T2, por lo que su reunión estará tanto en T1 como en T2 y, en consecuencia, en T . Análogamente, si la familia I es finita, la intersección de los conjuntos en la familia será un abierto de T . Lo que prueba lo afirmado.
El razonamiento anterior se puede extender a una familia cualquiera no vacía de topologías de un mismo conjunto. Si tenemos una familia de topologías, (Tk), k ∈ K, de un conjunto X y llamamos T a su intersección, tendremos que: el conjunto vacío y todo el conjunto están en cada una de las topologías, por lo que están en su intersección T .
Si U = (Ui), i ∈ I, es una familia de abiertos de T , la reunión de los conjuntos de la familia estará en cada Tk, por lo que la reunión estará en T .
Si U = (Ui), i ∈ I, es una familia finita de abiertos de T , la intersección de los conjuntos de la familia estará en cada Tk, por lo que dicha intersección estará en T .
Proposición 8.4.1. La intersección de una familia cualquiera de topologías de un conjunto es una topología, que es menos fina (o más débil) que cualesquiera de las topologías de la familia.
Topología Generada por Familias de Subconjuntos. Sea S una familia de subconjuntos de un conjunto X y sea la intersección de todas las topologías posibles de X que contienen a S. La topología discreta es una de esas topologías, por lo que dicha familia no es vacía. Decimos que es la topología de X generada por S. Dicha topología es la topología menos fina (o más débil) que contiene a S.
Proposición 8.4.2. Sea X un conjunto no vacío y sea S un conjunto de subconjuntos de X. Sea T la colección de reuniones arbitrarias de intersecciones de finitos elementos de S. Entonces, T contiene a S y está contenida en cualquier otra topología que contenga a S. Es decir que T =- Demostración. Ejercicio. Considerar la intersección de una familia vacía como el conjunto X y la reunion de una familia vacía como el conjunto vacío.
Subbase. Decimos que una familia de abiertos S de una topología T es una subbase de la topología, cuando T es la topología generada por S.
Base. Decimos que una familia de abiertos B de una topología T es una base de la topología cuando cada abierto de T es una reunión de elementos de B. Un abierto básico es un abierto de una base.
Cuando B sea una base de la topología de un espacio X y la topología quedé clara del contexto, podremos hablar de la base del espacio.
La importancia de bases y subbases reside en que propiedades topológicas de conjuntos abiertos preservadas por intersecciones finitas y reuniones necesitan tan solo verificarse en los elementos de una subbase. Análoga consideración para bases.
Cuando se trabaja alrededor de un punto p de un espacio es interesante considerar al conjunto V{p} formado por todas las vecindades del punto p. Una base para las vecindades de un punto p es una colección de abiertos, vecindades de p, tales que para cada vecindad U de p, hay un A en tal que A ⊂ U.
Ejemplo 8.4.1. En un espacio métrico, cada abierto es una reunión de bolas abiertas, por lo que la familia de todas las bolas abiertas es una base para la topología inducida por la métrica. Las bolas abiertas con centro en un punto p determinan una base para las vecindades del punto.
Ejemplo 8.4.2. (R2) Consideremos al plano con la topología usual. Las preimágenes por las proyecciones son franjas verticales (preimágenes de abiertos de intervalos en el eje X) y franjas horizontales (preimágenes de intervalos en el eje Y).
Sabemos que las celdas—subconjuntos que son productos de intervalos reales acotados (ver ejemplo 5.2.7.) de la sección 5.2.2, son intersecciones de franjas y son, por lo tanto, conjuntos abiertos.
Se puede verificar que para cada conjunto abierto U de R2 y para cada punto p del abierto, hay una celda de las anteriores que contiene al punto y está contenida en el abierto. Es decir que el conjunto de franjas es una subbase de la topología usual del plano.
Ejemplos 8.4.3 (Ejemplos generales).
- Cada topología es una base de ella misma.
- Cada base es una subbase.
- La familia de las intersecciones finitas de conjuntos de una subbase es una base.
Proposición 8.4.3. Sea X un espacio topológico. En orden a que una colección de abiertos B sea una base de la topología de X es necesario, y suficiente, que, para cada abierto no vacío U y cada x en U hay un elemento V de B tal que x ∈V ⊂ U.- Demostración. Supongamos que B fuera una base de X. Sea U un abierto cualquiera de X. Por la definición de base, U es una reunión de una familia (Vi) de abiertos de la base. Si x está en U, x está entonces en algún V = Vi; lo que prueba la necesidad de la condición. Supongamos que se cumple la condición. Sea U un abierto cualquiera no vacío, entonces para cada x de U sea Vx el abierto en B de la condición. Claramente, U es la reunión de todos tales Vx, x ∈ U.
Proposición 8.4.4. Sea f : X → Y una función cualquiera entre espacios. Entonces- (a) f es continua ⇔ la imagen inversa de cada abierto básico es abierto :⇔ la imagen inversa de cada abierto de una subbase es abierto.
- (b) f es abierta ⇔ la imagen de cada abierto básico es abierto.
- Demostración. Los resultados siguen directamente de las siguientes identidades de conjuntos:
Ejercicios 8.4
[editar]- Probar la proposición 8.4.2.
- (Bases) Sea X un espacio topológico.
- a) ¿Siempre hay una base para la topología de X?
- b) ¿Puede una topología tener dos bases distintas?
- c) ¿Pueden dos espacios topológicos diferentes tener bases iguales?
- Probar que cualquier abierto de la línea real es una reunión de intervalos abiertos disjuntos. (Sug: Cuando dos intervalos tiene intersección no vacía, su reunión es un intervalo.) Luego, una base de la topología usual de R consiste de ...
- Sea f : X → Y una biyección. Si X (resp. Y ) es un espacio topológico, se puede proveer a Y (resp. X) de una topología única tal que X y Y sean homeomórficos. Se dice que esa estructura topológica se obtiene por transporte de estructura.
- Sea f : X → Y una función del conjunto X en el espacio topológico Y. Definir T*(f) como el conjunto formado por todos los subconjuntos U de X que son preimágenes de abiertos de Y . Probar que T*(f) es una topología en X (la topología inducida por f) tal que f es continua y que es la menos fina de las topologías con esa propiedad.
- Sea X un espacio y sea A un subconjunto de X. Probar que la topología inducida por la inclusión i : A → X coincide con la topología relativa de subespacio definida en la sección 8.2.
- Sea f : X → Y una función del espacio X en el conjunto Y . Definir T*(f) como el conjunto formado por todos los subconjuntos V de Y cuyas preimágenes son abiertos de X. Probar que T*(f) es una topología en Y (la topología coinducida por f) tal que f es continua y que es la más fina de las topologías con esa propiedad.
- Hallar tres bases diferentes para la topología usual de R2.
- Se llama subbase (resp. base) de cerrados a una colección de conjuntos cerrados cuyos complementos forman una subbase (resp. base). Enunciar y probar teoremas acerca de subbases y bases de cerrados.
Métricas Equivalentes
[editar]El espacio vectorial Rn puede tener varias métricas diferentes; cada una de esas métricas induce una topología en Rn. ¿Cómo comparan esas topologías?
Métricas y Normas Equivalentes. Decimos que dos métricas de un mismo conjunto X son (topológicamente) equivalentes, cuando los abiertos definidos por una de ellas coinciden con los abiertos definidos por la otra. Es decir, cuando definen la misma topología. Análogamente, decimos que dos normas en un espacio vectorial E son equivalentes, cuando definen métricas equivalentes y, por lo tanto, la misma topología.
Por extensión de la terminología, diremos que una norma N1 de un espacio vectorial E es mas fina que una norma N2, cuando la topología inducida por N1 sea más fina que aquella inducida por N2, es decir que los abiertos respecto a la segunda norma son abiertos respecto a la primera. Para que se cumpla lo anterior, bastará con que cada bola abierta respecto a la segunda norma contenga una bola abierta respecto a la primera. Lo anterior pasa cuando la identidad id : E1 → E2 donde Ei es el espacio con norma Ni, i = 1, 2, sea continua.
Lema 8.5.1. Sea E un espacio vectorial y sea Ei el espacio E con norma ||•||i, i = 1, 2. Si hay un número positivo a tal que para todo x se cumple que ||x||2 ≤ a||x||1 entonces ||•||1 es más fina que ||•||2.
- Demostración. Basta probar que cada bola abierta de E2 es abierto en E1.Supongamos que ||x - p||2 < r. Entonces, cuando ||x - p||1 < r/a se tiene que
||x - p||2 ≤ a||x - p||1 < a(r/a) = r. Es decir que una bola de radio r respecto a ||•||2 siempre contiene a la bola de radio r/a respecto a ||•||1. Esto implica lo pedido.
Revisaremos las topologías inducidas por las normas estudiadas de Rn(norma–ciudad, norma euclídea y norma máxima).
Figura 8.1 La figura 8.1 ilustra gráficamente las equivalencias entre las normas ciudad, euclídea y máxima. Ver la sección 3.3.1.
Formalmente, tenemos lo siguiente.
Lema 8.5.2. Para todo x en Rn se cumple que
- (a) ||x||max ≤ ||x||e ≤ √(n)||x||max,
- (b) ||x||max ≤ ||x||c ≤ n||x||max.
-
Demostración. Probaremos (a) y dejaremos (b) como ejercicio. Sean x = (xi) y M = ||x||max = máx{|xi| : 1 ≤ i ≤ n}. Luego, hay un j, 1 ≤ j ≤ n tal que M = |xj|. Entonces, para todo i = 1, . . . , n, |x_i| ≤ |xi| = M. Tenemos, entonces, que
Proposición 8.5.3. Las normas ciudad, euclídea y maxima de Rnson equivalentes.- Demostración. Directo de los lemas anteriores.
Más adelante, veremos que dos normas cualesquiera de Rn son equivalentes.
Proposición 8.5.4. Dos normas ||·||1 y ||·||2 son equivalentes, cuando hay reales a y b positivos tales que
a ||·||1 ≤ ||·||2 ≤ b || · ||1.
- Demostración. Ejercicio.
Ejercicios 8.5
[editar]- Completar la demostración del lema 8.5.2.
- Probar la proposición 8.5.4.
- Sea <E, d> un espacio métrico y sea d' : E × E → R tal que d'(x, y) = mín {d(x, y), 1}. Probar que d' es una métrica en E que es topológicamente equivalente con d.
Las Sucesiones
[editar]Las sucesiones no tienen un rol tan destacado en los espacios topológicos generales, comparado con lo que pasa en espacios métricos.
La definición de convergencia es aquella de espacios métricos, pero usando solamente abiertos.
Definición. Sea X un espacio topológico, s=(s_n) una sucesión de puntos de X y p un punto de X. Decimos que la sucesión (sn) converge o tiende a p, ssi, para cada vecindad de p, casi todos los términos de lasucción pertenecen a la vecindad. En tal situación, decimos que p es un límite de los sn's.
A pesar de su similitud con la definición para espacios métricos, hay algunas diferencias significativas. Observemos, por ejemplo, que si tiene la topología indiscreta, una sucesión de puntos de tiene como punto límite a cualquier elemento de . Es decir que una sucesión puede converger a varios límites. La unicidad de límite requiere que el espacio sea Hausdorff; en tal situación hay un único límite. La demostración es análoga al caso de espacios métricos. (ver la proposición 7.2.1)
Proposición 8.6.1 En un espacio Hausdorff una sucesión tiene a lo más un límite.
Proposición 8.6.2. (Lema de la Sucesión). Sea un espacio topológico y un subconjunto de . Si es un punto límite de una sucesión de puntos diferentes de , entonces está en .
- Demostración. Por definición de límite, cada vecindad de contiene a casi todos los términos de la sucesión, por lo tanto, al menos un punto de diferente de .
Proposición 8.6.3. Sea una función continua. Entonces, para cada sucesión de , si converge a (no necesariamente único), entonces converge a .
- Demostración. Sea una vecindad de . Como es continua en , hay una vecindad de tal que está contenido en . Como casi todos los están en , casi todos los están en .
Observación 8.3. Se puede verificar que los recíprocos de las proposiciones anteriores son válidos solamente cuando es metrizable o satisface el primer axioma de enumerabilidad (hay una base enumerable de abiertos en la vecindad de cada punto).
Ejercicios 8.6
[editar]- Explicar el significado del enunciado " no es un punto límite de la sucesión ".
- Sean una sucesión de un espacio . Sea una biyección de en si mismo y sea . Probar que si converge a , también lo hace . Es decir que el orden de los términos no afecta la convergencia ni el límite de una sucesión.
- Probar la proposición 8.6.4.
Ejercicios del capítulo 8
[editar]- Probar que A = {(x, y) : 2 < x < 5} es un abierto de R2.
- Probar que C = {(x, y) : 2 < x < 5,-1 < y < -1} es un abierto de R2.
- (T1–topología de R) Sea A consistente del conjunto vacío y los complementos de subconjuntos finitos. Probar que A es una topología de R con respecto a la cual R no es Hausdorff. Denotaremos por RT1 a los Reales con esta topología. ¿Es id : R → RT1 continua? ¿abierta? ¿homeomorfismo?
- (Funciones Abiertas)
- a) Dar ejemplo de una función continua que no sea abierta.
- b) Dar un ejemplo de una función abierta que no es continua.
- c) Probar que la composición de dos funciones abiertas es abierta..
- (Funciones Cerradas)
- a) Dar ejemplo de una función continua que no sea cerrada.
- b) Dar un ejemplo de una función cerrada que no sea continua.
- Sea X un espacio topológico con topología T y sea X* = X ∪ {p}, donde
p no está en X.
Sea T* = {∅} ∪ {A ∪{p} : A ∈ T }. Probar que T* es una topología de X* tal que un subconjunto F de X es cerrado respecto a T, ssi, es cerrado respecto a T*. - Sea F un subespacio cerrado de X. Si f: X → Y es una función cerrada, entonces la restricción de f a F también es cerrada.
- Sea X un conjunto y sea (V{x}), x ∈ X, una familia no vacía de subconjuntos
de X tales que para cada x de X se cumple que:
- (1) x está en cada conjunto de V{x};
- (2) si A está en V{x} y B ⊂ A, entonces B está en V{x};
- (3) la reunión de una familia cualquiera de conjuntos de V{x} es un elemento de V{x}.
- (4) la intersección de una familia finita de conjuntos de V{x} es un conjunto de V{x}.
- (5) para cada A en V{x} hay un B en V{x} tal que A está en V{y} para cada y en B.
- Sea X un espacio topológico y Y un subespacio de X. Sea A un subconjunto de Y . Si A es abierto (resp. cerrado) en X, ¿lo es respecto a Y ?
Los Espacios Productos y Cocientes
[editar]Recordemos que espacio quiere decir espacio topológico, a menos que se indique algo distinto.
Introducción
[editar]Este capítulo está dedicado a la construcción de nuevos espacios a partir de espacios dados. Una construcción básica es la de subespacio, que vimos en el capítulo anterior. En este capítulo, veremos en la sección 9.3 como proveer de topología a un producto cartesiano de espacios. Luego, veremos en la sección 9.4 como proveer de topología a un conjunto cociente de un espacio. Finalmente, en la sección 9.5, veremos algunas construcciones interesantes.
Los Espacios Productos
[editar]El producto cartesiano de conjuntos nos permite formar un conjunto a partir de dos o más conjuntos. Hemos vistos celdas en R2 que son producto de dos intervalos reales. La representación gráfica de tal producto es un rectángulo con lados los intervalos factores. Tal representación nos es familiar y resulta adecuada y confiable para muchos aspectos. Consideremos sin embargo, la siguiente situación A ={a,b,c}, a, b, c arbitrarios, y B un segmento rectilíneo tal como [0,1] ¿cuál de las siguientes representaciones gráficas es la más adecuada?

Productos Cartesianos La respuesta lógica es cualquiera de ellas, no hay nada que nos indique lo contrario. Simplemente, usos tradicionales pueden favorecer una de ellas.
Ejemplo 9.2.1 (Cilindro) Si tomamos el producto cartesiano de la circunferencia unitaria S1 del plano con un intervalo, digamos [0,1], queremos pensar tal producto como un cilindro (sin tapas). Ver la siguiente figura

Cílindro como producto cartesiano Figura 9.1: Cílindro como producto cartesiano Sin embargo, las consideraciones anteriores nos dicen que va a depender de como se ubiquen los segmentos respecto a la circunferencia, queremos para un mismo y del segmento, los puntos (x1,y) y (x2,y) estén próximos cuando x1 y x2 lo estén en la circunferencia. En otras palabras, necesitamos una topología que pegue continuamente a los segmentos sobre la circunferencia.
El Producto Cartesiano de Conjuntos
[editar]Antes de introducir topología en un producto de espacios, revisaremos alguno hechos acerca del producto de conjuntos. Nos interesa considerar la generalización del producto de dos elementos a un producto de una familia cualquiera de conjuntos.
Supongamos que tenemos una familia [5] de conjuntos (Xi), i ∈ I. Cuando uno de los Xi sea vacío el producto será el conjunto vacío. En caso contrario, llamamos producto (cartesiano) de los Xi's al conjunto denotado por
y definido como el conjunto formado por todas las familias (xi), i ∈ I, tales que xi, es un elemento de Xi <ref>Suponemos la existencia de tales familias. Formalmente, para un conjunto de índices arbitrario, tal suposición requiere de un axioma especial llamado Axioma de Selección.} Cada uno de los Xi's es un factor del producto. Si k está en I, y x=(xi) es un elemento del producto, decimos que x_k es la coordenada o componente k (o k--ésima) de x. El producto anterior se presenta acompañado de una familia de funciones: las proyecciones, pri :X → Xi, que asocian a cada punto del producto, su i--ésima coordenada.
Claramente, esta noción de producto es una generalización del producto cartesiano usual, ya que podemos considerar a un par (x1, x2) como una familia con conjunto de índices I = {1,2} tal que xi está en Xi.
El producto cartesiano tiene la siguiente propiedad universal.
Proposición (Propiedad Universal del Producto Cartesiano) Sea (Xi), i ∈ I una familia de conjuntos no vacíos y sea X su producto, con las proyecciones pri. Sean Z un conjunto y fi :Z → Xi, i ∈ I, una familia de funciones. Entonces, hay una única función f: Z → X tal que pri ◦ f = fi (*).

Propiedad Universal del Producto - Demostración. Sigue de la relación (*) que tal f debe cumplir con f(z) = (fi(z)) lo que muestra su unicidad y existencia.
Los Espacios Productos
[editar]Volvamos a la consideración del rectángulo R = [a,b] x [c,d] (o región rectangular, si se prefiere) que representamos gráficamente en la figura 9.2.

Figura 9.2: Región Rectangular Esa representación, que es estándar, tiene varios supuestos implícitos. En primer lugar, suponemos que el rectángulo R esta contenido en un plano. En segundo lugar hay una suposición de preservación de cercanías.
Dos puntos, digamos (x1,y1) y (x2,y2) están próximos en la representación, cuando sus primeras coordenadas (x1 y x2) y sus segundas coordenadas (y1 y y2) lo están. Esto quiere decir que tenemos asociada a la imagen una topología. Puntos próximos en los factores, generan puntos próximos en el producto. Con esta idea en mente, veremos como, de forma general, podremos asociar una topología en el producto cartesiano de dos espacios topológicos que esté relacionada con la topología de los factores. La construcción que haremos tiene muchos usos en geometría y topología.
Sean X1, X2 espacios y sea X = X1 x X2. Sean pri : X1 x X2 → Xi, (x1,x2) ↦ xi, i=1,2. las proyecciones naturales del producto en sus factores. Las consideraciones intuitivas de la discusión anterior sugieren que debemos poner una topología en el producto de manera tal que esas funciones sean continuas. Naturalmente la topología discreta en el producto haría esas funciones continuas, pero no sería muy útil, ya que las proyecciones y cualquier otra función serían continuas; por lo que no habría una relación natural entre la topología de los factores y aquella del producto. Por lo que definiremos como topología producto a la topología menos fina entre las topologías que hacen que las proyecciones sean continuas. Es decir que las preimágenes de abiertos de los factores serán abiertos en el producto. Con esa definición, resulta que las celdas serían intersecciones de abiertos como los anteriores. En efecto, cuando U1 y U2 sean abiertos de X1 y X2 respectivamente, U1 x U2 es un abierto en X1 x X2, ya queLa topología producto deberá tener, por lo tanto, a las preimágenes de los abiertos de los factores como una subbase.
La definición anterior de producto puede generalizarse fácilmente a una familia finita de espacios topológicos. ¿Qué pasa cuando tenemos una familia arbitraria (<Xi, Ti>), i ∈ I, de espacios topológicos? Siguiendo lo hecho con el producto cartesiano de dos conjuntos, definimos la siguiente topología producto general.Definición. (Topología Producto) Sea (Xi), i ∈ I, una familia no vacía de espacios no vacíos y sea X su producto de conjuntos. Llamamos topología producto de X a la topología menos fina tal que las proyecciones sean continuas. Llamamos espacio topológico producto de los Xi's a X provisto con esta topología.
Sea X = ∏i X_I el espacio topológico producto de los Xi's. La definición implica lo siguiente.- Para cada abierto U de X_k, prk-1(U) es abierto en X. Tales preimágenes, con k en I cualquiera, forman una subbase de la topología del producto.
- Cada intersección finita de cada uno de esos abiertos se llama un abierto básico, porque forman una base de la topología producto.
- Un abierto del producto es un producto Π i ∈ Ui, donde cada Ui es un abierto en Xi, igual a Xi, excepto por una cantidad finita de los Ui's. (Recordemos que solamente las intersecciones de finitos abiertos tienen garantía de ser abiertos.)
- Cuando U es un abierto de X, se cumple que pri(U) (por la observación anterior) es un abierto de Xi; o sea que las proyecciones son funciones abiertas
- Tomando complementos, resulta que un conjunto cerrado es un producto prodi Fi donde los Fi son cerrados en Xi, iguales a Xi, excepto para una cantidad finita de los i.
- Cuando tenemos un producto de una familia finita de conjuntos, un abierto del producto es un producto de abiertos de los factores. Análogamente para los conjuntos cerrados.
Proposición (Propiedad Universal del Producto Topológico)
Sea (Xi), i ∈ I, una familia de espacios topológicos y sea fi :Z → Xi, i ∈ I, una familia de funciones continuas. Entonces, hay una única función continua f: Z → ∏i Xi tal que pri o f = fi, para todo i.

Propiedad Universal del Producto - Demostración. La existencia y unicidad de f proviene de la propiedad universal del producto cartesiano de conjuntos. Solamente necesitamos probar que f es continua. Sea U un abierto tal que U = pri-1(V), V un abierto de Xi---es decir que U es un abierto de la subbase que define al producto. Entonces,
Lo que prueba que f-1(U) es un abierto. La continuidad de $f$ sigue, entonces, de la proposición 8.4.4 parte (a), que garantiza la continuidad cuando se la comprueba la continuidad para los abiertos de una subbase.
Corolario 9.3.2 El producto topológico es único, excepto por homeomorfismo.
- Demostración. Sean P y P' productos topológicos de una familia Xi de espacios topológicos. Sigue de la proposición anterior aplicada a P como producto que hay una función continua f:P' → P tal que prif= { pri}'.
Simétricamente, tenemos una función continua g: P → P' tal que { pri}'g = pri. De donde se deduce que
pri fg = pri'g = pri Por la unicidad de la función anunciada por la proposición tenemos que fg=idP. Análogamente, gf=idP'. Luego, f y g son biyectivas, continuas, una inversa de la otra, por lo que son homeomorfismos.
Corolario 9.3.3 Sea f: Z → X una función de un espacio en el producto X = prodi Xi. Entonces, f es continua, ssi, la composición de f con cada proyección es continua.
-
Demostración. Ejercicio. (Mirar la demostración de la
proposición 6.5.5)
Producto de Funciones
[editar]Sean fi : Xi → Yi, i=1,2, un par de funciones. Llamamos producto cartesiano de esas funciones a la función de X1 x X2 → Y1 x Y2 denotada por f1 x f2 y tal que (f1 x f2) (x1, x2) := (f1(x1), f2(x2)).
Proposición 9.3.4 El producto cartesiano de dos funciones continuas (resp. abiertas) es un función continua (resp. abierta).
- Demostración. Ejercicio.
Pregunta Fundamental Cuando X y Y tienen una cierta propiedad topológica ¿qué podremos decir de su producto?
El Conjunto de Cantor
[editar]Presentamos en esta sección a un subconjunto muy interesante de los Reales, que usaremos para ejemplos y ejercicios más adelante. Resultará que el llamado "conjunto de Cantor será una extraordinaria figura plana, que por su estructura parecerá desafiar algunas de nuestras intuiciones geométricas preconcebidas---que están usualmente basadas en nuestras intuiciones preconcebidas a partir de los espacios Euclídeos de dimensiones 2 y 3.
Presentaremos inicialmente tres objetos geométricos, que posteriormente veremos son homeomorfos entre sí. La primera versión es un producto infinito de espacios topológicos.
Producto de Espacios Discretos. Sea An = {0,2}, n ≥ 1, una familia de espacios, todos iguales entre si, con dos elementos y la topología discreta. Sea
Expansiones Ternarias Especiales. Sea
Podemos pensar a C3 como las expansiones ternarias (es decir, usando 3 en lugar de 10) para las expansiones de los números reales en [0,1] donde la cifra 1 no aparece.Recordemos que en las expansiones decimales (base =10) se cumple que 0.9999 ... = 1, lo que permite exigir unicidad en la representación, cuando las expansiones decimales finitas se reemplazan usando la igualdad anterior, para tener siempre expansiones decimales infinitas no nulas para los racionales diferentes de 0.
Análogamente se tiene en expansión ternaria que 0.222223 =1 . En efecto, 0.2222 ... 3 es una serie geométrica de razón 1/3 con termino inicial 2/3, por lo que su suma es igual a
Adoptando el convenio anterior, reemplazaremos expansiones ternarias finitas o adonde aparezca unj 1, por expansiones infinitas con ... 2222 ...3, excepto para el 0. Se tiene que C3 representa a todos los números reales en [0,1] cuya expansión ternaria no contiene 1's.
Notemos que la correspondencia es una biyección de CP en C3.
Presentación Gráfica. Esta presentación es más fácil de visualizar. Se basa en el siguiente procedimiento de división de un intervalo cerrado: dividir al a intervalo cerrado en tres partes iguales, y eliminar el interior de los subintervalos del centro para quedarse con los intervalos cerrados de los extremos. Para la construcción empezamos con el intervalo [0,1] y aplicamos el prpcedimentyo a es intervalo. Continuamos aplicando reiteradamente a cada intervalo cerrado que vaya apareciendo.
Conjunto de Cantor El proceso comienza con el intervalo I = [0,1]. Aplicando el procedimiento descrito, obtenemos
Dividamos cada uno de los intervalos de F1 y formemos F2 como arriba, o sea excluyendo el interior del subintervalo del centro. Es decir que,
Continuando de esta manera, generamos una sucesión (Fn) de conjuntos cerrados en R. Llamamos Conjunto de Cantor a la intersección de todos los Fn y que simbolizaremos aquí por .
¿Qué podemos decir de ? Después de todas las exclusiones,¿quedará algo? Observemos que los puntos de los extremos de los subintervalos son preservados en las sucesivas divisiones, así que 1/3, 1/9, ..., 1/3^n, ... son todos puntos de . No son los únicos puntos como se puede verificar. En F1 están todos los números tales que la primera cifra de su expansión ternaria no es 1. Recordemos que 1/3 = 0.02222...3. En F2 se eliminan todos los números cuya segunda cifra en la expansión ternaria es 1. y así sucesivamente. Lo que muestra que este conjunto coincide con C3
Como cada Fn es una reunión finita de intervalos cerrados, Fn es cerrado. Por lo que su intersección, es un subconjunto cerrado de [0,1] ⊂ R.
Sea α un punto de , entonces cualquier intervalo abierto centrado en α contiene números cuya expansión ternaria tiene al menos un 1, por lo que ese intervalo no puede estar contenido en . Es decir que el conjunto de Cantor no tiene puntos interiores (o sea que es nunca denso).
Computemos el largo de la reunion de intervalos removidos, sumando los largos de los segmentos removidos.
La serie es geométrica con razón 2/3 y término inicial 1/3, luego
Ese resultado implica que el largo de lo que queda, que debe ser igual al largo del segmento [0,1], o sea 1, menos el largo de lo removido, lo que nos dice que el largo del conjunto de Cantor debe ser 1-1=0. !!!!!
Cardinalidad. La cantidad de elementos del conjunto de Cantor es infinita, como fue observado anteriormente. Sin embargo, se trata de un infinito comparable al de los Reales, que es mayor que el infinito de los Naturales. Para ver lo anterior, basta considerar cada expansión ternaria de un elemento de
y cambiar cada 2 que allí aparece por 1. El resultado son todas las expansiones binarias (base 2) de los números en [0,1], que muestra lo indicado.
Largo del Conjunto de Cantor}. El Conjunto de Cantor es un subconjunto de los reales que contiene infinitos números entre 0 y 1, ambos extremos incluidos. Resulta natural preguntarse por su largo. Computaremos dicho largo, mirando al largo de su complemento, que restaremos de 1 (el largo del intervalo [0,1]).
Computemos el largo de la reunion de intervalos removidos, sumando los largos de los segmentos removidos.
La serie es geométrica con razón 2/3 y término inicial 1/3, luego
El largo del Conjunto de Cantor debe ser igual al largo del segmento [0,1]---o sea 1---menos el largo de lo removido, o sea 1-1=0. !!!!!Ejercicios 9.3
[editar]Cuando Z = X x Y, prX, prY denotan las proyecciones sobre X (Z → X) y sobre Y (Z → Y), respectivamente.
- (Propiedades del Producto de Conjuntos) Sean A, A1, A2 ⊂ X y B, B1, B2 ⊂ Y. Se cumple que
- (A1 ∪ A2) x B = (A1 x B) ∪ (A2 x B).
- (A1 ∪ A2) x (B1 ∪ B2) = (A1 x B1) ∪ (A1 x B2) ∪ (A2 x B1) ∪ (A2 x B2).
- (A1 ∩ A2) x B = (A1 x B) ∩ (A2 x B).
- (A1 x B1) ∩ (A2 x B2) = (A1 ∩ A2) x (B1 ∩ B2).
- (A1 x B1) \ (A2 x B2) = (A1 \ A2) x B1 ∩ A1 x (B1 \ B2).
- (A x B)c = Ac x Y ∪ X x Bc.
- Sea A ⊂ X, entonces prX-1(A) = A x Y ⊂ X x Y.
- (Funciones y Producto Cartesiano) Sea f:X → Y. Llamamos
gráfico de f al subconjunto Γ f de X x Y tal que
- Un subconjunto Z de X x Y es el gráfico de una función X → Y, ssi, para todo a en X se cumple que Z ∩ {a} x Y contiene exactamente un punto.
- Sea f:X → Y, A ⊂ X, B ⊂ Y.
- f(A) = prY ( Γ f ∩ (A x Y )) = prY ( Γ f ∩ prX-1 (A)).
- f-1(B) = prX( Γ f ∩ (X x B)).
- La restricción de prX a Γ f es una biyección.
- La restricción de prY a Γ f es inyectiva, ssi, f es inyectiva.
- Sea H la hipérbola {(x,y): xy=1}. Probar que H es cerrado en R2, pero que su proyección en el eje X no lo es. Es decir que las proyecciones canónicas no son funciones cerradas.
- Sean X, Y y Z espacios topológicos. Probar los enunciados
siguientes.
- X x Y ≅ Y x X.
- X x (Y x Z) ≅ (X x Y) x Z ≅ X x Y x Z.
- X x {p} ≅ X.
- X ≅ Y ⇒ X x Z ≅ Y x Z.
- Probar que Rn con la topología usual es homeomórfico con el producto de n copias de R. Análogamente, el cubo unitario In (como subespacio de Rn) es homeomorfo al producto de n copias del intervalo I=[0,1].
- Probar que f:X → Y es continua, ssi, la proyección de X x Y sobre X restringida a Γf es continua.
- Sea W ⊂ X x Y. Si W es abierto entonces prX(W) es abierto. Concluir que las proyecciones son funciones abiertas. ¿Son funciones cerradas?
- Sea Z = X x Y. Sean A ⊂ X y B ⊂ Y.
- A x B es abierto en Z, ssi, A es abierto en X y B es abierto en Y.
- A x B es cerrado en Z, ssi, A es cerrado en X y B es cerrado en Y.
- Cl(A x B) = Cl(A) x Cl(B).
- ¿Será cierto que Int(A x B) = Int(A) x Int(B)?
- ¿Será cierto que Fr(A x B) = Fr(A) x Fr(B)? En caso negativo, hallar una fórmula para Fr(A x B)?
- Los resultados del ejercicio anterior se pueden generalizar al producto cartesiano de una cantidad finita de espacios topológicos. ¿Cuáles, si alguna, se pueden generalizar a un producto arbitrario de espacios topológicos?
- Probar que el producto de dos espacios Hausdorff es un espacio Hausdorff.
- Sea C el conjunto de Cantor. Probar que
- C no interseca a ]1/2,2/3[.
- C no interseca el intervalo para cualquier par de enteros s y k.
- Probar que el espacio de Cantor no es un espacio discreto, pero que su topología coincide con la topología producto (proyecciones son continuas).
- El ejercicio anterior muestra que el producto de infinitos espacios discretos no es necesariamente discreto. ¿Qué pasa con un producto finito de espacios discretos?
Los Espacios Cocientes
[editar]Conjuntos Cocientes
[editar]Sea X un conjunto no vacío y R una relación de equivalencia en X (o sea que es reflexiva, simétrica y transitiva). Llamamos R--clase de equivalencia o simplemente clase de equivalencia de un elemento x de X, al subconjunto de X denotado por [x] y que está formado por todos los y en X que son equivalentes (respecto a R) con X. Cada elemento de una clase de equivalencia se denomina un representante de la clase.
Las clases de equivalencia forman una partición de X, o sea una colección de subconjuntos no vacíos disjuntos entre si y cuya reunión es todo el conjunto. En efecto, como cada x está en [x] (reflexividad) se tiene que las clases de equivalencia no son vacías y que su reunión es igual a X. Supongamos que z fuera un elemento tanto de [x] como de [y]. Entonces, para todo w en [x] se cumple que w ∼ x, x ∼ z y z ∼ y, luego z ∼ y, o sea que w está en [y]. Conclusión, [x] ⊂ [y]. Por la simetría de la situación, tenemos que [y] ⊂ [x], por lo que concluimos que [x] = [y].
Llamamos partición} de un conjunto X a una familia de subconjuntos no vacíos de X disjuntos dos a dos y cuya reunión es todo el conjunto.
Los resultados anteriores muestran que cada relación de equivalencia en un conjunto induce una partición del conjunto cuyos elementos son las clases de equivalencia de la relación.
Supongamos ahora que tenemos una partición de X. Esa partición define una relación de equivalencia en el conjunto de la manera siguiente. Dos elementos están relacionados cuando, y solo cuando, pertenecen al mismo subconjunto de la partición. Cada conjunto de la partición es entonces una clase de equivalencia respecto a esa relación.
Sea X un conjunto cualquiera no vacío y R una relación de equivalencia. Llamamos conjunto cociente de X por la relación R al conjunto formado por todas las clases de equivalencias de R, al que denotamos por X/R. La función ν de X en X/R que asigna a cada x de X su clase de equivalencia se llama suprayección canónica o natural. o también la función cociente.
Ejemplo 9.4.1 Sea f:X → Y un función cualquiera. Definimos una relación x ∼f y en X cuando f(x)= f(y). Es fácil ver que se trata de un relación de equivalencia que denotamos por ∼f o Rf. Las clases de equivalencia son las preimágenes f-1(y), donde y está en f(X). Denotaremos al conjunto cociente por X/f.
El conjunto cociente tiene la siguiente propiedad universal.
Proposición (Propiedad Universal del Conjunto Cociente)
Sea ∼ una relación de equivalencia en un conjunto X y sea ν : X → X/ ∼ la suprayección canónica. Sea f:X → Y una función compatible con la relación de equivalencia---es decir que x ∼ y ⇒ f(x) = f(y), o equivalentemente f es constante en las clases de equivalencia. Entonces, hay una única función inyectiva f*: X/ ∼ → Y tal que f* ° ν = f cuya imagen es f(X). Cuando la función f es suprayectiva, f* es biyectiva.
Propiedad Universal del Cociente -
Demostración. En order de que f* o ν = f, se debe cumplir que f*([x]) = f(x). Solamente es necesario verificar que tal definición no depende del representante escogido en la clase [x]. Observemos que cuando y está en [x] se cumple, por las hipótesis, que f(y) = f(x), lo que prueba que f* está bien definida.
Notemos que f*([x]) = f*([y]) implica que f(x) = f(y). Lo que, a su vez, implica que [x]=[y]. Esto prueba la inyectividad de f*. Claramente si f es suprayectiva, se tiene que para todo y en Y, hay un x en X con f(x)= y, lo que implica que f*([x]]) = y, probando la suprayectividad de f*.
Nomenclatura. La función f* se dice que es la función deducida de f por paso al cociente.
Ejemplo 9.4.2 Sea g:X → Y un función suprayectiva cualquiera. El conjunto Y puede identificarse (como conjunto) con el conjunto cociente X/g. En efecto, por paso al cociente de g, se tiene que la función g^* :X/g → Y es una biyección.
Ejemplo 9.4.3 Definamos una relación ∼Z en R tal que x ∼Z y , ssi, x-y es un número entero. Claramente, esa relación es de equivalencia. Denotaremos por R/Z al correspondiente conjunto cociente.
Consideremos ahora a una función f : R → R periódica con (menor) periodo igual a 1, o sea tal que para todo t se cumple que f(t+1) = f(t). Probaremos que x ∼f y ⇔ x ∼Z y.
Debemos probar que para cualquier t, cuando m sea entero se cumplirá que f(t+m) = f(t) (*). Tal resultado es evidente si m=0 o m=1. Supongamos que m >0 y que se sabe que f(t+m) = f(t). Entonces, f(t+(m+1)) = f((t+m) + 1 ) = f(t+m) = f(t). Por inducción, tenemos entonces que la relación (*) es válida cuando m es positivo. Sea m <0, entonces f(t+m) = f(t+m + (-m)) = f(t); lo que concluye la prueba.
Por lo tanto, las clases de equivalencia de ambas relaciones coinciden, por lo que sus conjunto cocientes coinciden? ¿Qué más podemos decir del conjunto cociente R/Z (= R/f)? Esperemos a estudiar la topología de la situación.
Cocientes Topológicos
[editar]Sea X un espacio. Una relación de equivalencia R en X o lo que es lo mismo una partición (a veces llamada descomposición en algunos textos de Topología) definen un conjunto cociente, X/ R y una suprayección
ν: X → X/R. Nuestro propósito es dotar a X/R con una topología que haga que la suprayección canónica sea continua. Claramente la topología indiscreta cumple con esa condición, pero no es la más interesante, ya que no refleja nada especial de la partición La respuesta adecuada será la topología cociente que definiremos a continuación.Definición. (Topología Cociente) Sean ν: X → X/R como arriba. Llamamos topología cociente a la topología más fina que hace que ν sea continua. Esto es, la topología que contiene a todas las otras topologías en que ν es continua. Esto implica, que un subconjunto U de X/R es abierto, ssi, su preimagen por ν es abierto en X. En tal situación decimos que X/R es el espacio cociente relativo a la relación R o también respecto a la función cociente ν.
Es usual en Topología, llamar identificación a cualquier función f:X → Y entre espacios tal que la topalgia de Y sea tal que un subconjunto de A es abierto, ssi, f-1(A) es abierto. Esto implica que f es continua y que la topología de Y coincide con la topología de X/f, o sea que Y ≅ X/f.La propiedad universal de los conjuntos cocientes produce una propiedad universal semejante para los espacios cocientes.
Proposición 9.4.2 (Propiedad Universal de los Espacios Cocientes)
Sea R una relación de equivalencia en el espacio topológico X. Sea ν la suprayección canónica sobre el espacio cociente X/R. Sea f:X → Y una función continua compatible con la relación R, o sea tal que x R y implica que f(x) = f(y). Entonces, hay una única función inyectiva continua f* : X /R → Y tal que f = f* o ν. Tal función es biyectiva cuando f es suprayectiva.
-
Demostración. La existencia de la función f* sigue de la propiedad universal de los conjuntos cocientes. Necesitamos tan sólo mostrar que se trata de una función continua. Sea V un abierto de Y y consideremos f-1(V), como
f es continua se trata de un abierto de X. Por la descomposición, f =
f* o ν, tenemos que
Lo que muestra que {f*}-1(V) es abierto, probando la continuidad de f*.
Veremos, en ejemplos, que aunque f sea suprayectiva, la función f* no es necesariamente un homomorfismo, a pesar de ser biyectiva.
Advertencia. Las topologías cocientes pueden, a pesar de la simpleza de su definición, ser bastante patológicas.
Ejemplo 9.4.4 Sean X = [0,2] ⊂ R, Y={0,1} y sea f:X → R tal que f(x) = 0 si x está en [0,1[ y f(x) = 1 si x está en [1,2]. El espacio cociente X/f tiene dos elementos, la clase del 0 y la clase del 1. ¿Cómo es la topología de X/f. Como ν-1([0]) = [0,1] se tiene que el conjunto que contiene solamente a la clase del 0 es un abierto en X/f. Vemos entonces que la clase del 1 es cerrado. Así que X/f tiene la topología de Sierpinski.
Notemos que f* es biyectiva, pero no es un homeomorfismo que Y (como subespacio de R tiene la topología discreta que es diferente de aquella de Sierpinski. Notemos que si f* es la función obtenida de f por paso al cociente, se tiene que f*([0]) = 0 y f*([1]) = 1; lo que muestra que f* es biyectiva, pero no es un homeomorfismo por la diferencia de las topologías.
El siguiente lema muestra que la condición sobre los abiertos de la topología cociente tiene una contrapartida equivalente con cerrados.
Lema 9.4.3 Sea f:X → Y una función entre espacios cualesquiera. Las siguientes propiedades son equivalentes.
- Un subconjunto A de Y es abierto en Y, ssi, f-1(A) es abierto en X.
- Un subconjunto A de Y es cerrado en Y, ssi, f-1(F) es cerrado en X.
- Demostración. Para cualquier función f:X → Y y subconjunto Z de Y se cumple que
De donde se obtiene en forma inmediata la equivalencia (a) ⇔ (b).
La próxima proposición da condiciones para que una función biyectiva, obtenida por paso al cociente, sea un homeomorfismo.
Proposición 9.4.4 Sea f:X → Y una función suprayectiva que es abierta o cerrada .La función f*: X/f → Y obtenida por paso al cociente de f es un homeomorfismo. Es decir que f es una identificación (función cociente)
- Demostración. Sea h= (f*)-1 y ν:X → X/f canónica. Observemos que para todo x en X, f*(ν(x)) = f(x) implica que ν(x) = h(f(x)), o sea que ν= h o f.
Sea U un abierto de X/f. Entonces, ν-1(U) es abierto, pero entonces, f-1(h-1(U)) = ν-1(U) es abierto, Como f es abierta, se tiene que f(f-1(h-1(U))) es abierto en Y, pero como f es suprayectiva,
h-1(U) = f(f-1(h-1(U))), lo que prueba que h es continua. Luego, f* es un homeomorfismo.
Razonamiento análogo para cuando f es cerrada.
Pregunta Fundamental Cuando X tiene una cierta propiedad, ¿qué podemos decir de un espacio cociente de X?
Ejercicios 9.4
[editar]- Probar que dada una relación de equivalencia R en un espacio X, el espacio cociente X/R es único, excepto por homeomorfos. Es decir que dos espacios cocientes para la misma relación son siempre homeomorfos.
- Sea X un conjunto cualquiera no vacío. La relación de igualdad = es una relación de equivalencia en X. ¿Qué relación hay entre X y X /=?
- Sea h : [0,1) → S1 tal que f(t) = (cos(2π t), sen(2π t). Probar que h es biyectiva, continua, pero noes un homeomorfismo.
- Sea f:X → Y continua. Definir en X una relación ∼f por x ∼f y ↔ f(x) = f(y). Probar que ∼f es una relación de equivalencia y describir el espacio cociente.
- Sea X = R2 \ {(0,0)}. Definir relaciones R tal que (x,y) R (x',y'), ssi, hay un α >0 tal que x = α x', y = α y'. Probar que el espacio cociente es homeomorfo a una circunferencia.
- Probar que R2 ≅ S1 x ]0, +∞[.
- Sea f: R → R tal que f(x) = x2. Describir el espacio R/f (ver ejercicio anterior).
- Sea f: R → R tal que f(x) = sen(x). Describir el espacio R/f.
}}
Mirando al ejemplo 9.4.4, vemos que un espacio puede ser Hausdorff, pero su cociente no.
Construcción de Conjuntos
[editar]
Cinta de Moebius Gran parte de los ejemplos consiste en hacer todos los puntos de un subconjunto del espacio equivalentes entre si. Sea X un espacio y A un subconjunto de X. Consideremos la partición de X formada por A y por un conjunto de un elemento, para los elementos en el complemento de A. Llamamos contracción de X por A al espacio cociente correspondiente, al que denotaremos por X/A.
Ejemplo 9.5.1 Consideración intuitiva: Sea X un intervalo cerrado de R, digamos [0,1]. Si pegamos 0 con 1, el resultado que se obtiene es una figura homeomórfica a una circunferencia.
Más formal, "pegar" quiere decir que queremos ``identificar 0 con 1. ¿Cómo podemos hacerlo? Simplemente usando una relación de equivalencia donde haya una clase de equivalencia que contenga al 0 y al 1; es decir, haciendo una contracción con A={0,1}. La correspondiente partición sería tal que cada x ≠ 0,1 aporta {x} a la partición, y el único elemento con dos elementos es {0,1}, Sea R la relación definida por esa partición, entonces X/R contiene un punto por cada x ≠ 0,1 y un punto donde se identifican 0 y 1. Notemos que usando la terminología de contracciones, el espacio cociente es [0,1]/{0,1}.
Busquemos una función continua suprayectiva f:[0,1] → S1 (S1 es la circunferencia unitaria) tal que f(0) = f(1) y f(x) = f(y) implica que x=y, cuando 0 < x, y <1. Si esa función es además abierta o cerrada, se tendría una identificación (proposición 9.4.4).
Una posible función es f:[0,1] → S1 tal que f(t) = (cos(2π t), sen(2π t)). Claramente, f es una función continua suprayectiva tal que f(0) = f(1). Sea g:X/f → S1, la función biyectiva que se obtiene al pasar f al cociente. Notemos que f es una función cerrada. Conjuntos cerrados básicos de X son [0,a] con 0 ≤ a < 1 y [b,1] con 0 < b ≤ 1. Entonces, claramente, f([0,a]), el arco desde P= (0,1) a Q=(cos(2π a), sen(2π a)) es un subconjunto cerrado de S1 (intersección de la bola cerrada con centro en el punto medio entre P y Q, de radio la mitad de la distancia de P a Q, con S1. Análogamente, para el otro conjunto cerrado básico. Luego, por la proposición citada, g : X/f → S1 es un homeomorfismo.
Ejemplo 9.5.2. Anteriormente, en el ejemplo 9.4.3, vimos que la relación x ∼Z y, ssi, x-y es un número entero, producía un espacio cociente que al denotamos por R/Z. Considerando al espacio cociente R/ f con f(t) = (cos(2π t), sen(2π t)) y procediendo como en el ejemplo anterior, concluimos que R/Z ≅ S1.
Ejemplo 9.5.3 Sean X, Y espacios topológicos y sea Z = X x Y. Sea x0 un punto de X, definamos una relación de equivalencia, por (x1,y1) R (x2, y2) ↔ y1 = y2.
Se puede observar que la clase de equivalencia de (x,y) consiste de todos los pares cuya segunda coordenada es igual a y. En la representación como ``rectángulo del producto cartesiano, se trata de segmentos paralelos (uno por cada y en Y) al eje de X. Se verifica que prY : X x Y → Y es una identificación, o sea que Y es homeomorfo al correspondiente conjunto cociente.
Ejemplo 9.5.4 (Cilindro) (Intuición) Consideremos un rectángulo y seleccionemos dos de sus lados opuestos. Cada línea paralela a uno de los lados no seleccionados corta a esos dos lados. Identifiquemos esos puntos de corte, o sea imaginemos que pegamos los lados opuestos haciendo corresponder tales puntos de corte. ¿Qué obtenemos? ... un tubo; formalmente llamado cilindro (sin tapas).
Cílindro como espacio cociente Ficura 9.4:Cílindro como espacio cociente Suponiendo un rectángulo R con vértices (1,0), (1,1), (-1,1) y (-1,0). Definamos una relación en R por (x,y) ∼ (x',y'), ssi, x = 1, x'=-1, y=y' o x =-1, x'=1, y=y', si x &neq; 1 o -1, (x,y) \sim (x',y') solamente cuando x = x', y = y'. R es una relación de equivalencia. Las clases de equivalencia son {(x,y)} cuando x ≠ ± 1, y arbitrario, y {(-1,y)(1,y)}, y cualquiera. Una (función) identificación posible es: h: R → C: (x,y) = (cos(π x), sen(π x),y) donde C = S1 x [0,1] (cilindro).
Ejemplo 9.5.5 (Cinta (o banda) de Moebius) Consideremos nuevamente un rectángulo y seleccionemos dos lados opuestos. Peguemos nuevamente los lados opuestos, pero después de girar por media vuelta uno de ellos. Mirar la figura.

Toro como conjunto cociente ¿Qué obtenemos? ... una superficie conocida como ``cinta de Moebius. Si la lectora o lector no tiene experiencia con este objeto, una experiencia interesante será construir en papel una cinta de Medius (empezar con un rectángulo mucho más largo que ancho: una cinta y pegar los lados menores después de una media vuelta). El resultado será un modelo concreto de la cinta de Moebius. Después de hecho lo anterior, como curiosidad, cortar por el centro de la cinta obtenida ¿qué pasa? Un aspecto importante de la cinta es que tiene una solamente una cara.
Ejemplo9.5.6 (Toro) Una superficie muy interesante es aquella llamando toro, que resulta de hacer girar una circunferencia alrededor de un eje que no la corta. La palabra «toro» proviene del latín ``torus, que significa algo así como ``protuberancia.

Toto Objetos de la vida real que tienen forma de toro son las superficies de los flotadores o de una rosquilla. Topológicamente,un toro se define como el espacio producto S1 x S1. Se puede, también, generarlo como espacio cociente de la manera indicada en la figura, empezando con un rectángulo, pegamos por lados opuestos, obteniendo un cilindro. Luego, pegamos las dos bocas del cilindro.
Ejemplo 9.5.7 (Plano Proyectivo). Sea X = R3 \ {(0,0,0)}. Definir una relación ∼ tal que (x1,x2,x3) ∼ (y1,y2,y3), ssi, hay un número real α ≠ 0 tal que xi = α yi, i=1,2,3. Claramente, la relación ∼ es de equivalencia. El espacio cociente, se llama el plano proyectivo y se denota por . Los puntos del plano proyectivo corresponden a líneas pasando por el origen y se simboliza por [x1:x2:x3] al punto que es la clase de equivalencia de (x1,x2,x3).Un plano en R3 que pasa por el origen genera una línea del plano proyectivo.
Sea la función cociente natural. Para cada i = 1, 2, 3, sea
Se verifica que cada Ui es un abierto homeomórfico a R3.
Ejercicios 9.5
[editar]- Sea C el cilindro S1 x I donde I=[0,1]. Definir una relación de equivalencia (x,y) R (x',y), ssi, y' = y = 1.
Explicar por qué C/R puede ser llamado ``sombrero cónico.
- Probar que C/R es homeomorfo a un disco cerrado del plano.
- Sea A = {(x,y): y=1}, mostrar que C/A = C/R.
- Sea X el producto de una bola cerrada del plano con un intervalo cerrado, digamos . Si se define una relación R tal que (x,y,t) R (x',y',t'), ssi, t=t'=1, explicar por que podemos decir que el cociente X/R es un cono sólido. es la bola unitaria de \R2.
- Sea Bn cualquier espacio homeomorfo a la bola de radio 1 y centro el origen de Rn. Sea Sn-1 la esfera unitaria de Rn.
- Mostrar que podemos identificar Sn con un subespacio de Bn+1.
- Probar que Bn+1/Sn ≅ Sn+1.
- Probar que un toro y X = S1 x S1 son homeomorfos.
Ejercicios del capítulo 9
[editar]- Sean X={0,1} con la topología discreta y sea Y = X x X con la topología producto. Listar todos los abiertos de Y. ¿Es Y un espacio discreto?
- Sean X={0,1} el espacio de Sierpinski (topología = {∅,{0}, X}) y sea Y = X x X con la topología producto. Listar todos los abiertos de Y.
- En el texto se indicó que el producto cartesiano de dos funciones continuas era continuo. Cuando se tiene una familia f_α : X_α → Y_α , α en I, donde I es un conjunto arbitrario, podemos definir de manera análoga un producto f = ∏α fα tal que f ((xα ))= (fα (xα )). Cuando las fα son continuas, es f necesariamente continua?
- Sea Xi, i ∈ I una familia de espacios topológicos discreto y sea X su producto topológico. ¿Es X necesariamente discreto?
- Cuando g1, g2 son funciones abiertas, también lo es su producto g1 x g2.
- Sea X un espacio cualquiera e I = [0,1] ⊂ R. Sea A = {(x,1): x ∈ X } ⊂ X x I. Sea CX = X/A, el cono basado en X}.
- Si X= Sn entonces CX es homeomorfo a la bola cerrada de radio 1 y centro el origen, Bn+1, n ≥ 1.
- Sea I2 el cuadrado unitario de R2. ¿Cómo podría describirse CX?
- Escribir una relación de equivalencia R en X x I tal que CX = X x I / R.
- Sea X un espacio cualquiera. Se define una partición en X x I, donde I=[-1,1] ⊂ R, integrada por N = {(x,1): x ∈ X},
S = {(x,-1): x ∈ X} y cada punto en el complemento de S ∪ N generando una clase con un único elemento. El conjunto cociente se denota por SX y se llama la suspensión de X.
- Si X= S1 entonces SX= S2 la esfera unitaria de R3
- Si Y fuera un triángulo ordinario (unión de tres segmentos), ¿cómo podríamos describir a SY? ¿Que relación hay entre SY y SX.
- (Homeomorfismos)
- Probar que [0,1]/[1/4,3/4] ≅ [0,1].
- Describir el espacio cociente [0,1]/{1/3,1}. Comparar con una letra del alfabeto.
- Si el punto medio del lado curvo se identifica con el punto medio del segmento rectilíneo de la letra D, ¿qué letra obtenemos?
- Construir otros ejemplos análogos a las situaciones anteriores.
- (Proyección Estereográfica) Sea S la esfera unitaria tridimensional (x2 +y2 +z2 =1) pero sin su polo norte N = (0,0,1). Sea Y el plano z=0 Sea P un punto cualquiera de la esfera. La línea qua pasa por N y P corta el plano en un punto π(P). Probar que π es un homeomorfismo.
Los Espacios Conexos
[editar]Introducción
[editar]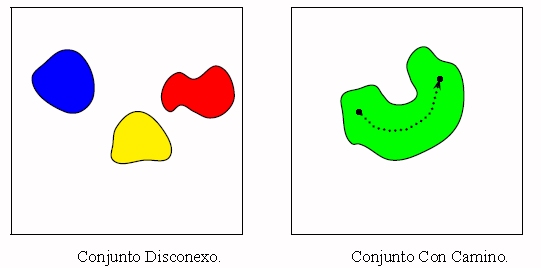
Conexo significa intuitivamente algo formado por un solo pedazo, que está conectado, no separado. Un archipiélago (conjunto de islas) es un ejemplo de un espacio con varias partes separadas. Tales espacios se llamarán disconexos, mientras que una isla será un ejemplo de un espacio conexo (sin partes). Veamos un ejemplo matemático. Consideremos al espacio topológico R* formado por los reales no nulos. R* es la reunión de dos partes separadas: los reales positivos, R+, y los reales negativos, R-. Ambos subconjuntos son conjuntos abiertos que son disjuntos entre si; y serán las partes topológicas del espacio. Vemos, además, intuitivamente, que no hay un camino continuo posible de un real positivo a un real negativo. La ausencia de un punto introduce un abismo infranqueable (continuamente) entre las dos partes. En una situación plana no sucede necesariamente lo anterior. Resulta intuitivamente claro que dos puntos de R2* (el plano sin el origen) pueden unirse por un camino.
En este capítulo, analizaremos las nociones de conexo y de conexo por caminos. Un espacio será conexo por caminos cuando hay un camino continuo entre dos cualesquiera de sus puntos. Veremos que esas dos nociones son topológicas, es decir que cuando un espacio tiene una de esas propiedades, cualquier espacio homeomorfo también la tiene. Lo anterior nos servirá, a veces, para distinguir entre espacios topológicos. Por ejemplo, las consideraciones sobre caminos en R* y R2* nos indicará que esos espacios no pueden ser homeomorfos.
La formalización de dichas nociones y su uso en el estudio de espacios topológicos son un ejemplo de bella matematización de intuiciones.
Las Definiciones Básicas
[editar]Iniciaremos nuestro estudio con los espacios conexos por ser, como veremos, más generales que los espacios conexos por caminos. Postergaremos ejemplos importantes hasta ver espacios conexos por caminos, ya que será más fácil, usualmente, verificar dicha condición y, además, todo espacio conexo por caminos resultará ser conexo. El recíproco de lo anterior, sin embargo, no es válido en general.
La definición de espacio conexo abstrae de lo ilustrado en el ejemplo acerca de R*. Allí, vimos que había dos subconjuntos abiertos disjuntos (los positivos y los negativos) cuya reunión era todo el espacio.
Definición. (Espacio Conexo)
- Un espacio X es conexo, ssi, cuando con U, V abiertos no–vacíos, se cumple que
- Un espacio disconexo es un espacio que no es conexo.
- Un subespacio de X es conexo, cuando lo es respecto a su topología relativa.
Ejemplos 10.2.1.- R* es un espacio disconexo.
- Cualquier espacio o subespacio consistente de un único punto es conexo.
Disconexión, división, separación. Sea X un espacio topológico y sean A y B un par de subconjuntos propios abiertos disjuntos cuya reunión es X; lo que implica que X es disconexo. Diremos que el par A, B son (o determinan) una disconexión del espacio. También, podremos decir que definen una división del espacio.
La formalización de dichas nociones y su uso en el estudio de espacios topológicos es un ejemplo de bella matematización de intuiciones.Conjuntos Abiertos–Cerrados. Sea X un espacio topológico disconexo, con una división dada por A y B. Como, entonces, B es el complemento del abierto A, tenemos que B es cerrado; lo mismo pasa con A.
Diremos que un conjunto es abierto–cerrado cuando sea abierto y cerrado a la vez.
En cualquier espacio X, el subconjunto vacío y todo el espacio X son abiertos y cerrados. En un espacio conexo, de acuerdo con la definición, estos son los únicos conjuntos abierto–cerrados posibles. Al contrario, cuando haya un subconjunto propio no vacío A de X que sea abierto–cerrado, se tendrá que X es disconexo, con una disconexión dada por A y su complemento.
Ejemplo 10.2.2. Sea X un espacio topológico discreto con más de un punto. Como cada subconjunto es abierto y cerrado, el espacio no es conexo.
Ejemplo 10.2.3. Sea X = [0, 1] ∩ ]2, 3] (subconjunto de la línea real) . Probaremos que X es disconexo.
Sea A = [0, 1]. Observemos que en la topología relativa de X, como A = X ∩ (−1, 3/2), se tiene que A es abierto. Claramente es cerrado. Luego A es abierto–cerrado. Como no es vacío, el espacio X es disconexo. Los subespacios [0, 1] y ]2, 3] forman una disconexión de A.
La siguiente proposición muestra que en la línea real, la noción de conexión coincide con la noción de intervalo.
Proposición 10.2.1 (conectividad en la Línea Real). Un subespacio no vacío de la línea real es conexo, ssi, es un intervalo. En particular, la línea real es un espacio conexo.
- Demostración.
Sea X un subconjunto de R no vacío y conexo. Supongamos que X no es un intervalo. Esto implica que hay números x, y, z tales que x < y < z, con x, z en X, pero tales que y no está en X. Entonces,
X = (X ∩ ]−∞, y[) ∪ (X ∩ ]y,+∞[ ) es una disconexión de X. Como esto contradice la hipótesis, X debe ser un intervalo.
Supongamos ahora que X es un intervalo de R. Si X consiste de un punto, entonces X es conexo. Supongamos que X no fuera conexo, por lo que habría subconjuntos propios no vacíos A y B de X,abiertos–cerrados, tales que X = A ∪ B y A ∩ B = ∅. Sean x ∈ A, z ∈ B, donde, sin perdida de generalidad, podemos suponer que x < z. Como X es un intervalo, [x, z] es un subconjunto de X. Sea y definido como y = sup{w : [x,w] ⊂ A}. Ya que x ≤ y ≤ z, y está en X. :Como A es cerrado, y debe ser un punto de A. Luego, y < z. Entonces, para todo r > 0, y + r debe ser un punto de B, como r es arbitrario, se tiene que y pertenece a la clausura de B y como B es cerrado, debe estar en B. Pero esto implica que A y B no son disjuntos. Luego, X debe ser conexo.
En el ejemplo 10.2.3, vemos que un espacio conexo (R) puede contener subespacios disconexos. Vemos, también, que un espacio disconexo puede tener subespacios conexos.
C=== La Conectividad y las Funciones Continuas === Teorema 10.2.2.La imagen de un espacio conexo por una función continua es un conjunto conexo.
-
Demostración.
Sea f : X → Y una función continua. Supongamos que f(X) es disconexo. :Entonces, hay abiertos no vacíos disjuntos A y B tales que f(X) está contenido en A∪B. Pero, entonces, f−1(A) y f−1(B) son abiertos no vacíos cuya reunión es todo X. Además son disjuntos, ya que x en f−1(A) ∩ f−1(B) implica que f(x) está en A y en B, lo que es imposible.
Corolario 10.2.3. Ser conexo (resp. disconexo) es una propiedad topológica.
- Demostración. Si X es conexo y f : X → Y es un homeomorfismo, entonces Y = f(X) es conexo.
Corolario 10.2.4. Sea f : X → Y continua, donde X es conexo y Y es discreto. Entonces, f es constante.
Corolario 10.2.5. Sea f : X → R continua. Si X es conexo, su imagen en R es un intervalo.
Este corolario tiene interesantes aplicaciones al Análisis Real, por ejemplo el teorema del valor intermedio y sus aplicaciones (ver el Teorema A del primer capítulo y los ejercicios de la sección).
Criterio para Separación. La siguiente proposición nos da un criterio para disconexión.
Proposición 10.2.6. Un espacio topológico X es disconexo, ssi, hay una función suprayectiva continua de X en el espacio discreto {0, 1}.
-
Demostración. Suponer que existe función de f : X → {0, 1} suprayectiva y
continua. Como {0, 1} es disconexo, por la proposición anterior, X no puede ser
conexo.
Sea A,B una separación de X. Definiendo f(x) = 0 si x está en A y f(x) = 1
si x está en B, obtenemos una función suprayectiva, que además es continua, ya
que la imagen inversa de cualquier abierto en {0,1} es abierto en X.
Gráfica de una Función Real Continua. Sea f : I ⊂ R→ Run a función continua, donde I es in intervalo y consideremos la gráfica de f como un subconjunto de R2.
- Sea g : I → R2 tal que g(x) = (x, f(x)). Claramente g es continua por coordenadas, por lo que es continua. Como su imagen es precisamente la gráfica de f, concluimos que dicha gráfica es conexa.
El resultado anterior es la formulación matemática de la expresión que “una función continua tiene una gráfica que puede dibujarse sin levantar el lápiz”.
- Una función real definida en un intervalo es continua, ssi, su gráfica es conexa.
Ejercicios 10.2
[editar]- Sean A = [0, 1[, B = [1, 2] y C = A ∪ B subconjuntos de la línea real. Probar que C es conexo aunque A y B son disjuntos. Explicar.
- Dibujar dos subconjuntos conexos del plano, cuya intersección no sea conexa.
- Probar que el subconjunto de los Racionales no es conexo como subconjunto de la línea real. &&&
- Sean A la 1–vecindad de (−1, 0), B la 1–vecindad de (0, 1) y C = A ∪ B.. Probar que
- C es disconexo.
- Sea D = C ∪ {(0, 0)}. Probar que no puede haber una función continua tal que la restricción a A (resp. B) sea constante con valor 0 (resp. 1). ¿Es D conexo?
- Probar que ser conexo y ser disconexos son propiedades topológicas.
- Sea ¿Es C conexo? Justificar.
- Probar que, de acuerdo a la definición, el conjunto vacío no es disconexo; por lo que debe ser conexo.
- Probar que los siguientes enunciados son equivalentes.
- a) X es conexo.
- b) X no puede dividirse entre dos subconjuntos disjuntos no vacíos abiertos.
- c) X no puede dividirse entre dos subconjuntos disjuntos no vacíos cerrados.
- d) Los únicos subconjuntos abierto–cerrados de X son X y el conjunto vacío.
- e) Los únicos subconjuntos de X con frontera vacía son X y el conjunto vacío.
- f) Cualquier función continua de X en un espacio discreto es constante.
- g) X no puede expresarse como la reunión de dos conjuntos no vacíos tales que cada uno de ellos es disjunto de la clausura del otro.
- Enunciar equivalencias para espacio disconexo, correspondientes al ejercicio anterior.
- Probar que cuando el producto de dos espacios no vacíos X × Y es un espacio conexo, también lo son X y Y . Generalizar a productos arbitrarios.
- Sean X, Y conexos. Probar que X × Y (con la topología producto) es conexo. Sugerencia: suponer que hay una función continua f : X × Y en el espacio discreto {0, 1} y probar que es constante. Ver ejercicio sobre equivalencias para la noción de conexo. Generalizar a productos arbitrarios. Aplicar lo anterior para concluir que Rn y In (cubo unitario) son conexos.
- Cuando un subespacio X es conexo ¿lo será un subconjunto del mismo? ¿Un espacio cociente X/R?
- Si los conjuntos A y B forman una division de un espacio topológico X y Y es un subespacio conexo de X, entonces Y es un subconjunto de A o un subconjunto de B.
- Sean A y B subconjuntos conexos cuya intersección no es vacía. Probar que
su reunión es conexa. Generalizar a una familia de conexos con intersección
no vacía.
Aplicaciones al Análisis Real. - (Teorema del Valor Intermedio) Sea f : [a, b] → Res continua, entonces para cualquier z entre f(a) y f(b), hay un x entre a y b tal que f(x) = z.
- (Existencia de Ceros) Sea f : [a.b] → Rcontinua. Si f(a)f(b) < 0 entonces hay un c entre a y b tal que f(c) = 0.
- Probar que dado un número real positivo a hay un número real positivo c tal que c3 = a.
- (Teorema del Punto Fijo.) Sea f : [0, 1] → [0, 1] continua. Entonces, hay un z en [0, 1] tal que f(z) = z. (Sug. Si f(0) = 0 o f(1) = 1 no hay nada más que probar. En caso contrario, estudiar la función g(x) = x − f(x).)
- Probar que cualquier función continua f de [a, b] en [a, b] tiene un punto fijo. (Sugerencia: probar que si X y Y son homomeomórficos entonces cada función continua de X en X tiene un punto fijo, ssi, cada función continua de Y en Y tiene un punto fijo. Luego usar que [a, b] es homeomorfo a [0, 1].)
Los Subespacios Conexos
[editar]Sea X un espacio topológico y Y un subespacio de X. ¿Cuándo Y es disconexo? Sigue de la definición que debe haber un par de abiertos A y B de X, tales que
- (i) La reunión de los abiertos relativos A ∩ Y y B ∩ Y contiene a Y, lo que implica que Y ⊂ A ∪ B.
- (ii) La intersección de A ∩ Y y B ∩ Y no puede contener puntos de Y, es decir
que debe ser un subconjunto del complemento de Y .
- (iii) Los abiertos relativos A ∩ Y y B ∩ Y deben ser no vacíos.
Claramente, esas tres condiciones son, también, suficientes para garantizar que tales abiertos de X definen una división de Y .
La siguiente proposición nos da un criterio para que un par de subconjuntos de un subespacio definan una división del mismo.
Proposición 10.3.1. Si Y es un subespacio de X, una división de X es un par de conjuntos disjuntos no vacíos A y B cuya reunión es Y y tales que ninguno de ellos contiene un punto de acumulación del otro.
- Demostración.
Supongamos que A y B definen una disconexión de Y . Entonces, A es abierto–cerrado en Y. Recíprocamente, supongamos que A y B son conjuntos no vacíos disjuntos cuya reunión es Y y tal que ninguno de ellos contiene un punto de acumulación del otro. Como cl(A) ∩ B = ∅ (clausura respecto a X), tenemos que
cl(A) ∩ Y = cl(A) ∩ (A ∪ B) = (cl(A) ∩ A) ∪ (cl(A) ∩ B) = A. Análogamente, cl(B) ∩ Y = B. Lo que muestra que A y B son cerrados en Y . :Como cada uno de ellos es el complemento en Y del otro, son también abiertos en Y ; lo que muestra que forman una división de Y.
Lema 10.3.2. Si los conjuntos A y B forman una division de un espacio topológico X y Y es un subespacio conexo de X, entonces Y es un subconjunto de A o un subconjunto de B.
-
Demostración. Como A y B son abiertos en X, los conjuntos A∩Y y B ∪Y son abiertos disjuntos de Y cuya reunión es igual a Y . Si ambos subconjuntos fueran no vacíos, determinarían una división de Y, por lo tanto, uno de ellos debe ser vacío. Por lo que Y debe estar contenido en A o en B.
Proposición 10.3.3. Sea X un espacio topológico. Sea A un conjunto conexo y sea B tal que A ⊂ B ⊂ Cl(A). Entonces, B es conexo. En particular, Cl(A) es conexo.
- Demostración. Supongamos que los abiertos disjuntos C y D determinan una disconexión de B. Por el lema anterior, A debe estar contenido en
uno de esos conjuntos, digamos que A está contenido en C.
Luego, B ⊂ Cl(A) ⊂ Cl(C). Como C y D son una desconexión de B, no puede haber intersección de Cl(C) con D, lo que contradice que D sea un subconjunto no vacío de B. Luego, B debe ser conexo.
Proposición 10.3.4. Sea X un espacio topológico. Sea (Ai) una familia de subconjuntos conexos de X cuya intersección no es vacía. Entonces A = ∪{Ai} es un conjunto conexo.
- Demostración. Ver ejercicios.
Ejercicios 10.3
[editar]- Si los conjuntos A y B forman una division de un espacio topológico X y Y es un subespacio conexo de X, entonces Y es un subconjunto de A o un subconjunto de B.
- Sean A, B subconjuntos de un espacio topológico X tales que A es conexo, B es abierto–cerrado, y A ∩ B ≠ ∅. Entonces, A ⊂ B.
- Sean A y B subconjuntos conexos cuya intersección no es vacía. Probar que su reunión es conexa.
- Sea (Ai), 1 ≤ i ≤ n, una familia finita de conexos tales que Ai ∩ Ai+1 ≠ ∅, i = 1, . . ., n − 1. Entonces, la reunión de los conjuntos es conexa. (cadena de conjuntos conexos).
- Sea (Ai), i∈I, una familia de conjuntos conexos de un espacio X tal que la intersección de la familia no es vacía. Entonces, su reunión es conexa,
Las Componentes Conexas
[editar]Sea X un espacio topológico y sean x, y puntos de X. Decimos que “x está conectado con y”, ssi, hay un subconjunto conexo que contiene ambos puntos. Claramente la relación “estar conectados” es una relación de equivalencia. Denotaremos, en esta sección, por Cx a la clase de equivalencia de la relación anterior, que contiene a x. Sea A un conjunto conexo que contiene a x. Entonces, todos los elementos de A están relacionados con x, por lo que son elemento de Cx, es decir que A está contenido en Cx. Luego, Cx es la reunión de los subespacios conexos que contienen a x. Como dicha reunión tiene intersección no vacía concluimos que se trata de un conjunto conexo. Como son clases de equivalencias, si y está en Cx se tiene que Cy = Cx.
Llamaremos componentes conexas a las clases de equivalencia anteriores. Sigue de la discusión anterior que cada componente es un subespacio conexo de X que es maximal con respecto a esa propiedad. Un espacio es conexo cuando tiene solamente una componente conexa, el mismo espacio.
Como la clausura de un conexo es un conjunto conexo, la clausura de una componente debe coincidir con la componente, lo que implica que las componentes son conjuntos cerrados.
La siguiente proposición resume nuestra discusión sobre componentes conexas.
Proposición 10.4.1. Sea X un espacio topológico.
- (a) Cada punto x de X está contenido en exactamente una componente conexa de X.
- (b) Cada subconjunto conexo está contenido en una única componente conexa.
- (c) Cada componente conexa es un conjunto cerrado.
Ejemplos 10.4.1.
- Sea X = R* = {t ∈ R : t ≠ 0}. X no es conexo porque no es un intervalo; sus componentes son los reales positivos y los reales negativos.
- En el ejemplo 10.2.3, X = [0, 1]∪]2, 3], los subespacios [0.1] y ]2, 3] son las componentes conexas de X.
- En un espacio topológico discreto, cada punto define una componente conexa.
Espacios Totalmente Disconexos. Son aquellos espacios donde cada punto es una componente conexa. Notemos que los espacios con un sólo punto son conexos y totalmente disconexos. Cualquier subespacio discreto es totalmente disconexo.
Espacios Localmente Conexos. Son aquellos espacios donde cada punto tiene una vecindad que contiene una vecindad abierta conexa del punto.La línea real es un ejemplo de un espacio localmente conexo.
Proposición 10.4.2. Sea X un espacio localmente conexo. Cada componente conexa de un subespacio abierto Y de X, es un conjunto abierto. En particular, las componentes conexas de X son conjuntos abiertos.
- Demostración. Sea C una componente de Y y x un punto de C. Como X es
localmente conexo y Y es una vecindad de x, hay un vecindad abierta V de x que
es conexa y abierta en X. Como Y es abierto, la topología de V como subespacio
de X es la misma que la topología como subespacio de Y, luego, V es conexo en Y. Luego, V ⊂ C, ya que C es maximal. Lo que prueba que C es abierto.
Ejercicios 10.4
[editar]- Probar que la relación “estar conectados” es una relación de equivalencia.
- Un subconjunto no vacío conexo que es abierto y cerrado es una componente conexa.
- Sea X un espacio topológico con una cantidad finita de componentes. Probar que cada componente es un conjunto abierto–cerrado.
- Sean X, Y espacios homeomorfos. Probar que hay una correspondencia biyectiva entre las componentes de ambos espacios.
- ¿Cuántas componentes conexas tiene un espacio topológico indiscreto?
- Dar un ejemplo de un espacio topológico finito que no sea totalmente indiscreto.
Los Caminos
[editar]En la próxima sección, veremos una manera diferente de conexión, la conexión por caminos. Allí, veremos que un espacio es conexo por caminos, cuando haya un camino entre dos puntos cualesquiera del espacio.
¿Qué es un camino?
Definición. (Camino, Trayectoria) Sea X un espacio topológico no vacío y sean x, y puntos de X.
- Llamaremos trayectoria (continua) de x a y, a una función continua
σ : [a, b] ⊂ R → X tal que σ(a) = x y σ(b) = y. x es el punto de inicio y y el punto final de la trayectoria.
- Llamaremos camino de de x a y al conjunto de puntos de una trayectoria de x a y.El camino asociado a la trayectoria σ se simbolizará por {σ}.
- Llamamos punto inicial del camino, o de la trayectoria, al x, mientras que y e>s su punto final. Ambos puntos son los extremos del camino, o de la trayectoria.
Cada trayectoria define un camino, pero puede haber varias trayectorias diferentes para el mismo camino. Cada trayectoria define un camino, pero puede haber varias trayectorias diferentes para el mismo camino. Decimos que un camino es cerrado cuando su punto inicial coincide con su punto final.[6]
Ejemplo 10.5.1. Sea E = R2. Una trayectoria de x a y es σ: [0, 1] → Rtal que σ(t) = (1 − t)x + ty. El camino definido por σ, {σ}, es el segmento lineal con extremos x y.
Ejemplo 10.5.2. Sean σ1, σ1 : [0, 2π] → R2 tales que:
- σ1(t) = (cos(t), sen(t)) y
- σ2(t) = (cos(2t), sen(2t)).
Notemos que ambas trayectorias tienen como imagen la circunferencia unitaria. Ambas empiezan en (1,0) y terminan en el mismo punto. La diferencia entre ambas trayectorias es que, pensando cinemáticamente, la segunda recorre la circunferencia con el doble de rapidez que la primera. Lo que hace que la segunda recorra dos veces la circunferencia, mientras la primera lo hace solo una vez.
El último ejemplo muestra que, conceptualmente, camino y trayectoria son nociones relacionadas, pero diferentes entre si. En estudios geométricos resulta, a veces, necesario distinguir entre ambas nociones. Un camino es un objeto geométrico (conjunto de puntos), una trayectoria que define al camino es una parametrización del camino, lo que representa una manera de recorrer el camino. En general, las nociones geométricas son aquellas que dependen del camino y no de una trayectoria en particular del mismo.
Al contrario, en el contexto topogeométrico lo único que nos interesará, por ahora, es que haya un camino entre dos puntos del espacio, por lo que es tradicional usar camino como sinónimo de trayectoria (continua); lo que haremos en este capítulo. Lo que será importante para nuestras consideraciones será que los caminos (como subconjuntos) son subconjuntos conexos del espacio (ya que son imágenes de conexos).
Simbolizaremos por x ↝ y a un camino de x a y (o sea una función σ continua de algún intervalo [a, b] ⊂ R en el espacio con σ(a) = x y σ(b) = y. Diremos, también, que el camino une su punto inicial con su punto final.
Observemos que el dominio de una trayectoria puede ajustarse a ser cualquier intervalo, por ejemplo, sea σ: [a, b] → X una trayectoria y sea f : [c, d] → [a, b] tal queClaramente, f es continua y f(c) = a y f(d) = b. Además, σ ◦ f : [c, d] → X es un trayectoria que define el mismo camino que σ.
Notemos que caminos pueden concatenarse, en el sentido que dados caminos x ↝ y y y ↝ z, tenemos un camino x ↝ z. (Posiblemente, será necesario ajustar los dominios de los caminos, para definir la concatenación).
Ejercicios 10.5
[editar]- Probar que cuando hay una trayectoria de x a y, hay otra de y a x.
- Sean σ_1, σ_2 : [0, 1] → R2 tales que σ_1(t) = (1, t) y σ_2(t) = (1−t, 1). Probar que σ_1 : (1, 0) ↝ (1, 1) y que σ_2 : (1, 1) ↝ (0, 1). Escribir las ecuaciones para el camino de (1, 0) a (0, 1) recorriendo los caminos anteriores.
- Sea X un espacio topológico no vacío. Probar que la relación x y es una relación de equivalencia en X. Describir en palabras la clase de equivalencia de un punto x. Definir componente conexas por caminos y enunciar algunas de sus propiedades.
- Sea S2 la esfera unitaria de R3, o sea que Probar que dos puntos cualesquiera de S2 pueden unirse por un camino continuo.
La Conexión por Caminos
[editar]Definición. (Conexo por Caminos)
- Un espacio X es conexo por caminos, ssi, para todo x, y hay una camino (continuo) de x a y, esto es hay una función continua σ : [0, 1] → X tal que
σ(0) = x, y σ(1) = y. - Un espacio X es localmente conexo por caminos cuando cada uno de sus puntos tiene una vecindad abierta que es conexa por caminos.
- Un subconjunto Y de un espacio topológico es conexo por caminos (resp. localmente conexo por caminos) cuando lo sea con respecto a la topología relativa.
Recordemos que x ↝ y simboliza a un camino de x en y. Es fácil verificar que x ↝ y es una relación de equivalencia cuyas las clases de equivalencia se llaman las componentes conexas por caminos del espacio.
Proposición 10.6.1. Cada intervalo de la línea real es conexo por caminos.
- Demostración. Sean a, b numeros reales tales que a < b y que pertenecen a un mismo intervalo. Sea σ(t) = a + t(b − a). Claramente, σ es continua y tal que σ(0) = a y σ(1) = b. Lo que prueba el resultado.
La siguiente proposición, aparte de sus implicaciones teóricas, nos será muy útil para probar que ciertos espacios son conexos.
Proposición 10.6.2. Los espacios conexos por caminos son conexos.
- Demostración. Supongamos que X no fuera conexo. Entonces, tendríamos que X = U ∪V donde U, V ⊂ X son conjuntos abiertos no vacíos y tales que U∩V = ∅. Sean x ∈ U y y ∈ V. Por la hipótesis de conectividad por caminos, hay una función continua σ : [0, 1] → X tal que σ(0) = x, y
σ(1) = y. Entonces, [0, 1] = σ-1(U) ∪
σ-1(V ) es una disconexión de [0, 1], lo que contradice la conectividad de [0, 1]. Luego, X debe ser conexo.
La conectividad por caminos implica a la conectividad, pero el recíproco no es válido como lo muestra el ejemplo siguiente.
Ejemplo 10.6.1 (La curva seno del topólogo).
Curva Seno de los Topólogos (El nombre proviene de uso como ejemplos de libros de topología.) Sean
- A = {(x,y): x=0, -1 ≤ y ≤ 1}
- B la gráfica de la función f:(0,1] →, f(t) = sen(1/t), o sea que
B= {(x,y): 0 <x ≤ 2/π, y = sen(1/x)}; - C = A \cup B.
- (i) que cada punto de A es un punto de acumulación de B y
- (ii) que la función f no puede extenderse a una función continua cuyo dominio incluya al 0. Luego, C coincide con la clausura de B, por lo que es conexo; pero, por (ii0, no hay camino continuo uniendo los puntos de A con los puntos de B, es decir que C no es conexo por caminos.
Gráficamente, podemos también apreciar que C tampoco es localmente conexo.
Proposición 10.6.3. Las bolas abiertas y las cerradas de Rn son conexas por caminos.
- Demostración. Sea B una bola (abierta o cerrada) con centro en el punto a y radio r. Sea b un punto de B. La función σ(t) = a+t(b−a) define un camino continuo desde a hasta b. Sea x = a+t(b−a) con 0 ≤ t ≤ 1 un punto cualquiera de la Imagen de σ. Entonces, cuando 0 < t < 1 (o sea x ≠ a, b) tenemos que:
Lo que prueba que x está en B.
El argumento anterior muestra que dados x, y cualesquiera tenemos caminos de a hasta x y de a hasta y. Recorriendo el primer camino en sentido inverso, seguido por el segundo camino, obtenemos un camino de x hasta y.
Corolario 10.6.4. Las bolas abiertas y cerradas de Rn son conexas.
Corolario 10.6.5. Los espacios Rn son conexos por caminos, localmente conexos y conexos.
- Demostración. Como las bolas son conexas por caminos, concluimos que Rn es localmente conexo por caminos. Dos puntos cualesquiera son siempre elementos de una misma bola cerrada con centro en el origen y radio igual a la mayor de las distancias de esos puntos al origen. La conectividad sigue de la proposición anterior.
Usaremos el siguiente lema para la próxima proposición..
Lema 10.6.6. Cuando dos espacios son conexos por caminos y su intersección también lo es, entonces su reunión es conexa por caminos.
- Demostración. Sean X, Y los espacios. Sea U = X ∪ Y y sean x, y puntos
de U. Cuando ambos pertenecen a X o a Y, hay un camino que los conecta.
Supongamos, entonces, que x es un punto de X y y es un punto de Y . Sea z un
punto de la intersección de X con Y . Por las hipótesis tenemos que x ↝ z ↝ y es un camino continuo de x a y,
Proposición 10.6.7. Cuando n ≥ 1, la esfera unitaria Sn = {x ∈ Rn+1 : |x| = 1} es conexa, conexa por caminos y localmente conexa. S0 = {1,−1} es totalmente disconexa (espacio discreto).
- Demostración. Notemos que x = (xi) está en S = Sn, ssi,
Si n = 1, S1 es la circunferencia unitaria. Podemos representar cada punto de S1 como (cos(t), sen(t)), 0 ≤ t ≤ 2π . La representación anterior es única excepto para p = (1, 0) que corresponde a t = 0 y t = 2π. Asociaremos la coordenada 0 con (1,0). Sea q un punto con coordenada s. El camino definido por σ(t) = (cos(t), sen(t)), 0 ≤ t ≤ s une continuamente p con q. Lo que muestra, que dados dos puntos q1, q2, el camino q1 ↝ p ↝ q2 une ambos puntos. Eso muestra que S1 es conexa por caminos, por lo que es conexa.
Supongamos, ahora, que n > 1 y sea S+ = {x ∈ Sn : xn+1 ≥ 0} y S− = {x ∈ Sn : xn+1 ≤ 0}. Entonces, S = S+ ∪ S- y S+ ∩ S- = Sn-1.
Sea φ: S+ → B = B[0;1] ⊂ Rn tal que φ(x1, ..., xn, xn+1) = (x1, . . ., xn) (la proyección sobre el hiperplano ecuatorial). Entonces, φ es continua con inversa dada por la función continua
Por lo que, S+ es homeomorfa a B. Como sabemos que B es conexa por caminos, concluimos que S+ es conexa por caminos. Procediendo de manera análoga, concluimos que S- es conexo por caminos. sigue entonces, que S es la reunión de dos espacios conexos por caminos, cuya intersección es, por inducción sobre n ≥ 2, conexa por caminos. Por el lema, tenemos que S es localmente conexa; por lo que es conexa. Dejamos la conectividad local de ejercicio.
Corolario 10.6.8. Las esferas de radio cualesquiera son conexas, conexas por camino y localmente conexas por caminos.
- Demostración. Sea S = Sn la esfera unitaria de C, y sea S′ = S(s; r) una esfera de centro a y radio r en S+.
Si a = 0, la función x &8614; rx is un homeomorfismo que envía S en S′. :Supongamos ahora que a es un punto cualquiera y que S′′ = S(0; r) es la esfera de centro el origen y radio r. La traslación que envía el origen en a es un homeomorfismo de S′′ en S′, lo que prueba el resultado.
Corolario 10.6.10. Rn \ {0}, n > 1, es un espacio conexo, conexo por caminos y localmente conexo por caminos.
- Demostración. Sean x, y dos puntos diferentes del origen. Cuando el segmento lineal con extremos x y y no contiene al origen, dicho segmento provee un camino de x a y. Supongamos que el origen está entre x y y. Sea v = (1/|x − y|)(x − y), v es un vector unitario. Sin perdida de generalidad, podemos suponer que x = tv y y = s(−v) con t, s > 0. Como la esfera unitaria es conexa por caminos, hay un camino de v a −v, por lo que tenemos un camino de x a y dado por x ↝ v ↝ (−v) ↝ y. Lo que muestra la conectividad por caminos y, en consecuencia, la conectividad. La conectividad local sigue de que Rn \ {0} is abierto.
Proposición 10.6.10. Un espacio X que es conexo y localmente conexo por caminos es conexo por caminos.
- Demostración. Sea x un punto de X y sea Cx el subconjunto de X formado por todos los puntos y tales que hay un camino de x a y. Como X es localmente conexo por caminos, cada y en Cx tiene una vecindad abierta Uyque es conexa por caminos. Luego, para cada punto z en Uy hay un camino desde x a z, x ↝ y ↝ z.
Luego, Cx is open.
Razonando de manera análoga, se concluye que X \ Cx abierto.Por la conexidad de X, concluimos que Cx = ∅ o X \ Cx = ∅. En consecuencia, X es conexo por caminos.
Proposición 10.6.11. Sea f : X → Y continua. Cuando X es conexo por caminos entonces su imagen por f también lo es.
- Demostración. Supongamos que X es conexo por caminos y que x′ = f(x),
y′ = f(y) son puntos de f(X). Por la hipótesis hay un camino σ de x a y. Por lo tanto, f ◦ : x′ = f(x) y′ = f(y).
Corolario 10.6.12. “Conexo por caminos” es una propiedad topológica.
Proposición 10.6.13. El producto topológico de dos espacios conexos (resp. conexo por caminos) es conexo (resp. conexo por caminos).
- Demostración. Sean X1 y X2 los espacios y X su producto.
(Caso Conexo) Supongamos queX fuera disconexo. Entonces, habría una función continua f : X → {0, 1}. Sea (a, b) un punto de X. Definamos funciones g1 : X1 → X tal que x1 ↦ (x1, b), y g2 : X2 → X tal x2 ↦ (a, x2). Claramente ambas funciones, g1, g2, son continuas. Luego, f ◦ gi, i = 1, 2, es continua.
Como cada Xi es conexo, la imagen por f ◦ gi tiene que ser conexa. Luego, f ◦ gi debe ser constante. Luego, f(x, b) = f(g1(x)) = f(a, b) para todo x en X. Análogamente, f(a, y) = f(g2(y)) = f(a, b). Se tiene entonces que f es una función constante.
Esto contradice la suposición de que la imagen de f tiene dos puntos. Por lo tanto, tal función no existe, por lo que el producto es conexo. .
(Conexión por caminos) Sean (a, b) y (c, d) puntos de X. Como X1 y X2 son conexos por caminos, hay caminos &sigma1 : a ↝ c, y &sigmaq;2 2 : b d. Luego, (σ1, σ2) : (a, b) ↝ (c, d).
Ejemplo 10.6.2. Un toro T = S1 × S1 es conexo por caminos.
Ejercicios 10.6
[editar]- Sea f : I → R continua. Probar que cuando el intervalo I es cerrado, la gráfica de f es conexa por caminos.
- Sea X un espacio topológico. Sea Cx el conjunto de puntos de un espacio topológico X unidos al punto x de X.
- Cada x de X, x está en Cx.
- Para todo x, y en X, si y está en Cx, entonces x está en Cy.
- Para todo x, y, z de X, si y está en Cx, z está en Cy, entonces z está en Cx.
- Para todo x, Cx es conexo por caminos.
- Todo A conexo por caminos que contiene a x, está contenido en Cx.
- Un conjunto X es conexo por caminos, ssi, X = Cx para algún x de X.
- Sea f : I → R continua. Probar que cuando el intervalo es cerrado, la gráfica de f es conexa por caminos.
- Sea (Xi) una familia de espacios y sea X su producto. Si todos los espacios
son localmente conexos y todos, excepto popr una cantidad finita de ellos,
son conexos, entonces X es localmente conexo.
- Probar que I = [0, 1] no es homeomorfo a S1.
- Probar que Sn (n > 1) no es homeomorfa a 1.
- Sean I = [0, 1] y J =]0, 1[. Probar que
- J es homeomorfo a un subconjunto de I, e I es homeomorfo a un subconjunto de J, pero
- I no es homeomorfo a J.
Ejercicios del Capitulo 10
[editar]- ¿Cuáles de los enunciados siguientes son válidos? En caso afirmativo, dar
una razón; en caso contrario, producir un contraejemplo.
- a) Los subespacios de espacios conexos son conexos.
- b) Los subespacios de espacios localmente conexos son localmente conexos.
- c) Los espacios conexos por caminos son conexos.
- d) Hay una cantidad finita de componentes conexas de un espacio.
- e) La reunion de intervalos de la línea real es un conjunto conexo.
- f) La intersección no vacía de intervalos de la línea real es un conjunto conexo.
- Sea X un espacio topológico. Sea A un subconjunto de X.
- Si A es conexo ¿qué podemos decir de su interior, clausura y frontera?
- Si el interior (resp. la clausura, la frontera) de A es conexo, ¿qué podemos decir de A.
- Sea C un componente de un conjunto A de un espacio localmente conexo.
Demostrar que:
- a) int(C) = C ∩ int(A).
- b) fr(C) ⊂ fr(A).
- c) Si A es cerrado, entonces fr(C) = C ∩ fr(A).
- Sean A y B subconjuntos cerrados y no vacíos de un espacio X. Si su reunión e intersección son conexos, entonces A y B son conexos.
- Decimos que dos conjuntos A y B están separados, ssi, ninguno de ellos
contiene puntos de acumulación del otro.
- Probar que si A ∩ B = ∅ y ambos son abiertos o ambos cerrados, entonces están separados.
- Suponer que A y B están separados. Probar que
- A ∪ B abierto implica que A y B son abiertos,
- A ∪ B cerrado implica que A y B son cerrados.
- Demostrar que, en un espacio métrico, cuando d (A, B ) > O, entonces A y B están separados. Dar un ejemplo que pruebe que el recíproco no necesariamente es válido.
- Un espacio es disconexo cuando es la reunión de dos conjuntos separados.
- Cuando A y B son conjuntos conexos no separados, entonces A ∩ B es conexo.
- Sea A un subconjunto conexo de un espacio localmente conexo. Entonces, A es localmente conexo.
- Probar que el producto de espacios localmente conexo es localmente conexo.
- Probar que el cubo unitario, In es conexo, conexo por camino y localmente conexo.
- Sea E un espacio topológico y sea A y B subconjuntos conexos tales que A ∩ cl(B) ≠ ∅. Probar que A ∪ B es conexo.
- Sea ~c la relación de equivalencia definida por las componentes. Probar que X/~c es totalmente disconexo.
- Probar que espacios discretos son localmente conexos.
- El espacio cociente de un espacio localmente conexo es localmente conexo.
- Sea A un subconjunto de un espacio topológico X. Si C es un subespacio conexo de X que interseca A y su complemento, entonces debe intersecar su frontera.
- En un espacio X los siguientes enunciados son equivalentes.
- X es localmente conexo.
- Cada componente conexa de un subconjunto abierto de X es un conjunto abierto.
- Los conjuntos abiertos conexos forman una base de la topología de X.
- Sea E un espacio normado que consideraremos como espacio topológico inducido por la norma.
- Cuando la esfera unitaria (||x|| = 1) tiene una propiedad topológica, cualquier esfera también la tiene.
- Cuando el cubo unitario, In, tiene un propiedad topológica, cualquier caja cerrada (ver ejemplo 5.2.7) también la tiene.
- Sea E un espacio normado. Un subconjunto K de E es convexo, ssi, para todo x, y en K,K contiene al segmento lineal que une dichos puntos. Probar que conjuntos convexos son conexos por caminos.
- Sea M = {(x, y) ∈ R2 : y > x2}. Probar que M es conexo por caminos.
- Sea E un espacio normado y sean x, y puntos de E. Un camino de x a y
es un camino poligonal, ssi, hay una sucesión p0, ..., pn de puntos tales
que (I) p0 = x, pn = y; y (ii) hay un segmento lineal uniendo pi con pi+1, i = 0, n − 1.
- Probar que un conjunto es conexo por caminos cuando hay un camino poligonal entre dos de sus puntos.
- Dar un ejemplo de un espacio conexo por caminos, para él cual no siempre es posible hallar un camino poligonal entre dos de sus puntos.
- Sea S = [0, 1] ⊂ R, pero provisto con la topología de complementos finitos, o sea que los cerrados de S son S o los subconjuntos finitos. Probar que en esta topología S es conexo y conexo por caminos.
- ¿Es conexo el espacio RT1? (ver definición en el ejercicio 10 al final del capítulo 8). En caso negativo, ¿cuáles son sus componentes?
Los Espacios Compactos
[editar]Introducción
[editar]La compacidad es una propiedad muy importante de los espacios topológicos. Sin embargo, no resulta fácil dar una descripción intuitiva de la misma. La idea de compacto es de algo que cabe en un espacio pequeño. Para nosotros, topológicamente hablando, los espacios finitos serán espacios “pequeños”. Sin necesariamente mucha precisión, podemos decir que los conjuntos compactos serán espacios topológicamente semejantes a los conjuntos finitos. Una definición formal aparecerá más adelante.
Por la importancia de los conjuntos compactos y de las nociones asociadas, hemos adoptado una estructura especial en este capítulo. Después de dar una definición general de la compacidad y ver algunas de sus propiedades generales, haremos un estudio detallado de la compacidad para subconjuntos de la línea real; en particular una serie de nociones equivalentes. Posteriormente, veremos la compacidad en los espacios normados Rn. Luego, estudiaremos la noción en un espacio métrico cualquiera. Obviamente, cualquier propiedad de compactos en espacios métricos será valida para la línea real y los Rn. Es decir que habrá resultados cuyas demostraciones podrán aparece tres veces, primeramente para línea real, luego para los espacios normados de dimensión finita y luego para los espacios métricos. ¿Por qué esta redundancia? En primer lugar, porque ilustra el desarrollo de la noción. En segundo lugar, veremos demostraciones diferentes para una misma propiedad, dependiendo del ambiente. Finalmente, podremos ver que las propiedades equivalentes o implicadas por la compacidad, no son las mismas para espacios generales que para los Rn’s. Algunas propiedades importantes para los compactos de espacios Rn—en particular, la línea real—como la característica de ser cerrados y acotados, no son válidas en general. Por esa razón, nuestra definición de compacidad será dada en términos de familias de abiertos (cubiertas) que contienen al espacio o conjunto en cuestión, ya que la experiencia muestra que es la más provechosa.
Cubiertas, subcubiertas
[editar]Definición. (Cubiertas, Subcubierta) Sea X un espacio topológico, A un subconjunto de X. Decimos que una familia G de subconjuntos de X es una cubierta o recubrimiento del conjunto A o que cubre al conjunto A, cuando la reunión de los conjuntos de la familia contiene al conjunto A.
Una subcubierta G′ de una cubierta G de A es un subconjunto de G que también cubre a A.
Decimos que se trata de una cubierta abierta cuando cada conjunto de la cubierta es un conjunto abierto.
Notemos que una familia G de subconjuntos de un conjunto A será una cubierta de A, cuando para cada x de A hay un conjunto U en G que contiene a x.Ejemplo 11.2.1. Sea X = R y sea G la familia de intervalos ]z − 1, z + 1[, z en Z. Claramente G es una cubierta abierta de R.
Ejemplo 11.2.2. Sea X = [0, 1], r un racional positivo, y sea G el conjunto de r–vecindades de puntos racionales de X. Claramente, G es una cubierta abierta de X.
Ejemplo 11.2.3. Aunque las cubiertas abiertas serán aquella más interesantes para nosotros, podremos tener cubiertas de cerrados o de conjuntos que no son ni abiertos ni cerrados. Consideremos a F = {[z − 1, z + 1] : z ∈ Z}, que es claramente una cubierta cerrada de R. Omitiendo en cada uno de esos conjuntos uno de los extremos, todavía tendremos una cubierta.
Ejemplo 11.2.4. Sea X = {x1, ... , xn} un conjunto finito de un espacio topológico.
Sea G = {Gi : i ∈ I} una cubierta abierta de X. Mostraremos que hay una subcubierta finita de G que cubre a X, independiente del tamaño del conjunto de índices I. En efecto, para cada k, k = 1, 2, . . . n, hay un abierto en G que denotaremos por Gk que contiene a xk. Claramente la reunión de esos n abiertos cubre al conjunto X.
Ejercicios 11.2.
[editar]- Hallar la reunión y la intersección de cada una de las familias siguientes de subconjuntos de la línea real.
- , , .
- , , .
- , , .
- Sea una cubierta abierta de un espacio .
- Un subconjunto de es abierto, ssi, hay un tal que es abierto en .
- Una función es continua, ssi, para cada , la restricción de a es continua.
- Dos topologías de son iguales, ssi, inducen la misma topología relativa en cada .
Los Espacios Compactos
[editar]Inspirados en el ejemplo de los conjuntos finitos (11.2.4), daremos la siguiente definición de compacidad.
Definición. (Espacios y Conjuntos Compactos) Decimos que espacio topológico es compacto, ssi, cada cubierta abierta de X tiene una subcubierta finita. Un subconjunto de un espacio topológico es un subconjunto compacto cuando es un espacio compacto respecto a la topología relativa.
- Los espacios finitos son compactos.
- La línea real no es compacta. El cubrimiento del ejercicio 11.2.1 no tiene un subcubrimiento finito de R.
La siguiente proposición sigue inmediatamente de la definición.
Proposición 11.3.1. Sean X un espacio topológico y Y un subconjunto de X. Y es compacto, ssi, para todo familia de abiertos (en X) que cubren Y , hay una subfamilia finita de dicha familia que también lo cubre.
Antes de entrar en detalles de los espacios compactos, veremos condiciones duales para la compacidad, o sea en términos de cerrados.
Consideremos una familia (Fi) de cerrados en un espacio compacto X tal que la intersección de sus miembros sea vacía. Entonces, el complemento de tal intersección será todo X. Como el complemento de la intersección de los Fi’s es la reunión de los complementos de los Fi’s, y tales complementos son abiertos, tenemos que determinan una cubierta abierta de X. Como X es compacto, hay una familia finita de tales abiertos cuya reunión será igual a todo X; por lo que sus complementos—que es una familia finita de los Fi’s—tendrá intersección vacía. Lo anterior, produce la siguiente caracterización de la compacidad.
Proposición 11.3.2. En un espacio compacto, una familia de cerrados tiene intersección vacía, ssi, una subfamilia finita tiene intersección vacía.
Introduciremos una terminología que nos ayudará a escribir de manera más concisa algunas proposiciones.
Propiedad de la Intersección Finita. Decimos que una familia de conjuntos tiene la propiedad de la intersección finita (PIF), cuando cada subfamilia finita tiene intersección no vacía.
Usando esa terminología, sigue de la discusión anterior la siguiente proposición.
Proposición 11.3.3. Un espacio topológico X es compacto, ssi, cada familia de cerrados en X que tiene la propiedad de la intersección finita, tiene intersección no vacía.
Algunas veces, resultará más cómodo esta versión de la compacidad para probar que un conjunto ees compacto.
Sucesiones Anidadas de conjuntos. Sea X un conjunto. Una sucesión (A_n), n ∈N, de subconjuntos de X se llama anidada, ssi, para todo m, n en N.se cumple que m > n implica que A_m ⊂ A_n.
Sea (A_n) una sucesión anidada de conjuntos no vacíos. Sean n_1 < n_2 < ... < n_k, Entonces, Ank esta contenido en cada uno de los Ani ’s anteriores,por lo que está contenido en su intersección. Hemos, así, probado el siguiente lema.
Lema 11.3.4. Sea (A_n), n ∈ N, una sucesión anidada de subconjuntos no vacíos cualesquiera de un conjunto X, Entonces la familia de los A_n’s tiene la propiedad de intersección finita.
Aplicando el lema a una familia anidada de cerrados no vacíos en un espacio compacto, obtenemos la siguiente proposición.
Proposición 11.3.5 (Cerrados Anidados). Sea (F_n), n ∈ N, una familia anidada de cerrados no vacíos de un espacio compacto X. Entonces, la intersección de los F_n no es vacía.
Espacios y Conjuntos Compactos
[editar]Un subconjunto de un espacio compacto no necesita ser compacto. Por ejemplo, veremos, más adelante, que I = [0, 1] es compacto, pero su interior no lo es (ver ejercicio 5) sin embargo, los subconjunto cerrados siempre son compactos.
Proposición 11.4.1. Cualquier subespacio cerrado de un espacio compacto es compacto.
- Demostración. Sea F un cerrado en el espacio compacto X. Sea (Gi) una cubierta
abierta de F. Entonces, los Gi’s junto con el complemento de F cubren
X. Como X es compacto, una familia finita de los Gi’s, eventualmente con Fc
incluido, cubren a X y, por lo tanto, a F. Luego, F es compacto.
La linea real no es compacta ya que la cubierta C = { ]n, n + 2[ : n ∈ Z} no tiene subcubierta finita posible. Por la misma razón, ni el intervalo abierto ]0,+∞[ ni el intervalo cerrado [0,+∞[ son compactos. La siguiente proposición muestra, sin embargo, que hay otrosintervalos que son compactos.
Proposición 11.4.2. El intervalo [0, 1] de la línea real es compacto.
- Demostración. Probaremos que cualquier cubrimiento de [0, 1] tiene un subcubrimiento finito. Sea (Ui), i∈I, un cubrimiento abierto de [0, 1]. Si I fuera finito no hay más que probar. Supongamos, por lo tanto, que I fuera infinito. Sea A el subconjunto
de [0, 1] formado por todos los x en [0, 1] tales que hay un subcubrimiento
finito de [0, x]. El conjunto A no es vacío porque al menos 0 está en A. Como,
además, A está acotado superiormente por 1, tenemos que A tiene supremo, digamos
s ≤ 1. Como [0, 1] es cerrado, s está en [0, 1]. Si s = 1, hemos probado
la proposición. Suponer que s < 1. Entonces [0, s] está cubierto por una cantidad
finita de los Ui’s. Al menos uno de ellos contiene a s, digamos Uk.
Como está en el interior de , hay un intervalo abierto , , totalmente contenido en . Pero, entonces
[0, s + r/2] está totalmente contenido en el subcubrimiento finito y s + r/2 > s,
lo que es un absurdo. Luego, s = 1, y la proposición está probada.
Teorema 11.4.3. La imagen continua de un compacto es compacto.
- Demostración. Sea f : X → Y continua y sea K ⊂ X compacto. Sea (Ui) una
cubierta abierta de f(K). Cada Ui = Vi ∩ f(K) donde Vi es un abierto de Y .
La reunión de los Vi cubre a f(K), por lo que sus preimágenes f-1(Vi) cubren
K. Pero, como K es compacto una familia finita de esas preimágenes cubre a K.
Como K ⊂ f-1(Vi1) ∪ ...∪ f-1(Vim) implica que f(K) ⊂ Vi1 ∪ ... Vim, tenemos la compacidad de f(K).
Corolario 11.4.4. Compacidad es una propiedad topológica. Si X y Y son homeomórficos, se cumple que X es compacto, ssi, Y es compacto.
Corolario 11.4.5. Cualquier intervalo cerrado y acotado de la línea real es compacto.
- Demostración. El intervalo [0, 1], por la proposición 11.3.7, es compacto y como
la función f : [0, 1] → [a, b] tal que f(t) = (b − a)t + a es biyectiva y continua,
se tiene el resultado.
Corolario 11.4.6 (Intervalos Anidados). Sea (Jn) una sucesión anidada de intervalos cerrados y acotados de R, entonces la intersección de los Jn’s no es vacía. Además, cuando la sucesión de los diámetros de los Jn tiende a 0, dicha intersección contiene solamente un punto.
- Demostración. Ejercicio.
Ejemplo 11.4.1. Sea ϕ : [0, 1] → R2 tal que ϕ(t) = (cos(2π t, sen(2π t)). La función ϕ es claramente continua, por lo que imagen S1, la circunferencia unitaria es un subconjunto compacto de R2.
Proposición 11.4.7. Cualquier subconjunto cerrado y acotado de R es compacto.
- Demostración. Sea F cerrado y acotado. Por ser acotado, hay un número M tal
que F ⊂ [−M,M], Por el último corolario [−M,M] es compacto y, por la proposición
11.3.6, cualquier subconjunto cerrado de un compacto es compacto de R2.
Ejemplo 11.4.2. Hay espacios donde un conjunto cerrado y acotado no es compacto.
Consideremos al subespacio Q de R con la topología relativa y sea B = [0, 1] ∩ Q. B es cerrado y acotado en Q.
Sea θ = √2/2 y sea Fn = [θ − 1/n, θ + 1/n], n ∈ N, n ≥ 4. Cada Fn es un cerrado en R, por lo que Hn = Fn ∩ B es un cerrado de B. Observando que m > n implica que Hm ⊂ Hn, vemos que la familia de los Hn’s es una familia de cerrados de B que tiene la propiedad de intersección finita. Peor, claramente, ∩n Fn = {θ}, por lo que ∩n Hn = ∅ (ya que θ no está en B). Luego, B no puede ser compacto.
La Compacidad en Espacios Hausdorff
[editar]Volvamos a espacio generales, pero suponiendo que son Hausdorff. Recordemos que llamamos espacio Hausdorff a un espacio topológico donde cualquier par de puntos distintos pueden separarse por abiertos disjuntos. Es decir, dados x, y, x ≠ y hay vecindades abiertas Vx y Vy tales que x ∈ Vx, y ∈ Vy y Vx ∩ Vy = ∅.
La siguiente proposición puede ser considerada como un recíproco parcial de la proposición 11.4.6.
Proposición 11.4.8. Un subconjunto compacto de un espacio Hausdorff es cerrado.
- Demostración. Sea X un espacio topológico Hausdorff y sea A un subconjunto
compacto de X. Si K = X o vacío, el resultado es trivial. Supongamos que
∅ ≠ K ≠ X y sea z un elemento del complemento de K. Como X es un espacio
Hausdorff, para todo x en K podemos hallar una vecindad Vx de x y una vecindad
Ux de z tales que Vx ∩ Ux = ∅. Claramente, los Vx’s determinan una cubierta abierta
de K. Como K es compacto una familia finita de ellos, digamos Vx1, ... , Vxm
cubren a K. Sea U la intersección de los correspondientes Uxi’s. Entonces,
ya que Luego,
Lo que implica que U ∩ K = ∅, o sea que U ⊂ Kc. Es decir que Kc es abierto, por lo que K es cerrado.
Corolario 11.4.9. En un espacio métrico, los conjuntos compactos son cerrados y acotados.
- Demostración. Sea E un espacio métrico y sea K un subconjunto compacto no
vacío de E. (El caso vacío es trivial). Como espacios métricos son Hausdorff,
sigue de la proposición que K es cerrado. Consideremos el cubrimiento de K
formado por las bolas abiertas de radio 1 y centro en cada elemento de K. Dicha
familia de abiertos cubre a K y, por ser K compacto, hay una familia finita de
ellos que contiene a K. Como cada bola es acotada y la reunión finita de acotados
es acotado y K está contenido en esa reunión tenemos que K es acotado.
Corolario 11.4.10. Sea X un espacio Hausdorff compacto. Un subconjunto F de X es compacto, ssi, es cerrado.
- Demostración.
Sea un espacio métrico y sea un subconjunto compacto no vacío de . (El caso vacío es trivial). Como espacios métricos son Hausdorff, sigue de la proposición que es cerrado. Consideremos el cubrimiento de formado por las bolas abiertas deradio 1 y centro en cada elemento de . Dicha familia de abiertos cubre
a y, por ser compacto, hay una familia finita de ellos que contiene a . Como cada bola es acotada y la reunión finita de acotados es acotada y está contenido en esa reunión tenemos que es acotado.
El siguiente ejemplo muestra que el converso del corolario anterior no es válido en general; lo que complicará el estudio de compactos en espacios métricos.
Ejemplo 11.4.3. Espacio métrico donde un conjunto cerrado y acotado no es compacto.
Sea un espacio métrico discreto infinito. Claramente, es cerrado y acotado, pero no es compacto.
La siguiente proposición resultará, más adelante, útil para probar que ciertas funciones son homeomorfismos.
Proposición 11.4.11. Sean X, Y espacios tales que X es compacto y Y es Hausdorff. Si f : X → Y es biyectiva y continua, entonces f es un homeomorfismo.
- Demostración. Sea f : X → Y biyectiva y continua. Probaremos que para cada abierto A de X, f(A) es abierto en Y , para eso es suficiente mostrar que cada
cerrado F de X tiene una imagen f(F) cerrada en Y. Si F es vacío, su imagen
es vacía y, en consecuencia es cerrada. Supongamos que F no es vacío, sigue, entonces, de
la proposición 11.4.1 que F es compacto. Luego por el teorema 11.4.3, f(F) es
compacto. Pero, un compacto en un espacio Hausdorff es cerrado (ver la proposición 11.4.8).
Terminología. Los espacios compactos Hausdorff tienen muchas propiedades agradables. Además muchos de los espacios compactos interesantes son Hausdorff, por lo que hay varios autores (Bourbaki, Dixmier, por ejemplo) que incluyen la hipótesis de Hausdorff en la definición de compacto. En tales situaciones, se usan nombres tales como cuasicompactos para nuestros compactos.
Ejercicios 11.4
[editar]- Explicar cuando un espacio no es compacto de acuerdo a la definición.
- Explicar cuando un espacio no es compacto de acuerdo a la proposición 11.3.3.
- Explicar cuando un espacio topológico discreto es compacto. Examinar, a continuación, un espacio topológico indiscreto.
- Probar las afirmaciones no probadas en los ejemplos 11.2.1 y 11.2.4.
- Probar que ]0, 1[ no es compacto.
- Probar el corolario 11.3.11.
- Sea X = I2 el cuadrado unitario, {(x, y) : 0 ≤ x, y ≤ 1}. La familia C de bolas con centro en un punto del cuadrado y radio 1/10 cubre a X. Probar que hay una subcubierta finita de C que también lo cubre.
- La reunión de una familia finitas de subconjuntos compacto es compacto.
- Sea X un espacio infinito con la topología de complementos finitos. Entonces, X es compacto.
- . Cuando el producto de espacios no vacíos es compacto, entonces, cada factor es compacto. El recíproco es válido, pero no es fácil de probar, ver más adelante el teorema de Tychonoff.
- Sea X un espacio y B una base de la topología de X. Cada cubierta de X por abiertos de B tiene una subcubierta finita, ssi, X es compacto.
- Sea X un espacio compacto y R una relación de equivalencia en X. Entonces, el espacio cociente X/R es compacto.
- Sea S = [0, 1] ⊂ R pero provisto con la topología de complementos finitos, o sea que los cerrados de S son S o los subconjuntos finitos. Probar que en esta topología cualquier subespacio de S, en particular los subconjuntos abiertos, son compactos. ¿Por qué esto no contradice el resultado de la proposición 11.3.13?
La Línea Real
[editar]Antes de continuar un estudio general de la compacidad, examinaremos la compacidad donde todo comenzó: la línea real. Veremos varias equivalencias para la compacidad y algunas aplicaciones.
Claramente, como la línea real es un espacio métrico no acotado, sigue del corolario 11.4.10, que no puede ser compacta. Como los intervalos abiertos son homeomórficos a la línea real, tenemos que los intervalos abiertos no pueden ser compactos. En el lado positivo, sabemos que los subconjuntos cerrados y acotados de R son compactos (ver la proposición 11.4.7).
En el capítulo 1 insinuamos, mediante los teoremas B y C, que los intervalos cerrados y acotados eran algo especial—respecto a otro tipo de intervalos. La respuesta es que son compactos. Presentamos, usando tal noción, pruebas de tales teoremas.
Teorema B. (Acotamiento de Funciones) Sea f : [a, b] → R una función continua, entonces hay un real positivo M tal que para todo x en [a, b] se cumple que −M ≤ f(x) ≤ M. En palabras, la función f es acotada.
Teorema C. (Existencia de Máximos y Mínimos Absolutos) Sea f : [a, b] → R una función continua entonces hay números c y d tales que a ≤ c, d ≤ b con f(c) ≤ f(x) ≤ f(d), para todo x en [a, b]. En palabras, la función f alcanza máximos y mínimos absolutos.
- Demostración. Sea J = [a, b], por el teorema 11.5.3, la imagen de J por f es un subconjunto compacto de R, por lo tanto, cerrado y acotado (corolario 11.3.14).
Lo que muestra en forma inmediata el teorema B. La acotación implica la existencia
de un ínfimo, digamos c, y un supremo, digamos d, de f(J). Como f(J) es
cerrado, tales números pertenecen a f(J), lo que prueba el teorema C.
Un análisis de la prueba, muestra inmediatamente que los resultados de los teoremas mencionados son válidos si reemplazamos [a, b] por cualquier subconjunto compacto de R.Observación 11.1. Los resultados de los teoremas anteriores se usan (a veces, implícitamente) en el primer curso de Cálculo, especialmente cuando de trata de hallar máximos o mínimos. Una demostración usando solamente la axiomática de los Reales se puede hallar en Spivak [16].
El resultado de que una función continua es acotada se usa, en cursos de Cálculo, para probar que la existencia de la integral de funciones continuas. El resto de esta sección estará dedicado a estudiar propiedades equivalentes a la compacidad de subconjuntos de R. Tales propiedades están contenidos en el siguiente teorema, que resume muchos de los resultados del Análisis del siglo XIX. La demostración del teorema se hará a través de varios lemas, cuyas demostraciones serán interesantes por si mismas. La lectora o lector deberá estar atento a ver cuáles de esas propiedades se generalizan a Rn, a espacios métricos cualesquiera y, finalmente, a espacios topológicos generales.
Teorema 11.5.1 (Teorema de la Compacidad en R). Sea A un subconjunto no vacío de R. Los enunciados siguientes son equivalentes.
- (a) A es compacto.
- (b) A es cerrado y acotado.
- (c) Cada subconjunto infinito de A tiene un punto de acumulación en A.
- (d) Cada sucesión de elementos de A tiene una subsucesión convergente.
- (e) Cada función continua de A en R es acotada.
Antes de continuar con la discusión de esas propiedades introduciremos algunos nombres para las propiedades contenidas en el teorema.
Bolzano–Weierstrass. Decimos que un subconjunto A de un espacio X (cualquiera) tiene la propiedad de Bolzano–Weierstrass o que es un espacio B–W, ssi, cada conjunto infinito de A tiene un punto de acumulación en A. Algunos autores llaman a esta propiedad compacidad enumerable.
Compacidad secuencial. Un subconjunto A de un espacio X es secuencialmente compacto, ssi, cada sucesión de elementos de A tiene una subsucesión convergente en A.Seudocompacidad. Un subconjunto A de un espacio X es seudocompacto cuando toda función real continua definida en A es acotada.
El teorema establece que cada una de esas propiedades es, en la línea real, equivalente a la compacidad.
Como en cualquier espacio métrico un conjunto compacto es cerrado y acotado (ver corolario 11.4.10), sigue de la proposición 11.4.7 el siguiente resultado;
Proposición 11.5.2 (Teorema de Heine–Borel para la Línea Real). Un subconjunto de la línea real es compacto, ssi, es cerrado y acotado.
Esta equivalencia de la compacidad será usada frecuentemente en lo que sigue. En el corolario 7.5.3, vimos que toda sucesión real acotada tiene una subsucesión convergente. Esto implica que cualquier conjunto infinito acotado (que contiene, por lo tanto, a una sucesión acotada) tiene un punto de acumulación. Esta propiedad es muy importante, por lo que la enunciaremos a continuación como una proposición, y daremos otra demostración de la misma. Tal demostración será útil en las generalizaciones..
Proposición 11.5.3 (Bolzano–Weierstrass en R). Todo subconjunto infinito y acotado de R tiene un punto de acumulación.
- Demostración. Sea A un conjunto infinito y acotado. Como A es acotado, está contenido en un intervalo cerrado y acotado, digamos [a, b]. La idea de la demostración es construir una sucesión anidada de intervalos cuyos diámetros tiendan a cero, tomar la intersección de tales conjuntos, que contendrá a un único elemento
(ver corolario 11.4.6) y probar que ese único elemento es el punto de acumulación
deseado.
Sea J0 = [a, b]. Dividamos en intervalo J0 por su punto medio en dos subintervalos. Escogemos al subintervalo que contiene infinito puntos de A y le llamamos J1. Al menos uno de ellos debe tener infinitos elementos, cuando ambos tengan infinitos elementos seleccionamos el subintervalo de la izquierda. Notemos que el diámetro de J1 es igual a la mitad del diámetro de J0, es decir que δ(J1) = (b − a)/2.
Supongamos construidos de la manera anterior, J2, ... , Jk tales que
- (i) Jk contiene infinitos puntos de A,
- (ii) Jk ⊂ Jk−1 ⊂ ... ⊂ J1 ⊂ J0, y
- (iii) δ(Jk) = (b − a)/2k. (diámetro).
Observación 11.2. Notemos que el subconjunto N de la línea real es infinito, pero no tiene punto de acumulación. Es decir que la condición de acotado es esencial.
Lema 11.5.4. Un subconjunto infinito A de la línea real es compacto, ssi, tiene la propiedad de Bolzano–Weierstrass.
- Demostración. (⇒) Subconjuntos compactos son acotados, por lo que el
la proposición 11.5.3 implica A tiene un punto de acumulación. Como conjuntos compactos
son cerrados, dicho punto de acumulación está en el conjunto.
(⇐) Sea A un subconjunto de la línea real con la propiedad B-W. Si A es finito, trivialmente tenemos que A es cerrado y acotado, por lo tanto, compacto. Supongamos, entonces, que A es infinito. Probaremos que es cerrado y acotado. Sea z un punto de acumulación de A. Entonces, hay una sucesión (xn) de puntos de A que convergen a z. Entonces, z es un punto de acumulación de {xn : n ∈ N} ⊂ A. Por la hipótesis, z está en A, lo que implica que A es cerrado. Supongamos ahora que A no fuera acotado, digamos superiormente. Sea x1 un punto cualquiera de A tal que x1 > 1. Como A no está acotado superiormente, podemos hallar un x2 > 2 tal que x1 < x2. Análogamente (por inducción), cuando hemos hallado x1 < x2 < ... < xn con xn > n, podremos hallar un xn+1 tal que n + 1 < xn+1. Por inducción, obtendremos una sucesión no acotada, por lo que el conjunto S de los términos de la sucesión así formada es infinito y no acotado. Por la hipótesis, debe haber un punto de acumulación de S, que será el límite de una subsucesión (yn) de (xn). Luego, por ser convergente, la sucesión (yn) debe ser acotada (ver 7.2.8), pero por la generación de los xn’s debe ser no acotada. Esta contradicción concluye la prueba. El caso acotado inferiormente queda de ejercicio.
Lema 11.5.5. Un subconjunto de la línea real es compacto, ssi, es secuencialmente compacto.- Demostración. Usaremos la caracterización de compacto como cerrado y acotado.
(⇒) Sea A un conjunto compacto, o sea cerrado y acotado y sea (sn) una sucesión en A. Por ser acotado A, hay un real m tal que
A ⊂ [−m,m]. Consideremos al subconjunto S = {sn} de A formado por los términos de la sucesión. Si S fuera finito, entonces hay al menos un término cuyo valor se repite infinitas veces, definiendo una subsucesión convergente. En caso contrario. la proposición 11.5.3 nos dice que hay un punto de acumulación de S, o que produce una sucesión de S convergente al punto de acumulación. Tal sucesión es la subsucesión deseada. (⇐) Sea A un conjunto secuencialmente compacto. Sea p un punto de acumulación de A. Sabemos que entonces hay una sucesión de números en A diferentes de p, que converge a p. Por la hipótesis, p está en A, o sea que A es cerrado. Supongamos que A no fuera acotado. Entonces, podremos hallar una sucesión (xk) tal que |xk| ≥ k. Tal sucesión no es acotada, lo mismo que cualquier subsucesión de ella, por lo tanto, no puede tener una subsucesión convergente a un punto de A.
Lema 11.5.6. Un subconjunto A de R es compacto,ssi, cada función real continua definida en A es acotada.- Demostración. (⇒) Ejercicio. (Sug.Mirar la prueba de los teoremas B y C; o usar el teorema 11.4.3.)
(⇐) Consideremos la función valor absoluto restringida a A. Como valor absoluto es una función continua, la hipótesis de seudocompacidad implica que es acotada. Luego, A es un conjunto acotado. Probaremos que también es cerrado. Supongamos que no, y sea z un punto de la clausura de A que no está en A. Entonces, para todo x en A, |x − z| > 0 y acotado. Lo que implica que la función x → 1/|x − z| es continua, pero no es acotada. Contradicción. Lo que prueba el resultado..
Con los lemas 11.5.4, 11.5.5 y 11.5.6 se concluye al prueba del teorema 11.5.1.
Notemos que las equivalencias fueron hechas en cada lema con la propiedad de cerrado y acotado. Podríamos haber adoptado otro esquema, como se sugiere en el siguiente esquema.
Equivalencias de Compacidad Dejaremos al cuidado del lector de tratar de producir una demostración siguiendo ese esquema, o cualquier otro para la parte cíclica de la derecha. Las equivalencias directa con la definición de compacto son usualmente complicadas. ¿Cuáles de las equivalencias pueden extenderse a Rn? ¿a espacios métricos cualesquiera? ¿a espacios topológicos cualesquiera? ¿Cuáles de las equivalencias pueden extenderse a Rn? ¿a espacios métricos cualesquiera? ¿ a espacios topológicos cualesquiera?
Ejercicios 11.5
[editar]- Probar que los intervalos abiertos (acotados o no), así como los intervalos semiabiertos (acotados o no) no son conjuntos compactos.
- Hallar un cubrimiento abierto del intervalo (0, 1) que no tenga recubrimiento finito.
- Hallar un cubrimiento abierto de la línea real que no tenga recubrimiento finito. ¿Por qué esto implica que los intervalos abiertos no son compactos?
- El Conjunto de Cantor es compacto.
- Probar que la propiedad de intervalos encajados (ver corolario 11.4.6) implica la propiedad de Bolzano–Weierstrass (ver también a la proposición 11.5.3).
- Sea f : [a, b] → [c, d] una función continua estrictamente creciente (x < y =⇒ f(x) < f(y)) tal que f(a) = c y f(b) = d. Probar que f es un homeomorfismo.
- Suponga conocido que el cubo unitario I2 de R2
- a) Cualquier “cuadrado ] − M,M[ × ] − M,M[, donde M es un real positivo cualquiera, es compacto.
- b) La circunferencia y círculo con centro en el origen y radio 1 son conjuntos
- c) Cualquier bola cerrada de R2 es un conjunto compacto.
- Probar que la propiedad de Bolzano–Weierstrass (proposicion 11.5.3) para I2. Es decir que cada subconjunto infinito A de I2 tiene un punto de acumulación en A.
El Teorema de Tychonoff
[editar]La extensión del estudio de la compacidad a Rn y otros espacios requiere relacionar la compacidad de un producto a la compacidad de los factores. Esto se logra con el teorema de Tychonoff, que es uno de los teoremas más famosos e importantes de la topología.
Teorema 11.6.1 (Tychonoff). El producto de una familia cualquiera de conjuntos compactos es compacto.
El teorema, con la generalidad indicada, requiere para su demostración de algunas nociones avanzadas de la teoría de conjuntos (axioma de selección, lema de Tukey) que están fuera del alcance de este texto. Nos limitaremos, en consecuencia, al caso de una familia finita, lo que será suficiente para nuestros propósitos. Usaremos en la demostración el siguiente lema general.
Lema 11.6.2. Sea X un espacio topológico y B = (Bi: i∈I) una base de los abiertos de X. Si cada cubierta de X por abiertos de B tiene una subcubierta finita, entonces X es compacto.
- Demostración. Sea (Uj), j en J, una cubierta abierta de X. Cada abierto de la cubierta es una reunion de abiertos de la base. Supongamos que Uj = ∪k Bj,k, con cada Bj,k es un abierto de la base y los base y los k’s están en un subconjunto K de I. Luego,
Lo que implica que los Bj,k’s determinan una cubierta de X. Por la hipótesis, dicha cubierta tiene una subcubierta finita, digamos C1, C2, ...Cm. Cada Ci es alguno de los Bj,k, por lo que está contenido en, digamos, Uj,k . Luego,
Lo que muestra que la cubierta original tiene una subcubierta finita, es decir que X es compacto.
Teorema 11.6.3 (Teorema de Tychonoff finito). El producto de una familia finita de espacios topológicos compactos es compacto.- Demostración. Probaremos que el producto de dos espacios compactos Z = X × Y es compacto. El resultado seguirá entonces por inducción.
Usaremos el lema anterior para la demostración. Consideraremos la base de
abiertos de Z consistente de los abiertos de la forma U ×V , donde U es un abierto
de X y V un abierto de Y .
Sea B = {Ui × Vi : i ∈ I} una cubierta de Z; probaremos que hay una
subcubierta finita de B.
Sea x0 un punto de X y consideremos al subespacio {x0} × Y de Z. Dicho
subespacio es homeomórfico a Y ; por lo que es compacto. La familia B es una
cubierta de tal subespacio, por lo que hay un subconjunto finito Jx0 de I, tal que
la familia C = (Uj × Vj), j ∈ Jx0, es una subcubierta de {x0} × Y .
Sin perdida de generalidad, podemos suponer que cada elemento de esa subcubierta
contiene a {x0}×Y (si algún elemento de la subcubierta no contuviera a
ese subespacio, lo podemos eliminar de la subcubierta, y el resultado continuaría
cubriendo a {x0} × Y ).
Sea Ux0 = ∪ {Uj : j ∈ Jx0}. Entonces, tenemos que, para j en Jx0,
Lo que muestra que la familia C es una cubierta abierta de Ux0 × Y . Consideremos ahora la familia (Ux), x∈X, donde Ux se obtiene como arriba. Como X es compacto hay un subconjunto finito {x1, x2, ... , xm} de X tal que Ux1 ∪Ux2 ∪...∪Uxm cubre a X. Sea J = Jx1 ∪Jx2 ∪...∪Jxm. J es un conjunto finito, por ser reunión de finitos. Sea (x, y) un punto de Z, entonces hay un k tal que x pertenece a Uxk , 1 ≤ k ≤ m. Luego, (x, y) está en Uxk × Y , conjunto que, por el trabajo inicial, está contenida en Uj × Vj, j ∈ Jxk. Luego, la familia (Uj×Vj ), j∈J es una subcubierta finita de B. Lo que prueba queX×Y es compacto.
Sea Xi, i = 1, ... , m una familia finita de espacios compactos. Sabemos que el teorema es válido cuando m = 2. Si el teorema fuera valido para productos de k compactos, entonces tendremos para k + 1 espacios compactos que
Como, por lo anterior, la expresión de la derecha es el producto de dos espacios compactos, se tiene que el teorema es válido para el producto de (k + 1) espacios compactos. Por inducción, tenemos el resultado.
Observación. ¿Por qué la demostración dada para el producto de dos compactos no sirve para un producto general?
Básicamente, porque los abiertos de las bases—en el caso general—no tienen la forma indicada en la prueba del caso finito. La demostración del teorema general requiere de un lema semejante al lema 11.5.2 con subbases en lugar de bases. Tal demostración aparece, entre otros, en Simmoms [15].
Ejercicios 11.6
[editar]1. Probar que el cílindro y la cinta de Moebius son espacios compactos.
La Compacidad en Rn
[editar]La teoría de los conjuntos compactos en Rn es semejante a la teoría en a línea real, como veremos en esta sección. Esto se debe, en primer lugar, a que conjuntos cerrados y acotados son compactos. Nuestro primeros resultados, serán los análogos a aquellos en el corolario 11.4.5 y en la proposición 11.4.7. Aplicando el teorema de Tychonoff al cubo unitario In, vemos que se trata de un conjunto compacto, ya que I = [0, 1] es compacto y
In = I × ... × I (n veces).En forma más general, tenemos el siguiente resultado.
Lema 11.7.1. El cubo C(0;M) = {(xi) ∈ Rn : para todo i, − M ≤ xi ≤ M} es compacto.
- Demostración. C(0;M) = J × ... × J (n veces), donde J = [−M,M]. El resultado sigue del teorema de Tychonoff.
Veremos que el teorema básico de la compacidad de Rn, es totalmente análogo al teorema correspondiente (teorema 11.4.1) para la línea real. Dos resultados fueron importantes en las demostraciones del teorema mencionado. Veremos los correspondientes análogos para Rn.
Proposición 11.7.2 (Teorema de Heine–Borel para Rn). Un subconjunto de Rn es compacto, ssi, es cerrado y acotado.
- Demostración. Cualquier conjunto compacto de un espacio métrico es cerrado y
acotado. El enunciado recíproco, sigue de que un conjunto acotado está contenido
en un cubo centrado en el origen, que es compacto. Por lo que un subconjunto
cerrado de él, será compacto.
Proposición 11.7.3 (Bolzano–Weierstrass en Rn). Todo subconjunto infinito y acotado de Rn tiene un punto de acumulación en A.
- Demostración. La idea de la demostración es análoga a aquella de la proposición
11.5.3. Sea A un conjunto infinito y acotado. Como es acotado, está contenido
en un cubo cerrado, digamos C. La idea de la demostración es construir
una sucesión anidada de intervalos cuyos diámetros tiendan a cero, tomar la intersección
de tales conjuntos, que contendrá un único elemento y ver que ese único
elemento es el punto de acumulación deseado.
Ilustraremos la construcción para el caso n = 2. Sea A un conjunto infinito
acotado de Rn. Entonces, habrá un cuadrado C0 centrado en el origen que contienea A. Dividiendo C0 por líneas que pasa por los puntos medios de sus lados, obtendremos
cuatro cuadrados cuya reunión es C0, Al menos uno de ellos, digamos C1
contiene infinitos puntos de A. Repitiendo con C1 el procedimiento anterior, obtendremos
C2. Por inducción, obtenemos una sucesión anidada Cn de cerrados con
diámetro tendiendo a cero. El resto de la prueba es idéntica al de la proposición
citada.
Las equivalencias de compacidad en Rn son totalmente análogas a aquellas de la línea real, ya que tenemos el siguiente teorema.Teorema 11.7.4 (Compacidad en Rn). Sea A un subconjunto no vacío de Rn. Los enunciados siguientes son equivalentes.
- (a) A es compacto.
- (b) A es cerrado y acotado.
- (c) A es B–W (compacto enumerable). Cada subconjunto infinito de A tiene punto de acumulación en A.
- (d) A es secuencialmente compacto. Cada sucesión de tos de A tiene una subsucesión convergente en A.
- (e) A es seudocompacto. Cada función continua definida en A es acotada.
La demostración de la proposición quedará de ejercicio. Básicamente, las demostraciones del teorema correspondiente para la línea real, se pueden extender al caso de Rn. Además, en próxima sección probaremos esas equivalencias para espacios métricos cualesquiera, con la excepción de cerrado y acotado que no es válida en general. Vale la pena, para entender la riqueza de relaciones envueltas tratar de hacer las demostraciones con las herramientas que tenemos.
Sugerencias para las demostraciones.
- Cerrado y acotado implica B–W. Ver el lema 11.5.3.
- B-W, ssi, secuencialmente compacto. Ver la proposición11.5.5
- Secuencialmentre compacto implica cerrado y acotado. Ver el lema 11.5.5.
- Cerrado y acotado, ssi, seudocompacto. Ver el lema 11.5.6.
Ejemplo 11.7.1. Cuando A un espacio seudocompacto, A es compacto (cerrado y acotado).
Resolución. Consideremos la función || · || restringida a A. Como norma es una función continua, la hipótesis de seudocompacidad implica que es acotada. Luego, A es un conjunto acotado. Probaremos que también es cerrado. Supongamos que no, y sea z un punto de la clausura de A que no está en A. Entonces, para todo x en A, d(x, z) > 0 y acotado. Lo que implica que la función x ↦ 1/d(x, z) es continua, pero no es acotada. Contradicción. Lo que prueba el resultado.
Aplicaciones
[editar]Usaremos los resultados anteriores para dirimir una antigua interrogante. Probaremos que los espacios normados de dimensión finita son topológicamente equivalente a los espacios euclídeos Rn.
Proposición 11.7.5. Todas las normas de Rn son topológicamente equivalentes.
- Demostración. Sea N.una norma cualquiera (o sea se cumple lo especificado en la definición 3.5) y sea || • || la norma euclídea usual. Probaremos que hay reales m y M tales que para todo x en Rn se cumple que
m||x|| ≤ N(x) ≤ M||x||. (*)Sigue entonces de la proposición 8.5.4 que las normas serán equivalentes. Sea e1, ... en la base canónica de Rn y sea x = ∑i xi ei. Sea M = n máx{N(x) : 1 ≤ i ≤ n}. Como solamente el vector nulo tiene norma 0, se tiene que M es un número positivo.
Además
Pero, como siempre se cumple que |xi| ≤ ||x||, concluimos que
En particular, N(x − y) ≤ M||x − y||, lo que implica que N.es una función continua de E en R. Sea S = Sn−1 la esfera unitaria, que sabemos que es un conjunto compacto. Por lo que N.alcanza máximo y mínimo en S. Sea m dicho mínimo que será un número positivo, ya que ninguno de los vectores de la esfera es nulo. La relación es válida cuando x = 0. Suponiendo x ≠ 0, sea c = ||x||-1. Entonces ||cx|| = 1, lo que implica N(cx) = |c|N(x) ≥ m, es decir que N(x) ≥ m/|c| = m||X||.
Observación 11.3. El resultado anterior requiere esencialmente que el espacio normado sea de dimensión finita.Ejercicio 11.7
[editar]- Probar que cualquier bola cerrada y cualquier esfera de Rn son conjuntos compactos.
- Probar que las celdas de Rn, productos de intervalos cerrados de los factores, son conjuntos compactos.
- Probar que conjuntos abiertos no vacíos de Rn no son conjuntos compactos.
La Compacidad en los Espacios Métricos
[editar]Históricamente, la idea de la compacidad surgió de tratar de extender los teoremas clásicos del Análisis, teorema 11.7.4 de la sección anterior, a espacios métricos generales, especialmente a espacios de funciones. Queremos probar para espacios métricos cualesquiera el análogo al teorema citado. El mayor obstáculo para la extensión es que, en general, cerrado y acotado no implica compacto. Basta con considerar un espacio métrico discreto infinito E. Claramente es cerrado y acotado, pero no puede ser compacto, ya que la colección de {x}, x en E es una cubierta abierta de E que no admite subcubierta finita.
Como nuestras pruebas para Rn se basaban principalmente en las equivalencias de compacto con cerrado y acotado, necesitaremos nuevas pruebas. Debido a la generalidad, tendremos que proceder con bastante delicadeza, es decir con argumentos muy sutiles. La exposición está basada principalmente en el texto de Simmons.
Equivalencias de Compacidad
[editar]Probaremos, a continuación, las siguientes equivalencias.
Empezaremos con la siguiente equivalencia.
Proposición 11.8.1. Un espacio métrico E tiene la propiedad B–W, ssi, es secuencialmente compacto.
- Demostración. Supondremos que el espacio E es secuencialmente compacto y
probaremos B–W. Sea X un subconjunto infinito de E. Como X es infinito, podemos
formar una sucesión (xn) de puntos diferentes de X. Por la hipótesis, dicha
sucesión tiene una subsucesión convergente a un punto de X. El límite de esa sucesión
es un punto de acumulación de los términos de la subsucesión que forman
un subconjunto de X, por lo que dicho límite es un punto de acumulación de X.
Supongamos, ahora, que se cumple la propiedad de B–W. Sea (xn) una sucesión
en E. Consideremos al conjunto S = {xn} formado por los términos de
la sucesión. Si S es finito, un valor de los términos se repite infinitas veces, la
subsucesión constante asociada con dicho valor es convergente. Si S es infinito,
por la hipótesis, hay un punto de acumulación de S. Dicho punto es un punto de
acumulación de S, por lo que podemos extraer una subsucesión que converge a
dicho punto de acumulación.
Proposición 11.8.2. Cada espacio métrico compacto tiene la propiedad B–W.
- Demostración. Sea E un espacio métrico compacto y sea A un subconjunto infinito de A. Supongamos que A no tuviera un punto de acumulación. Entonces,
para cada x de E, hay una bola abierta con centro en x que no contiene punto
alguno de A, excepto x cuando x está en A. La reunión de esas bolas abiertas es
una cubierta de E, por la compacidad de E hay una subfamilia finita que cubre a
E y, en particular a A. Por lo que A debe ser finito. Esto contradice la hipótesis,
luego A debe tener un punto de acumulación.
Figura 11.1: Implicaciones en un Espacio Métrico Para completar nuestras equivalencias, bastará con probar que en cada espacio
métrico secuencialmente compacto es compacto. Esto será establecido usando dos conceptos auxiliares, que son interesantes por si mismos, el número de Lebesgue de una cubierta de abiertos y la noción de espacio totalmente acotado.
Número de Lebesgue
[editar]Sea (Gi) una cubierta abierta de un espacio métrico E. Para cada x de X hay un abierto de la cubierta que contiene una r–vecindad de x. Si escogemos otro punto, y repetimos el mismo proceso, podremos hallar una r′–vecindad del nuevo punto totalmente contenida en un abierto de la cubierta. En general, el radio de la bola abierta conteniendo al punto variará de punto en punto. Sin embargo, en algunos casos, un mismo radio servirá para todos los puntos, como veremos más adelante. Tal situación merece un nombre especial.
Definición. (Número de Lebesgue) Llamamos número de Lebesgue de una cubierta (Gi) de un espacio métrico E a un número λ, ssi, cada subconjunto de E cuyo diámetro es menor que λ está totalmente contenido en alguno de los abiertos de la cubierta.
Necesitaremos el siguiente resultado para la prueba de la próxima proposición.Lema 11.8.3. Sea A un subconjunto de un espacio métrico E tal que δ(A) = r y tal que A ∩ B(x;r) ≠ ∅. Entonces, A está contenido en B(x;2r).
- Demostración. Sea y un elemento de A y z un elemento de la intersección. Entonces,
d(y, x) ≤ d(y, z) + d(z, x) < r + r = 2r.
Proposición 11.8.4 (Lema de las Cubiertas de Lebesgue). Cuando un espacio métrico es secuencialmente compacto, cada cubierta abierta del espacio tiene un número de Lebesgue.
- Demostración. Sea E un espacio métrico secuencialmente compacto y sea
(Gi)i∈I una cubierta de E. Digamos que un conjunto es “grande” si no está contenido
en un abierto de la familia. Si no hay conjuntos grandes, cualquier número
positivo servirá como nuestro número de Lebesgue, a. Supongamos, ahora, que
hubiera conjuntos “grandes” y sea a′ el ínfimo de sus diámetros. Claramente,
0 ≤ a′ ≤ +∞. Si a′ = +∞, cualquier número positivo servirá como nuestro
λ. Si a′ > 0, entonces λ = a′ servirá para nuestra proposición. Veremos, a continuación,
que si a = 0, obtendremos una contradicción. Como cada conjunto
grande tiene al menos dos elementos, y a′ = 0, concluimos que para todo n > 0,
hay un conjunto grande Cn tal que 0 < δ(Cn) < 1/n. Escojamos un punto xn
en cada Cn. Como E es secuencialmente contacto, la sucesión (xn) tiene una
subsucesión (yn) convergente a un punto y de E. Tal punto está en uno de los
elementos de la cubierta, digamos Gj , j ∈ I. Hay, por lo tanto, una r–vecindad
de y totalmente contenida en Gj . Sea B la r/2–vecindad de y, como yn → y, hay
un n1 tal que n ≥ n1 implica que yn está en B. Sea n0 tal que 1/n0 < r/2 y
n0 ≥ n1. Como δ(Cn0) < 1/n0 < r/2, concluimos, usando el lema previo, que
Cn0 ⊂ B(y;r) ⊂ Gj . Lo que contradice que Cn0 fuera grande. Luego, a′ > 0.
ε–redes, Total Acotamiento
[editar]Definición. (ε–redes, Total Acotamiento) Sea E un espacio métrico. Un subconjunto A de E es una ε–red de E, ε > 0, ssi, A es finito y (B"(x)), x en A. es una cubierta de E.
Decimos que E es totalmente acotado, ssi, para cada ε > 0 hay una ε–red de E.
Proposición 11.8.5. Cada espacio secuencialmente compacto es totalmente acotado.
- Demostración. Sea E un espacio métrico secuencialmente compacto y sea ε > 0
dado. Escojamos un a1 en E y consideremos la bola abierta B1 = B(a;ε). Si
X = B1, entonces {a1} es una ε–red para E. En caso contrario hay un a2 fuera de B1 y consideramos la ε–vecindad B2 = B(a2;ε). Si B1 ∪ Bub>2</s cubre a X, entonces
{a1, a2} es un ε–red para E. Supongamos que hemos generado de esa manera a1, a2, ... ak, donde Bi una ε- vecindad de ai. Si la reunion B1 ∪ ... ∪ Bk cubre a
X, el conjunto {a1, ... , ak} es una ε–net para E. En caso contrario, hallamos un ak+1 fuera de la reunión anterior y formamos Bk+1 como la ε–vecindad de ak+1.
Si ninguna reunión de los Bi’s así obtenidos cubre a E, habremos generado una
sucesión (an) que no tiene subsucesión convergente (d(ak+1, ai) ≥ ε, para i ≤ k),
lo cual contradice que E fuera secuencialmente compacto. Por lo que el proceso anterior debe finalizar en una cantidad finita de pasos, generando una ε–red para E.
Usando las proposiciones anteriores, probaremos lo que nos resta de las equivalencias de la figura 11.1.Proposición 11.8.6. Cada espacio métrico secuencialmente compacto es compacto.
- Demostración. Sea E une espacio métrico secuencialmente compacto y sea (Gi)
una cubierta abierta de E. Por la proposición 11.8.4 la cubierta tiene un número
de Lebesgue λ. Sea r = λ/3 y sea A = {a1, ... , am} una ε–red para E. Sea Bk la
ε–vecindad de ak. Entonces, (i) la reunión de los Bk cubre a E y (ii) el diámetro
de cada Bi es menor que 2ε < λ. Luego, cada Bk está contenido en uno de los
Gi, digamos GIk , 1 ≤ k ≤ m. Luego, la reunión de los Bk (que cubre a E) está
contenida en la reunión de los Gik, que es, por lo tanto, una subcubierta finita de
E. Conclusión, E es compacto.
Resumen
[editar]Teorema 11.8.7 (Compacidad en Espacios Métricos). Sea E un espacio métrico. Los enunciados siguientes son equivalentes.
- (a) E es compacto.
- (b) E tiene la propiedad B–W.
- (c) E es secuencialmente compacto.
- (d) E es totalmente acotado y cada cubierta tiene un número de Lebesgue.
Ejercicios 11.8
[editar]- Sea A un subconjunto compacto de un espacio métrico compacto. ¿Es necesariamente compacto el complemento de A?
- Sea A un subconjunto compacto de un espacio métrico E y sea f : E → F una función continua en un espacio métrico E. Probar que si y es un punto de la frontera de f(A), hay un x en A tal que f(x) = y.
- Un espacio métrico totalmente acotado es acotado.
- Probar que, en los Reales, acotado y totalmente acotado son equivalentes. ¿Es eso cierto para R2? ¿para un espacio métrico cualquiera?
- Considerar a los Reales con la métrico discreta 0–1. Probar que se trata de un espacio acotado que no es totalmente acotado.
- Todo espacio compacto es seudocompacto, ¿será cierto que un espacio métrico seudocompacto es compacto?
Compacidad y Completitud
[editar]Hay interesantes relaciones entre la completitud (cada sucesión de Cauchy es convergente) y la compacidad, como veremos a continuación.
Proposición 11.9.1. Sea E un espacio métrico. Los enunciados siguientes son equivalentes.
- (a) E es compacto.
- (b) E es totalmente acotado y completo.
-
Demostración. (a) ⇒ (b). Como E es compacto es totalmente acotado. Como
es compacto es secuencialmente compacto, por lo que cada sucesión de Cauchy
tiene una subsucesión convergente; pero esto implica que la sucesión es convergente,
por lo que el espacio es completo.
(b) ⇒ (a). (Simmons) Probaremos que E es secuencialmente compacto. Como E es completo, bastará con probar que cada sucesión tiene una subsucesión de Cauchy. Sea (x1n) un sucesión tal que S1 = {x1n} es un conjunto infinito; para simplicidad de la exposición denotaremos la sucesión por su conjunto de términos (la razón del doble subscript se verá más adelante). Como E es totalmente acotado, hay un cubrimiento finito por bolas abiertas de radio 1/2. Luego, S1 debe contener una subsucesión S2 = {x21, x22, ... } que está contenida en una de esas bolas. Aplicando nuevamente el acotamiento total a bolas de radio 1/3, se ve que hay una subsucesión S3 = {x3n : n=1,2, ...} que está totalmente contenida en una bola de radio 1/3. Inductivamnete, continuamos hallamos Sk = {xk1, xk2, ... } totalmente contenido en una bola de radio 1/k, k = 4, 5, . . . . SeaS = {x11, x22, x33, ... }.La sucesión así definida es una subsucesión de S1. La construcción de la sucesión muestra que es de Cauchy.
Corolario 11.9.2. Un subconjunto cerrado de un espacio completo es compacto, ssi, es totalmente acotado.
- Demostración. Un subespacio cerrado de un espacio completo es completo.
La Continuidad Uniforme
[editar]La siguiente proposición establece una propiedad de las funciones continuas con dominio un compacto que tiene profundas consecuencias en Análisis y otras ramas de la matemática. Enunciaremos la proposición para discutir de forma más precisa su significado; la demostración aparecerá más tarde.
Proposición 11.10.1. Sea f : E → F continua entre espacios métricos con E compacto. Entonces, para todo ǫ > 0 hay un δ > 0 tal que para todo x, y en E se cumple que
d(x, y) < δ ⇒ d(f(x), f(y)) < ε¿Cuál es la diferencia con continuidad? Diremos que una función que satisface la propiedad de la proposición es uniformemente continua. Analizaremos a continuación cuál es la diferencia con la continuidad que hemos usado hasta ahora.
La definición de continuidad para f : E → F, continua en cada punto de E, establece que para todo p de E, para todo ε > 0 hay un δ > 0 tal que para todo x se cumple que
d(x, p) < δ ⇒ d(f(x), f(p)) < ε.Aparte de una diferencia en notación, pareciera no haber demasiada diferencia. Para apreciar mejor lo diferente, escribiremos en forma simbólica total las definiciones y haremos semejantes las notaciones. Simbólicamente, tenemos
Continuidad. ∀y ∈ E, ∀ε > 0, ∃δ > 0, ∀x ∈ E, d(x, y) < δ ⇒ d(f(x), f(y)) < ε.
Continuidad Uniforme. ∀ε > 0, ∃δ > 0, ∀y ∈ E, ∀x ∈ E, d(x, y) < δ ⇒ d(f(x), f(y)) < ε.
Observemos que no hay diferencia entorno a la implicación, la diferencia está en la posición del cuantificador referente a y. ¿Qué significa esto? En el caso de la continuidad, el δ que existe depende tanto del y como del ε, es decir que para puntos diferentes del espacio, pudiera ser que no habrá un δ que funciones con todos los puntos (y); mientras que en el caso de la continuidad uniforme podemos hallar un δ que funciona uniformemente con todos los puntos del espacio. La proposicion 11.6.6 establece que tal situación siempre sucede cuando el dominio de la función es compacto.
- Demostración de la proposición 11.9.1. Sea f : <E, d1> → <F, d21> continua y sea ε > 0 dado. Para cada y de F, consideremos la bola abierta de radio ε/2 con centro en y. Las preimágenes (imagen inversa) de esas bolas forman un cubrimiento de E. Como E es compacto, es secuencialmente compacto, y tiene, por lo tanto, un
número de Lebesgue del cubrimiento, digamos δ > 0. Si x y x′ son elementos
de E tales que d1(x, x′) < δ, entonces {x, x′} tiene diámetro menor que δ, por lo que está contenidos en una de las preimágenes de bolas usadas arriba; luego f(x)
y f(x′) pertenecen a una de las bolas de radio ε/2, por lo que d21(f(x), f(x′)) <
ε.
La Compacidad en Espacios Topológicos
[editar]Las propiedades equivalentes de los teoremas de compacidad en espacios métricos no se pueden extender a espacios topológicos cualesquiera. La aparición de “acotado” en algunas de las equivalencias, sugieren claramente que tales equivalencias no hacen sentido en espacios topológicos arbitrarios.
En el lado positivo, se tiene la siguiente cadena de implicaciones, cuyas demostraciones daremos más adelante.

Compacidad en Espacios Topológicos Se puede hallar ejemplos que muestran que las implicaciones son estrictas.
Proposición 11.11.1. Cualquier espacio compacto es B–W (compacto enumerable).
-
Demostración. Sea X un espacio compacto y sea A un subconjunto finito de X.
Supongamos que A no tiene punto de acumulación. Entonces, A y cualquier subconjunto
de A, son cerrados. Como A es infinito, hay una sucesión (xn) de puntos
de A, diferentes entre si. Sea An = {xk : k ≥ n}, n = 1, 2, . . . . Cada An es cerrado y la familia de los An es una secuencia anidada que tiene, por lo tanto, la propiedad de la intersección finita. Sin embargo, ∩ An es vacío, por lo que X no pude ser compacto; lo que contradice la hipótesis. Luego, A debe tener un punto de acumulación en X.
Proposición 11.11.2. Cualquier espacio B–W (compacidad enumerable) es seudocompacto.
-
Demostración. Sea X un espacio con la propiedad de B–W. Supongamos que hay
una función continua f : X → R que no es acotada. Sin perdida de generalidad
supondremos que f no es acotada superiormente (en caso contrario, usar −f).
Como n no es acotada superiormente, para todo n en N podremos hallar un xn
tal que f(xn) > n. El conjunto S = {xn : n ∈ N} contiene infinitos puntos, ya que en caso contrario, f(S) sería acotado, lo que contradice la definición de los xn’s. Como el espacio X es B−W, el conjunto S tiene un punto de acumulación, digamos y en X. Sea z = f(y), como f es continua, z es un punto de acumulación de f(S). Sea m el menor entero tal que z < m. Por la definición de los xn, hay
solamente una cantidad finita de xk tales que f(xk)< m. Sea r el mínimo entre las distancias de esos f(xk) a z, y de la distancia de z a m. Entonces, la r–vecindad de z no contiene puntos de f(S), lo que congradice su condición de punto de acumulación de ese conjunto. Luego, f dbe ser acotada.
Proposición 11.11.3. Cualquier espacio secuencialmente compacto es B–W.
-
Demostración. Sea X un espacio secuencialmente compacto. Sea A un subconjunto
infinito de X. Como X es infinito, podemos formar una sucesión (xn) con
los elementos de X. Por ser X secuencialmente compacto, hay una subsucesión
ynk> de los (xn) convergente a un punto y. Tal y es un punto de acumulación del conjunto de los ynk> y, por lo tanto, de los (xn), o sea que y es un punto de acumulación de A. Luego, X es B–W.
Una de las mayores dificultades con espacios topológicos arbotrarios reside en que sucesiones pueden tener más de un punto límite y que puntos de acumulación de un conjunto no son necesariamente límites de sucesiones de puntos del conjunto.
Ejercicios 11.11
[editar]- Hallar un ejemplo de espacio topológico donde una sucesión tiene dos puntos límites diferentes.
Espacios Localmente Compactos
[editar]La línea real no es compacta, pero cada punto est;a contenido en un conjunto compacto, el punto a está contenido en ]a−r, a+r[. Esta situación es compartida por muchos de nuestros ejemplos importantes.
Definición. (Relativamente y Localmente Compacto) Un subconjunto A de un espacio topológico X es relativamente compacto, ssi, su clausura es compacta.
Un espacio Hausdorff es localmente compacto, ssi, cada punto del espacio tiene una vecindad relativamente compacta.
Ejemplos 11.12.1.- Los espacios euclídeos Rn son localmente compactos.
- Cualquier espacio compacto es localmente compacto, todo el espacio es una vecindad compacta de cualquiera de sus puntos.
- Un espacio discreto infinito es localmente compacto, pero no compacto; por ejemplo, los Naturales.
Proposición 11.12.1. Sea X un espacio topológico. Los enunciados siguientes son equivalentes.
- X es localmente compacto.
- Para cada x en X y cada vecindad U de X, hay una vecindad abierta relativamente compacta V de x tal que V ⊂ Cl(V ) ⊂ U.
- Para cada compacto C y abierto U ⊃ C hay un abierto relativamente compacto V tal que C ⊂ V ⊂ Cl(V ) ⊂ U.
- X tiene una base que consiste de abiertos relativamente compactos.
- Demostración. (a) ⇒ (b). Para cada x hay una vecindad W tal que Cl(W) es compacta. Como se cumple que Cl(W) es un espacio regular (ver proposición 3.1 en capítulo 12), y Cl(W) ∩ U es una vecindad de x en Cl(W), hay una vecindad abierta G tal que contenido en Cl(W) tal que G ⊂ ClCl(W)(G) ⊂ Cl(W) ∩ U. Por definición de topología relativa, G = H ∩ Cl(W), donde H es un abierto en X. Luego, V = H ∩ Cl(W) es la vecindad buscada.
(b) ⇒ (c). Para cada c en C, sea V una vecindad de c relativamente compacta
cuya clausura está contenida en U. Como C es compacto, una familia finita de
tales vecindades cubre a C y su reunión es una vecindad de C que tiene clausura compacta.
(c) ⇒ (d). Sea B la familia de todos los abiertos relativamente compactos.
Como {x} es compacto, (c) implica que B es una base.
(d) ⇒ (a). Trivial.
Proposición 11.12.2. Sea f : X → Y , continua y abierta. Si X es localmente compacta entonces Y es localmente compacta.
- Demostración. Sea y en Y y sea x en X tal que f(x) = y. Sea U una vecindad abierta relativamente compacta de x. Como f es abierta, f(U) es una vecindad abierta de y. Como Cl(U) es compacta, también lo es f(Cl(U)), y como
Cl(f(U)) ⊂ Cl(f(Cl(U)) = f(Cl(U)), tenemos que Cl(f(U)) es compacta.
Ejercicios 11.12
[editar]- Los Racionales como subespacio de los Reales no es localmente compacto.
- Probar que una reunión finita de abiertos relativamente compactos es relativamente compacta. ¿Que se puede decir de su intersección?
- Sea X relativamente compacto. Cualquier subespacio abierto o cerrado de X es también relativamente compacto.
- El producto de espacios relativamente compactos es compacto.
Ejercicios del Capítulo 11
[editar]- Sea A un conjunto compacto de un espacio métrico E. Cuando U es una vecindad abierta de A (o sea A ⊂ U), hay un número real positivo tal que {x ∈ X : d(x,A) < ε} esta contenido en U.
- Sea A un subconjunto cerrado y conexo de Rn. Sea V la r–vecindad de A. Probar que V es conexo por caminos.
- Sea E un espacio métrico compacto. Cuando la clausura de cada bola abierta es la bola cerrada de igual centro y radio, se cumple que cada bola del espacio es conexa.
- Sea A un subconjunto de Rn. A es compacto, ssi, cada función continua con valores reales es acotada.
- Sean F y G subconjuntos disjuntos de un espaciométrico E. Si F es cerrado y G compacto, entonces d(F,G) > 0.
- Sea U un conjunto abierto que contiene un subconjunto compacto A de un espacio métrico E. Probar que hay un r > 0 tal que U contiene a Vr(A) = {x ∈ E : d(x,A) < r}.
- Sea A un subconjunto cerrado y conexo de Rn, y sea V una r–vecindad cerrada de A (V = {x ∈ Rn : d(x < A) ≤ r}). Probar que V es conexa por caminos.
- Sea E un espacio métrico compacto. Sea f : X → X continua tal que d(f(x), f(y)) < d(x, y) para todo x, y, x ≠ y. Entonces, f tiene un punto fijo único (o sea x tal que f(x) = x).
- ¿Cuando la reunión de una familia de compactos es compacta en un espacio
cualquiera?
- X es un espacio T0, ssi, para todo x, y en X, al menos uno de ellos está contenido en un abierto que no contiene al otro.
- X es un espacio T1, ssi, para todo x, y en X, cada uno de ellos está contenido en un abierto que no contiene al otro.
- X es un espacio T2 o Hausdorff, ssi, para todo x, y en X hay abiertos disjuntos, cada uno de los cuales contiene exactamente a uno de los dos puntos. Es decir que haya abiertos que separan los puntos. Siguiendo el uso tradicional, continuaremos usando el nombre Hausdorff para estos espacios.
- (Espacio T0) X = {a, b}, con topología TX= {∅ ,X, {b}}. X es T0, pero no T1.
- (Espacio T1) Sea X un espacio infinito, por ejemplo los Naturales, y sea TX el conjunto formado por el conjunto vacío y todos los subconjuntos cuyo complemento es finito. Si x, y son puntos diferentes de X entonces X \ {y} es una vecindad de x que no contiene a y. Análogamente, X \{x} es una vecindad de y que no contiene a x. Observemos que cualquier vecindad de x difiere de una vecindad de y por a lo más una cantidad finita de elementos, por lo que no son disjuntas. Es decir que X es T1, pero no T2.
- Los espacios métricos son espacios Hausdorff (T2).
- Decimos que una propiedad de un espacio topológico es hereditaria, cuando cada subespacio tiene la propiedad. Probar que las propiedades Ti, i = 0, 1, 2 son hereditarias.
- Sea f : X → Y continua e inyectiva. Probar que si Y es Hausdorff, X también los es.
- Probar que cada espacio T1 con una base finita es un espacio finito y discreto.
- Sea X un espacio infinito y sea T la topología generada por abiertos que tienen complementos finitos. Probar que X es T1, pero no Hausdorff.
- Sea X un espacio topológico. Las afirmaciones siguientes son equivalentes.
- a) X es Hausdorff.
- b) La intersección de las vecindades cerradas de un punto x es {x}.
- c) Cuando una sucesión en X converge, tiene un único límite.
- El producto de una familia de espacios Hausdorff es un espacio Hausdorff.
- Sea X un espacio topológico y sea D= {(x, y) ∈ X × X : x = y} (la diagonal principal del producto). Probar que X es un espacio Hausdorff, ssi, D es un subconjunto cerrado de X × X. Probar que R con la topología de complementos finitos es un espaco T1, pero no T2.
- Heinrich Franz Friedrich Tietze 1880–1964, Austriaco
- Pavel Samuilovich Urysohn (1898–1924), Ucraniano.
- Probar que subespacios de espacios regulares (resp. completamente regulares, normales, completamente regulares) también lo son.
- Los espacios completamente normales son normales.
- Sea X un espacio regular y p un punto de X y F un cerrado que no contiene a p. Entonces, hay abiertos tales que uno de ellos contiene a p y el otro a F y cuyas clausuras son disjuntas.
- Sea X un espacio topológico. Probar que X es un espacio T0, ssi, para todo x, y en X, x ∉ cl{y} o y ∉ cl{y}, ssi, x ≠ y implica que cl{x} ≠ cl{y}.
- Sea X un espacio topológico. Definamos una relación de equivalencia R en X, por x R y, ssi, cl{x} = cl{y}. Probar que el espacio cociente es T0.
- Sea X un espacio topológico y sea ∼ la relación en X tal que x ∼ y, ssi, x ∈ cl{y}. La relación es reflexiva y simétrica. La relación es antisimétrica, ssi, el espacio es T0.
- Sea Xi, i ∈ I una familia no vacía de espacios topológicos no vacíos y sea X su producto topológico. Probar que X es un espacios Tk, k = 0, 1, 2, ssi, cada espacio Xi lo es.
- Sean f, g : X → Y continuas y supongamos que Y es Hausdorff.
- El conjunto {x ∈ X : f(x) = g(x} es un conjunto cerrado.
- La gráfica de f, {(x, y) ∈ X × Y : y = f(x)} es cerrado en X × Y .
- Si f y g coinciden sobre un subconjunto denso, entonces son iguales.
- Sea X un espacio topológico y sea R una relación de equivalencia en X, sea g : X → X/R the canonical suprayección. Si (1) R es cerrado en X ×X y (2) g es una función abierta, entonces X/R es Hausdorff.
- La única topología Hausdorff en un espacio finito es la topología discreta.
- Subespacios de espacios regulares son regulares.
- Sea X = {a, b, c} y sea T = {∅ ,X, {a}, {b, c}}. Probar que < X, T > satisface la propiedad T3, pero no es regular.
- Un espacio X es completamente regular, ssi, es T1 y satisface la propiedad
T3 1/2 para cada p de X y conjunto cerrado F que no contiene a p, hay una
función continua de X en [0, 1] tal que f(p) = 0 y f(F) = {1}. (Advertencia:
la terminología no está estandarizada, algunos autores intercambian
el significado de completamente regular y T3 1/2. También son llamados espacios de Tychonoff).
- Cada espacio completamente regular es regular.
- Producto de espacios completamente regulares son completamente regulares.
- Sean f, g : X → Y funciones continuas, Y un espacio Hausdorff. Probar que {x ∈ X : f(x) = g(x)} es cerrado. Dar un ejemplo mostrando que la condición Hausdorff es esencial.
- Sea X un espacio topológico Hausdorff y f una función continua de X en si mismo. Probar que el conjunto formado por los puntos fijos de F es cerrado. Dar un ejemplo, mostrando que la condición Hausdorff es esencial.
- Probar que cuando f, g : X → Y son continuas, Y es Hausdorff, y A es un subconjunto denso en X. Entonces, si f|A = g|A, se cumple que f = g.
- (i) El producto AB es invertible, con (AB)−1 = B−1A−1, y
- (ii) La inversa de A es invertible con (A−1)−1 = A.
- (i) LA(x + y) = A(x + y) = Ax + Ay = LA(x) + LA(y)
- (ii) LA(αx) = A(αx) = αAx = αLA(x).
- (a) T preserva la norma (o largo de los vectores), ||T(x)|| = ||x||.
- (b) T preserva el origen, T(0) = 0.
- (c) T preserva la ortogonalidad (perpendicularidad) entre vectores.
- (d) La composición de transformaciones ortogonales es ortogonal.
- (e) Cuando T es biyectiva, su inversa es ortogonal.
- (i) (AB)t AB = BtAtAB = Bt(AtA)B = BtB = I, o sea que el producto de ortogonales es ortogonal.
- (ii) Recordemos que cuando A es ortogonal, su inversa es At. Entonces, la relación
- o sea que A−1 es ortogonal. Esto concluye la prueba.
- En el texto, se dice que la función determinante es suprayectiva, explicar porque eso es cierto.
- La función A ↦ At de Mn(R) en sí mismo es continua.
- Hallar la norma euclídea de cada una de las siguientes matrices.
- Sea G el conjunto de todas las matrices 2 × 2 cuyas entradas son todas números racionales. Probar que G es un subgrupo de GL(2) que no es cerrado en GL(2). ¿Cuál es la clausura de G en GL(2)?
- Los grupos GL(n) y SL(n) no son acotados como subconjuntos de Mn(R).
- GL(n) es por restricción de la distancia euclídea un espacio métrico. Luego, es un espacio completamente normal—ver teorema 12.3.5. ¿Qué se puede decir de SL(n) y de O(n)?
- Sean H un subgrupo cerrado de GL(n) y K un subgrupo cerrado de H. Probar que K es cerrado en GL(n).
- Probar que O+(n) es un subgrupo cerrado de O(n) y, por lo tanto, de GL(n). ¿Por qué O-(n) no puede ser un grupo? ¿Es O+(n) compacto, acotado?
- Sea UT(2) el conjunto de matrices 2×2 tal que el elemento bajo la diagonal es 0. Probar que UT(2) es un subgrupo cerrado de GL(2) .
- (Ortogonales de dimensión 1) (Matrices 1 × 1 se identifican con números reales) Probar que O(1) = {1,−1}. Identificar a O+(1).
- (Ortogonales de dimensión 2.)
- Probar que las matrices de la forma , θ real, son ortogonales con determinante 1.
- Probar que toda matriz ortogonal con determinante 1 tiene una matriz de la forma anterior. (Sug. Verificar que cualquier vector de largo 1 tiene la forma necesaria para aparecer como columna de la matriz. Usar que cuando (a, b) es un vector cualquiera, los únicos vectores de igual largo y ortogonales a él, son (−b, a) y (b,−a).)
- Sea J = Probar que J es ortogonal con determinante igual a −1.
- Sea ϕ : O-(2) → O+(2) la función que asocia a cada B en O-(2) con el producto JB. Probar que ϕ es un homeomorfismo.
- ¿Es O(2) conexo?
- Sea A una matriz n × n con determinante nulo. Para todo ε > 0 hay una matriz B tal que ||B − A|| < ε y el determinante de B no es nulo.
- Sea A una matriz n × n y sea B la matrix (n + 1) × (n + 1) tal que
Probar que A es ortogonal, ssi, B lo es. Usar el resultado para probar que podemos considerar a O(n) como un subgrupo cerrado de O(n + 1).
- Sea A una matriz n×n con determinante no nulo. Probar que hay un ε > 0 tal que para toda matriz B tal que max{|bij − aij |1 ≤ i, j ≤ n} < ε, se cumple que det(B) ≠ 0.
- Sea una base ortonormal de . Sean y vectores de , cuyas matrices de coordenadas respecto a la base son las matrices , y respectivamente. Entonces, se cumple que
- Sea una matriz con determinante nulo. Para todo hay una matriz tal que y el determinante de no es nulo.
- Considerar el espacio normado y sea la serie de potencias definida en el ejercicio 4 del final del capítulo sobre Sucesiones. Para cada matrix , es otra matriz, la matriz exponencial de . Para toda matriz se cumple que
- .
- , y en .
- es invertible y .
- .
Luego, define una función de en GL(n) que es central en la teoría de grupos de Lie, grupos donde las operaciones son derivables (en el sentido del Cálculo Infinitesimal) y, por lo tanto, continuas.
- Las funciones Lg : G → G :: x ↦ gx (multiplicación, o traslación, por g por la izquierda), Rg : G → G :: x ↦ xg (multiplicación, o traslación, por g por la derecha) y cg : G → G :: x ↦ gxg−1 (conjugación por g), son homeomorfismos.
- Tomar inversos, x ↦ x−1, es un homeomorfismo.
- Si U es una vecindad de e, entonces gU y Ug son vecindades de g. Viceversa, cuando V es una vecindad de g, g−1V y Vg−1 son vecindades de e.
- Observemos, primeramente, que para todo x en G se cumple que Le(x) = ex = x, lo que implica que Le = idG (la función identidad en G.
Sigue de la definición de multiplicación por la izquierda, que para todo g, h,
x en G, se cumple que
Es decir que .
Tomando h = g−1, se concluye que LgLg−1 = Le = idG; de donde concluimos que Lg es invertible y que su inversa es Lg−1. Notemos que x ↦ gx es igual a x ↦ (x, g) * ↦ xg, lo que implica que Lg es composición de continuas, luego es continua. Como su inversa es del mismo tipo, dicha inversa es continua; luego, se trata de un homeomorfismo. El resto de las afirmaciones de (a) queda de ejercicio.
- Tomar inversa es su propia inversa.
- Trivial, ya que traslaciones por la izquierda o derecha son homeomorfismos. En el grupo topológico Rn con la suma vectorial, las “multiplicaciones por la izquierda” son las traslaciones ta : x ↦ a + x. En esta caso, como la suma es conmutativa, las traslaciones por la derecha coinciden con las traslaciones por la izquierda.
- (a) gF y Fg son cerrados.
- (b) gU y Ug son abiertos.
- (c) UZ y ZU son conjuntos abiertos.
- (d) U−1 es abierto y F−1 es cerrado.
- (a) Si U es una vecindad del neutro, hay una vecindad V del neutro tal que V −1 ⊂ U.
- (b) Si U es una vecindad del neutro, hay vecindades V, W del neutro tales que
- (c) Si U es una vecindad del neutro, hay vecindades V, W del neutro tales que
- (d) Si U es una vecindad del neutro, hay una vecindad simétrica V del neutro tal
- (e) Si U es una vecindad del neutro, hay una vecindad simétrica V del neutro tal
- (i) Hay una vecindad U de x que no contiene a e;
- (ii) Hay una vecindad W de e que no contiene a x.
- (a) Si A y B son compactos entonces AB también lo es.
- (b) Si A es cerrado y B es compacto, AB es cerrado.
- El producto A × B es, por el teorema de Tychonoff, compacto. AB es la imagen de A × B por (x, y) ↦ xy.
- Sea x un elemento del complemento de AB, entonces A y xB-1 son disjuntos. Aplicando el lema 14.1.8, podemos hallar una vecindad U del neutro tal que UA no interseca a xB-1. Entonces, U-1x no interseca AB, o sea que AB es cerrado.
- Sea G un subgrupo topológico, A un subconjunto cualquiera no vacío.
- Sea x un punto de G tal que para toda vecindad U del neutro x está en xU ∩ A ≠ ∅, entonces x está en la clausura de A.
- Sea y un punto de G tal que para toda vecindad U del neutro x está en UA, entonces x está en la clausura de A.
- Usar cualesquiera de las afirmaciones de los ejercicios anteriores para dar una condición para que un punto x no esté en la clausura de A.
- Sean G un grupo topológico, g un punto de G, A y B subconjuntos cualesquiera no vacíos, y U una vecindad del neutro. Probar que A ∩ UxB ≠ ∅, ssi, U-1A ∩ xB ≠ ∅.
- Un subgrupo cerrado que no es abierto: Z en R. Un subgrupo que no es ni cerrado ni abierto: Q en R.
- Sean A y B subconjuntos de un grupo topológíco G.
- Cl(A) Cl(B) ⊂ Cl(AB).
- Cl(A-1) = Cl(A)-1.
- x Cl(A)x−1 = Cl(x A x−1).
- Usar los resultados del ejercicio anterior para probar que si H es un subgrupo (resp. subgrupo normal) de un grupo topológico G, entonces Cl(H) también lo es.
- Sea G un grupo T0, A y B subconjuntos de G.
- Si para todo a en A, b en B se cumple que ab = ba, entonces para todo a en Cl(A) y b en Cl(B) se cumple que ab = ba.
- Si H es un subgrupo abeliano (conmutativo) de G, entonces Cl(H) también lo es.
- Sea G un grupo topológico con neutro e. La clausura de {e} es un subgrupo normal de G que es el menor (respecto a la inclusión) de los subgrupos cerrados de G.
- Un homomorfismo continuo de G en H es un homomorfismo de grupos que, además, es continuo como función.
- Un homomorfismo abierto es un homomorfismo continuo que, además, es abierto.
- Un isomorfismo continuo es una biyección que es un isomorfismo de grupos y que es continuo.
- Un isomorfismo–homeomorfismo o isomorfismo topológico, es un isomorfismo de los grupos que también es un homeomorfismo.
- Un automorfismo topológico es un isomorfismo topológico de un grupo en si mismo.
- La función exponencial usual es un isomorfismo topológico entre el grupo aditivo de los Reales y el grupo multiplicativo de los Reales positivos.
- La función identidad es un automorfismo de cualquier grupo topológico.
- La función determinante de GLn en R* es un homomorfismo continuo.
- Sea E un espacio normado. La multiplicación por un escalar no nulo en E es un homomorfismo de la estructura aditiva que es un isomorfismo topológico.
- Probar la proposición 14.3.1.
- La composición de dos homomorfismos continuos (resp. abiertos, isomorfismos continuos, isomorfismos–homeomorfismos) es también continuo (resp. abierto, isomorfismo continuo, isomorfismo–homeomorfismo).
- Sea f : G → H un homomorfismo de grupos. f es un homomorfismo continuo, ssi, para cada vecindad del neutro eH de H hay una vecindad U de eG tal que f(U) ⊂ V.
- Sea f : G → H un homomorfismo de grupos. Probar que cuando H es un espacio T1, el núcleo de f, ker(f) = {x ∈ G : f(x) = eH}—que siempre es un subgrupode G—es cerrado como subespacio de G.
- El conjunto cociente G/H es un espacio con la topología más fina tal que la suprayección canónica es continua,
- La suprayección canónica es además abierta.
- Si H es normal en G, G/H es un grupo topológico con las operaciones que hacen que la suprayección canónica sea un homomorfismo de grupos.
- Sea E un espacio normado. Verificar que con respecto a la suma E es un grupo topológico.
- La composición de homomorfismos continuos es un homomorfismo continuo.
- Cualquier grupo finito (cantidad finita de elementos) es un grupo topológico respecto a la topología discreta.
- Sean X un espacio topológico y G un grupo topológico. Sean f, g : X → G dos funciones continuas. Probar que las funciones h : x ↦ f(x)g(x) y k : x ↦ f(x)−1 son continuas.
- ¿Cuáles de los siguientes subgrupos del grupo aditivo de los Reales son cerrados? (a) Z, (b) √2 Z, (c) Z + √2 Z.
- Dar ejemplo de un subgrupo de un grupo topológico que
- a) es cerrado, pero no abierto;
- b) no es ni cerrado ni abierto.
- Sea G = R2 con la suma de vectores. Sean v1, v2 vectores no nulos tales
que ninguno de ellos es un múltiplo del otro. Verificar que los siguientes
subconjuntos son subgrupos topológicos de G.
- a) A = {α v1 : α ∈ R}.
- b) B = {m v1 : m ∈ Z}.
- c) C = {m1v1 + m2v2 : m1,m2 ∈ Z}.
- d) D = {mv1 + α v2 : m ∈ Z, α en R}.
- Sea G = R2 con la suma de vectores. Sean v un vector no nulo y H = {qv : q ∈ Q}. Probar que H es un subgrupo de R2. pero que no es cerrado. ¿Cuál es la clausura de H?
- Cualquier subgrupo cerrado que tiene una cantidad finita de clases laterales es también abierto.
- Un subgrupo H de un grupo topológico es un subespacio discreto, ssi, H contiene un punto aislado.
- Un subgrupo abierto H de G es cerrado (o sea un subgrupo topológico). (Sug. Probar que las clases laterales de H diferentes de H forman un conjunto abierto.)
- Sean G un grupo topológico con neutro e, U una vecindad de E, y n un entero positivo. Probar que hay una vecindad simétrica V de e tal que V n ⊂ U.
- Sea V una vecindad simétrica de V del neutro e. Probar que ∩n≥1 Vn es un subgrupo abierto–cerrado.
- Una base de las vecindades del neutro es una colección de abiertos C tal que
para cada U del neutro e, hay un V en C tal que V ⊂ U.
- Sea C una base de las vecindades del neutro y sean A := {xU : x ∈ G, U ∈ C} y B := {Ux : x ∈ G, U ∈ C}. Probar que tanto A como B son bases de la topología de G.
- Hay una base de las vecindades del neutro consistente únicamente de vecindades simétricas.
- En el texto vimos que la clausura de un subgrupo es siempre un subgrupo. ¿Será siempre válido que el interior de un subgrupo es un subgrupo?
- Probar que el producto de dos grupos topológicos es un grupo topológico.
- Sea G un grupo cualquiera. Probar que G con la topología discreta es un grupo topológico.
- Sea H un subgrupo de un grupo topológico, probar que si H tiene al menos un punto interior, entoces H es abierto.
- Sea H un subgrupo conexo de G. La preimagen de cualquier componente conexa de G/H es una componente conexa de G.
- Sea H un subgrupo de G tal que G/H es un espacio regular. Entonces, H es cerrado (ver proposición 14.4.5).
- Sea G un grupo topológico y V una vecindad simétrica del neutro e.
- Sea W = &cupn≥1 Vk es un subgrupo abierto y cerrado de G.
- Si G es conexo, G = W. Es decir que V es un conjunto generador de G, o sea que cualquier g en G es producto de elementos de V.
- Sea G un grupo topológico y H un subgrupo de G. Si hay una vecindad U del neutro de G tal que Cl(U) ∩ H es cerrado, entonces H es un subgrupo topológico (cerrado).
- Sea G un grupo topológico localmente compacto, H un subgrupo de G. Entonces G/H es localmente compacto.
- Sean G1 un grupo de matrices m×m y G2 un subgrupo de matrices n×n. Sea G = G1 × G2 el grupo producto (con operación por coordenadas). G puede considerarse como un grupo de matrices (m + n) × (m + n) con elemento típico
donde A es un elemento de G1 y B un elemento de G2. Probar que G es un grupo matricial, subgrupo cerrado de GL(m + n).. Generalizar lo anterior a un producto de una cantidad finita de grupos matriciales.
- Probar que <Rn, +> (+ es la suma de vectores) es un grupo matricial. (Sugerencia: usar el ejercicio anterior y el ejemplo 15.1.2.)
- Sea θ el ángulo π/3 (= 60◦). La rotación por θ alrededor del origen está
dado por la transformación lineal con matriz
- Probar que ρ6 = id y que ρk ≠ id, cuando k = 1, ... , 5.
- Sea C6 = {id, ρ, . . . , ρ5}. Probar que C6 es un grupo matricial.
- (a) La composición de dos traslaciones es una traslación, tatb = ta+b.
- (b) La inversa de una traslación es una traslación, (ta)−1 = t−a.
- (c) Las traslaciones son isometrías.
- (d) Las traslaciones son homeomorfismos.
- Sean p y q dos puntos de E, probar que hay una traslación que envía p en q.
- Sea p un punto y sea Euclp el conjunto formado por todas las isometrías que
fijan p.
- a) Probar que Euclp es un subgrupo de Eucl(E).
- b) Sea q = ta(p). Probar que Euclp = ta Euclq t−a. (Ambos grupos son conjugados.)
- Sean p y q dos vectores de E de igual largo, probar que hay una transformación ortogonal que envía p en q.
- (Simetría central con centro en c.) Sea c un punto de E. Sea σc(p) = 2c − p.
- La transformación σc fija c y envía cada punto p distinto de c en un punto p′ tal que c es el punto medio entre p y p′.
- σc2 = id.
- σc es una isometría.
- Sea σ0 la simetría con centro el origen. Probar que
- (i) σ0es una transformación ortogonal y
- (ii) σc = tcσct−c.
- Sean c y d puntos diferentes. Probar que σcσd = σdσc es una traslación.
- Las isometrías son homeomorfismos del espacio en si mismo.
- Probar que el grupo de las traslaciones Tras(E) es isomorfo al gruo aditivo de Rn.
- A es invertible, ssi, B lo es.
- A es ortogonal, ssi, B lo es.
- det(A) = 1, ssi, det(B) = 1.
- Sigue del lema 13.4.3
- Se tiene, usando lema 13.4.2, que BBt = T(A; 0)T(At; 0) = T(AAt, 0).
- Trivial, ya que det(B) = det(A).
- (Representación Matricial de los Grupos Finitos) Sea (ei) la base canónica de Rn; o sea ei es un vector cuyas componentes son todas nulas, excepto la i–ésima que es igual a 1.
Sea G = {g1 = e, g2, ... , gn} un grupo. Identificar cada gi con ei. i = 1, ... , n. Es decir que consideramos a los vectores de Rn como sumas formalesα1g1 + · · · + αngn. Con cada g asociamos la transformación lineal Lg cuya matriz tiene como columnas a los vectores ggi. Si ggi = gj , Lg envía ei en ej . Probar que la función L : G → GL(n) tal que g ↦ Lg es un homomorfismo cuya imagen es un subgrupo cerrado de GL(n). Es decir que cada grupo finito es un grupo matricial.
- (Toro) Llamamos Toro (de dimensión 2) al espacio S1 ×S1, que puede pensarse
como la superficie de una rosquilla.
- Investigar las propiedades topológicas del toro. ¿Es compacto? ¿Es conexo? ¿Es acotado?
- Como S1 es un grupo topológico, el toro también lo es. ¿Es conmutativo?
- Sea Z2 el subconjunto de R2 formado por todos los puntos con ambas coordenadas enteras, Probar que Z2 es un subgrupo cerrado y que R2/Z2 es homeomórfico a T.
- Generalizar el ejercicio anterior a G = Rn y H = Zn. Probar que G/H es homeomórfico al producto de n copias de S1.
- GL(n) no es compacto para todo n ≥ 1. SL(n) no es compacto para todo n ≥ 2.
- Sea G un grupo matricial y H un subgrupo cerrado de G, entonces H es matricial.
- ¿Es compacto el grupo afín GA(n)?
- Sea G un subgrupo compacto de GL(n), entonces cada elemento de G tiene determinante igual a 1 o −1.
- . Sea
- H es un subgrupo de SL(2).
- El grupo SO(2) es un subgrupo de SL(2).
- Sea η: SO(2) × H → SL(2) tal que (A,B) ↦ AB. Probar que η es un homeomorfismo que no es un homomorfismo de grupos.
- ↑ Postulados son enunciados cuya validez aceptamos. En lugar de `postulado podremos decir axiomas. Los teoremas y las proposiciones son afirmaciones cuya validez debemos probar.
- ↑ Hay dos versiones de Naturales dependiendo de la inclusión del 0 en los Naturales. La tendencia actual es a incluirlo.
- ↑ RAHT, Fundamentos del Análisis, 2013 [2]
- ↑ En Álgebra hay una noción de conjunto cerrado respecto a una operación, para indicar que cuando los operandos están en un conjunto, el resultado de la operación con esos operandos, también está en el conjunto. Para distinguir las dos nociones, en este texto ``cerrado algebraicamente significará cerrado en el sentido del Álgebra.
- ↑ Suponemos a menos que se diga lo contrario que las familias no son vacías.
- ↑ Cerrado como camino es distinto de conjunto cerrado.
- ↑ La transpuesta At de una matriz A, es la matriz que se obtiene cambiando las filas por las columnas de A.
- ↑ Las traslaciones son las “traslaciones por la izquierda” L g del lema 14.1.1, del grupo aditivo de Rn. Algunas de las propiedades de la sección se pueden deducir utilizando los resultados del lema citado.
Las Propiedades de Separación
[editar]Introducción
[editar]En varios de los capítulos anteriores, hemos visto aparecer la propiedad de Hausdorff aparecer en varios resultados importantes.Recordemos que un espacio tiene dicha propiedad, cuando dados dos puntos distintos del espacio, hay abiertos disjuntos tales que cada uno de ellos contiene a exactamente uno de los puntos dados. En este capítulo estudiaremos propiedades análogas de separación, algunas más fuertes y otrás más débiles. Usaremos la notación tradicional de espacios Ti, i = 0, 1, 2, ... introducida por Alexandroff y Hopf (Topologie, 1935).
Generalizaremos la terminología de separación de la siguiente manera: diremos que hay abiertos que separan dos subconjuntos A y B, cuando haya abiertos disjuntos U y V tales que U contiene a A y V a B.
Cuando estudiamos los conjuntos disconexos, vimos que hay funciones reales que permiten distinguir a conjuntos disconexos. Resulta útil, especialmente en Análisis, disponer de ese tipo de funciones, por lo que en la sección 12.3.4 se hallará algunos resultados más profundos al respecto,Definiciones y Propiedades
[editar]Iniciaremos nuestro estudio con algunos tipos simples de separación.
Definición. (Propiedades de Separación) Sea X un espacio topológico.
Claramente, un espacio T2 es T1, y un espacio T1 es T0. Los siguientes ejemplos mostrarán que las inclusiones son estrictas. Además, notemos que un espacio topológico indiscreto con más de un punto no es T0 — el único abierto no vacío es todo el espacio.
Ejemplos 12.2.1. Los ejemplos siguientes, aunque tienen un aire artificial, permiten ver que cada condición es más restrictiva que la anterior.Sea X un espacio T1 y sea p un punto de X. Cada punto del complemento de {x} está contenido en un abierto que no contiene a p, o sea que está totalmente contenido en el complemento indicado. Luego, dicho complemento es un conjunto abierto. Luego, {x} es cerrado. Esta propiedad caracteriza a los espacios T1.
Proposición 12.2.1. Un espacio topológico es T1, ssi, cada punto es cerrado.
-
Demostración. X es T1 ⇐⇒ cada punto tiene un complemento abierto, ⇐⇒ cada punto es cerrado.
Sigue de la proposición que los subconjuntos finitos de espacios T1 son cerrados. En particular, los espacios Hausdorff tienen la misma propiedad. Las siguientes proposiciones refuerzan la intuición de que compactos (al menos en espacios Hausdorff) se comportan como puntos.
Los espacios Hausdorff tienen interesantes propiedades de separación. La siguiente proposición establece que un punto y un conjunto compacto que no lo contengan pueden ser separados.
Proposición 12.2.2. Sean X un espacio Hausdorff, C un subconjunto compacto de X, y p un punto que no está en C. Entonces, hay abiertos disjuntos U, V tales que U contiene a p y V a C.
- Demostrración.
Sea z un punto de C. Como el espacio es Haudorff hay abiertos $U_z$ y $V_z$ que separan p de z, o sea que p está en Uz y z está en Vz, con Uz y Vzdisjuntos. La familia de los Vz, z en C forman una cubierta abierta de C. Como C es compacto, una subfamilia de tales abiertos cubre a C, digamos que son V1, ... , Vm. Sean Ui, i=1,..., m los correspondientes U1's,y sea U = ∩ {Ui ; 1 ≤ i ≤ m} y V = ∪ {Vi: 1 ≤ i ≤ m. Claramente, U y V son abiertos con p en U y C contenido en V. Probaremos que son disjuntos.
Sigue en forma inmediata de la proposicion que un subconjunto compacto de un espacio Hausdorff es cerrado. Resultado que vimos anteriormente como proposición 10.2.6.
La proposición anterior, se puede generalizar de la siguiente manera.
Proposición 12.2.3. En un espacio Hausdorff, abiertos separan a conjuntos compactos.
-
Demostración. Sean C y D conjuntos compactos disjuntos de un espacio de Hausdorff X. Sigue de la proposición 12.2.2 que para todo x en C hay una vecindad abierta Ux de x y una vecindad Vx de D tales que Ux ∩ Vx = ∅.
La familia de abiertos Ux, x ∈ C, forman una cubierta de X, por lo que hay una familia finita de ellos que cubre a C, digamos, los Ux_i con i = 1, ... ,m. Sea U la reunión de todos esos conjuntos. Sea V la intersección de los correspondientes Vx_i’s. Claramente
V contiene a D y U ∩ V = ∅ .
Ejercicios 12.2
[editar]
Los Espacios Regulares y Normales
[editar]-
Advertencia. La terminología acerca de estos espacios no está estandarizada,
al contrario de la terminología usada en la sección anterior. Cuando visitando
un libro de topología, resulta conveniente ates de mirar a los teoremas, ver
los convenios sobre la terminología usada.
Definición. (Espacio Regular) Un espacio X es un espacio regular, ssi, es T1 (cada punto es cerrado) y se cumple la siguiente propiedad:
(Propiedad T3.) Abiertos separan puntos de conjuntos cerrados. Es decir que para cada punto p y cada conjunto cerrado C tal que p no está en C, hay abiertos disjuntos U, V tales que p está en U y C está contenido en V.
Algunos autores llaman regular a un espacio que satisface la condición T3, pero no necesariamente T1, y llaman completamente regular a lo que aquí llamamos regular.Definición. (Espacio Normal) Un espacio es normal o T4, ssi, es T1 y se cumple la siguiente propiedad.
(Propiedad T4.) Abiertos separan conjuntos cerrados. Es decir, si H y K son subconjuntos cerrados, hay abiertos disjuntos U, V tales que U contiene a H y V contiene a K.
Observación 12.1. Notemos que las condiciones T3 y T4 corresponden a las proposiciones 12.2.2 y 12.2.3 reemplazando compactos por cerrados.Los Espacios Regulares
[editar]Proposición 12.3.1. Un T1–espacio X es regular si, y sólo si, para cada punto p y cada abierto U que contiene a p hay un abierto V cuya clausura está contenida en U.
-
Demostración. Supongamos que X es regular y que el punto p está contenido en el abierto U. Como X es regular, hay abiertos disjuntos V y W tales que p está en V y W contiene a X \ U. Como, W ∩ V = ∅ , se tiene que W ∩ Cl(V) = ∅ , lo que implica que Cl(V) ⊂ U.
Recíprocamente, sea p un punto cualquiera de X y F un cerrado que no contiene
a p. Entonces X \ F es un abierto que contiene a p, luego hay un abierto V
que contiene a p y cuya clausura está contenida en X \ F. Entonces, X \ V es un
abierto conteniendo a F.
Proposición 12.3.2. Sean un espacio, un punto de y un subconjunto cerrado de . Hay abiertos que separan y cuyas clausuras son disjuntas.
- Demostración. Por la proposición 12.3.1 hay un abierto que contiene a y cuya clausura está contenida en el complemento de , , Por la misma proposición, hay un abierto que contiene a y tal que . Entonces, y son los abiertos deseados.
Los Espacios Normales
[editar]Proposición 12.3.3. Si H y K son subconjuntos cerrados de un espacio normal X, hay abiertos con clausuras disjuntas, uno de ellos contiene a H y el otro a K.
Proposición 12.3.4. Un espacio Hausdorff compacto es normal.
-
Demostración. Como cada conjunto conjuntos cerrado en un espacio compacto es compacto (ver 11.4.1), sigue de la proposición 12.2.3 que, en un espacio Hausdorff compacto, abiertos separan cerrados.

Las propiedades de separación de espacios topológicos.
La Separación y los Espacios Métricos
[editar]Sea E un espacio métrico, p un punto de E y U un abierto que contiene a p. Luego, hay una bola abierta B(p; r) que contiene a p y está contenida en U. Entonces, B(p; r/2) es un abierto contenido en U cuya clausura está contenida en B(p; r) y, por lo tanto en U. Sigue de la proposición 12.3.1 que E es regular.
Probaremos que los espacios métricos tienen la siguiente propiedad:
(Propiedad T5.) Si H y K son dos subespacios separados (en el sentido de los espacios conexos, ninguno de ellos contiene puntos de acumulación del otro) entonces hay abiertos separando los conjuntos.Un espacio T1 se llama completamente normal cuando tienen la propiedad T5. Los espacios completamente normales son normales.
Teorema 12.3.5. Los espacios métricos son completamente normales.
-
Demostración. Sea E un espacio métrico y sean H y K subconjuntos separados.
Sea U el conjunto formado por todos los puntos p tales que d(p,H) < d(p,K) y
sea V el conjunto formado por todos los puntos p tales d(p,H) > d(p.K). Claramente,
tales conjuntos son disjuntos H ⊂ U, ya que d(h,H) = 0 y d(h,K) > 0
para todo h en H. Análogamente, K ⊂ V . Probaremos que H es abierto. Sea x
cualquier punto de U y sea δ= d(x, k) − d(x,H). Tenemos para y en B(x;δ/2)
que d(x,K) ≤ d(x, y) + d(y,K) < δ/2 + d(y,K), de donde d(y,K) + δ/2 >
d(x,K) = d(x,H) + δ; lo que implica que d(y,K) > d(x,H) + δ/2. Es decir
que y está en U; por lo que U es abierto.
En forma análoga, se prueba que V es abierto.
Los resultados sobre los espacios vistos anteriormente muestra que las propiedades de separación son abstracciones de propiedades de los espacios métricos.
La Separación por Funciones
[editar]Esta sección contiene tres resultados importantes, especialmente para el Análisis, pero que no usaremos en el resto del libro. Por esa razón, solamente los enunciaremos, pero referiremos a la literatura para las demostraciones, ver por ejemplo Simmons [15].
Proposición 12.3.6. (Lema de Urysohn) Sea X un espacio normal y sean A y B subconjuntos cerrados disjuntos de X. Entonces, hay una función continua de X en [0, 1] tal que f(A) = {0} y f(B) = {1}.
Proposición 12.3.7 (Lema de la extensión de Tietze). Sea X un espacio normal y F un subconjunto cerrado de X. Suponer que tenemos una función f : A → [a, b] ⊂ R continua. Entonces, hay una extensión g : X → [a, b] de f, o sea que la restricción de g a F coincide con f.El siguiente lema responde a la pregunta de cuando un espacio topológico X es metrizable, es decir cuando hay una métrica en X cuya topología inducida coincide con la topología del espacio.
Proposición 12.3.8 (Lema de la Metrización de Urysohn). Cada espacio normal X con una base con una cantidad contable de elementos (se pueden escribir como una sucesión), es metrizable.
Ejercicios 12.3
[editar]Ejercicios del Capítulo 12
[editar]
La Topología de las Matrices
[editar]Introducción
[editar]En este capítulo, y en los dos siguientes, presentaremos aplicaciones de lo visto anteriormente a ciertos grupos geométricos. Los grupos geométricos son objetos algebraicos asociados a nociones geométricas. En nuestro caso, se tratará de la geometría de los espacios Euclídeos Rn.
Los grupos (abstractos o generales) se estudian en los cursos de Álgebra Abstracta, lo necesario para este capítulo está resumido en el apéndice C. Los principales grupos geométricos aparecerán como conjuntos de matrices, por lo que iniciaremos el capítulo estudiando la topología de las matrices n × n. En la tercera sección, generalizaremos lo visto en grupos de matrices a grupos topológicos cualesquiera. Finalmente, aplicaremos lo anterior a la topología de los grupos geométricos. Para concretar lo anterior consideremos a GL(n). (grupo lineal) que será el conjunto de todas las matrices n×n cuyo determinante no es nulo. Este conjunto como veremos, puede considerarse un subconjunto de Rn2, por lo que resulta natural preguntarse por la topología del mismo: ¿es abierto o cerrado? ¿es conexo? ¿es compacto? Además de presentar alguna matemática interesante por sí mismo, queremos, como dijimos arriba, mostrar como se aplican los conceptos vistos a esos conjuntos de matrices.
Este capítulo requiere un conocimiento básico de Álgebra Lineal. Cuando una lectora o lector no posea dicho conocimiento, puede hallar algunas dificultades en la lectura del mismo. Sin embargo, en cualquier caso, creemos que la lectura de estos capítulos puede ser provechoso, usando algo de fe para los resultados de Álgebra Lineal.
El Espacio Métrico de las Matrices
[editar]Simbolizaremos por Mn(R) al conjunto formado por todas las matrices n × n con entradas en los Reales. Cada matriz A = [aij ] puede identificarse con un punto de Rn2 , colocado las filas, ordenadamente, una tras otra. Es decir que aij ⇆ b(i−1)n+j .
Ejemplo 13.2.1. En M2(R),
La identificación de Mn(R) con Rn2 provee, por lo tanto, a Mn(R) con la estructura de espacio normado y, en consecuencia, con la métrica deducida de tal norma. Luego, podremos aplicar a Mn(R) las nociones métricas y topológicas vistas anteriormente.
Cada subconjunto de Mn(R) será un subespacio con la topología relativa. Cualquier métrica de Rn2 define la misma topología en Mn(R), pero como estamos interesados en los grupos geométricos usaremos la norma euclídea, a menos que se indique lo contrario.
Recordemos que las proyecciones (o coordenadas) pi : (x1, ... , xm) ↦ xi, 1 ≤ i ≤ m de Rm en R son funciones continuas. Recordemos, también, que una función f : E → Rm, en particular m = n2, es continua, ssi, la composición con cada una de las proyecciones es continua, o como diremos si es continua por coordenadas.
Cuando A = [aij}] sea una matriz , denotaremos las coordenadas como pares i,j o ij con . Así la coordenada ij de la matriz A es .
Las Operaciones Matriciales son Funciones Continuas
[editar]La suma, resta, y producto de matrices n × n, son funciones continuas
Rn2 × Rn2 → Rn2 .
También es continua la multiplicación por escalar. Para probar lo anterior, basta con ver la continuidad por coordenadas. En efecto, sean A = [aij ] y B = [bij ] matrices en Mn(R) = Rn2. Las coordenadas ij de la suma, resta y multiplicación son, respectivamente,
aij + bij, aij − bij y ∑k aik bkj.
Como dichos valores son polinomios en las coordenadas de los operandos, vemos que son funciones continuas. (Ver la sección 6.5.3). Resumimos la discusión anterior en la siguiente proposición.
Proposición 13.2.1. La suma, resta y multiplicación son operaciones continuas en Mn(R).
Se verifica que la suma y la multiplicación son asociativas, que la multiplicación es distributiva respecto a la suma. La suma es conmutativa, pero la multiplicación no lo es. La matriz identidad I es una matriz cuyas entradass en la diagonal principal son todas iguales a 1 y las demas entradas son nulas. Se verifica que para toda matriz A se cumple que AI = IA = A.
Ejemplo. La matriz identidad de es .El determinante es una función de Mn(R) en R definida comoLa Función Determinante y el Grupo Lineal
[editar]donde la suma corre sobre todas las permutaciones de los elemento del conjunto {1, 2, ... , n} y es el signo de la permutación. Se verifica la siguiente importante relación (a la que nos referiremos como la identidad básica del determinante).
Sigue de la definición que el determinante de la matriz identidad es igual a 1.
Decimos que una matriz A es invertible cuando hay una matriz tal que . Dicha matriz es única y se denota .
Sigue de la identidad~{IBD} que cuando una matriz es invertible se cumple que
Por lo que el determinate de una matriz invertible no es cero. Se verifica que el converso es válido, por lo que una matriz es invertible, ssi, su determinante no es nulo. En particular la matriz identidad es invertible.
Notemos que cuando es invertible, . Simbolizaremos por GL(n) al conjunto formado por todas las matrices n × n
invertibles. Cuando A y B son matrices invertibles, se cumple que
En la terminología de Álgebra Abstracta, las propiedades anteriores, conjuntamente con la asociatividad del producto, hacen que GL(n) tenga una estructura de grupo (ver definición C.1), al que llamamos el grupo lineal (real de dimensión n). Con esa terminología, la relación básica establece que el determinante es un homomorfismo (ver definición C.4) de grupos entre los grupos GL(n) y R* (los Reales no nulos) que se verifica, además, que es suprayectivo. Sigue de la teoría de grupos, que la preimagen de cualquier subgrupo de R* será un subgrupo de GL(n) (ver D.4.2). En particular, la preimagen del subgrupo {1} de R* es un subgrupo de GL(n), al que llamamos el (sub)grupo lineal especial y que denotamos por SL(n).
Proposición 13.2.2. La función determinante es continua.
- Demostración. Sigue de la definición que se trata de un polinomio en las coordenadas,
por lo que es continua.
Corolario 13.2.3. El grupo lineal GL(n) es un subconjunto abierto de Mn(R).
El grupo lineal especial SL(n) es un subconjunto cerrado (topológicamente) de GL(n).
- Demostración. Como det : Mn(R) → R es continua y GLn(R) es la preimagen por determinante de R* (reales no nulos), que es un subconjunto abierto
de R, se tiene que GL(n) es abierto.
Por su parte, SL(n) es la preimagen por el determinante del subconjunto cerrado
{1} en R*.
Proposición 13.2.4. La asociación a cada matriz invertible A = [aij ] de su inversa es una función continua.
- Demostración. Tenemos, por la Regla de Cramer, que
donde Cij es el ij–cofactor (el determinante de la matriz (n − 1) × (n − 1) que se obtiene a partir de A por eliminación de la i–ésima fila y la j-ésima columna). Sigue de la regla de Cramer que cada coordenada de la inversa es igual a un cociente de dos funciones continuas, el numerador siendo una suma de funciones continuas (determinantes), el denominador otra fución continua (también un determinante). Luego, es continua.
Corolario 13.2.5. La función es un homemorfsimo de GL(n) en si mismo.
- Demostración. La función es su propia inversa (como función) ya que
La Conjugación
[editar]Sea G un grupo. Se llama conjugación por (un elemento) g de G, a la función del grupo en sí mismo tal que x ↦ gxg−1 (el conjugado por g de x).
Proposición 13.2.5. La conjugación es un homeomorfismo para todo g.
- Demostración. La conjugación cg es la composición de la multiplicación por la izquierda por g, con la multiplicación por la derecha por g−1
Lo que prueba que es continua. Notemos que . Es decir que . Si , se tiene que . Es decir que es invertible como función, y la función inversa es continua, ya que también es una conjugación. Recordemos que decimos que un subgrupo es normal en G cuando los conjugados de cada uno desus elementos es un elemento del subgrupo. Por ejemplo, SL(n) es normal en GL(n),
ya que para toda A en SL(n) y B en GL(n) se cumple que
det(BAB−1) = det(B) det(A) det(B−1) = det(A) = 1.
Las Matrices y las Transformaciones Lineales
[editar]Cualquier matriz , , define una función de en si mismo, asignando a cada de el vector . Identificamos a los vectores con matrices (vectores columnas) y usamos la multiplicación general de matrices (filas por columnas).
Simbolizaremos por o simplemente por dicha función. Se cumple que
Tales propiedades establecen que la función LA es una transformación ineal (en la terminología del Álgebra Lineal). En los cursos de Álgebra Lineal, se prueba que una vez seleccionada una base B de un espacio vectorial, podemos representar a cada transformación lineal T por una matriz TB (llamada matriz de coordenadas de T) tal que las funciones A ↦ LA y T ↦ TB son inversas una de la otra. Las columnas de la matriz de coordenadas son las coordenadas de las imágenes de los vectores de la base.
Las Matrices Ortogonales
[editar]Definición. (Transformación Ortogonal) Sea E = Rn el espacio Euclídeo de dimensión n. Una transformación lineal T es ortogonal, ssi, preserva el producto interior, es decir, ssi, para todo x, y en E se cumple que
(TO)
Proposición 13.2.4. Cuando T es transformación lineal ortogonal se cumple lo siguiente:
- Demostración. Ejercicio
Sea B = {v1, ... , vn} un base ortonormal de E, o sea que los vectores vi tienen largo 1 y son mutuamente ortogonales. Lo que podemos simbolizar como que vi · vj = δij , donde δij es el delta de Kronecker, definido como δij = 1, cuando i = j, y 0 en caso contrario.
Cuando T es ortogonal, sigue de la proposición anterior, que las imágenes de los vectores de una base ortonormal forman un conjunto ortonormal de vectores, que se verifica que también es una base ortonormal del espacio.
Supongamos que A = [aij ] es la matriz de una transformación lineal ortogonal respecto a una base ortonormal. Llamando w1, ... ,wn a las columnas de la matriz A, tenemos que dicho conjunto de vectores es ortonormal. Esto implica que para todo 1 ≤ i, j ≤ n se cumple que wi · wj = δij (o sea igual a 1 cuando i = j y 0 en caso contrario). Con la notación introducida arriba, tenemos que
Luego,(*)
Sea B = [bη,μ] = At la transpuesta de A [7]. Entonces, bη,μ = aμ,η . Escribiendo (*) usando los bη,μ, tenemos que
(**)
Podemos interpretar el número de la derecha como el elemento en la posición (i, j) del producto BA = At A. Por las relaciones obtenidas, esos elementos son nulos si i ≠ j y son 1 si i = j. Es decir que hemos probado que
(MO )
Notemos que la relación implica que A es invertible y que su inversa es At.
Simbolizaremos por O(n) al conjunto formado por todas las matrices que satisfacen la relación (MO). Claramente, ese conjunto no es vacío ya que la (matriz) identidad I tiene esa propiedad. Recordando que el determinante de una transpuesta es igual al determinante de la matriz original,por lo que usando la relación (MO) tenemos que
1 = det(I) = det(AtA) = det(At) det(A) = det(A)2.
Luego, el determinante de una matriz ortogonal puede ser 1 o −1. La matriz identidad es una transformación ortogonal con determinante igual a 1. Sea A una matriz cuyos elementos fuera de la diagonal principal son nulos, y todos los elementos de su diagonal son 1, excepto el último que es -1.
Claramente, AAt=I, por lo que A es ortogonal y su determinante es igual a −1. Sigue de esa discusión, que la restricción de la función determinante a O(n) tiene como imagen al espacio discreto {1,−1}, concluimos que O(n) es disconexo como espacio topológico.Denotaremos por O+(n) (resp. O-(n)) al subconjunto de O(n) formado por todas las matrices ortogonales con determinante igual a 1 (resp. −1).
Proposición 13.2.5. O(n) es un subgrupo de GL(n), al que llamaremos grupo ortogonal (de dimensión n).
- Demostración. Recordemos que la matriz identidad es un elemento de O+(n). Sean A, B matrices ortogonales. Entonces,
Sea A = [Aij ] una matriz ortogonal. Entonces, usando la norma euclídea, tenemos que:
Como las columnas de la matriz A forman un conjunto ortonormal, tenemos que la norma de cada columna es igual a 1. Por lo que reagrupando la suma anterior por columnas, tendremos que
Por lo que ||A|| = √n. Lo que implica que O(n) es un conjunto acotado.Consideremos ahora, la función A ↦ At A de Mn(R) en sí mismo. Es fácil ver que esa función es continua, A ↦ (At ,A) *→ AtA. Como O(n) es la preimagen por esa función de {I}, vemos que O(n) es cerrado. Como es cerrado y acotado en Rn2, por el teorema de Heine–Borel (11.5.5), O(n) es un conjunto compacto.
Proposición 13.2.6. El grupo O(n) es un subgrupo compacto de GL(n).
Ejemplo 13.3.1 (Grupo no Acotado). El grupo SL(2) no es acotado en M2(R).
En efecto, sea Entonces, det(A) = 1 y ||A|| = √(n2 + 2). Lo que muestra que el grupo lineal especial no puede ser acotado.
Ejercicios 13.2
[editar]Referencias
[editar]
Los Grupos Topológicos
[editar]Definiciones y Propiedades Básicas
[editar]Los grupos topológicos son grupos (en el sentido de Álgebra Abstracta; ver C.1) provistos con una topología compatibles con las operaciones del grupo. Tales objetos aparecen en diversas ramas de la matemática y tienen, incluso, aplicaciones importantes en Física
Nuestro ejemplo básico es G = GL(n). Vimos, en el capítulo anterior, que tanto la multiplicación de matrices y la función "tomar inversas" en G son funciones continuas, lo que conecta la parte algebraica con la parte topológica. Dichas propiedades se abstraen en la siguiente definición.
Definición. (Grupo Topológico) Un grupo topológico G es un grupo provisto de una topología tal que la operación del grupo y la operación unaria (x ↦ x−1, tomar inversos) son funciones continuas.
Nuestro primer ejemplo es, por supuesto, GL(n). Con la topología usual tenemos, que además, son grupos topológicos: los Reales con la suma, los Reales no nulos con la multiplicación. También, Rn con la suma de vectores es un grupo topológico y, en particular, las matrices n × n con la suma.Veremos, a continuación, algunas propiedades generales de los grupos topológicos. Aunque nuestro interés es el estudio de los grupos de matrices, algunos resultados generales sobre grupos topológicos son relativamente fáciles de obtener y servirán de aplicaciones a nuestros conceptos topológicos generales. Además, la abstracción, como siempre, ilumina las relaciones entre los conceptos y puede simplificar algunas consideraciones. Por lo que, en esta sección, trabajaremos principalmente con grupos topológicos abstractos.
Lema 14.1.1. Sean G un grupo topológico, g un elemento cualquiera del grupo, y e el elemento neutro del grupo.
- Demostración parcial.
Observación 14.1. Sigue directamente del lema anterior que para cualquier subconjunto A de un grupo topológico G, los subconjuntos A, gA, Ag, gAg−1 y A−1 son homeomórficos entre si. Tenemos, como consecuencia inmediata la siguiente proposición.
Lema 14.1.2. Sea G un grupo topológico. Sean U, F y Z subconjuntos de G tales que U es abierto, F es cerrado y Z es cualquiera. Sea g un elemento cualquiera. Entonces,
- Demostración. Los resultados siguen de la observación anterior. Los detalles quedan
de ejercicios. Observar que UZ = ∪z∈Z Uz.
Observación. El producto (como subconjuntos del grupo) de dos conjuntos abiertos es abierto ¿vale lo mismo para conjuntos cerrados? Ver ejercicio 5.
Homogeneidad de los Grupos Topológicos
[editar]Decimos que un espacio topológico X es un espacio homogéneo, cuando para todo x, y en X hay un homeomorfismo f de X en sí mismo tal que f(x) = y.
Los grupos topológicos son espacios homogéneos, ya que sigue del lema anterior que dados puntos x, y del grupo, se cumple que Lg(x) = y cuando g = yx−1. Cuando un espacio es homogéneo las propiedades locales (propiedades alrededor de un punto) son las mismas para cualquiera de los puntos. Resulta natural entonces, en el caso de los grupos topológicos, estudiar las vecindades del elemento neutro, como representante de cualquiera de los puntos de un grupo topológico.
Las vecindades del elemento neutro
[editar]Denotaremos por V_e al conjunto formado por todas las vecindades del neutro e. Sigue de la continuidad de la multiplicación y de que ee = e que dada una vecindad U de e, hay vecindades V, W de e, tales que VW ⊂ U. Análogamente, como tomar inversos es continuo y e−1 = e, para cualquier U vecindad de e, hay una vecindad V tal que V −1 ⊂ U, Combinando los resultados anteriores y observando que e−1e = e, dada una vecindad U del neutro e, hay vecindades V, W de e tales que V −1W ⊂ U.
Resultará conveniente para algunas demostraciones considerar vecindades simétricas. Una vecindad V del neutro es simétrica, ssi, V −1 = V. Dada cualquier vecindad U del neutro, la vecindad V = U ∩ U−1 es simétrica y contenida en U.
Finalmente, Si U es una vecindad del neutro, hay una vecindad W tal que W2 ⊂ U. Si V es una vecindad simétrica contenida en W, tenemos que V2 ⊂ U. Registraremos los resultados anteriores en la siguiente proposición.
Proposición 14.1.3. Sea G un grupo topológico.
VW ⊂ U.
V −1W ⊂ U.
que V ⊂ U.
que V2 = V V ⊂ U.
Observación 14.3. Sea G un grupo topológico y sea A un subconjunto cualquiera no vacío de G. Entonces, para cada vecindad U del neutro, UA es un abierto que contiene a A (ea = a). Si A = {g}, Ug es una vecindad de g.
Las propiedades de Separación
[editar]Convenios. Sea G un grupo topológico. Cuando especifiquemos un tipo especial de grupo, el adjetivo usado podría referirse a la estructura algebraica o a la topológica del grupo. Usualmente, los adjetivos se referirán a la estructura topológico: cerrado, abierto, compacto, conexo, etc. La única excepción será normal, ya que siempre lo usaremos para referirnos al significado algebraico (contener todos los posibles conjugados). Grupos con la propiedad de separación normal, se indicarán como grupos topológicamente normales.
Las definiciones de las propiedades topológicas de separación se hallan en el capítulo 12.
El siguiente lema muestra que los grupos topológicos tienen la propiedad de separación T3.
Lema 14.1.4. Sea G un grupo topológico. Entonces, para cada vecindad U del neutro, hay una vecindad V del neutro tal que Cl(V ) ⊂ U.
- Demostración. Sea V una vecindad simétrica del neutro tal que V2 ⊂ U. Sea x un elemento de la clausura de V, entonces la vecindad xV de x interseca en forma no vacía a V. Esto implica que hay v1, v2 en V tales que xv1 = v2. De donde,
∈ V V^{-1} = V V \subset U.</math>
Sigue directamente del lema anterior y de la proposición 12.3.1, la siguiente proposición
Proposición 14.1.5. Sea G un grupo topológico T1, entonces G es regular, y, por lo tanto, Hausdorff.
(Para la noción de espacio regular, ver la sección 12.3.)
Sean G un grupo topológico T0 y G* el complemento de {e}. Probaremos que G* es abierto. Sea x en G*. Por estar en un espacio T0 al menos una de las alternativas siguientes es válida.
La alternativa (i) implica que x es un punto interior de G*. Supongamos válida la alternativa (ii) y sea V una vecindad simétrica contenida en W. Entonces xV es una vecindad de x. Si e estuviera en xV, habrá un v tal que e = xv. Pero esto implica que v = x−1 y como v es simétrica, v = (v−1)−1, tendríamos que x estaría en V. Luego, xV no contiene a e; lo que implica que x es interior de G*. Por lo tanto G* es un abierto. En consecuencia, {e} es cerrado. Por la homogeneidad, cada {x} = Lx(ε) es cerrado. En consecuencia, el grupo G como espacio topológico es T1. Sigue de la proposición anterior que, también, es Hausdorff. Hemos probado, así, la siguiente proposición.
Proposición 14.1.6. En un grupo topológico, se cumple que T0 ⇐⇒ T1 ⇐⇒ T2 (Hausdorff).
Corolario 14.1.7. Un grupo topológico T0 es regular.
Observación 14.4. En la literatura matemática hay gran variedad acerca de cuáles propiedades de separación debe tener un grupo topológico. Algunos autores agregan a la definición que dimos la exigencia de que sean espacios T1. Los últimos resultados muestran que podemos suponer indistintamente T0, T1 o Hausdorff. Como nuestros ejemplos de interés son los grupos de matrices, que son subconjuntos de espacios métricos, tenemos que son automáticamente Hausdorff, no necesitaremos una restricción especial.
Lema 14.1.8. Sean F y C subconjuntos disjuntos de un grupo topológico G. Si F es cerrado y C es compacto, hay una vecindad U del neutro e tal que UC ∪ CU es disjunta de F. Si G es localmente compacto, se puede seleccionar U de modo que Cl(UC ∪ CU) es compacta.
- Demostración. Para cada x en C hay una vecindad Vx del neutro tal que xVx no interseca a F. Por un resultado en la proposición 14.1.3, hay una vecindad Wx del neutro tal que (Wx)2 ⊂ Vx.
Como C es compacto, hay una colección finita de
abiertos Wi, Wi = xiWxi, i = 1,..., n que cubre a C.
Sea U1 = ∩i Wi, entonces,
Lo que prueba que CU1 no interseca a F. Análogamente, podemos hallar un U2 tal que U2C no interseca a F. Poniendo U = U1 ∩ U2 se obtiene la vecindad deseada.
Cuando G es localmente compacto, escogemos vecindades Vx que tengan clausura compacta, y procedemos como arriba.
Proposición 14.1.3. Sean A y B subconjuntos de G.
- Demostración.
Ejercicios 14.1
[editar]Los Subgrupos Topológicos
[editar]Sea G un grupo, topológico o no. Recordemos que un conjunto no vacío H determina un subgrupo de G (lo que simbolizamos por H < G), cuando HH−1 ⊂ H (ver definición de subgrupo en C.2). Veremos, a continuación, que cualquier subgrupo de un grupo topológico es un grupo topológico. Para simplicidad de la expresión, diremos “las operaciones del grupo” para referirnos conjuntamente a la operación del grupo junto con tomar inversos (operación unaria).
Proposición 14.2.1. Sea G un grupo topológico y H < G, entonces H es un grupo topológico.
- Demostración. Sean x, y elemento de H y z = xy. Sea W* una vecindad de z
en H. Entonces, hay una vecindad W de G tal que W* = W ∩ H. Luego, hay
vecindades U, V tales que x está en U, y está en V y tales que UV −1 ⊂ W. Sean
U* = U ∩ H, V * = V ∩ H. Entonces, U*(V *)−1 ⊂ W*W ∩ H; lo que implica que las operaciones en H son continuas.
Subgrupos Topológicos. Resulta de la experiencia que un subgrupo de un grupo topológico tiene propiedades "agradables" cuando como subespacio topológico es cerrado. Por lo que es costumbre llamar subgrupos topológicos a tales subgrupos. Además, resultará que los subgrupos abiertos como subconjuntos de G, serán cerrados.
Proposición 14.2.2. Un subgrupo H de un grupo topológico G que sea abierto como subconjunto, será cerrado topológicamente.
- Demostración. Si H = G el resultado es trivial. Supongamos que g es un elemento de G que no está en H. Entonces, gH (= Lg(H)) es una vecindad abierta de g que es disjunta de H, por lo que el complemento de H es abierto. Luego, H es cerrado.
Ejemplos 14.2.1.
Definición. (Subgrupo Topológico) Sea G un grupo topológico y sea H un subgrupo (algebraico) de G. Decimos que H es un subgrupo topológico de G, ssi, H es cerrado como subespacio topológico de G.
Naturalmente que si deseamos que el subgrupo trivial {e} sea un subgrupo topológico, debemos suponer que el grupo es un espacio T0 (o T1 o Hausdorff).. Para la próxima proposición, recordemos que un subgrupo H de G se dice que es normal en G, cuando todos los conjugados de sus elementos son elementos de H; es decir, cuando para todo g en G se cumple que cg(H) = gHg−1 ⊂ H.Proposición 14.2.3. Sea G un grupo topológico cualquiera. Sea H la intersección de todas las vecindades del neutro. Entonces, H es un subgrupo normal de G.
- Demostración. Sean h1, h2 elementos de H. Sea U una vecindad del neutro, por el
lema 14.1.2, hay vecindades V, W del neutro tal que VW−1 ⊂ U. Luego, como
h1 está en V y h2 está en W, se tiene que h1h2−1 está en U. Como U era arbitraria,
se tiene que h1h2−1 está en H, Lo que prueba que H es un subgrupo de G.
Como cada conjugación es un homeomorfismo y cg(e) = e se tiene para cada
vecindad U del neutro, cg(U) = gUg−1 es también vecindad del neutro. Lo que prueba que H es normal en G.
La próxima proposición muestra que la clausura de cada subgrupo es un subgrupo topológico.
Proposición 14.2.3. Sea G un grupo topológico y sea H un subgrupo G, entonces CL(H) < G, o sea es un subgrupo topológico de G. Cuando H es normal, Cl(H) también lo es. Si H es abierto, entonces Cl(H) = H.
- Demostración. Sean x, y elementos de H. Sea W una vecindad de xy−1 y sean
U, V vecindades de x y y, respectivamente, tales que UV −1 ⊂ W. Por definición
de clausura, hay u, v de H tales que u está en U y w en V, por lo que uv−1 está
en UV −1 ⊂ W. Luego, xy−1 está en H, lo que prueba que Cl(H) es un grupo.
Supongamos que H es normal en G. Sea g un elemento cualquiera de G y x
un elemento de H. Sea V una vecindad de gxg−1 y sea U una vecindad de x tal
que gUg−1 ⊂ V. Como x está en H, hay un z en H que está en U, y por lo tanto
gzg−1 está en H (normalidad) y en V. Es decir que gxg−1 está en overlineH, lo
que prueba que se trata de un subgrupo normal.
Supongamos que H es abierto. Si x está en H, entonces x está contenido en
el abierto xH (homeomórfico a H). Por lo que xH debe interceptar H, lo que
implica que x estará en HH−1 = H. luego, Cl(H) ⊂ H, por lo que se tiene que
Cl(H) = H.
Ejercicios 14.2
[editar]Los Homomorfismos Continuos
[editar]Definición. (Homomorfismo Continuo) Sean G y H grupos topológicos.
La composición de dos homomorfismos continuos (resp. abiertos, isomorfismos topológicos) es también continuo (resp. abierto, isomorfismo topológico).
Ejemplos 14.3.1.
Convenios. Sea G un grupo topológico. Cuando especifiquemos un tipo especial de grupo, el adjetivo usado especificará si se refiere a la estructura algebraica o a la topológica del grupo. Los adjetivos se referirán usualmente a la estructura topológica: cerrado, abierto, compacto, conexo, etc. La única excepción será normal, ya que siempre lo usaremos para referirnos al significado algebraico (contener todos los posibles conjugados).
Proposición 14.3.1. Sean G, H grupos topológicos y sea f : G → H un homomorfismo de grupos. f es continua (resp. abierta), ssi, es continua (resp. abierta) en el neutro.
- Demostración. Ejercicio
Ejercicios 14.3
[editar]
Grupos Cocientes, Espacios Homogéneos
[editar]Sea G un grupo y H un subgrupo de G. Se verifica que x ∼ y ↔ x−1y ∈ H es una relación de equivalencia cuyas clases de equivalencia son los conjuntos de la forma xH = {xh : h ∈ H} (clase lateral izquierda de x respecto a H). Denotamos por G/H al conjunto cociente de la relación, o sea al conjunto formado por todas las clases laterales respecto a H. El conjunto G/H no es necesariamente un grupo, a menos que H sea normal en G (o sea que H contiene a todos sus conjugados. Ver C.5).
G/H es un espacio topológico cuando se lo provee (canónicamente) con la topología más fina tal que la suprayección canónica η : G → G/H, η : x ↦ xH, sea continua. Sigue de esa definición que U* es abierto en G/H, ssi, η−1(U*) es un abierto de G. Equivalentemente, una subconjunto F* de G/H es cerrado, ssi, η-1(F*) es cerrado. La definición, también, implica que η es abierta.
Supongamos ahora que H fuera un subgrupo normal de G. Probaremos que G/H es un grupo topológico con la operación natural del grupo cociente,
xH * y H = (xy)H Sean xH, yH dos puntos de G/H y sea zH = xyH. Sea U* = η(U) una vecindad de zH en G/H. Como la multiplicación es continua en G, hay vecindades V de x y W de y, tales que VW ⊂ U. Entonces, V * = η(V ) y W* = η(W) son vecindades de xH y yH, respectivamente, y tales que V *W* ⊂ U*. Lo que prueba que la multiplicación en G/H es continua. De manera análoga se verifica que tomar inversos es continua en G/H. Es decir que G/H es un grupo topológico.
Resumimos lo anterior en la siguiente proposición.
Proposición 14.4.1. Si G un grupo topológico y H un subgrupo de H, entonces se cumple lo siguiente.
Proposición 14.4.2. Sea G un grupo topológico, H un subgrupo de G, ν : G → G/H la suprayección natural, y f : G → X continua tal que x, y en H implica que f(x) = f(y). Entonces, hay una función continua inyectiva f* : G/H → X tal que f* ◦ ν = f. Cuando f es abierta o cerrada, f* es un homeomorfismo sobre su imagen. Si, además, H es normal en G y X un grupo topológico, f es un homomorfismo.
-
Demostración. Directo de la propiedad universal de los espacios cocientes (ver la proposición 9.4.1). La parte acerca de homeomorfismo sigue de la proposición 9.4.4.
Corolario 14.4.3. Sea f : G → G′ un homomorfismo continuo de grupos topológicos. El núcleo de f, ker(f) = {x ∈ G : f(x) = e′}, e′ neutro de G′, es un subgrupo normal de G. Además, si G′ es Hausdorff, entonces ker(f) es un subgrupo topológico.
- Demostración. La parte de subgrupo normal es estándar de Álgebra Abstracta. Si G′ es Hausdorff, {e′} es cerrado y ker(f) = f−1({e′}).
Proposición 14.4.4. Sea G un grupo topológico y H un subgrupo de G. Entonces, G/H es un espacio homogéneo.- Demostración. El siguiente diagrama de funciones continuas y abiertas es conmutativo,
donde g un elemento cualquiera de G y L*gH
es la función obtenida por
paso al cociente de η ◦ Lg.

Como ν◦ Lg es una función abierta, obtenemos que LgH* es un homeomorfismo tal que Por lo que dados xH, yH, se tiene que cuando g = x-1y. Es decir que G/H es un espacio homogéneo.
Proposición 14.4.5. Sea G un grupo topológico y H un subgrupo cerrado de G. Entonces, G/H es un espacio que satisface la condición de separación .
- Demostración. Para todo g en G, η−1(η(g)) = gH = Lg(H); como H es cerrado y Lg es un homeomorfismo, tenemos que η(g) es cerrado en G/H. Como cada punto es cerrado, se tiene que G/H es un espacio T1. (ver proposición 11.3.1.)
Sean p un punto cualquiera y F un subconjunto cerrado de G/H tales que p no está en F.
Como G/H es homogéneo, sin perdida de generalidad podemos suponer que p = eH = H. Como F es cerrado hay un U* abierto tal que p ∈ U*
y F ∩ U* = ∅. Entonces, η−1(U*) es un abierto de G, por lo que hay una vecindad W de e tal que W−1W ⊂ Wη−1(U*). El conjunto η−1(F) es abierto (14.1.2).
Como η es abierta, tanto U = η(W) y V = η(nu−1(F) son abiertos en G/H.
Además, p está en U y F ⊂ V.
Probaremos que U ∩ V = ∅. Supongamos que hay un z ∈ U ∩ V, entonces hay
g1, g2 en W y g en η(F), tales que z = η(g1) = η(g1g). Luego, habrá un h ∈ H tal que g1h = g2g, lo que implica que g2−1 g1 = gh−1. Llamando k al valor común, tenemos que k = g2−1 g1 está en W−1W ⊂ η−1(U*), luego η(k) está en U*.
Por otra parte, k = gh−1 implica que η(k) está en F. Es decir que k ∈ F ∩ U* = ∅. Luego, U ∩ V = ∅.
Notemos que podemos usar la última proposición para probar que un grupo topológico T1 es regular. En efecto, la hipótesis T1 implica que {e} es cerrado y G es homeomórfico a G/{e}.
Subgrupos, Grupos Cocientes y Compacidad
[editar]Proposición 14.5.1. Sea G un grupo topológico y H un subgrupo topológico de G. Si G es compacto (resp. localmente compacto) entonces H y G/H también lo son.
- Demostración. La afirmación sobre H sigue de que H es cerrado (ver 11.3.13).
Cuando G es compacto, G/H es la imagen de un compacto por una función continua,
luego es compacto.
Supongamos ahora que G es localmente compacto. Sea a* = η(a) un elemento
de G/H. Sea U una vecindad de a en G tal que Cl(U) es compacto.
Entonces, η(U) es compacto en G/H y debe ser cerrado, ya que G/H es Hausdorff
(ver 14.1.13)). Como U ⊂ Cl(U) se tiene que η(U) ⊂ η(Cl(U)). Luego la clausura
de η(U) debe esta contenida en η(Cl(U)). Por lo que concluimos que η(U) es un conjunto
compacto. Sea U* la vecindad de a* consistente de todos los xH que tiene
intersección no vacía con U, claramente U* coincide con η(U), lo que implica que
Cl(U*) es compacta; o sea, G/H es localmente compacto.
Proposición 14.5.2. Sea G un grupo y H un subgrupo topológico compacto. Entonces, la suprayección canónica η : G → G/H es cerrada.
- Demostración. Sea F ⊂ G un subconjunto cerrado y x un elemento de G que no está en FH, por lo que η(x) no está en η(F) (si FH = G, la imagen de F es trivialmente cerrada en G/H). Como FH es cerrado (por 14.1.9), hay un abierto U de x que es disjunto de FH. Luego η(U) es un abierto disjunto de η(F), lo que implica que el complemento de η(F) es abierto. Luego, la suprayección es
cerrada.
Proposición 14.5.3. Sea G un grupo y H un subgrupo topológico. Cuando H y G/H son compactos, entonces G también lo es.
- Demostración. (Chevalley [2]) Sea η : G → G/H la suprayección canónica y sea Φ una familia de cerrados con la propiedad de intersección finita (cada subfamilia finita de miembros de Φ tiene intersección no vacía). Probaremos que hay un elemento común a todos los miembros de Φ, por lo que el resultado seguirá de la proposición 11.3.3.
Sin perdida de generalidad, podemos suponer que la intersección de una familia finita de miembros de Φ es también un miembro de Φ.
Como H es compacto, tenemos que η es cerrado, por lo que η(Φ) es una familia de cerrados en G/H con la propiedad de intersección finita; como G/H es compacto hay un elemento
comun a todos los cerrados en η(Φ), digamos x*.
Sea x en G tal que η(x) = x* y sea U en V_e (vecindades del neutro de G). Luego, Ux es una vecindad de x tal que η(Ux) interseca cada η(F) con F en Φ.
Por lo que para cada F en Φ tenemos que F ∩ UxH ≠ ∅, lo que implica que U_1F ∩ xH ≠ ∅. Sea
Probaremos que Φ1 tiene la propiedad de intersección finita. En efecto, sean F1,..., Fm cerrados de Φ1 y U1,..., Um vecindades del neutro, entoncesdonde F = ∩i Fi y U = ∩iUi. Como xH es imagen homeomórfica de H, es un conjunto compacto, y Φ1 es una familia de cerrados de xH con PIF, hay un y en xH que pertenece a todos los miembros de Φi y, en consecuencia, a todos los U-1F. Si para F fijo, consideramos lo anterior para toda vecindad U del neutro, tenemos que y pertenece a la clausura de F, pero como F es cerrado pertenece a F. Luego, y es común a todos los F’s en Φ.
Observación 14.5. Hay una proposición análoga para el caso de H y G/H localmente compactos.
Subgrupos, Grupos Cocientes y Conexidad
[editar]Proposición 14.6.1. Sea G un grupo topológico. La componente conexa Ge que contiene al elemento neutro, es un subgrupo normal cerrado de G.
- Demostración. Sea C cualquier subconjunto conexo de G, entonces para todo g en G se cumple que
gC y Cg son conexos (traslaciones izquierdas y derechas son homeomorfismos).
Luego, para g en Ge, Geg−1 debe ser conexo, lo que implica que Geg−1 ⊂ Ge,
ya que contiene a e = gg−1. Por lo que GeG−1
e ⊂ Ge, lo que implica que Ge es
un grupo, Análogamente, tenemos que para cualquier g de G, gGeg−1 debe ser
una componente de G, pero como claramente contiene al neutro, debe ser igual
a Ge. Esto dice que Ge es normal (contiene a todos su conjugados). Finalmente, componentes conexas son siempre conjuntos cerrados.
El conjunto cociente G/Ge (que tiene una estructura natural de grupo, ya que
Ge es normal) tiene tantos elementos como componentes conexas de G y su topología
es discreta.
Proposición 14.6.2. Sea G un grupo topológico y sea H un subgrupo cerrado conexo de G, si H y G/H son espacios conexos entonces G también lo es.
- Demostración. Supongamos que G no fuera conexo y sea G = U ∪ V una descomposición
de G. Como la suprayección canónica η : G → G/H es abierta se
tiene que η(U) y η(V ) son abiertos de G/H tales que G/H = η(U)∪η(V ). Como
G/H es conexo, dichos abiertos tienen intersección no vacía. Sea [g] (la coclase
de g) un elemento de dicha intersección. Entonces, gH ∩ U y gH ∩ V son abiertos
relativos en gH, cuya reunión es gH y que tiene intersección no vacía, lo que
implica que gH es disconexo, lo que es imposible ya que gH es homeomórfico a
H—es igual a Lg(H). Luego, G debe ser conexo.
Ejercicios del Capítulo 14
[editar]
Los Grupos Matriciales
[editar]Los Grupos Matriciales
[editar]Volvemos en este capítulo a los grupos de matrices, especialmente a aquellos relacionados con aspectos geométricos. Todos esos grupos son grupos topológicos. Entre ellos, los m'as interesantes serán aquellos que llamaremos \textit{grupos matriciales} (en la literatura en inglés, ``matrix groups), cuya definición daremos a continuación.
Definición. (Grupo Matricial) Llamaremos grupo matricial a cualquier grupo topológico que sea isomorfo-homeomorfo a un subgrupo cerrado de algún grupo lineal general.
Grupos de matrices cerrados como subespacios son, por lo tanto, grupos matriciales. Sigue de los trabajos previos que los grupos SL(n) y O(n) son grupos matriciales. Igualmente, SO(n) = O+(n) = SL(n) ∩ O(n), ya que es la intersección de dos cerrados. Recordemos que la proposición 14.2.2 establece que subgrupos abiertos soncerrados. Hay, sin embargo, subgrupos cerrados que no son abiertos, por ejemplo Z en R.
Sigue de los trabajos previos que los grupos SL(n) y O(n) son grupos matriciales. Igualmente, SO(n) = O+(n) = SL(n) ∩ O(n), por lo que es un subgrupo cerrado de GL(n), ya que es la intersección de dos cerrados.
Mostraremos, a continuación, otros interesantes grupos de matrices que son grupos matriciales. Para probar la cerradura topológica, recurriremos, muchas veces, al siguiente lema.Lema 15.1.1 (Lema–C). Sea A un subconjunto de GL(n) tal que todas las matrices en A tienen nulas iguales coordenadas. Entonces, A es cerrado en GL(n).
- Demostración. Sean p1, ... , pk las proyecciones correspondientes a las coordenadas que
son nulas. Entonces, el conjunto
es un conjunto cerrado ya que es una intersección de finitos cerrados. Como A = F ∩ GL(n), A
es cerrado en la topología relativa de subespacio de GL(n).
Ejemplo 15.1.1. Sea ( Matrices 2 × 2 triangulares superiores especiales)
Observado que la coordenada 2,1 es nula para todas las matrices de G, sigue del Lema C, que G es un subconjunto cerrado de SL(2) y, por lo tanto, de GL(2).
Veamos que se trata de un grupo, subgrupol de GL(2). Claramente, la identidad I está en G (x = 0). Sea . Entonces,
Luego, A(x)A(−x) = A(x + (−x)) = A(0) = I, lo que prueba que el producto de dos matrices de G y la inversa de cada matriz en G, están en G. Por lo tanto, G = SUT(2) es un subgrupo cerrado de GL(2), o sea que se trata de un grupo matricial.
Ejemplo 15.1.2. (Usamos la notación del ejemplo anterior) Sea A : R → SUT(2) tal que x ↦ A(x). Por la relación obtenida arriba, tenemos que A es un homomorfismo, que como función es claramente biyectiva, por lo que es un isomorfismo de grupos, que es claramente continuo, lo mismo que su inversa. Lo que prueba que el grupo aditivo de los reales <R,+> es isomorfo–homeomorfo a un grupo matricial; o sea que es un grupo matricial.
Ejercicios 15.1
[editar]
E l Grupo Euclídeo
[editar]Sea E un espacio euclídeo. Una isometría T de E es una transformación biyectiva de E en si mismo que preserva la distancia entre puntos, es decir que
d(T(x), T(y)) = d(x, y). Se notará que tal noción es la generalización de la noción de congruencia del plano. Denotaremos por Eucl(E) al conjunto de todas las isometrías de E. Dicho conjunt La noción de isometría apareció en la sección 4.2.2, donde se probó que las isometrías determinan un grupo de transformaciones, al que llamaremos el grupo euclídeo de E---que sea un grupo implica que la composición de dos isometrías y la inversa de una isometría son isometrías. Denotaremos por Eucl(E)$ al grupo Euclídeo de E. En una próxima sección, probaremos que es un grupo matricial, aunque tal hecho no es aparente de la definición.
Las Traslaciones
[editar]Los primeros ejemplos de isometrías son las traslaciones. Una traslación por un vector a es la transformación que denotaremos por ta y que será tal que ta(x) = a + x [8]. Notemos que la traslación por el vector nulo, t0, coincide con la identidad id.
Proposición 15.2.1 (Propiedades de las Traslaciones).
- Demostración. Tenemos que ta(tb(x)) = ta(b+x) = a+(b+x) = (a+b)+x =
ta+b(x). Luego, ta ◦ tb = ta+b.
Poniendo b = −a, obtenemos que tat−a = t0 = id. Lo que acaba la prueba.
de (a) y (b). Como
d(ta(x), ta(y)) = d(a + x, a + y) = ||(a + x) − (a + y)|| = ||x − y|| = d(x, y),
vemos que las traslaciones son isometrías.
Finalmente, sabemos que las isometrías son homeomorfismos (ver el ejemplo 8.3.4 del capítulo 8).
Denotaremos por Tras(E) al conjunto formado por todas las traslaciones de E. Sigue de las partes (a) y (b) de la proposición, que se trata de un grupo de transformaciones, que por (c) es un subgrupo del grupo de las isometrías. Más adelante, probaremos que se trata de un grupo matricial.
Las Transformaciones Ortogonales
[editar]Recordemos que las trasformaciones ortogonales son las transformaciones lineales que preservan el producto interior. Sigue de la proposición 13.3.1 que el grupo O(n) de las transformaciones ortogonales es un subgrupo de Eucl(E). Recordemos que las transformaciones ortogonales preservan el origen, por lo que, excepto por t0 = id, las traslaciones no pueden ser transformaciones ortogonales.
La estructura del Grupo Euclídeo
[editar]Sea f : E → E una isometría cualquiera y supongamos que f(0) = a. Entonces, t−af es una isometría (composición de isometrías) y (t−af)(0) = t−a(f(0)) = t−a(a) = −a + a = 0. Es decir que t−af = u, donde u es una isometría que fija el origen. Luego f = tau. Por lo que podemos afirmar lo siguiente.
Proposición 15.2.2. Cada isometría es el producto de una traslación por una isometría que preserva el origen.
Veremos, después de algunos lemas que las isometrías que fijan el origen son ortogonales.
Lema 15.2.3. Una isometría u que preserva el origen, preserva largos.
- Demostración. ||u(x)|| = ||u(x)−u(0)|| = d(u(x), u(0)) = d(x, 0) = ||x−0|| =
||x||.
Lema 15.2.4. Una isometría u que preserva largos es ortogonal.
- Demostración. Por ser isometría. se tiene que d(u(x), u(y)) = d(x, y) de donde
||u(x) − u(y)||2 = ||x − y||2.
Usando el lema del cuadrado del binomio (3.2.2), se tiene entonces que
||u(x)||2 − 2u(x) · u(y) + ||u(y)||2 = ||x||2 − 2x · y + ||y||2.
De donde, u(x) · u(y) = x · y.
Lema 15.2.5. Sea u una isometría ortogonal. Entonces, u es lineal._
- Demostración. Notemos que por ser u ortogonal, preserva origen y largos.
Sea B = {e_1, ... , e_n} una base ortonormal del espacio. Como u preserva
largos, es ortogonal. Luego, u(B) = {u(e_1), ... , u(e_n)} es un conjunto ortonormal.
Sea A la matriz cuyas columnas son u(e_i), 1 ≤ i ≤ n, por lo que la transformación
lineal L = L_A es ortogonal. Sea h = L−1 u. Observemos que h es una isometría
tal que para cada i, 1 ≤ i ≤ n, se cumple que h(e_i) = e_i. Sea x = \&sum_i x_ie_i y
supongamos que h(x) = ∑α_ie_i. Entonces,
αi = h(x) · e_i = h(x) · h(e_i) = x · e_i = x_i. Lo que implica que h(x) = x. Como x era arbitrario, esto nos dice que h = id. Luego, L−1 u = id, lo que implica que u = L, es decir que u es lineal. Notemos, además, que al ser u lineal y cumplirse que u(x) = 0 implica que x = 0 (ya que se preservan largos), por lo que tenemos que u es biyectiva (o sea un isomorfismo lineal).
Proposición 15.2.6. Cada isometría es el producto de una traslación por una transformación lineal ortogonal biyectiva.
Corolario 15.2.7. Las isometrías son siempre transformaciones biyectivas.
Ejercicios 15.2
[editar]Suponemos que E es un espacio euclídeo de dimensión n.
El Grupo Afín
[editar]El grupo afín es la generalización del grupo euclídeo, donde una isometría es el producto de una traslación por una transformación (lineal) ortogonal.
Definición. (Grupo Afín) Llamamos transformación afín a un transformación que es el producto de una traslación por una transformación lineal biyectiva cualquiera.
Sigue de los trabajos anteriores que las isometrías son transformaciones afines, cuya parte lineal es ortogonal. En particular, las traslaciones son trasformaciones afines (producto de una traslación por la identidad---que es lineal). Esto implica que habrá transformaciones afines que no preservan el origen, por lo que no pueden ser lineales.
(♠) Geométricamente las transformaciones afines son importantes porque se puede probar que una transformación biyectiva envía líneas sobre líneas si, y sólo si, es afín.
Veamos, a continuación, que las transformaciones afines determinan un grupo. Sean f = tvA y g = twB dos transformaciones afines. Entonces, para todo x en E, se tiene quePor lo que la composición de transformaciones afines es una transformación afín. Notemos, también, que
donde w = −A−1(v).
En consecuencia, las transformaciones afines determinan un grupo de transformaciones que llamamos el grupo afín y que denotamos por GA(n) o GAn(R).
Proposición 15.3.1. Las transformaciones afines determinan un grupo de transformaciones al que llamamos el grupo afín y denotamos por GA(n) o GAn(R).
Notemos que el grupo lineal está contenido en el grupo afín, ya que cualquier A en GL(n) es igual a t0A, por lo que es afín. Es decir que el grupo afín contiene al grupo lineal, y a todos sus subgrupos. .
Representación matricial de GA(n)
[editar]En esta sección, veremos que el grupo afín es un grupo matricial, construyendo un homomorfismo continuo inyectivo del grupo afín GA(n) en el grupo GL(n + 1), cuya imagen. Dicha representación tendrá, posteriormente, otras aplicaciones
Sean A una matriz n × n y v un vector cualquiera de Rn, asociaremos con el par (A, v) la matriz (n + 1) × (n + 1) que denotaremos por T(A, v) y que definiremos como
Los siguientes lemas mostrarán que las matrices de la forma T(A, v) forman un subgrupo de GL(n + 1). Lema 15.4.1. T(A; v)T(B;w) = T(AB;Aw + v)
- Demostración. Computación directa.
Comparar el resultado del lema con lo visto para el producto de dos transformaciones afines.
Lema 15.4.2. Sean A en GL(n), v en Rn. Entonces, T(A, v) es invertible, con inversa
- Demostración. Usando la relación en lema 15.4.1, se tiene que
El siguiente lema nos ayudará para nuestros propósitos.
Lema 13.4.4 (Lema–D). Sea A en GL(n), B = T(A, 0). Entonces,
Demostración.
Sean
Sigue de los lemas anteriores que , determinan subgrupos de GL(n + 1) que además, por el Lema–C, cada uno de ellos es cerrado (topológicamente).
Definamos ϕ : GA(n) → GL(n + 1) tal que ϕ(tcA) = T(A, c). Sigue del lema 14.3.2, que ϕ es un homomorfismo de grupos. Como T(A, v) = In+1, ssi, A = In y v = 0, concluimos que ϕ es inyectivo, por lo que GA(n) es isomorfo a su imagen, que es precisamente . Como ese isomorfismo y su inverso (definido en su imagen) son claramente continuos, concluimos que el grupo afín es un grupo matricial.
Se tiene también, por el Lema–D, que: , , y lo que implica respectivos isomorfismos homeomórficos. Resultados que usaremos más adelante.
I=== El Grupo Euclídeo ===
Proposición 15.3.4. Sea Tras(n) el grupo de las traslaciones de Rn. Sea tv la traslación por el vector v. Entonces. ϕ(tv) = ϕ(I, v), donde I es la matriz identidad. ϕ induce un isomorfismo algebraico entre Tras(n) y el subgrupo = {T(A, V ) : A = I} de . Lo que implica que Tras(n) es un grupo matricial.
- Demostración. Sigue de 15.3.1 que T(I, v)T(I,w) = T(I, v + w), lo que prueba
que la restricción de ϕ a Tras(n) es un isomorfismo de grupos de Tras en .
Claramente, ϕ es también un homeomorfismo, y Tras(n) es cerrado en GA.
Proposición 15.3.5. El grupo Euclídeo es un grupo matricial.
- Demostración. Basta con observar que si tv es una traslación y A es ortogonal, entonces,
ϕ(v,A) = T(A, v) = T(A, Iv) = T(I, v)T(A, 0).
Los Grupos Ortogonales y Las Esferas
[editar]En esta sección, continuaremos usando las notaciones introducidas en la sección anterior.
Supongamos que nuestro espacio es Rn+1 provisto de una base ortonormal (e1, ... , en, en+1). Probaremos que O(n) puede identificarse con las transformaciones en O(n + 1) que fijan en+1.
Sea σ una transformación ortogonal en O(n + 1) que fija a en+1. Sea [aij] la matriz de σ. Como σ(en+1) = en+1 se tiene que ai,n+1 = δi,n+1 (δ de Kronecker), o sea que el único elemento no nulo de esa columna es a n+1,n+1 que es igual a 1. Por su parte, la última fila de la matriz de σ es un vector unitario. Es decir que .
Pero, como an+1,n+1 = 1, tenemos que an+1,j = 0 cuando j ≤ n. Es decir que σ es un elemento de GO, o sea que GO está formado por todas las transformaciones ortogonales de Rn+1 que fijan en+1. Usando la identificación de O(n) con GO tenemso que podemos considerar a O(n) como un subgrupo de O(n + 1) que fija en+1.
Sea τ una transformación ortogonal en O(n + 1) que fija a en+1. Sea [aij ] la matriz de τ . Como τ (en+1) = en+1 se tiene que ai,n+1 = δi,n+1 (δ de Kronecker), o sea que el único elemento no nulo de esa columna es an+1,n+1 que es igual a 1.
Por su parte, la última fila de la matriz de τ es un vector unitario. Es decir que . Pero como an+1,n+1 = 1, tenemos que an+1,j = 0 cuando j < n. Es decir que τ es un elemento de , o sea que está formado por todas las transformaciones ortogonales que fijan en+1. Identificando con O(n) tenemos la identificación anunciada.
Sean, ahora, σ, τ dos ortogonales de O(n + 1) que fijan a en+1. Entonces,Por lo tanto, σ−1τ está en O(n). La relación entre σ y τ definida como que σ−1τ ∈ O(n) es una relación de equivalencia en O(n+1) cuyas clases de equivalencias son los subconjuntos de la forma σO(n) (todos los productos de σ por un elemento de O(n)).
Denotamos por O(n+1)/O(n) al correspondiente conjunto cociente con la topología inducida por la función η : O(n + 1) → O(n + 1)/O(n) tal que η(σ) = σO(n) (la clase de equivalencia de σ). Se tiene que η es continua y abierta (envía abiertos en abiertos).
Sea Sn la esfera unitaria de Rn+1 o sea el conjunto formado por todos los vectores de largo 1. Cada transformación ortogonal actúa en Sn---, ya que preserva largos, envía puntos de Sn en Sn. Consideremos la órbita de en+1, o sea el subconjunto de Sn formado por todos los σ(en+1) con σ en O(n+1). Dado v en Sn, siempre hay una transformación ortogonal σ tal que σ(en+1) = v; basta tomar una base ortonormal (v1, ... , vn+1 = v) y definir σ como la transformación cuya matriz tenga como columnas a los vectores de la base anterior.Definamos una función π : O(n + 1) → Sn tal π(σ) = &sigma(en+1). Notemos que por lo anterior (i) π es suprayectiva y (ii) π(σ) = π(&tau) ⇐⇒ &sigma-1τ ∈ O(n).
Cuando σ = [aij ] entonces σ(en+1)t = [a1,n+1 ... an+1,n+1]; lo que prueba que π es una función continua.
Por lo que hay una función π*: O(n + 1)/O(n) → Sn tal que el diagrama en la figura 15.1 es conmutativo.

Figura 15.1: Cociente homeomórfico a la Esfera Sn. La función π* es biyectiva y continua. Como O(n+1)/O(n) es compacto (imagen continua de compacto) y Sn es Hausdorff (subconjunto de un espacio métrico), entonces por la proposición 11.3.16, π* es un homeomorfismo. Tenemos, en consecuencia, la siguiente proposición.
Proposición 15.4.1. Sea n ≥ 1 entonces .
Grupos Ortogonales Especiales
[editar]Una revisión de los argumentos anteriores, muestra que los razonamientos anteriores son válidos para los SO(n), Por lo que se obtiene el siguiente resultado.
Proposición 15.4.2. Sea n ≥ 1 entonces SO(n + 1)/SO(n) ∼= Sn.
Proposición 15.4.3. Los grupos SO(n) son conexos, para todo n.- Demostración. (Inducción) Si n = 1, SO(1) = {1} es conexo. Supongamos probado que SO(n) es conexo. Entonces, como SO(n + 1)/ SO(n) ≅ Sn y sabemos
que Sn es conexo (ver proposición 10.6.7) y SO(n) lo es por hipótesis, SO(n+1) también es conexo, por la proposición 14.1.18.
Ejercicios del Capítulo 15
[editar]Referencias
[editar]
¿Cuál de los enunciados equivalentes usaremos? Depende de la situación. Para efectos teóricos, usualmente la versión (V) es conveniente. Cuando se trabaja con funciones numéricas u operaciones con funciones, la definición original puede resultar más conveniente.
Cuando el dominio o el codominio sea un espacio normado escribiremos las distancias en términos de normas, o de valor absoluto en el caso de los Reales. Por ejemplo, cuando E y F sean espacios normados, tendremos que f:E → F será continua en un punto p de E, ssi,
-
(VI) para todo ε > 0, hay un δ > 0 tal que para todo x se cumple que
La noción de continuidad presentada aquí es la noción local. Con esto queremos decir que depende solamente de lo que pasa en el punto y en los puntos suficientemente próximos a ese punto. En consecuencia, para los efectos de probar continuidad en un punto, podemos tomar una vecindad suficientemente "pequeña" para nuestros propósitos. En particular, cuando se trate de una r--vecindad del punto, podremos escoger el valor de r a nuestra conveniencia, siempre que se trate de un número positivo.
Tenemos también una versión global de continuidad que recordamos a continuación.
Una función f de un espacio métrico E en un espacio métrico F es continua (en el espacio) E, ssi,
es continua en cada punto de E.Sigue de la definición que para probar la continuidad de una función en (todo) el espacio E, bastará con probar la continuidad en un punto p cualquiera de E.
Ejercicios 6.2
[editar]Propiedades Generales
[editar]Nuestra primera proposición nos garantiza la existencia de funciones continuas, aunque sean relativamente triviales.
Proposición 6.3.1. Las funciones constantes son continuas.
- Demostración. Sea f:E → F una función constante entre espacios métricos. Sea p un punto de E y sea V una vecindad de f(p). Entonces para cualquier vecindad U de p. tenemos que
Luego, f es continua en p. Como p era arbitrario, la función es continua en E.
Proposición 6.3.2. La función identidad 1E: E → E es continua.
- Demostración. Sea p un punto cualquiera de E y sea V una vecindad de 1E(p) (= p). Entonces U=V es una vecindad de p tal que f(U) = V.
Notemos que la identidad en los Reales es la función que en cursos de Cálculo se presenta como f(x) = x, para todo x real.
La siguiente proposición tiene tanto importancia teórica como práctica, como veremos en los ejemplos posteriores.
Proposición 6.3.3 (Composición de Continuas) Sean f:E → F y g: F → G funciones.
- Demostración. \quad
Proyecciones. Recordemos que llamamos i--ésima proyección de Rn en R a la función pri que asigna a cada punto (xk) de Rn, su i--ésima coordenada. Como, para todo x=(xk) se cumple que |xi| ≤ ||x||, tenemos que para que |xi-pi| sea menor que ε, es suficiente con tomar ||x-p||< δ = ε. Por lo que tenemos la siguiente proposición.
Proposición 6.3.4. Las proyecciones de Rn en R son funciones continuas.
Observaciones y Ejemplos
[editar]Antes de ir a otros ejemplos, revisaremos lo que implica la continuidad y los procedimientos generales para probar continuidad.
El siguiente resultado será de gran ayuda para probar continuidad local.
Lema 6.3.5 (Lema H) Sea f: E → F continua en un punto p de E. Si hay un número positivo M y una vecindad U de p tal que para todo x en esa vecindad se cumple que
Entonces, f es continua en p.
- Demostración. (Consideración intuitiva.) Sigue de la desigualdad en la hipótesis, que dado ε > 0, d(f(x) , f(p)) será menor que tal ε > 0, cuando Md(x,p) lo sea; es decir cuando d(x,p) < ε/M. Esta última relación nos sirve, por lo tanto, para estimar el valor adecuado de δ.
(Demostración.) Sea ε>0 dado. Tomando δ = ε/M, se tiene que
Lo que prueba la continuidad deseada.
Ejemplo 6.3.1. Usar el lema H para probar que 1E:E → E es continua.
Sea un punto cualquiera de E. Como
d(f(x), f(p)) = d(x, p) = 1 * d(x, p), aplicando el lema H con M =1, se obtiene el resultado.
Ejemplo 6.3.2. Probar que f:R → \R::t ↦ 3t + 5 es una función continua en cualquier punto a de R.
Solución. Notemos que |f(t) - f(a)| = 3|t - a|, por lo que el resultado sigue del lema H.
Ejemplo 6.3.3. La función radical de R0+ en R, x ↦ √{x} es continua en todo su dominio.
Solución. Sea p ≠ 0. Se tiene que
(1)
En una p/2--vecindad de p se cumple que -p/2 < x - p < p/2 de donde x > p/2 y, por lo tanto, √{x} > √{p/2} > √{p}/{2}. Por lo que, √{x} + √{p} > (3/2)√{2}. Luego, .Usando la última desigualdad en (1), tenemos que
Por el Lema H, tenemos la continuidad en p.La continuidad en 0, sigue de que √(x) < ε ←→ x < ε2, lo que muestra que tomando δ = ε2, se cumplirá la condición para continuidad.
Observación 6.1. Observemos, en el último ejemplo, que a pesar de la continuidad en 0, no hay número M>0 tal que para todo x>0 en una vecindad de 0 se cumpla que f(x) < Mx.
En efecto, supongamos que tal M existiera, entonces se tendría que
Como para cualquier vecindad U de 0, podemos hallar un número natural N tal que n > N, lo que implica que 1/n está en la vecindad U, lo que a su vez implica que n2 > n, concluimos que 1/n2 está en la vecindad U. Como 1/√{1/n2} = n y los naturales no tienen cota superior, concluimos que es imposible la existencia de tal M.
Es decir que el criterio dado en el lema H es suficiente, pero no necesario; en otras palabras, el recíproco del lema H no es válido.
Ejemplo 6.3.4. La función valor absoluto, x ↦ |x| es continua.
Basta con recordar que y aplicar el lema H.
(☩) En los cursos de Cálculo, esta función se usa para ilustrar que la afirmación derivable implica continuidad no tiene converso, ya que la función valor absoluto es continua en 0, pero no derivable en 0. Notemos que la gráfica de esa función tiene una punta, Nuestra experiencia con gráficas de funciones nos puede dar la impresión que las gráficas de funciones son siempre curvas suaves. Sin embargo, se puede ver que la "suavidad" de una gráfica está asociada más bien con la derivabilidad que con la continuidad. Por ejemplo, las gráficas producidas por un electrocardiograma o un sismográfo son generalmente continuas.
A continuación, examinaremos una situación de discontinuidad.
Ejemplo 6.3.5. Repetimos el ejemplo 4.3.3. Sea f:R → R tal que f(x) = 1, cuando x > 0, y f(x) = 0, cuando x ≤ 0. Veremos que f no puede ser continua en 0. Cualquier bola abierta con centro en 0 y radio δ contiene números positivos, si x0 es uno de ellos, entonces f(x0) - f(0) = 1 - 0 = 1. Por lo que no importa que δ escojamos la distancia entre esas imágenes será igual a 1, por lo que no puede hacerse tan pequeña como queramos (por ejemplo 1/2).
En el último ejemplo, la gráfica de la función tiene un "salto" en 0. El salto mide 1. Cualquier salto impide, por las mismas razones del ejemplo, la continuidad de la función. Por eso, tienen algo de razón quienes dicen que una función continua es aquella cuya gráfica se puede dibujar sin tener que levantar el lápiz del papel
¿Cuántos saltos puede admitir una función?
¿Cuántas discontinuidades puede admitir una función?
El siguiente ejemplo muestra que una función que es discontinua en cada uno de los puntos de su dominio.Ejemplo 6.3.6 (La función de Dirichlet) Sea f : [0,1] → R tal que f(x) = 0 cuando x es racional, y f(x) = 1 cuando x es irracional.
Como en cualquier vecindad de un irracional hay un racional, se tiene que la función no puede ser continua en un irracional i, ya que una r--vecindad del número 1 con r<1 no contendrá imágenes de racionales. Como también se cumple que en la vecindad de cada racional, hay un irracional, se tiene que no puede ser continua en los racionales.
¿Cómo es la gráfica de esta función?
Otros Ejemplos de Funciones Continuas
[editar]Con el fin de tener variados ejemplos de continuidad, usaremos un teorema que enunciaremos a continuación, pero que probaremos en la sección 6.5.4.
Teorema de las Operaciones. Sean f, g : E → R funciones continuas en un punto p (resp. en todo E). Entonces se cumple que la suma, la resta, el producto y el cociente de f y g son continuas en p (resp. en todo E).
Usaremos el resultado del teorema para poder mostrar una variedad de ejemplos.
Ejemplo 6.3.7. Las funciones potencias pn : t ↦ tn de R en R son continuas.
El caso n = 1 está contenido en la proposición 6.3.2, donde probamos que la identidad era continua.
El caso n = 2, resulta del producto de la identidad consigo misma; esto es p2 = p1p1. El caso general, pn+1, es el producto de p1 con pn; por lo que el resultado sigue por inducción.
Ejemplo 6.3.8. Suponiendo que sen, cos y exp son funciones continuas, se concluye la continuidad de las siguientes funciones.
Ejercicios 6.3
[editar]La Continuidad Global
[editar]La continuidad global de una función, o sea cuando la función es continua en cada punto de su dominio, es muy importante en las consideraciones topogeométricas, por lo que estudiaremos algunas de sus caracterizaciones. La siguiente proposición muestra criterios necesarios y suficientes para la continuidad global, en términos de abiertos, sin referencia directa a puntos.
Proposición 6.4.1 Sea f: E → F una función. Son equivalentes:
-
(i) f es continua en E.
(ii) Para todo abierto V de F, su preimagen (f-1(V)) es abierto en E.
(iii) Para todo cerrado W de F, su preimagen (f-1(W)) es cerrado en E.
-
Demostración. Recordemos que f-1(V) = \{x ∈ E: f(x) ∈ V\}.
(i) implica (ii). Sea V un abierto de F. Si f-1(V) es vacío, es abierto. Supongamos que f-1(V) no es vacío y sea p un punto de ese conjunto. Entonces, f(p) está en V. Aplicando la alternativa (V) de las definiciones locales de continuidad, tenemos que hay una vecindad W de p, tal que f(W) ⊂ V. Luego, hay un abierto U vecindad de p y contenido en W. Entonces, U ⊂ W ⊂ f-1(f(W)) ⊂ f-1(V). Lo que muestra que f-1(V) es abierto.
(ii) implica (i). Sea p un punto cualquiera de E. Sea V una vecindad abierta de f(p). Entonces, U = f-1(V) es una vecindad abierta de p tal que f(U) ⊂ V, lo que prueba la continuidad en p. Como p era arbitrario, concluimos la continuidad en todo E.
(ii) equivalente con (iii) (El resultado sigue de la identidad entre conjuntos que establece que la preimagen del complemento de un conjunto es igual al complemento de la preimagen del conjunto. Es decir que f-1(Ac) = (f-1(A))c. Supongamos que las preimágenes de abiertos son abiertos. Entonces, W cerrado en F implica que Wc es abierto en F, lo que implica que (f-1(W))c = f-1(Wc) es abierto (por la hipótesis), de donde f-1(W) es cerrado. Supongamos, ahora, que las preimágenes de cerrados son cerrados. Entonces, V abierto en F implica que Vc es cerrado en F; de donde por la hipótesis. f-1(Vc) = (f-1(V))c es cerrado, lo que implica que que f-1(V) es abierto en E.
Proposición 6.4.2. Sean E un espacio métrico y X un subespacio de E. La inclusión canónica i : X → E es continua.
-
Demostración. Sea V un abierto de E, entonces i-1(V) = V ∩ A, que es un abierto de X; lo que prueba la proposición.
Corolario 6.4.3. Sea f : E → F continua y sea X un subespacio no vacío de E. Entonces, la restricción de f a X, es continua.
- Demostración. , donde i es la inclusión de X en E.
Ejemplo6.4.1. Probar que el semiplano H= {(x,y) ∈ R2: y > 0\} es abierto (ver el ejemplo 5.2.1.).Solución. Consideremos la segunda proyección de R2 en R, pr2(x,y) = y. Como H es la preimagen por pr2 del intervalo abierto ]0, +∞[ y dicha proyección es una función continua (6.3.4.), el resultado sigue de la proposición anterior.
Ejemplo 6.4.2. Probar que la franja F= { (x,y) ∈ R2: 2 ≤ x ≤ 5\} es un conjunto cerrado.
Solución. F= pr2-1([2,5]), preimagen de un cerrado.
Ejemplo 6.4.3. Probar que la celda C= ]a,b[ x ]c,d[ de R2 es un conjunto abierto.
Solución. Ver la solución dada en el ejemplo 5.2.7. Con las herramientas actuales, basta con ver que C es la intersección de la preimagen por pr1 de ]a,b[ con la preimagen por pr2 de ]c,d[.
Proposición 6.4.4. Sea f: E → R continua. Entonces, U= {x ∈ E: f(x) > 0\} y V = \j{x ∈ E : f(x) < 0\} son abiertos, mientras que W = \j{x ∈ E: f(x) =0\} es cerrado en E.
-
Demostración. Basta con observar que U = f-1(]0,+∞[), V = f-1(]-∞,0[) y W = f-1({0}).
El lema siguiente se usará más adelante y tiene algunas notables aplicaciones.
Lema 6.4.5 (Lema K)(Estabilidad del Signo) Sea f:E → R una función continua en un punto p. Si f(p) ≠ 0 hay una vecindad abierta de p tal que para todo x en la vecindad se cumple que f(x) tiene el mismo signo que f(p).
-
Demostración. Supongamos que f(p) > 0. Entonces, p pertenece al abierto f-1(R+), preimagen de los Reales positivos. Luego, hay una vecindad de p cuyas imágenes son todas positivas. Análogamente cuando f(p) < 0.
Ejercicios 6.4
[editar]Las Funciones Numéricas
[editar]Llamamos funciones numéricas a las funciones cuyo dominio y codominio son subconjuntos de algún Rm y Rn respectivamente.
Sea f:A ⊂ Rm → Rn. Cuando m = 1, decimos que se trata de una función de una variable real; cuando m > 1, que se trata de una función de varias variables reales. Si n = 1, decimos que es una función real o con valores reales; y, en caso de que n > 1, decimos que es una función vectorial o con valores vectoriales.
Examinaremos la continuidad de los diferentes tipos de funciones.
Funciones Reales de una Variable Real
[editar]Sumar una constante o multiplicar por una constante una función continua, produce una función continua.
Proposición 6.5.1. Sea a un número real y sean f,g:R → R tales que f(t) = t + a y g(t) = at, las funciones f y g son continuas.
-
Demostración. Sea p un real cualquiera.
Notemos que |f(t) - f(p)| = |(t+a)- (p+a)| = |t-p|. Luego, podemos hacer |f(t)-f(p)| menor que un cierto ε, tomando |t-p| menor que ε. Como p es arbitrario, f es continua en R.
Por su parte, si a = 0, la función g es constante y, por lo tanto, continua. Supongamos que a ≠ 0.
Tenemos que |g(t) - g(p)| = |at - ap | = |a(t-p)| = |a|\, |t-p|. Luego, podemos hacer |f(t)-f(p)| menor que un cierto ε, tomando |t-p| menor que ε/|a|. Como p es arbitrario, g es continua en R.
En ambos casos, podríamos, alternativamente, haber invocado el lema H para probar la continuidad.
Corolario 6.5.2. La función t ↦ -t es continua.
Notemos, para futuras consideraciones, que tanto f como g de la proposición, para a ≠ 0 son biyectivas. Sus inversas tienen la misma forma, por lo que son también continuas.
Ejemplo 6.5.1 Para todo a, b reales, la función f:R → R tal que f(t) = at +b es continua.
Notemos que t ↦ at +b es la composición de t ↦ t+b con t ↦ at; lo que muestra lo afirmado.
Tomar recíprocos también produce una función continua.
Proposición 6.5.3. La función g: R \ {0} → R tal que g(t) = 1/t, es continua.
- Demostración. Como
, tenemos que
Suponiendo |t-p|<\delta, tenemos que
(*)
Necesitamos una cota superior para los valores 1/|t|, o equivalentemente una cota inferior para los valores de |t|. Supongamos que |t| > K>0, entonces 1/|t| < 1/K. Tomando una |p|/2--vecindad de p, vemos que para cualquier t en esa vecindad se cumple que |t| > |p|/2, por lo que una cota inferior es K=|p|/2. Por lo que sigue de (*) que(**)
Lo que implica que si queremos |g(t)- g(p)| < ε, debemos escoger δ tal que
Luego, tomando obtendremos que |g(t) - g(p)|< ε. Por lo que g es continua en p y, por lo tanto, continua en todo su dominio.
Funciones Reales de Varias Variables
[editar]Notemos que una función real de varias variables es una función de un subconjunto de Rn en R. Tal función es continua, ssi, para todo ε > 0 es posible hallar un δ tal que
Continuidad de las Operaciones con Números Reales.
[editar]Las operaciones algebraicas en los Reales son ejemplos básicos importantes de funciones reales de "varias variables".
Recordemos que las operaciones de suma y multiplicación son funciones de R2 en R.
Proposición 6.5.4. La función s: R x R → R::(x,y) ↦ x +y (suma), y la función m: R x R → R::(x,y) ↦ x*y (multiplicación) son continuas.
- Demostración.
(Continuidad de la Suma) Sea (p,q) un punto cualquiera de R2. Dada una ε--vecindad V de p+q, probaremos que hay una vecindad U de (p,q) tal que s(U) ⊂ V
Observemos que
(*)
Sea ε >0 dado. Sea r = ε/2 . Notemos que si podemos escoger x, y tales que |x-p| < r y |y-q| <r, entonces (*) implica que
lo que probaría la continuidad en (p,q).Seleccionemos U = ]p-r,p+r[ \times ]q -r, r+r[. Sabemos por trabajos previos que U es abierto y por construcción es una vecindad de (p,q). Luego, para todo (x,y) en U se cumple que |x-p|< r y |y-q|<r, lo que prueba el resultado.
(Continuidad de la multiplicación) Necesitaremos la siguiente identidad, cuya validez se prueba por computación directa.
(**)
(Idea: buscar acotamiento para cada uno de los sumandos en términos de cotas fijas para |x-p| y |y-q|, de modo que la suma en (**) sea menor que ε. )Sea δ un número posistivo tal que |x -p| < δ y |y-q| < δ. Tenemos, entonces que
Funciones con Valores Vectoriales
[editar]Examinaremos, inicialmente, el caso donde el codominio es un subconjunto de R2. Sea X un conjunto cualquiera y sean f1, f2 funciones de X en R. Usando ese par de funciones, podemos definir una función f:X → R2 tal que
En forma recíproca, supongamos dada una función f:X → R2 y consideremos las composiciones de f con las i--ésima proyecciones (i=1,2), lo que nos producirá funciones de X en R. Llamando fi a la composición de pri con f, tenemos que
Los desarrollos anteriores muestran que hay una correspondencia biyectiva entre F(X, R2) y el producto cartesiano de dos copias de F(X,R), que asigna a cada función de X en R2 sus componentes f1,f2. Usando esa correspondencia, identificaremos a ambos conjuntos, es decir que consideraremos f=(f1, f2).
Es fácil ver como el desarrollo anterior se generaliza a Rn. Cada función f:E → Rn se identifica con la n--upla de funciones (f1, ... , fn), donde fi = pri ° f. Llamamos componente de f a cada fi.Proposición 6.5.5. Sea E un espacio métrico y sea f:E → Rn. f es continua en un punto p de E, ssi, sus componentes lo son.
- Demostración. Sea f=(f1, ... ,fn) .
(⇒) Como fi = pri º f, i=1, ... ,n, el resultado sigue del teorema de composición de funciones continuas. Ver 6.5.5.
(⇐) Queremos probar que podemos lograr que
||f(x) = f(p)|| = ||(fi(x))- (fi(p))|| sea tan pequeño como queramos, tomando d(x,p) suficientemente pequeño.
Como fi, i=1,... , n es continua, para todo εi hay un δi tal que
(*)
Tomando ε1= ... = εn = η y δ = min{δ1, ... , δn}, la relación (*) se mantiene válida para δ y η. Luego, si d(x,p) < δ, tenemos que
Por lo tanto, dado ε > 0 cualquiera, tomando η = ε/√{n} obtendremos un δ que sirve para nuestros propósitos. Es decir que la función f es continua.
Espacios de Funciones Continuas
[editar]En el capítulo 4, introdujimos al conjunto F(X,R) (funciones de X en R) y a su subconjunto B(X,R), funciones acotadas de X en R.
En esta sección, estudiaremos la estructura algebraica de C(E,R), el conjunto de las funciones continuas de E en R, donde E es un espacio métrico. Recordemos que hay una suma de funciones, una multiplicación por escalar y un multiplicación de funciones definidas en C(E,R) por ser subconjunto de F(E,R). Recordemos sus definiciones,
Nuestro interés será examinar la relación entre la continuidad de las funciones y las operaciones indicadas. El resultado es el teorema de las operaciones anunciados en la sección 6.3.1.Teorema 6.5.6 (Teorema de las Operaciones) Sea E un espacio métrico. Si f y g son continuas de E en R, se tiene lo siguiente.
-
Demostración.
Corolario 6.5.7. Los resultados del teorema son válidos, reemplazando continuidad por continuidad en un punto.
- Demostración.
Mirar a las demostraciones de la proposición.
Aplicaciones del Teorema
[editar]Funciones Polinómicas. Las funciones polinómicas de R en R son funciones de la forma
Veremos que tales funciones son continuas. En primer lugar, por la proposición 6.3.2 la función t ↦ t es continua. El producto de esa función consigo mismo produce la función continua t ↦ t2. Usando inducción, se verifica que la función potencia enésima, pn(t)=tn, n entero positivo, es continua. Multiplicando esa función por constante, produce una función continua. Finalmente la suma de tales "términos" produce una función continua. Lo que muestra que las funciones polinómicas son continuas.
Las Funciones Racionales. Una función racional es el cociente de dos polinómicas. Sigue del teorema de las operaciones que el cociente de continuas es continua en todo su dominio.
Notemos que a pesar de lo que, a veces, se dice de la función f(x) = 1/x, esta función es continua en todo su dominio---que consiste de los reales no nulos.
Sea f: A ⊂ R → R una función. Podemos, a partir de f, formar una función g que sea un polinomio en f, es decir que
Cuando f sea continua, razonando como arriba (que es el caso donde f(t)=t) se ve que cuando f sea continua, también lo será g.Polinomios de Varias Variables
Sabemos (ver 6.3.4.) que las proyecciones son funciones continuas por lo que monomios de la forma
donde xi es la i--ésima proyección de Rn en R, son funciones continuas ya que son productos de funciones continuas. Como las funciones polinómicas de varias variables son sumas de tales monomios, tenemos que son continuas.Ejemplos 6.5.2. Sean x, y, z las coordenadas de R3. Entonces, las siguientes funciones son continuas.
(♠) También son continuas las siguientes funciones (suponemos que la función seno y la exponencial son continuas).
Abiertos y Cerrados de Rn
[editar]Un ejercicio del capítulo 5 pedía probar que el conjunto {(x,y) ∈ R2 : y < x2} era abierto en R2. Tales ejercicios y otros similares tienen una respuesta fácil mediante una visualización; sin embargo una demostración formal usando directamente las definiciones puede resultar engorrosa. Veremos, a continuación, que con las herramientas ahora disponibles, la resolución de esos problemas es casi trivial. Usaremos como herramienta teórica la proposición 6.4.4.
Ejemplo 6.5.3. Sea S = {(x,y) : y < x2}. Probar que se trata de un conjunto abierto.
Sea f:R2 → R tal que f(x,y)= y-x2. Observemos que la función es continua por ser un polinomio de sus coordenadas. Luego, por la proposición citada, como y < x2 es equivalente a y-x2<0, o sea f(x,y) < 0, tenemos por la proposición citada que S es un conjunto abierto. Considerando a la función continua f: x ↦ x2 vemos que (x,y)∈ H ⇐⇒ y < f(x). Sigue, entonces, de la proposición anterior, que H es abierto.
Ejemplo 6.5.4. Consideremos el conjunto H={(x,y) : xy = 1}. Probar que es cerrado.
La función f, f(x,y) = xy, es una función continua de R2 en R. H es la preimagen por f del conjunto cerrado {1}. Luego H es cerrado.
Las Gráficas de Funciones
[editar]Sea f : A ⊂ Rn → R una función. Llamamos gráfica de f al subconjunto de Rn+1 denotado por Graf(f) y definido por
Se tiene entonces que g: (x1, ... , xn,xn+1) = xn+1 - f(x1, ... , xn) es una función continua cuando f lo es. Como la gráfica de f es la preimagen por g de {0}, concluimos que es un conjunto cerrado.
Ejercicios 6.6
[editar]Los Límites
[editar]Esta sección consistirá de una breve presentación del concepto de límite (de los valores) de una función. Dicho concepto es muy importante en Cálculo y Análisis en general, pero no tanto en las consideraciones topogeométricas. En consecuencia, nuestra presentación se limitará a la definición y algunas proposiciones básicas. El resto está en los ejercicios.
En el desarrollo del Cálculo nos encontramos con funciones definidas en la vecindad de un punto, pero no necesariamente en el punto; típicamente, al computar derivadas. En tales situaciones, nos interesará saber si habrá un valor que podamos asignar a la función en ese punto, de manera que al extender el dominio de la función a ese punto resulte que la función sea continua en dicho punto.
Ejemplo 6.6.1. Sea . El dominio natural de la función anterior excluye solamente al 2, por lo que podemos afirmar que esa función está definida en cualquier punto de una vecindad de 2, excepto en el 2. Si simplemente intentamos evaluar en 2, nos encontraremos con 0/0 lo que es algo indeterminado. La pregunta natural es: ¿habrá un valor que podamos asignar en 2, de modo que la función obtenida extendiendo el dominio a 2, sea continua en 2?
Observando de que
para todo x ≠ 2, y que g(x) = x + 2 es una función continua en 2 con g(2) = 4, concluimos que el valor que se debe asignar a f en 2 para hacerla continua allí es 4.
En tal situación, decimos que 4 es el limite de los valores de f, para valores de x que se aproximan o tienden a 2.
El ejemplo se generaliza de la siguiente manera.
Definición. (Límite) Sean E y F espacios métricos, A un subconjunto de E, p un punto de acumulación de A. Sea f función cuyo codominio es un subconjunto de F y que está definida en A con la posible excepción de p. Sea L un punto de F.
Decimos que L es un límite de los valores de f cuando x tiende a p, ssi, hay una función g definida en una vecindad U de p, que es continua en p, y tal que
(♣) Intuitivamente, L es un valor que hace a f continua en p.
Primeramente, observemos que cuando haya un límite, tal valor será único. Por definición, si L y L' son limites de los valores de f cuando x tiende a p, se tendría que hay funciones continuas g y g' que coinciden en una vecindad de p con la excepción, a lo más, de p, donde se cumple que g(p) = L y g'(p) = L'. Sea ε = |L- L'| y supongamos que es positivo, o sea que L ≠ L'. Por las continuidades de g y g' en p concluimos que hay una vecindad U de p tal que para todo x en U se cumple que |g(x)-L| < ε/2 y |g'(x)-L| < ε/2. Luego, para todo x ≠ p se cumple que g(x) = g'(x) =f(x) y que
Como lo anterior, implica que ε < ε, hemos llegado a un absurdo. Por lo tanto, es imposible que ε sea positivo. Debe, por lo tanto, ser igual a cero, o lo que es lo mismo que L= L'.
Notación. Cuando exista el límite de los valores de f cuando x tiende a p, x en A, lo simbolizaremos por
Cuando el conjunto A quede claro del contexto, simplemente escribiremos
Cuando ese límite sea, digamos L, escribiremos también que
lo que leeremos: "cuando x tiende a p, f(x) tiende a L".Sigue de la definición anterior y de la definición de continuidad que afirmar que limx → p f(x) = L es equivalente a afirmar que para todo ε > 0 hay un δ>0 tal que
Observemos que el enunciado simbólico es casi idéntico a aquel que define la continuidad en p, con la excepción de que pedimos que 0 < d(x,p), es decir que estamos excluyendo de consideración al punto p. Notemos que si la función f es continua en p, el límite en p es f(p)
Las propiedades de límites se reducen, en consecuencia, a propiedades de funciones continuas.
Ejercicios 6.7
[editar]
Las Sucesiones y la Completitud
[editar]Introducción
[editar]Cada número real α tiene asociada una expansión decimal
α = a0.a1a2a3... Las truncaciones sucesivas producen una sucesión de números racionales
a0, a0.a1, a0.a1a2, a0.a1a2a3, ... cuyos valores se aproximan más y más a α. Cuando α es un número irracional, dichas aproximaciones constituyen la manera práctica de computar con esos números. Las sucesiones (y sus asociadas, las series) aparecen como maneras de evaluar números y funciones, aunque sea de forma aproximada. Recordemos, también, que en los cursos de Cálculo, se ve que podemos expresar ciertas funciones como series de potencias. Por ejemplo
Dicha serie sirve para evaluar la función seno con tanta exactitud como queramos, ya que para series de potencias podemos computar estimados acerca del error en la aproximación. Al valor computacional de las sucesiones, se agrega su valor teórico. Probaremos que cada punto de acumulación de un conjunto es el límite de una sucesión de puntos del conjunto. Suponemos relativa familiaridad con las sucesiones y series de un primer curso universitario de Cálculo, por lo que nos preocuparemos más de los aspectors teóricos que de los computacional.
Definiciones y Propiedades Básicas
[editar]Una sucesión s en un conjunto X es una familia de elementos de X cuyo conjunto de índices son los Naturales. Es decir que se trata de una función de los Naturales en X, donde lo más interesante son los valores que toma la función. Cuando s es una sucesión, como es usual con las familias, simbolizamos por sn a s(n)—término énésimo. Podemos simbolizar a una sucesión s de diversas maneras, tales como
s = (sn) = (s0, s1, . . . , sn, ... ). La importancia de que el conjunto de índices sean los Naturales reside en que podemos transportar el orden de los números naturales a los correspondientes términos de la sucesión. Así que podemos hablar del segundo término de la sucesión, que está antes que el quinto, etc. En la práctica, podemos tener sucesiones s cuyo primer término no es s0, sino que es sn0 donde n0 > 0. Por ejemplo, an = 1/n, n > 0. Sin embargo, para efectos teóricos, siempre podremos suponer, por una simple traslación de los índices, que el primer términio corresponde al 0. Por ejemplo, respecto al ejemplo mencionado, sn = 1/(n + 1), n ≥ 0.
Sean E un espacio métrico, A un subconjunto de E y p un punto de acumulación de A. Suponiendo que p no está en A, mostraremos que hay una sucesión de puntos de A que se acercan más y más a p. Más adelante, diremos que esa sucesión converge a p. El argumento que usaremos es igual al usado en la demostración de la proposición 5.3.2.
Supongamos que p no está en A, pero que está en su clausura, o sea que es un punto de acumulación de A. Entonces, por definición de punto de acumulación, cada vecindad de p contiene al menos un punto de A diferente de p. Usaremos bolas abiertas como vecindades. Sea r1 = 1, entonces la bola B(p; r1) contiene un punto, digamos p1 de A que no es igual a p. Como p1 ≠ p, tenemos que 0 < r2 = d(p1, p) < r1. Considerando ahora la bola B(p; r2), vemos que hay un p2 en A, diferente de p, y también de p1, tal que d(p2, p) < d(p1, p). Supongamos generada de la manera anterior la sucesión finita, p1, p2, . . . , pn de puntos de A diferentes de p y tales que
d(p1, p) > d(p2, p) > . . . > d(p, pn)>0.
Generamos un punto pn+1 de igual forma que los anteriores, es decir que pn+1 es un punto de la bola B(p; d(pn, p) diferente de p. Obtenemos así una sucesión cuyos términos pn, a medida de que n crece ,se aproximan cada vez más a p. Tal situación es un ejemplo de convergencia de una sucesión a un límite, nociones que definiremos a continuación. Notemos que cuando m ≥ n, B(p; rm) ⊂ B(p ; rn), lo que implica que pm está en B(p; rn). La situación anterior se abstrae en la siguiente definición.Definición. (Convergencia, Límite) Sea E un espacio métrico, p un punto de E. Decimos que una sucesión (sn) converge a p, ssi, para todo vecindad V de p hay un natural n0 tal que
n ≥ n0 ⇒ sn ∈ V. Cuando (sn) converge a p, decimos que la sucesión es convergente y que p es un límite de la sucesión. Una sucesión que no converge es una sucesión divergente.
En términos métricos, tenemos que
(Versión métrica del límite) Una sucesión (sn) converge a p, ssi, para todo ε > 0 hay un n0 tal quen ≥ n0 ⇒ d(xn, p) < ε. Otra manera de expresar la convergencia.
(Versión cardinal del límite.) Una sucesión (sn) tiene un límite p, ssi, para cada vecindad V de p, hay a lo más una cantidad finita de términos de la sucesión fuera de V .
Observación 7.1. Sea P(n) una propiedad de los términos de una sucesión (xn). Cuando la propiedad P se cumpla para todos los n a partir de un cierto n0, diremos que la propiedad se cumple para casi todo n, o que la sucesión finalmente alcanza esa propiedad.
Por ejemplo, la última versión de límite se puede expresar como, la sucesión (xn) converge a p, ssi, para cada vecindad de p, casi todos los términos de la sucesión están en V.
Proposición 7.2.1 (Unicidad de Límites). Sea E un espacio métrico. Cuando una sucesión converge, su límite es único.
- Demostración. Supongamos que p y q fueran límites diferentes de la sucesión
(xn). Sean U una vecindad de p y V una vecindad de q tales que U ∩ V = ∅ (propiedad de Hausdorff). Por definición de convergencia aplicada a p hay un n1 tal que n ≥ n1 implica que xn está en U. Análogamente, hay un n2 tal que n ≥ n2
implica que xn está en V . Sea n0 = máx{n1, n2}. Entonces,
n ≥ n0 ≥ n1, n2 ⇒ xn ∈ U y xn ∈ V ⇒ xn ∈ U ∩ V.
Como U y V son disjuntas, lo anterior es imposible. Luego, no puede haber límites
diferentes.
Notación Cuando una sucesión (sn) converge a un punto p, podemos, por lo tanto, decir que p es el límite de la sucesión. Representaremos esta situación, simbólicamente, por una cualquiera de las expresiones siguientes.
Ejemplo 7.2.1. La sucesión an = 1/n en R es convergente a 0.
Resolución. La prueba sigue de la propiedad arquimediana de los Reales (ver la sección 2.4.3). En efecto, dado un ε > 0, hay un n tal que 1/n < ε (2.4.6). Luego,
lo que prueba que límn (1/n) = 0.
Ejemplo 7.2.2. Sea s la sucesión de números reales tal que sn = (−1)n. Es decir que sn = 1, cuando n es par, y sn = -1, en caso contrario.
Notemos que para cualquier bola abierta con centro 1 (resp. −1) y radio 1/2, hay infinitos términos que quedan fuera de esa vecindad. Por lo que ni 1 ni −1 pueden ser límites de la sucesión. Sea a un número real diferente de 1 o −1 y sea r = (1/2) mín{d(a, 1), d(a,−1)}. Entonces, una bola con centro a y radio r no contiene puntos de la sucesión, están todos fuera. Conclusión, la sucesión no es convergente, ya que no tiene límite posible.
Ejemplo 7.2.3 (La sucesión de distancias). Notemos que dados una sucesión (xn) y un punto p, podemos asociarles una sucesión de números reales (an) cuyos
términos son an = d(xn, p). Sigue directo de la variante métrica de la definición de convergencia quexn → p ⇐⇒ d(xn, p) → 0. Una sucesión converge a un punto p, cuando la sucesión asociada con la distancia de los términos a p converge a 0.
La discusión previa a la definición muestra que en un espacio métrico, un punto de acumulación de un conjunto es un límite de una sucesión cuyos términos pertenecen todos al conjunto, pero que son diferentes del límite. Tenemos que lo anterior caracteriza a los puntos de acumulación.
Proposición 7.2.2. Sea A un subconjunto de un espacio métrico E. Un punto p es punto de acumulación de A, ssi, hay una sucesión de elementos de A diferentes de p que convergen a p.
-
Demostración. La existencia de tal sucesión fue probada arriba.
Supongamos que (xn) fuera una sucesión de puntos de A, pero diferentes de
p, que converge a p. Sea V una vecindad cualquiera de p, entonces hay un n0 tal que m ≥ n0 implica que xm está en V. Luego, V contiene puntos de A diferentes
a p, es decir que, p es un punto de acumulación de A.
Corolario 7.2.3. Sea E un espacio métrico y A un subconjunto de E. A es cerrado, ssi, cada sucesión convergente de puntos de A tiene su límite en A.-
Demostración. Un conjunto es cerrado, ssi, contiene a todos sus puntos de acumulación.
El conjunto de términos de una sucesión
[editar]Cuando (xn) sea una sucesión, denotaremos por {xn} al conjunto formado por todos los términos de la sucesión. Dicho conjunto puede ser infinito o finito. Analizaremos los posibles comportamientos de las sucesiones con respecto al cardinal (cantidad de elementos) de su conjunto de términos.
El conjunto de términos es finito. Sea (xn) tal que S = {xn} = {xn : n ∈ N} es un conjunto finito. La finitud de S implica que hay al menos un término cuyo valor se debe repetir infinitas veces. Cuando haya exactamente un único valor que se repita infinitas veces, dicho valor será el límite de la sucesión. Al contrario, cuando haya más de un valor que se repite infinitas veces, razonando como en el ejemplo 7.2.2, concluiremos que la sucesión no converge.
El conjunto de términos es infinito. Supongamos ahora que S = {xn} es infinito y que la sucesión converge a p. Supongamos que p no fuera un punto de acumulación de S. Entonces, habría una vecindad V de p que no tendría puntos de S diferentes de p. Como xn → p, hay un n0 tal que n ≥ n0 implica que sn está en V. Como p es el único punto de S en V. se debe tener que para n ≥ n0 se cumple que xn = p; lo que implica que S es finito. Luego, cuando {xn} es infinito y xn → p, p debe ser un punto de acumulación de S.
Si S tiene más de un punto de acumulación, razonando como en la prueba de que hay un único límite, vemos que la sucesión no puede converger. Resumimos la discusión en la siguiente proposición.
Proposición 7.2.4. Sea (xn) una sucesión y {xn} el conjunto formado por sus términos.
Ejemplo 7.2.4. Sea (xn) la sucesión con términos xn = 1 − (1/n) para n par y xn = −1 + 1/n si n es impar. Es fácil verificar que todos los términos son diferentes entre si para todo n > 1, por lo que hay infinitos términos. Además que 1 y −1 son puntos de acumulación de {xn}. Por lo que la sucesión no converge.
Observación. Sea una sucesión convergente a un punto . Sigue de la proposición que cuando es infinito, es un punto de acumulación de . Esto implica que para cualquier reordenamiento de los términos de la sucesión produce una sucesión que también es convergente a . Es decir que, en tal caso, el orden de los términos no es importante. En particular, cuando la sucesión convergente tiene sus términos dos a dos diferentes, la convergencia solamente depende de la ``topogeometría de sus términos. \end{rem}
Subsucesiones
[editar]Sea s =(sn) una sucesión. Una subsucesión de s es una sucesión cuyos términos son términos de (sn) preservando el orden relativo. En forma más precisa, sea j : N → N una función que preserva el orden, o sea tal que m < n implica que j(m) < j(n), entonces una subsucesión de (sn) asociada a la función j es la sucesión (tn) tal que tn = sj(n) . Una sucesión puede ser divergente y tener una subsucesión convergente. La sucesión del ejemplo 7.2.2, sn = (−1)n, tiene subsucesiones convergentes, por ejemplo, la sucesión de los términos pares converge a 1.
Proposición 7.2.5. Cuando una sucesión converge, todas sus subsucesiones convergen al mismo límite.
- Demostración. Sea (sn) tal que sn → p y sea (tn) una subsucesión con tn = sj(n) donde j :N → N es una función estrictamente creciente (o sea que preserva el orden).
Aserto: para todo n se cumple que j(n) ≥ n. Si n = 0, claramente j(0) ≥ 0 ya que es un número natural. Supongamos que j(k) ≥ k ≥ 0 para un k natural. Entonces, como k + 1 > k se debe tener que j(k+1) > j(k) ≥ k, lo que implica que j(k+1) ≥ k+1. Por inducción, tenemos la afirmación. Sea V una vecindad de p. Como sn → p, hay un natural n tal que m ≥ n implica que sm está en V . En particular, como j(n) ≥ n se cumple que para todo m ≥ n, tm = sj(m) está en V, ya que j(m) ≥ j(n) ≥ n.
Corolario 7.2.6. Cuando una sucesión tiene una subsucesión divergente, la sucesión es divergente.
Convergencia y Continuidad
[editar]La siguiente proposición muestra otra posible definición de continuidad en un punto.
Proposición 7.2.7 (Convergencia y Continuidad). Sea f : E → F una función entre espacios métricos. Sea p un punto de E. Las afirmaciones siguientes son equivalentes.
- Demostración.
((a)⇒(b)). Supongamos que f es continua en p y que xn → p. Tenemos que probar que f(x) → f(p). Por la continuidad de f en p, tenemos que para cada ε > 0 hay un δ > 0 tal que f(Bδ(p)) ⊂ Bε(f(p)). Como xn → p, hay un natural n0 tal que n ≥ n0 implica que xn está en Bδ(p). Luego, para n ≥ n0, f(xn) está en Bε(f(p)); lo que prueba que f(xn) → f(p).
((b) ⇒ (a).) Supondremos que f no es continua en p y probaremos que hay una sucesión (xn) que converge a p, pero tal que f(xn) no converge a f(p). Si f no es continua en p, entonces hay una vecindad V de f(p) tal que para todo vecindad U de p se cumple que f(U) no está contenida en V . Escojamos una sucesión Un de vecindades de p, Un = B1/n(p) y formemos una sucesión con xn ∈ Un tal que f(xn) no pertenece a V . Entonces, xn → p, pero f(xn) no converge a f(p).
Propiedades Métricas
[editar]Proposición 7.2.8. Una sucesión convergente en un espacio métrico es acotada, es decir hay un M tal que el conjunto de puntos de la sucesión está contenido en una bola de radio M alrededor del límite.
- Demostración. Ejercicio. Sugerencias: (i) Aplicar la definición de convergencia a la ε–vecindad del punto límite p con ε = 1. (ii) Definir M como el
máximo entre 1 y los d(xm, p), para aquellos m tales que xm no esta en la ε–vecindad.
Ejercicios 7.2
[editar]Las Sucesiones Reales
[editar]Una sucesión real es una sucesión cuyos términos son números reales. El conjunto formado por todas esas sucesiones es (todas las funciones de los Naturales en los Reales, que es un caso especial del espacio introducido en la sección 3.4/.
En ese conjunto hay definidas operaciones de suma, multiplicación y producto por constantes, que para las sucesiones son operaciones término a término. Es decir que cuando x = (xn) y y = (yn) son sucesiones reales y α una constantes (número real), se cumple que
Sucesiones constantes. Notemos que cada número real α produce una sucesión s = (α), cuyos términos son todos iguales a α y que podemos identificar con el número α. Con esa identificación, la multiplicación por constante es un caso particular de la multiplicación de dos sucesiones.
Sucesiones Acotadas. Una sucesión x = (xn) es acotada, cuando hay un número real tal que M tal que, para todo n en N, se cumple que |xn| ≤ M. M es una cota de la sucesión.
Se verifica (ver los ejercicios) que la suma y el producto de sucesiones acotadas es una sucesión acotada. Si denotamos por B(N, R) al conjunto de las funciones acotadas, se tiene entonces que se trata de una subalgebra de F(N, R). Sigue de la proposición 7.2.8 que cada sucesión convergente es acotada, por lo que SC(R) (sucesiones reales convergentes) es un subconjunto de las sucesiones acotadas. La próxima proposición muestra que se trata de una subálgebra del álgebra de las sucesiones acotadas.
Proposición 7.3.1 (Operaciones y Convergencia). Sean x = (xn), y = (yn) sucesiones de números reales tales que xn → a y yn → b. Entonces,
Es decir que SC(R) es una subálgebra de F(N,R).
- Demostración. Sea ε dado. Como xn → a (resp. yn → b) hay un entero n1, (resp
n2) tales que
Observación 7.2. Comparar la demostración anterior con la demostración del teorema 6.5.6
. Proposición 7.3.2. Sean (xn) una sucesión real tal que para todo n, xn ≠ 0. Si xn → a, a ≠ 0, entonces 1/xn → 1/a.
- Demostración. Ejercicio.
Proposición 7.3.3 (Teorema del Sandwich). Sean (xn), (yn) y (zn) sucesiones tales que para todo n se cumple que xn ≤ yn ≤ zn. Si xn → a y zn → a, entonces yn → a.
- Demostración. Ejercicio
. Proposición 7.3.4. Sean (xn), (yn) sucesiones reales tales que yn = xn+k, k un entero positivo. Ambas sucesiones convergen o divergen simultáneamente.
- Demostración. Ejercicio.
Notemos que en la proposición anterior, (yn) se obtiene de (xn) eliminando los primeros k términos. El resultado implica que lo único importante para la convergencia es, entonces, la “cola” de la sucesión. Es decir que en las hipótesis de proposiciones o teoremas donde aparece “para todo n”, podemos generalmente poner en sustitución “para casi todo n” (ver la observación 7.1).
Las Sucesiones en Espacios Normados
[editar]Sea un espacio normado, en particular uno de los espacios Euclídeos . La siguiente proposición resume los resultados sobre las sucesiones en .
Proposición 7.3.5. Sea un espacio normado y sean , sucesiones de puntos de .
La demostración queda de ejercicio.
Las Series
[editar]En cualquier espacio normado podemos definir series (informalmente, sumas infinitas). La definición general de serie es la misma que en los Reales.
Dada una sucesión , le asociamos la sucesión de sumas parciales , tal que
Es decir que , , , etc.
Decimos que la sucesión es sumable, cuando la sucesión asociada de sumas parciales es convergente. Denotamos al límite, cuando exista, por
o
y le llamamos serie definida por los Por abuso de lenguaje, llamamos serie a la suma infinita y decimos que la serie converge o diverge dependiendo de que el límite mencionado exista o no.En cualquier espacio normado podemos definir series (o sea sumas infinitas).Los siguientes resultados deberían ser conocido de los cursos de Cálculo. Sea
Ejercicios 7.3
[editar]Las Sucesiones de Cauchy
[editar]¿Podemos saber que una sucesión es convergente, aunque no sepamos su límite?
Sea (xn) una sucesión convergente a x en un espacio métrico E. Entonces, para todo ε > 0, hay un n0 tal que n ≥ n0 implica que d(xn, x) < ε/2. Luego, para todo m, n ≥ n0, tenemos que
La condición anterior es, en consecuencia, una condición necesaria para la convergencia de una sucesión. Podemos usarla para probar que una sucesión no es convergente (por ejemplo en la sucesión del ejemplo 7.2.2, los términos pares mantienen distancia de 2 de los términos impares, por lo que es imposible que tal sucesión converja). La condición se llama condición de Cauchy, y la definiremos formalmente a continuación.
Condición de Cauchy Una sucesión (xn) en un espacio métrico satisface la condición de Cauchy, ssi, para todo ε > 0 hay un n0 tal que
m, n ≥ n0 ⇒ d(xm, xn) < ε. Una sucesión de Cauchy es una sucesión que satisface la condición de Cauchy.
Sigue de la discusión inicial la siguiente proposición.
Proposición 7.4.1. Cada sucesión convergente es una sucesión de Cauchy.
La convergencia de una sucesión depende tanto de la sucesión como del espacio adonde está la sucesión. Por ejemplo, en los Reales, la sucesión 1/n es convergente a 0 y es, por lo tanto, una sucesión de Cauchy. Sin embargo, la misma sucesión no es convergente en ]0, 1], aunque continúa siendo una sucesión de Cauchy. Es decir que la condición de Cauchy aunque necesaria, no es suficiente. Por lo que, espacios adonde la condición de Cauchy sea suficiente para la convergencia merecen un nombre especial.
Definición. (Espacio Métrico Completo) Decimos que espacio métrico es un espacio (métrico) completo, ssi, toda sucesión de Cauchy es convergente. Un subespacio es completo, cuando toda sucesión de Cauchy del subespacio converge a un punto del subespacio.
Observación 7.3. Cuando un espacio normado es completo respecto a la métrica inducida, se dice que es un espacio de Banach.Probaremos, más adelante que los Reales son un espacio completo. De hecho, se puede mostrar que suponer que la condición de que toda sucesión de Cauchy de números reales sea convergente, es equivalente a la completitud de los Reales vía postulado del supremo.
La condición de Cauchy es estrictamente métrica, no hay formulación de la misma en términos solamente de abiertos. No obstante lo anterior, hay relaciones con la topología del espacio.
Ejemplo 7.4.1. El ejemplo anterior de la sucesión en X =]0, 1] sugiere que para “completar” ese espacio deberíamos agregar 0, es decir un punto de acumulación del conjunto que no está en el conjunto. La validez de esa intuición está contenida en la siguiente proposición.
Proposición 7.4.2. Sea E un espacio métrico. Cualquier subespacio completo X de E es cerrado.
- Demostración. Supongamos que X fuera completo. Sea p un punto de acumulación
de X. Por la proposición , hay una sucesión de puntos propLimPA de X que converge a
p. Como X es completo, p está en X; lo que implica que X es cerrado.
Tenemos, también, casi un converso de lo anterior.
Proposición 7.4.3. Sea E un espacio métrico completo. Un subespacio X de E cerrado es completo.
- Demostración. Supongamos que X fuera cerrado y que (xn) fuera una sucesión
de Cauchy en X. Al ser (xn) una sucesión de Cauchy en X, también lo es en E.
Como E es completo, la sucesión converge, digamos a p. Mostraremos que p está
en X. Consideremos el conjunto de términos de la sucesión. Si dicho conjunto
tiene finitos elementos, el límite de la sucesión es uno de ellos y, por lo tanto, el
límite está en X. En caso de que el conjunto sea infinito, tendremos que p es un
punto de acumulación del conjunto de términos y, en consecuencia, de X. Como
X es cerrado, dicho punto está en X. Es decir que la sucesión converge a un punto
de X.
Las sucesiones de Cauchy son sucesiones que casi convergen, solamente les falta el límite, por lo que comparten algunas de las propiedades de las sucesiones convergentes.
Proposición 7.4.4. Las sucesiones de Cauchy son acotadas.
- Demostración. Sea (xn) una sucesión de Cauchy. Tomando ε = 1 en la condición
de Cauchy. hallamos un n0 tal que para m, n ≥ n0 se tiene que d(xm, xn) < ε. En particular tomando n1 = n0 + 1, tenemos que para todo m > n1, d(xm, xn1) < 1.
Sea M = máx{1, d(xk, x<subn1) : k < n1}. Entonces, para todo n se cumple que
d(xn.xn1) ≤ M. Lo que muestra que el conjunto de términos de la sucesión es
acotado.
Vimos antes que hay sucesiones divergentes que pueden tener subsucesiones convergentes. Tal situación no ocurre con las subsucesiones de Cauchy (al igual que con las sucesiones convergentes).
Proposición 7.4.5. Cuando una sucesión de Cauchy (an) en un espacio métrico tiene una subsucesión convergente a q, entonces la sucesión converge a q.
- Demostración. Sea ε > 0 dado. Sea (ani) la subsucesión convergente a q. Como
(an) es sucesión de Cauchy, hay un natural k1 tal que
d(am, an) < ε/2, cuando m, n ≥ k1.
Como límni ani = q, podemos hallar un k2 tal que
d(ani , q) < ε/2, cuando ni ≥ k2.
Escogiendo k ≥ k2 tal que nk > k1, tenemos que para m ≥ k se cumple que
d(am, q) ≤ d(am, anm) + d(anm, q) < ε/2 + ε/2 = ε.
Ejercicios 7.4
[editar]La Completitud de los Reales
[editar]En el capítulo 2, introducimos la “completitud” de los Reales vía el postulado del supremo; “cada conjunto no vacío acotado superiormente tiene una supremo (cota superior estricta)”. En esta sección, mostraremos que R también es completo en el sentido de este capítulo, es decir que toda sucesión real de Cauchy es convergente. Daremos una prueba usando solamente resultados acerca de los Reales y de las sucesiones de Cauchy. Necesitaremos algunos resultados previos que nos mostrarán importantes propiedades adicionales de los números reales.
Proposición 7.5.1. Si (an) es una sucesión de números reales que es creciente (an ≤ an+1) y acotada superiormente, entonces (an) es convergente. Resultado análogo para una sucesión decreciente y acotada inferiormente.
- Demostración. Sea S el conjunto de términos de la sucesión, o sea S = {an : n ∈ N}. Como S es no vacío y acotado superiormente, tiene un supremo, digamos, a. Probaremos que a es un límite de la sucesión. Supongamos dado ε > 0, entonces a − ε no es una cota superior de S, por
lo que hay un n0 tal que an0 > a − ε. Luego, para todo m ≥ n0 se cumple que am > a − ε, de donde |a − am| = a − am < ε, lo que implica que límn an = a.
El resto de la proposición queda al cuidado del lector o lectora.
El siguiente lema nos ayudará en nuestro trabajo posterior.
Lema 7.5.2. Cualquier sucesión real (an) tiene una subsucesión que es o creciente o decreciente.
- Demostración. (Spivak) Llamemos “punto cumbre” de la sucesión a un n tal que
m > n implica am < an.
Caso 1. La sucesión tiene infinitos puntos cumbres. Digamos n0 < n1 < n2 < Entonces la subsucesión an0 > an1 > an2 > ... es una sucesión decreciente.
Caso 2. La sucesión tiene una cantidad finita de puntos cumbres. Sea n0 un natural mayor que todos los puntos cumbres. Como n0 no es punto cumbre, hay un n1 > n0 tal que an1 ≥ an0 . Como n1 no es punto cumbre, hay un n2 > n1 tal que an2 ≥ an1. Continuando de esta manera (formalmente, por inducción) obtenemos una subsucesión (ani) que es creciente.
Corolario 7.5.3 (Bolzano–Weierstrass). Toda sucesión acotada tiene una subsucesión convergente.
Teorema 7.5.4 (Completitud de Cantor). Toda sucesión de Cauchy es convergente. Es decir que R es un espacio métrico completo.
- Demostración. Las sucesiones de Cauchy son acotadas (proposición 7.4.4) Por la
propiedad de Bolzano–Weierstrass (corolario anterior) tiene entonces una subsucesión
convergente. Pero, cuando una sucesión de Cauchy tiene una subsucesión
convergente, la sucesión es convergente (ver la proposición 7.4.5).
Espacios de Sucesiones
[editar]Introduciremos dos espacios normados y, por lo tanto, métricos basados en sucesiones reales especiales. El primero de esos espacios consistirá de los sucesiones acotadas con norma definida por
||(xn)||sup := sup{xn : n ∈ N}. Tal espacio es un caso particular del espacio de funciones acotadas introducido en la sección 3.4.
El espacio ℓ2: espacio de Hilbert
[editar]Definiremos otro espacio de sucesiones reales, denotado por ℓ2 y formado por todas las sucesiones reales (xn) tales que
Se verifica fácilmente que la suma de sucesiones y multiplicación por un real de sucesiones en ℓ2 son también sucesiones de ese espacio, lo que dice que ℓ2 tiene una estructura de espacio vectorial. Se define una norma en ℓ2, por
Ejemplo 7.6.1. Sea ei, la sucesión cuyos términos son todos nulos, excepto el i–ésimo que es igual a 1. Entonces,
Se puede verificar que ℓ2 con la distancia inducida por la norma definida arriba es un espacio métrico completo (ver Kolmogorov & Fomin [4]), o sea que es un espacio de Banach.
Ejercicio 7.6
[editar]Completación de un Espacio Métrico
[editar]Suponer que tenemos un espacio métrico X que no es completo. Las sucesiones de Cauchy son sucesiones que “casi” convergen; si no convergen es porque el límite no se halla en el espacio métrico X. Si X es un subconjunto de un espacio métrico E entonces, la clausura de X es un candidato para un espacio métrico cerrado que contiene a X. Sea Cl(X) dicha clausura, entonces se cumple que X es un subconjunto denso en Cl(X).
La siguiente proposición esteblece que para cada espacio métrico (sea o no subespacio de otro), podemos hallar un espacio métrico completo que contiene una imagen isométrica de X (que identificaremos con X).Proposición 7.7.1. Sea X un espacio métrico. Hay un espacio métrico completo Cl(X) y hay una isometría ϕ : X → X* tal que ϕ(X) es denso en bX . Identificando X con su imagen, podemos decir que cada espacio metrico está contenido en un espacio métrico completo.
Indicaremos, a continuación, los pasos de una construcción de bX a partir de X. Las demostraciones de las afirmaciones acerca de los pasos o detalles quedan como ejercicios.
Procedimiento para la construcción de la completación de un espacio métrico.
Sea X un espacio métrico, posiblemente incompleto.
Ejercicios del Capítulo 7
[editar]
Los Espacios Topológicos
[editar]Introducción
[editar]Hemos analizado, en los capítulos anteriores, las posiciones relativas de puntos y conjuntos usando métricas. Hay, sin embargo, situaciones interesantes donde la métrica no es lo más adecuado o, inclusive, puede que no haya una métrica posible; pero que nos interese tener una noción de proximidad. Aquí es donde entra la noción de espacio topológico donde la noción de proximidad será dada por abiertos en lugar de distancias.
Si examinamos lo hecho en los capítulos anteriores, todas las nociones importantes: vecindad, interior, exterior, clausura, puntos aislados, de acumulación, continuidad, etc. fueron definidas usando la noción de abierto. Por lo que podemos, a partir de una familia de abiertos, tener todas las nociones indicadas arriba. Eso es, precisamente lo que haremos en este capítulo. Nuestro punto de partida será las propiedades de abiertos contenidas en la proposición 5.2.2.Las Definiciones Básicas
[editar]Definición. (Topología, Espacio Topológico)Una topología en un conjunto X es un conjunto T de subconjuntos de X tal que:
Un espacio topológico es un par <X, T > donde T es una topología de X. Llamamos puntos del espacio a los elementos de X y (conjuntos) abiertos (de X) a los conjuntos de la topología.
Ejemplos 8.2.1.Convenios. Como es usual, cuando no haya riesgo de confusión acerca de la topología, hablaremos simplemente del espacio X. De ahora en adelante, además, “espacio” siempre querrá decir “espacio topológico”, a menos que digamos algo distinto.
Cuando digamos que una función f : X → Y es continua, implícitamente suponemos que X y Y son espacios (topológicos).
Los Puntos y los Conjuntos Especiales
[editar]La terminología asociada con espacios topológicos es básicamente la misma que aquella usada para espacios métricos. Enunciaremos las definiciones, principalmente para comparaciones y futuras referencias.
Definición. (Vecindad) Sea X un espacio topológico. Una vecindad de un conjunto A (resp. de un punto p) es cualquier conjunto que contenga un abierto que contenga a A (resp. a p).
Veremos, brevemente las definiciones de cerrado, interior, exterior, clausura y frontera. Revisar las definiciones para ver que formalmente coinciden con aquellas dadas en el capítulo 5.Definición. (Cerrado) Un subconjunto de un espacio topológico es cerrado, ssi, su complemento es abierto.
Definición. (Puntos Especiales) Sean X un espacio topológico, A un subconjunto de X y p un punto de X.
Definición. (Conjuntos especiales) Sea A un subconjunto de un espacio topológico.
Claramente las nociones coinciden con las correspondientes de espacios métricos. Queda de ejercicio:Cada espacio métrico define una topología. Resulta natural preguntarse si podriamos dotar a cada espacio topológico de una métrica de modo que la topología inducida por la métrica coincida con la topología del espacio. La respuesta es negativa, como se puede apreciar en el ejemplo 4 de 8.2.1.
Cuando en un espacio topológico haya una métrica cuya topología inducida coincide con la topología del espacio, diremos que el espacio es metrizable.
Suponiendo que el espacio fuera metrizable, ¿podemos del conocimiento de su topología recuperar la métrica?
La respuesta es negativa, como es fácil de ver. observando que cuando d es una métrica en el conjunto X, entonces d'(x, y) := 2d(x, y) es una métrica que genera los mismos abiertos que d. Más adelante veremos que las normas euclídeas, ciudad y máxima generan la misma topología en los Rn. Es decir que aún métricas muy diferentes pueden generar la misma topología (o sea la misma familia de abiertos).
Observación 8.1 (Topologías definidas por Cerrados). Observamos en el capítulo de abiertos y cerrados, que cerrado era una noción dual a la de abierto. Luego, cuando en un conjunto X tenemos una familia de conjuntos tal que:
tenemos una familia que tiene las propiedades de los cerrados en la proposición 5.3.5. Por lo que podemos definir una topología formada por los complementos de los conjuntos en .
Espacios Hausdorff
[editar]Un espacio Hausdorff es un espacio topológico tal que, para todo p, q en X con p ≠ q hay abiertos disjuntos U y V tales que p está en U y q está en V .
Decimos que tales abiertos separan puntos o distinguen puntos.
Los espacios métricos son espacios Hausdorff, así como los espacios discretos.
Subespacios
[editar]Sean X un espacio (topológico) y Y un subconjunto de X, ¿cuándo Y tendrá una topología relacionada con la topología de X?
La respuesta no consiste simplemente en usar los abiertos de X que son subconjuntos de Y. Miremos, por ejemplo, una situación con espacios métricos. Si X = R y Y = [0, 1], tenemos que [0, 1/2) es un conjunto abierto en Y, aunque no lo sea en X. Los abiertos de Y, recordemos, eran las intersecciones de abiertos de X con Y . Esto motiva la siguiente proposición.
Proposición 8.2.1. Sean <X, T> un espacio topológico, Y un subconjunto de X, y TY := {U ∩ Y : U ∈ T }. Entonces, TY es una topología en el conjunto Y .
-
Demostración. Claramente, el conjunto vacío (∅ = ∅ ∩ Y ) y Y = X ∩ Y están en TY. Sea (Ui), i ∈ I, una familia de conjuntos de TY . Por definición, para cada i en I, hay un abierto Vi de X tal que Ui = Vi ∩ Y. Entonces,
es un abierto de X y como
tenemos que está en TY.Análogamente, suponiendo que I fuera finito, tenemos que:
lo que prueba que W está en TY. En conclusión, TY es una topología.
Definición. (Subespacio). Sean <X, T > un espacio topológico, Y un subconjunto de X y TY la topología formada por la intersección de los abiertos de X con Y. Decimos que el espacio topológico <Y, TY > es un subespacio (topológico) de <X, T >. Llamamos topología relativa de Y (respecto a X) a la topología TY .
Cuando en el contexto queda claro acerca de que topología estamos hablando, decimos simplemente que Y es un subespacio de X y supondremos que su topología es la topología relativa.
Sea A ⊂ X. Aunque cada abierto A de X induce un abierto A ∩ Y de Y , el recíproco no es válido, en general.Proposición 8.2.2. Sea Y un subespacio abierto de X (o sea que Y es abierto en X). Entonces, A es abierto en Y , ssi, A es abierto en X.
- Demostración. Ejercicio
Ejercicios 8.2
[editar]
Como corolario, tenemos nuevamente que conjuntos finitos no pueden tener puntos de acumulación.
Proposición 5.3.3 (Caracterización métrica de los puntos de acumulación). Sea A un subconjunto de un espacio métrico E. Sea p un punto de E. Entonces, d(p,A) = 0, ssi, p está en A o es un punto de acumulación de A.
Bolas Cerradas y Esferas
[editar]Observaciones. Recordemos algunos hechos acerca de bolas cerradas y esferas.
Veamos que el apellido de cerradas es consistente con nuestro concepto de conjunto cerrado.
Proposición 5.3.4. Las bolas cerradas y las esferas son conjuntos cerrados.
La siguiente proposición es la dual de la proposición 5.2.2. sobre conjuntos abiertos.
Proposición 5.3.5 (Propiedades de los Cerrados). Sea E.un espacio métrico. Entonces,
-
Demostración. Sigue de la definición de cerrado y de la proposición
5.2.2, aplicando las leyes de Morgan (Ver la sección B.5.). Por ejemplo, si (Fi) es una familia de abiertos con intersección F, tenemos que


































































































































![{\displaystyle ||x||_{p}:={\sqrt[{p}]{|x_{1}|^{p}+|x_{2}|^{p}+\dots +|x_{n}|^{p}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4031391381990b7450689282f5182218d2f6094e)


























































![{\displaystyle B_{r}[p]:=\{x\in E:d(x,a)\leq r\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08d4bd493584b51a503ef4a9ea412d5c3530a847)

![{\displaystyle {\begin{array}{|c|c|c|c|}\hline r&B_{r}(a)&B_{r}[a]&S_{r}(a)\\\hline \hline 1/2&\{a\}&\{a\}&\emptyset \\\hline 1&\{a\}&X&X\setminus \{a\}\\\hline 2&X&X&\emptyset \\\hline \hline \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e55d4d709f77d1d2c322b2c1db7b4bacd95d86b)
![{\displaystyle d(f,g)=\sup\{|f(t)-g(t)|:t\in [a,b]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84473bcc671fb84f4da5d273994453898b09e78a)









![{\displaystyle B\#(+\infty ,1/2)=\{x\in \mathbb {R} :1<x\}=]1,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a39466bb174ba1ad88799022b3d091831729b063)



















































![{\displaystyle {\begin{array}{rcl}C&=&\{(x,y):a<x<b,c<y<d\}\\&=&\{(x,y):a<x<b\}\cap \{(x,y):c<y<d\}\\&=&pr_{1}^{-1}(]a,b[)\cap pr_{2}^{-1}(]c,d[).\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30b062b80a8a53dcf5ad858f3418bbc1c4121f02)




























































































![{\displaystyle t\mapsto {\sqrt[{3}]{t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/250f57cb6c0dbd48cadf77d2137db8c4492e78c1)



































![{\displaystyle F_{1}=[0,1/3]\cup [2/3,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec5136ef8c15235f000ece5aac11db7afc18e34)
![{\displaystyle F_{2}=[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1099cb543bd7eaa5b60a673999d892b2095fb98b)





![{\displaystyle ]{\frac {3s+1}{3^{k}}},{\frac {3s+2}{3^{k}}}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfa0756baf52cadd03513a9c09d579707de8e4cf)









![{\displaystyle U_{i}=\{[x_{1}:x_{2}:x_{3}]:x_{i}\neq 0\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/080f41097c69d5d3bd232a46f6d37391dc9420ff)
![{\displaystyle X=\mathbb {B} ^{2}\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa33539647944650545b7c851319dc23a362dc86)
















![{\displaystyle B_{n}=]-1/n,1/n[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf69dca3677011b2dd696ca05efc6a8154fc413f)

![{\displaystyle C_{n}=[-1/n.1/n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87f8df7ebf76ee4824c9edce1408d577e390920d)




![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle ]s-r,s+r[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00310cc66f39388b43be99f4698923084c576702)

![{\displaystyle U_{\alpha }\cap ]0,1[\subset U_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a945d0ddbaffe267d7012f6d7ef95aa209f82f)


























![{\displaystyle \det([a_{ij}]):=\sum _{\sigma }(-1)^{{\text{sgn}}(\sigma )}a_{i\,\sigma (i)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e569a6fa09a10816eae1623d70a7da15d09d949)


































![{\displaystyle [x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb77bc5344dd9dee000589fe8f708b70cb200afa)
![{\displaystyle [y_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0733aa435bd20b12b259b38350ab7b3e2bd2a9d)
![{\displaystyle x\cdot y=[x_{i}]^{t}[y_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a830960efc5dab77ae70fb4b552ba1b4935fcf5c)

















































