Matemáticas Universitarias/Espacios Métricos/Compactos

Introducción

La compacidad es una propiedad muy importante de los espacios topológicos. Sin embargo, no resulta fácil dar una descripción intuitiva de la misma. La idea de compacto es de algo que cabe en un espacio pequeño. Para nosotros, topológicamente hablando, los espacios finitos serán espacios “pequeños”. Sin necesariamente mucha precisión, podemos decir que los conjuntos compactos serán espacios topológicamente semejantes a los conjuntos finitos. Una definición formal aparecerá más adelante.

Por la importancia de los conjuntos compactos y de las nociones asociadas, hemos adoptado una estructura especial en este capítulo. Después de dar una definición general de la compacidad y ver algunas de sus propiedades generales, haremos un estudio detallado de la compacidad para subconjuntos de la línea real; en particular una serie de nociones equivalentes. Posteriormente, veremos la compacidad en los espacios normados Rⁿ. Luego, estudiaremos la noción en un espacio métrico cualquiera. Obviamente, cualquier propiedad de compactos en espacios métricos será valida para la línea real y los Rⁿ. Es decir que habrá resultados cuyas demostraciones podrán aparece tres veces, primeramente para línea real, luego para los espacios normados de dimensión finita y luego para los espacios métricos. ¿Por qué esta redundancia? En primer lugar, porque ilustra el desarrollo de la noción. En segundo lugar, veremos demostraciones diferentes para una misma propiedad, dependiendo del ambiente. Finalmente, podremos ver que las propiedades equivalentes o implicadas por la compacidad, no son las mismas para espacios generales que para los Rⁿ’s. Algunas propiedades importantes para los compactos de espacios Rⁿ—en particular, la línea real—como la característica de ser cerrados y acotados, no son válidas en general. Por esa razón, nuestra definición de compacidad será dada en términos de familias de abiertos (cubiertas) que contienen al espacio o conjunto en cuestión, ya que la experiencia muestra que es la más provechosa.

Cubiertas, subcubiertas

Definición. (Cubiertas, Subcubierta) Sea X un espacio topológico, A un subconjunto de X. Decimos que una familia G de subconjuntos de X es una cubierta o recubrimiento del conjunto A o que cubre al conjunto A, cuando la reunión de los conjuntos de la familia contiene al conjunto A.

Una subcubierta G′ de una cubierta G de A es un subconjunto de G que también cubre a A.

Decimos que se trata de una cubierta abierta cuando cada conjunto de la cubierta es un conjunto abierto.

Notemos que una familia G de subconjuntos de un conjunto A será una cubierta de A, cuando para cada x de A hay un conjunto U en G que contiene a x.

Ejemplo 11.2.1. Sea X = R y sea G la familia de intervalos ]z − 1, z + 1[, z en Z. Claramente G es una cubierta abierta de R.

Ejemplo 11.2.2. Sea X = [0, 1], r un racional positivo, y sea G el conjunto de r–vecindades de puntos racionales de X. Claramente, G es una cubierta abierta de X.

Ejemplo 11.2.3. Aunque las cubiertas abiertas serán aquella más interesantes para nosotros, podremos tener cubiertas de cerrados o de conjuntos que no son ni abiertos ni cerrados. Consideremos a F = {[z − 1, z + 1] : z ∈ Z}, que es claramente una cubierta cerrada de R. Omitiendo en cada uno de esos conjuntos uno de los extremos, todavía tendremos una cubierta.

Ejemplo 11.2.4. Sea X = {x₁, ... , x_n} un conjunto finito de un espacio topológico.

Sea G = {G_i : i ∈ I} una cubierta abierta de X. Mostraremos que hay una subcubierta finita de G que cubre a X, independiente del tamaño del conjunto de índices I. En efecto, para cada k, k = 1, 2, . . . n, hay un abierto en G que denotaremos por G_k que contiene a x_k. Claramente la reunión de esos n abiertos cubre al conjunto X.

Ejercicios 11.2.

1. Hallar la reunión y la intersección de cada una de las familias siguientes de subconjuntos de la línea real.
   1. $(A_{n})$, $n\in \mathbb {N}$, $A_{n}=[0,1/n)$.
   2. $(B_{n})$, $n\in \mathbb {N}$, $B_{n}=]-1/n,1/n[$.
   3. $(C_{n})$, $n\in \mathbb {N}$, $C_{n}=[-1/n.1/n]$.

   
   

2. Sea ${\mathcal {C}}$ una cubierta abierta de un espacio $X$.
   1. Un subconjunto $A$ de $X$ es abierto, ssi, hay un $B\in {\mathcal {C}}$ tal que $A\cup B$ es abierto en $B$.
   2. Una función $f:X\rightarrow Y$ es continua, ssi, para cada $B\in {\mathcal {C}}$, la restricción de $f$ a $B$ es continua.
   3. Dos topologías de $X$ son iguales, ssi, inducen la misma topología relativa en cada $B\in {\mathcal {C}}$.

Los Espacios Compactos

Inspirados en el ejemplo de los conjuntos finitos (11.2.4), daremos la siguiente definición de compacidad.

Definición. (Espacios y Conjuntos Compactos) Decimos que espacio topológico es compacto, ssi, cada cubierta abierta de X tiene una subcubierta finita. Un subconjunto de un espacio topológico es un subconjunto compacto cuando es un espacio compacto respecto a la topología relativa.

• Los espacios finitos son compactos.
• La línea real no es compacta. El cubrimiento del ejercicio 11.2.1 no tiene un subcubrimiento finito de R.

La siguiente proposición sigue inmediatamente de la definición.

Proposición 11.3.1. Sean X un espacio topológico y Y un subconjunto de X. Y es compacto, ssi, para todo familia de abiertos (en X) que cubren Y , hay una subfamilia finita de dicha familia que también lo cubre.

---

Antes de entrar en detalles de los espacios compactos, veremos condiciones duales para la compacidad, o sea en términos de cerrados.

Consideremos una familia (F_i) de cerrados en un espacio compacto X tal que la intersección de sus miembros sea vacía. Entonces, el complemento de tal intersección será todo X. Como el complemento de la intersección de los F_i’s es la reunión de los complementos de los F_i’s, y tales complementos son abiertos, tenemos que determinan una cubierta abierta de X. Como X es compacto, hay una familia finita de tales abiertos cuya reunión será igual a todo X; por lo que sus complementos—que es una familia finita de los F_i’s—tendrá intersección vacía. Lo anterior, produce la siguiente caracterización de la compacidad.

Proposición 11.3.2. En un espacio compacto, una familia de cerrados tiene intersección vacía, ssi, una subfamilia finita tiene intersección vacía.

---

Introduciremos una terminología que nos ayudará a escribir de manera más concisa algunas proposiciones.

Propiedad de la Intersección Finita. Decimos que una familia de conjuntos tiene la propiedad de la intersección finita (PIF), cuando cada subfamilia finita tiene intersección no vacía.

Usando esa terminología, sigue de la discusión anterior la siguiente proposición.

Proposición 11.3.3. Un espacio topológico X es compacto, ssi, cada familia de cerrados en X que tiene la propiedad de la intersección finita, tiene intersección no vacía.

Algunas veces, resultará más cómodo esta versión de la compacidad para probar que un conjunto ees compacto.

---

Sucesiones Anidadas de conjuntos. Sea X un conjunto. Una sucesión (A_n), n ∈N, de subconjuntos de X se llama anidada, ssi, para todo m, n en N.se cumple que m > n implica que A_m ⊂ A_n.

Sea (A_n) una sucesión anidada de conjuntos no vacíos. Sean n_1 < n_2 < ... < n_k, Entonces, A_nk esta contenido en cada uno de los A_ni ’s anteriores,por lo que está contenido en su intersección. Hemos, así, probado el siguiente lema.

Lema 11.3.4. Sea (A_n), n ∈ N, una sucesión anidada de subconjuntos no vacíos cualesquiera de un conjunto X, Entonces la familia de los A_n’s tiene la propiedad de intersección finita.

---

Aplicando el lema a una familia anidada de cerrados no vacíos en un espacio compacto, obtenemos la siguiente proposición.

Proposición 11.3.5 (Cerrados Anidados). Sea (F_n), n ∈ N, una familia anidada de cerrados no vacíos de un espacio compacto X. Entonces, la intersección de los F_n no es vacía.

---

Espacios y Conjuntos Compactos

Un subconjunto de un espacio compacto no necesita ser compacto. Por ejemplo, veremos, más adelante, que I = [0, 1] es compacto, pero su interior no lo es (ver ejercicio 5) sin embargo, los subconjunto cerrados siempre son compactos.

Proposición 11.4.1. Cualquier subespacio cerrado de un espacio compacto es compacto.

Demostración. Sea F un cerrado en el espacio compacto X. Sea (G_i) una cubierta abierta de F. Entonces, los G_i’s junto con el complemento de F cubren X. Como X es compacto, una familia finita de los G_i’s, eventualmente con F^c incluido, cubren a X y, por lo tanto, a F. Luego, F es compacto.

---

La linea real no es compacta ya que la cubierta C = { ]n, n + 2[ : n ∈ Z} no tiene subcubierta finita posible. Por la misma razón, ni el intervalo abierto ]0,+∞[ ni el intervalo cerrado [0,+∞[ son compactos. La siguiente proposición muestra, sin embargo, que hay otrosintervalos que son compactos.

Proposición 11.4.2. El intervalo [0, 1] de la línea real es compacto.

Demostración. Probaremos que cualquier cubrimiento de [0, 1] tiene un subcubrimiento finito. Sea (U_i), i∈I, un cubrimiento abierto de [0, 1]. Si I fuera finito no hay más que probar. Supongamos, por lo tanto, que I fuera infinito. Sea A el subconjunto de [0, 1] formado por todos los x en [0, 1] tales que hay un subcubrimiento finito de [0, x]. El conjunto A no es vacío porque al menos 0 está en A. Como, además, A está acotado superiormente por 1, tenemos que A tiene supremo, digamos s ≤ 1. Como [0, 1] es cerrado, s está en [0, 1]. Si s = 1, hemos probado la proposición. Suponer que s < 1. Entonces [0, s] está cubierto por una cantidad finita de los U_i’s. Al menos uno de ellos contiene a s, digamos U_k. Como $s$ está en el interior de $[0,1]$, hay un intervalo abierto $]s-r,s+r[$, $r>0$, totalmente contenido en $U_{\alpha }\cap ]0,1[\subset U_{\alpha }$. Pero, entonces [0, s + r/2] está totalmente contenido en el subcubrimiento finito y s + r/2 > s, lo que es un absurdo. Luego, s = 1, y la proposición está probada.

---

Teorema 11.4.3. La imagen continua de un compacto es compacto.

Demostración. Sea f : X → Y continua y sea K ⊂ X compacto. Sea (U_i) una cubierta abierta de f(K). Cada U_i = V_i ∩ f(K) donde V_i es un abierto de Y . La reunión de los V_i cubre a f(K), por lo que sus preimágenes f^-1(V_i) cubren K. Pero, como K es compacto una familia finita de esas preimágenes cubre a K. Como K ⊂ f^-1(V_i1) ∪ ...∪ f^-1(V_im) implica que f(K) ⊂ V_i1 ∪ ... V_im, tenemos la compacidad de f(K).

---

Corolario 11.4.4. Compacidad es una propiedad topológica. Si X y Y son homeomórficos, se cumple que X es compacto, ssi, Y es compacto.

Corolario 11.4.5. Cualquier intervalo cerrado y acotado de la línea real es compacto.

Demostración. El intervalo [0, 1], por la proposición 11.3.7, es compacto y como la función f : [0, 1] → [a, b] tal que f(t) = (b − a)t + a es biyectiva y continua, se tiene el resultado.

---

Corolario 11.4.6 (Intervalos Anidados). Sea (J_n) una sucesión anidada de intervalos cerrados y acotados de R, entonces la intersección de los J_n’s no es vacía. Además, cuando la sucesión de los diámetros de los J_n tiende a 0, dicha intersección contiene solamente un punto.

Demostración. Ejercicio.

---

Ejemplo 11.4.1. Sea ϕ : [0, 1] → R² tal que ϕ(t) = (cos(2π t, sen(2π t)). La función ϕ es claramente continua, por lo que imagen S¹, la circunferencia unitaria es un subconjunto compacto de R².

---

Proposición 11.4.7. Cualquier subconjunto cerrado y acotado de R es compacto.

Demostración. Sea F cerrado y acotado. Por ser acotado, hay un número M tal que F ⊂ [−M,M], Por el último corolario [−M,M] es compacto y, por la proposición 11.3.6, cualquier subconjunto cerrado de un compacto es compacto de R².

---

Ejemplo 11.4.2. Hay espacios donde un conjunto cerrado y acotado no es compacto.

Consideremos al subespacio Q de R con la topología relativa y sea B = [0, 1] ∩ Q. B es cerrado y acotado en Q.

Sea θ = √2/2 y sea F_n = [θ − 1/n, θ + 1/n], n ∈ N, n ≥ 4. Cada F_n es un cerrado en R, por lo que H_n = F_n ∩ B es un cerrado de B. Observando que m > n implica que H_m ⊂ H_n, vemos que la familia de los H_n’s es una familia de cerrados de B que tiene la propiedad de intersección finita. Peor, claramente, ∩n F_n = {θ}, por lo que ∩n H_n = ∅ (ya que θ no está en B). Luego, B no puede ser compacto.

---

La Compacidad en Espacios Hausdorff

Volvamos a espacio generales, pero suponiendo que son Hausdorff. Recordemos que llamamos espacio Hausdorff a un espacio topológico donde cualquier par de puntos distintos pueden separarse por abiertos disjuntos. Es decir, dados x, y, x ≠ y hay vecindades abiertas V_x y V_y tales que x ∈ V_x, y ∈ V_y y V_x ∩ V_y = ∅.

La siguiente proposición puede ser considerada como un recíproco parcial de la proposición 11.4.6.

Proposición 11.4.8. Un subconjunto compacto de un espacio Hausdorff es cerrado.

Demostración. Sea X un espacio topológico Hausdorff y sea A un subconjunto compacto de X. Si K = X o vacío, el resultado es trivial. Supongamos que ∅ ≠ K ≠ X y sea z un elemento del complemento de K. Como X es un espacio Hausdorff, para todo x en K podemos hallar una vecindad V_x de x y una vecindad U_x de z tales que V_x ∩ U_x = ∅. Claramente, los V_x’s determinan una cubierta abierta de K. Como K es compacto una familia finita de ellos, digamos V_x1, ... , V_xm cubren a K. Sea U la intersección de los correspondientes U_xi’s. Entonces,
$U\cap V_{x_{i}}=(\bigcap _{j=1}^{m}U_{j})\cap V_{x_{i}}=\emptyset ,$

ya que $U_{x_{i}}\cap V_{x_{i}}=\emptyset .$ Luego,

$U\cap \bigcup _{j=1}^{m}V_{x_{j}}=\bigcup _{j}(U\cap V_{x_{j}})=\emptyset .$

Lo que implica que U ∩ K = ∅, o sea que U ⊂ K^c. Es decir que K^c es abierto, por lo que K es cerrado.

---

Corolario 11.4.9. En un espacio métrico, los conjuntos compactos son cerrados y acotados.

Demostración. Sea E un espacio métrico y sea K un subconjunto compacto no vacío de E. (El caso vacío es trivial). Como espacios métricos son Hausdorff, sigue de la proposición que K es cerrado. Consideremos el cubrimiento de K formado por las bolas abiertas de radio 1 y centro en cada elemento de K. Dicha familia de abiertos cubre a K y, por ser K compacto, hay una familia finita de ellos que contiene a K. Como cada bola es acotada y la reunión finita de acotados es acotado y K está contenido en esa reunión tenemos que K es acotado.

---

Corolario 11.4.10. Sea X un espacio Hausdorff compacto. Un subconjunto F de X es compacto, ssi, es cerrado.

Demostración. Sea $E$ un espacio métrico y sea $K$ un subconjunto compacto no vacío de $E$. (El caso vacío es trivial). Como espacios métricos son Hausdorff, sigue de la proposición que $K$ es cerrado. Consideremos el cubrimiento de $K$ formado por las bolas abiertas deradio 1 y centro en cada elemento de $K$. Dicha familia de abiertos cubre a $K$ y, por ser $K$ compacto, hay una familia finita de ellos que contiene a $K$. Como cada bola es acotada y la reunión finita de acotados es acotada y $K$ está contenido en esa reunión tenemos que $K$ es acotado.

---

El siguiente ejemplo muestra que el converso del corolario anterior no es válido en general; lo que complicará el estudio de compactos en espacios métricos.

Ejemplo 11.4.3. Espacio métrico donde un conjunto cerrado y acotado no es compacto.

Sea $E$ un espacio métrico discreto infinito. Claramente, $E$ es cerrado y acotado, pero no es compacto.

---

La siguiente proposición resultará, más adelante, útil para probar que ciertas funciones son homeomorfismos.

Proposición 11.4.11. Sean X, Y espacios tales que X es compacto y Y es Hausdorff. Si f : X → Y es biyectiva y continua, entonces f es un homeomorfismo.

Demostración. Sea f : X → Y biyectiva y continua. Probaremos que para cada abierto A de X, f(A) es abierto en Y , para eso es suficiente mostrar que cada cerrado F de X tiene una imagen f(F) cerrada en Y. Si F es vacío, su imagen es vacía y, en consecuencia es cerrada. Supongamos que F no es vacío, sigue, entonces, de la proposición 11.4.1 que F es compacto. Luego por el teorema 11.4.3, f(F) es compacto. Pero, un compacto en un espacio Hausdorff es cerrado (ver la proposición 11.4.8).

---

Terminología. Los espacios compactos Hausdorff tienen muchas propiedades agradables. Además muchos de los espacios compactos interesantes son Hausdorff, por lo que hay varios autores (Bourbaki, Dixmier, por ejemplo) que incluyen la hipótesis de Hausdorff en la definición de compacto. En tales situaciones, se usan nombres tales como cuasicompactos para nuestros compactos.

Ejercicios 11.4

1. Explicar cuando un espacio no es compacto de acuerdo a la definición.
2. Explicar cuando un espacio no es compacto de acuerdo a la proposición 11.3.3.
3. Explicar cuando un espacio topológico discreto es compacto. Examinar, a continuación, un espacio topológico indiscreto.
4. Probar las afirmaciones no probadas en los ejemplos 11.2.1 y 11.2.4.
5. Probar que ]0, 1[ no es compacto.
6. Probar el corolario 11.3.11.
7. Sea X = I² el cuadrado unitario, {(x, y) : 0 ≤ x, y ≤ 1}. La familia C de bolas con centro en un punto del cuadrado y radio 1/10 cubre a X. Probar que hay una subcubierta finita de C que también lo cubre.
8. La reunión de una familia finitas de subconjuntos compacto es compacto.
9. Sea X un espacio infinito con la topología de complementos finitos. Entonces, X es compacto.
10. . Cuando el producto de espacios no vacíos es compacto, entonces, cada factor es compacto. El recíproco es válido, pero no es fácil de probar, ver más adelante el teorema de Tychonoff.
11. Sea X un espacio y B una base de la topología de X. Cada cubierta de X por abiertos de B tiene una subcubierta finita, ssi, X es compacto.
12. Sea X un espacio compacto y R una relación de equivalencia en X. Entonces, el espacio cociente X/R es compacto.
13. Sea S = [0, 1] ⊂ R pero provisto con la topología de complementos finitos, o sea que los cerrados de S son S o los subconjuntos finitos. Probar que en esta topología cualquier subespacio de S, en particular los subconjuntos abiertos, son compactos. ¿Por qué esto no contradice el resultado de la proposición 11.3.13?

La Línea Real

Antes de continuar un estudio general de la compacidad, examinaremos la compacidad donde todo comenzó: la línea real. Veremos varias equivalencias para la compacidad y algunas aplicaciones.

Claramente, como la línea real es un espacio métrico no acotado, sigue del corolario 11.4.10, que no puede ser compacta. Como los intervalos abiertos son homeomórficos a la línea real, tenemos que los intervalos abiertos no pueden ser compactos. En el lado positivo, sabemos que los subconjuntos cerrados y acotados de R son compactos (ver la proposición 11.4.7).

En el capítulo 1 insinuamos, mediante los teoremas B y C, que los intervalos cerrados y acotados eran algo especial—respecto a otro tipo de intervalos. La respuesta es que son compactos. Presentamos, usando tal noción, pruebas de tales teoremas.

Teorema B. (Acotamiento de Funciones) Sea f : [a, b] → R una función continua, entonces hay un real positivo M tal que para todo x en [a, b] se cumple que −M ≤ f(x) ≤ M. En palabras, la función f es acotada.

Teorema C. (Existencia de Máximos y Mínimos Absolutos) Sea f : [a, b] → R una función continua entonces hay números c y d tales que a ≤ c, d ≤ b con f(c) ≤ f(x) ≤ f(d), para todo x en [a, b]. En palabras, la función f alcanza máximos y mínimos absolutos.

Demostración. Sea J = [a, b], por el teorema 11.5.3, la imagen de J por f es un subconjunto compacto de R, por lo tanto, cerrado y acotado (corolario 11.3.14). Lo que muestra en forma inmediata el teorema B. La acotación implica la existencia de un ínfimo, digamos c, y un supremo, digamos d, de f(J). Como f(J) es cerrado, tales números pertenecen a f(J), lo que prueba el teorema C.

---

Un análisis de la prueba, muestra inmediatamente que los resultados de los teoremas mencionados son válidos si reemplazamos [a, b] por cualquier subconjunto compacto de R.

Observación 11.1. Los resultados de los teoremas anteriores se usan (a veces, implícitamente) en el primer curso de Cálculo, especialmente cuando de trata de hallar máximos o mínimos. Una demostración usando solamente la axiomática de los Reales se puede hallar en Spivak [16].

El resultado de que una función continua es acotada se usa, en cursos de Cálculo, para probar que la existencia de la integral de funciones continuas. El resto de esta sección estará dedicado a estudiar propiedades equivalentes a la compacidad de subconjuntos de R. Tales propiedades están contenidos en el siguiente teorema, que resume muchos de los resultados del Análisis del siglo XIX. La demostración del teorema se hará a través de varios lemas, cuyas demostraciones serán interesantes por si mismas. La lectora o lector deberá estar atento a ver cuáles de esas propiedades se generalizan a Rⁿ, a espacios métricos cualesquiera y, finalmente, a espacios topológicos generales.

Teorema 11.5.1 (Teorema de la Compacidad en R). Sea A un subconjunto no vacío de R. Los enunciados siguientes son equivalentes.

(a) A es compacto.

(b) A es cerrado y acotado.

(c) Cada subconjunto infinito de A tiene un punto de acumulación en A.

(d) Cada sucesión de elementos de A tiene una subsucesión convergente.

(e) Cada función continua de A en R es acotada.

---

Antes de continuar con la discusión de esas propiedades introduciremos algunos nombres para las propiedades contenidas en el teorema.

Bolzano–Weierstrass. Decimos que un subconjunto A de un espacio X (cualquiera) tiene la propiedad de Bolzano–Weierstrass o que es un espacio B–W, ssi, cada conjunto infinito de A tiene un punto de acumulación en A. Algunos autores llaman a esta propiedad compacidad enumerable.

Compacidad secuencial. Un subconjunto A de un espacio X es secuencialmente compacto, ssi, cada sucesión de elementos de A tiene una subsucesión convergente en A.

Seudocompacidad. Un subconjunto A de un espacio X es seudocompacto cuando toda función real continua definida en A es acotada.

El teorema establece que cada una de esas propiedades es, en la línea real, equivalente a la compacidad.

---

Como en cualquier espacio métrico un conjunto compacto es cerrado y acotado (ver corolario 11.4.10), sigue de la proposición 11.4.7 el siguiente resultado;

Proposición 11.5.2 (Teorema de Heine–Borel para la Línea Real). Un subconjunto de la línea real es compacto, ssi, es cerrado y acotado.

Esta equivalencia de la compacidad será usada frecuentemente en lo que sigue. En el corolario 7.5.3, vimos que toda sucesión real acotada tiene una subsucesión convergente. Esto implica que cualquier conjunto infinito acotado (que contiene, por lo tanto, a una sucesión acotada) tiene un punto de acumulación. Esta propiedad es muy importante, por lo que la enunciaremos a continuación como una proposición, y daremos otra demostración de la misma. Tal demostración será útil en las generalizaciones..

Proposición 11.5.3 (Bolzano–Weierstrass en R). Todo subconjunto infinito y acotado de R tiene un punto de acumulación.

Demostración. Sea A un conjunto infinito y acotado. Como A es acotado, está contenido en un intervalo cerrado y acotado, digamos [a, b]. La idea de la demostración es construir una sucesión anidada de intervalos cuyos diámetros tiendan a cero, tomar la intersección de tales conjuntos, que contendrá a un único elemento (ver corolario 11.4.6) y probar que ese único elemento es el punto de acumulación deseado. Sea J₀ = [a, b]. Dividamos en intervalo J₀ por su punto medio en dos subintervalos. Escogemos al subintervalo que contiene infinito puntos de A y le llamamos J₁. Al menos uno de ellos debe tener infinitos elementos, cuando ambos tengan infinitos elementos seleccionamos el subintervalo de la izquierda. Notemos que el diámetro de J₁ es igual a la mitad del diámetro de J₀, es decir que δ(J₁) = (b − a)/2. Supongamos construidos de la manera anterior, J₂, ... , J_k tales que

(i) J_k contiene infinitos puntos de A,

(ii) J_k ⊂ J_k−1 ⊂ ... ⊂ J₁ ⊂ J₀, y

(iii) δ(J_k) = (b − a)/2^k. (diámetro).

Repitiendo el proceso anterior con J_k, obtendremos un J_k+1 ⊂ J_k que tiene infinitos puntos de A y cuyo diámetro es igual a la mitad del diámetro de J_k, es decir, igual a (b − a)/2^k+1. Por inducción, obtenemos la sucesión de intervalos anidada anunciada. Luego, por el corolario 11.4.6, tenemos que la intersección de todos los J_n’s contiene exactamente un punto, digamos z. Probaremos que z es un punto de acumulación de A. Sea V una vecindad de z, por definición de vecindad hay un r > 0 tal que la bola abierta B(z; r) está contenida en V . Como la sucesión (b − a)/2ⁿ → 0, hay un n tal que m ≥ n implica que (b − a)/2^m < 2r, lo que implica que el intervalo Jm que contiene a z, está contenido en B(z : r) ⊂ V . Por lo que V contiene un punto (de hecho infinitos puntos) de A diferentes de z. Luego, z es un punto de acumulación de A.

---

Observación 11.2. Notemos que el subconjunto N de la línea real es infinito, pero no tiene punto de acumulación. Es decir que la condición de acotado es esencial.

Lema 11.5.4. Un subconjunto infinito A de la línea real es compacto, ssi, tiene la propiedad de Bolzano–Weierstrass.

Demostración. (⇒) Subconjuntos compactos son acotados, por lo que el la proposición 11.5.3 implica A tiene un punto de acumulación. Como conjuntos compactos son cerrados, dicho punto de acumulación está en el conjunto.
(⇐) Sea A un subconjunto de la línea real con la propiedad B-W. Si A es finito, trivialmente tenemos que A es cerrado y acotado, por lo tanto, compacto. Supongamos, entonces, que A es infinito. Probaremos que es cerrado y acotado. Sea z un punto de acumulación de A. Entonces, hay una sucesión (x_n) de puntos de A que convergen a z. Entonces, z es un punto de acumulación de {x_n : n ∈ N} ⊂ A. Por la hipótesis, z está en A, lo que implica que A es cerrado. Supongamos ahora que A no fuera acotado, digamos superiormente. Sea x₁ un punto cualquiera de A tal que x₁ > 1. Como A no está acotado superiormente, podemos hallar un x₂ > 2 tal que x₁ < x₂. Análogamente (por inducción), cuando hemos hallado x₁ < x₂ < ... < x_n con x_n > n, podremos hallar un x_n+1 tal que n + 1 < x_n+1. Por inducción, obtendremos una sucesión no acotada, por lo que el conjunto S de los términos de la sucesión así formada es infinito y no acotado. Por la hipótesis, debe haber un punto de acumulación de S, que será el límite de una subsucesión (y_n) de (x_n). Luego, por ser convergente, la sucesión (y_n) debe ser acotada (ver 7.2.8), pero por la generación de los x_n’s debe ser no acotada. Esta contradicción concluye la prueba. El caso acotado inferiormente queda de ejercicio.

---

Lema 11.5.5. Un subconjunto de la línea real es compacto, ssi, es secuencialmente compacto.

Demostración. Usaremos la caracterización de compacto como cerrado y acotado. (⇒) Sea A un conjunto compacto, o sea cerrado y acotado y sea (s_n) una sucesión en A. Por ser acotado A, hay un real m tal que
A ⊂ [−m,m]. Consideremos al subconjunto S = {s_n} de A formado por los términos de la sucesión. Si S fuera finito, entonces hay al menos un término cuyo valor se repite infinitas veces, definiendo una subsucesión convergente. En caso contrario. la proposición 11.5.3 nos dice que hay un punto de acumulación de S, o que produce una sucesión de S convergente al punto de acumulación. Tal sucesión es la subsucesión deseada. (⇐) Sea A un conjunto secuencialmente compacto. Sea p un punto de acumulación de A. Sabemos que entonces hay una sucesión de números en A diferentes de p, que converge a p. Por la hipótesis, p está en A, o sea que A es cerrado. Supongamos que A no fuera acotado. Entonces, podremos hallar una sucesión (x_k) tal que |x_k| ≥ k. Tal sucesión no es acotada, lo mismo que cualquier subsucesión de ella, por lo tanto, no puede tener una subsucesión convergente a un punto de A.

---

Lema 11.5.6. Un subconjunto A de R es compacto,ssi, cada función real continua definida en A es acotada.

Demostración. (⇒) Ejercicio. (Sug.Mirar la prueba de los teoremas B y C; o usar el teorema 11.4.3.)
(⇐) Consideremos la función valor absoluto restringida a A. Como valor absoluto es una función continua, la hipótesis de seudocompacidad implica que es acotada. Luego, A es un conjunto acotado. Probaremos que también es cerrado. Supongamos que no, y sea z un punto de la clausura de A que no está en A. Entonces, para todo x en A, |x − z| > 0 y acotado. Lo que implica que la función x → 1/|x − z| es continua, pero no es acotada. Contradicción. Lo que prueba el resultado..

---

Con los lemas 11.5.4, 11.5.5 y 11.5.6 se concluye al prueba del teorema 11.5.1.

---

Notemos que las equivalencias fueron hechas en cada lema con la propiedad de cerrado y acotado. Podríamos haber adoptado otro esquema, como se sugiere en el siguiente esquema.

Equivalencias de Compacidad

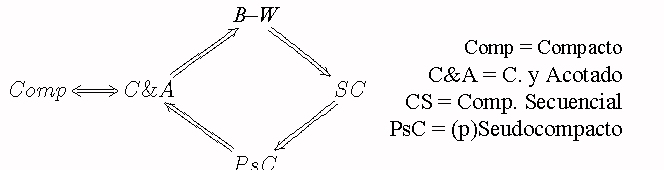
Dejaremos al cuidado del lector de tratar de producir una demostración siguiendo ese esquema, o cualquier otro para la parte cíclica de la derecha. Las equivalencias directa con la definición de compacto son usualmente complicadas. ¿Cuáles de las equivalencias pueden extenderse a Rⁿ? ¿a espacios métricos cualesquiera? ¿a espacios topológicos cualesquiera? ¿Cuáles de las equivalencias pueden extenderse a Rⁿ? ¿a espacios métricos cualesquiera? ¿ a espacios topológicos cualesquiera?

Ejercicios 11.5

1. Probar que los intervalos abiertos (acotados o no), así como los intervalos semiabiertos (acotados o no) no son conjuntos compactos.
2. Hallar un cubrimiento abierto del intervalo (0, 1) que no tenga recubrimiento finito.
3. Hallar un cubrimiento abierto de la línea real que no tenga recubrimiento finito. ¿Por qué esto implica que los intervalos abiertos no son compactos?
4. El Conjunto de Cantor es compacto.
5. Probar que la propiedad de intervalos encajados (ver corolario 11.4.6) implica la propiedad de Bolzano–Weierstrass (ver también a la proposición 11.5.3).
6. Sea f : [a, b] → [c, d] una función continua estrictamente creciente (x < y =⇒ f(x) < f(y)) tal que f(a) = c y f(b) = d. Probar que f es un homeomorfismo.
7. Suponga conocido que el cubo unitario I² de R²

   a) Cualquier “cuadrado ] − M,M[ × ] − M,M[, donde M es un real positivo cualquiera, es compacto.

   b) La circunferencia y círculo con centro en el origen y radio 1 son conjuntos

   compactos.

   c) Cualquier bola cerrada de R² es un conjunto compacto.

8. Probar que la propiedad de Bolzano–Weierstrass (proposicion 11.5.3) para I². Es decir que cada subconjunto infinito A de I² tiene un punto de acumulación en A.

El Teorema de Tychonoff

La extensión del estudio de la compacidad a Rⁿ y otros espacios requiere relacionar la compacidad de un producto a la compacidad de los factores. Esto se logra con el teorema de Tychonoff, que es uno de los teoremas más famosos e importantes de la topología.

Teorema 11.6.1 (Tychonoff). El producto de una familia cualquiera de conjuntos compactos es compacto.

El teorema, con la generalidad indicada, requiere para su demostración de algunas nociones avanzadas de la teoría de conjuntos (axioma de selección, lema de Tukey) que están fuera del alcance de este texto. Nos limitaremos, en consecuencia, al caso de una familia finita, lo que será suficiente para nuestros propósitos. Usaremos en la demostración el siguiente lema general.

Lema 11.6.2. Sea X un espacio topológico y B = (B_i: i∈I) una base de los abiertos de X. Si cada cubierta de X por abiertos de B tiene una subcubierta finita, entonces X es compacto.

Demostración. Sea (U_j), j en J, una cubierta abierta de X. Cada abierto de la cubierta es una reunion de abiertos de la base. Supongamos que U_j = ∪_k B_j,k, con cada B_j,k es un abierto de la base y los base y los k’s están en un subconjunto K de I. Luego,
$X\subset \bigcup _{j}U_{j}=\bigcup _{j}\bigcup _{j,k}B_{j,k}.$

Lo que implica que los B_j,k’s determinan una cubierta de X. Por la hipótesis, dicha cubierta tiene una subcubierta finita, digamos C₁, C₂, ...C_m. Cada C_i es alguno de los B_j,k, por lo que está contenido en, digamos, U_j,k . Luego,

$X\subset \bigcup _{j=1}^{m}C_{j}\subset \bigcup _{j=1}^{m}U_{j_{k}}.$

Lo que muestra que la cubierta original tiene una subcubierta finita, es decir que X es compacto.

---

Teorema 11.6.3 (Teorema de Tychonoff finito). El producto de una familia finita de espacios topológicos compactos es compacto.

Demostración. Probaremos que el producto de dos espacios compactos Z = X × Y es compacto. El resultado seguirá entonces por inducción. Usaremos el lema anterior para la demostración. Consideraremos la base de abiertos de Z consistente de los abiertos de la forma U ×V , donde U es un abierto de X y V un abierto de Y . Sea B = {U_i × V_i : i ∈ I} una cubierta de Z; probaremos que hay una subcubierta finita de B. Sea x₀ un punto de X y consideremos al subespacio {x₀} × Y de Z. Dicho subespacio es homeomórfico a Y ; por lo que es compacto. La familia B es una cubierta de tal subespacio, por lo que hay un subconjunto finito J_x0 de I, tal que la familia C = (U_j × V_j), j ∈ J_x0, es una subcubierta de {x₀} × Y . Sin perdida de generalidad, podemos suponer que cada elemento de esa subcubierta contiene a {x₀}×Y (si algún elemento de la subcubierta no contuviera a ese subespacio, lo podemos eliminar de la subcubierta, y el resultado continuaría cubriendo a {x₀} × Y ). Sea U_x0 = ∪ {U_j : j ∈ J_x0}. Entonces, tenemos que, para j en J_x0,
${\begin{array}{rcl}\{x_{0}\}\times Y&\subset &U_{x_{0}}\times Y=U_{x_{0}}\times \bigcup _{j}\{V_{j}:j\in J_{x_{0}}\}\\&=&\bigcup _{j}\{U_{x_{0}}\times V_{j}\}\subset \bigcup _{j}(U_{j}\times V_{j}).\end{array}}$

Lo que muestra que la familia C es una cubierta abierta de U_x0 × Y . Consideremos ahora la familia (U_x), x∈X, donde U_x se obtiene como arriba. Como X es compacto hay un subconjunto finito {x₁, x₂, ... , x_m} de X tal que U_x1 ∪U_x2 ∪...∪U_xm cubre a X. Sea J = J_x1 ∪J_x2 ∪...∪J_xm. J es un conjunto finito, por ser reunión de finitos. Sea (x, y) un punto de Z, entonces hay un k tal que x pertenece a U_xk , 1 ≤ k ≤ m. Luego, (x, y) está en U_xk × Y , conjunto que, por el trabajo inicial, está contenida en U_j × V_j, j ∈ J_xk. Luego, la familia (U_j×V_j ), j∈J es una subcubierta finita de B. Lo que prueba queX×Y es compacto.

Sea X_i, i = 1, ... , m una familia finita de espacios compactos. Sabemos que el teorema es válido cuando m = 2. Si el teorema fuera valido para productos de k compactos, entonces tendremos para k + 1 espacios compactos que

$\prod _{i=1}^{k+1}X_{i}=(\prod _{i=1}^{k}X_{i})\times X_{k+1}.$

Como, por lo anterior, la expresión de la derecha es el producto de dos espacios compactos, se tiene que el teorema es válido para el producto de (k + 1) espacios compactos. Por inducción, tenemos el resultado.

---

Observación. ¿Por qué la demostración dada para el producto de dos compactos no sirve para un producto general?

Básicamente, porque los abiertos de las bases—en el caso general—no tienen la forma indicada en la prueba del caso finito. La demostración del teorema general requiere de un lema semejante al lema 11.5.2 con subbases en lugar de bases. Tal demostración aparece, entre otros, en Simmoms [15].

Ejercicios 11.6

1. Probar que el cílindro y la cinta de Moebius son espacios compactos.

La Compacidad en Rⁿ

La teoría de los conjuntos compactos en Rⁿ es semejante a la teoría en a línea real, como veremos en esta sección. Esto se debe, en primer lugar, a que conjuntos cerrados y acotados son compactos. Nuestro primeros resultados, serán los análogos a aquellos en el corolario 11.4.5 y en la proposición 11.4.7. Aplicando el teorema de Tychonoff al cubo unitario Iⁿ, vemos que se trata de un conjunto compacto, ya que I = [0, 1] es compacto y
Iⁿ = I × ... × I (n veces).

En forma más general, tenemos el siguiente resultado.

Lema 11.7.1. El cubo C(0;M) = {(x_i) ∈ Rⁿ : para todo i, − M ≤ x_i ≤ M} es compacto.

Demostración. C(0;M) = J × ... × J (n veces), donde J = [−M,M]. El resultado sigue del teorema de Tychonoff.

---

Veremos que el teorema básico de la compacidad de Rⁿ, es totalmente análogo al teorema correspondiente (teorema 11.4.1) para la línea real. Dos resultados fueron importantes en las demostraciones del teorema mencionado. Veremos los correspondientes análogos para Rⁿ.

Proposición 11.7.2 (Teorema de Heine–Borel para Rⁿ). Un subconjunto de Rⁿ es compacto, ssi, es cerrado y acotado.

Demostración. Cualquier conjunto compacto de un espacio métrico es cerrado y acotado. El enunciado recíproco, sigue de que un conjunto acotado está contenido en un cubo centrado en el origen, que es compacto. Por lo que un subconjunto cerrado de él, será compacto.

---

Proposición 11.7.3 (Bolzano–Weierstrass en Rⁿ). Todo subconjunto infinito y acotado de Rⁿ tiene un punto de acumulación en A.

Demostración. La idea de la demostración es análoga a aquella de la proposición 11.5.3. Sea A un conjunto infinito y acotado. Como es acotado, está contenido en un cubo cerrado, digamos C. La idea de la demostración es construir una sucesión anidada de intervalos cuyos diámetros tiendan a cero, tomar la intersección de tales conjuntos, que contendrá un único elemento y ver que ese único elemento es el punto de acumulación deseado. Ilustraremos la construcción para el caso n = 2. Sea A un conjunto infinito acotado de Rⁿ. Entonces, habrá un cuadrado C₀ centrado en el origen que contienea A. Dividiendo C₀ por líneas que pasa por los puntos medios de sus lados, obtendremos cuatro cuadrados cuya reunión es C₀, Al menos uno de ellos, digamos C₁ contiene infinitos puntos de A. Repitiendo con C₁ el procedimiento anterior, obtendremos C₂. Por inducción, obtenemos una sucesión anidada C_n de cerrados con diámetro tendiendo a cero. El resto de la prueba es idéntica al de la proposición citada.

---

Las equivalencias de compacidad en Rⁿ son totalmente análogas a aquellas de la línea real, ya que tenemos el siguiente teorema.

Teorema 11.7.4 (Compacidad en Rⁿ). Sea A un subconjunto no vacío de Rⁿ. Los enunciados siguientes son equivalentes.

(a) A es compacto.

(b) A es cerrado y acotado.

(c) A es B–W (compacto enumerable). Cada subconjunto infinito de A tiene punto de acumulación en A.

(d) A es secuencialmente compacto. Cada sucesión de tos de A tiene una subsucesión convergente en A.

(e) A es seudocompacto. Cada función continua definida en A es acotada.

---

La demostración de la proposición quedará de ejercicio. Básicamente, las demostraciones del teorema correspondiente para la línea real, se pueden extender al caso de Rⁿ. Además, en próxima sección probaremos esas equivalencias para espacios métricos cualesquiera, con la excepción de cerrado y acotado que no es válida en general. Vale la pena, para entender la riqueza de relaciones envueltas tratar de hacer las demostraciones con las herramientas que tenemos.

Sugerencias para las demostraciones.

1. Cerrado y acotado implica B–W. Ver el lema 11.5.3.
2. B-W, ssi, secuencialmente compacto. Ver la proposición11.5.5
3. Secuencialmentre compacto implica cerrado y acotado. Ver el lema 11.5.5.
4. Cerrado y acotado, ssi, seudocompacto. Ver el lema 11.5.6.

Ejemplo 11.7.1. Cuando A un espacio seudocompacto, A es compacto (cerrado y acotado).

Resolución. Consideremos la función || · || restringida a A. Como norma es una función continua, la hipótesis de seudocompacidad implica que es acotada. Luego, A es un conjunto acotado. Probaremos que también es cerrado. Supongamos que no, y sea z un punto de la clausura de A que no está en A. Entonces, para todo x en A, d(x, z) > 0 y acotado. Lo que implica que la función x ↦ 1/d(x, z) es continua, pero no es acotada. Contradicción. Lo que prueba el resultado.

---

Aplicaciones

Usaremos los resultados anteriores para dirimir una antigua interrogante. Probaremos que los espacios normados de dimensión finita son topológicamente equivalente a los espacios euclídeos Rⁿ.

Proposición 11.7.5. Todas las normas de Rⁿ son topológicamente equivalentes.

Demostración. Sea N.una norma cualquiera (o sea se cumple lo especificado en la definición 3.5) y sea || • || la norma euclídea usual. Probaremos que hay reales m y M tales que para todo x en Rⁿ se cumple que
m||x|| ≤ N(x) ≤ M||x||. (*)

Sigue entonces de la proposición 8.5.4 que las normas serán equivalentes. Sea e₁, ... e_n la base canónica de Rⁿ y sea x = ∑_i x_i e_i. Sea M = n máx{N(x) : 1 ≤ i ≤ n}. Como solamente el vector nulo tiene norma 0, se tiene que M es un número positivo.

Además

$N(x)=N\sum _{i}x_{i}e_{i}\leq \sum _{i}|x_{i}|\,|N(e_{i})|\leq {\frac {M}{n}}\sum _{i}|x_{i}|.$

Pero, como siempre se cumple que |x_i| ≤ ||x||, concluimos que

$N(x)\leq {\frac {M}{n}}\sum _{i}|x_{i}|\leq M||x||.$

En particular, N(x − y) ≤ M||x − y||, lo que implica que N.es una función continua de E en R. Sea S = Sⁿ⁻¹ la esfera unitaria, que sabemos que es un conjunto compacto. Por lo que N.alcanza máximo y mínimo en S. Sea m dicho mínimo que será un número positivo, ya que ninguno de los vectores de la esfera es nulo. La relación es válida cuando x = 0. Suponiendo x ≠ 0, sea c = ||x||^-1. Entonces ||cx|| = 1, lo que implica N(cx) = |c|N(x) ≥ m, es decir que N(x) ≥ m/|c| = m||X||.

---

Observación 11.3. El resultado anterior requiere esencialmente que el espacio normado sea de dimensión finita.

Ejercicio 11.7

1. Probar que cualquier bola cerrada y cualquier esfera de Rⁿ son conjuntos compactos.
2. Probar que las celdas de Rⁿ, productos de intervalos cerrados de los factores, son conjuntos compactos.
3. Probar que conjuntos abiertos no vacíos de Rⁿ no son conjuntos compactos.

La Compacidad en los Espacios Métricos

Históricamente, la idea de la compacidad surgió de tratar de extender los teoremas clásicos del Análisis, teorema 11.7.4 de la sección anterior, a espacios métricos generales, especialmente a espacios de funciones. Queremos probar para espacios métricos cualesquiera el análogo al teorema citado. El mayor obstáculo para la extensión es que, en general, cerrado y acotado no implica compacto. Basta con considerar un espacio métrico discreto infinito E. Claramente es cerrado y acotado, pero no puede ser compacto, ya que la colección de {x}, x en E es una cubierta abierta de E que no admite subcubierta finita.

Como nuestras pruebas para Rⁿ se basaban principalmente en las equivalencias de compacto con cerrado y acotado, necesitaremos nuevas pruebas. Debido a la generalidad, tendremos que proceder con bastante delicadeza, es decir con argumentos muy sutiles. La exposición está basada principalmente en el texto de Simmons.

Equivalencias de Compacidad

Probaremos, a continuación, las siguientes equivalencias.

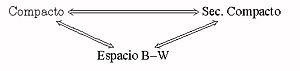
Empezaremos con la siguiente equivalencia.

Proposición 11.8.1. Un espacio métrico E tiene la propiedad B–W, ssi, es secuencialmente compacto.

Demostración. Supondremos que el espacio E es secuencialmente compacto y probaremos B–W. Sea X un subconjunto infinito de E. Como X es infinito, podemos formar una sucesión (x_n) de puntos diferentes de X. Por la hipótesis, dicha sucesión tiene una subsucesión convergente a un punto de X. El límite de esa sucesión es un punto de acumulación de los términos de la subsucesión que forman un subconjunto de X, por lo que dicho límite es un punto de acumulación de X. Supongamos, ahora, que se cumple la propiedad de B–W. Sea (x_n) una sucesión en E. Consideremos al conjunto S = {x_n} formado por los términos de la sucesión. Si S es finito, un valor de los términos se repite infinitas veces, la subsucesión constante asociada con dicho valor es convergente. Si S es infinito, por la hipótesis, hay un punto de acumulación de S. Dicho punto es un punto de acumulación de S, por lo que podemos extraer una subsucesión que converge a dicho punto de acumulación.

---

Proposición 11.8.2. Cada espacio métrico compacto tiene la propiedad B–W.

Demostración. Sea E un espacio métrico compacto y sea A un subconjunto infinito de A. Supongamos que A no tuviera un punto de acumulación. Entonces, para cada x de E, hay una bola abierta con centro en x que no contiene punto alguno de A, excepto x cuando x está en A. La reunión de esas bolas abiertas es una cubierta de E, por la compacidad de E hay una subfamilia finita que cubre a E y, en particular a A. Por lo que A debe ser finito. Esto contradice la hipótesis, luego A debe tener un punto de acumulación.

---

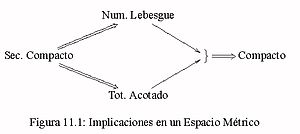
Figura 11.1: Implicaciones en un Espacio Métrico Para completar nuestras equivalencias, bastará con probar que en cada espacio

métrico secuencialmente compacto es compacto. Esto será establecido usando dos conceptos auxiliares, que son interesantes por si mismos, el número de Lebesgue de una cubierta de abiertos y la noción de espacio totalmente acotado.

Número de Lebesgue

Sea (G_i) una cubierta abierta de un espacio métrico E. Para cada x de X hay un abierto de la cubierta que contiene una r–vecindad de x. Si escogemos otro punto, y repetimos el mismo proceso, podremos hallar una r′–vecindad del nuevo punto totalmente contenida en un abierto de la cubierta. En general, el radio de la bola abierta conteniendo al punto variará de punto en punto. Sin embargo, en algunos casos, un mismo radio servirá para todos los puntos, como veremos más adelante. Tal situación merece un nombre especial.

Definición. (Número de Lebesgue) Llamamos número de Lebesgue de una cubierta (G_i) de un espacio métrico E a un número λ, ssi, cada subconjunto de E cuyo diámetro es menor que λ está totalmente contenido en alguno de los abiertos de la cubierta.

Necesitaremos el siguiente resultado para la prueba de la próxima proposición.

Lema 11.8.3. Sea A un subconjunto de un espacio métrico E tal que δ(A) = r y tal que A ∩ B(x;r) ≠ ∅. Entonces, A está contenido en B(x;2r).

Demostración. Sea y un elemento de A y z un elemento de la intersección. Entonces, d(y, x) ≤ d(y, z) + d(z, x) < r + r = 2r.

---

---

Proposición 11.8.4 (Lema de las Cubiertas de Lebesgue). Cuando un espacio métrico es secuencialmente compacto, cada cubierta abierta del espacio tiene un número de Lebesgue.

Demostración. Sea E un espacio métrico secuencialmente compacto y sea (G_i)i∈I una cubierta de E. Digamos que un conjunto es “grande” si no está contenido en un abierto de la familia. Si no hay conjuntos grandes, cualquier número positivo servirá como nuestro número de Lebesgue, a. Supongamos, ahora, que hubiera conjuntos “grandes” y sea a′ el ínfimo de sus diámetros. Claramente, 0 ≤ a′ ≤ +∞. Si a′ = +∞, cualquier número positivo servirá como nuestro λ. Si a′ > 0, entonces λ = a′ servirá para nuestra proposición. Veremos, a continuación, que si a = 0, obtendremos una contradicción. Como cada conjunto grande tiene al menos dos elementos, y a′ = 0, concluimos que para todo n > 0, hay un conjunto grande C_n tal que 0 < δ(C_n) < 1/n. Escojamos un punto x_n en cada C_n. Como E es secuencialmente contacto, la sucesión (x_n) tiene una subsucesión (y_n) convergente a un punto y de E. Tal punto está en uno de los elementos de la cubierta, digamos G_j , j ∈ I. Hay, por lo tanto, una r–vecindad de y totalmente contenida en G_j . Sea B la r/2–vecindad de y, como y_n → y, hay un n₁ tal que n ≥ n₁ implica que y_n está en B. Sea n0 tal que 1/n₀ < r/2 y n₀ ≥ n₁. Como δ(C_n0) < 1/n₀ < r/2, concluimos, usando el lema previo, que C_n0 ⊂ B(y;r) ⊂ G_j . Lo que contradice que C_n0 fuera grande. Luego, a′ > 0.

---

ε–redes, Total Acotamiento

Definición. (ε–redes, Total Acotamiento) Sea E un espacio métrico. Un subconjunto A de E es una ε–red de E, ε > 0, ssi, A es finito y (B"(x)), x en A. es una cubierta de E.

Decimos que E es totalmente acotado, ssi, para cada ε > 0 hay una ε–red de E.

Proposición 11.8.5. Cada espacio secuencialmente compacto es totalmente acotado.

Demostración. Sea E un espacio métrico secuencialmente compacto y sea ε > 0 dado. Escojamos un a₁ en E y consideremos la bola abierta B₁ = B(a;ε). Si X = B₁, entonces {a₁} es una ε–red para E. En caso contrario hay un a₂ fuera de B₁ y consideramos la ε–vecindad B₂ = B(a₂;ε). Si B₁ ∪ Bub>_{2</s cubre a X, entonces {a1, a2} es un ε–red para E. Supongamos que hemos generado de esa manera a1, a2, ... ak, donde Bi una ε- vecindad de ai. Si la reunion B1 ∪ ... ∪ Bk cubre a X, el conjunto {a1, ... , ak} es una ε–net para E. En caso contrario, hallamos un ak+1 fuera de la reunión anterior y formamos Bk+1 como la ε–vecindad de ak+1. Si ninguna reunión de los Bi’s así obtenidos cubre a E, habremos generado una sucesión (an) que no tiene subsucesión convergente (d(ak+1, ai) ≥ ε, para i ≤ k), lo cual contradice que E fuera secuencialmente compacto. Por lo que el proceso anterior debe finalizar en una cantidad finita de pasos, generando una ε–red para E.}

---

Usando las proposiciones anteriores, probaremos lo que nos resta de las equivalencias de la figura 11.1.

Proposición 11.8.6. Cada espacio métrico secuencialmente compacto es compacto.

Demostración. Sea E une espacio métrico secuencialmente compacto y sea (G_i) una cubierta abierta de E. Por la proposición 11.8.4 la cubierta tiene un número de Lebesgue λ. Sea r = λ/3 y sea A = {a₁, ... , a_m} una ε–red para E. Sea B_k la ε–vecindad de a_k. Entonces, (i) la reunión de los B_k cubre a E y (ii) el diámetro de cada B_i es menor que 2ε < λ. Luego, cada B_k está contenido en uno de los G_i, digamos G_Ik , 1 ≤ k ≤ m. Luego, la reunión de los B_k (que cubre a E) está contenida en la reunión de los G_ik, que es, por lo tanto, una subcubierta finita de E. Conclusión, E es compacto.

---

Resumen

Teorema 11.8.7 (Compacidad en Espacios Métricos). Sea E un espacio métrico. Los enunciados siguientes son equivalentes.

(a) E es compacto.

(b) E tiene la propiedad B–W.

(c) E es secuencialmente compacto.

(d) E es totalmente acotado y cada cubierta tiene un número de Lebesgue.

---

Ejercicios 11.8

1. Sea A un subconjunto compacto de un espacio métrico compacto. ¿Es necesariamente compacto el complemento de A?
2. Sea A un subconjunto compacto de un espacio métrico E y sea f : E → F una función continua en un espacio métrico E. Probar que si y es un punto de la frontera de f(A), hay un x en A tal que f(x) = y.
3. Un espacio métrico totalmente acotado es acotado.
4. Probar que, en los Reales, acotado y totalmente acotado son equivalentes. ¿Es eso cierto para R²? ¿para un espacio métrico cualquiera?
5. Considerar a los Reales con la métrico discreta 0–1. Probar que se trata de un espacio acotado que no es totalmente acotado.
6. Todo espacio compacto es seudocompacto, ¿será cierto que un espacio métrico seudocompacto es compacto?

Compacidad y Completitud

Hay interesantes relaciones entre la completitud (cada sucesión de Cauchy es convergente) y la compacidad, como veremos a continuación.

Proposición 11.9.1. Sea E un espacio métrico. Los enunciados siguientes son equivalentes.

(a) E es compacto.

(b) E es totalmente acotado y completo.

Demostración. (a) ⇒ (b). Como E es compacto es totalmente acotado. Como es compacto es secuencialmente compacto, por lo que cada sucesión de Cauchy tiene una subsucesión convergente; pero esto implica que la sucesión es convergente, por lo que el espacio es completo.
(b) ⇒ (a). (Simmons) Probaremos que E es secuencialmente compacto. Como E es completo, bastará con probar que cada sucesión tiene una subsucesión de Cauchy. Sea (x_1n) un sucesión tal que S₁ = {x_1n} es un conjunto infinito; para simplicidad de la exposición denotaremos la sucesión por su conjunto de términos (la razón del doble subscript se verá más adelante). Como E es totalmente acotado, hay un cubrimiento finito por bolas abiertas de radio 1/2. Luego, S₁ debe contener una subsucesión S₂ = {x₂₁, x₂₂, ... } que está contenida en una de esas bolas. Aplicando nuevamente el acotamiento total a bolas de radio 1/3, se ve que hay una subsucesión S₃ = {x_3n : n=1,2, ...} que está totalmente contenida en una bola de radio 1/3. Inductivamnete, continuamos hallamos S_k = {x_k1, x_k2, ... } totalmente contenido en una bola de radio 1/k, k = 4, 5, . . . . Sea
S = {x₁₁, x₂₂, x₃₃, ... }.

La sucesión así definida es una subsucesión de S₁. La construcción de la sucesión muestra que es de Cauchy.

---

Corolario 11.9.2. Un subconjunto cerrado de un espacio completo es compacto, ssi, es totalmente acotado.

Demostración. Un subespacio cerrado de un espacio completo es completo.

---

La Continuidad Uniforme

La siguiente proposición establece una propiedad de las funciones continuas con dominio un compacto que tiene profundas consecuencias en Análisis y otras ramas de la matemática. Enunciaremos la proposición para discutir de forma más precisa su significado; la demostración aparecerá más tarde.

Proposición 11.10.1. Sea f : E → F continua entre espacios métricos con E compacto. Entonces, para todo ǫ > 0 hay un δ > 0 tal que para todo x, y en E se cumple que

d(x, y) < δ ⇒ d(f(x), f(y)) < ε

¿Cuál es la diferencia con continuidad? Diremos que una función que satisface la propiedad de la proposición es uniformemente continua. Analizaremos a continuación cuál es la diferencia con la continuidad que hemos usado hasta ahora.

La definición de continuidad para f : E → F, continua en cada punto de E, establece que para todo p de E, para todo ε > 0 hay un δ > 0 tal que para todo x se cumple que

d(x, p) < δ ⇒ d(f(x), f(p)) < ε.

Aparte de una diferencia en notación, pareciera no haber demasiada diferencia. Para apreciar mejor lo diferente, escribiremos en forma simbólica total las definiciones y haremos semejantes las notaciones. Simbólicamente, tenemos

---

Continuidad. ∀y ∈ E, ∀ε > 0, ∃δ > 0, ∀x ∈ E, d(x, y) < δ ⇒ d(f(x), f(y)) < ε.

Continuidad Uniforme. ∀ε > 0, ∃δ > 0, ∀y ∈ E, ∀x ∈ E, d(x, y) < δ ⇒ d(f(x), f(y)) < ε.

---

Observemos que no hay diferencia entorno a la implicación, la diferencia está en la posición del cuantificador referente a y. ¿Qué significa esto? En el caso de la continuidad, el δ que existe depende tanto del y como del ε, es decir que para puntos diferentes del espacio, pudiera ser que no habrá un δ que funciones con todos los puntos (y); mientras que en el caso de la continuidad uniforme podemos hallar un δ que funciona uniformemente con todos los puntos del espacio. La proposicion 11.6.6 establece que tal situación siempre sucede cuando el dominio de la función es compacto.

Demostración de la proposición 11.9.1. Sea f : <E, d₁> → <F, d₂₁> continua y sea ε > 0 dado. Para cada y de F, consideremos la bola abierta de radio ε/2 con centro en y. Las preimágenes (imagen inversa) de esas bolas forman un cubrimiento de E. Como E es compacto, es secuencialmente compacto, y tiene, por lo tanto, un número de Lebesgue del cubrimiento, digamos δ > 0. Si x y x′ son elementos de E tales que d₁(x, x′) < δ, entonces {x, x′} tiene diámetro menor que δ, por lo que está contenidos en una de las preimágenes de bolas usadas arriba; luego f(x) y f(x′) pertenecen a una de las bolas de radio ε/2, por lo que d₂₁(f(x), f(x′)) < ε.

---

La Compacidad en Espacios Topológicos

Las propiedades equivalentes de los teoremas de compacidad en espacios métricos no se pueden extender a espacios topológicos cualesquiera. La aparición de “acotado” en algunas de las equivalencias, sugieren claramente que tales equivalencias no hacen sentido en espacios topológicos arbitrarios.

En el lado positivo, se tiene la siguiente cadena de implicaciones, cuyas demostraciones daremos más adelante.

Compacidad en Espacios Topológicos

Se puede hallar ejemplos que muestran que las implicaciones son estrictas.

Proposición 11.11.1. Cualquier espacio compacto es B–W (compacto enumerable).

Demostración. Sea X un espacio compacto y sea A un subconjunto finito de X. Supongamos que A no tiene punto de acumulación. Entonces, A y cualquier subconjunto de A, son cerrados. Como A es infinito, hay una sucesión (x_n) de puntos de A, diferentes entre si. Sea A_n = {x_k : k ≥ n}, n = 1, 2, . . . . Cada A_n es cerrado y la familia de los A_n es una secuencia anidada que tiene, por lo tanto, la propiedad de la intersección finita. Sin embargo, ∩ A_n es vacío, por lo que X no pude ser compacto; lo que contradice la hipótesis. Luego, A debe tener un punto de acumulación en X.

---

Proposición 11.11.2. Cualquier espacio B–W (compacidad enumerable) es seudocompacto.

Demostración. Sea X un espacio con la propiedad de B–W. Supongamos que hay una función continua f : X → R que no es acotada. Sin perdida de generalidad supondremos que f no es acotada superiormente (en caso contrario, usar −f). Como n no es acotada superiormente, para todo n en N podremos hallar un x_n tal que f(x_n) > n. El conjunto S = {x_n : n ∈ N} contiene infinitos puntos, ya que en caso contrario, f(S) sería acotado, lo que contradice la definición de los x_n’s. Como el espacio X es B−W, el conjunto S tiene un punto de acumulación, digamos y en X. Sea z = f(y), como f es continua, z es un punto de acumulación de f(S). Sea m el menor entero tal que z < m. Por la definición de los x_n, hay solamente una cantidad finita de x_k tales que f(x_k)< m. Sea r el mínimo entre las distancias de esos f(x_k) a z, y de la distancia de z a m. Entonces, la r–vecindad de z no contiene puntos de f(S), lo que congradice su condición de punto de acumulación de ese conjunto. Luego, f dbe ser acotada.

---

Proposición 11.11.3. Cualquier espacio secuencialmente compacto es B–W.

Demostración. Sea X un espacio secuencialmente compacto. Sea A un subconjunto infinito de X. Como X es infinito, podemos formar una sucesión (x_n) con los elementos de X. Por ser X secuencialmente compacto, hay una subsucesión y_nk> de los (x_n) convergente a un punto y. Tal y es un punto de acumulación del conjunto de los y_nk> y, por lo tanto, de los (x_n), o sea que y es un punto de acumulación de A. Luego, X es B–W.

---

Una de las mayores dificultades con espacios topológicos arbotrarios reside en que sucesiones pueden tener más de un punto límite y que puntos de acumulación de un conjunto no son necesariamente límites de sucesiones de puntos del conjunto.

Ejercicios 11.11

1. Hallar un ejemplo de espacio topológico donde una sucesión tiene dos puntos límites diferentes.

Espacios Localmente Compactos

La línea real no es compacta, pero cada punto est;a contenido en un conjunto compacto, el punto a está contenido en ]a−r, a+r[. Esta situación es compartida por muchos de nuestros ejemplos importantes.

Definición. (Relativamente y Localmente Compacto) Un subconjunto A de un espacio topológico X es relativamente compacto, ssi, su clausura es compacta.

Un espacio Hausdorff es localmente compacto, ssi, cada punto del espacio tiene una vecindad relativamente compacta.

Ejemplos 11.12.1.

• Los espacios euclídeos Rⁿ son localmente compactos.
• Cualquier espacio compacto es localmente compacto, todo el espacio es una vecindad compacta de cualquiera de sus puntos.
• Un espacio discreto infinito es localmente compacto, pero no compacto; por ejemplo, los Naturales.

Proposición 11.12.1. Sea X un espacio topológico. Los enunciados siguientes son equivalentes.

1. X es localmente compacto.
2. Para cada x en X y cada vecindad U de X, hay una vecindad abierta relativamente compacta V de x tal que V ⊂ Cl(V ) ⊂ U.
3. Para cada compacto C y abierto U ⊃ C hay un abierto relativamente compacto V tal que C ⊂ V ⊂ Cl(V ) ⊂ U.
4. X tiene una base que consiste de abiertos relativamente compactos.

Demostración. (a) ⇒ (b). Para cada x hay una vecindad W tal que Cl(W) es compacta. Como se cumple que Cl(W) es un espacio regular (ver proposición 3.1 en capítulo 12), y Cl(W) ∩ U es una vecindad de x en Cl(W), hay una vecindad abierta G tal que contenido en Cl(W) tal que G ⊂ Cl_Cl(W)(G) ⊂ Cl(W) ∩ U. Por definición de topología relativa, G = H ∩ Cl(W), donde H es un abierto en X. Luego, V = H ∩ Cl(W) es la vecindad buscada. (b) ⇒ (c). Para cada c en C, sea V una vecindad de c relativamente compacta cuya clausura está contenida en U. Como C es compacto, una familia finita de tales vecindades cubre a C y su reunión es una vecindad de C que tiene clausura compacta. (c) ⇒ (d). Sea B la familia de todos los abiertos relativamente compactos. Como {x} es compacto, (c) implica que B es una base. (d) ⇒ (a). Trivial.

---

Proposición 11.12.2. Sea f : X → Y , continua y abierta. Si X es localmente compacta entonces Y es localmente compacta.

Demostración. Sea y en Y y sea x en X tal que f(x) = y. Sea U una vecindad abierta relativamente compacta de x. Como f es abierta, f(U) es una vecindad abierta de y. Como Cl(U) es compacta, también lo es f(Cl(U)), y como Cl(f(U)) ⊂ Cl(f(Cl(U)) = f(Cl(U)), tenemos que Cl(f(U)) es compacta.

---

Ejercicios 11.12

1. Los Racionales como subespacio de los Reales no es localmente compacto.
2. Probar que una reunión finita de abiertos relativamente compactos es relativamente compacta. ¿Que se puede decir de su intersección?
3. Sea X relativamente compacto. Cualquier subespacio abierto o cerrado de X es también relativamente compacto.
4. El producto de espacios relativamente compactos es compacto.

Ejercicios del Capítulo 11

1. Sea A un conjunto compacto de un espacio métrico E. Cuando U es una vecindad abierta de A (o sea A ⊂ U), hay un número real positivo tal que {x ∈ X : d(x,A) < ε} esta contenido en U.
2. Sea A un subconjunto cerrado y conexo de Rⁿ. Sea V la r–vecindad de A. Probar que V es conexo por caminos.
3. Sea E un espacio métrico compacto. Cuando la clausura de cada bola abierta es la bola cerrada de igual centro y radio, se cumple que cada bola del espacio es conexa.
4. Sea A un subconjunto de Rⁿ. A es compacto, ssi, cada función continua con valores reales es acotada.
5. Sean F y G subconjuntos disjuntos de un espaciométrico E. Si F es cerrado y G compacto, entonces d(F,G) > 0.
6. Sea U un conjunto abierto que contiene un subconjunto compacto A de un espacio métrico E. Probar que hay un r > 0 tal que U contiene a V_r(A) = {x ∈ E : d(x,A) < r}.
7. Sea A un subconjunto cerrado y conexo de Rⁿ, y sea V una r–vecindad cerrada de A (V = {x ∈ Rⁿ : d(x < A) ≤ r}). Probar que V es conexa por caminos.
8. Sea E un espacio métrico compacto. Sea f : X → X continua tal que d(f(x), f(y)) < d(x, y) para todo x, y, x ≠ y. Entonces, f tiene un punto fijo único (o sea x tal que f(x) = x).
9. ¿Cuando la reunión de una familia de compactos es compacta en un espacio cualquiera?