Matemáticas/Geometría/Paralelogramos/Texto completo
Definición
[editar]Un paralelogramo es un cuadrilátero convexo cuyos pares de lados opuestos son iguales y paralelos dos a dos
Los paralelogramos son:
El cuadrado, que tiene todos sus lados de igual longitud.
El rectángulo, que tiene sus lados opuestos de igual longitud.
El rombo, que tiene todos sus lados de igual longitud, y dos pares de ángulos iguales.
El romboide, que tiene los lados opuestos de igual longitud y dos pares de ángulos iguales
El paralelogramo propiamente dicho
Propiedades
[editar]
El conjunto de los paralelogramos reúne en sí a varios subconjuntos de figuras geométricas, todas ellas con lados opuestos iguales y paralelos, por ejemplo los romboides, los rombos, los cuadrados y los rectángulos son todos subconjuntos pertenecientes al conjunto de los paralelogramos. El hecho de que varias figuras con algunas características distintas sean parte de los paralelogramos hace un poco más complejo el mencionar sus propiedades, puesto que existen propiedades que son comunes a toda la familia de paralelogramos, por ejemplo «lados opuestos iguales y paralelos», pero otras propiedades como ser «ejes de simetría de reflexión» pueden ser diferentes para cada subfamilia de paralelogramos.
Por el motivo anterior se mencionarán en primer término, las propiedades comunes a todos los paralelogramos (de cualquier subclase), luego algunas de las propiedades particulares que diferencian a las distintas clases o figuras de la familia, y finalmente algunas propiedades métricas.
Propiedades comunes de los paralelogramos
[editar]- Todo paralelogramo tiene cuatro vértices, cuatro lados, además cuatro ángulos interiores (es un subconjunto de los cuadriláteros)
- Los lados opuestos de un paralelogramo son paralelos (por definición), por lo cual nunca se intersectan.
- Los lados opuestos de un paralelogramo son de igual longitud, (congruentes).
- Los ángulos opuestos de un paralelogramo son iguales en medida.
- Los ángulos de dos vértices son suplementarios (suman 180°).
- La suma de los ángulos interiores de todo paralelogramo es siempre igual a 360°.
- El área de un paralelogramo es el doble del área de un triángulo formado por cualquiera de sus diagonales y los lados contiguos de la figura.
- El área de un paralelogramo es igual a la magnitud (módulo) del producto vectorial[1] de dos lados contiguos, considerados como vectores.[2]
- Todos los paralelogramos son convexos.[3][4]
- Cualquier recta secante coplanar corta al paralelogramos en dos y solo dos de sus lados.
- Las diagonales de un paralelogramo se bisecan entre sí.
- El llamado «centro» del paralelogramo se encuentra en el punto en que se bisecan sus dos diagonales.
- El «centro» del paralelogramo es también el baricentro del mismo.[5]
- Cualquier recta coplanar que pase por el «centro» de un paralelogramo divide a su superficie en dos partes iguales, o en dos trapecios congruentes.[6] El segmento que pasa por el punto medio se llama mediana, aun en el caso extremo de una diagonal.
- Cualquier recta coplanar que pase por el «baricentro»[5] de un paralelogramo es también «transversal de gravedad» del mismo.
- Cualquier transformación afín no degenerada transforma un paralelogramo en otro paralelogramo.
- Existe un número infinito de transformaciones afines que transforman a un paralelogramo dado en un cuadrado.
- Se puede establecer un homeomorfismo entre un paralelogramo y una circunferencia.[7]
- Una traslación, una rotación de un paralelogramo conservan la forma y el tamaño[8]
Propiedades particulares de distintos paralelogramos
[editar]- El paralelogramo «cuadrado», tiene simetría de rotación de orden 4 (90°)
- Los paralelogramos «romboide», «rombo» y «rectángulo», tiene simetría de rotación de orden 2 (180°)
- Si no tiene ningún eje de simetría de reflexión, entonces es un paralelogramo «romboide».
- Si tiene 2 ejes de simetría de reflexión diagonales, entonces es un paralelogramo «rombo».
- Si tiene 2 ejes de simetría de reflexión perpendiculares a sus lados, entonces es un paralelogramo «rectángulo».
- Si tiene 4 ejes de simetría de reflexión, entonces es un paralelogramo «cuadrado».
Algunas propiedades métricas comunes
[editar]- El perímetro de un paralelogramo es 2 (a + b), donde a y b son las longitudes de dos lados contiguos cualquiera.
- La suma de los cuadrados de los lados es igual a la suma de los cuadrados de las diagonales (véase la ley del paralelogramo).
- Para calcular el área de un paralelogramo, se puede considerar como una figura compuesta por dos triángulos congruentes y un rectángulo, trazando alturas de los vértices de los ángulos obtusos.
Fórmulas
[editar]
| Fórmulas del paralelogramo | |
|---|---|
| Área |
|
| Altura de a | |
| Altura de b | |
| Diagonales (ley de cosenos) |
|
| Ángulos | |
Cuadrado
[editar]Un cuadrado en geometría plana es un cuadrilátero regular; esto es una figura del plano con sus cuatro lados iguales, y sus cuatro ángulos que son de 90º. Sus dos únicas diagonales son de igual longitud y perpendiculares entre sí. Tiene 4 ejes de simetría, cuya intersección es el centro de la figura; dos ejes que pasan perpendicularmente por cada punto medio del par de lados opuestos; otros dos que pasan por vértices opuestos de la figura.[9][10][11] En algunas fuentes consideran el cuadrado como un rectángulo de cuatro lados iguales o un rombo con un ángulo recto. O un cuadrado es un cuadrilátero de cuatro ángulos rectos y cuatro lados iguales.[12][13]
Propiedades
[editar]Es el polígono que tiene sus lados opuestos paralelos y, por tanto, es un paralelogramo. Dado que sus cuatro ángulos internos son rectos, es también un caso especial de rectángulo, es un rectángulo equilátero. De modo similar, al tener los cuatro lados iguales, es un caso especial de rombo, es un rombo equiángulo. Cada ángulo interno de un cuadrado mide 90 grados o radianes, y la suma de todos ellos es 360° o radianes. Cada ángulo exterior del cuadrado mide 90° o radianes.
Entre los rectángulos que tienen el mismo perímetro, el cuadrado es el que tiene mayor área.[14]
- Sus diagonales se cortan en partes iguales.
- La intersección de sus diagonales es centro de simetría del cuadrado.
- Sus diagonales son iguales.
- Las perpendiculares, trazadas por el centro de simetría, son ejes de simetría del cuadrado.
- Sus diagonales son perpendiculares entre sí, bisectrices de los ángulos cuyos vértices conectan, y ejes de simetría del cuadrado.[15]
- El lado de un cuadrado circunscrito es igual al diámetro de la respectiva circunferencia.
- La diagonal de un cuadrado inscrito es igual al diámetro de la respectiva circunferencia.
Medidas
[editar]Perímetro
[editar]
Si un cuadrado C tiene lados que miden L, entonces, el perímetro es igual a 4L, pues los cuatro lados son iguales.
Expresión de la diagonal
[editar]La longitud de la diagonal se puede calcular mediante el Teorema de Pitágoras:
- y recíprocamente

Área
[editar]El área de un cuadrado es el producto de la longitud del lado por sí misma:
donde A el área y L el lado.
El área de un cuadrado es la mitad del cuadrado de la longitud de la diagonal D:
Rectángulo
[editar]
En geometría plana, un rectángulo es un paralelogramo cuyos cuatro lados forman ángulos rectos entre sí. Los lados opuestos tienen la misma longitud.
El perímetro de un rectángulo es igual a la suma de todos sus lados:
El área de un rectángulo es igual al producto de dos de sus lados contiguos:
Definición
[editar]Un rectángulo es una figura geométrica que posee cuatro ángulos interiores de 90º. Es un paralelogramo, es decir, todos sus lados son paralelos dos a dos.[16][17]
Propiedades
[editar]- Sus lados paralelos son iguales.
- Sus dos diagonales son iguales, y se bisecan mutuamente o se cortan en el punto medio común; (esta característica también lo define). Este punto es el centro de la figura, en el sentido que toda recta que pasa por él, corta al rectángulo en dos puntos equidistantes del centro, por lo que define una simetría respecto a un punto para puntos del rectángulo.[18]
- Se puede pavimentar el plano, repitiendo infinitos rectángulos.
- El rectángulo tiene dos simetrías axiales, respecto a ejes paralelos a sus lados y que pasan por el centro.[19]
- Posiblemente, de modo empírico, en el antiguo Egipto se obtuvo la terna pitagórica 3 - 4 - 5, como medidas de los lados y la diagonal de un rectángulo, y lo usaron en la cuerda del agrimensor de 15 nudos.[20][21]
- Si se unen los cuatro puntos medios de los cuatro lados, mediante cuatro segmentos, se obtiene un rombo cuya área es la mitad de la del respectivo rectángulo.
- Cualquier rectángulo se puede inscribir en una circunferencia, dos de cuyos diámetros coinciden con las diagonales del rectángulo.
- Usando como base de un triángulo una base del rectángulo y el punto medio de del lado opuesto, como vértice opuesto, resulta un triángulo isósceles de área igual a la mitad de la del rectángulo.
- Empleando como base de cualquier triángulo la base del rectángulo y como vértice opuesto un punto que dista como la altura del rectángulo, se obtiene una familia de triángulos equivalentes y cuyos vértices forman un lugar geométrico: la recta paralela a la base del rectángulo.[22]
- Si se unen los puntos medios M, N; P, Q de sendos lados de un rectángulo, mediante segmentos se genera el rombo MNPQ.[23]
Rectángulos con nombre propio
[editar]
- El cuadrado se puede considerar un caso particular del rectángulo, en el que todos sus lados tienen la misma longitud.
- El rectángulo áureo, también denominado rectángulo de oro o rectángulo Φ, es el rectángulo cuyos lados están en razón áurea. Si b y h son los lados, b/h = Φ. Para construirlo a partir de un cuadrado de lado AB, basta con determinar el punto medio M de uno de los lados AB, y trazar, con centro en el punto M, una circunferencia que pase por uno de los vértices C del lado opuesto.

- Rectángulo (rectángulo raíz de 2), aquel cuya relación entre base y altura es igual a la raíz cuadrada de dos. Si b y h son los lados, b/h = . El interés de este rectángulo radica en que si es dividido en dos mitades, por su lado más largo, los dos nuevos rectángulos obtenidos mantienen exactamente la misma proporción que el original, o sea que son también rectángulos raíz de 2. Es por ello que, entre otros usos, es el formato utilizado para dimensionar las hojas de papel según las normas DIN 476 e ISO 216.
Construcción partiendo del cuadrado: de forma similar al rectángulo áureo, se traza con centro en el punto A, una circunferencia que pase por el vértice opuesto C.
- Doble cuadrado, aquel cuyos lados están en la relación 2:1.
- Pantallas de televisión. Hasta la introducción de los monitores de alta definición, cuya relación [ancho:alto] habitual es [16:9], los sistemas de televisión convencionales utilizaban rectángulos con la proporción [4:3]. Dado que estas proporciones son fijas, basta con conocer la medida de la diagonal (normalmente expresada en pulgadas) para establecer el tamaño de la pantalla.
Rectángulos cruzados
[editar]
Un cuadrilátero cruzado (es decir, que se interseca a sí mismo) consiste en dos lados opuestos de un cuadrilátero junto con sus dos diagonales (véase antiparalelogramo). Del mismo modo, un rectángulo cruzado es un cuadrilátero cruzado formado por dos lados opuestos de un rectángulo junto con sus dos diagonales. Tiene la misma disposición de vértices que el rectángulo. Aparece como dos triángulos idénticos con un vértice común. La intersección geométrica no se considera un vértice propiamente dicho.
Un cuadrilátero cruzado a veces se asemeja a un lazo de pajarita o a una mariposa. Un marco rectangular de alambre toma la forma de un cuadrilátero cruzado cuando se hacen girar en un espacio tridimensional sus lados cortos en sentido opuesto. Un rectángulo cruzado a veces también se denomina un "ocho angular".
El interior de un rectángulo cruzado puede tener un densidad poligonal de ± 1 en cada triángulo, dependiendo de la orientación (en sentido de las agujas del reloj o en sentido contrario) con la que se recorrran.
Un rectángulo cruzado no es equiangular. La suma de sus ángulos interiores (dos agudos y dos obtusos), como en cualquier cuadrilátero cruzado, es de 720°.[24]
Un rectángulo y un rectángulo cruzado son cuadriláteros con las siguientes características en común:
- Los lados opuestos tienen la misma longitud.
- Las dos diagonales tienen la misma longitud.
- Tiene dos líneas de simetría de reflexión y simetría rotacional de orden 2 (180°).
Cuadrado, perfecto, y otros rectángulos
[editar]Un rectángulo puede ser embaldosado mediante cuadrados, rectángulos, o triángulos. Se dice que el recubrimiento es Perfecto[25][26] si todas las baldosas son semejantes, tiene un número finito de baldosas, y no hay dos baldosas del mismo tamaño. Si dos de estas baldosas son del mismo tamaño, se dice que el recubrimiento es imperfecto. En un recubrimiento perfecto (o imperfecto) triangulado, los triángulos deben ser rectángulos.
Un rectángulo tiene lados conmensurables sí y solo sí puede ser recubierto por un número finito de cuadrados distintos.[25][27] Lo mismo es cierto si las baldosas son triángulos isósceles desiguales.
Los recubrimientos de rectángulos con otras formas geométricas que han atraído la mayor atención son los de poliominós no rectangulares congruentes, permitiendo todas las rotaciones y reflexiones. También hay embaldosados mediante poliábolos congruentes.
Rombo
[editar]| Rombo | |
|---|---|
| Familia | Bipiramidal |
| Tipo | Cuadrilátero |
| Lados y vértices | 4 |
| Propiedades | convexo, isotoxal |
El rombo es un paralelogramo (y por tanto un cuadrilátero) cuyos cuatro lados son de igual longitud y cuyas diagonales se cortan perpendicularmente.
Definiciones equivalentes
[editar]
Un paralelogramo es un rombo si posee:
|
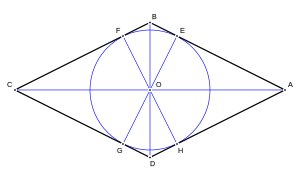

El rombo cuyos vértices son A, B, C y D, cumple las siguientes relaciones, respecto de sus lados:
- Sus cuatro lados: l, son iguales[29]
- Sus dos diagonales de respectivas longitudes:
siendo:
Propiedades
[editar]- Las diagonales son ejes de simetría.
- El punto de intersección O de las diagonales es el incentro del rombo.
- Las diagonales del rombo son perpendiculares entre sí, y satisfacen la relación:
- Las dos alturas: h, de un rombo tienen la misma longitud que el diámetro: d, de su circunferencia inscrita:
Si se observan los puntos de contacto de dicha circunferencia sobre dos lados opuestos cualesquiera de rombo se notará que los dos diámetros que unen a dichos puntos son cada uno de ellos paralelo a la respectiva altura y tienen medida exactamente igual a las mismas. Diámetro y alturas son la medida de la separación entre lados paralelos opuestos.
- Sean d1 una diagonal,d2 la otra diagonal, α el ángulo correspondiente, a lado del rombo, A el área del rombo, entonces se cumple:
- Si se unen los puntos medios H, I, J, K de sendos lados de un rombo usando segmentos de recta, resulta de la reunión de tales segmentos un rectángulo.[31]
- Si se inscriben en los cuatro triángulos, determinados por las diagonales, sendas circunferencias, cada una de estas es tangente , exactamente, a otras dos de ellas. Los cuatro centros de sendas circunferencias determinan, como vértices, un cuadrado, . El radio es
. El lado del cuadrado de vértices en los centros es 2r.[32]
Área
[editar]Hay diversas maneras de calcular el área del rombo:

- El área del rombo es igual al semiproducto de sus diagonales (diagonal mayor y diagonal menor):[33]
Viendo el triángulo OBC, rectángulo en O, su área es:
El rombo está formado por cuatro triángulos iguales:
Con lo que tenemos el área del rombo como el producto de sus dos diagonales dividido entre dos.

- El área también es igual al producto entre la base y la altura.
- siendo l el lado o la base; h la altura del rombo.
El rombo como paralelogramo, su área es el producto de la base por la altura.

- El área del rombo es igual al producto entre dos lados y el seno del ángulo comprendido entre estos.
Partiendo del triángulo PBC rectángulo en P, siendo BC la hipotenusa y PB la altura del rombo, tenemos que:
Equivalente a:
Con lo que queda determinada el área del rombo:
- Otra forma de hallar el área es a través del producto entre el semiperímetro y el radio del círculo inscrito en el rombomeones
- siendo 2l es el semiperímetro de rombo; r el radio del círculo inscrito.
Radio de la circunferencia inscrita
[editar]Cálculo del radio de la circunferencia inscripta
siendo A el área; l la base; r el radio de la circunferencia inscripta del rombo.
Dimensiones del rombo
[editar]

En un rombo podemos distinguir las siguientes dimensiones:
El lado l:
Las diagonales: D y d:
La altura h:
El rombo en el comercio y cosas de marca particular
[editar]- El logotipo de Mitsubishi, son tres rombos unidos a un punto en común cualquiera.
- La marca de los autos Renault lleva un rombo sin puntas, pero el centro del logotipo está formado también por un rombo.
- En la Televisión Española se indicaba con uno o dos rombos que el programa que empezaba no era apto para menores de 14 o 21 años, respectivamente. Los rombos aparecían durante unos segundos en la esquina superior derecha de la pantalla. La práctica se mantuvo entre 1962 y 1985. También hay que mencionar que esta es la figura que forma las 9 lunetas del logotipo del Canal 9.
- Las pastillas Juanola tienen una reconocible forma romboidal que durante años también fue utilizado para el diseño de su caja contenedora.
- En el juego de naipes, algunas cartas se llaman diamantes , que no son sino figuras en forma de rombo en esquinas opuestas de la correspondiente carta.
- Hay una novela de Europa oriental, que lleva por título Los aviones avanzan en rombo.
- El rombo se puede observar y reflejar por ejemplo en algo sencillo como lo es una cometa o aún una lámpara.
- Sobre las puertas de madera se tallan, encima de las planchas entre los marcos, rombos sobresalientes.
Romboide
[editar]
El Romboide un paralelogramo que tiene sus ángulos y sus lados iguales dos a dos.[34][35]
Esta figura recibe un nombre especial (aparte de ser un paralelogramo). El nombre romboide se aplica a otra figura, al cuadrilátero que tiene dos pares de lados consecutivos iguales (véase deltoide).[36]
Propiedades
[editar]Un romboide posee las siguientes propiedades:
- Tiene dos pares de lados opuestos, iguales y paralelos entre sí.
- Los ángulos contiguos son ángulos suplementarios.
- Sus diagonales no son perpendiculares.
- 2 ángulos agudos y 2 obtusos
- Es paralelogramo
- Tiene 4 vértices
- La suma de sus ángulos interiores da 360°, ya que es un cuadrilátero
Perímetro
[editar]Partiendo de un romboide, de lados a y b, y de altura h respecto a la base a, se puede determinar las siguientes características:
El perímetro de un romboide es:
Que es la suma de todos los lados.
Àrea
[editar]
El área se obtiene multiplicando la longitud de un lado, , por la distancia al lado opuesto, :
Referencias
[editar]- ↑ Siendo rigurosos, se sabe que el producto vectorial es una operación inválida para espacios de dos dimensiones ℝ2, pero siempre podemos imaginar a las figuras geométricas bidimensionales planas, como embebidas en un espacio euclidiano tridimensional ℝ3, ubicadas en un plano horizontal de cota cero, aun así el resultado de dicho producto sería un vector perpendicular al plano de la figura, es por esta razón que se dice que: «el área de un paralelogramo es igual solo al valor absoluto de la magnitud (o norma) de dicho vector y no al vector mismo».
- ↑ Puede plantearse que los vértices están en ℝ3
- ↑ Convexidad: El segmento de recta que reúne a cualquier par de puntos de un paralelogramo está siempre totalmente incluido en el mismo.
- ↑ Cualquiera recta que pase por un lado del paralelogramo determina que este quede totalmente en uno de los semiplanos que produjo la recta.
- ↑ 5,0 5,1 El centro de un paralelogramo coincide con su baricentro, si y solo si su densidad es uniforme.
- ↑ Fácil de comprobar gráficamente
- ↑ Topología de Schaumm
- ↑ Pastor- Santaló- Balanzat: Geometría Analítica
- ↑ Plantilla:Cita DRAE
- ↑ Real Academia de Ciencias Exactas, Física y Naturales, ed (1999). Diccionario esencial de las ciencias. Espsa. ISBN 84-239-7921-0. «Polígono regular de cuatro lados»
- ↑ Equipo editorial (en español). Enciclopedia didáctica de matemáticas. OCEANO. ISBN 84-494-0696-X. «Paralelogramo de cuatro ángulos rectos y cuatro lados iguales»
- ↑ Definición de Birkhoff
- ↑ A. Bouvier y M. George (en español). Diccionario de Matemáticas. AKAL. ISBN 84-7339-706-1. «rectángulo de cuatro lados iguales o un rombo de ángulos iguales y lados consecutivos perpendiculares»
- ↑ Cualquier manual de Cálculo, en el capítulo de extremos; para el caso Calculus de Spivak o el manual de Nathanson
- ↑ Repetto/Linkens/ Fesquet. Matemática Moderna. Geometría 2.
- ↑ Michel Helfgott. Geometría plana, Editorial Escuela Activa S. A.
- ↑ No se dice que tiene únicamente un ángulo de 90º; sobre la base de ello, el ángulo opuesto es de 90º, por ser paralelogramo; los dos restantes suman 180º, como son opuestos son iguales, cada cual mide 90º
- ↑ Julio Rey Pastor et al. Geometría Analítica
- ↑ Clemens: "Geometría. Con aplicaciones y solución de problemas"
- ↑ Alsina: "La recta de los números. Teorema de Albert Einstein"
- ↑ Hoffmann: Historia de la Matemática
- ↑ Michel Helfgott. Op. cit.
- ↑ G.M: Bruño. Elementos de Geometría
- ↑ Stars: A Second Look. (PDF). Retrieved 2011-11-13.
- ↑ 25,0 25,1 R.L. Brooks, C.A.B. Smith, A.H. Stone and W.T. Tutte (1940). «The dissection of rectangles into squares». Duke Math. J. 7 (1): pp. 312–340. doi:. http://projecteuclid.org/euclid.dmj/1077492259.
- ↑ J.D. Skinner II, C.A.B. Smith and W.T. Tutte (noviembre de 2000). «On the Dissection of Rectangles into Right-Angled Isosceles Triangles». J. Combinatorial Theory Series B 80 (2): pp. 277–319. doi:.
- ↑ R. Sprague (1940). «Ũber die Zerlegung von Rechtecken in lauter verschiedene Quadrate». J. fũr die reine und angewandte Mathematik 182: pp. 60–64.
- ↑ Juan Goñi: Formulario y conceptos de Matemática, ediciones Grupo Ingeniería, Lima
- ↑ Reiteración de la definición
- ↑ Goñi: Op. cit.
- ↑ G. M. Bruño. Elementos de Geometrías
- ↑ Se obtiene aplicando el área del triángulo en función del radio de la circunferencia inscrita y su semiperímetro
- ↑ Déplanche, Y. (1996). Diccio fórmulas. Área del rombo. Edunsa. pp. 22. ISBN 9788477471196. http://books.google.com/books?id=1HVHOwAACAAJ. Consultado el 24 de abril de 2011.
- ↑ Pedro Nuñez (1567). Libro de Algebra en Arithmetica y Geometria. Anvers. http://books.google.com/books?id=anVAEMqtIO0C&hl=es&pg=RA12-PA495#v=onepage&f=false. «Romboide es figura cuadrilátera, en la cual solamente los lados opósitos son iguales, y los ángulos no son rectos, y en esto es diferente del cuadrángulo rectángulo, que no es cuadrado»
- ↑ Julio Cesar Barreto Garcia. «Deducciones de las fórmulas para calcular las áreas de figuras geométricas a través de procesos cognitivos». Sociedad Canaria Isaac Newton de Profesores de Matemáticas.
- ↑ Josep Gascón. «Efectos del autismo temático sobre el estudio de la Geometría en Secundaria. Parte II: La clasificación de los cuadriláteros convexos». Revista SUMA Febrero 2004 (45): pp. 41-52. http://revistasuma.es/IMG/pdf/45/041-052.pdf. «(nota 2) Utilizo una definición de romboide, hoy en desuso, equivalente a la que dio Rey Pastor: un romboide es un cuadrilátero que tiene un eje de simetría que pasa por dos de sus vértices. [...] Como dice Puig Adam (1947, p. 68), se trata de una noción “más útil que la aplicación clásica que de esta palabra se hace para designar un paralelogramo que no sea rombo ni rectángulo, y que carece de interés”».









































