Matemáticas/Geometría/Ángulos/Relaciones entre Ángulos
En función de su posición
[editar]Ángulos adyacentes
[editar]Los que tienen un vértice y un lado común, y semirrectas opuestas, pero no tienen ningún punto interior común, y suman 180°.
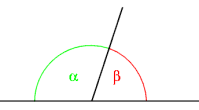
Ángulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.[1][2][3]
Ángulos consecutivos
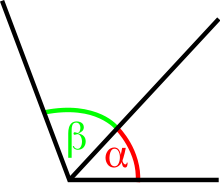
[editar]Tienen un lado y el vértice común.
Ángulos opuestos
[editar]Aquellos por el vértice y cuyos lados son semirrectas opuestas.


En geometría euclidiana dadas dos rectas r y s, del plano, que se cortan en el punto P, dos ángulos se dicen opuestos por el vértice cuando los lados de uno son semirrectas opuestas a los lados del otro ángulo.
En la figura los ángulos a, c y b, d son opuestos por el vértice. Dos ángulos opuestos por el vértice son congruentes.
En función de su amplitud
[editar]Ángulos congruentes
[editar]aquellos que tienen la misma amplitud, es decir, que miden lo mismo.
Los ángulos opuestos son congruentes debido a que una rotación de 180° sobre su vértice hace coincidir uno y el otro.
-
Los ángulos y son congruentes y opuestos por el vértice.
-
Una recta que corta dos paralelas generan ángulos congruentes.
-
Los ángulos opuestos de un paralelogramo son congruentes.
Ángulos complementarios
[editar]aquellos cuya suma de medidas es π/2 radianes o 90°.
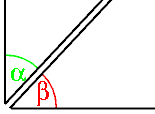
Los ángulos complementarios son aquellos ángulos cuyas medidas suman 90° (grados sexagesimales). Si dos ángulos complementarios son consecutivos, los lados no comunes de los dos forman un ángulo recto.
Así, para obtener el ángulo complementario de α, teniendo α una amplitud de 70°, se restará α de 90°:
- β = 90° – 70º = 20º
Sabiendo esto, dichos ángulos formarán siempre un triángulo rectángulo puesto que los ángulos en un triángulo rectángulo son uno de 90º y los otros dos deben sumar 90 (180º(grados totales de un triángulo)-90º=90º). Por tanto, el seno de α es igual al coseno de β y el seno de β igual al coseno de α puesto que pertenecen al mismo triángulo rectángulo.
La diagonal de un rectángulo también configura ángulos complementarios(90°) con los lados adyacentes.
Ángulos suplementarios
[editar]aquellos cuya suma de medidas es π radianes o 180°.
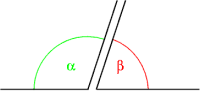
Dos ángulos y son ángulos suplementarios, si suman 180° (grados sexagesimales).
- Un ángulo es o tiene suplementario si es menor que 180º.
- El valor de 180º es el mismo que dos ángulos rectos, rad o grados centesimales.
Método de obtención
[editar]Aritmético
[editar]Para obtener el ángulo suplementario de un determinado ángulo , se restará a 180°, de manera que:
Propiedades
[editar]- Si dos ángulos son suplementarios de otros dos ángulos congruentes, también son congruentes entre sí.
- Los senos de los ángulos suplementarios son los mismos, por ejemplo:
- Los cosenos de los ángulos suplementarios son de igual valor absoluto, pero de signo inverso, como muestran los siguientes ejemplos:
Ángulos conjugados
[editar]aquellos cuyas medidas suman 2π radianes o 360°.

Dos ángulos conjugados con vértices coincidentes, tendrán sus lados comunes.
Así, para obtener el ángulo conjugado de β que tiene una amplitud de 110°, se restará β de 360°:
- α = 360°–110° = 250°
- el ángulo α (alfa) es el conjugado de β (beta).
- 360 grados sexagesimales equivalen a 2π radianes, o 400 grados centesimales.
Cuando dos rectas son cortadas por una tercera en distindo punto:[4]
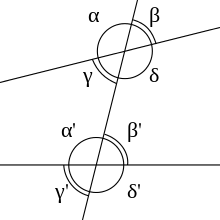
Ángulos alternos
[editar]ángulos dispuestos a distinto lado de una recta que corta otras dos pero que no comparten lado.
- o es alterno a o a
- o es alterno a o a
- y viceversa.
Ángulo alternos internos
[editar]ángulos comprendidos entre dos rectas pero situados a distinto lado de la recta cortante.
- es alterno interno a
- es alterno interno a
Ángulo alternos externos
[editar]ángulos no comprendidos entre dos rectas pero situados a distinto lado de la recta que corta.
- es alterno externo a
- es alterno externo a
Ángulos correspondientes
[editar]formados por dos paralelas y una transversal. Se encuentran en el mismo semiplano con respecto a la transversal y uno pertenece a la región interior y otro a la región exterior. Son congruentes.
- ↑ Principios y ejercicios de geometría. (Acisclo Fernández Vallín y Bustillo, 1864) pág. 12.
- ↑ Geometria: El Encanto de la Forma. pág. 12.
- ↑ Notas de clase. Geometría en el plano y en el espacio. (Ana Berenice Guerrero G., Univ. Nacional de Colombia) pág. 32.
- ↑ Diccionario esencial de las ciencias. Espasa. ISBN 84-239-7921-0.




















