Curso de relatividad general, gravitación y cosmología/Principios fundamentales de la Relatividad General
Principios fundamentales de la Relatividad General
[editar]¿Por qué es necesaria la Relatividad General?
[editar]Los éxitos explicativos de la teoría de la Relatividad Especial condujeron a la aceptación de la teoría por la mayor parte de los físicos. Antes de la formulación de la relatividad general existían por tanto dos teorías físicas incompatibles:
- La teoría especial de la relatividad que integraba adecuadamente el electromagnetismo, y que descarta explícitamente las acciones instantáneas a distancia.
- La teoría de la gravitación de Newton que explicaba la gravedad mediante acciones instantáneas a distancia.
La necesidad de buscar una teoría que integrase como casos límites particulares las dos anteriores requería la búsqueda de una teoría de la gravedad que fuese compatible con los nuevos principios relativistas introducidos por Einstein. Además de la formulación de una teoría relativista de la gravitación, hubo otra razón adicional. Einstein había concebido la teoría especial de la relatividad como una teoría aplicable sólo a sistemas de referencia inerciales, aunque realmente puede generalizarse a sistemas acelerados sin necesidad de introducir todo el aparato de la relatividad general. La insatisfacción de Einstein con su creencia de que la teoría era aplicable sólo a sistemas inerciales les llevó a buscar una teoría que proporcionara descripciones físicas adecuadas para un sistema de referencia totalmente general.
Esta búsqueda era necesaria, ya que según la Relatividad Especial ninguna información puede viajar a mayor velocidad que la luz, y por lo tanto no puede existir relación de causalidad entre dos eventos unidos por un intervalo espacial. Sin embargo, uno de los pilares fundamentales de la gravedad newtoniana, el principio de acción a distancia, supone que las alteraciones producidas en el campo gravitatorio se transmiten instantáneamente a través del espacio. La contradicción entre ambas teorías es evidente, puesto que asumir las tesis de Newton llevaría implícita la posibilidad de que un observador fuera afectado por las perturbaciones gravitatorias producidas fuera de su cono de luz.
Einstein resolvió este problema interpretando los fenómenos gravitatorios como simples alteraciones de la curvatura del espacio-tiempo producidas por la presencia de masas. De ello se deduce que el campo gravitatorio, al igual que el electromagnético, tiene una entidad física independiente y sus variaciones se transmiten a una velocidad finita en forma de ondas gravitacionales. La presencia de masa, energía o momentum en una determinada región de la variedad tetradimensional, provoca la alteración de los coeficientes de la métrica, en una forma cuyos detalles pormenorizados analizaremos en las secciones siguientes.

Un hito fundamental en el desarrollo de la teoría de la Relatividad General lo constituyó la enunciación por Albert Einstein en el año 1912 del principio de equivalencia, al que su autor calificó como "la idea más feliz de mi vida". Dicho principio supone que un sistema que se encuentra en caída libre y otro que se mueve en una región del espacio-tiempo sin gravedad se encuentran en un estado físico sustancialmente similar: en ambos casos se trata de sistemas inerciales.
En este punto hay una diferencia esencial entre la mecánica galileana y la general relativista: En la primera, de acuerdo con la ley de Newton, un cuerpo en caída libre no es un sistema inercial, sino que -por el contrario- describe un movimiento uniformemente acelerado que lo lleva a desplazarse hacia el centro de la masa. Por otro lado, un sujeto que se halle en reposo sobre la superficie de la tierra es un observador inercial.
Sin embargo, el principio de equivalencia llega a conclusiones totalmente contrarias: Son sistemas inerciales aquellos en los que el observador no experimenta ni aceleración ni atracción gravitatoria alguna, bien por hallarse en caída libre, bien por la inexistencia de grandes masas (que son las que originan la curvatura gravitatoria) en el espacio más cercano. Los cuerpos en caída libre son, por tanto, sistemas inerciales, pero no lo son los observadores situados en la superficie de la tierra (que experimentan una aceleración de origen gravitatorio de unos 9.8 metros por segundo al cuadrado). Es decir, son sistemas no inerciales aquellos en los que el observador, ora describe un movimiento acelerado no originado por la gravedad, ora experimenta los efectos de ésta.
En general, cualquier cuerpo que se mueva sin restricciones por un campo gravitatorio puede ser considerado como un sistema inercial. Es el caso de los planetas que orbitan en torno del Sol y de los satélites que orbitan alrededor de los primeros.
La contracción del tiempo provocada por la gravedad
[editar]La aceptación del principio de equivalencia por Albert Einstein le llevó a un descubrimiento ulterior: La contracción o curvatura del tiempo como consecuencia de la presencia de un campo gravitatorio, que quedó expresado en su artículo de 1911 "Sobre la influencia de la gravedad en la propagación de la luz".[1]
Supongamos que un fotón emitido por una estrella cercana se aproxima a la Tierra. En virtud de la ley de conservación del tetramomentum la energía conservada del fotón permanece invariante. Por otro lado, el principio de equivalencia implica que un observador situado en el fotón (que es un sistema inercial, es decir, se haya en caída libre) no experimenta ninguno de los efectos originados por el campo gravitatorio terrestre. De ello se deduce que la energía conservada del fotón no se altera como consecuencia de la acción de la gravedad, y tampoco lo hace la frecuencia de la luz, ya que, según la conocida fórmula de la física cuántica, la energía de un fotón es igual a su frecuencia (v) multiplicada por la constante de Planck (h): E = hν.

Ahora bien, si las observaciones las realizara un astrónomo situado en la superficie de la Tierra, esto es, en reposo respecto su campo gravitatorio, los resultados serían muy diferentes: El astronomo podría comprobar cómo el fotón, por efecto de su caída hacia la Tierra, va absorbiendo progresivamente energía potencial gravitatoria y, como consecuencia de esto último, su frecuencia se corre hacia el azul.[2] Los fenómenos de absorción de energía por los fotones en caída libre y corrimiento hacia el azul se expresan matemáticamente mediante las siguientes ecuaciones:
Donde es la energía medida por un observador en reposo respecto al campo gravitatorio (en este caso un astrónomo), el potencial gravitatorio de la región donde se encuentra éste, la energía conservada del fotón, la frecuencia de emisión, es la frecuencia percibida por el observador (y corrida hacia el azul) y la constante de Planck.
Ahora bien, en el párrafo anterior hemos demostrado que la energía conservada del fotón permanece invariante. Por tanto, ¿cómo se posible que exista esta divergencia entre los resultados de la medición de la energía obtenidos por el astrónomo () y la energía conservada del fotón ()? La única manera de resolver esta contradicción es considerando que el tiempo se ralentiza como consecuencia de la presencia de un campo gravitatorio. De este modo, la citada ecuación
puede escribirse de este modo:
Es decir, la frecuencia es igual al número de ciclos que tienen lugar en un determinado periodo de tiempo (generalmente, un segundo). Donde es el tiempo medido por un observador situado a una distancia infinita del cuerpo masivo (y por lo tanto no experimenta la atracción gravitatoria de éste), mientras que es el tiempo medido por un observador bajo la influencia del campo gravitatorio y en reposo respecto a este (como, por ejemplo, una persona situada sobre la superficie terrestre. De ahí se deduce que cerca de un cuerpo masivo el tiempo se ralentiza, siguiendo estas reglas matemáticas:
En una singularidad espacio-temporal (como las que existen en el interior de los agujeros negros), la densidad de masa-materia y el campo gravitatorio tienden al infinito, lo que provoca la congelación del tiempo y por lo tanto la eliminación de todo tipo de procesos dinámicos:


La contracción del tiempo debido a la presencia de un campo gravitatorio fue confirmado experimentalmente en el año 1959 por el experimento Pound-Rebka-Snider, llevado a cabo en la universidad de Harvard. Se colocaron detectores electromagnéticos a una cierta altura y se procedió a emitir radiación desde el suelo. Todas las mediciones que se realizaron confirmaron que los fotones habían experimentado un corrimiento hacia el rojo durante su ascenso a través del campo gravitatorio terrestre.
Hoy en día, el fenómeno de la contracción del tiempo tiene cierta importancia en el marco del servicio localizador GPS, cuyas exigencias de exactitud requieren de una precisión extrema: Basta con que se produzca un retraso de 0.04 microsegundos en la señal para que se produzca un error de posicionamiento de unos 10 metros. De ahí que las ecuaciones de Einstein hayan de ser tenidas en cuenta al calcular la situación exacta de un determinado objeto sobre la superficie terrestre.
Desde un punto de vista teórico, el artículo de Einstein de 1911 tuvo una importancia aún mayor. Pues, la contracción del tiempo conllevaba también, en virtud de los principios de la Relatividad Especial, la contracción del espacio. De ahí que fuera inevitable a partir de este momento descartar la existencia de un espacio-tiempo llano, y fuera necesario asumir la curvatura de la variedad espacio-temporal como consecuencia de la presencia de masas.
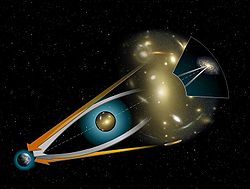
Finalmente, podemos hacer referencia a la desviación de los rayos de la luz como consecuencia de la presencia de un cuerpo masivo, fenómeno que da lugar a efectos ópticos como las lentes gravitacionales o los anillos de Einstein.
Frente de onda desviado. Lente gravitacional. Experimento de Eddington.


















