Curso de alemán para principiantes con audio/Lección 101b
Apariencia
- índice
- Lección 100b ← Lección 101b → Lección 102b
- Lección 101
- Mathematik auf Deutsch - 51
BM2501 - BM2510
[editar]BM2501
- Aufgabe:
- Ein Radfahrer legt die erste Wegstrecke mit einer Geschw. von 17 km/h in 15 Min. zurück.
- Wie schnell muss er die zweite Wegstrecke fahren, die 10 km lang ist, damit er eine Durchschnittsgeschwindigkeit von 22,5 km/h erreicht?
- (... damit er auf eine Durchschnittsgeschwindigkeit von 22,5 km/h kommt?)
Ein kleiner Tipp für die Lösung BM2501 - Lege, so wie in den vorhergehenden Weg-Zeit-Aufgaben, eine Tabelle an!
- Überlege Dir für die Einteilung der Tabelle welche Formel verwendet werden könnte!
3. Lösung BM2501 - Für den 2. Lösungsweg wurden zwei Zwischenergebnisse mit vielen Nachkommastellen berechnet, notiert und gerundet weiterverwendet.
- Dadurch sind im Endergebnis beide Nachkommastellen falsch.
- Das kann umgangen werden, indem wir das Ergebnis v2 als Variable verwenden und damit die Dauer für die 2. Teilstrecke ausdrücken: 10 km / v2.
- Diese Dauer verwenden wir in unserem Ansatz, mittlere Geschwindigkeit * Gesamtdauer = Gesamtstrecke:
- 22,5 km/h * (0,25 h + 10 km/v2) = 0,25 h * 17 km/h + 10 km
- Das ist mit Einheiten geschrieben, um den Ansatz kenntlich zu machen. Weiter ohne Einheiten (v2 in km/h):
- 22,5*(0,25 + 10/v2) = 0,25*17 + 10
- Links ausmultiplizieren und dabei, um die Zahlen zu vereinfachen, beide Seiten mit 4 multiplizieren:
- 22,5 + 900/v2 = 17 + 40 = 57
- 22,5 abziehen, den Kehrwert bilden und mit 900 multiplizieren:
- v2 = 900/34,5 ~= 26,1
- Den Bruch kann man im Kopf rechnen: 1800/69, 180/69 = 2 Rest 42, 420/69 = 6 Rest 6, 6/69 = knapp 0,1.
Antwortsatz BM2501 - Antwortsatz:
- Er muss die zweite Wegstrecke mit einer Geschwindigkeit von 26,1 km/h fahren, damit er eine Durchschnittsgeschwindigkeit von 22,5 km/h erreicht.
BM2502
- Aufgabe:
- Ein Wasserwerk kann ein Becken von 20.000 m3 Fassungsvermögen in 50 Min. füllen. Nun wurde eine 2. Zuleitung gebaut, durch die zusätzlich 250 m3/min in das Becken gepumpt werden.
- Wie lange dauert es nun, das Becken zu füllen?
Antwortsatz BM2502 - Beide Rohre zusammen füllen das Becken in 30,7 Minuten.
- Wir können noch die 0,7 Minuten in Sekunden umrechnen:
- Überschlagsrechnung:
- 1/2 min = 0,5 min = 30 s
- 3/4 min = 0,75 min = 45 s
- ---
- 1 min ≙ 60 s
- 1 s ≙ 1/60 min
- 0,7 min = 0,7 * 60 s = 42 s
- ---
- Also:
- Beide Rohre zusammen füllen das Becken in 30 Minuten und 42 Sekunden.
BM2503
- Aufgabe:
- ER braucht 3 Std. für eine bestimmte Arbeit (z. B. einen 10 m langen Graben graben)
- SIE braucht 8 Std. für die gleiche Arbeit.
- Wie lange brauchen sie, wenn sie beide zusammen die Arbeit erledigen?
Lösungsformel BM2503 - Zeit * Arbeitsleistung = Arbeitsmenge
- Zeit * Arbeitsgeschwindigkeit = Arbeitsmenge
- t * g = m
- [h] * [%/h] = [%]
Antwortsatz BM2503 - Wenn beide zusammen die Arbeit erledigen, dann brauchen sie 1,875 Std. dafür.
- ---
- Wie viel Stunden und Minuten sind das?
Antwort in Stunden und Minuten BM2503 - 1,875 Std.
- 1 Std und 0,875 Std.
- ---
- 1 h = 60 min
- 1 min = 1/60 h
- ---
- Für das „h“ in der nächsten Zeile können wir „60 min“ (sieh zwei Zeilen weiter oben) eintragen.
- 0,875 h = 0,875 * 60 min = 52,5 min
- ---
- 52,5 min sind 52 min und 0,5 min
- 0,5 min können wir im Kopf rechnen
- 0,5 ist 1/2
- Eine halbe Minute sind 30 Sekunden.
- ---
- Also:
- 1,875 Std. sind
- 1 Std. 52 Min. und 30 Sek.
BM2504
- Mischungsaufgabe:
- Es soll eine 45%-ige Lösung eines Frostschutzmittels angesetzt werden. Dafür stehen 55 Liter einer 30%-igen Lösung zur Verfügung und außerdem ein 70%-iges Konzentrat.
- Wie viel 70%-iges Konzentrat muss man dazu geben?
Lösungsformel BM2504 - Konzentration k (in Prozent)
- Volumen V (in Litern; Gesamtvolumen der verdünnten Lösung)
- reine Stoffmenge m (in Litern)
- [%] * [l] = [l]
- ---
- Beispiel:
- Zehn Liter einer 20%-igen Zuckerlösung enthalten 2 Liter Zucker.
- 20% = 20/100 = 1/5
- 20% * 10 = 2
- 20/100 * 10 = 2
- ---
- Fünfzehn Liter einer 20%-igen Zuckerlösung enthalten 3 Liter Farbe.
- 20% = 20/100 = 1/5
- 20/100 * 15 = 3
- 20% * 15 = 3
1. Fehlersuche BM2504 
Bild 7 - Wir setzen die mit einem online-Mischungsrechner gefundenen 33 Liter ein und füllen die Tabelle aus. Dann erhalten wir eine Tabelle mit den nebenstehenden Werten.
- Nun vergleichen wir unsere obige Rechnung mit diesen Werten und finden bis einschließlich Bild 6 keinen Fehler.
- ---
- Also sollte der Fehler in der abschließenden Rechnung stecken.
- Ein online-Rechner sagt uns ([3]), dass nach „x“ umgestellt gleich „33“ ist.
- Wo war unser Fehler?
- Warum haben wir „x=165“ rausbekommen?
2. Fehlersuche BM2504
BM2505
- Mischungskreuz

Andreaskreuz - ---
- Für solche Mischungsaufgaben wie in der vorherigen Übung wird üblicherweise mit einem Mischungskreuz gerechnet.

- Das Mischungskreuz besteht aus 5 Kästchen, die in Form eines Andreaskreuzes angeordnet sind.
- In die beiden linken Kästchen werden die Konzentrationen (p1 und p2 in Prozent) der beiden Lösungen eingetragen.
- In das zentrale Kästchen wird die Konzentration der Ziellösung in Prozent eingetragen.
- In die beiden rechten Kästchen kommt die Formel zur Berechnung der Anteile (Volumen V1 und V2 in Liter oder Milliliter), die die beiden Ausgangslösungen haben müssen, um auf die Konzentration der Ziellösung zu kommen.
- Die Anteile geben das Verhältnis der beiden Ausgangslösungen an.
- Je nach Aufgabenstellung ist einer der Wert unbekannt und kann als „x“ gekennzeichnet werden.
- ---

- Hier bezeichnen wir die Konzentration der 1. Lösung als „x%“ und der 2. Lösung als „y%“. Die Konzentration der Ziellösung bezeichnen wir hier mit „z%“.
- Im oberen rechten Kästchen steht der Anteil der 1. Lösung in Volumeneinheiten. Dieser errechnet sich aus der Differenz der Konzentration der 2. Lösung und der Ziellösung. Diese Differenz wird als Betrag (senkrechte Strich) geschrieben, da es keine neg. Zahl für Volumenanteile geben kann.
- | y% - z% |
- ---
- Im unteren rechten Kästchen steht der Anteil der 2. Lösung in Volumeneinheiten. Dieser errechnet sich aus der Differenz der Konzentration der 1. Lösung und der Konzentration der Ziellösung. Diese Differenz wird als Betrag (senkrechte Strich) geschrieben, da es keine neg. Zahl für Volumenanteile geben kann.
- | x% - z% |
- ---
- Die meisten Leute vergessen das Mischungskreuz wieder, wenn sie es nicht beruflich anwenden müssen. Aber man sollte wenigstens einmal davon gehört haben, um es bei Bedarf schnell wieder lernen zu können.
- ---

- Beispiel:
- Eine 20%-ige Stammlösung (z. b. Salzsäure) soll mit Wasser verdünnt werden, bis eine 15%-ige Lösung entsteht.
- Mit wie viel Wasser muss die 20%-ige Lösung verdünnt werden, damit 1 Liter 15%-ige Lösung rauskommt?
- Wir tragen für p1 20 % ein.
- Die 2. Lösung besteht nur aus Wasser, h. h. sie enthält nichts anderes außer Wasser. Sie enthält also z. b. 0 % Salzsäure. Deshalb tragen wir für p2 0 % ein.
- Die Konzentration de Ziellösung (15 %) kommt in das zentrale Kästchen und in die beiden rechten Kästchen kommen die Formeln für die Volumenanteile.
- Wenn wir die Volumenanteile ausrechnen, dann erhalten wir 15 bzw. 5.
- Man muss also 15 Teile einer 20%-igen Lösung mit 5 Teilen einer 0%-igen Lösung (also Wasser) zusammenkippen, um eine 15%-ige Lösung zu erhalten.
- Das kann man auch kürzen:
- Man muss also 3 Teile einer 20%-igen Lösung mit einem Teil Wasservermischen, um eine 15%-ige Lösung zu erhalten.
- ---
- Damit ist die Aufgabe allerdings noch nicht vollständig gelöst, denn es wir abschließend nach einem Volumen gefragt, das vorgegeben wird.
- Es soll 1 Liter 15%-ige Lösung angesetzt werden.
- Dazu müssen wir die Anteile der beiden Lösungen zusammenzählen:
- 3 + 1 = 4
- Wenn wir also 3 Teile der Lösung 1 mit Wasser zusammenkippen, dann erhalten wir zusammen vier Teile der Ziellösung. Diese Ziellösung soll ein Volumen von 1 Liter haben.
- Am besten rechnen wir den Liter in Mililiter um.
- 1 Liter = 1.000 ml
- 1000 ml : 4 Anteile = 250 ml je Anteil
- 3 Teile Lösung 1 (3 * 250 ml) sind 750 ml.
- 1 Teil Wasser sind 250 ml.
- Wir müssen also 750 ml 20%-ige Salzsäure mit 250 ml Wasser mischen um 1 Liter 15%-ige Salzsäure zu erhalten.
- Wenn wir unser urspüngliches Ergebnis „15 : 5“ nicht gekürz hätten, dann wären wir auf das gleiche Ergebnis gekommen.
- 15 + 5 = 20 (Wir müssen das Volumen der Ziellösung in 20 Anteile teilen)
- 1000 ml : 20 = 50 ml (1/20 der Ziellösung sind 50 ml)
- 15 Teile * 50 ml = 750 ml (Lösung 1)
- 5 Teile * 50 ml = 250 ml (Wasser = Lösung 2)
- Das Ergebnis ist das Gleiche.
BM2506
- Mischungskreuz
- ---
- Das Mischungskreuz ist eine anschauliche Methode, um die Verhältnisse zweier Komponenten für eine Mischung zu berechnen. In der Chemie wird es verwendet, um Konzentrationen und Mengenverhältnisse in Flüssigkeiten oder Mischungen aus festen Komponenten zu errechnen. Dies kommt beim Mischen gelöster Stoffe (z. B. Säuren, Salze oder Laugen) mit unterschiedlichen Ausgangskonzentrationen vor. Das Mischungskreuz ist eine Anwendung des Massenerhaltungssatzes bzw. der Erhaltung der Stoffmenge. Die Berechnungen über das Mischungskreuz funktionieren daher nur mit Massen oder Stoffmengen. Wenn man mit Volumina rechnen möchte, muss man vorher die einzelnen Volumina mit Hilfe der Dichte in eine Masse umrechnen. Man erhält dann als Ergebnis eine Masse. Diese lässt sich mit der Dichte (bzw. über eine Prozentrechnung) wieder in ein Volumen umrechnen (Dichte = Masse/Volumen in [g/ml] oder [kg/l]).
- Weiter dient das Mischungskreuz zur Berechnung der Anteile an festen Stoffen (z. B. Mehl, Gebäck), die zu einer gewünschten Mischung vermengt werden müssen, oder für Mischkalkulationen im kaufmännischen Kontext. Das analoge Vorgehen zur Bestimmung von Mischtemperaturen wird Richmannsche Mischungsregel genannt.
- ---
- Prinzip des Mischungskreuzes:
- Das Mischungskreuz ist eine Methode, mit der man die Massenanteile berechnen kann, die man benötigt, um aus zwei Stammlösungen, d. h. Lösungen mit bekannten Konzentrationen, eine Lösung mit einer bestimmten Zielkonzentration zu erzeugen. Da die Stoffmenge eines gelösten Stoffs bei einer Verdünnung konstant bleibt, gilt – unter der Voraussetzung, dass die Konzentration des gelösten Stoffes im Verdünnungsmittel null ist – dass das Produkt aus Konzentration c und Volumen V (als eine Definition der Stoffmenge) eines gelösten Stoffes konstant bleibt:
- Der Index 1 bezeichnet dabei den Ausgangszustand, der Index 2 den Endzustand. Ist der betrachtete Stoff in beiden Lösungen A und B vorhanden, so gilt
- mit dem Gesamtvolumen
- .
- ---
- Aufgabe:
- Zeige, wie sich die Gleichung
- durch Einsetzen von und durch Umformen in die Gleichung umwandeln lässt.
1. Lösungshinweis BM2506 - Das soll aus der Gleichung verschwinden, weil die Gleichung, in die letztendlich umgewandelt werden soll, kein enthält.
- ---
- Einsetzen bedeutet z. B. bei folgender Aufgabe:
- das durch die Formel zu ersetzen,
- so dass man zum Schluss
- erhält
2. Lösungshinweis BM2506 - Da die Variablen in den 3 Gleichungen ziemlich unübersichtlich sind
- könnte man sie durch einfachere Variablen ersetzen, um die Aufgabe übersichtlicher zu machen.
- Beispielsweise:
Lösung (Teil 1) BM2506 - Einsetzen von Gleichung 2 in Gleichung 1:
- Gleichung 1:
- Gleichung 2:
- So entfällt aus der Gleichung.
Lösung (Teil 2) BM2506 - Das Entziel ist die Umwandlung in die folgende Gleichung:
- ---
Anwendung der Lösung BM2506
BM2507
- Schema:

Schema Mischungkreuz am Beispiel einer Weizenmischung - Vereinfacht ausgedrückt, gibt es in jedem Mischungskreuz eine „Gewinnsorte“ und eine „Verlustsorte“ gegenüber der gewünschten Mischung – sie stehen auf der linken Seite. Die gewünschte Mischung steht immer in der Mitte. Ziel der Berechnung ist es, zu ermitteln, mit welchen Massenanteilen (sie werden auf der rechten Seite errechnet) der beiden Mischungspartner der Gewinn und Verlust gegenüber der Mischung ausgeglichen werden kann. Da sich die Massenanteile umgekehrt proportional zu Gewinn und Verlust verhalten, ergibt sich schematisch die „Berechnung über Kreuz“.
- Beispiel:
- Zwei Posten Weizen sollen so gemischt werden, dass eine Dezitonne der Mischung für 49 € verkauft werden kann. Der Verkaufspreis für Sorte A beträgt 52 €/dt, der für Sorte B beträgt 45 €/dt.
- a) In welchem Verhältnis müssen die beiden Sorten gemischt werden?
- b) Wie viel dt müssen von jeder Sorte genommen werden, wenn insgesamt 24 dt Mischung benötigt werden?
- Lösung a) Das Mischungsverhältnis ist 4:3. Die Mischung demnach 7 Teile.
- Lösung b) 7 Teile entsprechen 24 dt. 4 Teile von Sorte A sind demnach = 13,71 dt. 3 Teile von Sorte B sind = 10,29 dt. Beide Anteile ergeben zusammen 24 dt.
BM2508
- Anwendungen des Mischungskreuzes:
- Mischen von Flüssigkeiten:

Mischungskreuz - Auf der linken Seite des Mischungskreuzes werden die bekannten Ausgangskonzentrationen der Flüssigkeiten eingetragen.
- An den Kreuzungspunkt schreibt man die gewünschte Zielkonzentration der Mischung.
- Nun bildet man die Differenz aus der bekannten Konzentration links oben und der gewünschten Zielkonzentration in der Mitte und notiert das Ergebnis rechts unten. Dann bildet man die Differenz aus der bekannten Konzentration links unten und der gewünschten Zielkonzentration in der Mitte und schreibt das Ergebnis rechts oben auf. Negative Ergebnisse werden ohne Vorzeichen notiert (Betragsrechnung).
- Auf der rechten Seite des Mischungskreuzes erhält man dann als Ergebnis die „Anteile an der Gesamtmasse“ (nicht am Volumen!), mit denen man die gewünschte Zielkonzentration herstellen kann.
- Beispielrechnung 1 (Mischen mit reinem Wasser):
- Es soll eine 35-prozentige Säure mit Wasser so gemischt werden, dass sich eine Ziellösung von 6 % Säureanteil ergibt.
- Wie viel Wasser und wie viel Säure werden benötigt?
- Die Ausgangskonzentrationen auf der linken Seite sind 35 % für die Säure und 0 % für das Wasser, in der Mitte steht die gewünschte Zielkonzentration, in diesem Fall 6 %
- 35 – 6 ergeben 29 Teile,
- 0 – 6 ergeben 6 Teile, (Vorzeichen wird weggelassen)
- insgesamt sind es 35 Gesamtteile. Es werden folglich 6 Teile der 35-prozentigen Säure und 29 Teile Wasser benötigt, um eine 6-prozentige Säure herzustellen.
- Sollen 1000 g einer 6-prozentigen Ziellösung hergestellt werden, benötigt man demnach:
- 35-prozentige Säure: [1000 g / 35] * 6 = 171 g
- Wasser: [1000 g / 35] * 29 = 829 g
- Beispielrechnung 2 (Mischen mit einer zweiten Säuremischung):
- An Stelle von 0 % (für die Konzentration von Wasser) könnte links auch ein Wert für eine 15-prozentige Säure stehen:
- Bei einer Zielkonzentration von 22 % müssten dann
- 22 – 15 = 7 Teile 35-prozentige Säure und
- 35 – 22 = 13 Teile 15-prozentige Säure
- gemischt werden.
- Sollen 1000 g der 22-prozentigen Ziellösung hergestellt werden, benötigt man demnach:
- 35-prozentige Säure: [1000 g / ( 7+13 )] * 7 = 350 g
- 15-prozentige Säure: [1000 g / ( 7+13 )] * 13 = 650 g
BM2509
- Berechnung von Legierungen mit dem Mischungskreuz:
- Das Mischungskreuz eignet sich auch zur näherungsweisen Berechnung der Masseanteile in Legierungen von Metallen, z.B. der Anteile von Zink und Kupfer in einer Messinglegierung. Wegen der Kristallgitterstruktur von Metallen ergibt die Berechnung mit dem Mischungskreuz nur ungefähre Werte. Die Formeln zur genauen Berechnung finden sich im Artikel Stoffmengenanteil.
- Beispielrechnung:
- Für die Dichte einer Messinglegierung wurde durch Wägen und Volumenberechnung der Wert 8,32 g/cm³ ermittelt.
- Reines Zink besitzt nach Tabelle eine Dichte von 6,97 g/cm³ und Kupfer eine Dichte von 8,61 g/cm³.
- Auf der linken Seite des Mischungskreuzes setzt man die "Ausgangskonzentrationen" 6,97 (für reines Zink) und 8,61 (für reines Kupfer) ein.
- In die Mitte setzt man den Mischungswert 8,32 für Messing als Zielzahl ein.
- Nun wird diagonal subtrahiert:
- Subtrahiert man 8,32 von 8,61 ergibt sich 0,29 -- sind 29 Teile Zink
- Subtrahiert man 8,32 von 6,97 ergibt sich 1,35 -- sind 135 Teile Kupfer.
- 29 Teile + 135 Teile = 164 Teile = Gesamtmasse = 100 %
- 29 Teile entsprechen somit 17,7 % (=Zink). 135 Teile entsprechen 82,3 % (= Kupfer)
- Die vorhandene Messinglegierung besteht demnach aus ca. 18 % Zink und 82 % Kupfer.
- ---
- Mischkalkulation

Mischungskreuz - Das Mischungskreuz eignet sich auch zur Berechnung von Mischungsverhältnissen im kaufmännischen Kontext.
- Beispielrechnung:
- Teesorte 1 kostet 2,60 Euro pro 100 g, Teesorte 2 kostet 3,70 Euro pro 100 g. Berechnen Sie ein Mischungsverhältnis für eine Teemischung vom Preis 3,40 Euro pro 100 g.
- Subtrahiert man 2,60 von 3,40 ergibt sich 0,80 — sind 8 Teile Teesorte 2
- Subtrahiert man 3,40 von 3,70 ergibt sich 0,30 — sind 3 Teile Teesorte 1
- 8 Teile + 3 Teile sind 11 Teile. Man kann beispielsweise 800 g Teesorte 2 und 300 g Teesorte 1 zu 1,1 kg Teemischung zum Preis 3,40 Euro pro 100 g mischen.
- 8 Teile entsprechen somit ca. 73 % Teesorte 2; 3 Teile entsprechen ca. 27 % Teesorte 1.
BM2510
- Wie viel einer 10%-igen Lösung A muss mit wie viel einer 30%-igen Lösung B gemischt werden, um 20 ml einer 25%-igen Lösung zu erhalten?
- Löse die Aufgabe zuerst mit einer Tabelle und dann nochmals mit mit einem Mischungskreuz!
Antwortsatz BM2510 - Frage:
- Wie viel einer 10%-igen Lösung A muss mit wie viel einer 30%-igen Lösung B gemischt werden, um 20 ml einer 25%-igen Lösung zu erhalten?
- Löse die Aufgabe zuerst mit einer Tabelle und dann nochmals mit mit einem Mischungskreuz!
- ---
- Antwort:
- Man braucht 5 ml der Lösung A und 15 ml der Lösung B.
Lösung mit Mischungskreuz BM2509
- ---
- 5 + 15 = 20 (20 Teile)
- 20 : 20 = 1 (1 Teil entspricht 1 ml)
- 5 * 1 ml = 5 ml
- 15 * 1 ml = 15 ml
- Antwort:
- Wir brauchen 5 ml von A und 15 ml von B.
BM2511 - BM2520
[editar]BM2511
- Rechteck
- In der Geometrie ist ein Rechteck ein ebenes Viereck, dessen Innenwinkel alle rechte Winkel sind. Es ist ein Spezialfall des Parallelogramms (gleichwinkeliges Parallelogramm) und damit auch des Trapezes. Ein Sonderfall des Rechtecks ist das Quadrat, bei dem alle Seiten gleich lang sind (gleichseitiges Rechteck).
- Eigenschaften:
- Für jedes Rechteck gilt:
- Die Winkelsumme beträgt 360°.
- Die beiden Diagonalen sind gleich lang und halbieren einander.
- Gegenüberliegende Seiten sind gleich lang und parallel. (siehe: Bild 2)
- ---
- Fläche A (Synonym: Flächeninhalt A)
- A = a * b (Bild 1)
- oder auch:
- A = b * h (Breite b; Höhe h) (siehe: Bild 3)
- ---
- Umfang U
- U = 2a + 2b
- oder auch:
- U = 2b + 2h (siehe: Bild 2)
- ---

Bild 4: Winkelsumme 360° - Die Summe der Innenwinkel eines Rechtecks ist 360°.
- Ein Rechteck hat 4 rechte Winkel. Jeder rechte Winkel hat 90°.
- Ein Vollkreis hat ebenfalls 360°.
BM2512
- Flächeneinheiten am Dreieck berechnen:
- ---

Bild 1 - Dreieck:
- Bild 1: Dreieck mit der Breite b und der Höhe h.
- Das Dreieck in Bild 1 ist ganz allgemein ein Dreieck. Es ist nicht der Spezialfall eines rechtwinkligen Dreiecks.
- ---
- Fläche A (Synonym: Flächeninhalt A) eines Dreiecks
- Die Fläche eines Dreiecks berechnet sich aus der halben Höhe mal der Breite.
- oder
- ---

Bild 2 - Bild 2: Jedes Dreieck ist die Hälfte eines Parallelogramms.
- obere Zeile Bild 2: Hier wurde das Dreieck aus Bild 3 verdoppelt, um ein Parallelogramm zu erzeugen, und um damit zu zeigen, dass dieses Dreieck die Hälfte eines Parallelogramms ist.
- mittlere und untere Zeile Bild 2: Hier soll gezeigt werden, dass sich der Flächeninhalt eines Parallelogramms nach der gleichen Formel berechnet, wie die Fläche eines Rechtecks. Wir können uns vorstellen, dass ein Teil des Parallelogramms rechts abgeschnitten wird (rot; mittlere Zeile) und links wieder angesetzt wird (grün; untere Zeile). So erhalten wir das flächengleiche Rechteck, für das die Fläche wie bereits bekannt berechnet wird:
- A = b * h (oder A = a * h)
- Sowohl beim Rechteck als auch beim Parallleogramm wird mit dieser Formel zur Flächenberechnung die Fläche ermittelt.
- Was folgt daraus? Da ein Parallelogramm aus 2 Dreiecken besteht, kann man die Fläche eines Dreieck berechnen, indem man die Fläche des Parallelogramms berechnet (A=b*h) und diese dann halbiert, also nicht anderes macht als sie durch 2 zu teilen.
- oder anders geschrieben
- was nichts anderes ist als
- wie wir es schon von weiter oben kennen.
- ---

Bild 3 - Bild 3 veranschaulicht nochmals die Flächenberechnung eines Dreiecks. Das Dreieck wurde auf halber Höhe waagerecht abgeschnitten. Der obere linke (hellgrüne) Teil wurde nach links unten gedreht (dunkelgrüm). Der obere rechte (hellrote) Teil wurde nach rechts unten gedreht (dunkelrot). Wir erhalten so ein halb so hohes Rechteck wie das Dreieck (untere Hälfte des Dreiecks zusammen mit dunkelrotem und dunkelgrünem Teil), aber mit der gleichen Breite. Offensichtlich ist die Fläche dieses Dreicks:
-
- ---
-
Bild 4
-
Bild 5
- Jedes rechtwinkige Dreieck ist die Hälfte eines Rechteck.
- Für rechtwinklige Dreiecke ist das viel offensichtlicher, als für andere Dreieck. (siehe: Bild 4 und 5)
- Erkläre das mit Hilfe der Bilder 4 und 5!
- ---
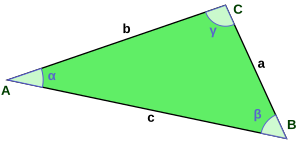
Bild 6 - Für den Umfang eines Dreiecks gibt es keine komplizierte Formel:
- U = a + b + c
- Die Höhe des Dreicks brauchen wir für die Berechnung des Umfangs nicht.
- ---

Bild 7: In einem Dreieck beträgt die Innenwinkelsumme stets . Die beiden blauen und roten Winkel sind Stufen- bzw. Wechselwinkel an parallelen Geraden und daher gleich groß. - Die Summe der Innenwinkel eines Dreiecks ist 180°.
- ---
-
Bild 1
-
Bild 2
-
Bild 3
-
Bild 4
- Nur an ebenen Dreiecken ist die Winkelsumme 180°.
- Bei sphärischen Dreiecken (Kugeldreieck; Dreieck auf Kugeln) ist die Winkelsumme größer als 180°.
- Die Winkelsumme eines Dreiecks auf einer Sattelfläche (Bild 4) ist – im Gegensatz zu einem sphärischen Dreieck oder allgemein einem Dreieck auf einer positiv gekrümmten Fläche – kleiner als 180°.
BM2513
- Flächeneinheiten am Trapez berechnen:
- ---

Bild 1: Trapez - Ein Trapez (von lateinisch trapezium, von der altgriech. Verkleinerungsform von trapeza „Tisch“) ist in der Geometrie ein ebenes Viereck mit zwei parallel zueinander liegenden Seiten.
- Ein Trapez kann man auch als ein Dreieck betrachten, bei dem die Spitze abgeschnitten ist.
- ---

Bild 2 - Fläche A (Synonym: Flächeninhalt A)
- oder anders ausgerückt
- ---
- Mittelwert:
- Das arithmetische Mittel (auch Durchschnitt) ist derjenige Mittelwert, der als Quotient aus der Summe der betrachteten Zahlen und ihrer Anzahl berechnet ist.
- Beispiel:
- Die zwei Zahlen 1 und 2 haben zum Beispiel den arithmetischen Mittelwert 1,5.
- .
- ---

Bild 3 - In der Formel zur Flächenberechnung eines Trapezes
- ist der Term der Mittelwert der beiden parallelen Seiten und .
- Dieser Mittelwert entspricht der roten Linie in Bild 3.
- ---

Bild 4 - Man kann sich die Flächenberechnung eines Trapezes bildlich so vorstellen, dass vom Trapez in der unteren rechten und linken Ecke ein Dreieck abgeschnitten wird, so dass das Trapez nur noch eine Breite von hat.
- Die abgeschnittenen Dreieck werden werden in die obere Hälfte gedreht, so dass sich nunmehr eine recheckige Fläche mit der Höhe und der Breite ergibt.
- Das entspricht der obigen Flächenformel
-
- ---

Bild 5 - Eine andere Möglichkeit die Flächenformel für das Trapez zu erklären ist, das Trapez in 2 Dreiecke zu unterteilen.
- Die Fläche von Dreieck 1 (rot) berechnet sich nach der von oben bekannten Formel für Dreiecke:
- (halbe Höhe mal Beite)
- In unserem konkreten Fall also
- Die Fläche des Dreieck 2 (grün) berechnet sich nach dem gleichen Schema:
- Und die Fläche des Trapezes ergibt sich aus der Summe dieser beiden Dreiecke 1 und 2.
- A = Dreieck 1 + Dreieck 2
- Aus dieser Formel können wir
- ausklammern und erhalten so die uns bereits bekannte Flächenformel für Trapeze:
BM2514
- Berechne folgende Flächen!

Bild 1: Berechne die Flächen der Dreiecke A, B, C und D! 
Bild 2: Berechne den Winkel Alpha! 
Bild 3: Berechne die Flächen F und G!
Lösung BM2514 - Bild 1:
- ---
- Bild 2:
- ---
- Bild 3:
BM2515
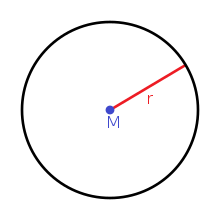
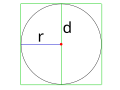
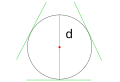
Bile 1: Mittelpunkt und Radius 
Bild 2: Durchmesser - Flächeninhalt und Umfang eines Kreises.
- Radius r
- Durchmesser d ()
- Mittelpunkt M
- Umfang U
- oder
-
Bild 3
-
Bild 4
- Wenn man die Formel für den Kreisumfang vergessen hat, dann kann man durch Überlegung den Kreisumfang ungefähr abschätzen. (grob schätzen; näherungsweise schätzen)
- Bild 3 und 4:
- Der Kreisumfang ist kleiner als 4 mal der Druchmesser. (4*d ist also unsere obere Grenze für den Kreisumfang)
- Das erkennt man daran, dass ein den Kreis umschließendes Quadrat vier Seiten von jeweils der Länge des Durchmessers hat. Es ist offensichtlich, dass wenn man diese 4 Seiten des Quadrates krümmt (beispielsweise aus Draht zu einer Rundung biegt), um den Kreisumfang zu bilden, dass dann einiges von den 4 Seiten des Quadrates als Überschuss übrig bleibt. (Die Linien überlappen sich.)
- ---
-
Bild 5
-
Bild 6
- Bild 5 und 6:
- Der Kreisumfang ist größer als 2 mal der Kreisdurchmesser. (2*d ist also unsere Untergrenze für den Kreisumfang)
- Das erkennt man, wenn man an den Kreis rechts und links 2 Linien von der Länge des Durchmessers anlegt und um den Kreis rumbiegt. Eine Linie vo der Länge des Durchmessers reicht niemals aus, um den Umfang eines halben Kreises abzudecken. Es bleibt eine Lücke.
- Wir stellen also fest:
- und
- Der Kreisumfang liegt also irgendwo zwischen zwei und vier mal den Kreisdurchmesser.
- ---
-
Bild 7
-
Bild 8
- Bild 7 und 8 demonstrieren uns, dass die Länge des Kreisumfangs irgendwo im Bereich um 3 liegen könnte.
- Der genaue Wert liegt bei 3,141592 ... und wird als Kreiszahl bezeichnet.
- Wir merken uns 3,14 für Pi.
BM2516
- Die alten Ägypter kannten zur Zeit des Pyramidenbaus schon die Kreiszahl .
- Sie rechneten aber mit dem Wert für .
- ---
- Beides ist also unser gerundetes Pi = 3,14
- ---
- Um wie viel Prozent weicht vom genaueren Wert 3,141592 ab?
Lösung BM2516 - Unser Grundwert G ist der wahre Wert für pi, also 3,141592
- 3,141592 (unser Grudnwert) entspricht also 100 %
- entspricht x Prozent
- ---
- ist um 0,04 % größer als .
BM2517
- Berechnung der Kreisfläche
- ---
- Kreisfläche A
- Radius r
- Die Einheit für die Fläche ist Quadratmeter [m2], also ein Quadrat mit der Kantenlänge 1x1 m.
- Auch wenn der Kreis rund ist, so wird dennoch die Fläche in Quadraten angegeben.
- ---

Bild 1 - Wenn einem wieder mal die Formel für die Berechnung der Kreisfläche entfallen ist, dann kann man sie sich herleiten oder zumindest näherungsweise bestimmen bzw. eingrenzen.
- Wie wir es oben bereits für den Kreisumfang getan haben wollen wir jetzt die Ober- und Untergrenze für die Kreisfläche abschätzen.
- Bild 1 zeigt einen Kreis, der von vier Quadraten abgedeckt ist. Die Quadraten haben die gleiche Kantenlänge wie der Kreisradius, so wie es am unteren rechten grünen Quadrat nochmals beschriftet ist. Die Fläche eines Quadrates ist somit r2. Da wir 4 dieser Quadrate haben und diese vier Quadrate zusammen eine größere Fläche als der Kreis abdecken, gilt:
- (das ist unsere Obergrenze für die Fläche des Kreises)
- ---

Bild 2 - Nun wollen wir die Untergrenze für eine mögliche Kreisfläche bestimmen.
- Wir gehen wieder von den vier Quadraten mit der Kantenlänge r aus. Diese vier Quadrate werden nochmals diagonal geteilt. Unten rechts ist das durch das blaue Dreieck angedeutet. Das blaue Dreieck liegt vollständig innerhalb des Kreises. Vier dieser Dreiecke (jeweils die Hälfte eines Quadrates) liegen also alle innerhalb des Kreises.
- Unsere Untergrenze für eine mögliche Kreisfläche ist also
- (das ist unsere Obergrenze für die Fläche des Kreises)
- Zwischen 2 und 4 liegt wieder unsere 3, mit der wir ziemlich nahe bei pi (3,14) liegen.
- Und schon haben wir die Kreisformel
- Statt mit dem Radius kann man die Kreisfläche auch mit dem Durchmesser d ausdrücken. Wie lautet die Formel dafür? Kannst du sie aus ableiten?
Lösung BM2517 - folglich ist
- Also setzen wir in die folgende Gleichung für ein.
- Das ist die Formel für die Berechnung der Kreisfläche mittels des Durchmessers d.
BM2518
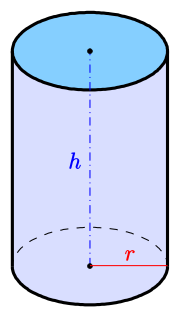
Bild 1: Zylinder - Zylinder
- ---
- Zylinder kann man sich als Kreis vorstellen, die in die 3. Dimension verlängert wurden, die in die 3. Demension wachsen.
- Ein Zylinder (lat. cylindrus von ‚rollen‘, ‚wälzen‘) ist im einfachsten Fall eine Fläche, deren Punkte von einer festen Gerade, der Achse, denselben Abstand r haben.
- Da solch eine Fläche unendlich ausgedehnt ist, beschneidet man sie normalerweise mit zwei parallelen Ebenen der Distanz h (s. Bild).
- Sind die Schnittebenen senkrecht zur Achse, entsteht ein senkrechter (oder gerader) Kreiszylinder mit Radius r und Höhe h. Die so beschnittene Fläche heißt Mantelfläche des Zylinders.
- ---
- Ein Zylinder ist ein dreidimensionaler Körper. Deshalb wird sein Volumen in Kubikmeter oder Kubikzentimeter angegeben.
- Der Kubikmeter (oder 'Meter hoch 3') ist die Maßeinheit für das Volumen im Internationalen Einheitensystem (SI), üblicherweise wird das Einheitenzeichen m3 verwendet. Ein Kubikmeter entspricht dem Volumen eines Würfels mit 1 Meter Kantenlänge.
- ---
- Das Volumen V des Zylinders berechnet sich aus der Fläche seiner Grundfläche (des Kreises auf dem er steht) mal seiner Höhe.
- ---
- Die Oberfläche des Zylinders ergibt sich aus der Summe der Grundfläche, der Deckfläche und der Mantelfläche (die seitliche Begrenzungsfläche). (Die Mantelfläche errechnet sich aus der Höhe des Zylinders mal dem Umfang des Kreises der Grundfläche.)
BM2519

Quader mit Raumdiagonale d - Quader
- ---
- Ein Quader ist ein Körper, der von sechs Rechtecken begrenzt wird.
- Ein Quader besitzt
- sechs Seitenflächen, die im rechten Winkel aufeinander stehen,
- acht rechtwinkelige Ecken (vier oben und vier unten) und
- zwölf Kanten, von denen jeweils vier gleiche Längen besitzen und zueinander parallel sind.
- Gegenüberliegende Flächen eines Quaders sind kongruent (deckungsgleich).
- ---
- V = a * b * c
- oder
- V = Länge l * Breite b * Höhe h
- ---
- Oberfläche
- Jeweils zwei der sich gegenüberliegende Seiten sind gleich groß. Wir haben alsp 3 mal je zwei gleich große Begrenzungsflächen des Quaders.
BM2520

Würfel - Würfel
- ---
- Ein Würfel ist eine Sonderform des Quaders, bei dem alle Kantenlängen gleich sind.
- Kantenlänge a
- Wie lauten die Formeln für die Volumenberechnung und Oberflächenberechnung eines Würfels mit de kantenlänge a?
Lösung BM2520 - (das ergibt sich aus )
- (das ergibt sich aus )
BM2521 - BM2530
[editar]- BM2521

- Kreis
- ---
- Ein Kreis ist eine ebene geometrische Figur. Er wird definiert als die Menge aller Punkte einer Ebene, die einen konstanten Abstand zu einem vorgegebenen Punkt dieser Ebene (dem Mittelpunkt) haben. Der Abstand der Kreispunkte zum Mittelpunkt ist der Radius oder Halbmesser des Kreises.
- ---
- Die Menge aller Punkte mit einer bestimmten Entfernung (Radius) zu einem zentralen Punkt (Mittelpunkt) nennt man Kreis.
- Der Durchmesser ist die Gerade, die von der einen Seite des Kreises durch den Mittelpunkt bis zur Begrenzungslinie auf der anderen Seite des Kreises geht.
- Radius r
- Durchmesser d
- Die Beziehung zwischen dem Druchmesser d und dem Umfang U ist (3,14)
- ---
- Berechne den Umfang des Kreises mit dem Radius 3 m! Gib die Antwort so genau wie möglich an!
Lösung BM2521 - (das ist die genaueste Antwort)
- (das ist nur ein gerundetes Ergebnis; das ist nur eine angenäherte Lösung)
- (das ist immer noch die genaueste Antwort)
BM2522
- Berechne die Fläche des Kreises mit dem Radius 3 cm! Gib die Antwort so genau wie möglich an!
Lösung BM2522 - (das ist die exakte Antwort)
- (das ist nur ein gerundetes Ergebnis; das ist nur eine angenäherte Lösung)
BM2523
- Aufgabe:
- Ein Autoreifen hat einen Durchmesser von 67,77 cm. Wie oft dreht sich der Reifen auf einer Fahrstrecke von 1 km?
Lösung BM2523 - 1 km = 1000 m
- 67,77 cm = 0,6777 m
- U = pi * d
- U = 3,141592 * 0,6777 m = 2,1290 m
- 1000 m : 2,1290 m = 469,7
- Das Rad dreht sich auf einer Strecke von einem Kilometer knapp 470 mal.
BM2524
- Ein Autoreifen mit einen Durchmesser von 66,09 cm hat sich in 53 Min. 88.483 mal gedreht. Wie schnell ist das Auto gefahren?
Lösung BM2524 - 1 km = 1000 m
- 66,09 cm = 0,6609 m
- U = pi * d
- U = 3,141592 * 0,6609 m = 2,076 m
- 2,076 m * 88.483 = 183690,708 m
- 183690,708 m = 183,69 km
- ---
- 60 min = 1 h
- 1 min = 1/60 h
- 53 min = x h
- 53 * 1/60 h = 0,8833 h
- ---
- v = s/t
- v = 183,69 km/0,8833 h
- v ≈ 208 km/h
- Das Auto ist 208 km/h gefahren.
BM2525
- Ein Zylinder hat die Höhe h = 10 m und den Durchmesser d = 8 m. Berechne sein Volumen, seine Oberfläche und den Umfang seiner Grundfläche!
Lösung BM2525 - U = 2 pi r
- r = d/2 = 8/2 = 4
- U = 2 * pi * 4
- U = 8 pi m
- ---
- Grundfläche:
- AG = pi * r2
- AG = pi * 42
- AG = 16 pi m2
- ---
- Mantelfläche:
- AM = U * h
- AM = 8 pi m * 10 m
- AM = 80 pi m2
- ---
- Gesamtfläche:
- A = 2 * Grundfläche + Mantelfläche
- A = 2 * 16 pi m2 + 80 pi m2
- A = 32 pi m2 + 80 pi m2
- A = 112 pi m2
- ---
- Volumen:
- V = Grundfläche * Höhe
- V = 16 pi m2 * 10 m
- V = 160 pi m3
BM2526
Lösung BM2526 - Die Fläche setzt sich aus drei Telflächen zusammen:
- v.l.n.r. Dreieck + Rechteck + Halbkreis
- Dieses Ergebnis ist natürlich falsch! Wo liegt der Fehler?
Korrektur der Lösung BM2526 - In dieser Formel ist der Halbkreis rechts falsch berechnet. Es wurde die Fläche für einen ganzen Kreis angesetzt ().
- Es muss also richtig lauten:
- Die Fläche beträgt ca. 439,25 Flächeneinheiten.
- ---
- Alternativ kann man das linke Dreieck zusammen mit dem Rechteck als Trapez betrachten und mit der entsprechenden Formel ausrechnen.
- A = Trapez + Halbkreis
- Das Ergebnis ist verständlicherweise das gleiche.
BM2527
- Umstellung einer Gleichung nach einer bestimmten Variablen
- ---
- Wir wollen die Gleichung v = s/t nach t umstellen.
- Die Umstellung einer Gleichung macht man mit der inversen (entgegengesetzten) Rechenoperation.
- Also „+“ ist die inverse Operation zu „-“, und umgekehrt.
- Und „*“ ist die inverse Operation zu „:“, und umgekehrt.
- ---
- Stelle v = s/t nach „t“ um!
Lösung BM2527-1
- ---
- Die jetzige Form der Gleichung ist eines Lösung für „s“. Man muss nur für die Variablen a, b und c die entsprechenden Zahlen einsetzen und ausrechnen und hat so das Ergebnis für „s“.
- Löse die Gleichung nach „b“ auf!
Lösung BM2527-2 - Üblicherweise wird die Gleichung so umgedreht, dass die Variable zum Schluss links steht.
- ---
- Hier nochmals das Umstellen der Gleichung, aber wesentlich kürzer und einfacher:
- ---
BM2528
- Löse die Gleichung nach „z“ auf!
Lösung BM2528
BM2529
- Rechne 100 °F in °C um!
- Grad Fahrenheit °F
- Grad Celsius °C
- Die Umrechnungsformel lautet:
- oder
- Temperatur in °C
- Temperatur in °F
Lösung BM2529-1 - 100 °F sind rund 37,8 °C.
- ---
- Rechne 22°C in °F um!
Lösung BM2529-2 - Dazu müssen wir die Formel nach TF auflösen
- In diese Formel könen wir nun 22°C für TC einsetzen.
- 22 °C sind 71,6 °F
BM2530
- Lineare Ungleichungen
- ---
- x + 5 > 2
- Das Umstellen von Ungleichungen erfolgt genauso wie bei Gleichungen.
- Einzige Ausnahme: Bei der Multiplikation oder Division mit negativen Zahlen dreht sich das „größer-als-Zeichen“ zum „kleiner-als-Zeichen“ um. (Dazu später mehr.)
- ---

- x + 5 = 2 // - 5
- x = -3
- ---
- x + 5 > 2 // - 5
- x > -3
- ---
- x + 5 < 2 // - 5
- x < -3
- ---
- x + 5 ≥ 2 // - 5
- x ≥ -3
- ---
- x + 5 ≤ 2 // - 5
- x ≤ -3
- ---
- Ungleichungen haben meist mehr als eine Zahl als Lösung. (manchmal auch keine Lösung oder unendlich viele Lösungen).
- Lineare Gleichungen haben gewöhnlich eine einzige Lösung (manchmal auch keine Lösung oder unendlich viele Lösungen).
BM2531 - BM2540
[editar]BM2531
- Welche Zahlen machen diese Aussagen wahr?
- 4 < 5 - 2y
Lösung BM2531-1
- ---
- 3x - 1 ≥ 7 + 2x
Lösung BM2531-2 - (Die Lösungsmenge besteht aus den Zahlen 8 und allen Zahlen, die größer als 8 sind, also auch 8,01; 9,9 usw.)
- Das schreibt man korrekt:
- (Alle x, für die gilt: x größer oder gleich 8.)
- Es gibt also unendlich viele Zahlen als Lösung. Das Zahlenintervall 8 bis plus unendlich ist die Lösungsmenge.
- ---
- 3x - 1 = 7 + 2x
Lösung BM2531-3 - (Die Lösungsmenge besteht lediglich aus der Zahl 8.)
BM2532
- Intervallnotation
- ---
- Das Intervall x < 2 geht von minus Unendlich bis ganz dicht an 2 ran, ohne die 2 selber mit zu enthalten. Das Intervall geht also bis 1,99999 ... oder anders ausgedrückt bis .
- ---

Bild 1 - Das Intervall x > 3 kann auf der Zahlengeraden mit einem Kreis dargestellt werden, der nicht ausgefüllt ist. Das zeigt an, dass das Intervall an diesem Punkt beginnt, dass aber der eigentliche Punkt nicht im Intervall enthalten ist. Das Intervall beginnt aber unendlich nahe bei dem ausgeschlossenen Startpunkt des Intervalls.
- Beispielsweise beginnt das Intervall x > 3 mit 3,1 oder noch dichter mit 3,0001 oder noch dichter 3,00000001 usw. Die Zahlen, die zum Intervall gehören gehen also unendlich dicht an die Zahl ran, die nicht zum Intervall gehört.
- Die Intervallschreibweise ohne Zahlengerade erfolgt mit runden bzw. eckigen Klammern. Die runde Klammer hat die gleiche Funktion wie der nicht ausgefüllte Kreis. Die runde Klammer zeigt also an, dass das Intervall bei einer bestimmten Zahl beginnt, dass aber diese Zahl selber NICHT zum Intervall gehört.
- Für das Intervall x > 3 ist die Intervallschreibweise
- Das Zeichen für „Unendlich“ ähnelt einer liegenden Acht. Da es die Zahl „Unendlich“ nicht gibt, kann sich unser Intervall nur an sie annähern. Also ist auch diese (größere) Seite durch eine runde Klammer begrenzt.
- Für könnte man auch schreiben.
- ---

Bild 2 - Das Intervall x < 3 geht von minus Unendlich bis 3, wobei das minus Unendlich und die 3 aber nicht dazu gehören. Deshalb ist das Intervall von zwei runden Klammern eingeschlossen.
- Bei der Intervallschreibweise wird die kleinere Zahl immer links geschrieben und die größere Zahl rechts. Die Anordnung ist also so wie auf dem Zahlenstrahl, der Größe nach von links nach rechts.
BM2533

Bild 3 - Das Intervall (x größer gleich 3) beginnt bei 3 (einschließlich 3) und endet bei plus Unendlich. Wenn der Endpunkt des Intervalls mit zum Intervall gehört, dann wird er auf dem Zahlenstrahl mit einem ausgefüllten Kreis (mit einem ausgefüllten Punkt) gekennzeichnet. Die Richtung, in die das Intervall geht wird mit einer Linie (evtl. farblich hervorgehoben) mit Pfeil markiert.
- In der Klammerscheibweise wird eine eckige Klammer verwendet, um zu zeigen, dass der Endpunkt des Intervalls mit zum Intervall gehört.
- plus Unendlich (und auch minus Unendlich) wird IMMER mit einer runden Klammer abgeschlossen, denn Unendlich gibt es nicht als Zahl, also kann es NICHT zum Intervall gehören, auch wenn es die Intervallgrenze darstellt.
- ---

Bild 4 - Das Intervall (x kleiner gleich 3) beginnt bei minus Unendlich und geht bis einschließlich Drei. Die Obergrenze ist 3 und wird auf der Zahlengeraden mit einem gefüllten Punkt markiert. In Klammerschreibweise wird die Obergrenze mit einer eckigen Klammer geschreiben, da die Intervallgrenze mit zum Intervall gehört. Die Untergrenze minus Unendlich wird mit einer runden Klammer abgeschlossen, da minus Unendlich selber nicht mehr mit zum Intervall gehört.
- Innerhalb der Klammern (eckig oder rund), stehen die beiden Zahlen für die Ober- und Untergrenue, wobeidie Untergrenze immer zuerst (links) angegeben wird. Beide Zahlen sind durch ein Semikolon oder Komma getrennt.
- Ein Komma kann aber irreführend sein, wenn Zahlen mit Nachkommastellen verwendet werden.
- sollte man besser mit Semikolon, statt mit Komma schreiben:
- oder so , je nachdem was gemeint ist.
- ---

Bild 5 - x = 3 ist keine Ungleichung, weshalb es dafür auch nur eine einzige Lösung gibt und nicht ein Intervall als Lösungsmenge. Folglich kann man auch nicht als Intervall auf der Zahlengeraden darstllen, sondern nur als Punkt.
- Normalerweise verwendet man dafür auch nicht die Intervallschreibweise, sondern schreibt diesen Punkt als Lösungsmenge:
- Man könnte auch ein Intervall mit der gleichen Ober- und Untergrenze angeben:
- , aber das wird selten so geschrieben und ist unüblich.
BM2534

Bild 6 - Eine gebräuchliche Variante der Darstelung von Zahlenintervallen auf einer Zahlengeraden ist die Verwendung von runden und eckigen Klammern auf der Zahlengeraden an Stelle von offenen und ausgefüllten Punkten.
- Die Bedeutung der Klammer ist die selbe, wie bei der Klammerschreibweise der Intervalle:
- Eine runde Klammer ersetzt also einen unausgefüllten Kreis und bedeutet, dass die Intervallgrenze selber nicht zum Intervall gehört, während eine eckige Klammer einen ausgefüllten Kreis ersetzt und bedeutet, dass diese Grenzstelle des Intervalls auf dem Zahlenstrahl mit zum Intervall gehört.
BM2535

Bild 7 - Eine weitere gebräuchliche Variante der Darstelung von Intervallen auf der Zahlengeraden ist die ausschließliche Verwendung von eckigen Klammern (auf runde Klammern wird dabei vollständig verzichtet).
- Die eine eckige Klammer wird wie bekannt verwendt, während für die runde Klammer (also für den nicht ausgefüllten Kreis) eine eckige Klammer verwendet wird, die vom Intervall weg zeigt.
- Diese Schreibweise mit ausschließlich eckigen Klammern kann man auch für die Klammerschreibweise verwenden:
- ⇒
- ⇒
- ⇒
- ⇒
BM2536
BM2537
- offenes Intervall
- (geschlossenes Intervall) = abgeschlossenes Intervall
- Wenn beide Intervallgrenzen (Ober- und Untergrenze) dem Intervall angehören, dann sprechen wir von einem abgeschlossenen Intervall.
- 1 ≤ x ≤ 3
- [1; 3]
- Die Untergrenze des Intervalls ist 1, die Obergrenze ist 3
- Das ist ein abgeschlossenes Intervall.
- ---
- Wenn beide Intervallgrenzen (Ober- und Untergrenze) NICHT dem Intervall angehören, dann sprechen wir von einem offenen Intervall.
- 2 < x < 5
- (2; 5)
- oder auch ]2; 5[ geschrieben.
- Die Untergrenze des Intervalls ist 2, wobei die 2 selber NICHT im Intervall enthalten ist.
- Die Obergrenze des Intervalls ist 5, wobei die 5 selber NICHT im Intervall enthalten ist.
- ---
- halboffenes Intervall
- Die eine Intervallgrenze ist offen und die andere ist abgeschlossen.
- Beispiele für halboffene Intervalle:
- 4 < x ≤ 7; (4; 7]; untere Intervallgrenze offen, obere Intervallgrenze abgeschlossen;
- 3 ≤ x < 6; [3; 6); untere Intervallgrenze abgeschlossen, obere Intervallgrenze offen;
- ; untere Intervallgrenze offen, obere Intervallgrenze abgeschlossen;
- ; untere Intervallgrenze offen, obere Intervallgrenze abgeschlossen;
BM2538
- x ≤ 5
- Wie schreibt man dieses Intervall?
- Wie nannt man diese Intervall auf der Zahlengeraden dar?
- Wie nennt man dieses Intervall?
- ---

Bild 2: Die Spitze hat nur EIN Ende. Die andere Seite hat ZWEI Enden (hier mit roten Punkten hervorgehoben). EINS ist kleiner als ZWEI. Die Spitze zeigt immer zum kleineren Wert. - „<“; „>“
- Manche verwechseln immern wieder das „größer-als-Zeichen“ mit dem „kleiner-als-Zeichen“.
- Eselsbrücke:
- Die Spitze des Zeichens zeigt immer zum kleineren Wert:
- 3 > 2
- 5 < 7
- 4 > 8 (Das ist natürlich falsch. Dann zeigt die Spitze auch nicht zur kleineren Zahl.)
BM2539
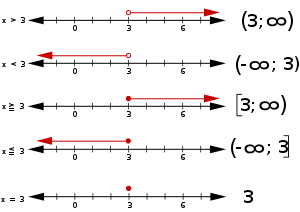
Bild 3 - Eselsbrücke für die Darstellung des Intervalls auf der Zahlengeraden:
- Dazu muss die Variable (hier „x“) immer auf der rechten Seite stehen, damit diese Eselsbrücke funktioniert.
- Die Spitze des größer- bzw- kleiner-als-Zeichens zeigt in die Richtung, in die der Strahl für das Invervall geht.
- Beispiel:
- x > 3; Die Spitze des „>“-Zeichens zeigt nach rechts. Das Intervall beginnt bei 3 und geht nach rechts.
- ---
- x < 3; Die Spitze des „<“-Zeichens zeigt nach links. Das Intervall beginnt bei 3 und geht nach links.
- Wenn die Spitze nach links zeigt, dann geht das Intervall nach links.
BM2540

Bild 4 - Wichtig ist, dass bei der Intervallschreibweise der kleine Wert (die kleine Zahl) immer links steht.
- (3; 5); Das ist die gleiche Reihenfolge wie auch auf der Zahlengeraden. Links die kleinen Zahlen, rechts die großen Zahlen. Das gilt auch für die negativen Zahlen.
- (-3; -5); Deshalb ist diese Intervallschreibweise falsch, denn minus 3 ist größer als minus 5.
- Richtig muss es heißen: (-5; -5).
- (-1; 0)
- (-9; 9)
- ; Das ist falsch. Es muss heißen .
- ---

Bild 5 - Das Intervall in Bild 5 startet nicht bei 3, sondern es endet bei 3.
- Es heißt also nicht (3; ...), sondern (...; 3).
- Das Intervall startet immer links, bei der kleineren Zahl.
- ---
- Die Zahlen auf dem Zahlenstrahl sind der Größe nach geordnet, von links nach rechts.
- Ebenso werden die Zahlen bei der Intervallschreibweise geordnet.
BM2541 - BM2550
[editar]BM2541
- Gib die Intervalle an!
- a) x ≤ -5
- b) x ≥ 4
Lösung BM2541 - a) x ≤ -5 ⇒
- b) x ≥ 4 ⇒
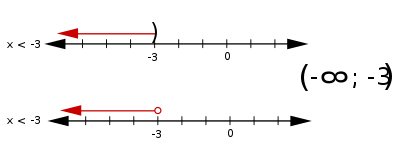
BM2542
- 3x - 5 ≤ 10
- Man kann versuchen die Lösung und das Intervall durch Ausprobieren zu finden.
- Wir setzen in 3x - 5 ≤ 10 ein:
- x = 0
- x = 6
- x = 5
- Welche dieser drei x-Werte erfüllen diese Ungleichung?
Lösung BM2542 - x = 0 ⇒ 3⋅0 - 5 ≤ 10 ⇒ - 5 ≤ 10 (wahr)
- x = 6 ⇒ 3⋅6 - 5 ≤ 10 ⇒ 13 ≤ 10 (falsch)
- x = 5 ⇒ 3⋅7 - 5 ≤ 10 ⇒ 10 ≤ 10 (wahr)
BM2543
- Nochmals die Ungleichung aus der vorherigen Übung, dieses mal aber mit „<“ statt „≤“
- 3x - 5 < 10
- Wir setzen wieder in 3x - 5 < 10 ein, um festzustellen ob mit diesen x-Werten die Ungleichung erfüllt ist:
- x = 0
- x = 6
- x = 5
Lösung BM2543 - x = 0 ⇒ 3⋅0 - 5 < 10 ⇒ - 5 < 10 (wahr)
- x = 6 ⇒ 3⋅6 - 5 < 10 ⇒ 13 < 10 (falsch)
- x = 5 ⇒ 3⋅7 - 5 < 10 ⇒ 10 < 10 (falsch)
BM2544
- Lineare Ungleichungen kann man genauso lösen, wie lineare Gleichungen.
- Die einzige Ausnahme bei Ungleichungen ist, dass bei einer Multiplikation mit einer negativen Zahl gleichzeitig das Verhältniszeichen („<“ oder „>“) umgedreht wird.
- Ebenso wird bei der bei der Division mit einer negativen Zahl im gleichen Schritt das Verhältniszeichen („<“ oder „>“) umgedreht.
- ---------------------------------------
- ---------------------------------------
- ---------------------------------------
- ---------------------------------------
- ---------------------------------------
BM2545
BM2546
- Wie eine Gleichung, so kann man auch eine Ungleichung umdrehen, also die rechte mit der linken Seite vertauschen. Dabei muss auch das Vergleichszeichen (Größer-als-Zeichen „>“ und das Kleiner-als-Zeichen „<“) mit umgedreht werden.
- 3 < 5 ⇒ 5 > 3 (Wenn 3 kleiner als 5 ist, dann ist 5 größer als 3.)
- a > b ⇒ b < a
- 5 > x ⇒ x < 5
- Bei Gleichheitszeichen kann man bekanntlich ebenfalls die Gleichung umdrehen:
- a = b ⇒ b = a
- Auch für „kleiner-gleich-Zeichen“ (≤; ≥) gilt, dass diese umgedreht werden, wenn die Ungleichung umgedreht wird. Schließlich sind diese Zeichen eine Kombination von „Kleiner-als-Zeichen“ und „Gleichheitszeichen“.
- a ≥ b ⇒ b ≤ a
- 5 ≥ x ⇒ x ≤ 5
BM2547
- Gib das Lösungsintervall an!
Lösung BM2547 - Lösung:
- --------------------------------
- Oder ein anderer Lösungsweg:
- Das ist die gleiche Lösung:
BM2548
- Gib das Lösungsintervall an!
Lösung BM2548 - Lösungsmenge L
BM2549
- Lineare Ungleichungen lösen
- ---
Lösung BM2549 - Zunächst vereinfacht man die Terme auf beiden Seiten, indem man die Klammern ausmultipliziert.
- linke Seite:
- ⇒
- Wir multiplizieren zwar mit minus Eins (also einer negativen Zahl), aber nicht die ganze Ungleichung sondern nur eine Seite der Ungleichung. Das bedeutet also NICHT, dass das „größer-als-Zeichen“ umgedreht wird.
- Es wird zwar multipliziert, aber auf jeder Seite für sich. Deshalb wird das Zeichen NICHT umgedreht.
- Das „größer-kleiner-Zeichen“ wird nur umgedreht, wenn die ganze Ungleichung (also beide Seiten gleichzeitig) mit einer neg. Zahl multipliziert (oder dividiert) wird.
- Das Ausmultiplizieren auf einer Seite dreht das Zeichen nicht.
- Das können wir auch begründen, indem wir erst die einer Seite ausmultiplizieren und erst in einem zweiten Schritt die andere Seite. Wann sollte man dann das Zeichen umdrehen? Nach dem Ausmultiplizieren der ersten oder der zweiten Seite? Oder soll man das Zeichen etwas zwei mal umdrehen, so dass es letztendlich unverändert bleibt?
BM2550
- Gib das Lösungsintervall an!
Lösung BM2550 - ---
- Oder
- índice
- Lección 100b ← Lección 101b → Lección 102b
- Lección 101











































































































































![{\displaystyle [m\cdot m\cdot m]=[m^{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da04f268f3d9486275cc40b90eba73fc33e9b16e)

![{\displaystyle [m^{2}\cdot m]=[m^{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4abce72848ff9000c16692107b0a542c00dbcae)
































![{\displaystyle [^{\circ }C]=([^{\circ }F]-32)\cdot \textstyle {\frac {5}{9}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a99bdcc2cac267a3fb3bedd395270e9d6102b0c2)






























![{\displaystyle (-\infty ;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90d7885874b3390fe2b9319af242464485c7c43)
![{\displaystyle [4,5,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba2a275fa8f0930b679a6a9a1a565f8823e346b0)
![{\displaystyle [4,5;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b3030a34e062b79ef50624af742eec9347493c9)
![{\displaystyle [4;5,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf9e249aa54b78fa0f3b53d220d22d5030e85d2)



![{\displaystyle [3;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c013875e8f3411efa42844ee4a93109c1a6c33e3)



![{\displaystyle ]3;\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b21c08f6047dbd90fd8f25b1300f67d47eb43fa)

![{\displaystyle ]-\infty ;3[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f6297bc199758fc8c99a64b4f24fa45a2c37f8e)

![{\displaystyle ]-\infty ;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f92a9c9f3a6bcd21f341b0dd2ba654e02ddb5487)

![{\displaystyle (3;\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/942c6b8e086e78b008d20b28229ce9110582c50f)

![{\displaystyle (-\infty ;5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae2c13189f4e1ef8c2b596c28d9ae2abd3ba80f)
![{\displaystyle ]-\infty ;5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80c94959479e808785aff89705bb8b39e35b1802)





![{\displaystyle (-\infty ;-5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/228b4512c6f73b32d7cd705b804d6b490448aa40)







![{\displaystyle ]-\infty ;-3[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27161163c9ae10e982bedde2e9bad4c51b23fe81)















![{\displaystyle L=\{\quad -\infty ;\textstyle {\frac {5}{4}}]\quad \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb0b27891cf2e3abbae5cb9122e4d8ae58d8003)



