Curso de alemán para principiantes con audio/Lección 072b
Apariencia
- índice
- Lección 071b ← Lección 072b → Lección 073b
- Lección 072
- Mathematik auf Deutsch - 22
BM1051 - BM1060
[editar]BM1051
- Beziehungen zwischen Mengen
- ---
- Wie wir wissen ist jede Zahl, die durch 4 teilbar ist, auch durch 2 teilbar. Wenn wir nun die Menge aller durch 4 teilbaren Zahlen M4 und die Menge aller durch 2 teilbaren Zahlen mit M2 bezeichnen, so können wir sagen:
- Jede Zahl a, die Element von M4 ist, ist auch Element von M2.
- d. h.:
- Wenn , so ,
- M4 = {0, 4, 8, 12, 16, 20, ...}
- M2 = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, ...}
- ---

Bild 1: Teilmenge - Umgekehrt gibt es aber Zahlen in M2, die nicht Element von M4 sind.
- Das können wir mit den Worten „nicht jede durch 2 teilbar Zahl ist auch durch 4 teilbar“ feststellen.
- Wir sagen: „M4 ist eine Teilmenge von M2“ und schreibe ndafür:
- (lies: M4 ist eine Teilmenge von M2)
- Bild 1 veranschaulicht diese Beziehung zwischen den Mengen M4 und M2. In ihm sind die Mengen als Flächen dargestellt., von denen die eine ['Sprechpause'] Teilfläche der anderen ist. Die Form und die Größe dieser Fläche kann beliebig gewählt werden, wenn nur diejeneige Fläche, die die Teilmenge M4 von M2 veranschaulicht, ganz innerhalb der Fläche liegt, die die Menge M2 darstellt.
- ---

Bild 2: Menge N = M - M sei die Menge aller ungeraden Zahln, die zwischen 40 und 45 liegen.
- N sei die Menge aller Primzahlen zwischen 40 und 45.
- M = {41, 43}
- N = {41, 43}
- Wir stellen fest, dass M und N dieselben Elemente enthalten.
- Wir sagen: „Die Mengen M und N sind gleich.“
- Wir schreiben: M = N
- ---
- Bei der Gleichheit von Mengen kommt es nicht auf die Reihenfolge ihrer Elemente an. So ist z. {2, 7, 9} dieselbe Menge wie {7, 2, 9}.
BM1052
- Bilde die Quersumme!
- --
- 24.036
- 311.201
- 37.415.214
- 40.023
- ---
- Welche der Zahlen sind durch 9 teilbar?
- Welche der Zahlen sind durch 3 teilbar?
BM1052
- Welche der folgenden Zahlen sind durch 6 teilbar?
- ---
- 756
- 2847
- 9462
- 5344
- 378.961
- 214.872
- 7392
- 30.462
- ---
- 576
- 4287
- 9552
- 3454
- 387.691
- 212.784
- 9732
- 30.624
BM1054
- Welche der folgenden Aussagen sind wahr?
- ---
- a) Wenn eine Zahl durch 8 teilbar ist, so ist sie auch durch 4 teilbar.
- b) Wenn eine Zahl durch 4 teilbar ist, so ist sie auch durch 8 teilbar.
- c) Wenn eine Zahl durch 6 teilbar ist, so ist sie auch durch 3 teilbar.
- d) Wenn eine Zahl durch 5 teilbar ist, so ist sie auch durch 10 teilbar.
- e) 13|221
- f) Wenn eine Zahl durch 9 teilbar ist, so ist sie auch durch 3 teilbar.
- g) Wenn eine Zahl durch 3 teilbar ist, so ist sie auch durch 9 teilbar.
- h) Wenn eine Zahl durch 3 teilbar ist, so ist sie auch durch 6 teilbar.
- i) Wenn eine gerade Zahl durch 3 teilbar ist, so ist sie auch durch 6 teilbar.
BM1055
- gemeinsame Vielfache
- gemeinsame Teiler
- ---
- zerlegen natürlicher Zahlen in Primfaktoren
- Primfaktorzerlegung (Teil 1)
- ---
- Die Primfaktorzerlegung ist die Darstellung einer natürlichen Zahl n als Produkt aus Primzahlen, die dann als Primfaktoren von nbezeichnet werden. Diese Darstellung ist (bis auf die Reihenfolge der Faktoren) eindeutig und zählt zu den grundlegenden und klassischen Werkzeugen der Zahlentheorie. Es ist bisher kein effizientes Faktorisierungsverfahren bekannt, um die Primfaktorzerlegung einer beliebigen Zahl zu erhalten.
- ---
- Die Primfaktorzerlegung ist die Darstellung der Zahl n als Produkt ihrer Primfaktoren. Da die Multiplikation kommutativ und assoziativ ist, ist die Reihenfolge der Primfaktoren unwichtig.
- Wenn n selbst eine Primzahl ist, so ist sie selbst ihr einziger Primfaktor.
- Gibt es mehr als einen Primfaktor, so wird n zusammengesetzte Zahl genannt.
- Ein Primfaktor p kann mehrfach auftreten; mehrfach auftretende Primfaktoren können mittels Exponenten-Schreibweise zusammengefasst werden.
- Üblicherweise werden die Primfaktoren aufsteigend geordnet geschreiben.
- ---
- Beispiele für Primfaktorzerlegungen
- (Primzahl)
- (Zweierpotenz)
- (Zehnerpotenz)
- ---
- Praktische Anwendung
- Aus der Primfaktorenzerlegung lässt sich erkennen, ob eine Zahl durch eine andere teilbar ist. Das kleinste gemeinsame Vielfache (kgV) und der größte gemeinsame Teiler (ggT) können leicht aus der Primfaktorzerlegung bestimmt werden. In der Bruchrechnung können Brüche durch den ggT von Zähler und Nenner gekürzt werden. Beim Addieren und Subtrahieren werden zwei Brüche auf das kgV der Nenner erweitert.
- ---
- Kryptographie
- Eine wichtige Rolle spielen Primzahlen in der Kryptographie. Verschlüsselungssysteme wie RSA basieren darauf, dass kein effizientes Faktorisierungsverfahren bekannt ist. So ist es innerhalb von Sekunden problemlos möglich, zwei 500-stellige Primzahlen zu finden und miteinander zu multiplizieren. Mit den heutigen Methoden würde die Rückgewinnung der beiden Primfaktoren aus diesem 999- oder 1000-stelligen Produkt dagegen sehr lange Zeit dauern.
- ---
- Es gibt Zahlen, die nur durch 1 und sich selbst teilbar sind. Diese werden Primzahlen genannt, z. B. 2, 3, 5, 7, 11... Zahlen, die keine Primzahlen sind, heißen zusammengesetzte Zahlen. Jede zusammengesetzte Zahl lässt sich in Primfaktoren zerlegen, d. h., dass man jede zusammengesetzte Zahl eindeutig als Produkt aus Primzahlen schreiben kann, z. B. 91 = 7 ⋅ 13.
BM1056
- Primfaktorzerlegung (Teil 2)
- ---
- Es sind häufig zwei Fragen, die sich in Bezug auf die Primzahlen stellen:
- Ist die vorliegende Zahl eine Primzahl?
- Wie läßt sich die vorliegende Zahl zerlegen?
- ---
- Wenn die vorliegende Zahl sehr klein ist, also kleiner als 90, dann kann man schon mit etwas Überlegung sagen, ob es sich um eine Primzahl handelt, oder nicht. Die 91 ist der erste kleine Stolperstein, da sie die erste Zahl ist, deren sämtliche Primfaktoren größer als fünf sind (91=7·13). Wer allerdings Primzahlen auswendig weiß, kann durchaus bis 127 und höher kommen. Aber wer lernt schon vier- oder mehrstellige Primzahlen auswendig (333667 mag da, z.B. wegen ihrer Eigenschaften, eine Ausnahme sein). Also braucht man ein Verfahren, um solche Zahlen auf ihre Primalität zu testen.
- ---
- Wenn man testen möchte, ob eine natürliche Zahl eine Primzahl ist, kommt einem vielleicht als erstes das Konsequente Durchtesten auf Teilbarkeit in den Sinn. Dabei testet man, ob es eine natürliche Zahl zwischen und gibt, die teilt. Existiert keine natürliche Zahl zwischen und gibt, die teilt, so ist eine Primzahl. Findet sich wenigstens eine Zahl zwischen und die teilt, so ist keine Primzahl.
- ---
- Beispiele:
- 7
- Keine Zahl zwischen 2 und 6 teilt 7 (ohne Rest), also ist 7 eine Primzahl.
- ---
- 9
- Teiler!
- Die 3 teilt 9 (ohne Rest), also kann 9 keine Primzahl sein.
BM1057
- Sieb des Eratosthenes
- ---
- Das Sieb des Eratosthenes ist ein Sonderfall. Im Gegensatz zu Verfahren, die einzelne Zahlen auf ihre Primalität prüfen, siebt das Siebverfahren aus einem vorgegebenen Zahlenbereich, von 2 bis zu einer vorgegebenen Obergrenze, alle Nichtprimzahlen aus, so dass nur die Primzahlen übrig bleiben.
- Dabei wird wie folgt vorgegangen. Jede natürliche Zahl zwischen 2 und der Obergrenze bekommt eine Art kleines Schild, auf der ihr Zustand bezüglich der Primalität geschrieben steht. Am Anfang werden alle Zahlen zwischen 2 und Obergrenze als Primzahl deklariert.
- Nun wird die erste Zahl genommen, das ist die 2, und nachgesehen, ob es eine Primzahl ist. Die 2 hat die Information Primzahl. Wenn also die 2 eine Primzahl ist, dann können alle Vielfachen von 2, angefangen mit 22 keine Primzahlen mehr sein. Dementsprechend wird auf allen Schildern der Vielfachen von 2, angefangen mit 22 bis Obergrenze, die Information von Primzahl auf Nichtprimzahl geändert. danach wird die nächste Zahl, das ist die 3, auf ihre Primalität getestet. Wieder werden, im Falle, das es sich um eine Primzahl handelt alle Vielfachen in ihrem Zustand von Primzahl auf Nichtprimzahl geändert.
- Das Ganze wird solange gemacht, bis man die Quadratwurzel von Obergrenze erreicht hat, weswegen es sinnvoll ist, als Obergrenze eine Quadratzahl einzusetzen. Wenn man z.B. ein Zahlenfeld von 2 bis 10.000 siebt, dann muß man nur bis 100 (genauer bis 101) testen, da 1002 = 10.000 ist. Alle Zahlen größer 100, die noch auf ihrem Schild Primzahl stehen haben, sind auch Primzahlen.
- ---
- Der Sinn des Sieb des Eratosthenes ist, Primzahltabellen zu erstellen, in denen man - bei kleineren Zahlen - nachsehen kann, ob es sich bei der gesuchten Zahl um eine Primzahl handelt.
BM1058
- Primfaktorzerlegung (Teil 3)
- ---
- Wenn wir eine Zahl in Faktoren zerlegen, die sämtlich Primzahlen sind, so sprechen wir von eier Zerlegung in Primfaktoren.
- Bei der Zerlegung in Primfaktoren beginnen wir am besten mit der kleinsten Primzahl unter den Teilern dieser Zahl.
- ---
- Beispiel:
- 42 in Primfaktoren zerlegen
- 42 = 2 * (21)
- 42 = 2 * (3 * 7)
- 42 = 2 * 3 * 7
- ---
- 72
- 72 = 2 * 36
- 72 = 2 * 2 * 18
- 72 = 2 * 2 * 2 * 9
- 72 = 2 * 2 * 2 * 3 * 3
- 72 = 23 * 32
BM1059
- Es soll die Zahl 315 in Primfaktoren zerlegt werden.
- Da 315 ungerade ist, enthält 315 nicht den Teiler 2.
- An der Quersumme 9 erkennen wir, dass 315 durch 3 teilbar ist. Die 3 ist also in diesem Fall die kleinste Primzahl unter den Teilern dieser Zahl.
- 315 = 3 * 105
- 315 = 3 * 3 * 35
- 315 = 3 * 3 * 5 * 7
BM1060
- Jede natürliche Zahl lässt sich nur auf eine einzige Art in Primfaktoren zerlegen.
- ---
- Zerlege 6.734.271.541 in Primzahlen! (Das geht nicht mit Stift und Papier, weil die Zahl zu groß ist. Suche Dir im Internet eine passende Seite dafür.)
Lösung BM1060 - 6.734.271.541 = 87.557 * 76.913
BM1061 - BM1070
[editar]BM1061
- Primfaktorzerlegung in Potenzschreibweise
- ---
- Aus der Zerlegung einer Zahl in Primfaktoren können wir alle Primzahlen in der Menge ihrer Teiler sofort ablesen, denn das sind ja gerade die in der Zerlegung auftretenden Primzahlen.
- ---
- Wir können diese Primzahlen zu einer Menge zusammenfassen.
- a) Menge der Primzahlen unter den Teilern von 42: {2, 3, 7}
- b) Menge der Primzahlen unter den Teilern von 72: {2, 3}
- c) Menge der Primzahlen unter den Teilern von 315: {2, 3, 7}
- ---
- Wir können durch die Primfaktorzerlegung einer Zahl aber nicht nur die Primzahlen unter ihren Teilern feststellen, sondern auch ermitteln, welche weiteren Teiler diese Zahl hat, indem wir auf alle möglichen Arten die Primfaktoren zu Produkten zusammenfassen.
- ---
- Beispiel:
- 72 = 2 * 2 * 2 * 3 * 3
- 72 = 2 * 2 * 2 * 3 * 3 = 2 * 36 (Teiler 2 und 26)
- 72 = 2 * 2 * 2 * 3 * 3 = 4 * 18 (Teiler 4 und 18)
- 72 = 2 * 2 * 2 * 3 * 3 = 8 * 9 (Teiler 8 und 9)
- 72 = 2 * 2 * 2 * 3 * 3 = 24 * 3 (Teiler 24 und 3)
- 72 = 2 * 2 * 2 * 3 * 3 = 12 * 6 (Teiler 12 und 6)
BM1062
- Bei der Zerlegung in Primfaktoren können gleiche Primzahlen auch mehrmals als Faktoren auftreten. Ein Produkt mit gleichen Faktoren können wir in abgekürzter Form schreiben.
- ---
- 8 = 2 * 2 * 2 = 23 (lies: zwei hoch drei)
- 81 = 3 * 3 * 3 * 3 = 34 (lies: drei hoch vier)
- 72 = 2 * 2 * 2 * 3 * 3 = 23 * 32
- ---
- 125 = 5 * 5 * 5 = 53
- In dieser Form geschreibene Produkte heißen Potenzen.
- Die kleine hochgesetzte Zahl heißt Exponent.
- Die kleine hochgestellte Zahl heißt Exponent.
- Die unten stehende Zahl heißt Basis.
- Der Exponent gibt an, wie oft die Basis als Faktor zu setzen ist.
- ---
- Mit Hilfe der Potenzschreibweise könne wir die Primfaktorzerlegungen kürzer schreiben.
- 315 = 32 * 5 * 7
- 72 = 23 * 32
- 432 = 24 * 33
BM1063
- Außer den durch die Primfaktorzerlegung gefundenen Teilern hat jede Zahl noch die 1 und die Zahl selber als Teiler.
- ---
- Beispiel:
- 72 = 2 * 2 * 2 * 3 * 3
- 72 hat noch die Teiler 1 und 72.
- ---
- Die Menge der Primzahlen unter den Teilern von 72 ist also eine Teilmenge der Menge aller Teiler dieser Zahl.
- A = Menge aller Teiler der Zahl 72
- A = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}
- B = Menge der Primzahlen unter den Teilern von 72
- B = {2, 3}
BM1064
- Zerlege die folgenden Zahlen in Primfaktoren!
- ---
- a) 25
- b) 42
- c) 48
- d) 50
- e) 81
- f) 121
- g) 152
- h) 240
- i) 440
- j) 625
- k) 840
BM1065
- Zerlege die folgenden Zahlen in Primfaktoren!
- ---
- a) 16
- b) 28
- c) 36
- d) 54
- e) 100
- f) 225
- g) 306
- h) 504
- i) 720
- j) 900
- k) 1000
BM1066
- Zerlege die folgenden Zahlen in Primfaktoren!
- ---
- a) 120
- b) 160
- c) 200
- d) 150
- e) 180
- f) 320
- g) 220
- h) 80
BM1067
- Zerlege die folgenden Zahlen in Primfaktoren!
- ---
- a) 180
- b) 256
- c) 372
- d) 2200
- e) 128
- f) 348
- g) 1400
BM1068
- Schreibe die folgenden Produkte als Potenzen!
- ---
- a) 2 * 2 * 2 * 2
- b) 3 * 3 * 3 * 3 * 3
- c) 4 * 4 * 4 * 4
- d) 10 * 10 * 10 * 10 * 10 * 10
- e) 2 * 2 * 2 * 2 * 2
- f) 3 * 3 * 3 * 3
- g) 9 * 9 * 9 * 9 * 9 * 9 * 9 *
- h) 10 * 10 * 10 * 10 * 10
BM1069
- Rechne die folgenden Potenzen aus!
- ---
- a) 23
- b) 53
- c) 83
- d) 45
- e) 104
- f) 24
- g) 34
- h) 105
- i) 63
- j) 72
BM1070
- gemeinsame Teiler
- gemeinsame Vielfache
- ---
- Eine natürliche Zahl kann Teiler auch von zwei oder mehr als zwei natürlichen Zahlen sein.
- ---
- 4 ist Teiler von 20, denn 20 = 4 * 5. Also 4|20
- 4 ist Teiler von 32, denn 32 = 4 * 8. Also 4|32
- Außer den Zahlen 20 und 32 gibt es noch andere Zahlen, die den Teiler 4 besitzen, z. B. 4, 16, 80, 104.
- ---
- Die Zahl 7 ist Teiler z. B. von 21, 35, 63, 147, 4711.
- --
- Eine natürliche Zahl, die Teiler von zwei oder von mehr als zwei Zahlen ist, heißt gemeinsamer Teiler dieser Zahl.
BM1071 - BM1080
[editar]BM1071
- teilerfremd
- ---
- Da die Zahl 1 Teiler einer jeden Zahl ist, ist sie auch stets gemeinsamer Teiler zweier beliebiger Zahlen. Wir wollen sie deshalb bei der Aufzählung gemeinsamer Teiler nicht aufführen.
- ---
- Natürliche Zahlen, die außer 1 keinen gemeinsamen Teiler haben, heißen zueinander teilerfremd.
- ---
- Beispiel:
- 15 und 16 sind teilerfremd
- 14 und 25 sind teilerfremd
- ---
- Eine natürliche Zahl kann Vielfaches auch von zwei oder von mehr als zwei natürlichen Zahlen sein.
- ---
- Die Zahl 72 ist Vielfaches der Zahl 6, denn 72 = 12 * 6
- Die Zahl 72 ist aber auch Vielfaches der Zahl 8, denn 72 = 9 * 8
- Außer der Zahl 72 gibt es noch weitere Vielfache der Zahlen 6 und 8, z. B. 96, 240, 24, 120.
BM1072
- gemeinsames Vielfaches
- ---
- Eine natürliche Zahl, die Vielfaches von zwei oder mehr als zwei natürlichen Zahlen ist, heißt gemeinsames Vielfaches dieser Zahlen.
- ---
- Da die Zahl 0 Vielfaches (nämlich das Nullfache) von jeder Zahl ist, ist die Zahl 0 auch gemeinsames Vielfaches zweier beliebiger Zahlen. Daher wollen wir bei der Bildung gemeinsamer Vielfacher die 0 nicht berücksichtigen.
BM1073
- Das kleinste gemeinsame Vielfache
- k.g.V.
- ---
- Unter allen gemeinsamen Vielfachen der Zahl 6 und 8 gibt es ein kleinstes gemeinsames Vielfaches, nämlich die Zahl 24.
- Es gibt zwar noch kleinere Vielfache von 6 und auch kleinere Vielfache von 8, aber kein kleineres gemeinsames Vielfaches.
- ---
- Die folgende Tabelle zeigt die Vielfachen von 6 und die Vielfachen von 8. Das kleinste gemeinsame Vielfache ist in der Tabelle grün markiert.
Vielfaches von 6 6 12 18 24 30 36 Vielfaches von 8 16 24 32 40 48 56
BM1074
- Wir können gemeinsame Vielfache von mehr als zwei Zahlen bilden.
- ---
- Es sollen gemeinsame Vielfache von 4, 9 und 10 ermittelt werden.
- a) 180 = 45 * 4 = 20 * 9 = 18 * 10
- b) 360 = 90 * 4 = 40 * 9 = 36 * 10
- c) 720 = 180 * 4 = 80 * 9 = 72 * 10
- ---
- Auch hier gibt es beleibig viele gemeinsame Vielfache, denn jedes Vielfache von 180 ist wieder gemeinsames Vielfaches von 4, 9 und 10.
- Für die Zahlen 4, 9 und 10 ist 180 das kleinste von allen gemeinsamen Vielfachen.
- ---
- Definition: Das kleinste gemeinsame Vielfache (k.g.V.) gegebener natürlicher Zahlen ist die kleinste von Null verschiedene Zahl, die durch alle gegebenen Zahlen teilbar ist.
BM1075
- Ermitteln des k.g.V.
- ---
- Das Produkt gegebener Zahlen ist stets ein gemeinsames Vielfaches dieser Zahlen, aber meistens nicht das kleinste gemeinsame Vielfache.
- Ein gemeinsames Vielfaches von 6 und 8 ist z. B. 6 * 8 = 48, das k.g.V. aber ist 24.
- ---
- So ermitteln wir das k.g.V.:
- ---
- 1. Schritt:
- Zerlege die gegebenen Zahlen in Primfaktoren!
- Beispiel:
- 6 = 2 * 3
- 8 = 2 * 2 * 2
- ---
- 2. Schritt:
- Schreibe die Produkte in Potenzschreibweise!
- Beispiel:
- 6 = 2 * 3
- 8 = 2 * 2 * 2 = 23
- ---
- 3. Schritt:
- Schreibe von den Potenzen mit gleicher Basis jeweils die mit dem größten Exponenten heraus!
- Beispiel:
- 6 = 2 * 3
- 8 = 2 * 2 * 2 = 23
- 23 * 3
- ---
- Primfaktoren, die nur einfach und nicht als Potenzen auftreten, werden in jeder Spalte einmal ausgewählt.
- Da die Zahl 8 im k.g.V. als Faktor enthalten sein muss, müssen wir 23 für das Bilden des k.g.V. auswählen.
- Weiterhin muss aber auch die Zahl 6 im k.g.V. als Faktor enthalten sein, d.h., das k.g.V. muss die Faktoren 2 und 3 enthalten. Der Faktor 2 ist schon in der bereits ausgewählten Potenz 23 enthalten. Deshalb brauchen wir nur noch einen Faktor 3 zu berücksichtigen.
- ---
- 4. Schritt:
- Bilde das Produkt der ausgewählten Potenzen!
- Beispiel:
- 6 = 2 * 3
- 8 = 2 * 2 * 2 = 23
- k.g.V.: 23 * 3 = 24
- Das k.g.V. ist 24.
- ---
- Dieses Verfahren ist besonders zweckmäßig, wenn man das k.g.V. größerer Zahlen berechnen will.
BM1076
- Es soll das k.g.V. von 840, 126 und 225 ermittelt werden.
- 840 = 2 * 2 * 2 * 3 * 5 * 7 = 23 * 3 * 5 * 7
- 126 = 2 * 3 * 3 * 7 = 2 * 32 * 7
- 225 = 3 * 3 * 5 * 5 = 32 * 52
- 23 * 32 * 52 * 7 = 12.600
- Das k.g.V. von 840, 126 und 225 ist 12.600.
- ---
- Um das k.g.V. zu ermitteln zerlegen wir also die Zahlen in Primfaktoren oder genauer gesagt: wir zerlegen die Zahlen in Potenzen von Primfaktoren.
- Um alle Primfaktoren übersichtlich aufzuschreiben, werden gleiche Primfaktoren am besten genau untereinander geschrieben:
840 = 2 * 2 * 2 * 3 * 5 * 7 = 23 * 3 * 5 * 7 126 = 2 * 3 * 3 * 7 = 2 * 32 * 7 225 = 3 * 3 * 5 * 5 = 32 * 52 k.g.V. 12.600 = 23 * 32 * 52 * 7
BM1077
- Die Zahl 12.600 ist ein gemeinsames Vielfaches der gegebenen Zahlen 840, 126 und 225.
- 12.600 ist aber auch das kleinste gemeinsame Vielfache.
- Würden wir auch nur einen Primfaktor fortlassen (= weglassen), so wären die gefundenen Zahln nicht mehr ein gemeinsames Vielfaches der gegebenen Zahlen.
- Streichen wir aus der Zahl 12.600 z. B. einen Faktor 2, so ist die Potenz 23 und damit die Zahl 840 nicht mehr als Faktor in der Zahl 12.600 enthalten.
- Beispiel:
- 840 = 2 * 2 * 2 * 3 * 5 * 7 = rrrrrrrrr * 3 * 5 * 7
- 126 = 2 * 3 * 3 * 7 = 2 * 32 * 7
- 225 = 3 * 3 * 5 * 5 = 32 * 52
- rrrrrrrrr * 32 * 52 * 7 = 1575
- ABER: 1575 ist NICHT das k.g.V. von 840, 126 und 225.
- ---
- Beim Kürzen von Brüchen müssen wir solche Zahlen finden, durch die Zähler und Nenner teilerfremd sind. Diese Zahlen müssen also gemeinsamer Teiler von Zähler und Nenner sein.
BM1078
- Ermittler in der folgenden Aufgabe die gemeinsamen Teiler!
- Gib an, welcher von ihnen der größte ist!
- ---
- a) 12 und 18
- b) 21 und 28
- c) 72 und 63
- d) 80 und 64
- ---
- e) 90 und 45
- f) 20 und 24
- g) 42 und 56
- h) 120 und 96
- ---
- i) 12, 18 und 40
- j) 16, 36 und 52
- k) 24, 28, 36 und 84
- ---
- m) 26, 25 und 130
- n) 48, 84 und 150
- o) 44, 56, 63 und 112
BM1079
- Schreibe von den folgenden Zahlenpaaren [a; b] diejenigen heraus, bei denen a und b zueinander teilerfremd sind!
- ---
- a) [8; 22]
- b) [41; 164]
- c) [19; 58]
- d) [21; 63]
- e) [256; 105]
- ---
- f) [19; 82]
- g) [23; 47]
- h) [11; 143]
- i) [36; 105]
- j) [243; 140]
BM1080
- Ermittle das k.g.V. von folgenden Zahlen!
- ---
- a) 4 und 6
- b) 9 und 12
- c) 4 und 5
- d) 24 und 27
- e) 25 und 35
- f) 60 und 80
- g) 18 und 48
- h) 4, 9 und 24
- ---
- i) 4 und 10
- j) 12 und 15
- k) 2 und 11
- m) 14 und 35
- n) 27 und 36
- o) 20 und 45
- p) 40 und 60
- q) 7, 12 und 21
BM1081 - BM1090
[editar]BM1081
- Ermittle durch Zerlegen in Primfaktoren das k.g.V. der folgenden Zahlen!
- ---
- a) 6, 8, 10, 12
- b) 12, 15, 18, 24
- c) 187, 44, 102
- d) 221,26, 6
- ---
- e) 6, 9, 12, 15
- f) 12, 16, 20, 24
- g) 143, 78, 44
- h) 221, 34, 6
BM1082
- In der folgenden Tabelle steht in der ersten Zeile das k.g.V. zweier Zahlen a und b.
- Ermittle die kleinste Zahl, die für b möglich ist!
k.g.V. 24 105 180 a 6 15 90 b
BM1083
- In der folgenden Tabelle steht in der ersten Zeile das k.g.V. zweier Zahlen a und b.
- Ermittle die kleinste Zahl, die für b möglich ist!
k.g.V. 36 105 180 a 12 21 60 b
BM1084
- Ermittle durch Zerlegen in Primfaktoren alle gemeinsamen Teiler der folgenden Zahlen!
- ---
- a) 28, 119, 63
- b) 36, 72, 81, 126
- c) 35, 112, 56
- d) 24, 48, 16, 128
BM1085
- größter gemeinsamer Teiler (g.g.T.)
- Brüche kürzen
- ---
- Jetzt wird es Zeit unsere Kenntniss vom k.g.V. praktisch anzuwenden.
- Es soll der Bruch gekürzt werden.
- Dazu suchen wir alle gemeinsamen Teiler von 56 und 84:
Teiler von 56 1 2 4 7 8 14 28 56 Teiler von 84 1 2 3 4 6 7 12 14 21 28 42 84 gemeinsame Teiler 2 4 7 14 28
- Damit haben wir die Zahlen gefunden, durch die wir kürzen können.
- ---
- gekürzt durch 2 ist gleich
- gekürzt durch 4 ist gleich
- gekürzt durch 7 ist gleich
- gekürzt durch 14 ist gleich
- gekürzt durch 28 ist gleich
- ---
- Unter allen gemeinsamen Teilern von 56 und 84 ist die Zahl 28 der größte gemeinsame Teiler.
BM1086
- größter gemeinsamer Teiler (g.g.T.)
- ---
- Der größte gemeinsame Teiler (g.g.T.) gegebener natürlicher Zahlen ist die größte Zahl, die alle gegebenen Zahlen teilt.
- ---
- Wenn wir einen Bruch so weit wie möglich kürzen wollen, um im Zähler und Nenner möglichst kleine Zahlen zu erhalten, müssen wir den gegebenen Bruch durch den g.g.T. von Zähler und Nenner kürzen. Im gekürzten Bruch sind dann Zähler und Nenner zueindander teilerfremd.
- Zum Ermitteln des g.g.T. gegebenener Zahlen brauchen wir nicht alle gemeinsamen Teiler dieser Zahlen aufsuchen. Ähnlich wie bei der Berechnung des k.g.V. können wir nämlich auch den g.g.T. mit Hilfe der Primfaktorzerlegung finden.
BM1087
- Ermittle durch Zerlegen in Primfaktoren den g.g.T. der folgenden Zahlen!
- ---
- a) 100, 125, 180
- b) 700, 550, 875
- c) 5083, 11339, 1955
- ---
- d) 225, 250, 324
- e) 350, 910, 875
- f) 4301, 13464, 4625
BM1088
- Kleinstes gemeinsames Vielfaches
- ---
- Das kleinste gemeinsame Vielfache (kgV) ist ein mathematischer Begriff. Sein Pendant ist der größte gemeinsame Teiler (ggT). Beide spielen in der Bruchrechnung.
- Das kleinste gemeinsame Vielfache zweier ganzer Zahlen und ist die kleinste positive natürliche Zahl, die sowohl Vielfaches von als auch Vielfaches von ist. Zusätzlich wird für den Fall oder das kgV definiert als .
- Die englische Bezeichnung lcm (least common multiple) für das kgV ist in mathematischen Texten ebenfalls verbreitet.
- ---
- Beispiel zur kgV-Berechnung
- Die Vielfachen von 12 sind: 12, 24, 36, 48, 60, 72, 84, 96, 108, …
- Die Vielfachen von 18 sind: 18, 36, 54, 72, 90, 108, …
- Die gemeinsamen Vielfachen von 12 und 18 sind also 36, 72, 108, …
- und das kleinste von diesen ist 36; in Zeichen:
- ---
- Berechnung über die Primfaktorzerlegung
- ggT und kgV kann man über die Primfaktorzerlegung der beiden gegebenen Zahlen bestimmen.
- Beispiel:
- Für das kgV nimmt man die Primfaktoren, die in mindestens einer der beiden Zerlegungen vorkommen, und als zugehörigen Exponenten den jeweils größeren der Ausgangsexponenten:
- ---
- Das kgV von mehreren Zahlen
- Man verwendet alle Primfaktoren, die in mindestens einer der Zahlen vorkommen, mit der jeweils höchsten vorkommenden Potenz, zum Beispiel:
- also:
- Man könnte auch zunächst berechnen und danach denn als eine zweistellige Verknüpfung auf den ganzen Zahlen ist das kgV assoziativ:
- Dies rechtfertigt die Schreibweise
BM1089
- Anwendungen des k.g.V. bei der Bruchrechnung
- ---
- Angenommen, man möchte die Brüche und addieren. Dazu müssen diese durch Erweitern auf einen gemeinsamen Nenner gebracht werden. Man könnte natürlich einfach mit multiplizieren, was ergibt. Der kleinstmögliche gemeinsame Nenner (der sog. Hauptnenner) ist aber . Die beiden Brüche werden auf diesen Nenner erweitert und dann addiert:
BM1090
- Größter gemeinsamer Teiler
- ---
- Definition:
- Eine ganze Zahl heißt ein größter gemeinsamer Teiler zweier ganzer Zahlen und , wenn gilt:
- Wenn ein (weiterer) Teiler von und von ist, so gilt .
- Man schreibt dann .
- ---
- Ist der größte gemeinsame Teiler zweier Zahlen und gleich , so sagt man, und sind teilerfremd.
- Bei der Definition des größten gemeinsamen Teilers fällt auf. dass nicht, wie der Name suggeriert, verlangt wird, dass der größte gemeinsame Teiler größer als alle anderen gemeinsamen Teiler ist.
- Stattdessen soll er ein Vielfaches aller gemeinsamen Teiler sein.
BM1091 - BM1100
[editar]BM1091
- Größter gemeinsamer Teiler
- ---
- Der größte gemeinsame Teiler (ggT) ist ein mathematischer Begriff. Sein Pendant ist das kleinste gemeinsame Vielfache (kgV). Beide spielen unter anderem in der Bruchrechnung eine Rolle.
- Er ist die größte natürliche Zahl, durch die sich zwei ganze Zahlen ohne Rest teilen lassen.
- Der ggT zweier ganzer Zahlen a und b ist eine ganze Zahl m mit der Eigenschaft, dass sie Teiler sowohl von a als auch von b ist und dass jede ganze Zahl, die ebenfalls die Zahlen a und b teilt, ihrerseits Teiler von m ist.
- Der Begriff „groß“ in ggT korreliert hochgradig mit der üblichen Ordnungsrelation > der ganzen Zahlen. Es gibt allerdings eine wichtige Ausnahme: Da die 0 Vielfaches einer jeden ganzen Zahl m ist, ist 0 in Teilbarkeitsfragen an „Größe“ nicht zu überbieten.
- Die englische Bezeichnung gcd (greatest common divisor) für ggT ist in mathematischen Texten ebenfalls verbreitet.
- Oft wird auch ( a , b ) als Kurzschreibweise für ggT ( a , b ) verwendet.
- ---
- Beispiel
- 12 ist durch die folgenden Zahlen ohne Rest teilbar: 1, 2, 3, 4, 6, 12.
- 18 hat diese Teiler: 1, 2, 3, 6, 9, 18.
- Die gemeinsamen Teiler von 12 und 18 sind also 1, 2, 3, 6 und der größte von diesen ist 6; in Zeichen:
- ---
- Berechnung über die Primfaktorzerlegung
- GgT und kgV kann man über die Primfaktorzerlegung der beiden gegebenen Zahlen bestimmen.
- Beispiel:
- Für den ggT nimmt man die Primfaktoren, die in beiden Zerlegungen vorkommen, und als zugehörigen Exponenten den jeweils kleineren der Ausgangsexponenten:
BM1092
- Der ggT von mehreren Zahlen
- ---
- Man verwendet alle Primfaktoren, die in jeder der Zahlen vorkommen, mit der jeweils kleinsten vorkommenden Potenz, zum Beispiel:
- also:
- Man könnte auch zunächst berechnen und danach denn als eine zweistellige Verknüpfung auf den natürlichen Zahlen ist der ggT assoziativ:
- Dies rechtfertigt die Schreibweise .
- ---
- Seien , und ganze Zahlen. Dann gilt:
- ---
- Anwendung bei der Bruchrechnung
- Beim Kürzen wird ein gemeinsamer Faktor von Zähler und Nenner eines Bruches entfernt, wobei sich der Wert des Bruches nicht ändert, z. B. . Kürzt man mit dem größten gemeinsamen Teiler von Zähler und Nenner, entsteht ein Bruch, der nicht weiter kürzbar ist. Zum Beispiel ist , also
BM1093
- Hauptnenner
- ---
- Beim Rechnen mit Brüchen in der Arithmetik, einem Teilgebiet der Mathematik, versteht man unter dem Hauptnenner oder Generalnenner mehrerer Brüche das kleinste gemeinsame Vielfache (kgV) der Nenner dieser Brüche.
- Sollen Brüche miteinander verglichen oder addiert werden, so werden sie dazu zunächst durch Erweitern auf einen gemeinsamen Nenner gebracht. Als gemeinsamen Nenner kann man immer den Hauptnenner verwenden, dies erlaubt in vielen praktischen Fällen auch die einfachste Rechnung.
- ---
- Beispiele:
- 1.) Vergleich
- Eine Möglichkeit zwei Brüche zu vergleichen, die weder Zähler noch Nenner gemeinsam haben, besteht darin, sie so zu erweitern, dass sie in Zähler oder Nenner übereinstimmen. Meistens bringt man sie dabei auf den gleichen Nenner, praktischerweise den Hauptnenner.
- Um beispielsweise festzustellen, ob größer oder kleiner als ist, kann man beide Brüche auf den Hauptnenner bringen und sieht dann:
- ---
- 2.) Addition und Subtraktion
- Um Brüche mit unterschiedlichen Nennern addieren oder subtrahieren zu können, muss man zuerst alle Brüche auf einen gemeinsamen Nenner erweitern. Dabei wird in der Regel der Hauptnenner bevorzugt, z.B.
- ist das kleinste gemeinsame Vielfache von , und und somit der Hauptnenner der drei zu addierenden Brüche.
BM1094
- Gemeinsamer Nenner im übertragenen Sinn
- (außerhalb der Mathematik)
- ---
- Gemeinsamer Nenner ist in der deutschen Sprache eine Metapher für Gemeinsamkeiten, beispielsweise gleiche Interessen in einer Gruppe von sonst sehr unterschiedlichen Menschen.
- ---
- Kleinster gemeinsamer Nenner
- Die Redewendung kleinster gemeinsamer Nenner bezeichnet einen Kompromiss oder Konsens auf niedrigstem Niveau. Im Zuge von Verhandlungen kann ein kleinster gemeinsamer Nenner mehrere Bedeutungen haben: z. B. fauler Kompromiss, außer Streit gestellte Punkte, mageres Ergebnis etc.
- In der Mathematik würde der Begriff kleinster gemeinsamer Nenner dem Begriff des kleinsten gemeinsamen Vielfachen (der Nenner von Brüchen, die man addieren möchte) entsprechen. Da aber z. B. in journalistischer Sprache der Begriff des kleinsten gemeinsamen Nenners [3] vorkommt (der mathematisch gesehen eindeutig unsinnig ist), scheint es zwecklos, solche sprachlichen Konstrukte mit mathematischer Begrifflichkeit zu unterlegen.
- ---
- Größter gemeinsamer Nenner
- Die Redewendung größter gemeinsamer Nenner bezeichnet einen Kompromiss oder Konsens auf höchstem, größtmöglichen Niveau.
- In Fällen in denen eine sehr geringe Gemeinsamkeit z.B. in Verhandlungen erzielt wird (in denen der größte gemeinsame Nenner klein ist) wird journalistisch vereinfachend der Begriff "Kleinster gemeinsamer Nenner" gebraucht.
BM1095
- Untersuche mit Hilfe der Teilbarkeitsregeln, ob die folgenden Zahlen durch 2, 3, 4, 5, 8, 9 oder 10 teilbar sind!
- ---
- a) 7.690
- b) 33.872
- c) 7.683.500
- d) 7.653.300
- ---
- e) 977.648
- f) 54.897.225
- g) 6.970
- h) 15.694
- ---
- i) 3.856.700
- j) 7.835.500
- k) 779.648
- m) 45.789.135
BM1096
- Ermittle das k.g.V. von folgenden Zahlen!
- ---
- a) 5 und 8
- b) 24, 36, 48
- c) 40, 24, 15
- d) 27, 36, 54
- ---
- e) 3 und 8
- f) 8, 24, 30
- g) 63, 18, 14
- h) 21, 56, 35
BM1097
- Kürze die folgenden Brüche, bis Zähler und Nenner jeweils teilerfremd sind!
- ---
- a)
- b)
- c)
- d)
- ---
- e)
- f)
- g)
- h)
- ---
- i)
- j)
- k)
- m)
- ---
- n)
- o)
- p)
- q)
BM1098
- Bruchrechnung
- ---
- Addition Subtraktion:
- ---
- Drei und Zwei
- Addiere
- Welche Zahl kommt im Zähler heraus, welche im Nenner?
- ---
- Äpfel und Birnen
- Addiere
- Gib ZÄHLER und NENNER des Ergebnisses an!
- ---
- Birnen, Bananen und Erdbeeren
- Berechne
- Gib Zähler und Nenner des Ergebnisses an!
- ---
- Nach dem Komma
- Ordne die Zahlen der Größe nach an!
- Welche ist die drittgrößte Zahl? Welche die größte? Rechne dazu die Zahlen in Dezimaldarstellung um und runde zur Überprüfung auf zwei Stellen nach dem Komma!
- ---
- Komma nach links
- Ordne die Zahlen der Größe nach an!
- Welche ist die drittgrößte Zahl? Rechne dazu die Zahlen in Deziamldarstellung um!
- ---
- Äpfel, Schwarzbeeren und Grafensteiner
- Berechne
- Welchen Wert hat Zähler und Nenner nach dem Kürzen?
- ---
- Kürzen
- Kürze die Brüche!
- .
- Gib die Lösung in der Form an!
BM1099
- Rationale Zahlen
- ---
- Die Menge aller rationalen Zahlen wird mit dem Formelzeichen (von „Quotient“ bezeichnet.
- Sie umfasst alle Zahlen, die sich als Bruch darstellen lassen, der sowohl im Zähler als auch im Nenner ganze Zahlen enthält.
- Die rationalen Zahlen werden – insbesondere in der Schulmathematik – auch als Bruchzahlen bezeichnet, während der Ausdruck Bruch (Dezimalbruch, Binärbruch, gewöhnlicher Bruch, gemischter Bruch ...) für bestimmte Schreibweisen einer rationalen Zahl verwendet wird.
- ---
- Definition der rationalen Zahlen
- Die Menge der rationalen Zahlen besteht aus der Menge der negativen rationalen Zahlen, der Zahl Null und der Menge der positiven rationalen Zahlen. Die Definition der rationalen Zahlen basiert auf der Darstellung rationaler Zahlen durch Brüche, also Paare ganzer Zahlen. Sie ist so aufgebaut, dass das Rechnen mit rationalen Zahlen wie gewohnt mit Hilfe ihrer Bruchdarstellungen durchgeführt werden kann, abstrahiert aber zugleich die rationale Zahl von ihren Bruchdarstellungen. Die rationalen Zahlen werden dabei nicht als vollkommen neue Dinge postuliert, sondern auf die ganzen Zahlen zurückgeführt.
BM1100
- Bruchrechnung
- ---
- Im engeren Sinn bezeichnet Bruchrechnung das Rechnen mit gemeinen Brüchen (manchmal auch gewöhnlichen Brüchen) in der „Zähler-Bruchstrich-Nenner-Schreibweise“ (siehe unten). Bruchrechnung gehört damit zur Arithmetik, einem Teilgebiet der Mathematik.
- In einem weiteren Sinn wird das Wort auch für das Rechnen mit rationalen Zahlen gebraucht, gleichgültig, in welcher Schreibweise sie vorliegen.
- Eine wichtigere Erweiterung besteht in der Zulassung von Bruchtermen, das sind Ausdrücke, die formal wie gemeine Brüche gebildet werden, bei denen aber Zähler und Nenner Terme sein können, die Variablen enthalten. Für diese Bruchterme gelten die Bruchrechenregeln sinngemäß. Das Rechnen mit Bruchtermen gehört aber zur Algebra.
- ---
- Die Regeln der Bruchrechnung beziehen sich auf die Grundrechenarten, also auf Addition, Subtraktion, Multiplikation, Division, sowie auf die Kehrwertbildung. Insbesondere bei Bruchtermen kommen auch Regeln für Potenzen und Wurzeln hinzu.
- Außerdem gibt es eine Kürzungs- und Erweiterungsregel, die eine Besonderheit der Bruchrechnung ist. Sie beruht auf dem Unterschied zwischen Bruch und Bruchzahl, der im folgenden Abschnitt genauer dargestellt wird.
- ---
- Die Bruchschreibweise, also die Schreibweise mit Bruchstrich, wird ganz allgemein in verschiedenen Bereichen der Mathematik, besonders in der Algebra, immer dann verwendet, wenn in der untersuchten Struktur die elementaren Bruchrechenregeln, insbesondere die Kürzungs- und Erweiterungsregel, gelten. Auch hier spricht man immer dann von „Bruchrechnung“, wenn diese Regeln angewendet werden.
- ---

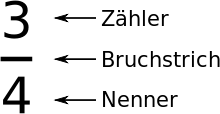
Das Ganze wird in vier gleiche Teile geteilt; drei davon sind hier gemeint. Oder: Drei Ganze werden gemeinsam in vier gleiche Teile geteilt; eines dieser gleichen Teile ist gemeint. - Bruch und Bruchzahl
- Die Bruchrechnung beruht darauf, dass sich das Ganze (die Eins aus dem Rechnen mit natürlichen Zahlen) noch unterteilen lässt. Einen Kuchen kann man zum Beispiel in vier Teile teilen. Wenn diese Teile gleich groß sind, so ist jedes Teil ein Viertel des Kuchens. Wenn, wie im Bild, eines der Viertel schon fehlt, so sind drei Viertel Kuchen dargestellt.
- ---
- Geschrieben wird dies gewöhnlich in der „Zähler-Bruchstrich-Nenner-Schreibweise“: Die Zahl unter dem Bruchstrich, der Nenner gibt an, in wie viele Teile das Ganze geteilt worden ist; die Zahl über dem Bruchstrich, der Zähler gibt an, wie viele Teile davon in diesem Falle gemeint sind. So erhält man einen Bruch. Man kann diesen auch so deuten: Der Zähler gibt an, wie viele Ganze gemeinsam in soviele gleich große Teile zu teilen sind, wie der Nenner angibt. (Man legt drei Kuchen übereinander und teilt den Stapel in vier gleiche Teilstapel.)
- Wird das Ganze (die Torte) stattdessen in acht Teile geteilt und werden davon sechs genommen, so ist das ein anderer Bruch: statt . Aber diese beiden Brüche stehen offenbar für die gleiche Menge Kuchen: Sie stehen für dieselbe Bruchzahl.
- ---
- Für jede Bruchzahl gibt es viele (unendlich viele) verschiedene Darstellungen, verschiedene Brüche, die alle denselben Wert (dieselbe Größe) verkörpern, aber auf unterschiedliche Weise. Von einem Bruch zum anderen gelangt man durch Erweitern und Kürzen. Dadurch ändert sich der Wert einer Bruchzahl nicht, man erhält aber für diese Zahl verschiedene Darstellungsweisen: verschiedene Brüche.
- ---
- Brüche lassen sich zunächst in gemeine Brüche (auch gewöhnliche Brüche genannt) und Dezimalbrüche (= Dezimalzahl, umgangssprachlich: „Kommazahl“) einteilen, daneben gibt es noch die Darstellung als gemischter Bruch. Wenn man von einem Bruch spricht, meint man in der Regel einen gemeinen Bruch, das Rechnen mit Dezimalbrüchen wird meistens nicht als Bruchrechnung bezeichnet.
- ---

Beschreibung eines gemeinen Bruches - Gemeine Brüche
- Gemeine Brüche werden im Allgemeinen durch eine Übereinanderstellung von Zähler und Nenner, getrennt durch einen waagerechten Strich, dargestellt:
- Zähler und Nenner eines Bruches sind ganze Zahlen. Dabei darf der Nenner nicht null sein, da eine Division durch Null nicht definiert ist.
- ---
- Jeder Bruch kann nämlich auch als Divisionsaufgabe verstanden werden. Dabei ist der Zähler der Dividend, der Nenner der Divisor:
- Das Entscheidende bei der Bruchrechnung ist, dass hier jede Division (außer durch null) möglich ist und ein einfach darstellbares Ergebnis hat, während ja im Bereich der ganzen Zahlen die Teilbarkeitsregeln gelten.
- ---
- Üblicherweise werden für Zähler und Nenner natürliche Zahlen verwendet und ein eventuell vorhandenes negatives Vorzeichen wird vor den Bruch gesetzt, also beispielsweise statt oder . Sind Zähler und Nenner negativ, so bezeichnet das nach den Regeln der Division von ganzen Zahlen den positiven Bruch:
- ---
- Bei einer Variante dieser Schreibweise, die oft verwendet wird, wenn gemeine Brüche in Texten vorkommen, werden Zähler, Bruchstrich und Nenner hintereinandergeschrieben und als Bruchstrich ein Schrägstrich verwendet, zum Beispiel 1/2, 3/8. Bei der Schreibweise mit Schrägstrich an Stelle des waagrechten Bruchstrichs werden (vor allem) einstellige Zähler und Nenner manchmal verkleinert über bzw. unter den Schrägstrich geschrieben: 6/7. Zu diesem Zweck existieren in vielen Druckzeichensätzen Sonderzeichen, wie zum Beispiel ¾ oder ½.
- índice
- Lección 071b ← Lección 072b → Lección 073b
- Lección 072



























































































































