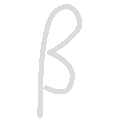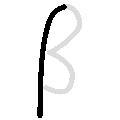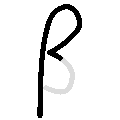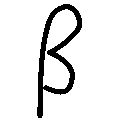Curso de alemán para principiantes con audio/Lección 066b
Apariencia
- índice
- Lección 065b ← Lección 066b → Lección 067b
- Lección 066
- Mathematik auf Deutsch - 16
BM751 - BM760
[editar]BM751
- Rauminhalt von Quadern
- ---
- Wie viele Ecken, Kanten und Flächen hat ein Quader?
- Was unterscheidet einen Quader von einem Würfel?
- Was haben ein Quader und ein Würfel gemeinsam?
Lösung BM751 - Ein Quader hat 8 Ecken, 12 Kanten und 6 Flächen.
- Bei einem Quader sind nur jeweils die beiden gegenüberliegenden Flächen gleich groß. Bei einem Würfel sind alle Flächen gleich groß.
- Beo Quadern und Würfeln sind alle Flächen rechtwinklig (Rechtecke oder Quadrate) und zwei gegenüberliegende Flächen sind jeweils parallel zueinander. (Anders als bei Pyramiden.)
FRAGE BM751a - Wie viel unterschiedlich große Flächen kann ein Quader haben und wie viel unterschiedliche Flächen kann ein Würfel haben?
- Kann ein Quader 4 unterschiedlich lange Kanten haben?
Lösung BM751a - Ein Quader kann 3 unterschiedlich große Flächen haben. Bei einem Würfel sind alle Flächen gleich groß.
- Ein Quader kann nicht 4 unterschiedlich lange Kanten haben, höchstens 3.
BM752

- Volumen
- ---
- Das Volumen (Pl. Volumen oder Volumina), auch: Raum- oder Kubikinhalt, ist der räumliche Inhalt eines geometrischen Körpers. Übliches Formelzeichen ist V.
- ---
- Wir ermitteln im Folgenden den Rauminhalt von Quadern, indem wir das Innere der Quader mit Einheitswürfeln ausfüllen.
- Wenn sich beim Messen der Kanten eines Quaders Längenangaben in vollen Zentimetern ergeben, so können wir das Innere des Quaders mit Einheitswürfeln von 1 cm Kantenlänge ausfüllen.
- Der Rauminhalt eins solchen Einheitswürfels beträgt dann 1 cm3.
- Wir zählen die Einheitswürfel und erhalten den Rauminhalt des Quaders.
- ---
- Wir können den Rauminhalt eines Quaders ermitteln, indem wir ihn schichtweise mit Einheitswürfeln ausfüllen. Es gibt dafür drei Möglichkeiten.
- verschiedene Schichten
- parallel zur Grundfläche
- parallel zur Vorderfläche
- parallel zur Seitenfläche
BM753

- 1. Möglichkeit:
- Wir füllen den Quader parallel zur Grundfläche schichtweise mit Einheitswürfeln aus (Bild 1).
- Es sind 3 Schichten mit je 5 * 2 Einheitswürfeln.
- 3 * (5 * 2) = 30
- c * (a * b)
- Rauminhalt: 30 Einheitswürfel
- ---

- 2. Möglichkeit:
- Wir füllen den Quader parallel zu eine Seitenfläche schichtweise mit Einheitswürfeln aus (Bild 2).
- Es sind 5 Schichten mit je 2 * 3 Einheitswürfeln.
- 5 * (2 * 3) = 30
- a * (b * c)
- Rauminhalt: 30 Einheitswürfel
- ---

- 3. Möglichkeit:
- Wir füllen den Quader parallel zur Vorderfläche schichtweise mit Einheitswürfeln aus (Bild 3).
- Es sind 2 Schichten mit je 5 * 3 Einheitswürfeln.
- 2 * (5 * 3) = 30
- b * (a * c)
- Rauminhalt: 30 Einheitswürfel
- ---
- Ergebnis:
- Wir ermitteln den Rauminhalt eines Quaders, indem wir ihn schichtweise mit Einheitswürfeln ausfüllen:
- Wir legen c Schichten mit je a * b Würfeln,
- oder wir legen a Schichten mit je b * c Würfeln,
- oder wir legen b Schichten mit je a * c Würfeln.
- ---
- Die Produkte sind gleich.
- Es gilt:
- c * (a * b) = a * (b * c) = b * (a * c) = a * b * c
BM754
- Durch den Vergleich des Rauminhalts eines gegebenen Quaders mit dem Rauminhalt eines Einheitswürfels können wir den Rauminhalt eines Quaders ermitteln.
- ---
- 1 m * 1 m * 1 m = 1 m * m * m = 1 m3
- ---
- Einheiten des Rauminhalts:
- Kubikmillimeter mm3
- Kubikzentimeter cm3
- Kubikmeter m3
- ---
- 1 cm3 = 1.000 mm3
- 1 cm3 = 1 cm * 1 cm * 1 cm
- 1 cm3 = 10 mm * 10 mm * 10 mm
- 1 cm3 = 1.000 mm * mm * mm
- 1 cm3 = 1.000 mm3
BM755

- Man kann den Rauminhalt eines Quaders ermitteln, ohne den Quader mit Einheitswürfeln auszufüllen.
- Der Quader in Bild 1 lässr sich zum Beispiel durch c Schichten mit b Stangen zu je a Einheitswürfeln ausfüllen.
- Der Rauminhalt beträgt a * b * c Einheitswürfel.
- ---
- Der Rauminhalt eines Quaders ist gleich dem Produkt aus der Länge a, der Breite b und der Höhe c.
- ---
- V = a * b * c
- ---
- Volumen = Länge * Breite * Höhe
- V = L * B * H
BM755
- Der Rauminhalt eines Quaders soll in Kubikzentimeter angegeben werden.
- Der Quader ist 30 cm lang, 9 cm breit und 1,45 m hoch.
Lösung BM755 - V = 30 * 9 * 145
- V = 39.150 cm3
BM756

- Oberflächen von Quadern
- ---
- Die Oberfläche eines Quaders wird von allen Begrenzungsflächen des Quaders gebildet. Der Inhalt der Oberfläche ist die Summe der Flächeninhalte aller Begrenzungsflächen.
- ---
- Wenn wir alle Begrenzungsflächen eines Quaders auf einem Zeichenblatt nachzeichnen, erhalten wir ein Netz dieses Quaders (Bild 1).
- Die Berechnung des Oberflächeninhalts eines Quaders mit der Länge a, der Breite b und der Höhe c addieren wir die Flächeninhalte seiner sechs Begrenzungsflächen.
- ---
- A = (a * b) + (b * c) + (a * b) + (b * c) + (a * c) + (a * c)
- A = [(a * b) + (b * c) + (a * c)] + [(a * b) + (b * c) + (a * c)]
- A = 2 * [(a * b) + (b * c) + (a * c)]
BM757

- Berechne den Rauminhalt und den Oberflächeninhalt eines Würfels von der Kantenlänge 5 cm!
- Vergleiche mit der Berechnung an Quadern.
Lösung BM757 - V = a3
- V = 53
- V = 1253 cm3
- ---
- A = 6 * a2
- A = 6 * 52
- A = 6 * 25
- A = 150 cm2
BM758


- Weitere Raummaße
- ---
- Der Rauminhlat kann auch mit Hilfe von Einheiten angegeben werden, die auf das Raummaß „1 Liter“ bezogen sind, zum Beispiel zwei Liter Milch (2 l Milch).
- Für die bessere Lesbarkeit wird hier in den Lektionen ein großes „L“ statt ein kleines „l“ verwendet, um den Buchstaben besser von der Ziffer „1“ unterscheiden zu können.
- 2 L Milch
- ---
- Es gilt: 1 L = 1 cm3 (Kubikdezimeter)
- 1 dm = 10 cm
- 1 cm3 = ein Würfel mit der Kantenlänge 10 cm * 10 cm * 10 cm
- 1 L = 10 cm * 10 cm * 10 cm = 1.000 cm3 = 1 dm3
- ---
- Länge 9,6 cm x Breite 6,3 cm x Höhe 20,1 cm
- V = 9,6 cm * 6,3 cm * 20,1 cm
- V = 1215,648 cm3
- V = 1,215 Liter //(Tetrapack: Der Behälter ist nicht randvoll.)
BM759
- Gib den Hubraum der Fahrzeuge jeweils in Liter an!
- ---
- Opel Corsa: 973 cm3
- Audi A6: 2.496 cm3
- BMW 730d: 2.993 cm3
- Ferrari 360: 3.586 cm3
- Mercedes-Benz S 500: 4.966 cm3
- Rolls-Royce Phantom: 6.749 cm3
- Reisebus Mercede Tourismo: 10.677 cm3
Lösung BM759 - Opel Corsa: 973 cm3 ≈ 1 L
- Audi A6: 2.496 cm3 ≈ 2,5 L
- BMW 730d: 2.993 cm3 ≈ 3 L
- Ferrari 360: 3.586 cm3 ≈ 3,5 L
- Mercedes-Benz S 500: 4.966 cm3 ≈ 5 L
- Rolls-Royce Phantom: 6.749 cm3 ≈ 7 L
- Reisebus Mercede Tourismo: 10.677 cm3 ≈ 10,5 L
BM760
- Strecken
- Die Länge wird gemessen in:
- mm, cm, m, km
- ---
- Flächen
- Der Flächeninhalt wird gemessen in:
- mm2, cm2, m2
- A = a * b
- ---
- Volumen
- Der Rauminhalt wird gemessen in:
- mm3, cm3, m3, Liter
- V = a * b * c
BM761 - BM770
[editar]BM761

- Grundriss eines Quaders
- ---
- Wenn wir eine quaderförmige Pappschachtel auf ein Zeichenblatt legen und sie von oben betrachten.
- Wir sehen fast keinen Körper mehr, sondern nur noch ein Rechteck.
- Wir zeichnen dieses Rechteck in natürlicher Größe auf das Zeichenblatt.
- Auf diese Weise erhalten wir den Grundriss des Quaders auf dem Zeichenblatt.
- ---
- Auf dem gezeichneten Grundriss können wir nur Länge und Breite des zugehörigen Quaders erkennen und messen.
- Die Höhe des Quaders können wir aus dem Grundriss nicht entnehmen.
- Die Kanten, die Deck- und Grundfläche verbinden, erscheinen in diesem Grundriss nur als Punkt.
BM762

- Es soll der Grundriss des Quaders in Bild 1 ermittelt werden.
- Eckpunkte der Grundfläche: A, B, C, D
- Eckpunkte der Deckfläche: E, F, G, H
- ---
- Die Kanten und (sowie und , und , und ) liegen senkrecht übereinander.
- Als Bild erscheint in der Grundrisstafel aber jeweils nur eine Strecke (Bildstrecke).
- Bildstrecke der Kanten und ist die Strecke mit den Endpunkten E', A' und F', B' usw.
- ---
- Die Kanten des Quaders, die parallel zur Zeichenebene verlaufen, erscheinen im Grundriss wieder als Strecken in wahrer Länge.
- Wenn eeine Seitenfläche des Quaders parallel zur Grundrisstafel leigt, dann ist eine STrecke im Grundriss gleichzeitig das Bild zweier Kanten des Quaders.
- Die Kanten, die senkrecht zur Zeichenebene verlaufen, erscheinen im Grundriss als Punkt.
BM763

- Anreißen, Reißbrett
- ---
- Als Anreißen wird das Anbringen von Maßlinien oder Bohrpunkten auf einer Werkstückoberfläche durch Einritzen oder Zeichnen genannt.
- Das Anreißen wird mit einem Stift, Kreide, einer Reißnadel oder einem Reißzirkel ausgeführt.
- Maße für Bohrungen, Schnitte und andere Bearbeitungen werden in Form von Gravuren oder gezeichneten Linien auf das Werkstück aus Holz, Metall oder Stein aufgebracht.
- Empfindliche Oberflächen oder solche, die keine Beschädigung erleiden sollen, können mit leicht lösbarem Papier beklebt werden, auf dem der Bleistiftriss erfolgt.
- Um den Riss auf metallischen Oberflächen besser sichtbar zu machen, werden spezielle dunkle, kupfersulfathaltige Lacke vor dem Anreißen auf das Werkstück aufgebracht und so die metallisch blanken Anrisse hervorgehoben. In der Praxis wird anstatt einer Anreißfarbe oft ein wasserfester Stift eingesetzt.
- ---
- Alle Anreißwerkzeuge sind Bestandteil der Metalltechnik. Sie finden sich vor allem in Werkstätten mit Kleinstserien- und Einzelfertigung, aber auch im Werkzeugbau von Großbetrieben.
- Um eine sinnvolle Haltbarkeit und eine erkennbare Ritzwirkung am Werkstück zu erreichen, sind diese Werkzeuge gehärtet oder tragen eine Spitze aus Hartmetall.
- Eine Reißnadel ist aus Stahl, Stahl mit Hartmetallspitze oder aus Messing. Typische Reißnadeln sind circa 20 bis 30 cm lang und haben einen Durchmesser von etwa 3 bis 4 mm. Meist sind sie beidseitig sehr lang angespitzt, wobei ein Ende nach circa 3 cm um 90 Grad abgewinkelt ist.
BM764

- Reißbrett
- Das Reißbrett (eigentlich Zeichenbrett genannt, gelegentlich auch Zeichenplatte oder Zeichenmaschine) dient technischen Zeichnern, Konstrukteuren und Architekten zum Erstellen technischer Zeichnungen und Bauzeichnungen, also zum Anfertigen von Grundrissen, Aufrissen, Schnitten und Perspektivdarstellungen. Der Name stammt noch aus der Zeit vor der Erfindung des Bleistiftes, als mit einem harten „Reißbley“ mehr geritzt als gezeichnet wurde. Ein Merkmal des Reißbrettes ist, dass die richtige Winkligkeit der Linien zueinander über eine Mechanik sichergestellt wird.
- ---
- Als Hilfsmittel zur Erstellung technischer Zeichnungen wurde das Reißbrett in den 1990er-Jahren durch den Einsatz von Computern mit entsprechender Software und häufig speziell angepassten Eingabegeräten Computer Aided Design (CAD) weitgehend verdrängt.
- ---
- Eine Reißschiene oder Zeichenschiene (auch T-Schiene - wegen der Ähnlichkeit mit dem Buchstaben „T“) ist ein Zeichengerät, das in Kombination mit Reißbrett und Reißzeug verwendet wird. Die Reißschiene unterstützt beim Zeichnen horizontaler und paralleler Linien. Sie dient als Basis für Zeichendreiecke und Schablonen, die an sie angelegt werden, um nichthorizontale Parallelen und Geraden zu zeichnen sowie Darstellungen mit Schablonen zu positionieren.
- ---

- Reißzwecke
- Eine Reißzwecke ist ein kurzer Nagel mit großem, gewölbtem Kopf aus Blech, der für den Aushang von Schriftstücken verwendet wird und leicht von Hand wieder entfernt werden kann.
- Die ursprüngliche Bestimmung der Reißzwecke war das Befestigen von Zeichnungen auf Reißbrettern. Diese Reißzwecken bestanden aus einer kurzen sehr spitzen Stahlnadel, die von einem flachen Kopf (über die Zeichenschienen und Schablonen gleiten können) aus Messing gehalten wurde. Moderne Reißzwecken haben in der Regel einen kleinen Plastiküberzug über dem Kopf, der die Verletzungsgefahr reduziert, wenn der Nagel sich vom Kopf löst und nach hinten durchrutscht.
- ---
- anreißen = einen skizzenhaften Entwurf zeichnen
- Beispiel: Als die Dimensionen besprochen waren begann er, das Bauteil am Reißbrett anzureißen.
- eine Skizze anreißen
BM765

- Grundriss
- ---
- Der Grundriss ist eine abstrahierte, zeichnerisch dargestellte, zweidimensionale Abbildung einer räumlichen Gegebenheit. Grundrissdarstellungen finden sich in technischen Zeichnungen, insbesondere jedoch in Bauzeichnungen.
- In der darstellenden Geometrie existieren neben Grundrissen zusätzlich Aufrisse, Ansichten und Schnitte.
- ---
- Die Bezeichnung Grundriss wird allerdings nicht nur für eine zeichnerische Darstellung, sondern auch für die räumlichen Verhältnisse als solche verwendet. So kann damit auch die Lage und Größe der Räume innerhalb eines Gebäudes angesprochen sein.
- ---
- Historisch lässt sich Grund-Riss mit „Boden-Zeichnung“ übersetzen. Die Grundrissdarstellung ist dementsprechend eine zeichnerische Abbildung der Bodenfläche. In der Architektur ist es allerdings üblich, den Grundriss als gedachten waagerechten Schnitt in zirka einem Meter Höhe anzulegen, beispielsweise um Fensteröffnungen darzustellen, die in der Regel nicht bis zum Boden reichen.
- ---
- Der Grundriss ist in der Mathematik die senkrechte Projektion eines Gegenstandes auf eine waagerechte Ebene.
- Mathematisch ist der Grundriss die senkrechte Projektion eines Gegenstandes auf eine waagerechte Ebene.
- ---
- Der Grundriss ist in der Architektur und im Bauwesen die maßstabsgetreue Darstellung eines waagerechten Schnittes eines Bauwerkes.
BM766
- Einheiten der Masse
- ---
- Milligramm; 1 mg
- Gramm; 1 g = 1.000 mg
- Kilogramm; 1 kg = 1.0000 g = 1 Mill. mg
- Tonne; 1 t = 1.000 kg
- 1 Zentner = 50 kg
- 1 Pfund = 500 g = ½ kg
BM767


- Waage
- wiegen
- ---
- Beim Wiegen vergleichen wir die die Masse eines Körpers mit der Masse eines Gewichtsstück (= Massestück).
- Zur Angabe der Masse eines Gegenstandes wählen wir nach Möglichkeit eine zweckmäßige Einheit.
- ---
- Masse
- Die Masse (auch Ruhemasse) ist eine Eigenschaft der Materie.
- Das Formelzeichen ist meist „m“.
- Die Masse wird außerhalb der Physik auch als Gewicht bezeichnet.
- Gewicht = Gewichtskraft: die Kraft auf einen Körper in einem Schwerefeld
- Das Gewicht ist die durch die Wirkung eines Schwerefeldes verursachte Kraft auf einen Körper.
- Die Gewichtskraft ist senkrecht nach unten gerichtet, was beinahe, aber nicht genau, der Richtung zum Erdmittelpunkt entspricht.
- ---
- In der Alltagssprache wird oft vom Gewicht eines Körpers gesprochen, ohne zu unterscheiden, ob damit seine Masse oder seine Gewichtskraft gemeint ist. Dennoch handelt es sich um sehr unterschiedliche physikalische Begriffe:
- die Masse ist ein Maß dafür, wie stark ein Körper ganz allgemein von Gravitationsfeldern beeinflusst wird und wie sehr er sich Beschleunigungen widersetzt (Trägheit).
- die Gewichtskraft hingegen gibt an, wie stark ein Körper konkret von der Erde oder dem Himmelskörper, auf dem er sich befindet, angezogen wird.
- Die Masse ist daher eine dem Körper innewohnende Eigenschaft, während die Gewichtskraft Resultat eines äußeren Einflusses auf den Körper ist.
- Demzufolge ist die Masse eines Körpers, unabhängig von dem Ort, an dem er sich befindet (Erde, Mond, Schwerelosigkeit, …), stets gleich, während die auf ihn wirkende Gewichtskraft von der Schwerebeschleunigung abhängt (auf dem Mond beträgt die Gewichtskraft nur ungefähr ein Sechstel von derjenigen auf der Erde, d. h. die Gewichtskraft eines Körpers der Masse 100 kg auf dem Mond entspricht ungefähr derjenigen, die auf der Erde auf einen Körper der Masse 16,5 kg wirkt; in der Schwerelosigkeit spürt man keine Gewichtskraft).
- ---
- Messgeräte zur direkten Feststellung einer Gewichtskraft sind Kraftmesser, beispielsweise Federwaagen. Allerdings verfälscht der statische Auftrieb das Ergebnis, was sich insbesondere bei Körpern geringer Dichte bemerkbar macht.
- ---
BM768
- 6 t = 6.000 kg
- 2,840 kg = 2 kg 840 g = 2840 g
- 3,035 kg = 3 kg 35 g = 3.035 g
- 5 Zentner = 250 kg
BM769

- Geldmaße
- 1 Euro = 100 Cent
- Wir unterscheiden Münzen und Banknoten.
- ---
- Die Euromünzen sind die in derzeit 19 Ländern der Europäischen Union sowie den Nicht-EU-Staaten Andorra, Monaco, San Marino und Vatikanstadt in Umlauf gebrachten Münzen der gemeinsamen europäischen Währung Euro. Ein Euro wird unterteilt in 100 Cent; es gibt acht Nennwerte für Münzen.
- ---
- Die Euromünzen wurden zusammen mit den Eurobanknoten ab dem 1. Januar 2002 eingeführt. Das Prägejahr der Münzen kann aber bis 1999 zurückgehen, also bis zu dem Jahr, in dem die Währung offiziell als Buchgeld eingeführt wurde.
- Im September 2014 waren rund 110 Mrd. Euromünzen mit einem Gesamtwert von fast 25 Mrd. Euro im Umlauf.
- In einigen Euroländern wurde die Ausgabe der 1- und 2- Cent-Münzen ganz eingestellt: Finnland, Niederlande und Irland.
- Während die ausgezeichneten Preise weiterhin auf 1 Cent genau sein können, werden die dann an der Kasse in bar zu zahlenden Gesamtbeträge auf den nächsten durch 5 Cent teilbaren Betrag gerundet, d. h. Beträge, die auf 1, 2, 6 oder 7 Cent enden, werden nach unten, Beträge, die auf 3, 4, 8 oder 9 Cent enden, nach oben gerundet.
- Da die 1- und 2-Cent-Münzen in der gesamten europäischen Währungsunion gesetzliches Zahlungsmittel sind, müssen sie aber von den Händlern angenommen werden.
- ---
- Es gibt Eurobanknoten mit sieben Nennwerten:
- 5-Euro-Banknoten
- 10-Euro-Banknoten
- 20-Euro-Banknoten
- 50-Euro-Banknoten
- 100-Euro-Banknoten
- 200-Euro-Banknoten
- 500-Euro-Banknoten
- ---
- Es werden zwar seit 2014 keine 500-Euro-Noten mehr gedruckt, der Schein wurde aber noch bis Anfang 2019, bis die Einführung der zweiten Serie abgeschlossen wurde, von den Notenbanken ausgegeben. Seine Gültigkeit im Zahlungsverkehr soll der Schein erst Jahre später – zusammen mit den anderen Banknoten der ersten Serie – verlieren. Bei den Notenbanken kann er zeitlich unbegrenzt eingetauscht werden.
BM770
- Zeitmaße
- ---
- Wir messen die Zeit eines Vorgangs (seine Dauer), indem wir sie mit einer festgelegten Einheit vergleichen.
- Es gibt die Sekunde (s), die Minute (1 min = 60 s), die Stunde (1 h = 60 min), den Tag (1 d = 24 h), die Woche (7 d), der Monat (4 Wochen + 0–3 d oder 28–31 d), das Jahr (1 a = 12 Monate oder 52 Wochen + 1–2 d oder 365–366 d), das Jahrzehnt (10 Jahre), das Jahrhundert (10 Jahrzehnte), das Jahrtausend (10 Jahrhunderte).
- ---
- Für Berechnungen setzen wir fest:
- 1 Woche = 7 Tage
- 1 Monat = 30 Tage
- 1 Jahr = 12 Monate = 360 Tage
- Wir berücksichtigen dabei nicht, dass der Februrar 28 oder 29 Tage hat.
- ---
- Sekunde s
- Minute min
- Stunde h (lat.: hora)
- Tag d (lat.: dies)
- ---
- 1 s
- 1 min = 60 s
- 1 h = 60 min = 60 * 60 min = 3.600 s
- 1 d = 24 h = 24 * 60 min = 1.440 min = 24 * 60 * 60 s = 86.400 s
BM771 - BM780
[editar]BM771
- 24 Stunden eines Tages
- ---
- Die Einteilung des Tages in zwölf Teile kommt vermutlich von einer Version der Sonnenuhr der alten Ägypter. Da die Zeiteinteilung lange mit Hilfe des Sonnenlichts geschah, konnte die Nacht nicht so einfach aufgeteilt werden. Später entdeckten ägyptische Astronomen 36 Sterne, die den Himmel in gleiche Teile aufteilten. Die Nacht konnte mit 18 dieser Sterne aufgeteilt werden. Jeweils drei Sterne wurden für die Morgen- und Abenddämmerung verwendet, da es zu dieser Zeit schwer war die Sterne zu erkennen. Die Zeit der totalen Finsternis wurde von den übrigen zwölf Sternen festgelegt. Zwischen 1550 und 1070 v. Chr. wurde dieses System vereinfacht, indem 24 Sterne genutzt wurden, wobei zwölf für die Nacht waren.
BM772
- 60 Minuten und 60 Sekunden
- ---
- Die Babylonier machten astronomische Berechnungen im 60er-System.
- Eratosthenes hat das 60er System genutzt, um einen Kreis in 60 Teile zu teilen. Damit hat er ein frühes System für Breitengrade aufgebaut.
- Ptolemäus hat die 360 Grad in zwei Stufen in jeweils wieder 60 Einheiten unterteilt. Die erste Einheit nannte er partes minutae prima - die Minuten -, die zweite partes minutae secundae - unsere Sekunden.
- ---
- Die Einheiten der Zeit sind nicht nach dem dekadischen Positionssystem erfolgt.
BM773
- Schaltjahr
- ---
- Als Schaltjahr wird ein Jahr im Kalender bezeichnet, das im Unterschied zum „normalen Jahr“ einen zusätzlichen Schalttag (den 29. Februar) enthält.
- Im gregorianischen Kalender – einem Sonnenkalender – findet in der Regel alle vier Jahre ein Schaltjahr mit einem Schalttag statt – der Februar hat dann 29 anstatt 28 Tage.
- Damit wird das Kalenderjahr dem die Jahreszeiten bestimmenden Sonnenjahr (Tropisches Jahr) angeglichen, das fast ¼ Tag länger ist als das 365 Tage lange „normale Jahr“.
- Das Tropische Jahr hat eine Länge von 365,24219 Tagen (ca. 365 Tage, 5 Stunden, 48 Minuten und 45 Sekunden).
- ---
- Der julianische Kalender wurde von Julius Caesar eingeführt.
- Er wurde 1582 durch den Gregorianischen Kalender abgelöst.
- Der Gregorianische Kalender ist nach Papst Gregor XIII. benannt.
- 1582 fand die Frühlingstagundnachtgleiche nach dem julianischen Kalender schon am 11. März statt. Für den Tag des Frühlingsanfangs war aber der 21. März festgelegt (erste Konzil von Nicäa im Jahr 325). Die aufgelaufene Differenz betrug somit 10 Tage. Auf Anordnung von Papst Gregor XIII. wurden 1582 zehn Kalendertage ausgelassen (auf den 4. Oktober folgte der 15. Oktober, wobei die Abfolge der Wochentage nicht verändert wurde: auf einen Donnerstag folgte ein Freitag). Damit künftig kein (oder kein wesentliches) Auseinanderlaufen zwischen Sonnen- und Kalenderjahr stattfindet, wurde die julianische vierjährige Schalttagsregelung ergänzt.
- ---
- Die gregorianische Schalttagsregelung besteht aus folgenden drei einzelnen Regeln:
- 1.) Die durch 4 ganzzahlig teilbaren Jahre sind Schaltjahre. Die mittlere Länge eines gregorianischen Kalenderjahres erhöht sich dadurch um einen viertel Tag von 365 Tagen auf 365,25 Tage.
- 2.) Säkularjahre, also die Jahre, die ein Jahrhundert abschließen (z.B. 1800, 1900, 2100 und 2200) sind keine Schaltjahre. Im Durchschnitt verringert sich dadurch die Länge des Kalenderjahres um 0,01 Tage von 365,25 Tage auf 365,24 Tage.
- 3.) Schließlich sind die durch 400 ganzzahlig teilbaren Säkularjahre doch Schaltjahre. Damit sind z.B. 1600, 2000 und 2400 jeweils wieder Schaltjahre. Die mittlere Länge des Kalenderjahres erhöht sich um 0,0025 Tage von 365,2400 Tage auf 365,2425 Tage (das sind 365 97⁄400 Tage).
- ---
- Seit dieser Regelung beträgt der Fehler bei der Länge des durchschnittlichen Kalenderjahres einen Tag pro ungefähr 3231 Jahren.
- Da in Wirklichkeit das tropische Jahr keine exakt konstante Länge hat, ist auch diese Differenz zwischen tropischem und gregorianischem Jahr nicht konstant. Rechnet man die derzeitige Verkürzung des tropischen Jahres um 0,5 s pro Jahrhundert ein, ergibt sich eine mit gleicher Rate größer werdende Differenz und daraus ein deutlich früherer bester Zeitpunkt zum Einfügen eines zusätzlichen Schalttages.
BM774

- Schaltsekunde
- ---
- Die Erde dreht sich minimal langsamer um sich selbst, als bei der Definition der Sekunde zugrunde gelegt wurde; ein tatsächlicher mittlerer Sonnentag dauert daher um Sekundenbruchteile länger als 86400 Sekunden. Dieser Effekt summiert sich. Von Zeit zu Zeit wird deshalb eine Schaltsekunde in die koordinierte Weltzeit (UTC) eingefügt, um sie mit der mittleren Sonnenzeit (UT1) möglichst synchron zu halten (es soll DUT1 < 0,9 s sein).
- ---
- In gewisser Weise sind Schaltsekunden mit Schalttagen vergleichbar: Da die Erde für die Umrundung der Sonne etwas länger als genau 365 Tage braucht, wird ein Schalttag eingefügt, bevor die Abweichung des Kalenders von der tatsächlichen astronomischen Situation einen ganzen Tag überschreitet. Und da ein mittlerer Sonnentag etwas länger als genau 86400 Sekunden dauert, wird eine Schaltsekunde eingefügt, bevor die Abweichung der Uhrzeit von der mittleren Sonnenzeit eine ganze Sekunde überschreitet.
- ---
- Da die Eigenrotation der Erde nicht perfekt konstant ist, erfolgt die Einfügung von Schaltsekunden bei Bedarf und nicht nach einem festen Muster.
- ---
- Schaltsekunden werden vom Internationalen Dienst für Erdrotation und Referenzsysteme festgelegt. Zuständig für die amtliche Zeit eines jeweiligen Landes ist jedoch meist eine jeweilige staatliche Einrichtung.
BM775
- Rechne um!
- ---
- 3 Monate in Tage
- 4 h in Minuten
- 2 h 45 min in Minuten
- 10 min 8 s in Sekunden
- 540 s in Minuten
- 168 h in Wochen
Lösung BM775 - 3 Monate = 90 d
- 4 h = 240 min
- 2 h 45 min = 120 min + 45 min = 165 min
- 10 min 8 s = 600 s + 8 s = 608 s
- 540 s = 9 min
- 168 h = 7 d = 1 Woche
BM776
- Bei der Darstellung von Zeitangaben gibt es mehrere Möglichkeiten:
- ---
- Angabe der Urhzeit: 7 Uhr 15 oder 7.15 Uhr oder 7:15
- Angabe des Datums: 7. März 1914 oder 7.3.1914 oder 1914-03-07
- Angabe einer Zeitdauer im Sport: Der offizielle Weltrekord beim Maratholauf (42,195 Kilometer) liegt bei 2:02:57. Er wurde am 28.09.2014 beim Berlin-Marathon vom Kenianer Dennis Kipruto Kimetto aufgestellt (erzielt; erreicht). Der offizielle Weltrekord beim Maratholauf liegt bei 2 Stunden 2 Minuten und 57 Sekunden.
BM777
- Lies folgende Angaben mit Monatsnamen!
- ---
- 12.5.1927
- 22.11.1849
- 2.1.2007
- 15.7.2013
- 9.9.1999
- ---
- Lies ausführlich folgende Zeitangaben!
- ---
- 11:41 min
- 3:36 min
- 4:12:09 h
- 1:07:26 h
BM778
- Es soll die Zeitdifferenz zwischen dem 3.2. und dem 15.7 eines Jahres berechnet weden.
- 1.) Wir ergänzen zum Monatsende (3.2. bis 28.2.) 25 Tage
- 2.) Wir zäheln die vollen Monate (4) 122 Tage
- 3.) Wir zählen die restlichen Tage (bis zum 14.7) 14 Tage
- 4.) Wir addieren (25 + 122 + 14 =) 161 Tage
BM779
- Wie viel Tage sind es vom 9.3. bis zum 21.10 eines Jahres?
Lösung BM779 - 1.) Wir ergänzen zum Monatsende (9.3. bis 31.3.) 23 Tage
- 2.) Wir zäheln die vollen Monate (6) 183 Tage
- 3.) Wir zählen die restlichen Tage (bis zum 21.10.) 21 Tage
- 4.) Wir addieren (23 + 183 + 21 =) 227 Tage
BM780
- Berechne den Zeitabstand von 8.47 Uhr bis 14.22 Uhr!
Lösung BM780 - 1.) Wir ergänzen zur vollen Stunde. 13 min
- 2.) Wir zählen die vollen Stunden. 5 h
- 3.) Wir zählen die restlichen Mnuten 22 min
- 4.) Wir addieren (13 min + 5 h + 22 min) 5 h 35 min
BM781 - BM790
[editar]BM781




- Zugfahrpläne lesen
- ---
- Mit Abfahrtszeit ist der Zeitpunkt bzw. die genau bestimmbare Uhrzeit gemeint, zu der ein Verkehrsmittel eine Haltestelle oder einen vergleichbaren Abfahrtsort verlässt.
- ---
- An Bahnhöfen gibt es zur Fahrgastinformation Aushangfahrpläne (auch als Fahrplanaushang bezeichnet) in sehr unterschiedlicher Form. Sie sind Ausschnitte aus dem Fahrplan, in dem alle Züge und deren Abfahrts- bzw. Ankunftsbahnsteige verzeichnet sind.
- Angegeben ist chronologisch geordnet allgemein das Endziel und die Abfahrtszeit eines Verkehrsangebots, meistens zusätzlich auch der Streckenverlauf.
- ---
- Wenn die Ankunftszeit wegen geringer Haltedauer annähernd gleich der Abfahrtszeit ist, genügt ein als „Fahrplan“ gekennzeichneter Aushang.
- Andernfalls werden getrennte Aushänge für ankommende („Ankunft“, weiß) und abfahrende („Abfahrt“, oft auf gelbem Papier) Verkehrsmittel angeboten. Der Ankunftsplan enthält alle am Bahnhof ankommenden Züge und eine Auswahl der Bahnhöfe, an denen der Zug hält (meist mit dortiger Abfahrtzeit).
- Angegeben wird auch der Ankunftsbahnsteig.
- ---
- Zugnummer
- Verkehrstag (verkehren = fahren)
- Verkehr
- Ankunftszeit
- Abfahrtszeit
- Kursbuch
- Sommerfahrplan
- Winterfahrplan
- Umsteigezeit
- Abfahrtstafel
- Zugzielanzeiger; Anzeigetafel; Zuginformation
- Elektronische Fahrplanauskunft
- ---
- Ein Kursbuch ist ein Verzeichnis von Fahrplänen für ein bestimmtes Gebiet – meist ein Land – und einen bestimmten Zeitraum. Die Fahrpläne der im Kursbuch enthaltenen Bahnstrecken (und Buslinien) sind jeweils einzeln in tabellarischer Form dargestellt.
- ---

- Zuggattungen:
- ICE - Intercity-Express (die schnellste Zuggattung der Deutschen Bahn AG) (mit Hochgeschwindigkeits-Triebzügen)
- IC - Intercity (Er verkehrt fast ausschließlich auf innerdeutschen Routen. Sein Pendant für den grenzüberschreitenden Verkehr ist der EuroCity.)
- RE - Regional-Express (Regional-Express steht für einen schnellen Zug, der Regionen an das Fernverkehrsnetz anbindet.)
- RB - Regionalbahn (Die Regionalbahn hat den klassischen Personenzug [P] und zuletzt den Nahverkehrszug [N] abgelöst. Vom Regional-Express unterscheidet sich die Regionalbahn durch kürzere Haltestellen-Abstände und -Laufwege, sowie niedrigere Reisegeschwindigkeit.)
- ---
- Werktag
- Bei Fahrplänen wird oft mittels ⚒ (Schlägel und Eisen) symbolisiert, dass ein Verkehrsmittel nur an Werktagen fährt. Dies schließt per Definition den Samstag ein. Die meisten Verkehrsmittel, bei denen das Symbol verwendet wird, fahren allerdings nicht an Samstagen, was dann zusätzlich angegeben wird („⚒ außer Sa“).
- Wochentage
- Mo
- Di
- Mi
- Do
- Fr
- Sa
- So
BM782

- Winkel und Winkelmessung
- ---
- Winkel:
- Scheitel
- Schenkel
- ---
- Ein Winkel ist in der Geometrie ein Teil der Ebene, der von zwei in der Ebene liegenden Strahlen (Halbgeraden) mit gemeinsamem Anfangspunkt begrenzt wird.
- Der gemeinsame Anfangspunkt der beiden Strahlen wird Scheitelpunkt des Winkels, Winkelscheitel oder kurz Scheitel genannt; die Strahlen heißen Schenkel des Winkels. Ein Winkel kann durch drei Punkte festgelegt werden, von denen einer den Scheitel des Winkels bildet und die beiden anderen auf je einem Schenkel des Winkels liegen.
- Die Winkelweite kann auch als Maß einer ebenen Drehung definiert werden.
- ---
- In der Geometrie sind zur Definition des Winkels als Objekt verschiedene Ansätze möglich. Dabei lassen sich zwei Typen unterscheiden:
- Der ungerichtete Winkel, der durch eine vorzeichenlose Winkelweite gekennzeichnet ist.
- Der gerichtete Winkel, der über eine Orientierung verfügt, und als Drehwinkel oder Winkelabstand gemessen wird.
BM783



- Darstellung des Winkels als Drehung
- ---
- Man kann auch sagen, dass ein Winkel durch eine Drehung eines Strahls oder einer Halbgeraden in einer Ebene um seinen bzw. ihren Anfangspunkt entsteht.
- Da es zwei verschiedene Möglichkeiten gibt, den Strahl zu drehen, muss zusätzlich die Drehrichtung angegeben werden:
- Linksdrehung: gegen den Uhrzeigersinn, auch mathematisch positiver Drehsinn genannt (Winkel ist positiv) - im Bild grün dargestellt.
- Rechtsdrehung: mit dem Uhrzeigersinn, auch mathematisch negativer Drehsinn genannt (Winkel ist negativ) - im Bild violett dargestellt.
- In der Mathematik ist es üblich, die Drehung gegen den Uhrzeigersinn – also im mathematisch positiven Drehsinn – auszuführen. Wenn die Drehung andersherum erfolgen soll, sollte dieses ausdrücklich angegeben werden.
- ---
- In der Geodäsie (Vermessungswesen) wird der Winkel im Uhrzeigersinn, also rechtsdrehend von 0 Gon bis 400 Gon gezählt. Da es in der Geodäsie per definitionem keine negativen Winkel gibt, ist der Drehsinn positiv. Analog zur Uhr, auch hier wird von 0 bis 24 h positiv, rechtsdrehend gezählt. Alle geodätischen Messinstrumente werden zur Richtungs- oder Winkelmessung rechtsherum gedreht.
BM784

- Bezeichnung von Winkeln
- ---
- ∡ oder ∠
- ---
- Winkel werden meistens mit kleinen griechischen Buchstaben, z. B. oder , bezeichnet.
- Ein Winkel ist ein Winkel zwischen zwei Halbstrahlen, Geraden, Kanten und ähnlichem. Er wird dann von ausgehend Richtung gezählt.
- Alternativ kann man die drei Punkte angeben, die den Winkel definieren, wobei der Scheitelpunkt immer in der Mitte steht, z. B. Winkel ABC oder . Dies bezeichnet den Winkel zwischen und , wobei im mathematisch positiven Drehsinn auf gedreht wird.
- Im englischen Sprachraum ist auch nur die Angabe des Scheitels üblich.
BM785
-
Alpha
-
Beta
-
Gamma
-
Delta
- Man verwendet zur Bezeichnung von Winkeln kleine griechische Buchstaben, zum Beispiel:
- Alpha α
- Beta β
- Gamma γ
- Delta δ
- Epsilon ε
- ---
- Dazu ordnen wir dem Winkel, bei dem die beiden Schenkel senkrecht aufeinanderstehen, die Maßzahl 90 zu.
- Einheit ist das „Grad“ (°).
- Die Größe des Winkels beträgt 90°.
- Einen Winkel von 90° nennt man „rechten Winkel“.
- Ein Grad ist also der 90. Teil eines rechten Winkels.
- ---
- Weitere Einheiten der Winkelgröße sind die Minute (') und die Sekunde ().
- ---
- die Sekunde 1
- die Minute 1' = 60
- das Grad 1° = 60' = 60 * 60' = 3600
- ---
- α = 90°
BM786


- Winkelmesser
- ---
- Zur Messung von Winkelgrößen wird der Winkelmesser verwendet.
- Um die Größe eines Winkels zu messen legen wir den Markierungspunkt des Winkelmessers an den Scheitelpunkt S des Winkels.
- Ein Schenkel des Winkels muss durch die Nullmarkierung des Winkelmessers gehen.
- (Wir sagen auch: Wir legen den Winkelmesser an einen Schenkel an.)
- Wir lesen auf der Einteilung beim zweiten Schenkel die Gradzahl ab:
- α = 60°
BM787


- Schätze die Größe der Winkel in Bild 1 und Bild 2!
- ---
- α
- β
- γ
- δ
Lösung BM787 - α = 35°
- β = 75°
- γ = 90°
- δ = 220°
BM788

- Wir teilen die Winkel nach ihrer Größe folgendermaßen ein:
- ---
- spitzer Winkel (Bild 1; Winkel α): kleiner als 90°
- rechter Winkel (Bild 1; Winkel β): 90°
- stumpfer Winkel (Bild 1; Winkel γ): größer als 90° und kleiner als 180° (90° < α < 180°)
- ---

- gestreckter Winkel (Bild 2): 180°
- ---

- überstumpfer Winkel (Bild 3): größer als 180° und kleiner als 360° (180° < α < 360°)
- ---

- Vollwinkel (Bild 4): 360°
BM789

- Zwischen zwei sich schneidenden Geraden gibt es vier Winkel. Jeweils zwei nebeneinander liegende summieren sich dabei zu 180°. Jeweils zwei gegenüberliegende Winkel sind gleich. Der Vollwinkel hat die Besonderheit, dass zwei der Winkel null sind.
- ---
- Zwei Geraden oder Strecken, die sich im rechten Winkel schneiden, nennt man zueinander orthogonal (= rechtwinklig). In einer Zeichnung wird der rechte Winkel durch einen Viertelkreis mit Punkt dargestellt.
BM790


- Zeichnen eines Winkels
- ---
- 1.) Wir zeichnen einen Strahl mit dem Anfangspunkt S (Scheitelpunkt S).
- 2.) Dann legen wir den markierungspunkt des Winkelmessers so an S an, dass der Strahl durch die Nullmarkierung des Winkelmessers geht.
- 3.) Wir markieren nun bei 60° an der Einteilung einen Punkt.
- 4.) Wir zeichnen den zweiten Strahl von S aus durch diesen Punkt und kennzeichnen den Winkel durch einen Kreisbogen.
BM791 - BM800
[editar]BM791
- Welchen Winkel bilden die beiden Zeiger einer Uhr? (Gib jeweils den kleineren der beiden möglichen Winkel an!)
- ---
- um 3.00 Uhr
- um 6.00 Uhr
- um 3.30 Uhr
- um 34.00 Uhr
- ---
- um 2.00 Uhr
- um 5.00 Uhr
- um 12.00 Uhr
- um 23.30 Uhr
BM792
- gebrochene Zahlen
- Bruchrechnung
- ---
- Die Summe zweier natürlicher Zahlen ist stets wieder eine natürliche Zahl.
- Bei der Subtraktion (Umkehrung der Addition) müssen wir die Zahlen so wählen, dass der Subtrahend größer als der Minuend ist, damit die Subtraktion ausführbar ist.
- ---
- Das Produkt zweier natürlicher Zahlen ist stets wieder eine natürliche Zahl.
- Bei der Division (Umkehrung der Multiplikation) müssen wir die Zahlen so wählen, dass der Dividend eine Vielfaches des Divisors ist, damit die Division ausfürhbar ist.
BM793
- 128 Bälle werden auf 28 Kinder aufgeteilt:
- 128 : 32 = 4
- ---
- Eine Tafel Schokolade wird auf 3 Kinder aufgeteilt:
- ABER: 1 : 3 ist im Bereich der natürlichen Zahlen nicht ausführbar.
- ---
- Wir geben solche Bruchteile von Einheiten mit Hilfe von Brüchen an.
- Ein Bruch ist ein Paar von natürlichen Zahlen, die durch den Bruchstrich' voneinander getrennt werden.
- Über dem Bruchstrich steht der Zähler, unter dem Bruchstrich steht der Nenner.
- ---
- Den Bruchteil der Rechnung 1 : 3 bezeichnen wir mit (ein Drittel).
- In den Bruch ist 1 der Zähler und 3 der Nenner.
- ---
- Der Nenner gibt an, in wie viel gleiche Teile das Ganze geteilt wird. Der Zähler gibt an, wie viel solcher Teile vorhanden sind
- ---
- Eine Tafel Schokolade wird auf 3 Kinder aufgeteilt:
- 1 : 3 =
- ---
- Wir wollen immer nur solche Brüche verwenden, deren Nenner von Nullen verschieden sind. Dagegen kann der Zähler eines Bruches aber Null sein.
BM794
- Gleichnamige Brüche
- Ungleichnamige Brüche
- ---
- Brüche, deren Nenner gleich sind, heißen gleichnamige Brüche.
- Brüche, deren Nenner verschieden sind, heißen ungleichnamige Brüche.
- ---
- gleichnamige Brüche: , , , ,
- ungleichnamige Brüche: , , , , , , ,
BM795
- Gib in denfolgenden Brüchen Zähler und Nenner an!
- ---
- , , ,
- , , ,
- , , ,
- (b ≠ 0), , ,
- (y ≠ 0), ,
BM796







- Brüche können wir geometrisch veranschaulichen.
BM797
- Zusammenfassung:
- Paare natürlicher Zahlen in der Form (b ≠ 0) heißen Brüche.
- Der Bruch besteht aus dem Zähler a, dem Nenner b und dem Bruchstrich.
BM798

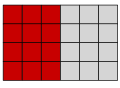
- In Bild 1 ist eine Kreisfläche in fünf gleiche Teile geteilt. Ein Teil stellt der Kreisfläche dar.
- 5 Teile stellen dann der Kreisfläche dar.
- ---

- In Bild 2 werden vier gleich große Kreisflächen jeweils in fünf gleiche Teile geteilt.
- Alle Bruchteile zusammen veranschaulichen den Bruch .
BM799
- Ein Rechteck ist 6 Einheiten lang und 4 Einheiten breit. Veranschauliche an diesem Rechteck folgende Brüche:
- a)
- b)
- c)
- d)
- e)
- f)
- g)
Lösung BM799 -
a (1/2)
-
b (1/3)
-
c (1/4)
-
d (1/6)
-
e (2/2)
-
f (3/3)
-
g (6/6)
-
BM800
- Veranschauliche an Rechtecken, die 6 cm lang und 1 cm breit sind, folgende Brüche:
- a)
- b)
- c)
- d)
- e)
Lösung BM800 -
a (4/2)
-
b (6/2)
-
c (6/3)
-
d (9/3)
-
e (12/6)
-
- índice
- Lección 065b ← Lección 066b → Lección 067b
- Lección 066
















![{\displaystyle [BA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28e56d00eabfbd70f8db2b8c78f8f536bce7d87b)
![{\displaystyle [BC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)