Administración de empresas/Estadística para los negocios/Prueba χ² (Chi-cuadrado)

PRUEB

A Χ² (CHI-CUADRADO)

Administración de empresas Proyecto de Aprendizaje Herramientas

Índice de contenidos

Datos bibliográficos (dar click para más información)
D. MURA, JOSEPH Administración: Una aproximación íntegra Estadística para los negocios Prueba χ² (Chi-cuadrado) 2015 En: https://es.wikibooks.org/wiki/Administración_de_empresas FUNDACIÓN WIKIMEDIA - PROYECTO WIKILIBROS, bajo licencia CC BY-SA 3.0

Esta obra está bajo la licencia CC BY-SA 3.0
(dar click para más información)

Esta obra está bajo la licencia CC BY-SA 3.0

Usted es libre de:

Compartir — copiar y redistribuir el material en cualquier medio o formato

Adaptar — remezclar, transformar y crear a partir del material para cualquier finalidad, incluso comercial.

Bajo las condiciones siguientes:

Reconocimiento — Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.

CompartirIgual — Si remezcla, transforma o crea a partir del material, deberá difundir sus contribuciones bajo la misma licencia que el original.

Índice

Principios

Administración de empresas/Estadística para los negocios/Índice de contenidos

Los principios tratados en este recuadro representan a los principios por los cuales se guía el libro. Aunque no se mencionen explícitamente en cada parte, se encuentran, aún así, ímplicitos.

La administración depende del contexto.
El recurso más valioso es el tiempo.
Las personas no son un recurso.
El éxito no es alcanzable directamente, o sea, no se puede pretender alcanzarlo mediante un plan de acción o la consecución de esfuerzos; sino que puede nacer o no como consecuencia de los resultados hechos o nuestras acciones.

Para Pruebas de Hipótesis con valores cuantitativos ver: Prueba de hipótesis (estadística)

Es un procedimiento estadístico que permite aceptar o rechazar una afirmación hecha con respecto a una cantidad cualitativa de datos determinada.

El procedimiento consta de siete (7) pasos.

Prueba de independencia

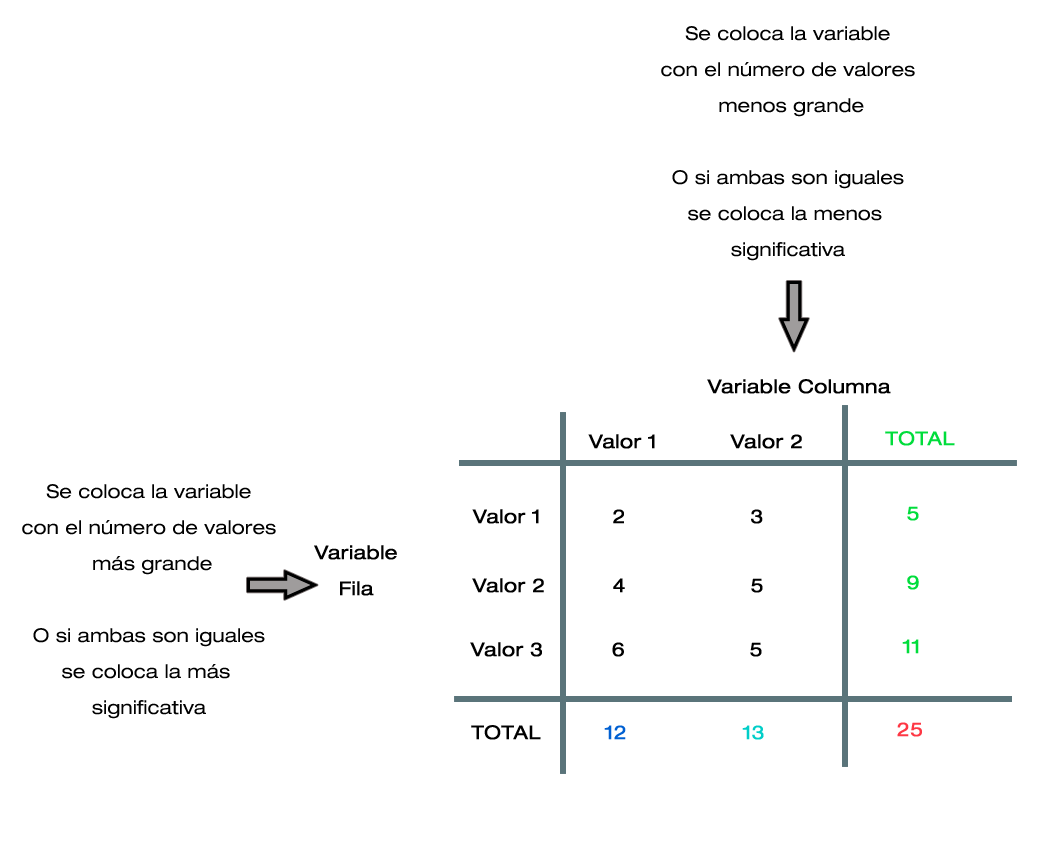
La información de las variables y de sus valores se representa a través del uso de una tabla, es necesario recalcar el hecho de que solamente pueden contarse los valores que estén entrecruzados entre sí (si valor 1 de la variable columna existe en el mismo lugar que valor 1 de la variable fila, se cuenta):

Ejemplo de uso:

Se realizó una encuesta en las personas sobre qué les parecía el servicio que brindaba una heladería y si les gustaba el sabor de sus helados.
Se obtuvieron los siguientes datos:

**Resultados de la encuesta**
Cliente	Calidad del servicio	¿Le gustó el sabor?
1	Bueno	Sí
2	Bueno	Sí
3	Malo	Sí
4	Malo	Sí
5	Malo	Sí
6	Malo	Sí
7	Malo	Sí
8	Malo	Sí
9	Regular	Sí
10	Regular	Sí
11	Regular	Sí
12	Regular	Sí
13	Bueno	No
14	Bueno	No
15	Bueno	No
16	Regular	No
17	Regular	No
18	Regular	No
19	Regular	No
20	Regular	No
21	Malo	No
22	Malo	No
23	Malo	No
24	Malo	No
25	Malo	No

En este caso:

La variable columna es Sabor del helado, porque tiene menos valores.
- Su valor 1 es Sí.
- Su valor 2 es No.
La variable fila es Calidad del servicio, porque tiene más valores.
- Su valor 1 es Bueno.
- Su valor 2 es Regular.
- Su valor 3 es Malo.

Con esto en cuenta se procede a realizar la tabla necesaria:

Procedimiento:

Sumar los valores tanto horizontal como verticalmente y anotar sus resultados en los extremos.
Del total de los valores horizontales (→ , 5 ; 9 ; 11): sumarlos y sacar un total nuevo (25).
Con este nuevo total, dividirlo entre cada uno de los números que lo formaron (5 ÷ 25 ; 9 ÷ 25 ; 11 ÷ 25) para hallar una proporción por cada fila (0.20 ; 0.36 ; 0.44).
Con estas proporciones, multiplicarlas por el total de los valores de cada columna (12 x 0.20 ; 12 x 0.36 ; 12 x 0.44 ; 13 x 0.20 ; 13 x 0.36 ; 13 x 0.44).
Anotar sus totales (2.4 + 4.32 + 5.28 ; 2.6 + 4.68 + 5.72) y comprobar que su resultado sumado es igual al de su columna (12 = 12 ; 13 = 13).

Hipótesis estadísticas

Se les denomina así a los supuestos (hipótesis) realizados con respecto a la relación de dos variables.

En este paso se definen dos tipos de hipótesis:

H_o: Hipótesis nula
H₁: Hipótesis alterna (de la cual se sospecha pudiera ser cierta, es planteada por el investigador)

Planteamiento único

Para este planteamiento solo debemos de comprobar dos suposiciones: si existe relación o no existe relación entre dos variables; por lo que...

Este tipo de desarrollo va de la forma: "¿Se podría afirmar que existe relación entre la calidad de servicio y el sabor del helado?"

En el cual se desea averiguar si existe relación entre la primera variable con la segunda variable.

Solo se puede distinguir un caso:

CASO ÚNICO
*H_o:No existe relación entre la primera y la segunda variable *H₁:Sí existe relación entre la primera y la segunda variable

Nivel de significancia (α)

Se le conoce así al error máximo adoptado al momento de rechazar la hipótesis nula (H_o) cuando es verdadera.

Dependiendo del tipo de de significación que se da al estudio, hay tres grados:

α = 0.01 → Muy significativo o de significación del 1%
α = 0.05 → Significativo o de significación del 5%
α = 0.10 → Poco significativo o de significación del 10% (rara vez usado)

Valor de la distribución 'χ²'

Véase: Tabla de la distribución: χ² (Chi-cuadrado), para valores de este tipo

En este paso se procede a ubicar el intervalo de confianza para poder rechazar o aceptar H_o.

Este valor solo puede ser hallado mediante la Tabla de Distribución χ².

Se usa la siguiente fórmula:

$\chi ^{2}=[(r-1)x(c-1)],\alpha$
Donde: $r$ = Número de valores en Variable Fila $c$ = Número de valores en Variable Columna $\alpha$ = Nivel de significancia
Ejemplo: Nivel de significancia del 1 % $\chi ^{2}=[(3-1)x(2-1)],0.01$ $\chi ^{2}=2,0.01$ Se procede a buscar el valor en la tabla χ² $\chi ^{2}=9.2104$

Estadístico de prueba 'χ²'

Se le conoce como Estadístico de Prueba al valor que resulta luego de aplicar una determinada fórmula a la información de la muestra tomada y que se utiliza para rechazar o aceptar la Hipótesis Nula (H_o) a través del Valor de la Distribución.

A continuación se muestra una fórmula detallada:

$\chi ^{2}=\Sigma {\frac {(O-E)}{E}}^{2}$

Donde:

$O$ = Cantidad de un valor con otro valor
$E$ = Resultado luego de multiplicarlo con su proporción correspondiente
$\Sigma$ = Suma total de todas las operaciones

Ejemplo:

Para ejemplificar esta fórmula se tomará en cuenta los valores de la siguiente tabla:

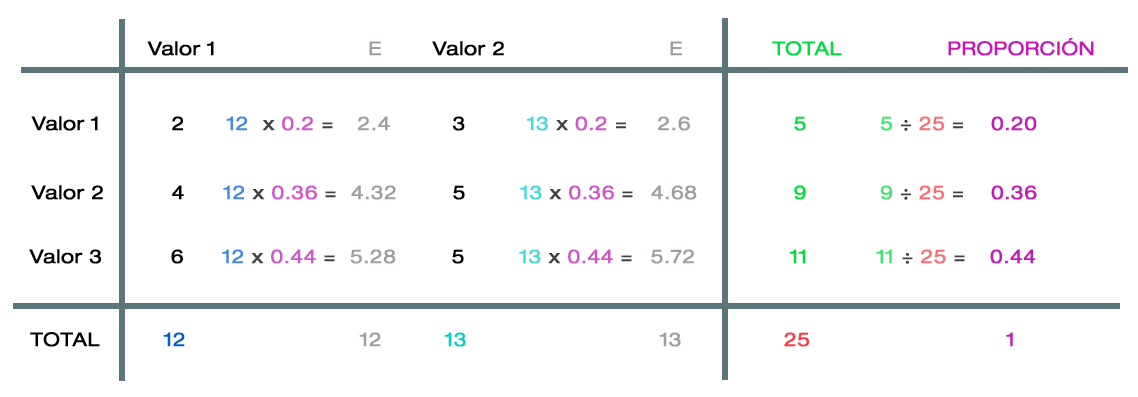
Se toman los valores necesarios y se reemplazan en la fórmula.

\chi ^{2}={\frac {(2-{\color {Gray}{\mbox{2.4}}})}{\color {Gray}{\mbox{2.4}}}}^{2}+{\frac {(3-{\color {Gray}{\mbox{2.6}}})}{\color {Gray}{\mbox{2.6}}}}^{2}+{\frac {(4-{\color {Gray}{\mbox{4.32}}})}{\color {Gray}{\mbox{4.32}}}}^{2}+{\frac {(5-{\color {Gray}{\mbox{4.68}}})}{\color {Gray}{\mbox{4.68}}}}^{2}+{\frac {(5-{\color {Gray}{\mbox{4.68}}})}{\color {Gray}{\mbox{4.68}}}}^{2}+{\frac {(6-{\color {Gray}{\mbox{5.28}}})}{\color {Gray}{\mbox{5.28}}}}^{2}+{\frac {(5-{\color {Gray}{\mbox{5.72}}})}{\color {Gray}{\mbox{5.72}}}}^{2}

Nótesese que los datos usados son de los valores entrecruzados y el resultado de multiplicar las proporciones de su fila.

Región de aceptación y rechazo

Una vez obtenidos los datos necesarios para poder realizar el procedimiento estadístico, se deberán de colocar en un gráfico que ilustre cómo se plantea; se determina si se acepta o se niega la hipótesis nula (H_o).

Caso único
chicuadrado

Los valores se sustituyen por cada uno de los puntos mencionados en la gráfica correspondiente. Puede resultarte algo parecido a esto:

Nivel de significancia del 5 %, con tres valores en la variable fila y dos valores en la variable columna

En este caso se rechaza H_o, por lo que se acepta H₁

Decisión

Important icon

Los niveles de significancia deben ser reemplazado por su similar literal

α = 0.01 o de significación del 1% → Muy significativo
α = 0.05 o de significación del 5% → Significativo
α = 0.10 o de significación del 10% → Poco significativo(rara vez usado)

Es la parte final del procedimiento de prueba de hipótesis, en la que redactamos una conclusión de todo el estudio realizado.

Esta parte tiene que incluir necesariamente: El nivel de significancia y la aceptación o rechazo de una existencia de relación entre dos variables (primera variable y segunda variable).

Ejemplo de una plantilla de redacción:

Se puede afirmar significativamente que sí existe relación entre la calidad del servicio y el sabor del helado.

Ejemplo según el gráfico:

Se rechaza H_o
Se puede afirmar significativamente que sí existe relación entre la calidad del servicio y el sabor del helado.