Wikichicos/Geometría/Capítulo 7. Circunferencia y círculo
Circunferencia
[editar]
|
La circunferencia es una línea curva plana y cerrada tal que todos sus puntos están a igual distancia del centro. |
Hay que distinguirla del círculo, cuyo lugar geométrico queda determinado por una circunferencia, y la región del plano que encierra esta.
Partes
[editar]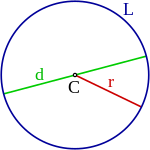
Elementos relevantes de la circunferencia:
- El centro es el punto equidistante a todos los puntos de una circunferencia. Señalado con el nombre en la figura.
- Un radio es cualquier segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio también es la longitud de los segmentos del mismo nombre. Señalado con el nombre en la figura.
- Un diámetro es cualquier segmento que une dos puntos de la circunferencia pasando por su centro. El diámetro también es la longitud de los segmento del mismo nombre. Señalado con el nombre en la figura.
- El perímetro es el contorno de la circunferencia y su longitud. Señalado con el nombre en la figura.
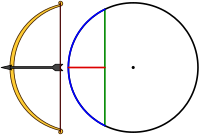
- Una cuerda es cualquier segmento que une dos puntos de una circunferencia. El diámetro es una cuerda de máxima longitud. Segmento verde en la figura.
- Un arco es cualquier porción de circunferencia delimitada por dos puntos sobre esta. Línea curva azul en la figura.
- Una semicircunferencia es cualquier arco delimitado por los extremos de un diámetro.
Perímetro
[editar]La longitud de una circunferencia en función del radio o del diámetro es:
donde es el número pi.

Longitud de una circunferencia
Obtener la longitud de una circunferencia que tiene un radio de 15 cm

- Longitud
- ;
- ;
- ;
- ;
- Longitud
Posiciones relativas respecto a la circunferencia
[editar]Los puntos
[editar]Posiciones de los puntos respecto de la circunferencia:

- Un punto exterior es el que está a una distancia mayor al radio de la circunferencia respecto la posición de su centro. (punto E)
- Un punto interior es el que está a una distancia menor al radio de la circunferencia respecto la posición de su centro. (punto I)
Las rectas
[editar]Posiciones de las rectas respecto de la circunferencia:

- Una recta exterior es cualquier recta que no tiene puntos en común con la circunferencia. (recta a)
- Una recta tangente es cualquier recta que toca la circunferencia en un único punto. (recta c)
- Una recta secante es cualquier recta que corta la circunferencia en dos puntos. (recta b)
Se llama punto de tangencia cada uno de los puntos que comparte la circunferencia con los diferentes elementos tangentes, es decir, el punto donde se produce la tangencia. (Puntos A y B).
En todo punto de la circunferencia se pueden hacer tangencias.
Posiciones entre circunferencias
[editar]- Una circunferencia es exterior a otra, si todos sus puntos son exteriores a esta otra. Véase la figura 1 y 8.
- Una circunferencia es interior a otra, si todos sus puntos son interiores a esta otra. Véase la figura 5.

- Una circunferencia es tangente exterior a otra, si tienen un único punto común y todos los demás puntos de una son exteriores a la otra. Véase la figura 2.
- Una circunferencia circundante es tangente exterior a otra, si tienen un único punto común. Véase la figura 7. (la circunferencia roja es tangente exterior a la azul)
- Una circunferencia es tangente interior a otra, si tienen un único punto común y todos los demás puntos de una son interiores a la otra. Véase la figura 4 (la circunferencia roja es tangente interior a la azul)
- Una circunferencia es secante a otra, si se cortan en dos puntos distintos. Véase la figura 3.
- Son coincidentes las circunferencias que tienen el mismo centro y el mismo radio, es decir, que todos los puntos de una son los de la otra y viceversa. Véase la figura 6.
Circunferencia inscrita y circunscrita
[editar]- Una circunferencia está inscrita en un polígono cuando sea tangente a todos los lados de dicho polígono, se dice que este polígono está circunscrito a la circunferencia.(fg.1)
- Una circunferencia está circunscrita a un polígono cuando todos los vértices de dicho polígono están sobre esta, se dice que este polígono está inscrito en la circunferencia.(fg.2)
-
Circunferencia inscrita en un cuadrado (fg.1)
-
Circunferencia circunscrita a un polígono (fg.2)
Círculo
[editar]
|
El círculo es una región del plano delimitada por una circunferencia y, por tanto, tiene asociada un área.[1] |
Perímetro
[editar]El perímetro de un círculo es el de su circunferencia y en función del radio o del diámetro tiene el valor:
donde es el número π, de la circunferencia.
Área
[editar]El área de un círculo de radio o diámetro , tendrá un valor:
- A =

Área de un círculo
Obtener el área de un círculo que tiene un radio de 15 cm

- Área
- A =
- A =
- A =
- A =
- Área
Regiones circulares
[editar]Elementos relacionados con partes de las regiones del círculo, (figura 1):

- El semicírculo es cualquier parte del círculo delimitada por un diámetro y el arco o semicircunferencia que determina este diámetro sobre su circunferencia.
(Véase la figura 2). - El segmento circular es cualquier parte del círculo delimitada por una cuerda y uno de los arcos que determina esta cuerda sobre su circunferencia. (Véase la figura 3).
- El sector circular es cualquier parte del círculo delimitada por dos radios y el arco que determinan estos lados sobre su circunferencia, por tanto, queda unívocamente determinada por un ángulo central. (Véase figura 4).
- La corona circular es la región del plano delimitada entre dos circunferencias concéntricas, exterior a la de radio menor e interior a la de radio mayor. (Véase figura 6).
- El trapecio circular es cualquier parte de la corona circular delimitada por un ángulo central. (Véase figura 5).
Área del sector circular
[editar]Para hallar el área de un sector circular se divide el área del círculo por 360 para hallar el área que corresponde a un grado y luego se multiplica por el número de grados del sector circular.

Área de un sector circular
Obtener el área de un sector circular de un círculo que tiene un radio de 15 cm

- Área del círculo
- A =
- A =
- A =
- A =
- Área del círculo
|
Área del sector circular
|
Referencias
[editar]- ↑ Real Academia de Ciencias Exactas, Física y Naturales, ed (1999). Diccionario esencial de las ciencias. Espsa. pp. 190. ISBN 84-239-7921-0. «Región del plano limitada...»
.....................................................................................................................................................
Ejercicios
[editar]
....................................................................................................................................................






















