Curso de alemán para principiantes con audio/Lección 079b
- índice
- Lección 078b ← Lección 079b → Lección 080b
- Mathematik auf Deutsch - 29
BM1401 - BM1410
[editar]BM1401
- Gleichung
- ---
- Unter einer Gleichung versteht man in der Mathematik eine Aussage über die Gleichheit zweier Terme, die mit Hilfe des Gleichheitszeichens („=“) symbolisiert wird. Formal hat eine Gleichung die Gestalt
- T 1 = T 2
- wobei der Term T 1 die linke Seite und der Term T 2 die rechte Seite der Gleichung genannt wird. Gleichungen sind entweder wahr beziehungsweise erfüllt (beispielsweise 1 = 1) oder falsch (beispielsweise 1 = 2).
- ---
- Die Werte der Variablen, für die die Gleichung erfüllt ist, heißen Lösungen der Gleichung.
- ---
- Gleichungssystem
- Sind zwei oder mehr Gleichungen angegeben, spricht man auch von einem Gleichungssystem, eine Lösung desselben muss alle Gleichungen simultan erfüllen.
- Beispiel:
- I) a + b = 10
- II) a * b = 24
- ---
- Bruchgleichung
- Unter einer Bruchgleichung versteht man in der (Schul-)Algebra eine Gleichung mit mindestens einem Bruchterm, der die Unbekannte im Nenner enthält.
- Beispiel:
- Durch Multiplikation mit dem Hauptnenner kann man eine Bruchgleichung auf einen einfacheren Gleichungstyp zurückführen.
Lösung BM1401 - Die Lösungsmenge ist:
BM1402
- Lösungsmenge
- ---
- Als Lösungsmenge bezeichnet die Mathematik die Menge der Lösungen einer Gleichung, einer Ungleichung, eines Systems von Gleichungen und Ungleichungen.
- ---
- Beispiele:
- Es ist jeweils eine Gleichung und ihre Lösungsmenge (L) für angegeben:
- , die Lösungsmenge ist ein Intervall
- , die Lösungsmenge ist eine Menge von Paaren x und y. Die Paare werden in runde Klammern geschrieben: (x; y). Dazu späte mehr.
- Ein Gleichungssystem:
- x + 2y = 8
- 2x + y = 7
- (Die Paare werden in runde Klammern geschrieben: (x; y). Dazu späte mehr.)
BM1403
- Wissenschaftliche Schreibweise von Zahlen
- Wissenschaftliche Zahlendarstellung
- ---
- Als wissenschaftliche Notation bezeichnet man die Exponentialdarstellung, auch traditionelle wissenschaftliche Notation oder Normdarstellung genannt:
- a * 10b
- Beispiel:
- 34.500
- 3,45 * 104
- ---
- Zehnerpotenzen werden in der elektronischen Datenverarbeitung und bei Taschenrechnern häufig mit e oder E dargestellt.
- Beispiel: 1,55 E5 := 1,55 · 105 = 155.000
- („:=“ bedeutet „ist definiert als“. )
- Die Abwandlungen des Gleichheitszeichens := oder =: werden in der Mathematik benutzt, um eine Definition einer Seite durch die andere Seite darzustellen. Dabei stehen die Doppelpunkte immer bei dem zu definierenden Objekt. Das früher dafür verwendete ≡ soll in diesem Sinne nicht mehr verwendet werden.
- Beispielsweise kann man die Menge A folgendermaßen definieren:
- ---
- a * 10b
- „b“ bezeichnet man als Exponenten. Der Exponent ist in der wissenschaftlichen Zahlendarstellung eine ganze Zahl (Ganzzahl).
- „a“ bezeichnet man als Mantisse.
- „a“ hat in der wissenschaftlichen Zahlendarstellung immer genau eine einzige Ziffer vor dem Komma.
- Natürlich ist die Ziffer vor dem Komma keine Null.
- „a“ hat immer nur eine, von Null verschiedene, linksseitige Dezimalstelle.
- ---
- 34,6 * 103 (FALSCH)
- 3,46 * 102 (RICHTIG)
- 0,346 * 101 (FALSCH)
BM1404

Eingabetaste für den Exponenten „b“ mit der Beschriftung „Exp“ (über der Taste „7“) - Wissenschaftliche Zahlendarstellung mit wissenschaftlichen Taschenrechnern
- ---
- Die meisten modernen Taschenrechner können Zahlen automatisch in wissenschaftlicher Notation darstellen. Bei sehr großen Zahlen oder sehr kleinen Dezimalbrüchen ist dies meist ohnehin nicht anders möglich.
- ---
- Wenn keine hochgestellten Ziffern zur Verfügung stehen, wird die folgende Schreibweise genutzt: aus 1·1018 wird 1 E18. Die Zahl 3200 z. B. kann somit auch 3,2 E3 notiert werden.
- ---
- Beispiel: Die Lichtgeschwindigkeit im Vakuum beträgt c = 299.792.458 m/s.
- das sind in wissenschaftlicher Schreibweise:
- 2,99792458 · 108 m/s
- ---
- Diese Schreibweise wurde von Physikern und Mathematikern schon seit langem verwendet, um sehr große und sehr kleine Zahlen angeben zu können. Noch heute wird deshalb die Gleitkommaschreibweise auf Taschenrechnern speziell als wissenschaftliches Format bezeichnet.
BM1405
- Wissenschaftliche Zahlendarstellung
- ---
- a) 123.400.000 schreibt man als 1,234 * 108
- b) 451 schreibt man als 4,51 * 102
- ---
- c) 92.384 schreibt man als 9,2384 * 104
- d) 0,000123 schreibt man als 1,23 * 10-4 (Zu negativen Exponenten in einer späteren Lektion mehr.)
- ---
- Sonderfälle:
- e) 7000 schreibt man als 7 * 103 (Es gibt kein Komma.) (7 * 103 = 7,0 * 103)
- f) 2,54 schreibt man als 2,54 * 100 (In der wissenschaftlichen Schreibweise schreibt man immer eine zehnerpotenz dazu. Nur „2,54“ zu schreiben wäre die Dezimalschreibweise.)
- ---
- Wir erinnern uns:
- a2 = a * a
- a1 = a
- a0 = 1
- ---
- 102 = 10 * 10
- 101 = 10
- 100 = 1
- ---
- 2,54 * 100 = 2,54 * 1 = 2,54
BM1406

6,02 * 1023 Taste EXP links unten über der 7 Taste - Varianten für die Schreibweise der wissenschaftlichen Zahlendarstellung:
- Statt 10 hoch einer Zahl wird für 10 ein kleines oder großes „E“ geschrieben.
- ---
- Da hochgestellte Exponenten wie z. B. 107 nicht immer in der Anzeige eines Taschenrechners dargestellt werden können, wird der Buchstabe E oder e oft verwendet um 10 hoch irgendwas darzustellen. „E“ bedeute also „* 10n“. Danach folgt der Wert des Exponenten „n“.
- ---
- 5e2 = 5 * 102 = 500
- 6,3E3 = 6,3 * 103 = 6300
- 7,3218E3 = 7,3218 * 103 = 7321,8
- 4,59e2 = 4,59 * 102 = 459
- 7,51E−9 = 7,51 * 10-9 = 0,000 000 007 51
- 6,72e9 = 6,72×109 = 6.720.000.000
- ---
- Auch in Computersprachen werden große Zahlen oft in wissenschaftlicher Schreibweise geschrieben.
- ---
- 3,5 * 102 or 35 * 101 or 350 * 100
- Die wissenschaftliche Schreibweise hat genau eine Ziffer vor dem Komma. Also ist nur die erste Zahlendarstellung die wissenschaftliche Schreibweise:
- 3,5 * 102
- ---
- Die meisten Taschenrechner und Computerprogramme stellen sehr große und sehr kleine Zahlen in wissenschaftlicher Notation (= wissenschaftliche Schreibweise) dar. Dazu haben Taschenrechner oft eine Tast mit der Beschriftung EXP (für Exponent), EEX (für enter exponent = engl. für Exponenten eingeben), EE, EX, oder E in Abhängigkeit vom jeweiligen Taschenrecher-Modell.
BM1407
- Lies die Zahlen vor!
- ---
- Abb. 1: ...
- Abb. 2: ...
- Abb. 3: ...
- ...
-
Abb. 1
-
Abb. 2
-
Abb. 3
-
Abb. 4
-
Abb. 5
-
Abb. 6
-
Abb. 7
-
Abb. 8
-
Abb. 9
-
Abb. 10
-
Abb. 11
-
Abb. 12
-
Abb. 13
-
Abb. 14
-
Abb. 15
-
Abb. 16
-
Abb. 17
-
Abb. 18
BM1408
- Variable
- ---
- Eine Variable ist ein Name für eine Leerstelle in einem logischen oder mathematischen Ausdruck. Der Begriff leitet sich vom lateinischen Adjektiv variabilis (veränderlich) ab. Gleichwertig werden auch die Begriffe Platzhalter oder Veränderliche benutzt. Als „Variable“ dienten früher Wörter oder Symbole, heute verwendet man zur mathematischen Notation in der Regel Buchstaben als Zeichen. Wird anstelle der Variablen ein konkretes Objekt eingesetzt, so ist darauf zu achten, dass überall dort, wo die Variable auftritt, auch dasselbe Objekt benutzt wird.
- ---
- x = 4 * 5
- 3 + n = 13
- a : b = 5
- ---
- Variable, die in einer Gleichung vorkommen, nannte man in den Schulbüchern der Mathematik bis in die 1960er Jahre auch Unbekannte oder Unbestimmte.
BM1409
- Gleichungen mit Variablen
- ---
- Gleichungen, in denen keine Variable auftritt, sind entweder wahre oder falsche Aussagen.
- Folgende Aussagen sind wahre Aussagen:
- 5 + 4 = 9
- 7 * 7 = 48
- ---
- Folgende Aussagen sind falsche Aussagen:
- 5 = 8
- 2,5 < 1,5 // eine Ungleichung
- ---
- Von Gleichungen mit Variablen können wir werde sagen, dass sie wahr sind, noch dass sie falsch sind. Es sind keine Aussagen. Wenn wir aber an die Stelle von Variablen Ziffern schreiben, so entstehen entweder wahre oder falsche Ausagen.
- ---
- Wir setzen in die Gleichungen „4 + x = 5,5“ und „3 * x = 21“ für „x“ Zahlen ein:
x 4 + x = 5,5 3 * x = 21 0 4 + 0 = 5,5 (falsch) 3 * 0 = 21 (falsch) 4 + = 5,5 (falsch) 3 * = 21 (falsch) 1,5 4 + 1,5 = 5,5 (wahr) 3 * 1,5 = 21 (falsch) 7 4 + 7 = 5,5 (falsch) 3 * 7 = 21 (wahr)
BM1410
- Wird eine Gleichung durch das Einsetzen einer Zahl zu einer wahren Aussage, so sagt man: „Diese Zahl erfüllt die betreffende Gleichung.“
- ---
- Welch gebrochenen Zahlen x erfüllen folgende Gleichungen?
- ---
- a) 2x = 6
- b) x = 5
- ---
- c) 2x + 1 = 5
- d) 9x = 6
- ---
- Manche Gleichungen weden von keiner Zahl, andere von nur einer Zahl und weider andere von mehreren Zahlen erfüllt.
- ---
- x - 5 = 2 (x ∈ ℕ)
- 4 : y = 0
- 4a = 10
- 0 * b = 0
- ---
- Die Lösungsmenge ist die Menge der Lösungen einer Gleichung.
- Mengen werden in geschweiften Klammern geschrieben.
- ---
- x - 5 = 2 (x ∈ ℕ); L = { } // die Lösungsmenge ist leer = leere Menge
- 4 : y = 0; ; L = { } // Die Lösungsmenge ist die leere Menge.
- 4a = 10; L = {2,5}
- 0 * b = 0; L = ℚ // Die Lösungsmenge ist die gesamte Menge der rationalen Zahlen. (ℚ)
BM1411 - BM1420
[editar]BM1411
- Leere Menge
- ---
- Die leere Menge kann auf zwei verschiedene Arten dargestellt werden.
- a) ∅
- b) { }
- ---
- Die leere Menge ist ein grundlegender Begriff aus der Mengenlehre. Man bezeichnet damit die Menge, die keinerlei Elemente enthält. Da Mengen über ihre Elemente charakterisiert werden und zwei Mengen genau dann gleich sind, wenn sie dieselben Elemente haben, gibt es nur eine einzige leere Menge.
- ---

Abbildung 1: leere Menge; { } 
Abbildung 2: Menge der Primzahlen bis 100 - c) {4; 7; 8; 40} // Diese Menge enthält drei Elemente. Die Elemente der Menge sind „4“, „7“ und „8“.
- d) { } // Diese Menge enthält keine Element. Diese Menge ist leer.
- ---
- Es folgen verschiedene Zeichen für die leere Menge
- e)
- Vor allem in der Schulmathematik wird die leere Menge auch gern durch eine leere Mengenklammer dargestellt: { } .
- Dieses Zeichen wirkt einem Missverständnis entgegen: Die leere Menge ist nicht nichts, sondern eine Menge, die nichts enthält.
- f) {} // Leere Menge, nur einfach ohne Leerzeichen zwischen der öffnenden und schließenden geschweiften Klammer geschrieben.
- g) // leere Menge (ein durchgestrichenes schmales Oval - eine typographische Variante)
- h) ∅ // leere Menge (ein durchgestrichener Kreis)
- (Das Durchmesserzeichen oder Durchschnittszeichen ⌀ ist typografisch etwas kleiner, als das Zeichen für die leere Menge: ∅)
- ---

Abb. 1: Mengendiagramm; {4; 7; 8; 40} - A = {4; 7; 8; 40}
- B = {8; 4; 40; 7}
- Die Mengen A und B sind identisch. Die Reihenfolge der Elemente ist egal.
- Mengen werden nur über ihre Elemente charakterisiert. Deshalb sind zwei Mengen genau dann gleich, wenn sie dieselben Elemente haben.
- A = B (Lies: Menge A gleich Menge B)
- ---
- Es gibt eine Menge, die keine Elemente enthält. Sie wir leere Menge genannt.
BM1412

Abb. 1: Teilmenge - Teilmengen
- ---
- Abb. 1 veranschaulicht diese Beziehung zwischen den Mengen M4 und M2. In ihm sind die Mengen als Flächen dargestellt, von denen die eine ['Sprechpause'] Teilfläche der anderen ist. Die Form und die Größe dieser Fläche kann beliebig gewählt werden, wenn nur diejeneige Fläche, die die Teilmenge M4 von M2 veranschaulicht, ganz innerhalb der Fläche liegt, die die Menge M2 darstellt.
- ---
- Beispiele: Diagramme mit Teilmengen und Schnittmengen
-
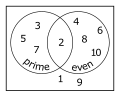
Abb. 3: links: Primzahlen; rechts: gerade Zahlen
-
Abb. 4: Mengen A, B, C und D
BM1413

Schnittmenge (rot); Venn-Diagramm - Schnittmenge
- ---
- Die Schnittmenge ist die Menge bestehend aus den gemeinsamen Elementen von mehreren Mengen.
- LIES:
- A geschnitten mit B ( ) ist definiert als ()
- die Menge { }
- der Elemente x für die gilt ... ( )
- dass x eine Element der Menge A ist ( )
- und ( )
- dass x eine Element der Menge B ist ( )
- ---
- Mathematik ist eine Sprache.
- Mathematik ist eine Sprache mit eigenen Worten und Symbolen.
- Mathematik ist wegen der Symbole eine sehr kompakte und genaue Sprache.
- ---
- Mit anderen Worten:
- Die Schnittmenge von A und B sind alle Elemente (x), die sowohl in der Menge A als auch in der Menge B liegen.
BM1414
- Verschiedene Darstellungen für Schnittmengen
- ---
- Abb. 1: Der rot markierte Bereich ist die Schnittmenge der beiden Mengen, die durch die Kreise links (Menge A) und rechts (Menge B) symbolisiert werden.
- Abb. 2 bis 3 zeigen nochmals den gleichen Sachverhalt, wobei die Mengen nur jeweils in anderen Farben dargestellt sind.
- Abb. 4: Das Element ek liegt in der Schnittmenge (LIES: A geschnitten mit B)
- In Abb. 5 ist die Menge der Teiler von 6 (links, in blau) und die Menge der Teiler von 33 (rechts, rot) dargestellt, sowie ihre Schnittmenge. (33 hat die Teiler 3 und 11, während 6 die Teiler 2 und 3 hat.)
-
Abb. 1
-
Abb. 2
-
Abb. 3
-
Abb. 4
-
Abb. 5
- ---
- Wesentlich mehr Schnittmengen ergeben sich, wenn sich 3 Mengen schneiden
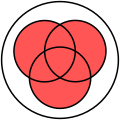
- In Abb. 4 überschneiden sich die Mengen A, B und C.
- Es werden 3 Schnittmengen gebildet, bei denen sich jeweils 2 Mengen schneiden und eine Schnittmenge, bei der sich alle 3 Mengen überschneiden. (Abb. 5)
-
Abb. 6
-
Abb. 7
BM1415

Vereinigungsmenge; (Venn-Diagramm) - Vereinigungsmenge
- ---
- Die Vereinigungsmenge ist die Menge der Elemente, die in mindestens einer Menge enthalten sind.
- ---
- LIES:
- vereinigt mit ( )
- ist ( )
- die Menge aller Elemente ( )
- die in oder in enthalten sind ( )
- Das „oder“ ( ) ist hier nicht-ausschließend zu verstehen: Die Vereinigung umfasst auch die Elemente, die in beiden Mengen enthalten sind.
- Das „oder“ ist also als „und/oder“ zu interpretieren.
- ---
- Mit anderen Worten:
- Die Vereinigung von und ist die Menge aller Elemente, die in oder in enthalten sind.
- ---
- ---
- (Die Menge aller „x“, für die gilt ...
- und (Die Menge aller „x“, für die gilt x > 9 und x < 15) = {10; 11; 12; 13; 14}
BM1416
- Vereinigungsmenge
- ---
- Beispiele:
- Abb. 1: (die Vereinigungsmenge von A und B; die Vereinigung von A und B)
- Abb. 2: Die Vereinigungsmenge von drei Mengen.
- Abb. 3: Die Vereinigungsmenge von zwei geometrischen Figuren (Würfel und Kugel)
- (Mengen sind nicht immer Zahlenmengen. Man könnte auch die Menge aller unregelmäßigen deutschen Verben definieren. Natürlich haben wir es in der Mathematik vorwiegend mit Zahlenmengen zu tun. Aber auch graphische Computerprogramme arbeiten mit Mengenoperationen.)
-
Abb. 1
-
Abb. 2
-
Abb. 3
BM1417


- Disjunkte Mengen
- ---
- Wenn Mengen keine gemeinsame Elemente enthalten, so sind sie disjunkt.
- ---
- In der Mengenlehre heißen zwei Mengen A und B disjunkt (lateinisch disjunctus = ‚getrennt‘), elementfremd oder durchschnittsfremd, wenn sie kein gemeinsames Element besitzen. Mehrere Mengen heißen paarweise disjunkt, wenn beliebige zwei von ihnen disjunkt sind.
- ---
- Zwei Mengen und sind disjunkt, wenn ihre Schnittmenge leer ist, wenn also gilt:
- ---
- Beispiele:
- Die Mengen und sind disjunkt, weil sie kein gemeinsames Element haben.
- Die Mengen und sind nicht disjunkt, da sie das Element gemeinsam haben.
- Die drei Mengen , und sind nicht paarweise disjunkt, da zumindest eine der drei möglichen Schnittmengen (nämlich ) nicht leer ist.
- ---
- Weitere Beispiele:
-
ein paarweise disjunktes Mengensystem
-
ein nicht paarweise disjunktes Mengensystem
- ---
- Eigenschaften:
- Die leere Menge ist disjunkt zu jeder beliebigen Menge.
- Beispiel: A := { }; B := {3; 5; 12}
- und sind genau dann disjunkt, wenn .
BM1418

Schnitt 
Vereinigung - Mengenoperationen:
- ---
- Schnittmenge: R ∩ S (Durchschnittsoperation)
- ---
- Vereinigungsmenge: R ∪ S (Vereinigung)
- Vereinigungsmenge: R ∪ S (Vereinigung)
- ---
- Teilmenge : (die Teilmenge ist keine Mengenoperationen.)
- ---

Eselsbrücke: ∧; A; AND - Verknpüfung von zwei Aussagen:
- ---
- und: ∧ (Gelesen wird die Konjunktion zweier Aussagen A sowie B meist als „A und B“.)
- Konjunktion:
- Gelesen wird die Konjunktion zweier Aussagen A sowie B meist als „A und B“. In der klassischen Logik ist die Konjunktion zweier Aussagen genau dann wahr, wenn beide verknüpfte Aussagen wahr sind.
- Gemeint sein kann mit dem Wort Konjunktion
- die verknüpfte Aussage als Ganzes (der Satz „A und B“)
- das Verknüpfungszeichen (Junktor)
- das Verknüpfungswort „und“
- ---
- oder: Schreibweise:
- Disjunktion:
- „A oder B (oder beides)“ sagt aus, dass mindestens eine der beiden beteiligten Aussagen wahr ist.
- Schreibweise:
- Das Disjunktions-Zeichen ( ) ähnelt dem Zeichen für die Vereinigungsmenge und erinnert an den Buchstaben „v“, mit dem das lateinische Wort „vel“ anfängt, das für ein solches nicht-ausschließendes Oder steht.
- ---
- Zusammenfassung:
- Schnittmenge: A ∩ B --- und: ∧ (Das Element ist in A und B enthalten.)
- Vereinigungsmenge: A ∪ B --- oder: (Das Element ist in A oder B enthalten. - gerne auch in beiden Mengen)
BM1419
- Leere Menge - ∅; { }
- ---

Abb. 1 - Die leere Menge ist Teilmenge jeder Menge, das heißt für jede Menge ist
- Abb. 1: blau (rechts) die Menge der Primzahlen von 1 bis 50; rot (links) die Menge der Primzahlen von 50 bis 100; grün (groß) die Menge der Primzahlen von 1 bis 100; grau (oben) leere Menge als Teilmenge der Menge der Primzahlen von 1 bis 100
- ---

Abb. 2 - Abb 2: Vereinigungsmenge: gelb (oben; Umrandung gestrichelt) Menge der Primzahlen von 1 bis 50; magenta (unten; Umrandung gepunktet) Menge der Primzahlen von 51 bis 100; links (rot) Menge der Primzahlen von 1 bis 100 bei denen die Quersumme gerade ist; rechts (blau) Menge der Primzahlen von 1 bis 100 bei denen die Quersumme ungerade ist
- Vereinigungsmenge
- grau (oben) leere Menge als Teilmenge der menge der Primzahlen
- schwarz (links; rechts; unten) leere Menge als Teilmenge einer Menge
- ---

Abb. 3 - Abb. 3: Disjunkte Mengen
- Wenn Mengen keine gemeinsame Elemente enthalten, so sind sie disjunkt.
- blau (rechts) Menge der Primzahlen von 1 bis 100, die eine ungerade Quersumme haben
- rot (links) Menge der Primzahlen von 1 bis 100, die eine gerade Quersumme haben
- Es gibt keine Überschneidungen, denn eine Quersumme kann nur gerade oder ungerade sein, aber nicht beides.
- ---

Abb. 4 - Abb. 4: Jede Menge bleibt bei Vereinigung (Vereinigungsmenge) mit der leeren Menge unverändert:
-
- ---

Abb. 5 - Für jede Menge ist der Durchschnitt (Schnittmenge) mit der leeren Menge die leere Menge:
-
- Der grün markierte Bereich ist die Schnittmenge. Dieser Bereich enthält keine Elemente, da er auch zur leeren Menge (links) gehört.
BM1420

- Teilmenge
- echte Teilmenge ( ⊂ ) (der Fall ist hier möglich)
- unechte Teilmenge ( ⊆ ) (hier ist garantiert )
- Obermenge - (Untermenge)
- ---
- Die mathematischen Begriffe Teilmenge und Obermenge beschreiben eine Beziehung zwischen zwei Mengen. Ein anderes Wort für Teilmenge ist Untermenge.
- ---
- ist eine Teilmenge von und ist eine Obermenge von , wenn jedes Element von auch in enthalten ist. Wenn zudem weitere Elemente enthält, die nicht in enthalten sind, so ist eine echte Teilmenge von und ist eine echte Obermenge von .
- ---
- Beispiele:
- {1, 2} ist eine (echte) Teilmenge von {1, 2, 3}.
- {1, 2, 3} ist eine (unechte) Teilmenge von {1, 2, 3}.
- {1, 2, 3, 4} ist keine Teilmenge von {1, 2, 3}.
- {1, 2, 3} ist keine Teilmenge von {2, 3, 4}.
- {} ist eine (echte) Teilmenge von {1, 2}.
- {1, 2, 3} ist eine (echte) Obermenge von {1, 2}.
- {1, 2} ist eine (unechte) Obermenge von {1, 2}.
- {1} ist keine Obermenge von {1, 2}.
- Die Menge der Primzahlen ist eine echte Teilmenge der Menge der natürlichen Zahlen.
- ---
- Weitere Beispiele als Mengendiagramme:
-
Abb. 2
-
Abb. 3
- Abb. 2: A ist eine echte Teilmenge von B ()
- Abb. 3: C ist zwar eine Teilmenge von B, aber keine echte Teilmenge von B ( ; bei unechten Teilmengen ist der Fall möglich)
- ---
- Die Zeichen für echte Teilmengen ( ⊂ ) und unechte Teilmengen ( ⊆ ) erinnern passender Weise an die Zeichen für Ungleichheit ≤ (kleiner oder gleich) und < < (kleiner als).
- ---
- Sprechweise:
- Statt „ ist eine Teilmenge von .“ wird auch „Die Menge ist in der Menge enthalten“ oder „Die Menge wird von umfasst.“ gesagt.
- Genauso wird statt „ ist eine Obermenge von .“ auch „Die Menge enthält die Menge .“ oder „Die Menge umfasst die Menge .“ gesagt.
- Wenn es nicht zu Missverständnissen kommen kann, wird auch „ enthält .“ usw. gesagt.
- ---
- Missverständnisse können insbesondere mit „Die Menge enthält das Element .“ entstehen.
BM1421 - BM1430
[editar]BM1421
- Wie viel?
- Aussagen darüber „wie viel“?
- Aussagen über die Menge.
- Mengenaussagen
- ---
- Bevor wir zur formalen Definition der echten und unechten Teilmenge kommen, müssen wir noch zwei neue Symbole einführen.
- ---
- (Für dieses auf den Kopf gestellte große A ließt man: „alle“.)
- Beispiel:
- (LIES: „für alle x Element der Menge A“)
- ---
- (Für dieses gespiegelte große E ließt man: „es gibt“.)
- Beispiel: (LIES: „es gibt ein x Element der Menge B“)
- ---
- Das (A) steht für All (engl. für alle).
- Das (E) steht für Existenz („es gibt“).
- ---
- Das nennt man Allquantor.
- Das nennt man Existenzquantor
- ---
- Die beiden gebräuchlichsten Quantoren sind der Existenzquantor (in natürlicher Sprache zum Beispiel als „mindestens ein“ ausgedrückt) und der Allquantor (in natürlicher Sprache zum Beispiel als „alle“ oder „jede/r“ ausgedrückt).
BM1422
- Mit dem Allquntor ( ) können wir nun die formalen Definition der echten und unechten Teilmenge vornehmen:
- ---

Abb. 1 - Abb 1: unechte Teilmenge (oft auch einfach nur als Teilmenge bezeichnet)
- Wenn und Mengen sind und jedes Element von auch ein Element von ist, nennt man eine Teilmenge von :
- (Sprich: „Alle x sind Element von A. Und alle x sind Element der Menge B.“
- ---
- Umgekehrt nennt man die Obermenge von genau dann, wenn Teilmenge von ist.
BM1423
- Eigenschaften der Teilmenge
- ---

Abb. 1 - Abb. 1: Die leere Menge ist Teilmenge jeder Menge:
- ---

Abb. 2 - Abb. 2: Jede Menge ist Teilmenge von sich selbst:
- ---

Abb. 3 - Abb. 3: Die einzige Teilmenge der leeren Menge ist die leere Menge:
- ---
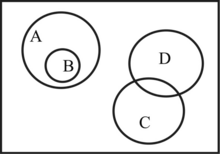
Abb. 4 - Welche Mengen erkennst du? Wie verahlten sich diese Mengen zueinander?
BM1424
- Teilmenge
- Schnittmenge
- Vereinigungsmenge
- ---
- Schnittmengen, Teilmengen und Vereinigungsmengen sind nicht nur mathematische Spielereien. Sie werden u. a. beim Entwurf von elektronischen Schaltungen benötigt.
- ---
- Beispiel 1:
- Eine Digitale Kreuzschaltung ist eine Kreuzschaltung, die mit Logikgattern realisiert wird. Bei einer Kreuzschaltung kann ein Schaltvorgang durch drei oder mehr Schalter unabhängig voneinander erfolgen, beispielsweise das An- und Ausschalten einer Lampe.
- ---
- Beispiel 2:
A B C Lampe 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1
- Eine Lampe soll durch bestimmte Muster dreier Schalter ein- oder ausgeschaltet werden. Die drei Schalter A, B und C sind entweder geschlossen (1) oder offen (0).
- ---
- Beispiel 3:
- Für Datenbankabfragen werden solche logischen Operationen sehr umfangreich eingesetzt.
- ---
- In der Mathematik sind alles Mengen.
BM1425
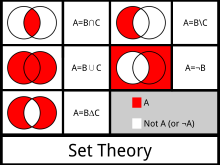
Mengentheorie - Es gibt noch 3 weitere Mengenoperationen:
- Differenz
- symmetrische Differenz
- Negation
- ---
- Differenz
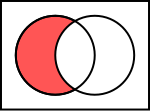
Differenz - Definition:
- LIES: Die Symmetrische Differenz ist definiert als ( := ) Menge aller „t“ für die gilt ( {t| ... } ) „t“ ist Element der Menge R oder „t“ ist Element der Menge S und „t“ ist nicht Element der Schnittmenge von R mit S.
- ---
- Die Operation kann aus den Grundoperationen abgeleitet werden:
- LIES: Die Symmetrische Differenz ist definiert als die Differenzmenge „R-S“ vereinigt mit der Differenzmenge „S-R“.
BM1426
- Beispiele für Mengenoperationen
- ---
- Wir betrachten die Mengen , und . Es gelten beispielsweise:
- ,
- , ,
- ---
- , , ,
- , ,
- ---
- Die leere Menge ist nicht Element der leeren Menge.
- Warum? - Die leere Menge in jeder Menge enthalten ist. Demnach müsste die leere Menge ja auch sich selbst enhalten. - FALSCH: Die leere Menge ist NICHT in jeder Menge (als Element) enthalten, sondern Teilmenge jeder Menge. - ABER: Wenn die leere Menge Teilmenge von jeder Menge ist, dann müsste sie doch auch ein Element davon sein. - NEIN, DENN: Die leere Menge hat überhaupt kein Element, also ist auch die leere Menge kein Element der leeren Menge. )
- Eine Menge, die nur die leere Menge als Element hat wäre {∅} also was anderes als nur ∅.
- Stellt man sich die Mengen als Kisten vor und ihre Elemente (meist sind es Zahlen) als Kugeln, dann wäre die leere Menge eine leere Kiste und die Menge {∅} wäre eine Kiste, in der sich eine weitere (leere) Kiste befindet.
- Bitte nicht durcheinander bringen und gut auseinander halten:
- a) „ist Element von“ („x ist Element von M“ oder mit Hilfe des Elementzeichens „x ∈ M“) und
- b) „ist Teilmenge von“
- Die Relation „ist Teilmenge von“ baut auf der Relation „ist Element von“ auf: Eine Menge A ist Teilmenge einer Menge B genau dann, wenn für jedes Element von A gilt, dass es auch Element von B ist.
- ---
- ---
- Und zum Schluss noch ein konkretes Beispiel:
- Die Menge aller zweistelligen „Schnapszahlen“ lautet . 33 ist ein Element dieser Menge, 23 ist es nicht.
- ---
- Das war es erst mal mit der Mengenlehre.
BM1427
- Lösen von Gleichungen der Form „a * x = b“ (a ≠ 0)
- ---
- Probieren hilft nicht immer.
- x - 3,1415 = 2,718
- ---
- Wir müssen die Gleichung a * x = b so umstellen, dass das allein auf einer Seite steht. Dazu dividieren wir beide Seiten durch a.
- a * x = b // :a
- =
- Das a auf der linken Seite können wir wegkürzen.
- Das a auf der linken Seite können wir kürzen.
- x =
- ---
- Nun geht auch die Aufgabe von oben leichter:
- x - 3{,}1415 = 2{,}718 // :
- FALSCH: Denn hier haben wir noch zusätzlich ein Subtraktion, die wir vorher los werden müssen. Also rechnen wir lieber:
- x - 3,1415 = 2,718 // + 3,1415
- x - 3,1415 + 3,1415 = 2,718 + 3,1415
- Jetzt hebt sich „- 3,1415 + 3,1415“ auf und wird Null, was wir nicht hinschreiben müssen.
- x = 2,718 + 3,1415
- Nicht vergessen: Punktrechnung vor Strichrechnung. Wir klammern die Summ auf der rechten Seite der Gleichung lieber ein, falls wir es nicht schon jetzt ausrechnen.
- x = (2,718 + 3,1415)
- Nun können wir den Trick von Oben mit der Division machen.
- x = (2,718 + 3,1415) // :
- Links kürzt sich im Zähler und Nenner weg und es bleibt nur x übrig. Das schreiben wir nicht noch mal extra auf.
- x = (2,718 + 3,1415) :
- x = (2,718 + 3,1415) *
- Jetzt brauchen wir ein großes Stück Papier oder einen Taschenrechner, falls wir nicht gut im Kopfrechnen sind.
- x = 5,8595 *
- x = 1,0254125
BM1428
- =
- Die Gleichung muss so lange umgestellt werden, bis x allein auf einer Seite steht. Üblicherweise sollte x auf der linken Seite stehen. Dann muss man nur noch die rechte Seite ausrechnen.
Lösung BM1428 - = // * x
- = // x auf der rechten Seite kürzen
- = 4 </math> // * 5
- = 4 * 5 // 5 auf der linken Seite kürzen; wir rechnen erst später aus
- 12x = 4 * 5 // : 12
- = // 12 auf der linken Seite kürzen
- x = // das rechnen wir im Kopf aus
- x = // und noch etwas kürzen
- x = // da geht noch was
- x = // fertig
- Aus jeder gegebenen lösbaren Gleichung lässt sich durch Umformen eine Gleichungder Form
- „x = c“ ode „c = x“ gewinnen, die dieselbe Lösung wie die ursprüngliche Gleichung hat.
- Diese Umformung bezeichnet man als Auflösen der Gleichung nach der betreffenden Variable.
- ---
- nach x auflösen
- die Gleichung nach x auflösen
- Lösen die gleichung nach y auf!
BM1429
- Die gesuchte Variable muss nach dem Auflösen (also nach der UmformungI isoliert auf einer Seite stehen.
- Üblicherweise ist die Variable x gesucht:
- =
- ansonsten muss angegeben werden, welche Variable gesucht ist - nach welcher Variblen also aufgelöst werden soll.
- ---
- =
- Löse nach b auf!
Lösung BM1429 - = // * b
- a = // * d
- ad = bc // : c
- = x
- x =
BM1430
- Die Division ist die Umkehrung der Multiplikation
- ---
- a) 5 * x = 35 //(1)
- b) x = 35 : 5 //(2)
- Weil die Division ist die Umkehrung der Multiplikation ist, ist Zeile b mit Zeile a identisch.
- Wir erhalten die Gleichung 2 aus der Gleichung 1, indem wir indieser beide Seiten durch 5 dividieren oder (was dasselbe ist) mit multiplizieren.
- ---
- c) 5 * x = 35 // : 5
- d) (5 * x) : 5 = 35 : 5
- e) x = 7
- ---
- oder:
- f) 5 * x = 35 // *
- g) * 5 * x = * 35
- h) x = 7
- ---
- Aus x = 7 kann man sofort ablesen, dass die Zahl 7 die Lösung der gegebenen Gleichung ist, denn 7 = 7 ist eine wahre Aussage. Deshalb betrachten wir die gegebenen Gleichung als gelöst, wenn wir sie auf diese Form gebracht haben.
- ---
- a = a
BM1431 - BM1440
[editar]BM1431
- Rechne! Mache eine Probe, wenn du das Ergebnis hast.
- ---
- a) y = 0,3
- b) 0,6t = 0,75
- c) =
BM1432
- Wir lösen Gleichungen der Form „ = b“ (a ≠ 0; b ≠ 0)
- Die Variable, nach der aufgelöst werdne soll, steht im Nenner eines Bruchs.
- a und b müssen ungeleich Null sein.
- Warum?
- Warum muss b ≠ 0 sein?
Lösung BM1432a - = b // * x
- a = b * x // : b (deshalb muss b ≠ 0 sein, denn die Division durch Null ist nicht definiert.
- = x
- Warum muss auch a ≠ 0 sein?
Lösung BM1432a - = b // * x
- a = b * x
- Wenn a = 0 wäre, also
- 0 = b * x
- dann müsste x = 0 sein, denn die Multiplikation einer beliebigen Zahl mit Null ergibt immer Null
- 0 = r * 0
- Aber x darf auch nicht Null sein, denn in der Ausgangsgleichung
- = b steht x im Nenner und bekanntlich ist die Division durch Null nicht definiert.
BM1433
- Rechne!
- ---
- a) = 5
- b) 4x = 12
- ---
- c) : x =
- d) 7a =
- ---
- e) 0,25z = 24
- f) 2,7x = 21,6
- ---
- g) = 38
- h) = 0,15
- Nachdem wir die Lösung ermitteln haben, führen wir in jedem Fall die Probe durch, indem wir die Lösung in die Ausgangsgleichung einsetzen. Dadurch vermeiden wir Rechenfehler.
BM1434
- Rechne!
- ---
- a) 3x = 9
- b) 9b =
- c) 0,5 w = 48
- --
- d) 2,3x = 18,4
- e) = 19
- f) = 0,05
BM1435
- Stelle je drei Gleichungen der Form „a * x = b“ auf, die folgende Lösungen haben!
- ---
- a) x = 2
- b) x =
- ---
- c) x =
- d) x = 3
- ---
- e) x =
- f) x =
BM1436
- Löse die folgenden Gleichungen!
- ---
- a) = 2
- b) = 1,2
- ---
- c) : x =
- d) 0,72 = 0,28 : x
BM1437
- Löse die folgenden Gleichungen!
- ---
- a) = 3
- b) = 1,5
- ---
- c) : x =
- d) 0,54 = 0,21 : x
BM1438
- Zeitreihe
- ---
- Eine Zeitreihe ist eine zeitabhängige Folge von Datenpunkten. Typische Beispiele für Zeitreihen sind Börsenkurse, Wahlabsichtsbefragungen oder Wetterbeobachtungen.
- Der Begriff Zeitreihe setzt voraus, dass Daten nicht kontinuierlich, sondern diskret - aber in endlichen zeitlichen Abständen anfallen. Aus einem zeitkontinuierlichen Messsignal (oder der kontinuierlichen Aufzeichnung eines Messsignals) kann eine Zeitreihe durch Abtastung gewonnen werden.
- ---
- Zeitreihen fallen in vielen Bereichen an.
- in der Finanzmathematik und der Finanzwirtschaft: Börsenkurse
- in der Ökonometrie: Bruttosozialprodukt, Arbeitslosenquote
- in der Biometrie: EEG
- in der Meteorologie: Temperatur, Windrichtung und -geschwindigkeit, usw.
- ---
- Zeitreihen sind Beobachtungen, die im Lauf der Zeit erhoben wurden. Bei der Analyse von Zeitreihen versuchen wir, die Beobachtungen durch den Faktor Zeit zu erklären. Wir suchen nach bestimmten Gesetzmäßigkeiten, nach denen diese Zeitreihen zustande kommen.
- Für die optische Unterstützung stellen wir eine Zeitreihe als Streudiagramm dar. Um den Verlauf, die Entwicklung des Merkmals darstellen, können wir die Punkte zu einer Kurve (Polygonzug) verbinden.
- Wir haben hier beispielsweise das Bruttoinlandsprodukt der Bundesrepublik Deutschland der Quartale 2001 bis 2005 gegeben. (Quelle: Statistisches Bundesamt Deutschland 2005)
Stichtag
Mrz 01
Jun 01
Sep 01
Dez 01
Mrz 02
Jun 02
BIP
514,51
522,63
531,51
544,91
519,19
531,66
Stichtag
Sep 02
Dez 02
Mrz 03
Jun 03
Sep 03
Dez 03
BIP
546,06
551,9
524,4
533,59
550,76
556,12
Stichtag
Mrz 04
Jun 04
Sep 04
Dez 04
Mrz 05
BIP
537,36
547,85
557,21
564,82
539,78

Zeitreihe des deutschen Bruttoinlandsprodukts (Milliarden €) für die Quartale der Jahre 2001 bis 2005
BM1439
- Bei wissenschaftlichen Untersuchungen, z. B. in der Physik oder der Chemie, werden häufig Messungen vorgenommen.
- ---
- Beispiel:
- Messung der Wassertemperatur während des Erwämens von Wassers. Um die Messpunkte besser auswerten zu können, ordnet man sie übersichtlich in Form einer Tabelle an.
- Wenn wir die Einzelmessungen nummerieren, erhalten wir eine Tabelle, die etwa folgendermaßen aussieht:
Laufende Nummer
der Messung1
2
3
4
5
6
7
8
9
10
Temperatur
in °C49,1
56,7
62,3
70,4
80,0
88,2
94,5
98,3
100,0
100,0
- Durch diese Messreihe wird jeder Nummer einer Messung, d. h. jeder natürlichen Zahl von 1 bis 10, eine gebrochene Zahl als Maßzahl der betreffenden Temperatur zugeordnet. Dabei sind die Messwerte, also die zugeordneten Zahln, nicht unbedingt auch natürliche Zahlen. Das richtet sich nach der jeweiligen Messgenauigkeit.
BM1440
- Maßzahl
- Maßeinheit
- ---
- 16,7 °C
- Maßzahl: 16,7
- Maßeinheit: °C
- 5 m
- 33 min
- 7,3 kg
BM1441 - BM1450
[editar]BM1441
- Zahlenfolge
- kurz: Folge
- ---
- Beispiel:
- Folge der Primzahlen: (2; 3; 5; 7; 11; 13; ...)
- Folge der geraden Zahlen: (2; 4; 6; 7; 8; 10; 12; ...)
- Folge der natürlichen Zahlen: (1; 2; 3; 4; 5; 6; 7; ...)
- ---
- Bei einer Folge ist die Reihenfolge der Elemente einer Folge genau festgelegt. Es gibt eine genau definierte Anordnung der Folgenglieder.
- Definition einer Folge:
- Für eine Folge schreibt man oder kurz .
- Meist wird der Buchstabe „i“, „n“ oder „k“ als Indexvariable benutzen.
- Man kann dementsprechend auch die Schreibweisen oder verwenden.
- das Folgeglied: Ein Folgenglied ist ein konkretes Element einer Folge. (an; ai oder ak)
- ---
- Beispiel:
- Die Folge der Quadratzahlen ist:
- ---
- Die einzelnen Elemente einer Folge werden Folgenglieder genannt. Die zu den einzelnen Folgengliedern zugeordneten natürlichen Zahlen nennt man Index. So ist beispielsweise das Folgenglied zum Index 4.
BM1442
- Bildungsgesetz einer Folge:
- Es gibt mehrere Möglichkeiten eine Folge anzugeben:
- a) Nennen aller Folgenglieder (nur für endliche Folgen möglich)
- b) Funktion (beispielseise: x = i * 2 + 0,5)
- c) Reihe
- d) Rekursion (Vorschrift, wie ein Folgenglied ai aus den vorhergehenden m berechnet werden kann. Beispiel: Fibonacci-Folge - siehe nächste Übung)
- e) Algorithmus
- ---
- zu e) Angabe über einen Algorithmus:
- Für manche Folgen gibt es eine klar definierte Konstruktionsvorschrift (Algorithmus), aber keine Funktionsvorschrift. Das bekannteste Beispiel ist die Folge der Primzahlen 2, 3, 5, 7, 11, ... Bereits den alten Griechen (möglicherweise auch Indern) war es bekannt, wie man immer weitere Glieder dieser Folge berechnet. Eine Möglichkeit ist, das Sieb des Eratosthenes anzuwenden. Es gibt jedoch keine Methode, zu einem gegebenen die -te Primzahl anzugeben, ohne zuvor die gesamte Folge von der ersten bis zur -ten Primzahl zu bestimmen. Wenn man nicht die zehnte oder die hundertste, sondern die -te Primzahl wissen möchte, erhöht dies den Rechenaufwand stark.
- ---
- zu a) Eine endliche Folge kann man angeben, indem man sämtliche Folgenglieder nennt. Bei einer unendlichen Folge geht das nicht, stattdessen muss man das Bildungsgesetz der Folge in anderer Form mitteilen.
- ---
- Folgen, deren Bildungsgesetz sich als Funktionsvorschrift oder Rekursion mitteilen lässt, werden zuweilen regelmäßige Folgen genannt.
BM1443
- Fibonacci-Folge
- ---
- Das bekannteste Beispiel für eine Folge, die sich wesentlich einfacher durch eine Rekursionsvorschrift als durch eine Funktionsvorschrift beschreiben lässt, ist die Fibonacci-Folge 0, 1, 1, 2, 3, 5, 8, ... Für sie ist , gegeben sind die zwei Anfangsglieder und sowie die Rekursionsvorschrift
- ---
- Die Fibonacci-Folge ist die unendliche Folge von natürlichen Zahlen, die (ursprünglich) mit zweimal der Zahl 1 beginnt oder (häufig, in moderner Schreibweise) zusätzlich mit einer führenden Zahl 0 versehen ist. Im Anschluss ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die unmittelbar danach folgende Zahl:
 |
- Die darin enthaltenen Zahlen heißen Fibonacci-Zahlen. Benannt ist die Folge nach Leonardo Fibonacci, der damit im Jahr 1202 das Wachstum einer Kaninchenpopulation beschrieb. Die Folge war aber schon in der Antike sowohl den Griechen als auch den Indern bekannt.
- Weitere Untersuchungen zeigten, dass die Fibonacci-Folge auch noch zahlreiche andere Wachstumsvorgänge der Pflanzen beschreibt. Es scheint, als sei sie eine Art Wachstumsmuster in der Natur.
- Die Fibonacci-Zahlen weisen einige bemerkenswerte mathematische Besonderheiten auf:
- Aufgrund der Beziehung zur vorherigen und zur folgenden Zahl scheint Wachstum in der Natur einem Additionsgesetz zu folgen.
- Die Fibonacci-Folge steht in einem unmittelbaren Zusammenhang zum Goldenen Schnitt. Je weiter man in der Folge fortschreitet, desto mehr nähert sich der Quotient aufeinanderfolgender Zahlen dem Goldenen Schnitt (1,618033...) an (beispielsweise 13:8=1,6250; 21:13=1,6154; 34:21=1,6190; 55:34=1,6176; etc).
- Diese Annäherung ist alternierend, d. h. die Quotienten sind abwechselnd kleiner und größer als der Goldene Schnitt.
BM1444
- Beispiel 1:
- Jeder natürlichen Zahl n (n>0) soll ihre Hälfte zugeordnet werden.
natürliche Zahl (n)
1
2
3
4
5
6
7
...
Hälfte der
nat. Zahl
( * n)...
- ---
- Beispiel 2:
n
1
2
3
4
5
6
7
8
9
10
11
12
20 - n
19
18
17
16
15
14
13
12
11
10
9
8
- In einer Folge hat jede Zahl entsprechend ihrer Position eine Nummer.
- Meist wird der Buchstabe „i“, „n“ oder „k“ als Indexvariable benutzen, um diese Nummer anzugeben.
- Die Indexvariable beginnt bei „1“ für die erste Zahl der Folge.
- Für Beispiel 2 kann man also angeben:
- a1 = 19; a3 = 17; a11 = 9
- ---
- Wenn wir die zugeordneten Zahlen in der Reihenfolge ihrer Nummerierung aufschreiben, so erhalten wir eine Zahlenfolge.
- Jedes Zahl einer Zahlenfolge heißt Glied einer Zahlenfolge.
- Die Nummer eines Gliedes ist diejenige natürliche Zahl, der dieses Glied zugeordnet ist.
- ---
- In der Folge (Beispiel 1) ; ; ; ; ; ; ; ...
- ist das Glied mit der Nummer 5.
BM1445
- In der Mathematik spricht man meist nur dann von Zahlenfolgen, wenn jeder natürlichen Zahl eine Zahl zugeordnet ist, wenn es also kein letztes Glied in der Zahlenfolge gibt.
- Auch die Dezimalstellen eines periodischen Deszimalbruchs bilden z. B. eine solche Zahlenfolge:
- Beispiel:
- 0,34260 34260 34260
- 0,34260
- (a) = (3; 4; 2; 6; 0; 3; 4; 2; 6; 0; 3; 4; 2 ... )
BM1446
- Gib von den folgenden Zahlenfolgen jeweils die ersten acht Gleider sowie das 10., 12. und 15. Glied an!
- ---
- a) Jeder natürlichen Zahl wird ihr Doppeltes zugeordnet.
- b) Jeder natürlichen Zahl wird ihr Dreifaches zugeordnet.
- c) Jeder natürlichen Zahl wird die Zahl zugeordnet, die man erhält, wenn man sie mit multipliziert.
- ---
- d) Jeder natürlichen Zahl wird die Zahl zugeordnet, die man erhält, wenn man sie mit multipliziert.
- e) Jeder natürlichen Zahl wird ihr Dreifaches, vermindert um 2,5 , zugeordnet.
- f) Jeder natürlichen Zahl wird ihr Doppeltes, vermindert um 1,5 , zugeordnet.
- ---
- g) Jeder natürlichen Zahl wird ihr Quadrat zugeordnet.
- h) Jeder natürlichen Zahl wird ihre dritte Potenz zugeordnet.
BM1447
- Proportionalität
- proportional
- ---
- Zwischen zwei veränderlichen Größen besteht Proportionalität, wenn sie immer in demselben Verhältnis zueinander stehen.
- ---
- Proportionale Größen sind verhältnisgleich, das heißt, bei proportionalen Größen ist die Verdopplung (Verdreifachung, Halbierung, …) der einen Größe stets mit einer Verdopplung (Verdreifachung, Halbierung, …) der anderen Größe verbunden, oder allgemein gesagt: Die eine Größe geht aus der anderen durch Multiplikation mit einem immer gleichen Faktor hervor. Das Verhältnis der beiden Größen wird Proportionalitätsfaktor oder Proportionalitätskonstante genannt.
- ---
- y = 5,3 * x
- ---
- Wir wollen Zahlenfolgen miteinander vergleichen, indem wir jeweils die einander entsprechenden Glieder der Zahlenfolgen miteinander vergleichen.
- Deshalb sollen diejenigen Glieder einander entsprechen, die inner halb der Zahlenfolge die gleich Nummer haben.
BM1448
- Proportionalität
- ---
- Beispiel 1:
1. Folge
5
10
15
20
25
30
2. Folge
7
13
19
25
31
37
- Beispiel 2:
1. Folge
2
4
6
8
10
12
2. Folge
4
8
12
16
20
24
- In beiden Beispielen ist jedes Glied der zweiten Folge größer als das entsprechende Glied der ersen Folge.
- Im Beispiel 2 erhalten wir jedes Glied der zweiten Folge durch Multiplikation des entsprechenden Gliedes der ersten Folge mit 2.
- oder umgekehr: Jedes Glied der ersten Folge ergibt sich durch Multiplikation des entsprechenden Gliedes der zweiten Folge .
- Das ist in der Folge in Beispiel 1 nicht der Fall.
- Die Beziehungen zwischen den beiden Folgen im Beispiel 2 heißt Proportionalität.
BM1449
- Proportionalität
- ---
- Beispiele:
- Bei einem Kauf ist die Mehrwertsteuer proportional dem Nettopreis; der Proportionalitätsfaktor ist der Mehrwertsteuersatz, beispielsweise 0,19 (=19 Prozent).
- Die Masse einer Flüssigkeit ist proportional ihrem Volumen.
- ---
- y = m * x
- Proportionalitätsfaktor m
- ---
- Proportionalität liegt genau dann vor, wenn dieses Verhältnis m konstant ist.
- ---
- Für „a proportional zu b“ verwendet man das Tilde-Zeichen „~“.
- ---
- Definition:
- Zahlenfolgen heißen zueinander proportional, wenn sich jedes Glied der einen Folge aus dem entsprechenden Glied der anderen Folge durch Multiplikation mit einem einheitlichen Faktor ergibt. Dieser Faktor heißt Proportionalitätsfaktor.
- ---
- Um festzustellen, ob zwei Zahlenfolgen zueinander proportional sind, bilden wir die Quotienten je zweier entsprechender Glieder. Sind diese Quotienten alle einander gleich, so sind die Zahlenfolgen zueinander proportional.
BM1450
- Stelle fest, welche der gegebenen Faktoren zueinandner proportional sind! Gib den Proportionalitätsfaktor an!
- ---
- a)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
- ---
- b)
0,2
4
10
0,175
- índice
- Lección 078b ← Lección 079b → Lección 080b







![{\displaystyle x^{2}\leq 4\qquad L=[-2;2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f836f63bbfc7073f9f3064e83a010629abcb93e)