Matemáticas/Bachillerato LOGSE/Combinatoria
La combinatoria estudia las diferentes formas en que se pueden agrupar u ordenar los elementos de un conjunto. El punto de partida será el principio de la multiplicación o estrategia del producto.
Principio de la multiplicación o estrategia del producto[editar]
- Ejemplo 1: Un equipo de baloncesto tiene que elegir un nuevo uniforme. Para ello debe escoger entre 4 camisetas y 5 pantalones con diferentes colores. ¿Cuántos uniformes distintos se pueden componer con las camisetas y pantalones disponibles?
- Para resolver este problema hemos de tener en cuenta que cada una de las camisetas se podrá combinar con cada uno de los pantalones disponibles. Si tuviéramos una única camiseta, podríamos componer 5 uniformes diferentes, resultado de combinar dicha camiseta con cada uno de los 5 pantalones. Si tuviéramos 2 camisetas, podríamos componer 5 uniformes distintos para cada camiseta, resultado de combinar cada camiseta con cada uno de los 5 pantalones. Tendríamos por tanto 2 · 5 = 10 combinaciones posibles. Siguiendo el mismo razonamiento, llegaríamos a la conclusión de que con 4 camisetas y 5 pantalones, podríamos componer 4 · 5 = 20 uniformes diferentes.
Lo que hemos utilizado es lo que se conoce con el nombre de principio de la multiplicación, que puede enunciarse de la siguiente forma:
| Principio de la multiplicación. Si tenemos a opciones para escoger un objeto, b opciones para elegir un segundo objeto, c opciones para escoger un tercero, etc., el número total de formas de combinar los distintos objetos es el producto a · b · c · ..... |
- Ejemplo 2: ¿Cuántos números de tres cifras se pueden formar con los dígitos 0, 1, 2, 3 y 4, sin que se repita ninguna cifra?
- Las opciones para escoger la primera cifra son cuatro, pues ésta no puede tomar el valor 0, ya que ningún número de tres cifras comienza por 0. Para la segunda cifra tendremos también cuatro opciones, pues aunque en este caso si puede tomar el valor 0, tendremos que descartar el valor que haya tomado la primera cifra, por no poderse repetir ninguna. Por último, para la tercera cifra tendremos tres opciones, resultado de descartar los valores empleados en las dos primeras cifras, para evitar repeticiones.
- Por tanto, aplicando el principio de la multiplicación, se obtiene que hay 4 · 4 · 3 = 48 números de tres cifras distintos con los dígitos indicados en el enunciado.
Diagrama de árbol[editar]
Un diagrama de árbol es una representación gráfica que ilustra las formas en las que se llevan a cabo las agrupaciones de elementos. Volviendo al ejemplo 1, si llamamos a las diferentes camisetas y a los distintos pantalones, obtendríamos el diagrama de árbol que se muestra en la figura 1. Si contamos los resultados, comprobamos que obtenemos los 20 que indicaba el principio de la multiplicación.
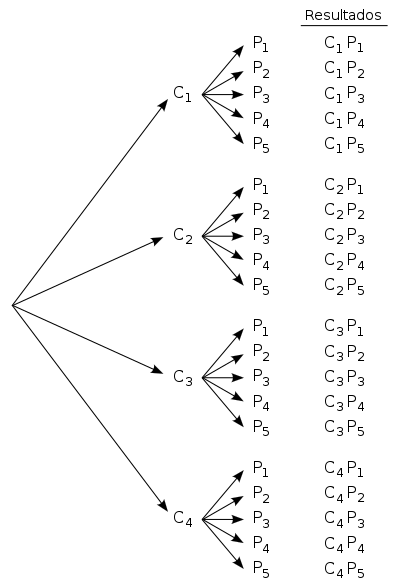
En los diagramas de árbol se emplea una nomenclatura propia, que describimos a continuación:
- Árbol: es el diagrama completo.
- Raíz: es el punto en el cual se origina el árbol. En la figura 1, la raíz sería el punto desde donde parten las cuatro flechas que llegan hasta las cuatro opciones de camiseta.
- Ramas: son las distintas bifurcaciones. En la figura 1 se corresponden con las flechas del gráfico.
- Nodos o nudos: son los puntos desde los que surgen nuevas bifurcaciones. En la figura 1, los nodos serían los puntos en los que tenemos las 4 opciones de camiseta: .
- Hojas: son los puntos finales, desde los cuales no surgen nuevas bifurcaciones. En la figura 1, las hojas son los puntos correspondientes a las 5 opciones de pantalón (todos los nombrados como , 20 puntos en total).
- Nivel: es el número de ramas que separa a un nodo u hoja de la raíz. La raíz corresponde al nivel 0 y, en la figura 1, las opciones de camiseta estarán en el nivel 1 y las de pantalón en el nivel 2.
- Camino: es cualquier recorrido por las ramas del árbol, desde la raíz hasta alguna de sus hojas. En la figura 1 tenemos 20 caminos diferentes.
Variaciones sin repetición[editar]
- Ejemplo 3: En una carrera de natación participan 8 nadadores. ¿De cuántas formas posibles pueden ocuparse los tres primeros puestos?
- Veamos las posibles opciones: Cualquiera de los nadadores participantes podría ser el primero, por lo que el número de opciones para escoger al primero es 8. El segundo puesto lo podría ocupar cualquiera de los nadadores restantes; por tanto, el número de opciones en este caso será 7. Por último, el tercer puesto lo podría ocupar cualquiera de los nadadores que no haya sido primero ni segundo; en este caso las opciones serán 6. Aplicando el principio de la multiplicación, habría 8 · 7 · 6 = 336 posibilidades distintas.
- A cada grupo de 3 nadadores, de los 336 posibles, le llamaremos variación de 8 elementos tomados de 3 en 3.
| Variaciones sin repetición o variaciones ordinarias de m elementos tomados de n en n (n m), son los distintos grupos de n elementos no repetidos que se pueden formar, escogidos de entre los m elementos posibles, de forma que en cada grupo haya algún elemento distinto, o tenga los mismos elementos que otro grupo, pero colocados en distinto orden. Cada uno de los posibles grupos es una variación. Se representa por o . |
Como el primero de los elementos puede ser cualquiera de los m disponibles, el segundo cualquiera de los (m – 1) restantes, el tercero cualquiera de los (m – 2) que quedan y así sucesivamente, aplicando el principio de la multiplicación se obtiene:
|
|
Permutaciones sin repetición. Factorial[editar]
Factorial[editar]
|
Sea el número natural n mayor que 1. Se conoce como factorial de n, y se representa por n!, al producto de los n primeros números naturales: |
Por convenio se definen 1! = 1 y 0! = 1 (son excepciones a la definición, ya que en ambos n no es mayor que 1).
- Ejemplo 4:
- 3! = 3·2·1 = 6
- 5! = 5·4·3·2·1 = 120
- 1! = 1
Teniendo en cuenta la definición de factorial de un número, se puede escribir la expresión para la obtención de las variaciones de m elementos tomados de n en n, de la siguiente forma:
|
|
Permutaciones sin repetición[editar]
- Ejemplo 5: En el bombo de un juego de lotería, quedan 5 bolas. ¿De cuántas formas podrán salir las cinco bolas?
- La primera bola en salir podrá ser cualquiera de las 5. La segunda bola tendrá que ser una cualquiera de las 4 restantes, etc. Si aplicamos a este problema la definición de variación sin repetición que ya hemos visto, se obtiene que las formas posibles de salir las bolas son:
En este caso, vemos que en todas las variaciones intervienen todos los elementos, y que la única diferencia entre una variación y otra está en el orden de dichos elementos. A las variaciones de n elementos tomados de n en n, se las llama permutaciones de n elementos.
|
Permutaciones ordinarias de n elementos son las distintas formas de ordenar dichos elementos. Cada forma de ordenarlos es una permutación. El número de permutaciones de n elementos se representa por , y su valor es: |
Permutaciones circulares[editar]
- Ejemplo 6: ¿De cuántas formas pueden colocarse 7 niños formando un círculo?
- Hay que tener cuidado, ya que no se trata de ordenar simplemente a los 7 niños, pues hay que tener en cuenta que si desplazamos a todos los niños un lugar hacia la derecha, se obtiene una ordenación idéntica a la anterior. En este caso no nos interesa la posición exacta de los niños dentro del círculo, sino la posición relativa entre ellos (no existe un primer niño, ni un último). Cuando el único orden que interesa es el orden relativo entre los n elementos, se dejará fijo a uno de los elementos y se permutará el resto de elementos de todas las formas posibles.
- Operando de esta forma se obtiene que el número de formas de posicionarse es:
|
A estas permutaciones se las llama permutaciones circulares de n elementos: |
Cuando no importa el orden. Combinaciones[editar]
Combinaciones sin repetición[editar]
- Ejemplo 7: A un concursante en un programa de televisión, le dejan elegir 3 regalos entre los siguientes: lavadora, frigorífico, lavavajillas, motocicleta, televisor y viaje. ¿Cuántas posibilidades de elección tiene el concursante?
- Se podría pensar en un principio, que se trata de las variaciones de 6 elementos tomados de 3 en 3, pero hay que tener en cuenta que hay distintas variaciones que dan lugar a la misma elección del concursante.
- Considérese el caso en que el concursante elige la motocicleta, el televisor y el viaje. Dentro del conjunto de todas las variaciones, dicha elección estaría repetida 3! = 6 veces, que son las distintas formas de ordenar dichos regalos. Por tanto, tendríamos que dividir el número de variaciones, entre el número de ordenaciones posibles de los regalos elegidos. En este caso:
|
Combinaciones ordinarias o combinaciones sin repetición de m elementos tomados de n en n (n m) son los distintos grupos que se pueden formar con los m elementos disponibles, de modo que en cada grupo haya n elementos distintos. En este caso para que dos grupos sean distintos, han de tener algún elemento diferente; no basta con que tengan distinto orden de colocación. Se representa por o y su valor viene dado por:
|
Números combinatorios[editar]
El número se conoce también como número combinatorio .
Propiedades de los números combinatorios[editar]
1.
- Demostración:
2.
- Demostración:
3.
- Demostración:
Triangulo de Tartaglia[editar]
A partir de las propiedades de los números combinatorios, se puede construir el llamado triángulo de Tartaglia o de Pascal, que permite obtener los valores de los números combinatorios sin necesidad de realizar las operaciones de la fórmula. Para obtener el triángulo se interpretan las propiedades de los números combinatorios de la siguiente forma:
- 1.Los extremos de las filas del triángulo toman el valor 1 (propiedad 1).
- 2.Todas las filas del triángulo son simétricas (propiedad 2).
- 3.Cada número se obtiene mediante la suma de los dos que tiene encima en el triángulo, excepto los extremos, cuyo valor es 1, según se indicó en el punto 1 (propiedad 3).
Con esto es muy sencillo construir el triángulo para las primeras filas. En la figura 2 se muestra el triángulo para las 10 primeras filas.
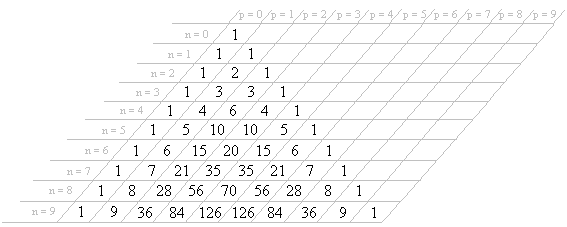
El valor correspondiente al número combinatorio , será el que se encuentra en la fila n y columna p del triángulo.
Así estaría en la fila n = 7 y p = 4, luego sería igual a 35.
Variaciones con repetición[editar]
- Ejemplo 8: ¿Cuántos números de tres cifras se pueden formar con los dígitos 1, 2, 3, 4 y 5?
- La primera cifra podrá ser una cualquiera de las 5. La segunda cifra también podrá ser una cualquiera de las cinco ya que puede repetirse, y lo mismo ocurre para la tercera cifra. Aplicando el principio de multiplicación, hay 5 · 5 · 5 = 125 números de tres cifras.
- Vemos que en este caso importa el orden, pues aún teniendo las mismas cifras, 123 y 231 son números diferentes. Además se han tomado 3 elementos de entre los 5 posibles, luego son variaciones, pero en este caso se puede elegir un elemento de los 5 más de una vez. A este tipo de variaciones se las llama variaciones con repetición.
|
Variaciones con repetición de m elementos tomados de n en n, son los distintos grupos de n elementos repetidos o no que se pueden formar, escogidos de entre los m elementos posibles. En este caso, dos grupos son distintos si tienen algún elemento diferente o si, siendo todos los elementos iguales, están colocados con distinto orden. Se representa por ó . |
Permutaciones con repetición[editar]
- Ejemplo 9: ¿Cuántas palabras de 5 letras, con sentido o sin él, se pueden formar con tres A y dos B?
- Se trata en este caso de obtener las distintas ordenaciones posibles de AAABB. Si las A fuesen distinguibles entre sí, y lo mismo ocurriera con las B, se trataría de ordenar 5 elementos distintos y estaríamos ante el caso de las permutaciones sin repetición visto anteriormente.
- Al ser indistinguibles, muchas de las permutaciones consideradas serán idénticas. Veamos, por ejemplo, el caso en que las 3 A aparezcan al principio de la palabra; la diferencia entre los casos en que las letras sean distinguibles e indistinguibles se recogen en la tabla siguiente (las hemos hecho distinguibles dotándolas de un subíndice).
| Indistinguibles | Distinguibles |
|---|---|
- Vemos que para el caso de las letras distinguibles, el número de palabras resulta de multiplicar las permutaciones de por las de , obteniéndose que el número de permutaciones es 3! · 2! = 12 , de las cuales sólo tenemos que considerar 1. Hemos considerado el caso en que las 3 A aparezcan al principio de la palabra; considerando todos los demás casos obtendremos que el número de palabras es
A partir del ejemplo anterior llegamos a la siguiente definición:
|
Dados n elementos, de los cuales el primer elemento se repite a veces, el segundo b veces, ..., el último r veces (a + b + ..... + r = n), llamaremos permutaciones con repetición de esos n elementos a los distintos grupos que se pueden formar, de forma que en cada grupo de n elementos, el primer elemento esté repetido a veces, el segundo b veces, ..., el último r veces. La única diferencia entre los grupos está en el orden de colocación de sus elementos distinguibles. El número de permutaciones con repetición de n elementos se representa por
|
Procedimiento para resolver problemas de combinatoria[editar]

El algoritmo representado en la figura 3 puede resultar de ayuda en la resolución de problemas de combinatoria. Partiremos del símbolo con la leyenda Inicio y seguiremos un camino que será función de las respuestas que demos a las preguntas de los rombos por los que pasemos. El camino concluye al llegar a uno de los rectángulos que nos indican el tipo de agrupamiento.
- Ejemplo 10: Utilizaremos el procedimiento de la figura 3 para resolver el problema del ejemplo 9.
- Partimos del inicio y descendemos a la primera pregunta: ¿Importa el orden? La respuesta en este caso es Sí, puesto que no es lo mismo AAABB que ABAAB.
- Seguimos la flecha correspondiente a la respuesta Sí y llegamos a la segunda pregunta: ¿Hay que utilizar todos los elementos? La respuesta vuelve a ser Sí, pues así nos lo indicaban en el enunciado del ejemplo 9.
- Seguimos de nuevo la flecha correspondiente a la respuesta Sí y llegamos a la tercera pregunta: ¿Hay elementos indistinguibles? La respuesta es de nuevo Sí, como ya se vió en el ejemplo 9.
- Siguiendo por último la flecha correspondiente a la respuesta Sí, llegamos al rectángulo que nos indica que se trata de Permutaciones con repetición.
- Ejemplo 11: Utilizaremos el procedimiento de la figura 3 con el problema del ejemplo 7.
- Partimos del inicio y descendemos a la primera pregunta: ¿Importa el orden? La respuesta en este caso es No, puesto que cuando el concursante elige tres regalos, pongamos por caso que sean lavadora, frigorífico y lavavajillas, el conjunto de premios que se llevará el concursante será el mismo, idependientemente de la forma en que se ordenen dichos premios.
- Siguiendo la flecha correspondiente a la respuesta No, llegamos al rectángulo que nos indica que se trata de Combinaciones.
Potencias de un binomio. Teorema del binomio[editar]
El Teorema del binomio de permite desarrollar la potencia de una suma o diferencia de dos monomios.[1]
Siendo .
Demostración[editar]
Demostraremos la fórmula anterior por inducción sobre N.
Base de inducción[editar]
Comprobamos que la fórumula se verifica para n = 1:
Paso de inducción[editar]
Se trata de comprobar que, si la fórmula se verifica para el valor n, entonces se verifica para n + 1.
Puesto que , se tiene
[...]
Importante[editar]
El teorema del binomio dio un vuelco cualitativo cuando el exponente de la potencia de un binomio , se considera un número racional; obviamente con una cantidad infinita de términos, si se trata de exponentes enteros negativos o números fraccionarios, y, correlativamente, los los números combinatorios que se se usan en dichos casos, difieren del típico número combinatorio de enteros no negativos.<ref> Banach, Stefan: "Cálculo diferencial e integral", ISBN 968-18-3949-8, (1991)
Notas y referencias[editar]
- ↑ A Isaac Newton le cupo ampliar para potencia racional que es un desarrollo infinito




























































