Matemáticas/Bachillerato LOGSE/Funciones
Concepto de función
[editar]Tipo de relación donde dada una variable o cantidad y procesada de acuerdo a unas condiciones preestablecidas da como resultado un único resultado.

Ej. Dado cualquier número se elevara al cuadrado y al resultado se le restara uno. Con este ejemplo de función se puede realizar la siguiente tabla donde los datos de la primera columna son datos arbitrarios y la segunda columna son datos obtenidos al procesar el dato de la izquierda.
| X | Y |
|---|---|
| 2 | 3 |
| 3 | 8 |
Observamos que a los datos de entrada se les llamó X y a los de salida se les llamó Y, entonces podemos escribir una formula que muestre lo anteriormente expresado: donde X es cualquier número, é Y es el valor que se obtiene al remplazar la X por el valor arbitrario.
Para dar una mayor idea al respecto y esperando que se profundice en el tema, diremos que una función es como una maquina que siempre le hace a lo que le introduzcan lo mismo, claro que de acuerdo a lo que le introduzcan dará un resultado diferente.
Producto inicial
(x) » » »
(función) Producto final
(y).
El anterior esquema representa un proceso industrial, matemáticamente podríamos decir que el producto inicial es como el valor izquierdo de la tabla, los valores de X; el producto final será el valor de Y que es lo que sale de la maquina, y finalmente la maquina será la función, la que convierte mediante un proceso propio de cada maquina un producto inicial en otro final.
Dominio de definición de una función
[editar]El dominio de una función es el conjunto de valores que pueden entrar para operar. Es decir, los valores que puede tener la variable independiente.
tiene como dominio todo número real ademas cuando tiene en coma.
tiene como dominio todo número real positivo incluído el cero
Discontinuidades. Continuidad
[editar]Una función es continua en un punto si, y solo si el límite de la función cuando tiende a tal punto tanto por la derecha y por la izquierda es el mismo, y es igual al valor que toma la función a tal punto.
La función es continua en el punto si se cumple la siguiente condición:

En caso de no cumplirse esta condición, la función es discontinua. Dicha discontinuidad puede ser evitable, si existen los límites por la derecha y por la izquierda (y son iguales, por lo tanto, existe el límite), pero no coinciden con el valor de la función (en tal caso, bastaría definir una nueva función "a trozos", de manera que se asignase el valor de los límites a la función en el punto para que esta fuese contínua), o inevitable, caso de que no existan o sean distintos.
La discontinuidad evitable también aparece cuando existe el límite y existe la imagen pero son diferentes.
Límites en un punto
[editar]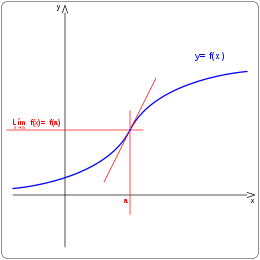
Una función f(x) es continua en un punto x=a si se cumplen la siguientes condiciones:
- Que el punto x=a tenga imagen.
- Que exista el límite de la función en el punto x=a.
- Que la imagen del punto coincida con el límite de la función en el punto.
Cálculo de límites cuando x -> a
[editar]Cálculo del límite de un cociente de polinomios cuando x -> a
[editar]Comportamiento de una función cuando x -> infinito
[editar]El comportamiento de una función cuando x tiende a son los distintos valores del , estos pueden ser ó . Si la función es un polinomio , siendo k el grado del polinomio,serà cuando , independiente si k es par o impar, y será cuando y k impar y será cuando y k par.
Ramas infinitas y asíntotas
[editar]En el estudio de la función, es importante analizar los puntos en los que esta tiende hacia el infinito (ramas infinitas), o las direcciones constantes que toma al alejarse hacia o (caso de que las haya). Una buena forma de enfocar este estudio podría ser el siguiente: localizar los puntos singulares de la función (denominador que se anula, logaritmo negativo ...), estudiar el límite en y por último buscar asíntotas verticales.
Asíntotas Verticales: Indican un valor a de la variable independiente x, tal que . Si ya hemos hecho un análisis del dominio de la función, encontrarlas es mucho más facil; son los ceros del denominador, los puntos en los que el argumento de un logaritmo se anula ... Para la posterior representación gráfica, es recomendable dibujar con trazo discontínuo las A. V. como rectas
Asíntotas Horizontales: Son tales que . Intuitivamente, es el valor al que se va acercando la función al crecer el valor de la variable independiente. Análogamente al caso anterior, es recomendable dibujar con trazo discontínuo la A.H. como una recta .
Asíntotas Oblícuas: a una dirección constante en el plano cartesiano. Para ello, es necesario calcular dos límites, que nos proporcionan diversa información:
- . Si , se trata de una rama parabólica de dirección OY; si es una rama infinita de dirección OX. Si , es una rama asintótica de pendiente k.
- Para determinar completamente dicha asíntota, tenemos que obtener el límite .
La asíntota será la recta de ecuación .
Comportamiento de una función cuando
[editar]Se calcula exactamente igual que cuando X-> infinito, pero teniendo en cuenta las reglas de los signos (ya sea suma, resta, multiplicación, división, potencia o raíz).