Los cuerpos redondos son aquellos que tienen, al menos, una de sus caras o superficies de forma curva.

Cilindro

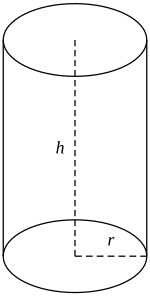
En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, denominada directriz del cilindro.

Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gausiana.

En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparamétrica de líneas paralelas.

Clasificación

Un cilindro puede ser: Su clasificación por la inclinación del eje, es decir del ángulo formado por la generatriz, los cilindros se clasifican en:

cilindro rectangular: si el eje del cilindro es perpendicular a las bases.
cilindro oblicuo: si el eje no es perpendicular a las bases.
cilindro de revolución: si está limitado por una superficie que gira 360° grados.

Superficie cilíndrica

La superficie cilíndrica está conformada por rectas paralelas, denominadas generatrices, las cuales contienen los puntos de una curva plana, denominada directriz del cilindro. La superficie lateral cilíndrica se obtiene mediante el giro de una recta alrededor de un eje.

Las superficies cilíndricas pueden ser

superficie cilíndrica de revolución: si todas las generatrices equidistan de un eje, paralelo a ella,
superficie cilíndrica de no revolución: si no existe un eje que equidiste de las generatrices.

Área de la superficie cilíndrica

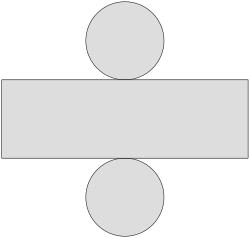
La superficie de un cilindro circular recto está conformada por el área de la base, circular en este caso: A = π r², pero como este cilindro tiene 2 bases se multiplica por 2, siendo el área total de las dos bases: A_b = 2 π r²

Además, el área lateral está formada por un rectángulo de altura "h" y de largo del perímetro del círculo L = 2 π r por lo que el área lateral es: A_l = 2 π r h

Por lo tanto, el área total, o área de la superficie cilíndrica es:

A = A_b + A_l

A = 2 π r² + 2 π r h

A = 2 π ( r² + r h )

A = 2 π r ( r + h )

Volumen del cilindro

El volumen de un cilindro es el producto del área de la base "A_b" por la altura del cilindro "h"

El volumen de un cilindro de base circular, es:

V = π r ²·h

Siendo la altura del cilindro la distancia entre las bases.

Cono

En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al punto donde confluyen las generatrices se llama vértice o cúspide.

Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.

Elementos

Directriz

Es una curva plana, por cuyos puntos pasa una recta que también pasa por un punto fijo.

Generatriz

Es la recta que pasa por el punto fijo y un punto de la directriz, la unión de estas rectas constituye la superficie cónica.

Base

Si la directriz es una circunferencia, el sólido limitado por la respectiva superficie cónica y el círculo que clausura la circunferencia se llama cono circular recto. Y el círculo respectivo se llama base del cono.

Vértice

Es el punto fijo exterior al plano de la directriz. Ordinariamente, las respectivas semirrectas originadas por el vértice, generan dos partes de la superficie llamadas mantos.

Altura

En un caso restringido de que un triángulo rectángulo ( como subconjunto bidimensional) gire en torno de uno de sus catetos, y se engendra un cono circular recto. Justamente, el cateto eje se llama, tanto como segmento y cuanto en medida altura del cono.

Cono (sólido geométrico)

Usualmente, se considera un círculo y un punto exterior al plano del círculo. La unión de todos los segmentos de extremo en un punto del círculo y extremo común, el punto exterior, se llama cono, considerado como un sólido geométrico.^[1]^[2]

Propiedades

Área de la superficie cónica

El área $A\,$ de la superficie del cono recto es:

A=A_{Base}+A_{Lateral}=\pi r^{2}+\pi ra\,\!

donde r es el radio de la base y a la longitud de la generatriz del cono recto.

La generatriz de un cono recto del triángulo rectángulo que conforma con la altura del cono y el radio de la base;

su longitud es: $a={\sqrt {h^{2}+r^{2}}}\,$ .

Desarrollo plano de un cono recto

El desarrollo plano de un cono recto es un sector circular y un círculo.

El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base.

La forma de calcular la distancia a en el desarrollo es con la ecuación de $a={\sqrt {h^{2}+r^{2}}}\,$

donde r es el radio de la base y h es la altura del cono.

El ángulo que está sombreado en la figura se calcula con la siguiente fórmula:

$\mathrm {{\acute {a}}ngulo} =360(r/a)\,$ .

Volumen de un cono

El volumen $V\,$ de un cono de radio $r\,$ y altura $h\,$ es 1/3 del volumen del cilindro que posee las mismas dimensiones:

V={\frac {\pi \cdot r^{2}\cdot h}{3}}\,\!

La ecuación se obtiene mediante $\int _{0}^{h}A(x)dx\,\!$ ,

donde $A(x)\,$ es el área de la sección perpendicular a la altura, con relación a la altura $h$ , en este caso $A(x)=\pi \left({\frac {rx}{h}}\right)^{2}$ .

Cono oblicuo

Un cono oblicuo es aquel cono cuyo eje de revolución no es perpendicular a su base.

Pueden ser de dos tipos: de base circular o de base elíptica. El de base elíptica es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje de revolución.

La base es un círculo o una elipse, y la altura es el segmento que contiene al vértice, siendo perpendicular al plano de la base; pero no es coincidente con el eje del cono.

Superficie y desarrollo

La superficie lateral de un cono oblicuo es un triángulo curvilíneo, con dos generatrices por lados y base semi-elíptica.

La superficie de la base de un cono oblicuo es un círculo o una elipse.

Volumen

La ecuación empleada para hallar el volumen de un cono oblicuo de base circular es similar a la del cono recto:

$V={\frac {\pi r^{2}h}{3}}$

donde $\scriptstyle r$ es el radio de la base y $\scriptstyle h$ la altura del cono oblicuo. La ecuación del volumen de un cono oblicuo de base elíptica es:

$V={\frac {\pi abh}{3}}$

siendo $\scriptstyle a$ y $\scriptstyle b$ los semiejes de la elipse y $\scriptstyle h$ la altura del cono oblicuo. La justificación de estas dos fórmulas se basa en el principio de Cavalieri cuyo enunciado es el siguiente:

Definición. Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces: igual volumen

Igualmente dentro del cálculo infinitesimal las fórmulas anteriores puede demostrarse sin necesidad del principio de Cavalieri.

Esfera

En geometría, una superficie esférica es una superficie de revolución formada por el conjunto de los puntos del espacio que equidistan de un punto llamado centro.

Los puntos cuya distancia es menor que la longitud del radio forman el interior de la superficie esférica. La unión del interior y la superficie esférica se llama bola cerrada en topología, o esfera, como en geometría elemental del espacio.^[3]Obviamente, la esfera es un sólido geométrico.

La esfera, como sólido de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro (Euclides, L. XI, def. 14).

Esfera proviene del término griego σφαῖρα, sphaîra, que significa pelota (para jugar). Coloquialmente hablando, se emplea la palabra bola, para describir al cuerpo delimitado por una esfera.

Geometría esférica

Como superficie

La esfera (superficie esférica) es el conjunto de los puntos del espacio tridimensional que tienen la misma distancia a un punto fijo denominado centro; tanto el segmento que une un punto con el centro, como la longitud del segmento, se denomina radio. En este caso se genera al rotar una semicircunferencia , usando como eje de rotación su diámetro.^[4] Este concepto se usa al definir la esfera en geometría analítica del espacio.

Como sólido

La esfera (sólido esférico) es el conjunto de puntos del espacio tridimensional que están, respecto del centro, a una distancia igual o menor que la longitud de su radio. Este concepto coincide con la definición de bola cerrada en el análisis real de ℝ³. Se genera al rotar un semicírculo, teniendo como eje de rotación su diámetro.^[5]

En esta situación, topológicamente, se puede hablar de frontera( Fr) el conjunto de puntos de la esfera de distancia igual al radio; interior ( Int), el conjunto de puntos de distancia menor que el radio; exterior (Ext), el conjunto de puntos de distancia mayor que el radio. Cumpliéndose que estos tres conjuntos forman una partición del espacio, de modo que son disjuntos dos a dos y la unión de los tres es el mismo espacio.^[6]

Propiedades

Cualquier segmento que contiene el centro de la esfera y sus extremos están en la superficie esférica, es un diámetro.^[7]
Cualquier sección plana de una esfera es un círculo.
Cualquier sección que pasa por el centro de una esfera es un círculo mayor, y si la sección no pasa por el centro es un círculo menor.
Si se da un círculo de una esfera, los extremos del diámetro perpendicular a aquel se llaman polos de dicho círculo.^[8]

Volumen

El volumen, $V\,$ , de una esfera se expresa en función de su radio $r\,$ como:

V={\frac {4\pi r^{3}}{3}}

Se puede considerar el volumen de una esfera como 2/3 del volumen del cilindro circunscrito a la esfera. Su base es un círculo del mismo diámetro que la esfera. Su altura tiene la misma medida que dicho diámetro:

V={\frac {2}{3}}(\pi r^{2}\cdot 2r)

Esta relación de volúmenes se adjudica a Arquímedes.

Es posible calcular el volumen de una esfera con un margen de error aproximado al 0.03% sin utilizar el valor de π:

V={\frac {67}{16}}r^{3}

Área

El área es 4 veces $\pi \,$ por su radio al cuadrado.

\ A=4\pi r^{2}

Demostración:

Arquímedes demostró que el área de la esfera es dos tercios respecto al del cilindro, usando esta definición:

A={\frac {2}{3}}(2r\cdot 2\pi r+2\cdot \pi r^{2})

A={\frac {2}{3}}(4\pi r^{2}+2\pi r^{2})

A={\frac {2}{3}}(6\pi r^{2})

A=4\pi r^{2}

Demostración:

El área de la esfera es también igual a la derivada de su volumen con respecto a $r\,$ .

V={\frac {4}{3}}\pi r^{3}=\int _{0}^{r}A(r)dr

{\frac {dV}{dr}}=A(r)=4\pi r^{2}

Toroide

{{

| direction = horizontal
| width     = 100
| footer    = Mitades inferiores y secciones longitudinales de las tres clases de toro
| image1    = Standard_torus-ring.png
| alt1      = ring
| caption1  = R > r:
 Toro de anillo
| image2    = Standard_torus-horn.png
| alt2      = horn
| caption2  = R = r:
 Toro de cuerno
| image3    = Standard_torus-spindle.png
| alt3      = spindle
| caption3  = R < r:
 Toro de huso

}}

En geometría, un toro o toroide es una superficie de revolución generada por una circunferencia que gira alrededor de una recta exterior coplanaria (en su plano y que no la corta) o, llanamente, la curva tridimensional que resulta de hacer girar una circunferencia alrededor de un eje que no la corta. La palabra «toro» proviene del latín torus, que significa «protuberancia», «elevación curva» (relacionado con latín "sterno" y griego στορέννυμι) y que ya en latín adquiere sentidos técnicos para designar objetos con esta forma geométrica específica, por ejemplo en arquitectura (Vitr.3.3.8), donde designa el «bocel» o «murecillo», que es una moldura redondeada de la base , con forma de hogaza de pan.^[9] Muchos objetos cotidianos tienen forma de toro: un dónut, una rosquilla, la cámara de un neumático, etc.

Geometría

Representación en sistema diédrico del toro.

El toro es semejante a un neumático hinchado o a una rosquilla (dónut o dona). Las ecuaciones paramétricas que lo definen son:

{\begin{cases}x=\cos \theta (R+r\cos \varphi )\\y=\sin \theta (R+r\cos \varphi )\\z=r\sin \varphi \end{cases}}

donde R es el trayecto entre el centro del conducto y el centro del toro, r es el radio del conducto, ambas constantes con r<R y θ, φ son ángulos que determinan el círculo completo, con $\theta ,\varphi \in [0,2\pi )$ .