Matemáticas/Geometría Analítica/Tridimensional/Hiperboloide
El hiperboloide es la superficie de revolución generada por la rotación de una hipérbola alrededor de uno de sus dos ejes de simetría. Dependiendo del eje elegido, el hiperboloide puede ser de una o dos hojas.
Para entenderlo mejor, se considera a continuación el caso de la hipérbola de referencia, cuya ecuación es
- ,
en el sistema de coordenadas (ver el esquema siguiente).
La revolución alrededor del eje de simetría rojo genera un hiperboloide conexo, mientras que la rotación alrededor del eje azul, que atraviesa dos veces la hipérbola, da un hiperboloide de dos hojas.
-
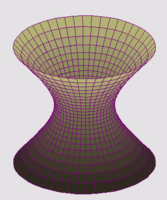
Hiperboloide de una hoja.
-
Hiperboloide de dos hojas.
Ecuaciones del hiperboloide
[editar]Ecuación Cartesiana
[editar]
Para hallar las ecuaciones de estas superficies, resulta más cómodo trabajar en el sistema de coordenadas , cuyos ejes son los de simetría. Sean X e Y las coordenadas en este sistema, entonces tenemos la igualdad:
es decir
- .
Luego, identificando los coeficientes de sendos vectores:
la ecuación inicial se escribe también xy = 1, es decir (X-Y)·(X+Y) = 1, luego:
Si se gira alrededor del eje Y, de vector director , entonces se otorga a la tercera coordenada Z el mismo papel que a X, por tanto Z y X aparecen bajo la misma forma en la ecuación, concretamente precedido del signo «+»:
Del mismo modo, Si se gira alrededor del eje X, de vector director , entonces Z aparece bajo la misma forma que Y en la ecuación, es decir con un signo «-»:
Reagrupando las coordenadas del mismo signo, cambiando los signos si hay dos negativos, y renombrando las variables para obtener el orden habitual x,y,z, se obtiene una de estas dos ecuaciones:
(una hoja) (dos hojas)
Se generalizan estos dos ejemplos así: un hiperboloide es una cuádrica cuya ecuación es, en un sistema de coordenadas adecuado, (con el centro situado en el centro de simetría, y cuyos planos son planos de simetría de la superficie), de la forma:
Estas superficies se obtienen, de las mostradas en el ejemplo, estirando en la dirección de los x por el factor a, multiplicando las distancias en los y por b, y en los z por c. Es decir que, fundamentalmente, tienen la misma forma.
Ecuación paramétrica
[editar]En un espacio euclídeo tridimensional, los puntos de la superficie del hiperboloide pueden ser parametrizados de la siguiente manera:
Parametrización sin usar las funciones hiperbólicas: