Matemáticas/Geometría Analítica/Parábola/Propiedades geométricas


De esta forma, una vez fijados una recta y un punto se puede construir una parábola que los tenga por directriz y foco respectivamente, usando el siguiente procedimiento: Se toma un punto T cualquiera de la recta, se lo une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la recta directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se pueden hallar tantos puntos de la parábola como sea necesario.
Vértice. Es el punto donde la parábola corta a su eje focal. Foco. Es un punto que se encuentra situado sobre el eje focal y la distancia
que se encuentra del vértice al foco, es la misma que del vértice a la Directriz.
Lado recto. La cuerda, perpendicular al eje focal, que contiene al foco y corta a dos puntos de la parábola.
Directriz. Línea recta donde la dist (P, F)= dist (P, D); PF PD = . Ver figura 1.
Eje focal. Recta que contiene el foco y es perpendicular a la directriz.
Parámetro p. Distancia del foco al vértice.
 |
 |
Lado recto
[editar]
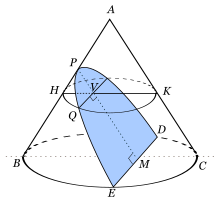
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto. La longitud del lado recto es siempre 4 veces la distancia focal.
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.
Tangentes a la parábola
[editar]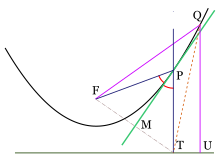
Un resultado importante en relación a las tangentes de una parábola establece: La tangente biseca el ángulo entre el foco, el punto de tangencia y su proyección.
Llamemos F al foco de una parábola, P a un punto cualquiera de la misma y T a la proyección de este sobre la directriz. Sea MP la mediatriz del triángulo FPT, el cual es isósceles por ser iguales las distancias FP y PT, como se ha visto. Luego MP biseca al ángulo FPT, restando verificar si es tangente a la parábola en el punto P.
Sea Q otro punto de la parábola y sea U su proyección en la directriz. Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.
