Matemáticas/Geometría Analítica/Elipse/Dibujo de la elipse

Dibujo de la elipse

Modo de dibujar la elipse conocido como "elipse del jardinero", mediante dos puntos fijos y una cuerda

Elipse “del jardinero”

El método se basa en la definición más corriente de la elipse, como lugar geométrico de los puntos cuya suma de distancias a los focos es constante. Los clavos o las chinchetas se colocan en el lugar de los focos, y la cuerda debe medir lo mismo que el eje mayor (2a). En el ejemplo de la foto al lazo de cuerda se le debe añadir la distancia de los focos. Con la cuerda tensa se mueve el lápiz o material de dibujo rodeando por completo los dos focos.

Se denomina “del jardinero” a este método porque sirve para trazar en el suelo elipses de gran tamaño y precisión suficiente, con medios modestos. Ver en la sección siguiente el modo de determinar los focos a partir de los ejes.

Modo de determinar los focos

El modo de determinar los focos a partir de los ejes, o un eje a partir de otro y los focos, se basa en la definición. Dibujados los dos ejes principales, se toma con el compás la medida a de la mitad del eje mayor. Haciendo centro en un extremo del eje menor, el compás cruza por el eje mayor en los focos.

Focos de la elipse, y dimensiones principales

Dado el eje mayor con los focos, la medida a aplicada a cada foco nos da arcos que se cruzan en los extremos del eje menor.

Dado un eje menor y la distancia de los focos, primero debemos hallar la recta sobre la que está el eje mayor, luego dibujar los focos a la distancia dada, y desde ellos tomar la distancia a los extremos del eje menor, que es la mitad del eje mayor.

Método de radios vectores

También denominado "por puntos"; con este método dibujamos un número suficiente de puntos mediante el compás. Como en el método tradicional visto antes usamos los radios vectores y la propiedad de que la suma de los radios vectores de un punto es igual a la medida del eje mayor.

Dados dos ejes principales y determinados los focos, se toman puntos al azar sobre el eje mayor entre el centro O y uno de los focos. Generalmente tres o cuatro, y preferiblemente cerca del foco por comodidad del dibujo.

Tomamos con el compás la distancia de un extremo del eje mayor (A) a cada uno de los puntos del eje (1). Haciendo centro en cada foco trazamos arcos con esa medida. A continuación tomamos el resto de la medida del eje mayor, desde el punto (1) al otro extremo (B), y con esa medida, haciendo centro de nuevo en los focos, cruzamos los arcos trazados antes. Las cruces nos dan puntos que pertenecen a la elipse.

Repitiendo la operación tantas veces como sea necesario obtenemos puntos de la elipse. Se completa el dibujo a mano o mediante plantillas de curvas.

Método de la tarjeta, compás de Arquímedes

Se puede dibujar la elipse mediante una regla de medir, un juego de escuadra y cartabón y un lápiz. Dibujamos los ejes principales con sus medidas, y determinamos los focos. Tomamos con la regla graduada, desde el 0, la distancia del centro al extremo del eje mayor, y después desde la marca del extremo del eje mayor, restamos la mitad del eje menor (ver dibujo). Apoyando el 0 de la regla en cualquier punto del eje menor y la diferencia calculada en el eje mayor, marcamos la medida del eje mayor. Para más claridad véase el dibujo.

Animación de los principios del Compás de Arquímedes o elipsógrafo

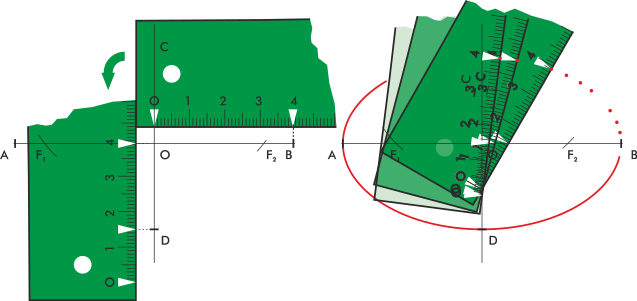
Esta misma operación se puede hacer con una tarjeta, y de ahí su nombre tradicional, haciendo marcas en el borde con las medidas dadas.

Para construirla con reglas y compás marcamos puntos arbitrarios en el eje menor. Tomando con el compás la medida de la mitad de la diferencia entre el eje mayor y el menor, hacemos centro en los puntos y señalamos puntos correspondientes en el eje mayor, a ambos lados. Dibujamos rectas desde los puntos del eje menor a sus correspondientes del eje mayor, prolongándolas. Sobre esas rectas, con el compás y desde cada punto del eje mayor, tomamos la medida de la mitad del eje menor, marcándola sobre la línea, lo que nos da los puntos de la elipse.

Existe una máquina sencilla (un elipsógrafo) hecha a base de guías o raíles y barras y llamada compás de Arquímedes, que se basa en este principio.

Construcción por afinidad

Partimos de las rectas de los ejes principales. Se dibujan dos circunferencias concéntricas cuyos diámetros sean los de la elipse. Para hallar un punto trazamos un radio cualquiera de la circunferencia mayor fuera de los ejes. Desde el extremo del radio trazamos una recta auxiliar, paralela al eje menor, hacia dentro de la circunferencia. Desde el punto donde el radio corta la circunferencia menor trazamos una recta auxiliar paralela al eje mayor, que cruce la línea auxiliar que acabamos de hacer. El punto donde se cortan las dos auxiliares pertenece a la elipse.

Repitiendo la operación se obtienen todos los puntos que sean necesarios; la elipse se completa a mano o con plantillas. Normalmente por comodidad el dibujo se sistematiza; en lugar de los radios dibujamos diámetros completos, los trazos auxiliares verticales y horizontales se hacen de una vez mediante paralelas a los ejes.

En este método se puede considerar una de las circunferencias como una doble transformación afín de la otra, y los puntos unidos por el mismo radio serían entonces afines. Una de las líneas auxiliares es la recta de afinidad de dos puntos (uno en la circunferencia, otro en la elipse), mientras la otra línea auxiliar da la reducción que corresponde

También se puede considerar la relación de las dos circunferencias una homología en la que el centro de homología coincide con el centro de una circunferencia, mientras su homóloga pertenece a un plano paralelo y también es concéntrica; estas homologías con rectas límite impropias son homotecias.

Por afinidad, a partir de conjugados

A partir de dos diámetros conjugados (A-B y C-D) se puede realizar la siguiente construcción, en la que hacemos afines los extremos del diámetro conjugado menor (C y C', la línea de afinidad en azul) con el de una circunferencia auxiliar de diámetro igual al mayor y perpendicular a él (en rojo), mientras el diámetro mayor es el eje de afinidad. Cada punto de la circunferencia es afín a otro de la elipse.

Por afinidad, dentro de un paralelogramo

Una construcción corriente para dibujar una elipse o un arco de elipse en un paralelogramo es hacerlo afín a otro ortogonal en el que podamos trazar un arco de circunferencia o una circunferencia completa. Esto es útil en particular para elipses proyectadas en axonométrica u otra proyección cilíndrica.

Como se ve en el dibujo hacemos que dos puntos sean afines, así como dos rectas que se corten en otra que hará de eje de afinidad. El resto consiste en ir trasportando puntos y rectas mediante otras rectas afines conocidas, normalmente los lados de los paralelogramos o sus diagonales (véase el dibujo).

En el cubo de la derecha se aprecia el principio que se aplica. Es importante señalar que en axonométrica este "truco" no equivale en general a un abatimiento.

Por haces proyectivos

Construcción por haces proyectivos, o del paralelogramo. En la variante tradicional ponemos tantos puntos en el eje menor como en los lados del rectángulo paralelos al eje menor; unimos estos desde los extremos del eje menor (C y D). Luego pasamos rectas desde esos extremos hasta los puntos del eje mayor, hasta cortar la recta correspondiente. Los puntos de cruce pertenecen a la elipse.

En la segunda imagen vemos el mismo procedimiento aplicado a dos diámetros conjugados; el rectángulo se hace romboide, pero sigue funcionando la construcción como una proyección afín de la otra.

En otra variante (ver imagen animada) dibujamos puntos a distancias iguales, proporcionales lado a lado, en un rectángulo exterior tangente a la elipse, que tiene los lados paralelos al eje menor de doble tamaño. Vamos uniendo en orden cada punto correspondiente como se ve en la imagen, desde los extremos el eje mayor. Los puntos que se cortan de las rectas correspondientes pertenecen a la elipse.

Construcción de la elipse según el método del paralelogramo

Existen métodos semejantes para trazar la parábola y la hipérbola.

La elipse como hipotrocoide

La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.

En una curva hipotrocoide, la circunferencia que contiene al punto generatriz, gira tangencialmente por el interior de la circunferencia directriz.

La elipse como caso particular de hipotrocoide. Datos: R = 10, r = 5, d = 1.

Anamorfosis de una circunferencia en una elipse

El artículo principal de esta categoría es Anamorfosis.

Determinada trasformación del plano (al deformar el plano cartesiano), se denomina anamorfosis. El término anamorfosis proviene del idioma griego y significa trasformar.

Al transformar una circunferencia o una elipse mediante una afinidad o una homología el resultado es otra elipse (o una circunferencia como caso especial de elipse).

Una circunferencia en un plano cartesiano no deformado.	Esta circunferencia se transforma en una elipse mediante una anamorfosis, donde el eje Y se ha contraído y/o el X se ha dilatado.	Otra modificación del plano contenedor; los ejes no se deforman ortogonalmente, sino que cada punto corresponde a otro según una homología de centro impropio (afinidad).
	Otra modificación del plano (homología)	Otra modificación del plano (libre, sobre un elipsoide)

En el caso de la circunferencia, si el plano cartesiano se divide en una red de cuadrados, cuando dicho plano se «deforma» en sentido del eje X, el Y, o ambos, la circunferencia se transforma en una elipse y los cuadrados en rectángulos. Este procedimiento era muy utilizado para realizar perspectivas ilusionistas, anamórficas, llamadas trampantojos.