Matemáticas/Geometría Analítica/Ecuación de la Recta/Ecuación General de la Recta
Ecuación de la recta en el plano
[editar]
En un plano cartesiano, podemos representar una recta mediante una ecuación general definida en dicho plano ya sea mediante coordenadas usando puntos y vectores, o bien funciones que especifican dichas coordenadas.
Pendiente y ordenada al origen
[editar]Dada una recta mediante un punto, , y una pendiente :
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente (ecuación punto-pendiente):
donde es la tangente del ángulo que forma la recta con el eje de abscisas X.
Ejemplos
[editar]a) La ecuación de la recta que pasa por el punto y que tiene una pendiente de es:
Sustituyendo en la ecuación anterior tenemos:
b) La ecuación de la recta que pasa por el punto y que tiene una pendiente de :
Demostración: Al sustituir los datos en la ecuación, resulta lo siguiente:
Forma simplificada de la ecuación de la recta
[editar]Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas es (0, b), podemos deducir, partiendo de la ecuación general de la recta, :
|
|
Esta es la segunda forma de la ecuación de la recta y se utiliza cuando se conoce la pendiente y la ordenada al origen, que llamaremos .
Forma segmentaria de la ecuación de la recta (ecuación simétrica)
[editar]Recta que corta el eje ordenado en y la abscisa en .
- .
Demostración: Si se plantea como problema encontrar la ecuación de una recta, conocidos y (la abscisa y ordenada al origen), se conocen dos puntos de la recta los cuales son los siguientes:
y
Con estos puntos se puede encontrar dicha ecuación, pero primero se debe calcular la pendiente:
Después se sustituye en la ecuación , usando cualquiera de los dos puntos, en este caso (a, 0):
y dividiendo toda la ecuación entre el término independiente :
Se obtiene la ecuación de la recta en su forma simétrica. Esta ecuación se suele utilizar para obtener la ecuación de una recta de la que se conocen sus intersecciones con los ejes y cuando, a partir de la ecuación de una recta, se desean conocer los puntos donde dicha recta interseca a los ejes.
Ecuación general de la recta
[editar]La ecuación general de una recta esta dada por la expresión con y ,,[1] donde representa la pendiente de la recta y señala la ordenada en el origen, datos suficientes para representar cualquier recta en el plano cartesiano.
Ecuación normal de la recta (primera forma)
[editar]La forma normal de la recta (Ecuación de Hesse):
Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo omega ω es el ángulo entre la perpendicular a la recta y la parte positiva del eje de ordenadas.[2]
Si en lugar del ángulo de la normal ω se emplea el ángulo de la recta α, entre la recta y el eje de las ordenadas:
Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo alfa α es el ángulo entre la recta y la parte positiva del eje de ordenadas, cuya tangente expresa el valor de la pendiente de la recta.
Demostración: Para obtener dicha ecuación a partir de una ecuación de la forma , primero se ha de calcular:
al dividir los parámetros de la ecuación por se obtiene que y . Finalmente sin excepción.[3]
Ecuación normal de la recta (segunda forma)
[editar]Tomando el valor positivo o negativo de la raíz según corresponda.
Rectas que pasan por un punto
[editar]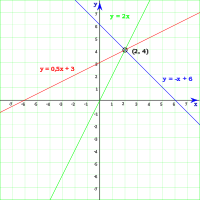
Para determinar las rectas del plano que pasan por el punto se usa la ecuación
- donde m toma cualquier valor real.
Demostración: La ecuación de la recta ha de ser:
Y ha de pasar por el punto , luego tendrá que cumplirse:
Despejando b, tenemos esta ecuación:
Sustituyendo b en la ecuación general de la recta:
Ordenando términos:
Esta ecuación define un haz de rectas en el plano que pasa por el punto , el valor de m es la pendiente de cada una de las rectas que forman parte del haz a excepción de la recta vertical por dicho punto.
Recta que pasa por dos puntos
[editar]Si pasa por dos puntos y , la ecuación de la recta puede expresarse como:
Demostración: Han de cumplir la fórmula general , resultando un sistema de dos ecuaciones con dos incógnitas m y b:
eliminamos la incógnita b, despejando en la primera ecuación y sustituyendo en la segunda:
agrupando términos:
despejando m:
este valor, m, es el de la pendiente de la recta que pasa por los dos puntos: y . Despejando ahora el valor de b de una de las ecuaciones del sistema, por ejemplo de la primera, tenemos:
y sustituyendo m, por su valor ya calculado;
Tenemos las dos incógnitas m y b despejadas, en función de las coordenadas de los dos puntos por los que tienen que pasar, entonces la ecuación general de la recta, con los parámetros ya calculados es:
Fórmulas para hallar "x" e "y" en una recta dada por coordenadas.
[editar]Tenemos una recta dada por dos puntos , de la cual queremos hallar y a lo largo de la misma. Obtenemos la pendiente y utilizamos las fórmulas respectivas para hallarlas:
Donde:
y : ordenada y abcisas a hallarse;
, , , : ordenadas y abcisas respectivas de los puntos A y B de la recta ;
: pendiente de la recta .
Fórmulas para hallar el punto de intersección de dos rectas dadas por sus puntos de coordenadas.
[editar]Para obtener las coordenadas del punto de intersección de dos rectas y , podemos utilizar la siguientes fórmulas.
Donde:
y : ordenada y abcisas de la intersección.
Recta que no pasa por el origen
[editar]En coordenadas polares una recta que pasa a una distancia d > 0, tiene una ecuación dada por:
Donde la pendiente de la recta viene dada por .
Rectas notables
[editar]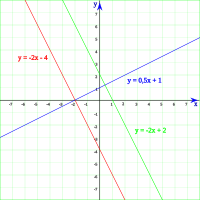
- La ecuación de una recta vertical responde a la ecuación general (constante).
- La ecuación de una recta horizontal responde a la ecuación general (constante).
- Una recta trigonoidal que pase por el origen O (0, 0), cumplirá la condición b = 0, siendo su ecuación: .
- Dos rectas cualesquiera:
- serán paralelas si y solo si . Además, serán coincidentes cuando:
- serán perpendiculares si y solo si , es decir:
Rectas en el plano como espacio vectorial y afín
[editar]Mediante dos puntos del plano afín
[editar]Dado dos puntos en el plano, P y Q, sobre una recta, se puede describir cada punto de ésta (es decir toda la recta) mediante la ecuación:
- donde puede tomar cualquier valor.
Ejemplo
[editar]Dados y , entonces la recta son los puntos tales que y .
Mediante un punto y un vector
[editar]Dado un punto y un vector en el plano, P y , queda totalmente definida una recta mediante la ecuación:
- donde puede tomar cualquier valor.
Ejemplo
[editar]Dados y (llamado vector director), entonces la recta son los puntos tales que y .
Rectas notables
[editar]- La ecuación de una recta vertical poseería un vector director del tipo .
- La ecuación de una recta horizontal poseería un vector director del tipo .
- Una recta por el origen, es una recta que pasa por el origen de coordenadas con .
- Dadas dos rectas cualesquiera
- serán paralelas si y solo si .
- serán perpendiculares si y solo si y son perpendiculares, es decir su producto escalar es cero.
Rectas como producto escalar
[editar]Toda recta ya sea de forma implícita, explícita o vectorial se puede expresar como producto escalar de vectores:
es decir, renombrando las constantes:
- Si por tanto el vector es perpendicular a la recta y a sus vectores directores, y por tanto a todas sus paralelas.
- ↑ Geometría Analítica ( 1980) Charles Lehmann; Editorial Limusa, ISBN 968-18-176-3; pg. 65
- ↑ R. Spiegel, Murray; Liu, John; Abellanas, Lorenzo (2000). «Cap 8 Fórmulas de geometría analítica plana». En McGraw-Hill Inc.. Fórmulas y tablas de matemática aplicada (2 edición). Madrid: Concepción Fernández. p. 20. ISBN 84-481-2554-1.
- ↑ Wooton, William. Geometría Analítica Moderna. México 1979. P.p. 90

























































































































