Matemáticas/Geometría Analítica/Circunferencia/Ángulos en una circunferencia

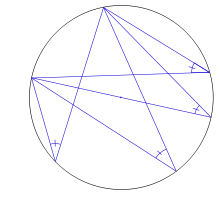
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos radios.
- La amplitud de un ángulo central es igual a la del arco que abarca.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.
- La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.
Ángulo exterior, si tiene su vértice en el exterior de la circunferencia
Circunferencia en un plano de ejes de referencia no ortogonales
[editar]
Para construir una circunferencia en el plano oblicuo, no se puede usar la misma ecuación que se usa en un plano ortogonal, por lo que es necesario introducir algunos conceptos que nos ayudarán a entender la construcción de tal ecuación. Tales conceptos son los de trigonometría. Dos diámetros de una sección cónica se denominan conjugados cuando toda cuerda paralela a uno de ellos es bisecada por el otro. Siguiendo esto, dos diámetros de la circunferencia perpendiculares entre sí son mutuamente conjugados. En una elipse dos diámetros son conjugados si y solo si la tangente a la elipse en el extremo de un diámetro es paralela a la tangente al segundo extremo.
Se debe tener presente que en este plano una ecuación de circunferencia se llamará así si se ve como tal. Es por esta razón que se descarta la ecuación anterior, porque en el plano oblicuo no parecerá circunferencia, sino una elipse.
