Usuario:Daniela.ceron.urzua

Mi nombre es Daniela Cerón. Docente Universitario, Candidata a Doctora en ciencias Mención Matemática. Creando Curso Los Números y sus Operaciones Nociones Fundamentales de los números Naturales, Enteros y Racionales

$\mathbb {Q} {\mbox{ Racionales }}{\begin{cases}\mathbb {Z} &{\mbox{Enteros }}{\begin{cases}\mathbb {N} &{\mbox{Naturales }}{\begin{cases}&{\mbox{1}}\\&{\mbox{Primos}}\\&{\mbox{Compuestos}}\end{cases}}\\0&{\mbox{Cero}}\\&{\mbox{Enteros negativos}}\end{cases}}\\&{\mbox{ }}\\&{\mbox{Fraccionarios}}{\begin{cases}&{\mbox{Fracciones propias}}\\&{\mbox{Fracciones impropias}}\end{cases}}\\\end{cases}}$

Números Naturales

Los Números Naturales son aquellos números que podemos ocupar ya sea para contar o para ordenar.

Los Números Naturales se denotan por $\mathbb {N}$ y es conjunto ordenado, esto quiere decir, que hay números naturales menores y mayores que otros.

¿Cuándo es menor?

Un número natural es menor que otro, si está colocado a la izquierda de él en la recta numérica.

Ejemplo: El número 6 está a la izquierda del número 9, lo que quiere decir, que 6 es menor que 9.

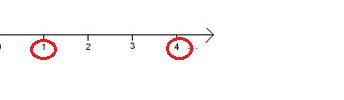
Ejemplo: El número 1 está a la izquierda del número 4, lo que quiere decir, que 1 es menor que 4.

El símbolo que nos indica menor que es: (<)

Por lo tanto, podemos decir que 1 < 4.

¿Cuándo es mayor?

Un número natural es mayor que otro, si está colocado a la derecha de él en la recta numérica. Ejemplo: El número 4 está a la derecha del número 3, lo que quiere decir, que 4 es mayor que 3.

Ejemplo: El número 4 está a la derecha del número 2, lo que quiere decir, que 4 es mayor que 2.

El símbolo que nos indica mayor que es: (>)

Por lo tanto, podemos decir que 4 > 2

Orden de los números naturales

Una propiedad muy importante que cumplen los números naturales, es que están totalmente ordenados. Dados dos números a y b, necesariamente tiene que verificarse una y sólo una de estas tres posibilidades:

• $a=b$ (a es igual a b)
• $a<b$ (a es menor que b)
• $a>b$ (a es mayor que b)

donde $a<b$ implica que existe un número natural $m$ tal que $a+m=b$. La definición es análoga para $a>b$, existe un número natural $m$ tal que $a=b+m$ Con respecto a la propiedad de orden, también existen los símbolos ≤ y ≥, que se definen como sigue:

• $a\leq b$ siempre que $a<b$ o bien $a=b$
• $a\geq b$ siempre que $a>b$ o bien $a=b$

Ejemplos

1. $2<3$, pues existe el número natural $1$ tal que $2+1=3$
2. $7>3$, pues existe el número natural $4$ tal que $7=3+4$
3. $10\leq 10$, pues $10=10$
4. $21\geq 15$, pues $21>15$ al existir el número natural $6$ tal que $21=15+6$

Ejercicio 1: De la misma manera que en los ejemplos anteriores, muestre que:

1. $5<8$
2. $11>8$
3. $5\leq 10$
4. $21\geq 7$

Ejercicio 2: En la siguiente tabla determine con los simbolos " $<$ " ó " $>$ " si los números son mayor que ó menor que:

Número	Simbolo	Número
6	.....	12
13	.....	12
23	.....	27
99	.....	110
112	.....	98

Antecesor y sucesor

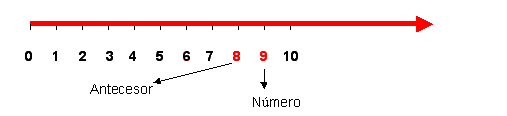
Todo número natural, a excepción del 1, lo antecede siempre un número natural más pequeño, al que denominaremos antecesor.

Ejemplo: 8 es el antecesor de 9.

Además, dado cualquier número natural, le sigue siempre otro número natural más grande, al cual denominaremos sucesor. Como consecuencia de esto, el conjunto de los números naturales es infinito.

Ejemplo: 4 es el sucesor de 3.

Ejercicio

No hay acuerdo total acerca de incluir al número 0 (cero) en el conjuntos de los números naturales pues hay buenas razones para incluirlo y para no incluirlo; usualmente textos escolares definen a los naturales como {0,1,2,...} y los textos universitarios suelen definir a los naturales como {1,2,...}.Así que nosotros denotaremos los números naturales por

$\mathbb {N} =\{1,\;2,\;3,\;4,\;5,\;...\;\}$

y cuando el cero este incluido lo denotaremos por

$\mathbb {N} _{0}=\{0,\;1,\;2,\;3,\;4,\;5,\;...\;\}$

Este conjunto de los Números Naturales se caracteriza porque:

• Tiene un número infinito de elementos

• Cada elemento tiene un sucesor y todos, excepto el 1, un antecesor

El sucesor de un número natural se obtiene sumando uno (+1); el antecesor se obtiene restando uno (-1).

Propiedades básicas de los números naturales

La suma es la operación matemética que resulta al reunir en una sola varias cantidades. También se conoce la suma como adición.

$a+b=c$

Los términos de la suma, a y b, se llaman sumandos y el resultado, c, suma. El símbolo que representa a la suma es +.

Ejemplo si a la cantidad 3 le añadimos la cantidad 2, obtenemos como resultado la cantidad 5

$3+2=5$

O bien, si tenemos 3 manzanas para comer y añadimos 2 manzanas mas obtenemos 5 manzanas para comer.

3 + 2 = 5 manzanas.

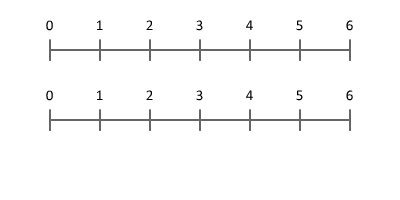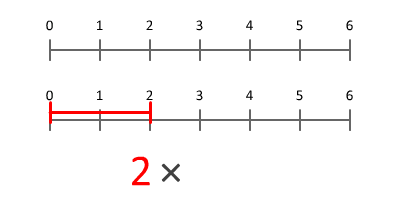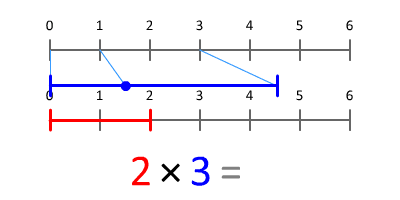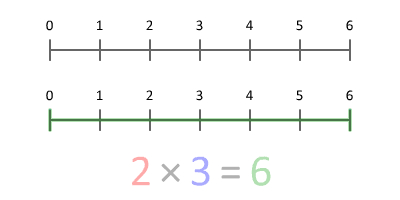
La multiplicación es una operación matemática que consiste en sumar un número tantas veces como indica otro número.

$a\times b=c$

Los términos de la multiplicación, a y b se denomina factores y el resultado c se denomina producto. El símbolo que representa a la multiplicación es $\cdot$ ó $\times$. También suele no anotarse el símbolo de multiplicación cuando lo que quiere multiplicarse son letras

$a\cdot b=a\times b=ab$

Ejemplo: Si multiplicando es 4 y el multiplicador es 3. Luego, el cuatro debe ser sumado 3 veces y nos queda 12.

$4\times 3=4+4+4=12$

$4\times 3=12$

Números Pares e Impares en los Números Naturales

En el conjunto de los números naturales hay elementos que son importante de reconocer, y que pasamos a definir.

Números pares: Los números pares son los números de la forma $2\times n$, donde $n$ un número natural.

Así, el conjunto de los números pares se puede representar de la siguiente manera

$\mathrm {pares} =\{0,\;2,\;4,\;6,\;8,\;...\;\}$

Números Impares: Los números impares son los números de la forma $2\times n-1$, donde $n$ un número natural.

Así, el conjunto de los números impares se puede representar de la siguiente manera

$\mathrm {impares} =\{1,\;3,\;5,\;7,\;...\;\}$

Es importante considerar las siguientes propiedades de los números pares e impares.

• " $PAR+PAR$ " ó " $IMPAR+IMPAR$ " es un número " $PAR$ " .

• " $PAR+IMPAR$ " ó " $IMPAR+PAR$ " es un número " $IMPAR$ ".

• " $PAR\times PAR$ " ó " $PAR\times IMPAR$ " ó " $IMPAR\times PAR$ " es un número " $PAR$ ".

• " $IMPAR\times IMPAR$ " es un número " $IMPAR$ ".

Ejemplos

Operación	Par o Impar	¿Por qué?
$22+14=36$	" $PAR$ "	$36=2\times 18$
$11+23=34$	" $PAR$ "	$34=2\times 17$
$12+33=45$	" $IMPAR$ "	$45=2\times 23-1$
$12\times 6=72$	" $PAR$ "	$72=2\times 36$
$13\times 7=91$	" $IMPAR$ "	$91=2\times 46-1$

Ejercicios

Operación	Par o Impar	¿Por qué?
$17+24=.......$	............	............
$14+4=.......$	............	............
$7+13=.......$	............	............
$6\times 11=.......$	............	............
$13\times 4=.......$	............	............

Propiedades de la Adición y Multiplicación

La adición y multiplicación de números naturales tiene varias propiedades entre ellas se encuentran:

• Clausura: la suma y el producto de números es, siempre, un número natural.

Ejemplos

1.

$2+2=4$

2.

• Asociatividad

Sean a,b y c números naturales, entonces

$(a+b)+c=a+(b+c)$

Ejemplo : ${\color {Blue}(3+5)+6=3+(5+6)}$

Error al representar (función desconocida «\begin{array}»): {\displaystyle \begin{array} \left(\underbrace{3 + 5}) + 6& = &3 + (\underbrace{5 + 6})\\ \underbrace{\quad 8 \quad + 6}& = &\underbrace{3 + \quad 11}\\ \qquad 14 & = & \quad 14 \end{array} }

Sean a,b y c números naturales, entonces

$(a\times b)\times c=a\times (b\times c)$

Ejemplo : ${\color {Blue}(3\times 5)\times 6=3\times (5\times 6)}$

Error al representar (función desconocida «\begin{array}»): {\displaystyle \begin{array} \left(\underbrace{3 \times 5})\times 6& = &3\times (\underbrace{5 \times 6}) ? \\ \underbrace{ \quad 15 \quad \times 6} & = & \underbrace{3\times \quad 30} \\ \qquad 90 & = &\quad 90 \end{array} }

• Conmutatividad

Sean a y b números naturales, entonces

$a+b=b+a$

Ejemplo 1: ${\color {blue}4+5=5+4}$

Error al representar (función desconocida «\begin{array}»): {\displaystyle \begin{array} \left(\underbrace{4 + 5})& = & (\underbrace{5 + 4}) ? \\ \quad 9 & = &\quad 9 \end{array} }

Ejemplo 2: ${\color {blue}2+1+5=5+1+2}$

Sean a y b números naturales, entonces

$a\times b=b\times a$

Ejemplo: ${\color {blue}2\times 3=3\times 2}$

Resta o Sustracción

Igual que la suma, la resta es una operación que se deriva de la operación de contar.

5 menos 2 igual al 3

Ejemplo

Si tenemos 6 ovejas y los lobos se comen 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaría el resultado y no necesitaría volver a contar las ovejas. Sabría que 6 - 2 = 4.

Los términos de la resta se llaman minuendo (las ovejas que tenemos) y sustraendo (las ovejas que se comieron los lobos) (observe que no tiene mucho sentido pensar en seguir comiéndose ovejas una vez que los lobos las devoraron a todas).

En términos simples, consiste en, a un número fijo, “quitarle” un número determinado, y ver qué resultado se obtiene. El símbolo que representa a la resta es -.

Ejemplo Imagine un segmento de recta de longitud b con el extremo izquierdo etiquetado a y el extremo derecho etiquetado c.

$c-a=b$

Por ejemplo, si tenemos un segmento de recta donde el extremo izquierdo es el número 5 y el extremo derecho es 12, la longitud de la recta es 7, es decir 12-5=7. En el ejemplo, el 12 es el minuendo, el 5 es el sustraendo, y el 7 es resta o diferencia.

Debemos observar que la resta no tiene la propiedad conmutativa ya que no es lo mismo a - b que b - a. Lo podremos notar cuando estudiemos los números enteros.

División

La división es repartir entre partes o grupos iguales. Éste es el resultado de una "repartición limpia".

En matemática, la división es una operación aritmética de descomposición que consiste en averiguar cuántas veces un número (divisor) está contenido en otro número (dividendo). El resultado de una división recibe el nombre de cociente y resto a lo que sobra o también lo nombran residuo. De manera general puede decirse que la división es la operación inversa de la multiplicación. Si el resto es cero la división se llama exacta y en caso contrario inexacta.

El símbolo que representa a la división es / o ÷.

Ejemplo

$20\div 4=5$

Si queremos dividir 20 en 4, nos preguntamos cuántas veces cabe 4 (divisor) en 20 (dividendo), y vemos que si sumamos el 5 un número de veces igual a 4, obtenemos 20. Luego, $20\div 4=5$.

$20\div 4=5$

La división no tiene la propiedad conmutativa, pues no es lo mismo $a\div b$ que $b\div a$.

Propiedades Aritméticas

Las Propiedades Aritméticas son expresiones combinadas de todas las operaciones que hemos visto hasta ahora y hay dos cosas importantes para los desarrollos de ejercicios combinados.

• Si el ejercicio no tiene paréntesis, el orden en que se operan los números es siempre: multiplicación y división, suma, resta.

Es importante considerar que se opera en orden de izquierda a derecha.

• Si el ejercicio tiene paréntesis, primero deben ser resueltos éstos, considerando que si el paréntesis está precedido por un signo menos, los signos interiores deben ser cambiados.

Ejemplos

1. Resolver la expresión

$24\times 3+15-40\div 20+7$

Solución: Como el ejercicio no presenta paréntesis, primero resolvemos la multiplicación, luego la división, para finalmente resolver las sumas y restas. Entonces tenemos que:

${\begin{alignedat}{2}24\times 3+15-40\div 20+7&=72+15-2+7\\&=92\\\end{alignedat}}$

2. Resolver la expresión

$(20+7)\div 3+2\times (10-7)+1$

Solución: la expresión tiene paréntesis, luego empezamos resolviendo por allí, para después respetar el orden: multiplicación, división, suma, resta. Entonces tenemos que:

${\begin{alignedat}{2}(20+7)\div 3+2\times (10-7)+1&=27\div 3+2\times 3+1\\&=9+6+1\\&=16\end{alignedat}}$

3. Resolver la expresión

$6\div 3\times 2$

Solución: en este caso, al no haber paréntesis que separen las operaciones división y multiplicación, se resuelve de izquierda a derecha, primero resolviendo la división $6\div 3$, y luego se multiplica por $2$, teniéndose que el resultado es $4$.

Ejercicios

1. $(3+5)\div (4-1)\times 7$
2. $4\times 20\div 4+5-1$
3. $5\div 5\times 4+20$
4. $3+[4\times (5-1)]+(4-2)$
5. $2-1+[(4-1)\times 4\div 2]+3$
6. $3\times 5\div 3+4-2$

Números Primos

Los Números Primos son aquellos números naturales mayores que 1 que son divisibles solamente por 1 y por sí mismo.

Es decir, si p pertenece IN. Diremos que p es un número primo si cumple con

• p>1
• p es divisible solamente por 1 y por sí mismo

Números Compuestos

Los números Compuestos son aquellos números mayores que 1 que no son primos. Es decir, números que pueden ser divididos por más números que el 1 y sí mismo.

Ejemplo

Números	Divisores	Naturaleza
2	1 y 2	Primo
3	1 y 3	Primo
4	1, 2 y 4	Compuesto
6	1, 2, 3 y 6	Compuesto
13	1 y 13	Primo
15	1, 3, 5,15	Compuesto

Ejercicio

Números	Divisores	Naturaleza
17	........	........
19	........	........
21	........	........

Una forma de saber si los números son primos o compuestos es ocupando una tablita llamada la criba de Eratóstenes. Funciona de la siguiente manera:

1. Escribamos una tabla de números, por ejemplo, entre 1 y 100.

2. Tarjamos el número 1.

3. Tarjamos los múltiplos de 2.

4. Tarjamos los múltiplo de 3.

5. Tarjamos los múltiplo de 5.

6. Tarjamos los múltiplo de 7.

Listo! Los números no tarjados corresponden a los números primos entre 1 y 100.

MCM

Múltiplo

Sea n ∈ $\mathbb {N} _{0}$. Definimos como múltiplo de n a todo número natural que contiene a n un número exacto de veces.

Por ejemplo, tenemos que el número 20 es múltiplo del número 4, pues 20 contiene a 4 un número igual a 5 veces. Por el contrario, el número 15 no es múltiplo del número 6, pues el 15 contiene al 6 un número igual a 2,5 veces, que no es un número natural.

Sea n ∈ $\mathbb {N}$. Definimos el conjunto de múltiplos de n como el conjunto formado por los números que se obtienen al multiplicar n por cada uno de los números naturales. A tal conjunto lo denotamos por M(n). Es decir:

$M(n)=\{n,\;2n,\;3n,\;4n,\;5n,\;...\;\}$

Así, por ejemplo tenemos que los múltiplos de 5 es el conjunto

$M(5)=\{5,\;10,\;15,\;20,\;25,\;...\;\}$

Mínimo Común Múltiplo (MCM) El MCM de dos o más números es el menor número que contiene exactamente a cada uno de los números dados. Por ejemplos, el MCM entre los números 4, 6 y 9 es el número 36, pues este es el número más pequeño que contiene a los tres números dados.

MCD

Divisor

Sea n ∈ $\mathbb {N}$. Definimos como divisor de n a todo número natural que está contenido en n un número exacto de veces.

Por ejemplo, tenemos que el número 9 es divisor de 18, pues el 9 está contenido en 18 un número igual a 2 veces. Por el contrario, el número 3 no es divisor de 10, pues el 3 está contenido en 10 un número de veces igual a 3,3, cantidad de veces no exacta.

Sea n∈ $\mathbb {N}$. Definimos el conjunto de divisores de n como el conjunto formado por todos los números que son contenidos por n un número exacto de veces. A tal conjunto lo denotamos por $D(n)$.

Así, por ejemplo tenemos que el conjunto de los divisores de 20 son

$D(20)=\{1,\;2,\;4,\;5,\;10,\;20\;\}$

pues cada uno de esos números está contenido en 20 un número exacto de veces.

Reglas de divisibilidad

Un número es divisible por:

• 2, cuando es par.

• 3, cuando la suma de sus cifras se puede dividir exactamente por 3.

• 4 , cuando sus dos últimas cifras son cero o bien forman un número que se puede dividir exactamente por 4.

• 5, cuando su última cifra es 0 ó 5.

• 6, cuando es divisible por 2 y 3 a la vez.

• 8, cuando sus tres últimas cifras son cero o bien forman un número que se puede dividir exactamente por 8.
• 9, cuando la suma de sus cifras se puede dividir exactamente por 9.

• 10, cuando su última cifra es cero.

Para el número 7, la regla no es fácil de retener. Por tanto, en caso de saber si un número es divisible por 7, se recomienda dividir. Si la división es exacta, entonces el número sí es divisible por 7; si la división no es exacta, entonces el número no es divisible por 7.

Como ejemplo, veamos por qué números podemos dividir el número 540, siguiendo las reglas antes enunciadas. Tenemos que el número es par y termina en 0. Luego, es divisible por 2, 5 y 10. También, sus dos últimas cifras forman el número 40, que es divisible por 4; luego 540 también es divisible por 4. Vemos que si sumamos sus cifras obtenemos 5+4+0=9, número que es divisible tanto por 3 como por 9. Luego, 540 es divisible por ambos. Como es divisible por 2 y 3, también lo es por 6. Y si hacemos las divisiones correspondientes, vemos que 540 no es divisible ni por 7 ni por 8. Esto se puede verificar fácilmente por el hecho de que $7\cdot 77=539$ y $7\cdot 78=546$, así como $8\cdot 67=536$ y $8\cdot 68=544$.

Máximo Común Divisor (MCD) El MCD de dos o más números es el mayor número que divide exactamente a cada uno de los números dados. Por ejemplo, para 24, 56 y 72, el MCD es el número 8, pues éste es el mayor número que divide exactamente a los números dados pues $24=8\cdot 3$, $56=8\cdot 7$ y $72=8\cdot 9$ y es fácil ver que no existe ningún número que divida, a la vez, al

Método para encontrar el MCM y el MCD

Para encontrar el MCM y el MCD de dos o más números dados, usaremos el método de la descomposición prima. Decimos que un número está expresado en su descomposición prima cuando el número está escrito como producto solamente de números primos. Para entender esto último, veamos la descomposición prima de algunos números:

$15=3\times 5$ $24=2\times 2\times 2\times 3$ $36=2\times 2\times 3\times 3$ $40=2\times 2\times 2\times 5$

Los procedimientos para determinar el MCM y el MCD de una cantidad de números fijos son: El MCM de dos o más números queda determinado por el producto de cada factor primo elevado al mayor exponente al que se encuentra. El MCD de dos o más números queda determinado por el producto de los factores primos comunes a todos los números, elevados al menor exponente con que se encuentren.

Para desarrollar la técnica descrita, buscamos el MCM y el MCD de los números 36, 48 y 120. Empezamos escribiendo las descomposiciones primas de cada número. Tenemos

$36=2^{2}\times 3^{2}$ $48=2^{4}\times 3$ $120=2^{3}\times 3\times 5$

Entonces, para el MCM usamos cada factor primo, una sola vez, elevado a la mayor potencia con la que aparece. En este caso, el MCM es:

${\begin{alignedat}{2}2^{4}\times 3^{2}\times 5&=16\times 9\times 5\\&=720\\\end{alignedat}}$

Para el MCD, usamos los factores primos que se repiten en todas las expresiones, elevados a su menor potencia. En este caso se repiten en todos el 2 y 3. Luego, el MCD es

${\begin{alignedat}{2}2^{2}\times 3&=4\times 3\\&=12\\\end{alignedat}}$

Finalmente tenemos una fórmula que nos permite relacionar mínimo común múltiplo y máximo común divisor. Si a y b son dos números naturales, entonces

$MCM\times MCD=a\times b$

Podemos chequear esta fórmula con los siguientes números $12$ y $18$.

$12=2^{2}\times 3$ $18=2\times 3^{3}$

Su MCD es:

$2\times 3=6.$

Entonces podemos calcular

$12\times 18=216.$

Números Enteros

Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, ...), los opuestos de los números naturales (..., −3, −2, −1) y al cero, 0.

El conjunto de todos los números enteros se representa por la letra ℤ = {..., −3, −2, −1, 0, +1, +2, +3, ...}, que proviene del alemán Zahlen («números», pronunciado [ˈtsaːlən]).

En la matemática moderna el conjunto de los números enteros al abarcar todos los enteros tanto negativos como positivos, representándolos en una recta numérica "llega" hasta el infinito hacia ambos lados, en rigor no existe un comienzo ni un final. La situación no cambiaría en el caso de usar el cero como "origen" para su localización.

Operaciones Básicas en ℤ

Adición: En los números enteros distinguimos dos casos para la adición.

• Enteros de igual signo: si los números tienen igual signo, se suman y se conserva el signo.
  

Ejemplos

$12+9=21$

Ambos números tienen el mismo signo positivo. Se suman y se conserva el signo.

$-12+-9=-21$

Ambos números tienen el mismo signo negativo. Se suman y se conserva el signo.

• Enteros de distinto signo: considerando ambos números como positivos, se hace la resta entre el número mayor y el menor, y al resultado se le mantiene el signo del número mayor.
  

Ejemplos

$5+-13=-8$

Los números enteros son de distintos signos. Al mayor, 13, se le resta el menor, 5, y al resultado, 8, se le conserva el signo del mayor, 13, que tiene signo negativo.

$-3+13=10$

Los números enteros son de distintos signos. Al mayor, 13, se le resta el menor, 3, y al resultado, 10, se le conserva el signo del mayor, 13, que tiene signo positivo.

Ejercicios

1. $5+3=....$
2. $8+-7=....$
3. $-2+-4=....$
4. $-12+9=....$
5. $10+11=....$
6. $15+-9=....$
7. $-25+10=....$
8. $-33+-12=....$

Multiplicación: Para multiplicar dos números enteros es necesario tener presente que el producto de dos enteros de igual signo es siempre positivo, mientras que el producto de dos enteros de distinto signo es siempre negativo.

Signo del N°	Multiplicación	Signo del N°	Signo del resultado
+	x	+	+
+	x	-	-
-	x	+	-
-	x	-	+

Ejemplos

$8\times 7=56\qquad (8\times 7=56;\quad +\times +=+)$

Error al representar (error de sintaxis): {\displaystyle –5 \times –10 = 50 \qquad (5 \times 10 = 50; \quad –\times – = +) }

Error al representar (error de sintaxis): {\displaystyle 12 \times –4 = –48 \qquad (12 \times 4 = 48; \quad + \times – = –) }

Error al representar (error de sintaxis): {\displaystyle -15 \times 5 = -45 \qquad (15 \times 5 = 45; \quad - \times + = –) }

Ejercicios:

(a) ${\begin{aligned}4\times 6&=.....\\\end{aligned}}$

(b) Error al representar (función desconocida «\begin{align}»): {\displaystyle \begin{align} –3 \times –10 & = ..... \\ \end{align}}

(c) Error al representar (función desconocida «\begin{align}»): {\displaystyle \begin{align} –15 \times –2 & = ..... \\ \end{align}}

(d) Error al representar (función desconocida «\begin{align}»): {\displaystyle \begin{align} –4 \times 10 & = ..... \\ \end{align}}

(e) ${\begin{aligned}15\times 8&=.....\\\end{aligned}}$

(f) Error al representar (función desconocida «\begin{align}»): {\displaystyle \begin{align} –7 \times 15 & = ..... \\ \end{align}}

(g) Error al representar (función desconocida «\begin{align}»): {\displaystyle \begin{align} 5 \times –12 & = ..... \\ \end{align}}

(h) Error al representar (función desconocida «\begin{align}»): {\displaystyle \begin{align} 8 \times –20 & = ..... \\ \end{align}}

Números Pares

Los números enteros se pueden subdividir en dos categorías, el conjunto de los números pares y el conjunto de los números impares.

Los números pares están formados por los números enteros múltiplos de 2, es decir, un número entero m es número par si y solo si existe otro número entero n tal que:

$m=2\times n$

Ejemplo 1

Supongamos que $n=2$, entonces $m=2\times 2=4$.

Ejemplo 2

Supongamos que $n=-2$, entonces $m=2\times -2=-4$.

Así tenemos que el conjunto de los números pares es:

$\{...,\;-6,\;-4,\;-2,\;0,\;2,\;4,\;6,\;...\}$

Números Impares

Los números impares está formada por los números enteros que no son múltiplos de 2, es decir, un número entero m es número impar si y solo si existe otro número entero n tal que:

$m=1+2\times n$

Ejemplo 1

Supongamos que $n=1$, entonces $m=1+2\times 1=1+2=3$

Recuerde que si son mas de dos operaciones se respeta la multiplicación y después la adición.

Ejemplo 2

Supongamos que $n=-1$, entonces $m=1+2\times -1=1+-2=-1.$

Así tenemos que el conjunto de los números pares es:

$\{...,\;-7,\;-5,\;-3,\;-1,\;1,\;3,\;5,\;7,\;...\}$

Resta o Sustracción en ℤ

Se define la sustracción de dos enteros como,

$a-b=a+(-b)=(-b)+a$

es decir, la sustracción se transforma en adición, sumando al minuendo el opuesto del sustraendo.

Ejemplo 1

$4-3=4+-3=-3+4=1$

Ejemplo 2

$5-7=5+-7=-7+5=-2$

Ejercicio: Calcule las siguientes sustraciones o restas

1. $6-5=.....$
2. $8-15=.....$
3. $15-2=.....$
4. $21-30=.....$
5. $45-60=.....$
6. $60-45=.....$

División en ℤ

La división en ℤ conserva la misma estructura que la multiplicación. Es decir, la división de dos números de igual signo es siempre positiva, mientras que la división de números de distinto signo es siempre negativa.

Signo del N°	División	Signo del N°	Signo del resultado
+	$\div$	+	+
+	$\div$	-	-
-	$\div$	+	-
-	$\div$	-	+

Ejemplos

Error al representar (error de sintaxis): {\displaystyle {\color{Blue}–10 \div –5 = 2 \qquad (10 \div 5 = 2 ; – \div – = + )}}

Error al representar (error de sintaxis): {\displaystyle {\color{blue}12 \div –4 = –3 \qquad (12 \div 4 = 3 ; + \div – = – )}}

Error al representar (error de sintaxis): {\displaystyle {\color{blue}-30 \div 5 = -6 \qquad (30 \div 5 = 6 ; – \div + = - )}}

Ejercicios:

(a) Error al representar (error de sintaxis): {\displaystyle –15 \div –5 = .... } (b) Error al representar (error de sintaxis): {\displaystyle 15 \div –5 = .... } (c) Error al representar (error de sintaxis): {\displaystyle –15 \div 5 = .... } (d) Error al representar (error de sintaxis): {\displaystyle –100 \div –20 = .... } (e) Error al representar (error de sintaxis): {\displaystyle 100 \div –20 = .... } (f) Error al representar (error de sintaxis): {\displaystyle –100 \div 20 = .... }

Propiedades Aritméticas en ℤ

Las Propiedades Aritméticas en ℤ al igual que en los números naturales son expresiones combinadas de todas las operaciones que hemos visto hasta ahora y hay dos cosas importantes para los desarrollos de ejercicios combinados.

• Si el ejercicio no tiene paréntesis, el orden en que se operan los números es siempre: multiplicación y división, suma, resta.

Es importante considerar que se opera en orden de izquierda a derecha.

• Si el ejercicio tiene paréntesis, primero deben ser resueltos éstos, considerando que si el paréntesis está precedido por un signo menos, los signos interiores deben ser cambiados.

Ejemplos

1. Resolver la expresión

$24\cdot (-3)+15+40:(-20)+7$

Solución: Como el ejercicio no presenta paréntesis, primero resolvemos la multiplicación, luego la división, para finalmente resolver las sumas y restas. Entonces tenemos que:

$24\cdot (-3)+15+40:(-20)+7=-72+15+-2+7=-52$

2. Resolver la expresión

$((-19)+7):3-2\cdot ((-10)-7)+1$

Solución: la expresión tiene paréntesis, luego empezamos resolviendo por allí, para después respetar el orden: multiplicación, división, suma, resta. Entonces tenemos que:

$((-19)+7):3-2\cdot ((-10)-7)+1=-12:3-2\cdot (-17)+1=(-4)-(-34)+1=-4+34+1=31$

3. Resolver la expresión

${\frac {(-6)}{3}}((-2)+1)$

Solución: en este caso, al no haber paréntesis que separen las operaciones división y multiplicación, se resuelve de izquierda a derecha, primero resolviendo la división ${\frac {(-6)}{3}}$, y luego se multiplica por ((-2)+1).Entonces tenemos que:

${\frac {(-6)}{3}}((-2)+1)=(-2)((-2)+1)=(-2)(-1)=2$

Valor Absoluto

Se interpreta como la distancia que hay entre un número y el cero.

Desde un punto de vista geométrico, el valor absoluto de un número real $a\,$ es siempre positivo o cero, pero nunca negativo. Formalmente se define como

$|a|=\left\{{\begin{array}{rcl}a,&{\mbox{si}}&a\geq 0\\-a,&{\mbox{si}}&a<0\end{array}}\right.$

Por definición, el valor absoluto de $a\,$ siempre será mayor o igual que cero y nunca número negativo.

Ejemplos

1. $|-2|=2$
2. $|15|=15$
3. $|2|+(-1)=2-1=1$
4. $|-3|+2=3+2=5$

Ejercicio: Evaluar

1. $|-21|=.....$
2. $|-7|=.....$
3. $|5|=.....$
4. $|-21|+4=.....$
5. $|7|-2=.....$
6. $|-21|-|2|=.....$
7. $|5|+|-4|=.....$

En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real Formalmente la distancia entre dos números reales a y b, que se escribe $d(a,b)$, se define como el valor absoluto de la diferencia de ambos números:

Error al representar (error de sintaxis): {\displaystyle d(a, b) = |b − a|}

Ejemplo La distancia entre −5 y 4 es:

Error al representar (función desconocida «\begin{alignat}»): {\displaystyle \begin{alignat}{2} d(−5, 4) & = |4 − (−5)| \\ & = |4 + 5| \\ & = |9| \\ & = 9 \end{alignat}}

Ejercicios

1. Calcule la distancia entre -2 y -5.
2. Calcule la distancia entre -2 y 4.
3. Calcule la distancia entre 5 y 10.
4. Calcule la distancia entre -6 y 3.

Propiedades Fundamentales

(a) $|x|\geq 0$ y $|x|=0$ si y solamente si $x=0$.

(b) Si $|a|>0$ y $|x|\leq a$, entonces $-a\leq x\leq a$.

(c) $|x+y|\leq |x|+|y|$ (Esta propiedad es llamada desigualdad triangular).

(d) $||x|-|y||\leq |x-y|$.

(e) $|xy|=|x||y|$.

Podemos chequear estas propiedades

(a) $|2|=2$, $|-3|=3$ y $|0|=0$.

(b) Si $|x|\leq 4$, se cumple $-4\leq -4,-3,-2,-1,0,1,2,3,4\leq 4$.

(c) Si $x=1$, $y=3$, es fácil ver que $|1+3|=4=|1|+|3|$. Si $x=3$, $y=-5$, se tiene que $|3-5|=|-2|=2<8=|3|+|-5|$.

(d) Si $x=3$, $y=-5$, se tiene que $||3|-|-5||=|3-5|=|-2|=2<8=|3-(-5)|$.

(e) Si $x=2$, $y=-3$, $|2\cdot (-3)|=|-6|=6=|2|\cdot |-3|=2\cdot 3$.

Números Racionales

En sentido amplio, se llama número racional a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero (una fracción común). El término racional alude a ración o parte de un todo, y no al pensamiento o actitud racional.

Definimos un número racional como un decimal finito o infinito periódico (por ejemplo, el número decimal finito 0,75 es la representación decimal del número racional 3/4. El número decimal infinito periódico 0,333... es la representación decimal del número racional 1/3). El número racional permite resolver ecuaciones del tipo ax = b, cuando a y b son números enteros (con «a» distinto de cero).

El conjunto de los números racionales se denota por $\mathbb {Q}$ por "Quotient" que significa «cociente» en varios idiomas europeos. Este conjunto de números incluye a los números enteros y es un subconjunto de los números reales. Una pregunta interesante (y muy difícil de resolver) es saber si algunos números más o menos familiares para nosotros como $\pi$, $e$ o ${\sqrt {2}}$ son números racionales (la respuesta en los casos es NO).

Las fracciones equivalentes entre sí –número racional– son una clase de equivalencia, resultado de la aplicación de una relación de equivalencia al conjunto denúmeros fraccionarios.

Historia

En el Antiguo Egipto ya se calculaba utilizando aquéllas cuyos denominadores son enteros positivos, como: cualquier fracción que escribimos con un numerador no unitario, los egipcios la escribían como suma de fracciones unitarias distintas, de ahí que las sumas de fracciones unitarias se conozcan como fracción egipcia. Además, se puede demostrar que cualquier número racional positivo se puede escribir como fracción egipcia.

El jeroglífico de una boca abierta (

) denotaba la barra de fracción (/), y un jeroglífico numérico escrito debajo de la "boca abierta", denotaba el denominador de la fracción.

|} Los babilónicos utilizaban fracciones cuyo denominador era una potencia de 60, mientras que los egipcios usaron, sobre todo, las fracciones con numerador igual a 1. En la escritura, la fracción la expresaban con un óvalo, que significaba parte o partido, y debajo, o al lado, ponían el denominador; el numerador no se ponía por ser siempre 1.

Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval.

En el siglo XIII Leonardo de Pisa, mejor conocido como Fibonacci, introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.

Construcción de los números racionales

Consideremos las parejas de números enteros $\left(a,b\right)$ donde $b\neq 0$ denotado por ${\frac {a}{b}}$, donde $a\,$ se le llama numerador y a $b\,$ se le llama denominador.

Al conjunto de estos números se le denota por $\mathbb {Q}$. Es decir $\mathbb {Q} =\left\{{\frac {p}{q}}\mid p\in \mathbb {Z} ,q\in \mathbb {Z} ,q\neq 0\right\}$

1. Ejemplo de la linea recta con los numeros racionales [[1]]

Si $p$ es un número entero entonces existe el número ${\frac {p}{1}}$ que equivale a $p$ y mantiene todas sus propiedades de entero. Es decir, se define ${\mathcal {I}}_{\mathbb {Q} }:\mathbb {Z\rightarrow \mathbb {Q} } ,\;{\mathcal {I}}_{\mathbb {Q} }\left(p\right)={\frac {p}{1}}$

Suma de los Números Racionales

Para sumar dos o más números racionales, nos podemos encontrar con varios casos.

Con el mismo denominador

Como se muestra, se suman los numeradores y se deja el mismo denominador:

Suma de fracciones de igual denominador

Con diferente denominador

${\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}$

Cuando tienen distinto denominador, se reduce a común denominador por medio del minimo común multiplo (m.c.m.) de los denominadores (no olvides convertir también el numerador de ambas fracciones ya que lo tengas), y resolverlas después sumando los numeradores:

${\frac {1}{6}}+{\frac {4}{9}}={\frac {3}{18}}+{\frac {8}{18}}={\frac {3+8}{18}}={\frac {11}{18}}$

m.c.m (6,9) = $2\cdot 3\cdot 3=18$

$18:6=3\cdot 1=3$

$18:9=2\cdot 4=8$

Suma de fracciones de distinto denominador

Suma de un racional con un número entero

Cuando nos encontramos con la posibilidad de sumar un número entero con una fracción, lo podemos resolver mediante dos formas

Mediante m.c.m

Para resolver mediante m.c.m, procederemos así:

• a) Transformarlo en fracción

Primero, transformamos la parte entera a una fracción con denominador 1.

$3+{\frac {2}{5}}={\frac {3}{1}}+{\frac {2}{5}}$

• b) Realizar el m.c.m y resolverlo bien

m.c.m (1,5) = $1\cdot 5=5$

$5:1=5\cdot 3=15$

$5:5=1\cdot 2=2$

${\frac {3}{1}}+{\frac {2}{5}}={\frac {15}{5}}+{\frac {2}{5}}={\frac {15+2}{5}}={\frac {17}{5}}$

Directamente

Se multiplica el número por el denominador y se le suma al numerador:

$3+{\frac {2}{5}}={\frac {(3\cdot 5)+2}{5}}={\frac {15+2}{5}}={\frac {17}{5}}$

Multiplicación de los Números racionales

Para multiplicar dos fracciones, unicamente es multiplicar el numerador de la primera fracción con el numerador de la segunda fracción, y hacer lo mismo con los denominadores.

${\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}$

${\frac {3}{6}}\cdot {\frac {2}{5}}={\frac {3\cdot 2}{6\cdot 5}}={\frac {6}{30}}$

Multiplicación de dos números racionales

Para multiplicar dos fracciones, se multiplican los denominadores y los numeradores por los denominadores y los numeradores de las respectivas fracciones

${\frac {1}{3}}\cdot {\frac {2}{5}}\cdot {\frac {4}{7}}\cdot {\frac {6}{8}}={\frac {1\cdot 2\cdot 4\cdot 6}{3\cdot 5\cdot 7\cdot 8}}={\frac {48}{840}}$

División de dos numeros racionales

Para dividir dos fracciones, se invierten numerador y denominador de la segunda fracción y luego se procede a multiplicar

${\frac {2}{3}}:{\frac {6}{5}}={\frac {2}{3}}\cdot {\frac {5}{6}}={\frac {2\cdot 5}{3\cdot 6}}={\frac {10}{18}}={\frac {5}{9}}$

¿Por qué no podemos dividir por 0?

Para poder entender porqué no podemos dividir por 0, empecemos por recordar la forma en la que hacemos la división. Tomemos por ejemplo el caso de la pregunta: “¿Cuánto es diez entre cinco?”

Para poder responder esa pregunta, necesitamos encontrar un número que al multiplicarlos por 5 nos resulte el número. El único número con esta propiedad es el número 2.

Ahora lo que nos preocupa es “¿Cuánto es diez entre cero?”. Para responder a esta pregunta necesitamos encontrar un número que multiplicado por cero nos resulta el número diez. Pero sabemos que cuando multiplico un número por cero, el resultado de esa multiplicación siempre es igual a cero. Entonces es imposible encontrar un número que satisfaga la condición impuesta por la pregunta que hemos hecho. En otras palabras, no podemos dividir diez entre cero.

Ahora consideremos otro caso. Todos sabemos también que cuando divido a un número por sí mismo, el resultado es igual a 1. Ahora surge la pregunta: “¿Es esto válido también para el cero?” Para descubrir la veracidad o falsedad de esto hagamos el mismo estudio que acabamos de hacer en el caso anterior.

${\frac {0}{0}}=?$

La nueva pregunta es: “¿por qué número debo multiplicar al número cero para obtener cero?”. La respuesta es que cualquier número multiplicado por cero da cero. Entonces, aquí no solamente tenemos una solución, sino un número infinito de ellas. Es importante hacer notar que no es que la solución sea infinito, puesto que cuando realizamos una operación con dos números (en este caso, división), el resultado es otro número. Por lo tanto, infinito no es un número, sino una expresión que indica que hay algo que no tiene fin.

Relaciones de equivalencia

• Se define la equivalencia ${\frac {a}{b}}={\frac {c}{d}}$ cuando $ad=bc\,$. Este concepto es importante porque permite explicar por qué hay infinitas maneras de representar un mismo número racional.

Un número racional que es equivalente a dos. Recuerde, hay infinitos racionales que hacen lo mismo

Orden de los Números Racionales

• Los números racionales positivos todos los números de la forma ${\frac {a}{b}}$ tales que $ab>0\,$

• Los números racionales negativos son todos los números de la forma ${\frac {a}{b}}$ tales que $ab<0\,$

• Se define el orden ${\frac {a}{b}}>{\frac {c}{d}}$ cuando $ad-bc>0\,$

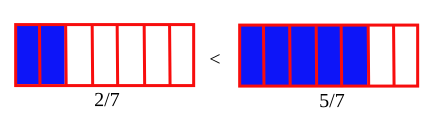
Para números racionales que tienen el mismo denominador hay que comparar los numeradores. La fracción con mayor numerador será mayor.

• Ejemplo:

${\frac {2}{7}}$ y ${\frac {5}{7}}$. La segunda fracción ${\frac {5}{7}}$ es mayor, ya que $5>2$.

De dos o más números racionales que tienen igual numerador es mayor la que tiene menor denominador.

• Ejemplo:

${\frac {2}{3}}$ y ${\frac {2}{5}}$. La mayor es ${\frac {2}{3}}$, ya que $3<5$.

Para fracciones con diferente numerador y denominador, se deben buscar fracciones equivalentes hallando el mínimo común denominador (reducir fracciones a común denominador). Para ello, se toma como denominador común el mínimo común múltiplo (mcm) de los denominadores y a partir de ahí estamos en el primer caso que ya hemos visto.

• Ejemplo:

${\frac {1}{4}}$ y ${\frac {2}{5}}$. El mínimo común denominador es 20, resultando ${\frac {5}{20}}$ y ${\frac {8}{20}}$. Como $5<8$, ${\frac {1}{4}}<{\frac {2}{5}}$.

Notación

• Los números de tipo ${\frac {-a}{b}}$ son denotados por $-{\frac {a}{b}}$

• Las sumas de tipo ${\frac {a}{b}}+{\frac {-c}{d}}$ son denotadas por ${\frac {a}{b}}-{\frac {c}{d}}$

• ${\frac {a}{b}}{\frac {c}{d}}$ denota a ${\frac {a}{b}}\times {\frac {c}{d}}$

• Todo número ${\frac {p}{1}}$ se denota simplemente por $p\,$.

Propiedades de la suma y multiplicación

• La suma en $\mathbb {Q}$ es asociativa, esto es:
  

${\frac {a}{b}}+\left({\frac {c}{d}}+{\frac {p}{q}}\right)=\left({\frac {a}{b}}+{\frac {c}{d}}\right)+{\frac {p}{q}}=\left({\frac {a}{b}}+{\frac {p}{q}}\right)+{\frac {c}{d}}$

• La suma en $\mathbb {Q}$ es conmutativa, esto es:
  

${\frac {a}{b}}+{\frac {c}{d}}={\frac {c}{d}}+{\frac {a}{b}}$

• La multiplicación en $\mathbb {Q}$ es asociativa, esto es:
  

${\frac {a}{b}}\times \left({\frac {c}{d}}\times {\frac {p}{q}}\right)=\left({\frac {a}{b}}\times {\frac {c}{d}}\right)\times {\frac {p}{q}}$

• La multiplicación se distribuye en la suma, esto es:
  

${\frac {a}{b}}\times \left({\frac {c}{d}}+{\frac {p}{q}}\right)=\left({\frac {a}{b}}\times {\frac {c}{d}}\right)+\left({\frac {a}{b}}\times {\frac {p}{q}}\right)$

Existencia de neutros e inversos

• Para cualquier número racional:

${\frac {a}{b}}$ se cumple que ${\frac {a}{b}}+{\frac {0}{1}}={\frac {a}{b}}$ entonces ${\frac {0}{1}}$ es el neutro aditivo de los racionales y se le denota por $0$

• Para cualquier número racional:

${\frac {a}{b}}$ se cumple que ${\frac {a}{b}}\times {\frac {1}{1}}={\frac {a}{b}}$ entonces ${\frac {1}{1}}$ es el neutro multiplicativo de los racionales y se le denota por $1$

• Cada número racional:

${\frac {a}{b}}$ tiene un inverso aditivo ${\frac {-a}{b}}$ tal que ${\frac {a}{b}}+{\frac {-a}{b}}=0$

• Cada número racional:

${\frac {a}{b}}$, con excepción de 0, tiene un inverso multiplicativo ${\frac {b}{a}}$ tal que ${\frac {a}{b}}\times {\frac {b}{a}}=1$

Otras operaciones de los números racionales

Cuando tenemos una unidad cualquiera, nos puede interesar una parte más pequeña para tomar. Así, si tenemos una tarta para ochos comensales, y estamos cuatro personas, lo normal seria que cada persona tomase dos trozos, expresados así:

${\frac {8}{8}}:4={\frac {8}{8}}\cdot {\frac {1}{4}}={\frac {8\cdot 1}{8\cdot 4}}={\frac {8}{32}}={\frac {8:4}{32:4}}={\frac {2}{8}}$

Lo que aquí se expresa es que cada persona cogería dos octavos de tarta, es decir, dos partes de las ocho que hay. Así, la parte de arriba (2) seria el numerador, y la parte de abajo (8), el denominador.

Existen situaciones en las que una fracción puede simplificarse dividiendo ambos términos entre un mismo número y resultar ambos valores enteros,

${\frac {12}{4}}={\frac {12:2}{4:2}}={\frac {6}{2}}$

La fracción original y la reducida son equivalentes, esto quiere decir tienen el mismo valor, aunque se escriban diferentes.

Si una fracción tiene términos que ya no se pueden simplificar más se denomina fracción irreducible.

Hallando el máximo común divisor (M.C.D.) de los dos términos y dividiendo ambos términos por él, se llega a una fracción irreducible.

Ejemplo:

Hallar la fracción irreducible de ${\frac {12}{4}}$:

$M.C.D.(12,4)=4$; dividiendo:

${\frac {12}{4}}={\frac {12:4}{4:4}}={\frac {3}{1}}$

Potenciacion de fracciones

Hay que decir que una potencia es aquella multiplicación donde se multiplica la base por si misma tantas veces como lo indique el exponente. Por lo que es una multiplicación de fracciones.

$\left({\frac {1}{2}}\right)^{3}={\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}={\frac {1^{3}}{2^{3}}}={\frac {1}{8}}.$

En caso de que la potencia sea negativa, debemos proceder mediante la siguiente fórmula

$\left({\frac {a}{b}}\right)^{-n}=\left({\frac {b}{a}}\right)^{n}.$

Esto se grafica con el siguiente ejemplo

$\left({\frac {1}{2}}\right)^{-3}=\left({\frac {2}{1}}\right)^{3}=2^{3}=2\cdot 2\cdot 2=8.$

Entre las otras propiedades importantes de potenciación tenemos las siguientes

a) Producto de potencias con la misma base:

$\left({\frac {a}{b}}\right)^{m}\cdot \left({\frac {a}{b}}\right)^{n}=\left({\frac {a}{b}}\right)^{m+n}.$

Por ejemplo

$\left({\frac {2}{3}}\right)^{3}\cdot \left({\frac {2}{3}}\right)^{4}=\left({\frac {2}{3}}\right)^{3+4}=\left({\frac {2}{3}}\right)^{7}={\frac {2^{7}}{3^{7}}}={\frac {128}{2187}}.$

b) División de potencias con la misma base

$\left({\frac {a}{b}}\right)^{m}:\left({\frac {a}{b}}\right)^{n}=\left({\frac {a}{b}}\right)^{m-n}.$

Por ejemplo

$\left({\frac {2}{3}}\right)^{3}:\left({\frac {2}{3}}\right)^{4}=\left({\frac {2}{3}}\right)^{3-4}=\left({\frac {2}{3}}\right)^{-1}={\frac {3}{2}}.$

c) Potencia de una potencia

$\left(\left({\frac {a}{b}}\right)^{m}\right)^{n}=\left({\frac {a}{b}}\right)^{mn}.$

Por ejemplo

$\left(\left({\frac {1}{2}}\right)^{3}\right)^{3}=\left({\frac {1}{2}}\right)^{9}={\frac {1}{512}}.$

d) Producto de potencias con el mismo exponente

$\left({\frac {a}{b}}\right)^{m}\cdot \left({\frac {c}{d}}\right)^{m}=\left({\frac {ac}{bd}}\right)^{m}.$

Por ejemplo

$\left({\frac {2}{3}}\right)^{4}\cdot \left({\frac {3}{5}}\right)^{4}=\left({\frac {2}{5}}\right)^{4}={\frac {2^{4}}{5^{4}}}={\frac {16}{625}}.$

Radicalización de fracciones

La radicalización es el proceso inverso a la potenciación. Para radicalizar una fracción, se extrae la raiz enesíma al numerador y denominador.

${\sqrt[{3}]{\frac {8}{27}}}={\frac {\sqrt[{3}]{8}}{\sqrt[{3}]{27}}}={\frac {2}{3}}$

${\sqrt {\frac {16}{20}}}={\frac {\sqrt {16}}{\sqrt {20}}}={\frac {4}{\sqrt {20}}}$

Racionalización

En el caso anterior, comprobamos que el denominador tenía una raíz cuadrada en su denominador. Para evitar tal situación, se debe multiplicar la raíz en el denominador consigo misma y por el numerador para así eliminar la raíz.

${\frac {4\cdot {\sqrt {20}}}{{\sqrt {20}}\cdot {\sqrt {20}}}}={\frac {4{\sqrt {20}}}{20}}={\frac {\sqrt {20}}{5}}$

Existe otro caso en el que el denominador tiene una suma de un número entero con un radical. Para racionalizar, debemos multiplicar por su conjugado (esto es, los mismos elementos pero con el signo cambiado), para así eliminar la raíz del denominador.

${\frac {3-{\sqrt {2}}}{3+{\sqrt {2}}}}={\frac {(3-{\sqrt {2}})(3-{\sqrt {2}})}{(3+{\sqrt {2}})(3-{\sqrt {2}})}}={\frac {(3-{\sqrt {2}})^{2}}{(3+{\sqrt {2}})(3-{\sqrt {2}})}}={\frac {9+2-6{\sqrt {2}}}{9-2}}={\frac {11-6{\sqrt {2}}}{7}}$

esto no les va a servir es muy malo

Expresión decimal

Es posible expresar una fracción como número decimal dividiendo el numerador entre el denominador:

Ejemplos:

${\frac {1}{2}}=1:2=0,5$

${\frac {2}{3}}=2:3=0,666...$

En las fracciones con denominador 10, 100, 1000, 10000... se recorrerá el punto hacia la izquierda tantos lugares como cifras cero haya.

• Un número decimal es un número racional de la forma ${\frac {a}{10^{n}}}$
• $\mathbb {D}$ denota al conjunto de los números de este tipo. Es decir $\mathbb {D} =\left\{{\frac {a}{10^{n}}}\mid {\frac {a}{10^{n}}}\in \mathbb {Q} \right\}$
• Expresión Racional de un número decimal: el número $a$ en base $10$ con un punto a $n$ lugares del extremo derecho, por ejemplo ${\frac {178}{10^{2}}}$ se denota como $1.78$

Ejemplo

${\frac {53}{1000}}=0.053$

${\frac {4}{10}}=0.4$

${\frac {4567}{100}}=45.67$

Representación decimal de los números racionales

Los números racionales se caracterizan por tener un desarrollo decimal cuya expresión sólo puede ser de tres tipos:

• Exacta o decimal finito: la parte decimal tiene un número finito de cifras. Ejemplo:

${\frac {8}{5}}=1,6$

• Periódica pura o decimal finito periódico: toda la parte decimal se repite indefinidamente. Ejemplo:

${\begin{array}{rcl}{\cfrac {1}{7}}&=&0,142857142857\dots \\&=&0,{\overline {142857}}\end{array}}$

• Periódica mixta o decima finito semiperiódico: no toda la parte decimal se repite. Ejemplo:

${\begin{array}{rcl}{\cfrac {1}{60}}&=&0,01666\dots \\&=&0,01{\overline {6}}\end{array}}$

En efecto, al aplicar el algoritmo para dividir un entero por otro, sólo existen un número finito de restos posibles. Siendo la sucesión de restos infinita, aparecerá forzosamente un mismo resto en dos posiciones distintas. A partir de ellas, el cálculo se repite igual. Ejemplo:

${\begin{array}{r}0,1428571\ldots \\7{\overline {)10\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,}}\\30\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\\20\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\\60\;\,\;\,\;\,\;\,\;\,\;\,\;\,\\40\;\,\;\,\;\,\;\,\;\,\;\,\\50\;\,\;\,\;\,\;\,\;\,\\10\;\,\;\,\;\,\;\,\\\vdots \;\,\;\,\;\,\;\,\end{array}}$

Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera: Léase el artículo entero en Wikipedia:Número Periódico

• Decimales exactos o finitos: Se escribe en el numerador la expresión decimal sin la coma (como un número entero), y en el denominador un uno seguido de tantos ceros como cifras decimales. Ejemplo: $34,65={\frac {3465}{100}}$
• Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma, y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo. Ejemplo: $15,3434\dots ={\frac {1534-15}{99}}$
• Decimales periódicos mixtos: Tendrá como numerador la diferencia entre $a$ y $b$, donde $a$ es el número escrito sin la coma, y $b$ es el número sin la parte decimal periódica, escritos ambos como números enteros. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya. Ejemplo: Sea el número $12,345676767\dots$ entonces $a=1234567\,$ y $b=12345\,$, por lo que el número buscado será ${1234567-12345} \over {99000}$.

Valor absoluto para números racionales e irracionales

Ya hemos estudiado la función valor absoluto pero trabajar con números racionales e irracionales, aumenta el tipo de problemas y complejiza el estudio que debemos hacer.

Ejemplos

$(a)\left|{\frac {1}{2}}\right|={\frac {1}{2}}.$

$(b)\left|{\frac {-3}{5}}\right|={\frac {3}{5}}.$

$(c)\left|-{\sqrt {3}}\right|={\sqrt {3}}.$

$(d)\left|{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}\right|={\frac {\sqrt {3}}{2}}-{\frac {1}{2}}.$

Esto ocurre pues ${\sqrt {3}}-1>0.$

$(e)\left|-{\frac {2}{3}}+{\frac {3{\sqrt {3}}}{2}}+{\frac {5}{3}}-{\frac {\sqrt {3}}{2}}\right|=\left|1+{\sqrt {3}}\right|=1+{\sqrt {3}}.$

Potencias

Es una forma abreviada de escribir una multiplicación de factores iguales

          base $2^{3}$exponente

La base corresponde al factor que se repite El exponente indica cuantas veces debe repetirse dicho factor Se lee 2 elevado a 3.

Ejemplo

         $2^{3}=2x2x2=8$

Potencia en base 10 Toda potencia de base 10 es igual a la unidad seguida de tantos ceros indica el exponente.

Ejemplo

       $10^{3}=10x10x10=1000$

Multiplicación de potencias de igual base El producto de potencias de igual base es otra potencia de la misma base y cuyo exponente es la suma de sus exponentes.

Ejemplo

       $2^{3}x2^{2}x2^{4}=2^{3+2+4}=2^{9}$

División de potencias de igual base El cociente de dos potencias de igual base es otra potencia de la misma base y cuyo exponente es la resta de los exponentes.

Ejemplo

        $2^{6}:2^{3}=2^{6-3}=2^{3}$

Potencia de una potencia La potencia de una potencia es otra potencia es otra potencia de igual base y cuyo exponente es el producto de los exponentes.

Ejemplo

        $(3^{3})^{2}=3^{3x2}=3^{6}$

Potencia de base fraccionaria y exponente natural Para elevar una fracción a una potenciase eleva tanto el numerador como el denominador al exponente.

Ejemplo

        $({\frac {2}{4}})^{2}={\frac {2}{4}}x{\frac {2}{4}}={\frac {4}{16}}$