Convolución de 2 variables y Cálculo de Respuesta de Sistemas LTI mediante ella [editar]
En esta sección añadimos problemas de convolución
Problema 6 02 08[editar]
Para el circuito RLC que se muestra en la figura, determine (R=3,L=2,C=K=2):
- La respuesta al escalón
- La respuesta al impulso
- La respuesta a

Problema 7 02 08[editar]
Considere un sistema LTI cuya respuesta al impulso es la función  . ¿Es este sistema causal?. Justifique su respuesta.
. ¿Es este sistema causal?. Justifique su respuesta.
Calcule y grafique la salida del sistema a las señales:


Problema 8 02 08[editar]
El sistema de la pregunta anterior se coloca en cascada con un segundo sistema cuya respuesta al impulso es  , donde
, donde  . ¿Es este segundo un sistema causal?
. ¿Es este segundo un sistema causal?
Determine y grafique la respuesta de la cascada de sistemas a las entradas del problema anterior
Problema 9 02 08[editar]
Considere la cascada de dos sistemas. El primero, que llamaremos S1, comprime (operación sobre el tiempo) la señal de entrada por un factor de 2, i.e.,  . El segundo (S2) es un circuito RC (filtro pasabajos) con RC=1. Si la señal de entrada es
. El segundo (S2) es un circuito RC (filtro pasabajos) con RC=1. Si la señal de entrada es  calcule la salida de la cascada de ambos si:
calcule la salida de la cascada de ambos si:


¿Serán idénticas las salidas?, ¿deberían serlo?.
Problema 10 02 08[editar]
Considere la señal  y tengamos un sistema cuya respuesta al impulso es
y tengamos un sistema cuya respuesta al impulso es  . Calcule y grafique la respuesta a las siguientes señales:
. Calcule y grafique la respuesta a las siguientes señales:
 . T>1
. T>1 .
. .
.- ¿Puede generalizar su resultado a cualquier h(t)y x(t)?
Problema 11 02 08[editar]
Grafique cada una de las señales y realice las siguientes convoluciones:
 .
. .
. .
. .
. .
.
Resuelto por Ender Valdivieso Carnet 06-40411
Ejercicio 1
 .
.
 .
.
Gráfica de  .
.

Gráfica de  .
.
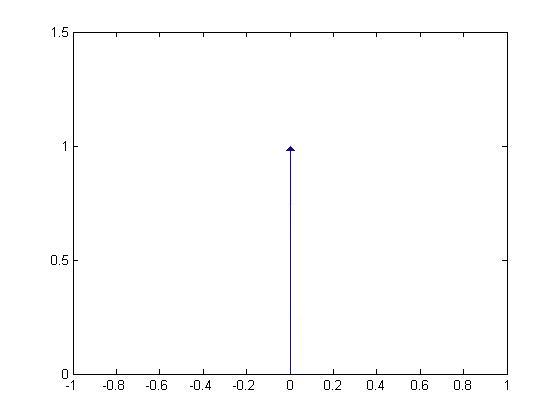
A priori conocemos que la función delta  es el elemento neutro en la convolución. Por ende, debemos obtener la misma señal como salida. Al realizar los cálculos tenemos:
es el elemento neutro en la convolución. Por ende, debemos obtener la misma señal como salida. Al realizar los cálculos tenemos:

Para 



Gráfica de #  .
.

Ejercicio 2
 .
.
 .
.
Gráfica de  .
.

Gráfica de  .
.
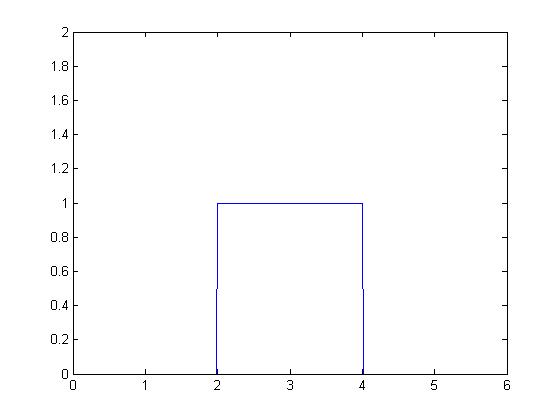


Para 


Para 


Para 


Enotonces la función  quedaría de la forma
quedaría de la forma

Gráfica de #  .
.

Ejercicio 3
 .
.
 .
.
Gráfica de  .
.

Gráfica de  .
.
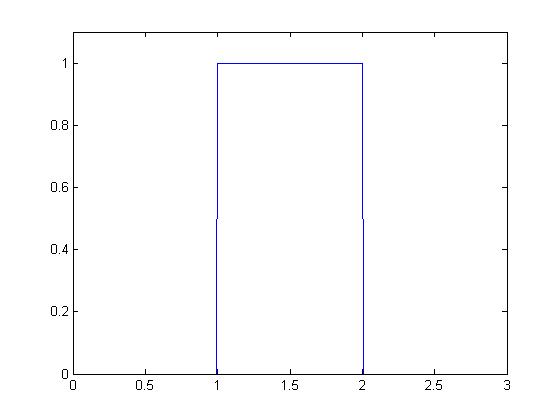


Para 


Para 


Para 


Para 


Para 


La función sería  para cualquiero otro valor de
para cualquiero otro valor de 
En síntesis, la función sería de la forma

Gráfica de #  .
.

Ejercicio 4
 .
.
 .
.
Gráfica de  .
.

Gráfica de  .
.
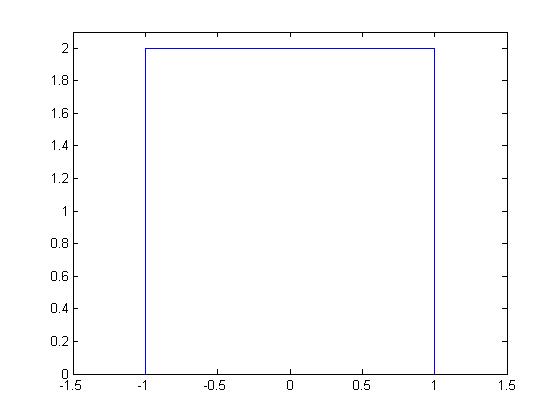


Para 


Para 


Para 


En síntesis, la función sería de la forma

Gráfica de #  .
.

Ejercicio 5
 .
.
 .
.
Gráfica de  .
.
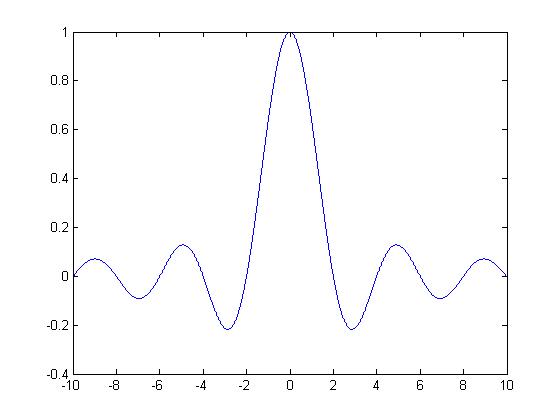
Gráfica de  .
.



Para todo tiempo se cumple que

Una versión imprimible se encuntra en el siguiente archivoArchivo
Sean,



Determine:


Subsección 1 Problema 1[editar]
Realizado Por: Jesús Querales #05-38758
1. 
Haciendo,


Por definición tenemos que la convolución esta dada por:

Estableciendo,


Entonces resulta,


Usando la propiedad de filtrado del impulso,

Subsección 2 Problema 1[editar]
Realizado Por: Alexander Gamero #05-38196
En el intervalo donde esta definido  ,
, ![{\displaystyle [0,2]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c930c6b148a1afeee1a559f22d76ee3262a73a56) ,
, 
Por lo que se puede reescribir 
Al ser  una señal periódica (
una señal periódica ( ), se puede convolucionar
), se puede convolucionar  con un período de
con un período de 
Para  ,
,

Entonces, utilizando la definición de convolución;

Esta convolución se calcula graficamente de la siguiente manera:






 para todo lo demás
para todo lo demás
Para hallar la señal periódica  reemplazamos
reemplazamos  , resultando:
, resultando:
 '
'


























































































































![{\displaystyle [0,2]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c930c6b148a1afeee1a559f22d76ee3262a73a56)
















