La idea del cálculo integral consiste en calcular, en general, superficies curvilíneas, es decir, el área entre la gráfica de una función y el eje-x.
Estamos de acuerdo con la siguiente notación:
S
=
∫
a
b
f
(
x
)
d
x
{\displaystyle S=\int _{a}^{b}f(x)\,\mathrm {d} x}
Es la integral definida de la función f(x) de variable x , entre los límites de a a b . Se pretende que la zona entre la curva y el eje x, como en la imagen de arriba, es la superficie S . Más específicamente, es que esta es una integral de Riemann (por ejemplo, Riemann), hay también integrante líneas generales.
El cálculo integral se refiere al cálculo de integrales tales.
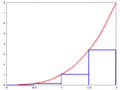
Aspecto geométrico [ editar ] Para hacer la integral de manera sistemática "de vuelta al espacio", que es abordado por las llamadas sumas superior e inferior de rectángulos cada vez más precisos.
Las áreas de los rectángulos ahora se pueden calcular fácilmente, así que tenemos un límite superior y un límite inferior para la zona.
∫
0
1
x
2
d
x
{\displaystyle \int _{0}^{1}x^{2}\mathrm {d} x}
>
R
1
{\displaystyle >R_{1}\,}
+
R
2
{\displaystyle +R_{2}\,}
+
R
3
{\displaystyle +R_{3}\,}
+
R
4
{\displaystyle +R_{4}\,}
=
1
4
⋅
0
2
{\displaystyle ={\frac {1}{4}}\cdot 0^{2}}
+
1
4
⋅
(
1
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {1}{4}}\right)^{2}}
+
1
4
⋅
(
2
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {2}{4}}\right)^{2}}
+
1
4
⋅
(
3
4
)
2
,
donde cada rectangulo
1
4
largo y tan alto
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {3}{4}}\right)^{2},\qquad {\text{donde cada rectangulo }}{\tfrac {1}{4}}{\text{ largo y tan alto}}}
=
0,218
75
{\displaystyle =0{,}21875\,}
Analógamente la suma superior calculada:
∫
0
1
x
2
d
x
{\displaystyle \int _{0}^{1}x^{2}\mathrm {d} x}
<
R
1
{\displaystyle <R_{1}\,}
+
R
2
{\displaystyle +R_{2}\,}
+
R
3
{\displaystyle +R_{3}\,}
+
R
4
{\displaystyle +R_{4}\,}
+
1
4
⋅
(
1
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {1}{4}}\right)^{2}}
+
1
4
⋅
(
2
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {2}{4}}\right)^{2}}
+
1
4
⋅
(
3
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {3}{4}}\right)^{2}}
+
1
4
⋅
(
4
4
)
2
{\displaystyle +{\frac {1}{4}}\cdot \left({\frac {4}{4}}\right)^{2}}
=
0,468
75
{\displaystyle =0{,}46875\,}
Entonces vale:
0,218
75
<
∫
0
1
x
2
d
x
<
0,468
75
{\displaystyle 0{,}21875<\int _{0}^{1}x^{2}\mathrm {d} x<0{,}46875}
Para un enfoque general [ editar ] Aqui se tiene para la n-esima suma por defecto
U
n
{\displaystyle U_{n}}
U
n
=
1
n
⋅
0
2
+
1
n
⋅
(
1
n
)
2
+
1
n
(
2
n
)
2
+
1
n
⋅
(
3
n
)
2
+
⋯
+
1
n
⋅
(
n
−
1
n
)
2
{\displaystyle U_{n}={\frac {1}{n}}\cdot 0^{2}+{\frac {1}{n}}\cdot \left({\frac {1}{n}}\right)^{2}+{\frac {1}{n}}\left({\frac {2}{n}}\right)^{2}+{\frac {1}{n}}\cdot \left({\frac {3}{n}}\right)^{2}+\cdots +{\frac {1}{n}}\cdot \left({\frac {n-1}{n}}\right)^{2}}
y la n-esima suma por exceso
O
n
{\displaystyle O_{n}}
O
n
=
1
n
⋅
(
1
n
)
2
+
1
n
(
2
n
)
2
+
1
n
⋅
(
3
n
)
2
+
⋯
+
1
n
⋅
(
n
n
)
2
{\displaystyle O_{n}={\frac {1}{n}}\cdot \left({\frac {1}{n}}\right)^{2}+{\frac {1}{n}}\left({\frac {2}{n}}\right)^{2}+{\frac {1}{n}}\cdot \left({\frac {3}{n}}\right)^{2}+\cdots +{\frac {1}{n}}\cdot \left({\frac {n}{n}}\right)^{2}}
Y para sacar el valor exacto de la Integral, definimos formalmente
∫
1
2
x
2
d
x
=
lim
n
→
∞
U
n
=
lim
n
→
∞
O
n
{\displaystyle \int _{1}^{2}x^{2}\mathrm {d} x=\lim _{n\to \infty }U_{n}=\lim _{n\to \infty }O_{n}}
que en el caso es la igual.
Primero sacamos por la suma por exceso:
O
n
=
1
n
⋅
(
1
n
)
2
+
1
n
(
2
n
)
2
+
1
n
⋅
(
3
n
)
2
+
⋯
+
1
n
⋅
(
n
n
)
2
|
factorizamos por
1
n
, quadriere die
B
r
u
¨
c
h
e
{\displaystyle \left.O_{n}={\frac {1}{n}}\cdot \left({\frac {1}{n}}\right)^{2}+{\frac {1}{n}}\left({\frac {2}{n}}\right)^{2}+{\frac {1}{n}}\cdot \left({\frac {3}{n}}\right)^{2}+\cdots +{\frac {1}{n}}\cdot \left({\frac {n}{n}}\right)^{2}\qquad \right|{\text{ factorizamos por }}{\tfrac {1}{n}}{\text{, quadriere die }}\mathrm {Br{\ddot {u}}che} }
=
1
n
[
1
2
n
2
+
2
2
n
2
+
3
2
n
2
+
⋯
n
2
n
2
]
|
resolvemos
1
n
2
las potencias
{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {1^{2}}{n^{2}}}+{\frac {2^{2}}{n^{2}}}+{\frac {3^{2}}{n^{2}}}+\cdots {\frac {n^{2}}{n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ resolvemos }}{\tfrac {1}{n^{2}}}{\text{ las potencias}}}
=
1
n
[
1
n
2
⋅
(
1
2
+
2
2
+
3
2
+
⋯
+
n
2
)
]
con
1
2
+
2
2
+
3
2
+
.
.
.
+
n
2
=
1
6
n
(
n
+
1
)
(
2
n
+
1
)
{\displaystyle ={\frac {1}{n}}\left[{\frac {1}{n^{2}}}\cdot \left(1^{2}+2^{2}+3^{2}+\cdots +n^{2}\right)\right]\qquad {\text{ con }}1^{2}+2^{2}+3^{2}+...+n^{2}={\tfrac {1}{6}}n(n+1)(2n+1)}
=
1
n
[
n
(
n
+
1
)
(
2
n
+
1
)
6
n
2
]
|
resolviendo el parentesis,
1
n
se simplifica
{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {n(n+1)(2n+1)}{6n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ resolviendo el parentesis, }}{\tfrac {1}{n}}{\text{se simplifica}}}
=
(
n
+
1
)
(
2
n
+
1
)
6
n
2
{\displaystyle ={\frac {(n+1)(2n+1)}{6n^{2}}}}
=
2
n
2
+
3
n
+
1
6
n
2
{\displaystyle ={\frac {2n^{2}+3n+1}{6n^{2}}}}
=
2
n
2
6
n
2
+
3
n
6
n
2
+
1
6
n
2
{\displaystyle ={\frac {2n^{2}}{6n^{2}}}+{\frac {3n}{6n^{2}}}+{\frac {1}{6n^{2}}}}
=
1
3
+
1
2
n
+
1
6
n
2
{\displaystyle ={\frac {1}{3}}+{\frac {1}{2n}}+{\frac {1}{6n^{2}}}}
Con lo que el valor limite será:
lim
n
→
∞
O
n
=
lim
n
→
∞
1
3
+
1
2
n
+
1
6
n
2
=
1
3
{\displaystyle \lim _{n\to \infty }O_{n}=\lim _{n\to \infty }{\frac {1}{3}}+{\frac {1}{2n}}+{\frac {1}{6n^{2}}}={\frac {1}{3}}}
Para la suma por defecto se tiene
U
n
=
O
n
−
1
n
⋅
1
2
{\displaystyle U_{n}=O_{n}-{\frac {1}{n}}\cdot 1^{2}}
y de todos modos analógamente
lim
n
→
∞
U
n
=
1
3
{\displaystyle \lim _{n\to \infty }U_{n}={\frac {1}{3}}}
entonces tenemos:
∫
0
1
x
2
d
x
=
1
3
{\displaystyle \int _{0}^{1}x^{2}\mathrm {d} x={\frac {1}{3}}}
La sabiduría de las Matemáticas "La diferenciación es un arte, la integración de un arte" ya se ha señalado, no existe un procedimiento general para la determinación (exacto) de una integral , es decir, en particular, la función potencial. Hay técnicas como la integración por partes o por sustitución, con la que uno - es parte integral de - pero incluso con una buena "mente matemática".
Otros conceptos son parte integral de la integral de Lebesgue y la integral de Stieltjes, una superior y un límite inferior de la zona.

























![{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {1^{2}}{n^{2}}}+{\frac {2^{2}}{n^{2}}}+{\frac {3^{2}}{n^{2}}}+\cdots {\frac {n^{2}}{n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ resolvemos }}{\tfrac {1}{n^{2}}}{\text{ las potencias}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2c1a4355649e813d9add23cee6ada80056f717)
![{\displaystyle ={\frac {1}{n}}\left[{\frac {1}{n^{2}}}\cdot \left(1^{2}+2^{2}+3^{2}+\cdots +n^{2}\right)\right]\qquad {\text{ con }}1^{2}+2^{2}+3^{2}+...+n^{2}={\tfrac {1}{6}}n(n+1)(2n+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f4550483fde2812f5a4f423a882625aedc2fae)
![{\displaystyle =\left.{\frac {1}{n}}\left[{\frac {n(n+1)(2n+1)}{6n^{2}}}\right]\qquad \qquad \qquad \right|{\text{ resolviendo el parentesis, }}{\tfrac {1}{n}}{\text{se simplifica}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ef71ca256fd34451e47890a5b8a7e85dfd41ba5)







