Electricidad/Campo eléctrico
El concepto de campo se refiere a la realización de un modelo de una magnitud física que presenta cierta variación sobre una región del espacio. En ocasiones campo se refiere a una abstracción matemática para estudiar la variación de una cierta magnitud física; en este sentido el campo puede ser un ente no visible pero sí medible. Históricamente fue introducido para explicar la acción a distancia de las fuerzas de gravedad, eléctrica y magnética, aunque con el tiempo su significado se ha extendido substancialmente.
En física el concepto surge ante la necesidad de explicar la forma de interacción entre cuerpos en ausencia de contacto físico y sin medios de sustentación para las posibles interacciones.
La acción a distancia se explica, entonces, mediante efectos provocados por la entidad causante de la interacción, sobre el espacio mismo que la rodea, permitiendo asignar a dicho espacio propiedades medibles. Así, será posible hacer corresponder a cada punto del espacio valores que dependerán de la magnitud del cuerpo que provoca la interacción y de la ubicación del punto que se considera.
Los campos más conocidos en física clásica son el campo electromagnético, superposición, de los campos electrostático y magnético, y el campo gravitatorio.
Por tipo de magnitud, atendiendo a la forma matemática de los campos pueden ser clasificados de la siguiente forma:
- Campo escalar: aquel en el que cada punto del espacio lleva asociada una magnitud escalar. (campo de temperaturas de un sólido, campo de presiones atmosféricas...)
- Campo vectorial: aquel en que cada punto del espacio lleva asociado una magnitud vectorial (campos de fuerzas,...).
- Campo tensorial: aquel en que cada punto del espacio lleva asociado un tensor (campo electromagnético en electrodinámica clásica, campo gravitatorio en teoría de la relatividad general, campo de tensiones de un sólido, etc.)
El campo eléctrico representa, en cada punto del espacio afectado por la carga, una propiedad local asociada al mismo. Una vez conocido el campo en un punto no es necesario saber qué lo origina para calcular la fuerza sobre una carga u otra propiedad relacionada con él.
Así, si se coloca una carga de prueba en un punto cualquiera del espacio en donde está definido un campo eléctrico, se observará la aparición de atracciones o de repulsiones sobre ella. Una forma de describir las propiedades de este campo sería indicar la fuerza que se ejercería sobre una carga determinada si se trasladara de un punto a otro del espacio. Al utilizar la misma carga de prueba es posible comparar la intensidad de las atracciones o repulsiones en los distintos puntos del campo. La carga de referencia más simple, a efectos de operaciones, es la carga unidad positiva. La fuerza eléctrica que en un punto cualquiera del campo se ejerce sobre la carga unidad positiva, tomada como elemento de comparación, recibe el nombre de intensidad del campo eléctrico y se representa por la letra E. Por tratarse de una fuerza, la intensidad del campo eléctrico es una magnitud vectorial que viene definida por su módulo E y por su dirección y sentido.
Interacciones entre dos cargas Q y q[editar]
Considérese una carga Q fija en una determinada posición (ver figura). Si se coloca otra carga q en un punto , a cierta distancia de Q, aparecerá una fuerza eléctrica actuando sobre q.
Si la carga q se ubica en otros puntos cualesquiera, tales como , etc., evidentemente, en cada uno de ellos, también estaría actuando sobre q una fuerza eléctrica, producida por Q. Para describir este hecho, se dice que en cualquier punto del espacio en torno a Q existe un campo eléctrico originado por esta carga.
Obsérvese en la figura que el campo eléctrico es originado en los puntos , , etc., por Q, la cual, naturalmente, podrá ser tanto positiva (la de la figura) como negativa. La carga q que es trasladada de un punto a otro, para verificar si en ellos existe, o no, un campo eléctrico, se denomina carga de prueba.
El campo eléctrico puede representarse, en cada punto del espacio, por un vector, usualmente simbolizado por y que se denomina vector campo eléctrico.
El módulo del vector en un punto dado se denomina intensidad del campo eléctrico en ese punto. Para definir este módulo, considérese la carga Q de la figura, generando un campo eléctrico en el espacio que la rodea. Colocando una carga de prueba q en un punto , se verá que sobre ella actúa una fuerza eléctrica. La intensidad del campo eléctrico en estará dada, por definición, por la expresión:
La expresión anterior permite determinar la intensidad del campo eléctrico en cualquier otro punto, tales como , , etc. El valor de E será diferente para cada uno de ellos.
De obtemos , lo cual significa que si se conoce la intensidad del campo eléctrico en un punto, es posible calcular, usando la expresión anterior, el módulo de la fuerza que actúa sobre una carga cualquiera ubicada en aquél punto.
Campo eléctrico creado por una carga puntual[editar]
El campo que crea una carga puntual se deduce a partir de la ley de Coulomb.
Consideremos una carga de prueba , colocada a una distancia r de una carga punto . La fuerza entre ambas cargas estará dada por:
La intensidad del campo eléctrico en el sitio en que se coloca la carga de prueba está dada por:
y por lo tanto resulta:
- =
donde es un vector unitario en la dirección radial, = es la llamada permitividad del vacío y es la constante de Coulomb cuyo valor es . La unidad de intensidad de campo eléctrico es (newton por culombio) o (voltio por metro).
Representación gráfica del campo eléctrico[editar]
Una forma muy útil de esquematizar gráficamente un campo es trazar líneas que vayan en la misma dirección que dicho campo en varios puntos. Esto se realiza a través de las líneas de fuerza, líneas imaginarias que describen, si los hubiere, los cambios en dirección de las fuerzas al pasar de un punto a otro. En el caso del campo eléctrico, puesto que tiene magnitud y sentido se trata de una cantidad vectorial, y las líneas de fuerza o líneas de campo eléctrico indican las trayectorias que seguirían las partículas si se las abandonase libremente a la influencia de las fuerzas del campo. El campo eléctrico será un vector tangente a la línea de fuerza en cualquier punto considerado.
La relación entre las líneas de fuerza (imaginarias) y el vector intensidad de campo, es la siguiente:
- La tangente a una línea de fuerza en un punto cualquiera da la dirección de E en ese punto.
- El número de líneas de fuerza por unidad de área de sección transversal es proporcional a la magnitud de E. Cuanto más cercanas estén las líneas, mayor será la magnitud de E.
No es obvio que sea posible dibujar un conjunto continuo de líneas que cumplan estos requisitos. De hecho, se encuentra que si la ley de Coulomb no fuera cierta, no sería posible hacerlo.
Si un elemento de superficie de área es atravesado por líneas y si la intensidad del campo eléctrico en el centro del elemento de superficie es E, se tiene que:
EL subíndice n indica que es normal a E. Para convertir esta proporcionalidad en ecuación se elige como constante de proporcionalidad. Así, se espacian arbitrariamente las líneas de fuerza de modo que, en cualquier punto, el número de líneas por unidad de superficie y la intensidad del campo eléctrico esté ligado por la relación:
Considérense, ahora, las líneas de fuerza que salen de una carga puntual positiva q y una esfera de radio r arbitrario rodeando la carga y de modo que ésta se encuentre en el centro. La intensidad del campo eléctrico en todos los puntos de la superficie de esta esfera es:
En consecuencia, el número de líneas por unidad de superficie es el mismo en todos los puntos de la superficie y está dado por:
Las líneas de fuerza atraviesan la superficie perpendicularmente puesto que E tiene una dirección radial. El área de la esfera es ,lo que implica que el número de líneas que atraviesan la superficie es:
Esto demuestra que si el valor del exponente de r, en la ley de Coulomb, no fuera 2, el número de líneas de fuerza no solo estaria dado por el valor de q, también sería inversamente proporcional a alguna potencia de r y por ello seria imposible dibujar un conjunto continuo de líneas que cumplan los requisitos indicados más arriba.
Para la construcción de líneas de fuerza se debe tener en cuenta lo siguiente:
- A.- Por convención, las líneas deben partir de cargas positivas y terminar en cargas negativas y en ausencia de unas u otras deben partir o terminar en el infinito.
Una carga puntual positiva dará lugar a un mapa de líneas de fuerza radiales, pues las fuerzas eléctricas actúan siempre en la dirección de la línea que une a las cargas interactuantes, y dirigidas hacia fuera porque una carga de prueba positiva se desplazaría en ese sentido. En el caso del campo debido a una carga puntual negativa el mapa de líneas de fuerza sería análogo, pero dirigidas hacia ella ya que ese sería el sentido en que se desplazaría la carga positiva de prueba. Como consecuencia de lo anterior, en el caso de los campos debidos a varias cargas, las líneas de fuerza nacen siempre de las cargas positivas y por ello son denominadas manantiales y mueren en las negativas por lo que se les llama sumideros.
- B.- Las líneas de fuerza jamás pueden cruzarse.
Las líneas de fuerza o de campo salen de una carga positiva o entran a una negativa. De lo anterior se desprende que de cada punto de la superficie de una esfera, suponiendo forma esférica para una carga, puede salir o entrar solo una línea de fuerza, en consecuencia entre dos cargas que interactúan solo puede relacionarse un punto de su superficie con solo un punto de la otra superficie, y ello es a través de una línea, y esa línea es la línea de fuerza.
Si se admitiera que dos líneas de fuerza se interceptan, entonces se podría extender la superficie de la otra carga hacia el lugar donde se interceptan las líneas que se mencionan y se podría concluir que dos líneas entran o salen de una superficie de una carga eléctrica. Con esto se está contradiciendo lo postulado inicialmente. En consecuencia, es imposible que dos líneas de fuerza se intercepten.
Por otra parte, si las líneas de fuerza se cortaran, significaría que en dicho punto E poseería dos direcciones distintas, lo que contradice la definición de que a cada punto sólo le corresponde un valor único de intensidad de campo.
- C.- El número de líneas fuerza que parten de una carga positiva o llegan a una carga negativa es proporcional a la cantidad de carga respectiva.
- D.- La líneas de fuerza deben ser perpendiculares a las superficies de los objetos en los lugares donde conectan con ellas.
Esto se debe a que en las superficies de cualquier objeto, sin importar la forma, nunca se encuentran componentes de la fuerza eléctrica que sean paralelas a la superficie del mismo. Si fuera de otra manera, cualquier exceso de carga residente en la superficie comenzaría a acelerar. Esto conduciría a la aparición de un flujo de carga en el objeto, lo cual nunca se observa en la electricidad estática.
Las representaciones anteriores reflejan el principio de superposición. Ya sea que las cargas ostenten el mismo signo o signo opuesto, las líneas de fuerza se verán distorsionadas respecto de la forma radial que tendrían si las cargas estuvieran aisladas, de forma tal, que la distorsión es máxima en la zona central, o sea, en la región más cercana a ambas. Si las cargas tienen la misma magnitud, la representación resulta simétrica respecto de la línea media que las separa. En el caso opuesto, predominará la influencia de una de ellas dando lugar a una distribución asimétrica de líneas de fuerza.
Ecuación de las líneas de fuerza[editar]
Siendo el campo tangente a las líneas de fuerza, se cumple:
donde la función describe la forma de la línea de fuerza.
Si tenemos una sola carga puntual, todas las líneas de fuerza son líneas rectas que parten de la carga. En este caso la razón entre y es una constante, por lo tanto:
que la ecuación de una recta que pasa por el origen, como era de esperar.
El Campo Electrico producido por una distribución discreta de cargas[editar]
Caso general[editar]
Para determinar el campo eléctrico producido por un conjunto de cargas puntuales se calcula el campo debido a cada carga en el punto dado como si fuera la única carga que existiera y se suman vectorialmente los mismos para encontar el campo resultante en el punto. En forma de ecuación:
Campo eléctrico creado por un dipolo eléctrico[editar]
A continuación se analiza el campo eléctrico creado por una distribución de dos cargas de igual magnitud y de signo opuesto conocida como Dipolo eléctrico.
A. Campo eléctrico en los puntos de la bisectriz del eje del dipolo[editar]
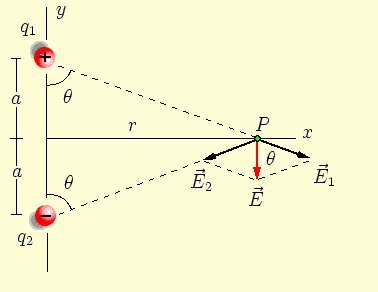
Según el principio de superposición, el campo eléctrico en el punto es la suma vectorial de los dos campos creados por ambas cargas:
Por el teorema de Pitágoras se cumple que la distancia entre cualquiera de las cargas y el punto es:
Y como ambas cargas son de igual magnitud se cumple:
Las componentes y poseen la misma magnitud pero apuntan en sentidos opuestos, por lo tanto:
En consecuencia, para efectuar la suma vectorial, sólo se deberán tener en cuenta a las componentes , es decir, la suma vectorial de y apuntan verticalmente hacia abajo, y siendo , se cumplirá que:
Teniendo en cuenta que:
y sustituyendo esta expresión y la de en la expresión de se obtiene:
Si >> se puede omitir a en el denominador y la ecuación se reduce a:
El producto se denomina momento del dipolo eléctrico. Entonces, se puede volver a escribir la ecuación de como:
Y si r>>a, es decir, para puntos distantes a lo largo de la bisectriz del eje del dipolo como:
B. Campo eléctrico en los puntos del eje del dipolo[editar]
Puntos fuera de la línea de unión de las cargas[editar]
Como en el caso anterior, según el principio de superposición, el campo eléctrico en el punto es la suma vectorial de los campos creados por ambas cargas.
Se observa que, al estar ambos vectores sobre el eje , se cumple:
Por tanto, a efectos de calcular la suma vectorial, solo deben tenerse en cuenta las componentes y .
En consecuencia las magnitudes del campo debidas a y serán respectivamente:
Como ambas componentes, y , apuntan en sentidos contrarios:
O sea:
Siendo el momento del dipolo eléctrico:
Y si >> :
Puntos sobre la línea de unión de las cargas[editar]
La magnitud de para puntos ubicados entre las cargas, tales como el punto , puede deducirse mediante un razonamiento similar al anterior. La diferencia estriba en que las componentes, y , apuntan en el mismo sentido y por ello se suman en lugar de restarse:
Siendo:
Por tanto:
Siendo el momento del dipolo eléctrico:
C. Otros puntos[editar]
Considérese un dipolo eléctrico y un punto de coordenadas tal como el representado en la figura.
Se cumple que:
En base a lo anterior, los campos generados por cada carga serán:
Para determinar el campo en se aplica el principio de superposición por lo cual se debe efectuar la suma vectorial de los campos creados por ambas cargas.
Se calculan, entonces, las componentes :
Las componentes serán:
Sumando se obtiene para la componente total:
Y para la componente total:
Campo generado por un cuadrupolo eléctrico lineal en su bisectriz[editar]
Un cuadrupolo eléctrico lineal es una distribución de cargas formada por dos dipolos alineados de forma opuesta de forma tal que sus cargas positivas se encuentran superpuestas (Ver figura).
Para determinar el campo eléctrico producido por el cuadrupolo sobre los puntos pertenecientes a su bisectriz, de acuerdo al principio de superposición, se deben sumar las contribuciones debidas a las cargas positivas y las producidas por las negativas.
El campo producido por cada carga positiva será:
Obsérvese que las componentes paralelas al cuadrupolo serán nulas, por lo tanto el campo total producido por ambas cargas positivas será:
El campo producido por cada carga negativa será:
Por simetría, las componentes paralelas al cuadrupolo, se cancelan, por lo tanto, sólo deben ser tenidas en cuanta las componentes colineales con la bisectriz.
Teniendo en cuenta que , el valor de cada componente colineal con la bisectriz será:
y el aporte total correspondiente a ambas cargas negativas será:
Por lo tanto, el campo total será:
O sea:
El Campo Eléctrico producido por una distribución continua de cargas[editar]
Caso general[editar]
Si se dispone de una distribución lineal continua de carga, el campo producido en un punto cualquiera puede calcularse dividiendo la carga en elementos infinitesimales dq. Entonces, se calcula el campo d E que produce cada elemento en el punto en cuestión, tratándolos como si fueran cargas. La magnitud de d E está dada por:
El campo resultante en el punto se encuentra, entonces, sumando; esto es, integrando; las contribuciones debidas a todos los elementos de carga, o sea,
Si la distribución continua de carga que se considera tiene una densidad lineal de carga , entonces .
Por lo tanto,
Campo eléctrico generado por una línea infinita de carga y densidad lineal de carga λ constante[editar]
La figura muestra una porción de una línea infinita de carga de densidad lineal de carga uniforme .
La magnitud de la contribución de campo eléctrico sobre el punto P debida al elemento de carga está dada por:
(1)
El vector tiene las componentes:
y
El signo menos delante de indica que apunta en la dirección negativa de las x.
Por tanto, las componentes x e y de en el punto P, están dadas por:
y
En estas expresiones debe ser cero porque todo elemento de carga a la izquierda de la perpendicular que une P con la línea de carga tiene un elemento correspondiente a la derecha, de modo que sus contribuciones al campo en la dirección de las x se anulan mutuamente. Así pues, apunta exactamente en la dirección de las y. Como las contribuciones a de la mitad derecha y de la mitad izquierda de la línea de carga son iguales, se puede escribir:
sustituyendo la expresión (1) en esta ecuación, se tiene:
(2)
Siendo , se tiene , diferenciando esta expresión resulta: y sustituyendo en (2) se obtiene:
(3)
Si se tiene en cuenta que: , y , se puede establecer que:
Sustituyendo en la expresión (3) se obtiene
Obsérvese que cuando , y cuando , , por lo tanto:
Por lo tanto:
Campo eléctrico generado por dos hilos paralelos, infinitos y de densidad de carga uniforme[editar]
Campo eléctrico en un punto B exterior[editar]
El campo eléctrico en el exterior de los hilos es la suma de los campos eléctricos que generan ambos, como apuntan en sentido opuesto, se restan.
Sea el campo debido al hilo cargado positivamente y el generado por el hilo con carga negativa. Se tiene, entonces:
Operando, la expresión anterior se reduce a:
Campo eléctrico en un punto A entre los hilos[editar]
El campo eléctrico entre los hilos es la suma de los campos eléctricos respectivos, como ambos campos apuntan en el mismo sentido, se suman.
Sea el campo debido al hilo cargado positivamente y el generado por el hilo con carga negativa. Se tiene, entonces:
Operando, la expresión anterior se reduce a:
Campo eléctrico generado por un anillo de densidad de carga uniforme sobre los puntos de su eje[editar]
La figura muestra un anillo de carga q y radio a. Considérese un elemento diferencial del anillo de longitud ds, localizado en la parte superior. Este elemento contiene una carga dada por:
siendo la circunferencia del anillo. Este elemento produce un campo eléctrico diferencial dE en el punto P. El campo resultante E se encuentra integrnado los efectos de todos los elementos que constituyen el anillo. Por simetría, este campo resultante debe estar en el eje del anillo. Así pues, solamente la componente dE paralela a este eje contribuye al resultado final. La componente perpendicular al eje se anula por una componente igual y opuesta que produce el elemento de carga situado en el lado opuesto del anillo. Así la integral general de vector se transforma en una integral escalar .
La cantidad dE será:
Según la figura, se tiene:
Como para un punto P, x tiene el mismo valor para todos los elementos de carga y, por tanto, no es una variable, se obtiene:
La integral es simplemente la circunferencia del anillo y, en consecuencia, se obtiene:
Esta expresión de E se reduce E=0 para x =0 ya que, en tal caso, cada componente perpendicular al eje se anula, como antes, con una componente iguale y opuesta que produce el elemento de carga situado en el lado opuesto del anillo y la componente paralela al eje vale cero.
Para x >> a, se puede omitir a en el denominador de esta ecuación, dando:
Este es un resultado esperado porque a distancias suficientemente grandes el anillo se comporta como una carga punto q.
La Ley de Gauss[editar]
En física y en análisis matemático, la ley de Gauss relaciona el flujo eléctrico a través de una superficie cerrada y la carga eléctrica encerrada en esta superficie. De esta misma forma, también relaciona la divergencia del campo eléctrico con la densidad de carga.
Véase el articulo de Wikipedia (http://es.wikipedia.org/wiki/Ley_de_Gauss)
El Potencial Eléctrico[editar]
El potencial eléctrico en un punto se mide por el trabajo eléctrico (w) efectuado al transportarse la carga eléctrica positiva (qo) desde ese punto hasta el infinito
Véase el articulo de Wikipedia (http://es.wikipedia.org/wiki/Potencial_el%C3%A9ctrico)
Recomiendo que quien use este material, preste especial atención a las variables en el anillo de carga, que pueden ser, acorde a la zona explorada, derivadas de una parte anterior a la examinada en este articulo





















![{\displaystyle [N/C]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/484d80762c1591ede24e57be4310ca6ba9956414)
![{\displaystyle [V/m]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22cf42fd2a5336783a7e9e2464bf5e86514f4cfa)











































![{\displaystyle E={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(r-a)}^{2}}}-{\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(r+a)}^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{{(r-a)}^{2}}}-{\frac {q}{{(r+a)}^{2}}}\right]={\frac {1}{4\pi \epsilon _{0}}}\ 4aq\ {\frac {r}{{(r^{2}-a^{2})}^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e84ff5a496e9fd8911adcaf67ead2c388a50c3b)







![{\displaystyle E={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{l^{2}}}+{\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(2a-l)}^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{l^{2}}}+{\frac {q}{{(2a-l)}^{2}}}\right]={\frac {1}{4\pi \epsilon _{0}}}q{\frac {2a}{l^{2}(2a-l)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a227dfceb8a9838e2c6974b6b7c664f877b310d)





![{\displaystyle {{E_{r}}_{1}}_{x}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x+a)}^{2}+y^{2}}}\cos \alpha ={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x+a)}^{2}+y^{2}}}{\frac {x+a}{\sqrt {{(x+a)}^{2}+y^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q(x+a)}{{\left[{(x+a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/397ee16c9f4b5b09797df39ed010a74bfd71f1ed)
![{\displaystyle {{E_{r}}_{2}}_{x}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x-a)}^{2}+y^{2}}}\cos \beta ={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x-a)}^{2}+y^{2}}}{\frac {x-a}{\sqrt {{x-a)}^{2}+y^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q(x-a)}{{\left[{(x-a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/019f82b3158e52f4b4e413007e9e3995990d5726)

![{\displaystyle {{E_{r}}_{1}}_{y}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x+a)}^{2}+y^{2}}}\sin \alpha ={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x+a)}^{2}+y^{2}}}{\frac {y}{\sqrt {{(x+a)}^{2}+y^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {qy}{{\left[{(x+a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cd18442af36835db7bddf9e1c17670f505e3247)
![{\displaystyle {{E_{r}}_{2}}_{y}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x-a)}^{2}+y^{2}}}\sin \beta ={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(x-a)}^{2}+y^{2}}}{\frac {y}{\sqrt {{x-a)}^{2}+y^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {qy}{{\left[{(x-a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39ca6570c79a68af8c82d2506b6008e767b20122)
![{\displaystyle E_{x}={\frac {1}{4\pi \epsilon _{0}}}q\left\lbrack {\frac {x+a}{{\left[{(x+a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}-{\frac {x-a}{{\left[{(x-a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}\right\rbrack }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35e9428347f62a93de323378548483b9b84bc3b2)
![{\displaystyle E_{y}={\frac {1}{4\pi \epsilon _{0}}}q\left\lbrack {\frac {y}{{\left[{(x+a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}-{\frac {y}{{\left[{(x-a)}^{2}+y^{2}\right]}^{\frac {3}{2}}}}\right\rbrack }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e6a2c23dcb850c705ba097539376803821bd699)







![{\displaystyle E={\frac {q}{2\pi \epsilon _{o}}}\left[{\frac {1}{r^{2}}}-{\frac {r}{{(r^{2}+d^{2})}^{\frac {3}{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26dca8158f84945bc91970ff01c8b1998c634d91)






























![{\displaystyle E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}\int _{\theta =0}^{\theta ={\frac {\pi }{2}}}\cos \theta d\theta ={\frac {\lambda }{2\pi {\epsilon }_{0}y}}{\Bigg [}\sin {\frac {\pi }{2}}-\sin 0{\Bigg ]}={\frac {\lambda }{2\pi {\epsilon }_{0}y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ba91d37efef6ede96ec050ce8dafd71397e2ecd)
















