Ecuaciones diferenciales ordinarias/Ecuaciones diferenciales de primer orden/Campos de direcciones
Campos de direcciones; isoclinas[editar]
Considérese una función diferenciable en un punto . La recta tangente a la gráfica de en el punto viene dada por la ecuación
Es bien sabido que esta recta es localmente muy similar a la gráfica de cerca del punto . Este hecho es de gran ayuda para entender de manera cualitativa ecuaciones diferenciales cuando no es posible encontrar una solución de la misma.
La idea es trazar pequeños segmentos de recta que serán tangentes a la gráfica de la solución de una ecuación diferencial, ya que éstos sugerirán la forma de la curva integral correspondiente a una solución de la ecuación diferencial. Ilustremos esta idea con un ejemplo.
Consideremos la ecuación diferencial
| (1.13) |
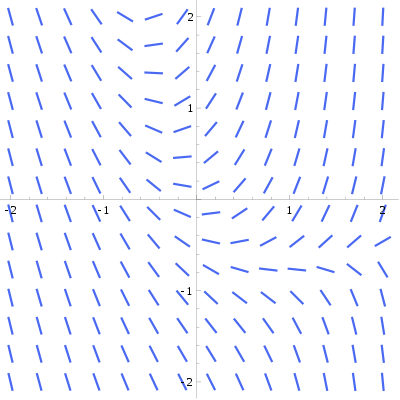
Puesto que esta definida para cualesquiera , somos libres de elegir cualquier valor para e . Por ejemplo, en el origen, vemos que vale 0. Trazamos entonces un pequeño segmento de recta de pendiente 0, el cual será localmente similar a la curva integral que pasa por el origen. En el punto , vemos que vale 1, y así trazamos un otro pequeño segmento de recta que pase por el punto y tenga pendiente . Si continuamos este proceso de manera similar, eligiendo diversos puntos , obtendremos una imagen que nos indicará la forma que tienen algunas de las curvas integrales de la ecuación diferencial ()
. El conjunto de todos estos segmentos de recta es lo que se conoce como un campo de direcciones, y a cada uno de estos pequeños segmentos se dice un elemento lineal del campo de direcciones. La figura 1.3 muestra un campo de direcciones para la ecuación diferencial ()
.
Fig. 1.3
Una vez que tenemos un campo de direcciones adecuado, es posible hacer un bosquejo de alguna curva integral que pase por algún punto específico. La animación siguiente muestra como, siguiendo la dirección indicada por los segmentos de recta del campo de direcciones, es posible dibujar la curva integral correspondiente a la solución particular sujeta, por ejemplo, a las condiciones iniciales .
Archivo:Point in a direction field1.gif
Animación 1.1
Crear un campo de direcciones por lo regular es tedioso y cuesta demasiado tiempo, a menos que para esto programemos un ordenador para generar un campo de direcciones. Sin embargo, cuando queremos tener una idea de como luce el campo de direcciones correspondiente a alguna ecuación diferencial dada sin usar un ordenador, entonces dibujamos elementos lineales a lo largo de curvas llamadas isoclinas. Para explicar de que se trata esto, supongamos que tenemos la ecuación diferencial de primer orden
Una isoclina resulta ser el conjunto de todos los puntos del plano tales que , donde es una constante dada (de modo que las isoclinas son curvas de nivel de ). Por lo tanto, todo elemento lineal que se encuentre a lo largo de una isoclina deberá tener pendiente igual a .
Ejemplo 1.5:
Consideremos la ecuación diferencial
| (1.14) |
La isoclina que probablemente querremos considerar primero es aquella en la que . En tal caso tenemos que
A lo largo de esta isoclina, los elementos lineales del campo de direcciones correspondiente a la ecuación diferencial ()
tienen todos pendiente igual a 0, por lo que podemos hacer una gráfica como la que se muestra en la figura 1.4.
Fig. 1.4
Podemos dibujar más isoclinas. En la figura 1.5 se muestran las isoclinas para las cuales es igual a .
Fig. 1.5